Received 21 June 2014; revised 20 July 2014; accepted 19 August 2014

ABSTRACT

A generalized method which helps to find a time-dependent Schrödinger equation for any static potential is established. We illustrate this method with two examples. Indeed, we use this method to find the time-dependent Hamiltonian of quasi-exactly solvable Lamé equation and to construct the matrix 2 × 2 time-dependent polynomial Hamiltonian.

Keywords:

Quasi-Exactly Solvable, Time-Dependent Hamiltonian

1. Introduction

Another direction of investigation of quasi-exactly solvable Schrödinger is the study of time-dependent Hamiltonian. Time-dependence can be set through the potential. A first step is the direction was done in [1] . This is related to the quasi-exactly solvable sextic anharmonic oscillator potentials. The Schrödinger equation is now considered with a time-dependent potential,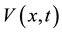

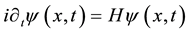, (1)

where

. (2)

The time-dependent potentials constructed from the well-known family of quasi-exactly solvable sextic anharmonic oscillator potentials

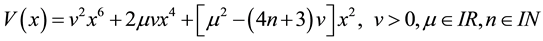(3)

are of the following form [1]

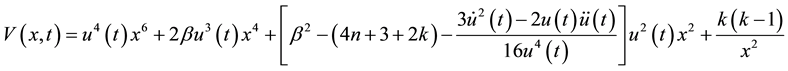, (4)

where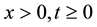, is a non-negative integer, 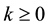, 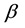is real constant and 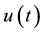is an arbitrary function of 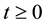which is positive. If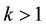, the last term in the above potential 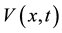may be viewed as a centrifugal term in radial equation with 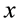playing the role of radial coordinate. The domain of the definition of the potential (4) may be extended to the real line if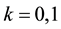. After some algebraic manipulations, one has obtained the algebraic solutions of the Equation (1) of the form

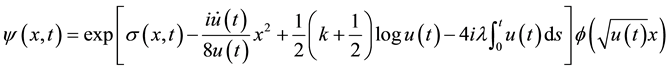, (5)

where the function is in terms of an arbitrary function,

. (6)

In this paper, we will construct time-dependent Schrödinger equation for any potential. It means that we will find algebraic solutions namely of that equation and one can build a time-dependent potential from any non time-dependent one. Note here that the static potential considered can be either quasi-exactly solvable (QES) or simply exactly solvable [2] -[4] . It is understood that we will generalize the formalism considered in Ref. [1] where the authors have constructed a time-dependent Schrödinger equation for only one family of quasi-exactly solvable sextic anharmonic oscillator potentials.

2. Construction of a Time-Dependent Schrödinger Equation

The main results are summarized by the following proposition:

2.1. Proposition

Let be a potential and be a solution of the eigenvalue equation

(7)

with eigenvalue. Let be a positive (and derivable) function of. Then, the solution of the Schrödinger equation

(8)

with time-dependent potential

(9)

is given by

(10)

Proof of the Proposition

We will discuss here an original method to construct time-dependent Hamiltonians which possess algebraic eigenvectors. Let us consider the Schrödinger equation,

, (11)

with is an eigenfunction with eigenvalue of the Hamiltonian

. (12)

Note here that this Hamiltonian (or the potential) doesn’t depend on time explicitly, it means that doesn’t enter neither in the eigenvalue, nor in the eigenfunction. Let us pose

(13)

As a consequence, the spectral Equation (11) is written as

. (14)

Let us pose and extend the effective potential of the above equation noted by adding a new term and consider a full Schrödinger equation of the form

. (15)

The next step is to determine the unknown function so that one can deduce the time-dependent algebraic solutions of the Equation (15) and relate it to (14). Obviously, the above Equation (15) can be developed as follows

, (16)

which can be rewritten

. (17)

Manifestly, this equation can be written in terms of (i.e. the first derivative terms of must be omitted (must vanish)) only if the following condition is imposed

(18)

with this expression of the function, the Equation (17) takes the following form

. (19)

Replacing the expression by its equivalent one in this above equation, i.e. as it is given in (14), one can write

, (20)

which can be rewritten

. (21)

From this equation, the added term to the initial potential in (15) is easily expressed as

. (22)

Replacing in this equation by expression (18) and after some algebraic manipulations, one can write

(23)

where.

One can easily remark that is real and non-dependent on the eigenvalue only if it is expressed as

. (24)

This is possible due to the following condition

. (25)

Solving the above differential equation and after some algebraic manipulations, one can easily obtain the expression of the function

. (26)

With this expression of the function, the algebraic solutions of the time-dependent Schrödinger equation

, (27)

with the time-dependent potential

(28)

are determined as

(29)

where is an arbitrary positive function of and is the eigenvector of the equation

. (30)

It means that one has constructed a time-dependent potential from the potential which is non time-dependent. This is the generalization of the particular case of potentials considered in Ref. [1] . This is a particular case of ours because one can replace the original potential (i.e. the potential which is non time-de- pendent) in Equation (28) by any one which leads to a time-dependent potential associated to the above solutions as it is given by the Equation (29). These solutions are expressed in terms of the eigenvalues of the Schrödinger equation. The values of depend on a potential considered, i.e. when the potential is quasi-exactly solvable, only a part of the eigenvalues is found algebraically whereas when the potential considered is exactly solvable, all eigenvalues are calculated explicitly. So, we have constructed a generalized formula which helps to find time-dependent potentials, it means that one can deduce for a non time-dependent potential its associated time-dependent one. In the next step, we will use this method established previously, i.e. we will manipulate simply the Equation (28) and Equation (29) respectively to construct the time-dependent Lamé potential and the algebraic solutions of Schrödinger equation. We will also apply the above method to the known QES matrix polynomial operator [5] [6] and interesting remarks will be pointed out.

2.2. Example 1: Construction of Time-Dependent Lamé Potential

In this section, along the same lines of the above method, i.e. simply from the Equation (28), we will transform the non time-dependent potential associated to the Lamé equation into the time-dependent one. The Lamé equation is quasi-exactly solvable and the original form is as follows [7] [8]

, (31)

where the Lamé potential is

. (32)

is the eigenvalue of the Lamé Hamiltonian and is the Jacobi elliptic function with modulus. This function is periodic (i.e. the Lamé potential is also periodic) with period which denotes the complete elliptic integral of the first type, i.e.

. (33)

Replacing the potential in the Equation (28) by the above Lamé potential (32), we find the following time-dependent Lamé potential

. (34)

It is easily observed that this last term in of (34) isn’t periodic so that it spoils the periodicity of the above time-dependent Lamé potential. The above time-dependent Lamé potential (34) can become periodic only if the following condition is satisfied

,

,

,

,

,

,

,

,

, (35)

where is a real constant.

From the expression of (i.e. (35), the Lamé potential (34) can be now expressed in time as follows

. (36)

From the above expressions (35) and (36), the time-dependent Schrödinger Equation (1) is of the following form

. (37)

Referring to the Equation (29) and Equation (35), the algebraic solutions of this Schrödinger equation are obtained

(38)

Note that one can deduce from a non time-dependent potential (for which the eigenvalues exist) its corresponding time-dependent one by using the general formula established in Equation (28) while the algebraic solutions of the Schrödinger equation are found from the Equation (29).

2.3 Example 2: Extension to Matrix Time-Dependent Schrödinger Equation

The goal of this section is to construct a matrix time-dependent Schrödinger equation by the above method used to find the time-dependent potential of the non coupled Lamé equation. Let us consider the following matrix Hamiltonian [5] [6]

, (39)

where the potential is 2 × 2 Hermitian matrix of the form

(40)

where are the Pauli matrices, is the matrix identity, are free real parameters and is an integer. can be written in the matrix form as follows

, (41)

where

(42)

In this case, the usual non time-dependent eigenvalue Schrödinger equation is of the form

, (43)

where

, (44)

with and are respectively the eigenfunction and the eigenvalue of the matrix Hamiltonian. Referring to the original method established in the section 2, one can assume

,

. (45)

From this change of variable, the Equation (43) takes the following form

,

,

, (46)

where

(47)

After the change of function as

, (48)

one can write the matrix time-dependent Schrödinger equation such that the initial potential acquires a supplementary term as it was done in the method established previously in the Equation (15)

, (49)

which leads to

. (50)

In the next step, we will calculate the function so that the algebraic solutions of the time- dependent Schrödinger equation are deduced. From the above Equation (50), the following system is obtained

(51)

Obviously, the two equations of the above system (51) can be linear respectively in and (i.e. the first derivatives of and are omitted) only if the following system is satisfied

(52)

One can solve the first equation (or the second equation) in (or in) of this Equation (52) in order to find the expression of

. (53)

From this expression of, as a consequence, the Equation (50) is written as follows

(54)

In the next, the idea is to find the unknown function, for this, one has to consider the derivative with respect to in the second expression of the above equation and after some algebraic manipulations, the Equation (54) is written as fallows

(55)

where and.

From the Equation (46), this equality can be considered

(56)

in the above Equation (55) and accordingly one can write

. (57)

As it has shown in the above method, this expression of leads to the Equation (24), Equation (25) and Equation (26).

Finally, from the expression of (26), one can deduce the algebraic solutions of the matrix time-de- pendent Schrödinger equation as follows

. (58)

3. Conclusion

In this paper, referring to sextic anharmonic potentials considered in Ref. [1] , we have established a generalized method which helps to construct time-dependent potential for any non time-dependent one.

Indeed, we have applied this method to construct the time-dependent potential of Lamé equation. Along the same lines of the method, we have constructed a time-dependent potential associated to the matrix polynomial Hamiltonian which was also studied in [5] [6] and interesting remarks have been pointed out.

References