Open Journal of Microphysics
Vol.3 No.1(2013), Article ID:28222,4 pages DOI:10.4236/ojm.2013.31002
Estimates of Tritium Produced Ratio in the Blanket of Fusion Reactors
Physics Department, Mazandaran University, Babolsar, Iran
Email: *m.mahdavi@umz.ac.ir
Received December 18, 2012; revised January 20, 2013; accepted January 28, 2013
Keywords: Tritium Breeding Ratio; Reactor Blanket; Lithium; Fusion
ABSTRACT
For the preparation of tritium fuel as the main and rare fuel of reactors in the fusion reactors, the reactor blanket must be designed so that it provides enough tritium breeding ratio. The tritium breeding ratio, TBR, in the blanket of reactors should be greater than one, (TBR > 1), by applying lithium blanket. The calculations for proposed parameters (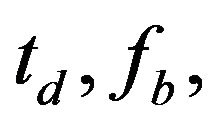 η and
η and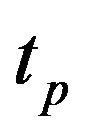 ), indicate that the estimated tritium breeding ratio is greater than one. The calculated TBR = 1.04 satisfies the tritium provision condition.
), indicate that the estimated tritium breeding ratio is greater than one. The calculated TBR = 1.04 satisfies the tritium provision condition.
1. Introduction
The first generation of controlled fusion devices reactive for the release of energy reaction is the following;
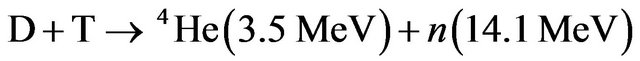 (1)
(1)
The reaction free energy is 17.6 MeV, about 80 and 20 percent of the energy carried by neutrons and alpha particles respectively [1]. More neutrons are produced in the blanket of lithium where they produce tritium. The neutrons may escape through the blanket or are absorbed by structural material. Tritium is naturally limited resources and also radioactive. Radioactive tritium spontaneously decays to 3He, an electron 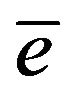 and an antineutron
and an antineutron , with a half life of 12.3 years in process of beta-decay:
, with a half life of 12.3 years in process of beta-decay:
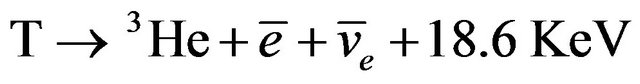 (2)
(2)
Unlike the stable isotope deuterium, which makes up 156 ppm of hydrogenon earth, tritium has a relatively short shelf life because of the radioactive decay (Equation (2)), so tritium is most efficiently used a few years after its manufacture. Consequently, its production requires special management. For a fusion reaction to be economically profitable, tritium breeding ratio(TBR), should be greater than one. The tritium breeding ratio is defined as the average number of tritium atoms bred per tritium atom burn in the reaction 1. One of methods can be achieved in fusion reactor TBR greater than one, using of lithium containing blankets with neutron multiplier. The interaction of neutrons with lithium blanket with pure tritritium will be produced as follows [2,3]:
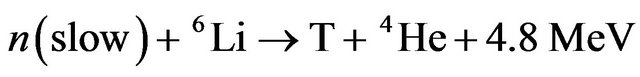 (3)
(3)
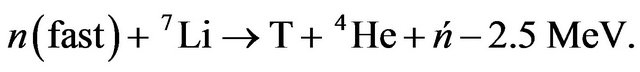 (4)
(4)
The lithium abundance in Equations (3) and (4) are 7.5 and 92.5 respectively. With proper selection of materials blanket structure and geometry, the loss of neutrons can be minimized by absorption or escape from the blanket. Nearly all of the neutrons that slow down to thermal energies from their initial 14.1 MeV, can be absorbed by 6Li and can generate tritium. Another way to produce large tritium breeding ratio is to include neutron multipliers such as beryllium and lead, in lithium blankets. Neutron multiplet will occur as the following:
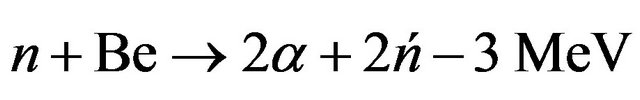 (5)
(5)
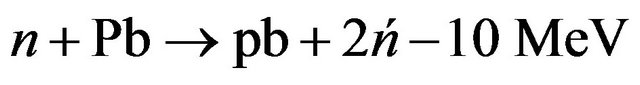 . (6)
. (6)
The variation of cross section versus energy for the important reactions for tritium breeding are shown in Figure 1.
2. Theory
Tritum mass consumption rate can be estimated for a reacctor with the power PF GW, during a year as follows:
 (7)
(7)
A and N0 are Tritium mass numbers and Avogadro’s number respectively. According to Equation (7), it 56 Kg
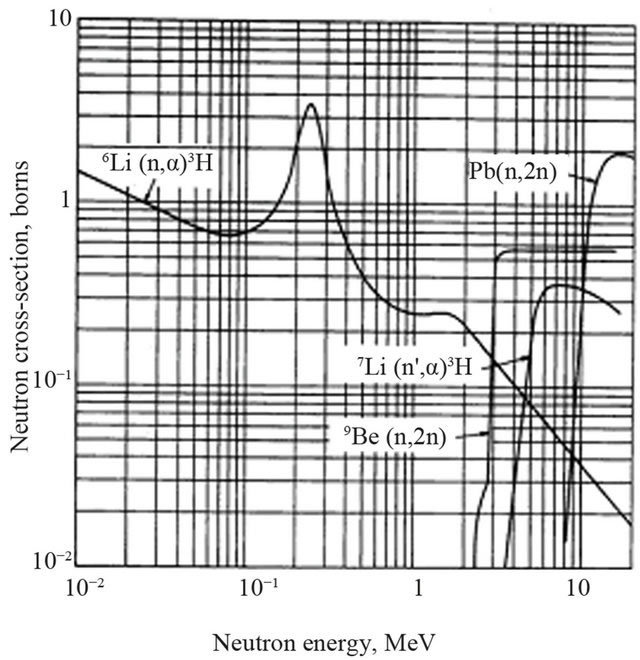
Figure 1. The variation of cross sections versus of energy for the important reactions for tritium breeding [2].
of tritium should be burned per year for producing 1 GW energy. The burnup fraction consumption parameter, (fb), is required for estimating the tritium. Also, The tritium is not consumed, is collected and is used in the burning cycle. For reactors with the steady state power, the values of the tritium breeding ratio should be closed to one. According to reaction Equation (1), the time dependence of number densities of tritium and deuterium in the plasma are given as following [4,5]:
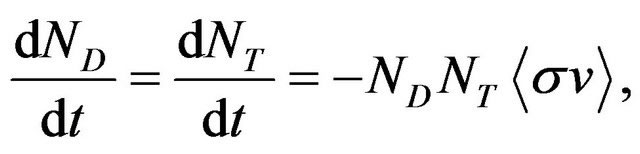 (8)
(8)
where reaction rate ,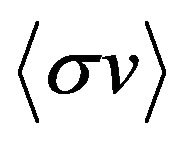 , is given by [6]:
, is given by [6]:
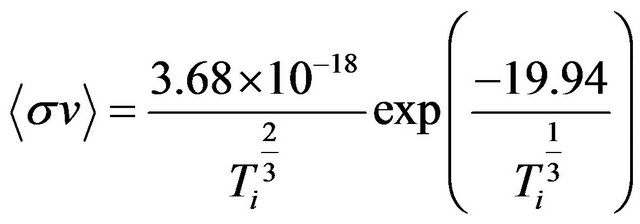 (9)
(9)
where Ti is ion temperatures in keV. Suppose the reactor is stoichiometrically fueled so ND = NT = N, Then one can readily solve Equation (7) to find that the number density 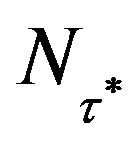 at time
at time  is related to the number den-- sity N0 at the time of fuel injection by:
is related to the number den-- sity N0 at the time of fuel injection by:
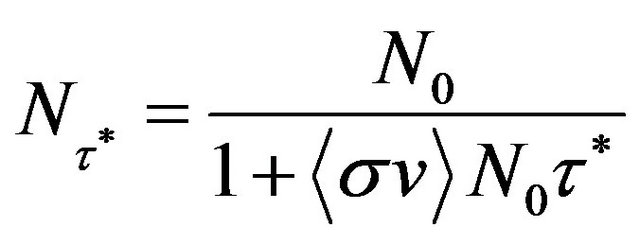 (10)
(10)
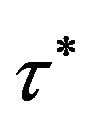 is effective confinement time:
is effective confinement time:
 (11)
(11)
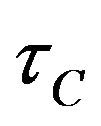 is the ion confinement time, R is fraction of the ions that escape the plasma can recombine. Finally, the tritium burnup fraction is:
is the ion confinement time, R is fraction of the ions that escape the plasma can recombine. Finally, the tritium burnup fraction is:
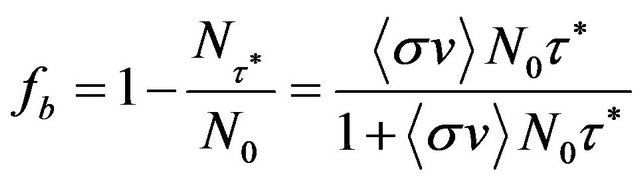 (12)
(12)
Figure 2 shows the burn up fraction consumption over time. Fraction of fuel consumption depends on three factors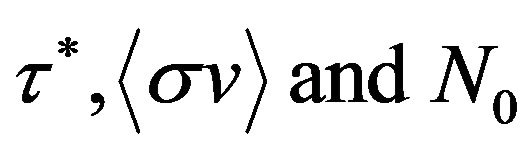 . By considering the tritium radioactive decay rate,
. By considering the tritium radioactive decay rate, 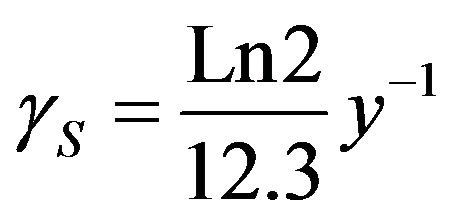 and the loss rate
and the loss rate 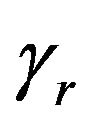
in the reprocessing of unburn tritium, the inventory of tritium is given by:
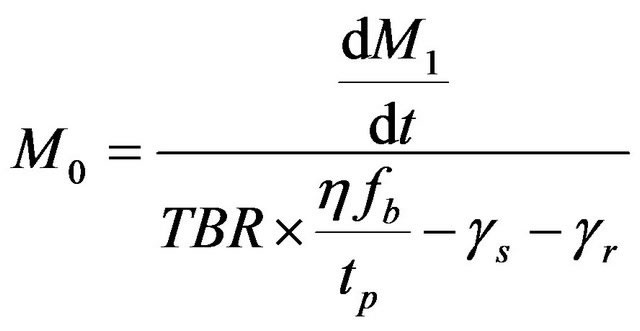 (13)
(13)
where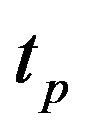 , is a mean time to clean up or recycle the tritium and
, is a mean time to clean up or recycle the tritium and 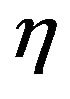 is improved efficiency of tritium injected into the plasma. if tritium production rate,
is improved efficiency of tritium injected into the plasma. if tritium production rate, 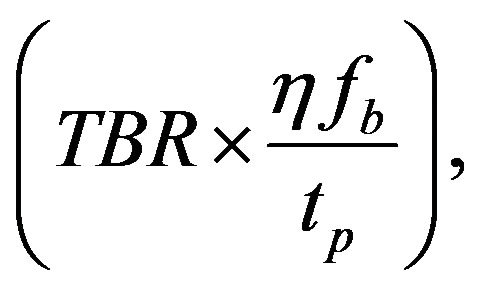 is larger than the tritium loss rate,
is larger than the tritium loss rate, 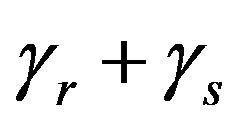 ,and amount TBR to be considered one, the mass inventory can approximate by:
,and amount TBR to be considered one, the mass inventory can approximate by:
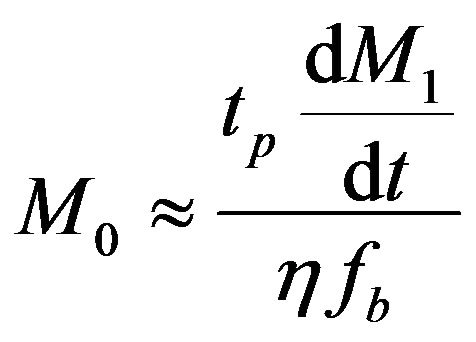 (14)
(14)
The Fusion reactor blanket must be designed so that the lost tritium in radioactive decay can be produced and reconstructed [7]. In addition, after the doubling time, 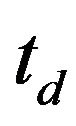 , enough extra tritium should be produced to provide the initial inventory for an identical reactor. The total inventory of tritium in the reactor is:
, enough extra tritium should be produced to provide the initial inventory for an identical reactor. The total inventory of tritium in the reactor is:
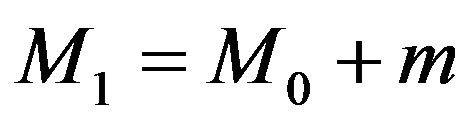 (15)
(15)
where m, is produced mass in the reactor blanket. Radio-

Figure 2. Burnup fraction to effective confinement time with Ti = 20 keV and N0 = 1020 m−3.
active decay at the rate, 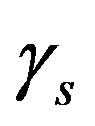 , and losses at the rate,
, and losses at the rate, 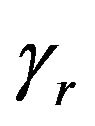 in the reprocessing loop, burning and breeding will cause the refueling mass to change at the rate:
in the reprocessing loop, burning and breeding will cause the refueling mass to change at the rate:
 (16)
(16)
In Equation (16), the First term is tritium production rate, Second term is the decay rate of tritium in the blanket, the third sentence is the decay rate and initial mass loss of tritium and the last sentence is tritium mass consumption rate. To calculate TBR the net production rate coefficient, (κ), is required. By replacing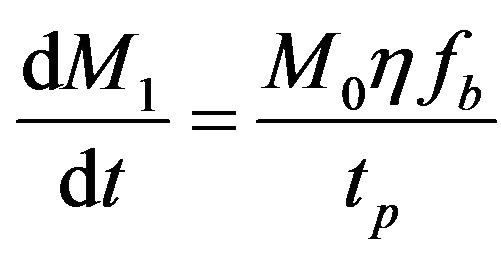 from Equation (14) in Equation 16, the Equation (16) can be rewritten as:
from Equation (14) in Equation 16, the Equation (16) can be rewritten as:
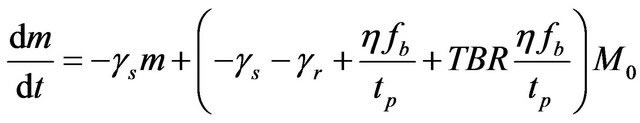 (17)
(17)
Using Equation (17), the coefficient of production rate can be calculated as:
 (18)
(18)
Then Equation (17), can be rewritten as:
 (19)
(19)
If there is no breeding in blanket, m = 0 and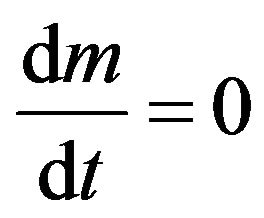 Equation (16) gives Equation (13). The time depended mass in the reactor blanket can be calculated Equation (19) under the assumption of a positive tritium production rate, (κ > 0), and assuming m = 0 at time t = 0, as;
Equation (16) gives Equation (13). The time depended mass in the reactor blanket can be calculated Equation (19) under the assumption of a positive tritium production rate, (κ > 0), and assuming m = 0 at time t = 0, as;
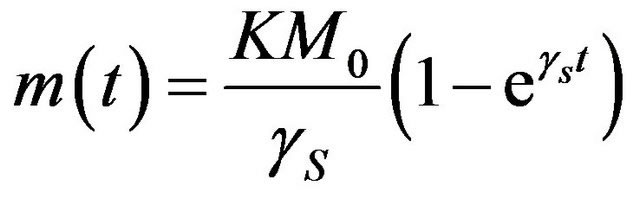 (20)
(20)
and at the doubling time, 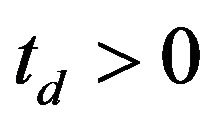 , we have:
, we have: :
:
 (21)
(21)
Then the cofficient of net production rate will be defined as;
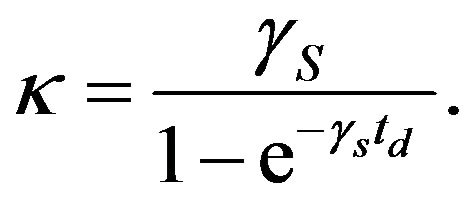 (22)
(22)
For simplicity, consider sufficiently short doubling times,  (a few years), that there is negligible radioactive decay of the tritium
(a few years), that there is negligible radioactive decay of the tritium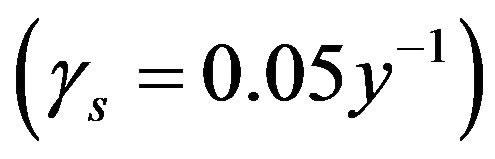 then
then 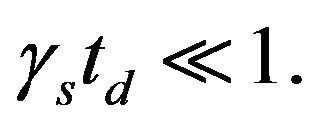 Equation (22) can be approximated as follows:
Equation (22) can be approximated as follows:
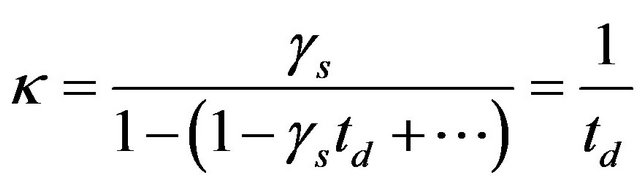 (23)
(23)

Figure 3. Tritium breeding ratio to recycle time with different of burn up fraction consumption parameters ( and
and ) and η = 0.5.
) and η = 0.5.
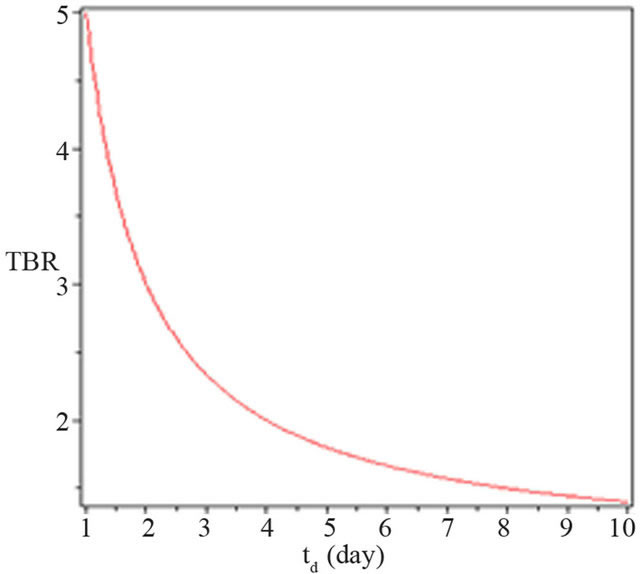
Figure 4. Tritium breeding ratio to doubling time with parameters , η = 0.5 and
, η = 0.5 and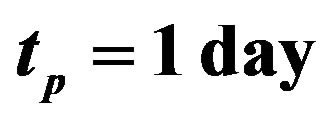 .
.
the tritium production rate is larger than the radioactive decay rate and tritium loss rate. Then we can approxi mate Equation (22) by 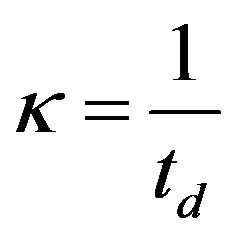 and neglect
and neglect 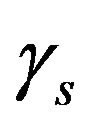 and
and 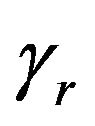 in Equation (18) to find that the required tritum breeding rate is:
in Equation (18) to find that the required tritum breeding rate is:
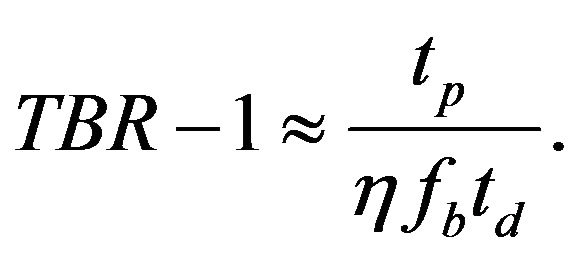 (24)
(24)
3. Conclusion
In this scheme, the ratio of tritium breeding in reactors with lithium blanket is estimated by considering of the possible reactions in the plasma and reactor blanket, Tritium breeding ratio based on the recycle time and doubling time are plotted in Figures 3 and 4. Figure 3 shows that TBR increases by the increasing of recycle time with different of burn up fraction consumption parameters (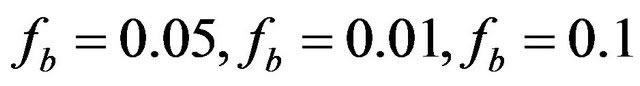 and η = 0.5). Also, it can be seen that with increasing the doubling time, tritium breeding ratio is always greater than one (Figure 4). For example, with parameters
and η = 0.5). Also, it can be seen that with increasing the doubling time, tritium breeding ratio is always greater than one (Figure 4). For example, with parameters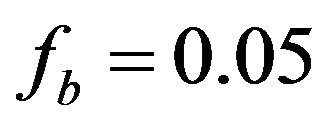 , η = 0.5 and
, η = 0.5 and 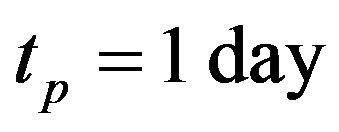 with a doubling time,
with a doubling time,  the tritium breeding ratio is approximately 1.04. This amount will secure the condition of fule supply, then for a reactor design with TBR > 1, it is necessary that the doubling time, the tritium burn fraction and the injection efficiency must be longer and the recycling time must be smallest.
the tritium breeding ratio is approximately 1.04. This amount will secure the condition of fule supply, then for a reactor design with TBR > 1, it is necessary that the doubling time, the tritium burn fraction and the injection efficiency must be longer and the recycling time must be smallest.
REFERENCES
- J. Yu and G. Yu,” Fission-Fusion Neutron Source,” Joural of Nuclear Material, Vol. 386-388, 2009, pp. 949- 953.
- T. Nakagawa, H. Kawasaki and K. Shibata, “Curves and
- Tables of Neutron Cross Section in JENDL-3.3(Part Ⅰ and Ⅱ),” Japan Atomic Energy Research Institute, Fukushima, 2002.
- C. Q. Sh and Y. X. Ln, “Tritium and Materials for Protection of Tritium Permeation,” Atomic Energy Publishing House, Beijing, 2002.
- A. Harms, K. F. Schoepf, G. H. Miley and D. R. Kingdon, “Principles of Fusion Energy,” World Scientific Publishing Co. Pte. ltd., Singapore City, 2002.
- S. Atzeni and J. Meyer-ter-Vehn, “Ineartial Fusion,” Oxford University Press, Oxford, 2004.
- S. Glasstone and R. Loveberg, “Controlled Thermonuclear Reactions,” van Norstrand, Princeton, 1960.
- M. Nishikawa, “Tritium Balance in a D-T Fusion Reactor,” Fusion Science and Technology, Vol. 59, No. 2, 2011, pp. 350-362.
NOTES
*Corresponding author.

