Open Journal of Geology
Vol.04 No.09(2014), Article ID:50132,44 pages
10.4236/ojg.2014.49034

13C-18O bonds in precipitated calcite and aragonite: an ab initio study

Jie Yuan*, Zhigang Zhang, Yigang Zhang

Key Laboratory of Earth and Planetary Physics, Institute of Geology and Geophysics, Chinese Academy of Science, Beijing, China

Email: *yuanjie@mail.iggcas.ac.cn

Copyright © 2014 by authors and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Received 26 July 2014; revised 20 August 2014; accepted 13 September 2014

ABSTRACT

The 13C-18O bonds in carbonates are potential single-phase geo-thermometers. However, their theoretical distributions (noted as ∆47s) in CO2 degassed from calcite and aragonite with phosphoric acid are unclear. Thus, the isotope reactions of 13C-18O bonds on the growing surfaces of calcite (0001) and aragonite (001) planes were investigated using ab initio techniques. 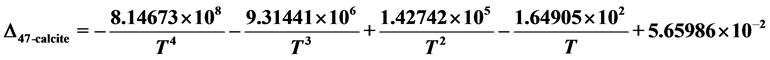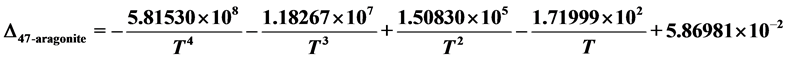It was found that these reactions determined 13C-18O clumped isotope signatures in bulk calcite and aragonite minerals with novel ∆47 polynomials: and for temperatures ranging from 260 to 1500 K. These theoretical results were in good agreement with the experimental data. In addition, the influence of phosphoric acid on these polynomials was at the level of 0.01‰.

Keywords:

13C-18O bonds, Clumped isotope, Calcite and aragonite, Ab Initio calculation

1. Introduction

Since first catching the attention of geochemists in 2004, the 13C-18O bonds in carbonates have become new geo-thermometers. It is first noted that the isotope reaction:

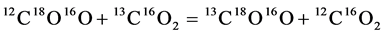(1)

is a geo-thermometer if the relative concentration of 13C18O16O in the CO2 (i.e. 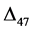(CO2), see definition in the Methods section) is determined via mass spectrometry (MS) [1] [2] . Ghosh et al. (2006) [3] and (2007) [4] then studied multiply substituted carbonate isotopologues in calcite and aragonite minerals:

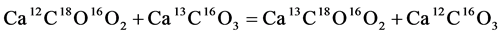(2)

by dissolving carbonates with phosphoric acid [5] - [8] and obtaining different (CO2) values at specific temperatures. The authors suggested that the 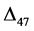value reflected the formation temperature of carbonates and

developed polynomials (e.g. 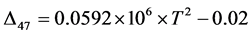in [3] ) by fitting their experimental data.

The relationship of the associated variables in the experiment is:

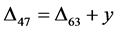, (3)

where 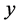represents the phosphoric acid fractionation factor and 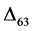represents the relative concentration of Mass63 in carbonate Mass60 isotopologues (see definition in the Methods section) [9] . The theoretical explanation for observed values depends on the ability to define 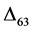and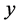; however, the appropriate approach is under debate. Schauble and Eiler (2004) [10] , Schauble et al. (2006) [11] and Hill et al. (2014) [9] (SSH)

performed theoretical calculations of (approximately 0.40‰ for calcite and aragonite at 25˚C) and

suggested the phosphoric acid digestion fractionation factor‰ at 25˚C. The theoretical analy-

sis by Guo et al. (2009) [12] provided a value of‰ (25˚C) for these two minerals. The com-

bination (or) agrees with the observed (=0.6460‰ (25˚C) [3] ); however, both

and are inconsistent with y ≤ 0.14‰, which was recommended by Ghosh et al. (2006). There-

fore, new strategies for understanding observed values for are required.

Herein, we described the results of our investigation of the equilibrium reaction (2) at the interfaces between calcite/aragonite crystals and water using ab initio techniques. Notably, new results for 13C-18O bonds in these minerals were obtained. In addition, the influence of the phosphoric acid digestion process on the signals was discussed.

2. Method

2.1. Carbonate isotopologues reacting on calcite and aragonite surfaces

The 13C-18O bonds in carbonates are isotope signals on growing surfaces during precipitation from solution. As shown by crystal growth models (e.g. the “growth entrapment model” [13] - [15] and the “surface kinetic model” [16] ), the bulk carbonate crystal records the isotopic information on its growing surface during precipitation from solution. Natural carbonate samples include stalactites and otoliths [4] [17] , teeth and bones [18] , corals [3] , foraminifera and coccoliths, etc. [3] [4] [11] [17] - [22] , which are made up of calcite and aragonite.

For clumped 13C-18O isotopes reacted on calcite and aragonite surfaces (Figure 1(a) and Figure 1(b), respectively):

, (4)

for which the equilibrium constant is noted as K3866| (illustrating the doubly substituted isotopologues

in the reaction):

, (5)

where the brackets indicate the concentrations of matter [10] [11] , “|” represents the surface, and the 13C-18O clumped bonds in this reaction remain in the calcite or aragonite [13] - [16] .

For the isotopologues in the groups of the carbonate minerals:

, (6)

Figure 1. Clusters for the (a) calcite (0001) and (b) aragonite (001) surfaces. The carbonate groups (carbon, grey; oxygen red) of interest are located at the centre of the 1st layers of the solids, and are surrounded by water molecules (hydrogen, white). Also plotted are the lengths of the first 2 shortest Ocarbonate group— Hwater bonds and the thickness of the first 3 water layers perpendicular to the calcite (0001) surface. The effects of the different oxygen sites (not shown) in the groups are also considered in the calculations.

where

and Mass(13C16O16O18O) accounts for 94% of the Mass 63 concentration [3] [9] [11] [12] .

In physical experiments, the carbonate minerals are dissolved with phosphoric acid to produce CO2 [3] [4] [20] . For isotopologues of CO2 degassed from the carbonates:

, (7)

where, and Mass(13C18O16O)

accounts for 97% of the Mass 47 concentration [1] [2] [10] .

2.2. Ab initio calculations

To investigate reaction (4), the structures of carbonate groups were constructed on calcite (0001) (Figure 1(a)) and aragonite (001) (Figure 1(b)) surfaces using ab initio techniques. Both interfacial clusters [23] [24] had three layers of periodic atoms (calcite, 75; aragonite, 51) to represent each crystal and six water molecules to represent the solution. The atoms in the crystals were terminated with charge points (calcite, 0.333; aragonite, 0.222) [25] at 1 Å along the broken Ca-O bond [26] . The Ca, C and O positions before optimization were the same as those in the lattices, with a = 4.99 Å and c = 17.06 Å for calcite [27] and a = 4.96 Å, b = 7.97 Å and c = 5.74 Å for aragonite [28] .

The carbonate groups of interest were located at the centre of each structure and the isotope effect on these carbonate groups from the next-nearest atoms was considered [9] [26] [29] . All of the calculations for these clusters were implemented in the Gaussian09 code [25] using the HF theoretical method [30] , and the 6-31G* basis set [31] [32] , which are suitable for all of the C, Ca and O elements.

The theoretical equilibrium constant for reaction (4) was calculated using the equation:

, (8)

for which the value of the RPFR (short for reduced partition function ratio [1] [2] [9] - [11] [33] [34] ) is given by:

, (9)

where is the molecule, and represent the heavy (13C, 18O) and light (12C, 16O) isotopes for element E and, with representing Planck’s constant, the frequency of the clusters (see Supplementary Materials) calculated using the Gaussian09 code [25] , is the Boltzmann’s constant and is the temperature (in the range from 260 to 1500 K) (Guo et al., 2009; Schauble et al., 2006). This temperature range is sufficient for studying the precipitation of calcite and aragonite near 0˚C (the freezing point of water [17] ) and 1200˚C (for metamorphic rocks [3] ). Note that the symmetry numbers were 1 for both optimized clusters because of their C1 symmetry (see Supplementary Materials).

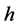
For calculation of the RPFR, a scaling factor (SF) should be used [11] [29] [35] and is predicted by:

, (10)

with the values for for the carbonate groups on the calcite (0001) surface presented in Table 1. By comparing the listed experimentally observed and theoretically calculated harmonic frequencies obtained using this equation, the value of the SF was determined to be 1.0613 for the HF/6-31G* level in the present study.

The theoretical values for were then calculated using the equation:

, (11)

which provides results with an accuracy of 94% [3] [9] [11] [12] . All of the values for calcite and aragonite were obtained by averaging the values for three different oxygen sites (O1, O2 and O3) [9] [11] [12] on each of the two surfaces (see Supplementary Materials).

Re-writing Equation (3) gives the present phosphoric acid fractionation factor:

, (12)

where represents the fitted polynomials from [3] [4] [20] and represents the values obtained using Equation (11).

3. Results

3.1. Optimized structures and harmonic frequencies

The optimized structures for the calcite and aragonite interfaces are in agreement with experimental observations. In the calcite structure, the O atoms in the water molecules were located at 1.70 - 2.80 Å from and perpendicular to the (0001) surface (Figure 1(a)); such values agree well with the vertical data for a (10 - 14) surface: 2.2 - 3.2 Å according to a molecular simulation (MD) study [36] and 2.29 - 3.45 Å as determined via X-ray scattering observations [37] .

These structures are also consistent with basic theories on crystal surface chemistry. Both the orientation of the atoms and the bond lengths in the clusters (see Supplementary Materials) slightly deviate from the pure crystal lattice positions [27] [28] ; this variation is reasonable [38] due to the termination of the periodic atom layers that are connected to molecules [39] .

The ab initio harmonic vibrational frequencies (in cm−1), and standard C and O elemental masses for the carbonate groups on the calcite (0001) surface are listed in Table 1, which also includes experimental vibrational data for carbonate groups on a calcite surface determined via laser Raman spectroscopy and infrared analysis [40] . The calculated vibrations for the symmetric stretch and asymmetric stretching bands of the carbonate groups are 1211, 1212 and 1213 cm−1 and are less than the observed values. On the other hand, the calculated out-of-plane bending and in-plane-bending bands at 988, 779 and 799 cm−1 are greater than the observed values.

The harmonic frequencies for the groups with different isotopic masses on the calcite surface are presented in Table 2. It can be seen from this data that when the heavier 13C substitutes the lighter 12C isotope in xC16O16O16O2−|, does not change; however, , and decrease by 29, 2 and 2 cm−1, respectively. These trends are in agreement with the corresponding vibrations in bulk calcite [26] . In addition, when heavier (13C, 18O) isotopes substitute lighter (12C, 16O, respectively) isotopes, the asymmetric stretching (and) bands under interfacial conditions do not change, which is different from the decreasing trends of and in bulk calcite [26] .

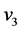
Table 1. Vibrational bands (in cm−1) of carbonate groups on the (0001) surface of calcite and the scaling factor (Scott and Radom, 1996).

aFrom Forbes et al. (2011)

(a) (b)

Table 2. Comparison of the frequencies (in cm−1) of carbonate groups on the calcite surface (this study) and in bulk calcite (Rustad et al. (2008)) and their ratios (vi/v1, in unit 1).

a| stands for the surface of the crystal; b“icce” stands for inner-crystal-chemical environments.

The calculated values are presented in Figure 2 and Figure 3 and Tables 3-6. In Table 4, it can be seen that for calcite at 25˚C, the values for O2 and O3 are slightly lower (−0.02‰) and higher (0.02‰), respectively, than the mean value (0.65‰), while that of O1 equals the mean value (Figure 2(a)). In contrast, for aragonite at 25˚C, the values for O2 and O3 are slightly higher (0.01‰ and 0.03‰, respectively) than the mean value (0.66‰), whereas that of O3 is lower (−0.04‰) than the mean value (Figure 2(b)). The variations in the values for the different sites are partly due to the varying lengths of the O(in carbonate group)-H(in water) bonds, which range from 1.88 to 1.92 Å in calcite (Figure 1(a)) and from 1.81 to 2.01 Å in aragonite (Figure 1(b)).

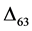
The values for the phosphoric acid fractionation factor y (Equation (12)) are shown in Figure 4 and Table 5. For temperatures ranging from 0˚C to 50˚C, the values in the present study were found to be

,

, and

(Figure 4). These values were thus on the order

of 0.01‰ in this temperature range, which is in good agreement with the value suggested by Ghosh et al. (2006) (‰). In addition, the polynomials determined for both minerals decreased extremely slowly with increasing temperature (approximately −0.0002‰/˚C), which is consistent with the trend reported by Ghosh et al. (2006) (−0.016‰/˚C). Note that the slope calculated in the present study for was 0.0005‰/˚C.

Because the values for y calculated in the present study are so small:

, (13)

where is given by Equation (11). Equation (13) provides results with an accuracy of 98%-G (=(abs (0.658 − 0.01)/0.658)) × 100% for calcite at 25˚C in Table 5) and 95%-D (=(abs(0.658 − 0.032)/0.658)) × 100% for calcite at 25˚C in Table 5). This equation also demonstrates why both the and values calculated in the present study can be placed on the ordinate in Figure 2. Furthermore, the values calculated in this study agreed well with the experimentally determined values for both minerals (Figure 2).

3.3. Uncertainty of the present predictions

Possible errors in the ab initio calculations were first considered. A series of factors influence the accuracy of the calculated K3866| values, including the quality of the exchange density functional and the level of the basis

(a) (b)

Figure 2. Values for ∆47 and ∆63 as a function of temperature (K) for (a) calcite and (b) aragonite. The theoretical (this study TS O1, red solid line; TS O2, blue solid line; TS O3, cyan solid line; TS mean, black solid line) and experimental (Ghosh et al. (2006), black crosses; Ghosh et al. (2007), black dots; Dennis and Schrag (2010), black diamonds; Eagle et al. (2010), black circles; Tripati et al. (2010), black squares) data are illustrated. The best polynomial fittings for the means of the ∆47 and ∆63 values for both calcite and aragonite obtained in the present study are shown in Table 3.

Figure 3. Comparison of this results of the present study (TS, black solid) obtained at the HF/6-31G*/1.0613(SF) level to other theoretical and experimental results for calcite ∆47 values from 0˚C to 100˚C. Data points for the data taken from Ghosh et al. (2006) (black dashed), Dennis and Schrag (2010) (blue dashed), and combined Guo et al. (2009) (cyan dashed) were calculated using their fitted polynomials. The data points for Hill et al. (2014) at the B3LYP/6-311++G(2d,dp)(un-scaled) level were illustrated by adding the experimental y (0.232 ± 0.015‰) (cross solid) and theoretical y (0.220‰, Guo et al., 2009) (cross dashed) values. Also shown are the results for ∆47-aragonite obtained in the present study (red solid line).

set; thus, the harmonic frequencies, as well as the error of the scaling factor and the Teller-Redlich product rule [41] [42] used in Equation (9). The use of the Teller-Redlich product rule simplifies the calculation of the RPFR [33] [34] with an uncertainty of less than 10−5, as shown in previous theoretical calculations [11] [26] [29] [43] . The standard error for the SF = 1.0613 was not determined because only one experimental vibrational spectrum [40] has been published. The quality of the theoretical method and the level of the basis set consist of systemic errors in the harmonic frequencies; however, it is clear that the systemic errors are partially cancelled out due to the division of the two RPFRs during calculation of the K3866| values [11] .

The uncertainties in the calculated y values derive from the accuracies of both the calculated s values and the experimentally fitted polynomials. As shown above for Equation (11), the values obtained using

Table 3. Parameters for the polynomial fitting to calculated best-estimate ∆63 and ∆47 values (Equation (13)) from different studies and the corresponding temperature ranges (K).

The form of each fit is ∆47/63 (T) = A/T4 + B/T3 + C/T2 +D/T + E. Our polynomials reproduce ∆63 within 0.26% for both calcite and aragonite from 260 to 1500 K. Present ∆47∆63 is given by Equation (13) within 0.01‰.

Table 4. Site-specific effects of ∆63 in the present study.

the calculated K3866| values have an accuracy within 0.03‰. The external precision of the values is 0.01‰ - 0.02‰, with a related temperature precision of ±2˚C [3] , and the run-to-run reproducibility and internal counting statistics in [20] were 0.029‰ and 0.012‰, respectively. That is, the accuracies of the experimental values are at the level of 0.01‰. Therefore, the errors in the y values determined in the present study are on the order of 0.01‰, and the precision of the temperature is ±2˚C [3] [4] [9] [12] [20] .

3.4. Fractionations for 13/12C, 18/16O and 14/12C

The accuracy of the calculated results obtained in the present study was then evaluated by comparing the calculated and experimentally obtained 13/12C and 18/16O fractionations for calcite and aragonite. For RPFR(13/12C-calcite) at 25˚C (Table 6 and Table 7), the estimated value of 1.2761 was greater than previously reported results (e.g. 1.2037 [44] , 1.1973 [45] , 1.20430 [11] , 1.1994 [26] and 1.2078 [9] ). The calculated value of 1.2785 for RPFR(13/12C-aragonite) at 25˚C, was also greater than previously reported results (e.g. 1.20669 [11] , 1.2014 [26] and 1.2110 [9] ). In contrast, the calculated value of −1.9‰ for ∆13CCalcite-Aragonite = 1000 × ln (RPFR (13/12C-calcite)/RPFR(13/12C-aragontie)) was in good agreement with the value reported previously for low-temperature equilibrium experiments (−1.7 ± 0.4‰, 25˚C) [46] [47] .

For RPFR(18/16O-calcite) at 25˚C, is the calculated value of 1.1355 was again larger than previously reported results (e.g. 1.1018 [48] , 1.1040 [44] , 1.10328 [11] and 1.1060 [9] ). The calculated value of 1.1394 for RPFR(18/16O-aragonite) at 25˚C was also larger than previously reported results (e.g. 1.098 [48] , 1.10319 [11] , 1.0737 [49] and 1.1075 [9] ). On the other hand, the calculated value for ∆18OCalcite-Aragonite of −3.4‰ at 25˚C, was less than the experimentally obtained results (−0.6‰ [31] [50] and −1.4‰ at 25˚C, [49] ). The difference in the magnitudes of the ∆18O valued may be due to the influence of the acid fractionation factor (1.01107 and 1.01049 for calcite and aragonite, respectively) [11] [51] .

The present results may be applied to the study of the climate history of the Paleozoic, Precambrian and Ce-

Table 5. Comparison of ∆47, ∆63 and y for different experimental and theoretical predictions. The ∆47 and ∆63 values for the data taken from Ghosh et al. (2006), Guo et al. (2009), Schauble et al. (2006), Dennis and Schrag (2010) and Hill et al. (2014) were calculated from their fitted polynomials, and the corresponding y values were copied from these references. The ∆63-T values in the present paper were calculated at the HF/6-31G* level with a scaling factor of 1.0613, and our y values were calculated using the equation ∆47 (published)-∆63-T. For a detailed comparison, the ∆47 values at specific temperatures taken from Ghosh et al. (2006) and our results are illustrated. See discussions in the text.

aThe subscript “c” represents calcite.

aThe subscripts “exp” and “G” stand for experimental and Ghosh et al. (2006), respectively; bthe subscript “a” represents aragonite; cthe subscript “D” represents Dennis and Schrag (2010).

aThe subscript “fit” represents the fitted polynomials from corresponding works.

nozoic [17] , including the variation of the 14C concentration in atmosphere in the Quaternary Period [52] . Thus, polynomials for the RPFR(14/12C) for calcite and aragonite were determined and are provided in Table 6 and Table 7.

Table 6. Parameters for the polynomial fitting to the calculated best-estimate RPFRs for 13/12C, 18/16O and 14/12C in calcite and aragonite from 260 to 1500 K.

The form of each fit is RPFR (T) = A/T4 + B/T3 + C/T2 + D/T + E. These reproduce RPFR within 1.10‰ (13/12C), 0.14‰ (18/16O), 1.5‰ (14/12C) for calcite and within 1.2‰ (13/12C), 0.16‰ (18/16O), 1.5‰ (14/12C) for aragonite from 260 to 1500 K.

Table 7. RPFRs for 13/12C, 18/16O and 14/12C in calcite and aragonite at 25˚C.

Figure 4. Comparison of the acid digestion fractionation factor y for (a) calcite and (b) aragonite for experimental fittings and theoretical results at temperatures from 0˚C to 50˚C. The legends are shown in the middle of both figures. The subscripts “G-T” and “D-T” for our y values represent “Ghosh et al. (2006)—This work” and “Dennis and Schrag (2010)—This work”, respectively. The normals (R2) of the residuals are also shown. See discussions in the text.

4. Discussion

4.1. Comparison with previous studies

Present predictions describe the statistical relationship between observed values and increasing temperatures. For instance, the values obtained in the present study are in agreement with those reported in [3] within 0.008‰ (calcite) and 0.004‰ (aragonite) at 23˚C (Table 5). This good agreement indicates that the equilibrium isotope reaction (2) occurring on the growing surfaces of these crystals is the source of the experimental data. The values calculated in the present study were also in agreement with those reported by Dennis and Schrag (2010) within −0.013‰ (calcite) and −0.017‰ (aragonite) at 25˚C. However, at temperatures above or below 25˚C, the trend in their data is systemically different from that observed for the results obtained in the present study (Figure 3). As they stated, the difference may be due to 1) impurities in the precipitated calcite, 2) non-equilibrium isotope fractionation with water, and 3) “inter-lab differences in sample preparation and IRMS analysis”. If these factors were to be considered, it is possible that the data would be in better agreement.

The calculated results obtained in the present study were also compared to previously reported theoretical results (Figure 3, Table 3 and Table 5). At 25˚C, the present calculated values of 0.653‰ (calcite) and 0.657‰ (aragonite) were greater than the value (approximately 0.40‰ for both minerals) obtained using lattice dynamics [11] and cluster models [9] . In addition, the calculated values for calcite systemically deviated from those reported by Guo et al. (2009) (Figure 3). Furthermore, the values obtained in the present study were in agreement with [3] but far lower than the conventionally accepted value of 0.22(3)‰ ( [9] [12] [20] ), regardless of whether or was used in Equation (12) (Figure 4 and Table 5). This difference is due to different interpretations of the recrystallization process for carbonate samples (see Section 4.2).

Notably, all of the theoretical results obtained in the present study (RPFR(13/12C), RPFR(18/16O), K3866|, and values) differed from previously reported results. The difference is in part due to the dissimilarity of vibrations (as required in Equation (9)) for carbonate groups at the crystal-water interface (Figure 1) and in the inner crystal environment [9] [11] [26] . Examples can be seen in Table 2, including the frequencies on the calcite surface at the HF/6-31G* level (this work) and in bulk calcite at the PBE/6-31G*/3-21G level [26] . Note that the frequencies are compared using the ratio, because the differences in the magnitudes due to the different calculation levels are cancelled out using this approach, which indicates the property of the ith vibration in corresponding clusters. This comparison revealed that: 1), , and on the surface are similar to those in the bulk crystal, whereas the C-O asymmetric stretching vibrations and are very close to on the calcite surface, but approximately 1.3 times greater than in bulk calcite. As a result, the differences in the results obtained in the present and previous studies are mainly due to the C-O asymmetric stretching vibrations and at the calcite interface.

In addition, the different coordinate atoms (CAs) of the O atoms in the carbonate group in the two different environments also contribute to the difference in the results obtained in the present and previous studies. The CAs of the O atoms include hydrogen, carbon and calcium atoms for both the calcite and aragonite surfaces (Figure 1), whereas the CAs for the O atoms in inner crystal environment consist of only carbon and calcium atoms [9] - [11] [26] .

4.2. Information behind the conventional 0.22(3)‰ value for y

In Ghosh et al.’s (2006) study, the technical process for analysing the recrystallized CaCO3 from, for example, sample 47413 is shown in Figure 5. This process involved seven steps that can be classified as physical or chemical processes. Steps 1, 4 and 6 were physical processes and did not involve chemical reactions and thus were assumed to have little or no influence on the final and values.

The remaining four chemical processes play key roles in determining the 0.22(3)‰ value for y. Step 2, which corresponds to the horizontal left arrow in Figure 6, includes the reaction:

, (14)

which produces a uniform distribution of different isotopes in the system, but does not change the total chemical composition, including the isotopic of the system, if a “sealed Pt capsule (ideally without air in it)” is used [3] [4] [12] .

In reality, air would be present in the Pt capsules if step 2 in both Ghosh et al.’s (2006) and Guo et al.’s (2009) experiments was performed in air rather than under a vacuum or atmosphere of a noble gas. In this condition, reactions (15) and (16) below occur during the melting process and contribute to a decrease in the K3866 value.

Steps 3 and 5 involve significant isotopic reactions. Step 3 corresponds to the vertical-down arrow in Figure 6. When quenched in air, isotopes in the melted CaCO3 sample (including CO2, CO and O2 gases) exchange with gases in the air. Take CO2 as an example:

(15)

and

. (16)

Figure 5. Simplified technical processes for sample 47413 in Ghosh et al. (2006). See details for each step in Ghosh et al. (2006) and Guo et al. (2009). See discussions of the physical (left) and chemical (right) processes in the text.

Figure 6. Schematic of the ∆63 and ∆47-T paths for the 47413 coral sample during recrystallization. The value for the phosphoric acid digestion fractiona- tion factor in the present study is shown at the bottom of the figure.

Previous experiments (C isotope, [53] ; O isotope, [44] [49] ) showed that due to these two isotope exchange reactions, calcite is enriched in light 12C and 16O isotopes and loses heavy 13C and 18O isotopes at temperatures above 700˚C, resulting in an increase in the concentration of 12C-16O bonds and a decrease in the concentration of 13C-18O bonds in the sample. Therefore, the values for K3866 (Equation (5)), (Equation (6)) and (Equation (7)) decrease. Furthermore, the magnitude of this decline and the extent of the two exchange reactions (Equations (15) and (16)) depend on the concentrations of the isotopes in the CO2 and the length of the quenching time [54] .

When digesting CO2 from a sample (step 5), phosphoric acid reacts with recrystallized carbonates [5] [8] ) and the phosphoric acid fractionation factor is at the level of 0.01‰ according to our calculations. Thus, we suggest that the intercepts (0.28‰, 47413 aragonite coral; 0.22‰, MZ carbonate; 0.14‰, Sigma carb in Ghosh et al. (2006) and 0.234, re-crystallized MZ; 0.210, NBS19 standard; 0.243, Sigma carbonate in Guo et al. (2009)) represent residual isotope information for the corresponding original CaCO3 samples after reaction with air.

5. Conclusions

Ab initio calculations of 13C-18O clumped isotope reactions on growing surfaces of calcite (0001) and aragonite (001) planes were performed. On the basis of the calculated results, the following conclusions can be drawn:

1) These reactions determine the clumped isotope signatures in bulk carbonate crystals and the corresponding information after dissolution using phosphoric acid. Over the temperature range from 260 to 1500 K, the calculated polynomial for calcite was found to be:

and that for aragonite:

.

2) A comparison of the present results with previously reported experimental data suggests that the phosphoric acid influences the degassing of CO2 from the carbonates at a level of just 0.01‰. It is therefore thought that the conventional intercept of 0.22(3)‰ is due to C and O isotope reactions between CaCO3 and air.

Acknowledgements

We would like to thank Dr Wang Xu in IGGCAS for helpful discussions on the process of phosphoric acid digestion. All of the calculations were performed at the IGGCAS computer simulation lab. This work was supported by the National Natural Science Foundation of China (Grant No. 90914010, 41020134003 and 41303047). The authors would like to thank Enago (www.enago.cn) for the English language review.

References

  1. Wang, Z.G., Schauble, E.A. and Eiler, J.M. (2004) Equilibrium Thermodynamics of Multiply Substituted Isotopologues of Molecular Gases. Geochimica et Cosmochimica Acta, 68, 4779-4797. http://dx.doi.org/10.1016/j.gca.2004.05.039
  2. Eiler, J.M. and Schauble, E. (2004) (OCO)-O-18-C-13-O-16 in Earth’s Atmosphere. Geochimica et Cosmochimica Acta, 68, 4767-4777.
  3. Ghosh, P., Adkins, J., Affek, H., Balta, B., Guo, W.F., Schauble, E.A., Schrag, D. and Eller, J.M. (2006) 13C-18O Bonds in Carbonate Minerals: A New Kind of Paleothermometer. Geochimica et Cosmochimica Acta, 70, 1439-1456. http://dx.doi.org/10.1016/j.gca.2005.11.014
  4. Ghosh, P., Eiler, J., Campana, S.E. and Feeney, R.F. (2007) Calibration of the Carbonate “Clumped Isotope” Paleothermometer for Otoliths. Geochimica et Cosmochimica Acta, 71, 2736-2744. http://dx.doi.org/10.1016/j.gca.2007.03.015
  5. Mccrea, J.M. (1950) On the Isotopic Chemistry of Carbonates and a Paleotemperature Scale. The Journal of Chemical Physics, 18, 849.
  6. Swart, P.K. (1991) The Oxygen and Hydrogen Isotopic Composition of the Black Sea. Deep Sea Research Part A. Oceanographic Research Papers, 38, S761-S772.
  7. Swart, P.K. (1991) Factors Affecting the Oxygen Isotopic Composition of the Black Sea. Black Sea Oceanography, 351, 75-88.
  8. Swart, P.K., Burns, S.J. and Leder, J.J. (1991) Fractionation of the Stable Isotopes of Oxygen and Carbon in Carbon-Dioxide during the Reaction of Calcite with Phosphoric-Acid as a Function of Temperature and Technique. Che- mical Geology: Isotope Geoscience Section, 86, 89-96.
  9. Hill, P.S., Tripati, A.K. and Schauble, E.A. (2014) Theoretical Constraints on the Effects of pH, Salinity, and Temperature on Clumped Isotope Signatures of Dissolved Inorganic carbon Species and Precipitating Carbonate Minerals. Geochimica et Cosmochimica Acta, 125, 610-652.
  10. Schauble, E.A. and Eiler, J.M. (2004) Theoretical Estimates of Equilibrium 13C-18O Clumping in Carbonates and Organic Acids. Eos, Transactions American Geophysical Union, 85, 11A-0552.
  11. Schauble, E.A., Ghosh, P. and Eiler, J.M. (2006) Preferential Formation of 13C-18O Bonds in Carbonate Minerals, Estimated Using First-Principles Lattice Dynamics. Geochimica et Cosmochimica Acta, 70, 2510-2529. http://dx.doi.org/10.1016/j.gca.2006.02.011
  12. Guo, W.F., Mosenfelder, J.L., Goddard, W.A. and Eiler, J.M. (2009) Isotopic Fractionations Associated with Phosphoric Acid Digestion of Carbonate Minerals: Insights from First-Principles Theoretical Modeling and Clumped Isotope Measurements. Geochimica et Cosmochimica Acta, 73, 7203-7225. http://dx.doi.org/10.1016/j.gca.2009.05.071
  13. Watson, E.B. and Liang, Y. (1995) A Simple Model for Sector Zoning in Slowly Grown Crystals: Implications for Growth Rate and Lattice Diffusion, with Emphasis on Accessory Minerals in Crustal Rocks. American Mineralogist, 80, 1179-1187.
  14. Watson, E.B. (2004) A Conceptual Model for Near-Surface Kinetic Controls on the Trace-Element and Stable Isotope Composition of Abiogenic Calcite Crystals. Geochimica et Cosmochimica Acta, 68, 1473-1488. http://dx.doi.org/10.1016/j.gca.2003.10.003
  15. Watson, E.B. (1996) Surface Enrichment and Trace-Element Uptake during Crystal Growth. Geochimica et Cosmochimica Acta, 60, 5013-5020. http://dx.doi.org/10.1016/S0016-7037(96)00299-2
  16. DePaolo, D.J. (2011) Surface Kinetic Model for Isotopic and Trace Element Fractionation during Precipitation of Calcite from Aqueous Solutions. Geochimica et Cosmochimica Acta, 75, 1039-1056. http://dx.doi.org/10.1016/j.gca.2010.11.020
  17. Eiler, J.M. (2011) Paleoclimate Reconstruction Using Carbonate Clumped Isotope Thermometry. Quaternary Science Reviews, 30, 3575-3588. http://dx.doi.org/10.1016/j.quascirev.2011.09.001
  18. Eagle, R.A., Schauble, E.A., Tripati, A.K., Tuetken, T., Hulbert, R.C. and Eiler, J.M. (2010) Body Temperatures of Modern and Extinct Vertebrates from 13C-18O Bond Abundances in Bioapatite. Proceedings of the National Academy of Sciences of the United States of America, 107, 10377-10382. http://dx.doi.org/10.1073/pnas.0911115107
  19. Came, R.E., Eiler, J.M., Veizer, J., Azmy, K., Brand, U. and Weidman, C.R. (2007) Coupling of Surface Temperatures and Atmospheric CO2 Concentrations during the Palaeozoic Era. Nature, 449, 198-201. http://dx.doi.org/10.1038/nature06085
  20. Dennis, K.J. and Schrag, D.P. (2010) Clumped Isotope Thermometry of Carbonatites as an Indicator of Diagenetic Alteration. Geochimica et Cosmochimica Acta, 74, 4110-4122. http://dx.doi.org/10.1016/j.gca.2010.04.005
  21. Saenger, C., Affek, H.P., Felis, T., Thiagarajan, N., Lough, J.M. and Holcomb, M. (2012) Carbonate Clumped Isotope Variability in Shallow Water Corals: Temperature Dependence and Growth-Related Vital Effects. Geochimica et Cos- mochimica Acta, 99, 224-242.
  22. Tripati, A.K., Eagle, R.A., Thiagarajan, N., Gagnon, A.C., Bauch, H., Halloran, P.R. and Eiler, J.M. (2010) 13C-18O Isotope Signatures and “Clumped Isotope” Thermometry in Foraminifera and Coccoliths. Geochimica et Cosmochimica Acta, 74, 5697-5717. http://dx.doi.org/10.1016/j.gca.2010.07.006
  23. Hammer, B., Morikawa, Y. and Norskov, J.K. (1996) CO Chemisorption at Metal Surfaces and Overlayers. Physical Review Letters, 76, 2141-2144. http://dx.doi.org/10.1103/PhysRevLett.76.2141
  24. Xu, Y., Ruban, A.V. and Mavrikakis, M. (2004) Adsorption and Dissociation of O-2 on Pt-Co and Pt-Fe Alloys. Journal of the American Chemical Society, 126, 4717-4725. http://dx.doi.org/10.1021/ja031701+
  25. Frisch, M.J., Trucks, G.W., Schlegel, H.B., Scuseria, G.E., Robb, M.A., Cheeseman, J.R., Montgomery, J.J.A., Vreven, T., Kudin, K.N., Burant, J.C., Millam, J.M., Iyengar, S.S., Tomasi, J., Barone, V., Mennucci, B., Cossi, M., Scalmani, G., Rega, N., Petersson, G.A., Nakatsuji, H., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J., Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Klene, M., Li, X., Knox, J.E., Hratchian, H.P., Cross, J.B., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R.E., Yazyev, O., Austin, A.J., Cammi, R., Pomelli, C., Ochterski, J.W., Ayala, P.Y., Morokuma, K., Voth, G.A., Salvador, P., Dannenberg, J.J., Zakrzewski, V.G., Dapprich, S., Daniels, A.D., Strain, M.C., Farkas, O., Malick, D.K., Rabuck, A.D., Raghavachari, K., Foresman, J.B., Ortiz, J.V., Cui, Q., Baboul, A.G., Clifford, S., Cioslowski, J., Stefanov, B.B., Liu, G., Liashenko, A., Piskorz, P., Komaromi, I., Martin, R.L., Fox, D.J., Keith, T., Al-Laham, M.A., Peng, C.Y., Nanayakkara, A., Challacombe, M., Gill, P.M.W., Johnson, B., Chen, W., Wong, M.W., Gonzalez, C. and Pople, J.A. (2009) Gaussian 09, Revision A.01. Gaussian, Inc., Wallingford.
  26. Rustad, J.R., Nelmes, S.L., Jackson, V.E. and Dixon, D.A. (2008) Quantum-Chemical Calculations of Carbon-Isotope Fractionation in CO2 (g), Aqueous Carbonate Species, and Carbonate Minerals. Journal of Physical Chemistry A, 112, 542-555. http://dx.doi.org/10.1021/jp076103m
  27. Maslen, E.N., Streltsov, V.A. and Streltsova, N.R. (1993) X-Ray Study of the Electron-Density in Calcite, CaCo3. Acta Crystallographica Section B-Structural Science, 49, 636-641.
  28. Jarosch, D. and Heger, G. (1986) Neutron-Diffraction Refinement of the Crystal-Structure of Aragonite. Tschermaks mineralogische und petrographische Mitteilungen, 35, 127-131.
  29. Liu, Y. and Tossell, J.A. (2005) Ab Initio Molecular Orbital Calculations for Boron Isotope Fractionations on Boric Acids and Borates. Geochimica et Cosmochimica Acta, 69, 3995-4006. http://dx.doi.org/10.1016/j.gca.2005.04.009
  30. Kohn, W. and Sham, L.J. (1965) Self-Consistent Equations Including Exchange and Correlation Effects. Physical Review, 140, A1133-A1138. http://dx.doi.org/10.1103/PhysRev.140.A1133
  31. Patterson, W.P., Smith, G.R. and Lohmann, K.C. (1993) Continental Paleothermometry and Seasonality Using the Iso- topic Composition of Aragonitic Otoliths of Freshwater Fishes. In: Climate Change in Continental Isotopic Records, American Geophysical Union, Washington DC, 191-202. http://dx.doi.org/10.1029/GM078p0191
  32. Petersen, J., Kieffer, M., Lilic, D., Rathlev, N. and Andersen, V. (1982) Influence of Autologous Monocytes on the Pokeweed Mitogen-Induced Generation of Immunoglobulin-Secreting Cells in Man. Scandinavian Journal of Haematology, 29, 273-282.
  33. Bigeleisen, J. and Mayer, M.G. (1947) Calculation of Equilibrium Constants for Isotopic Exchange Reactions. Journal of Chemical Physics, 15, 261. http://dx.doi.org/10.1063/1.1746492
  34. Urey, H.C. (1947) The Thermodynamic Properties of Isotopic Substances. Journal of the Chemical Society, 562-581.
  35. Scott, A.P. and Radom, L. (1996) Harmonic Vibrational Frequencies: An Evaluation of Hartree-Fock, Moller-Plesset, Quadratic Configuration Interaction, Density Functional Theory, and Semiempirical Scale Factors. Journal of Physical Chemistry, 100, 16502-16513. http://dx.doi.org/10.1021/jp960976r
  36. Kerisit, S. and Parker, S.C. (2004) Free Energy of Adsorption of Water and Calcium on the {10(1)over-bar-4} Calcite Surface. Chemical Communications, 1, 52-53.
  37. Geissbuhler, P., Fenter, P., DiMasi, E., Srajer, G., Sorensen, L.B. and Sturchio, N.C. (2004) Three-Dimensional Structure of the Calcite-Water Interface by Surface X-Ray Scattering. Surface Science, 573, 191-203. http://dx.doi.org/10.1016/j.susc.2004.09.036
  38. Fenter, P., Geissbuhler, P., DiMasi, E., Srajer, G., Sorensen, L.B. and Sturchio, N.C. (2000) Surface Speciation of Calcite Observed in Situ by High-Resolution X-Ray Reflectivity. Geochimica et Cosmochimica Acta, 64, 1221-1228. http://dx.doi.org/10.1016/S0016-7037(99)00403-2
  39. Myers, D. (1999) Surfaces, Interfaces, and Colloids: Principles and Applications. 2nd Edition, John Wiley & Sons, Inc., New York.
  40. Forbes, T.Z., Radha, A.V. and Navrotsky, A. (2011) The Energetics of Nanophase Calcite. Geochimica et Cosmochimica Acta, 75, 7893-7905. http://dx.doi.org/10.1016/j.gca.2011.09.034
  41. Angus, W.R., Bailey, C.R., Ingold, C.K., Leckie, A.H., Raisin, C.G., Thompson, J.W. and Wilson, C.L. (1935) Infra- Red Spectrum of Hexadeuterobenzene and the Structure of Benzene. Nature, 136, 680.
  42. Wilson, E.B.J., Decius, J.C. and Cross, P.C. (1955) Molecular Vibrations: The Theory of Infrared and Raman Spectra. Dover, New York.
  43. Zeebe, R.E., Sanyal, A., Ortiz, J.D. and Wolf-Gladrow, D.A. (2001) A Theoretical Study of the Kinetics of the Boric Acid-Borate Equilibrium in Seawater. Marine Chemistry, 73, 113-124. http://dx.doi.org/10.1016/S0304-4203(00)00100-6
  44. Chacko, T., Mayeda, T.K., Clayton, R.N. and Goldsmith, J.R. (1991) Oxygen and Carbon Isotope Fractionations between CO2 and Calcite. Geochimica et Cosmochimica Acta, 55, 2867-2882.
  45. Deines, P. (2004) Carbon Isotope Effects in Carbonate Systems. Geochimica et Cosmochimica Acta, 68, 2659-2679. http://dx.doi.org/10.1016/j.gca.2003.12.002
  46. Romanek, C.S., Grossman, E.L. and Morse, J.W. (1992) Carbon Isotopic Fractionation in Synthetic Aragonite and Calcite: Effects of Temperature and Precipitation Rate. Geochimica et Cosmochimica Acta, 56, 419-430.
  47. Rubinson, M. and Clayton, R.N. (1969) Carbon-13 Fractionation between Aragonite and Calcite. Geochimica et Cosmochimica Acta, 33, 997-1002.
  48. Kieffer, S.W. (1982) Thermodynamics and Lattice-Vibrations of Minerals: 5. Applications to Phase-Equilibria, Isotopic Fractionation, and High-Pressure Thermodynamic Properties. Reviews of Geophysics, 20, 827. http://dx.doi.org/10.1029/RG020i004p00827
  49. Chacko, T. and Deines, P. (2008) Theoretical Calculation of Oxygen Isotope Fractionation Factors in Carbonate Systems. Geochimica et Cosmochimica Acta, 72, 3642-3660. http://dx.doi.org/10.1016/j.gca.2008.06.001
  50. Tarutani, T., Clayton, R.N. and Mayeda, T.K. (1969) Effect of Polymorphism and Magnesium Substitution on Oxygen Isotope Fractionation between Calcium Carbonate and Water. Geochimica et Cosmochimica Acta, 33, 987-996.
  51. Kim, S.T. and Oneil, J.R. (1997) Equilibrium and Nonequilibrium Oxygen Isotope Effects in Synthetic Carbonates. Geochimica et Cosmochimica Acta, 61, 3461-3475. http://dx.doi.org/10.1016/S0016-7037(97)00169-5
  52. Yuan, J. and Liu, Y. (2012) Quantum-Mechanical Equilibrium Isotopic Fractionation Correction to Radiocarbon Dating: A Theory Study. Journal of Radioanalytical and Nuclear Chemistry, 292, 335-338. http://dx.doi.org/10.1007/s10967-011-1563-3
  53. Scheele, N. and Hoefs, J. (1992) Carbon Isotope Fractionation between Calcite, Graphite and CO2: An Experimental- Study. Contributions to Mineralogy and Petrology, 112, 35-45. http://dx.doi.org/10.1007/BF00310954
  54. Levine, I.N. (1995) Physical Chemistry. 4th Edition, McGraw-Hill, Inc., New York.

Appendix A. Supplementary Materials

Supplementary Materials can be found in the online version.

This file includes the optimized structures and frequencies for different isotopes of calcite and aragonite at HF/6-31g(d).

Note: the frequencies for calcite in Table 1 are calculated using the standard masses of the C and O elements, as is required by Scott and Radom, 1996. See details in the reference.

Summarized coordinate atoms of O in the interested carbonate group from the following optimized structures:

The CAs of O atoms are four for both calcite and aragonite. Bonds connecting O atom and its coordinate atoms are labeled in gray. All bond lengths are in unit Å. Three different oxygen sites (O1, O2 and O3) for both clusters are also shown.

NOTES

*Corresponding author.

Journal Menu >>