Open Journal of Geology
Vol.3 No.1(2013), Article ID:26810,12 pages DOI:10.4236/ojg.2013.31002
The Application of Geostatistical Methods to Prepare the 3D Petrophysical Model of Oil Reservoir
Department of Geology, Ferdowsi University of Mashhad, Mashhad, Iran
Email: *h_amanipoor@yahoo.com
Received July 4, 2012; revised August 9, 2012; accepted September 12, 2013
Keywords: 3D Petrophysical Model; Geostatistical Method; Variogram; Anisotropic Structure
ABSTRACT
In this study, the petrophysical parameters such as density, sonic, neutron, and porosity were investigated and presented in the 3D models. The 3D models were built using geostatistical method that is used to estimate studied parameters in the entire reservoir. For this purpose, the variogram of each parameter was determined to specify spatial correlation of data. Resulted variograms were non-monotonic. That shows anisotropy of structure. The lithology and porosity parameters are the main causes of this anisotropy. The 3D models also show that petrophysical data has higher variation in north part of reservoir than south part. In addition to, the west limb of reservoir shows higher porosity than east limb. The variation of sonic and neutron data are similar whereas the density data has opposed variation.
1. Introduction
During drilling, preparing cores from formations around well are time-consuming and expensive. Cutting rocks are not reliable to interpret because they were mainly small, mixed, and flushed by drilling fluid. Petrophysical logs that are based on measurements of physical properties of rock are an appropriate tool to obtain more information about nature of oil and gas reservoirs. These logs always represent continuous illustration of reservoir rock properties. Lithology, porosity, permeability, net pay thickness, and percentage of water and oil saturation are most important parameters for reservoir studies that can be easily calculated using the petrophysical data [1].
Porosity and lithology have a significant influence on the behavior of hydrocarbon reservoirs. There are two types of porosity that include total porosity and effective porosity. Total porosity is proportion of total empty space to total volume mass regardless of internal relation of pores. Effective porosity is ratio of related pores to total volume mass. Total porosity of rock mass may be significant while effective porosity is low. In this case, permeability will be low. Because effective porosity has a significant efficacy on oil production, it is applied for all engineering calculations of reservoir studies. Therefore, estimation of porosity distribution is an appropriate tool for investigation of porosity variation and its effect on other parameters.
The Bangestan calcareous reservoir in studied oil field that was composed of Ilam and Sarvak Formations was located in a flat plain, without any surface outcrop. A trend of this field is similar to the Zagros fold-trust belt trend, namely the NW-SE trend. It has been demonstrated that no any type of fault has been detected in this field.
The purpose of this study is modeling of the Ilam Formation. The lithology of studied reservoir layer was mainly composed of calcareous rocks with some intervals of thin inter layers of shale (Figure 1). Based on the alternation of permeable and impermeable layers, the the Ilam Formation is divided into three zones. This formation had no primary porosity and secondary porosity was mainly from cracks, fracture and cavities.
2. Porosity Logs
Sonic, density, and neutron logs are frequently referred to as porosity logs. In each log, an emitted signal interacts as it passes through the formation, and is detected either up or down hole of the source, as follows:
Ÿ Sonic Log: Source is sonic waves. The formation refracts the waves and the receiver detects transmitted acoustic waves and identifies travel time.
Ÿ Density Log: Source emits gamma rays, which are considered energy photons, interacting with electrons causing loss of energy. From the loss of energy, the density of the formation can be obtained.
Ÿ Neutron Log: A reaction between radioactive elements emits fast neutrons, which collide with the nuclei
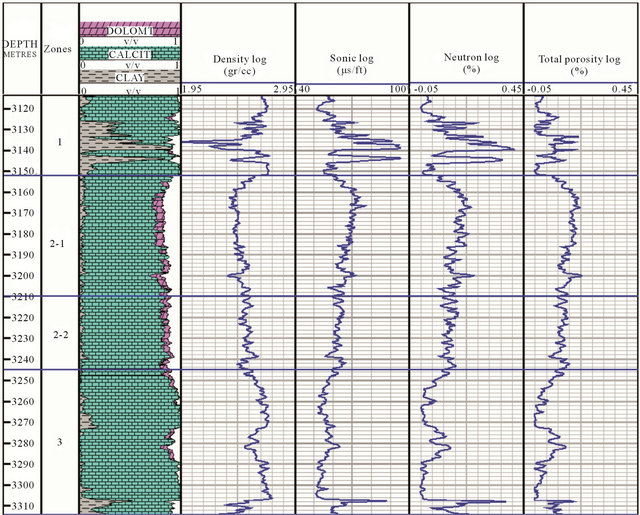
Figure 1. Lithology and porosity logs.
of other atoms, most importantly hydrogen nuclei. Detectors count the slowed neutrons deflected back to the tool. Apparent neutron porosity can be obtained based on the hydrogen index.
Neutron log is important log for determining porosity. Neutron and density log data show total porosity while sonic log shows primary porosity. Porosity can be calculated using one porosity log or combination of two or three porosity logs. Figure 1 shows the sonic, density, neutron, and total porosity logs. In this study, the total porosity was calculated using three porosity logs. This reservoir has no primary porosity and secondary porosity is mainly from cracks, fracture and cavities.
3. Geostatistical Estimation and 3D Modeling
Geostatistical estimation of rock’s petrophysical properties consists of two steps: a) variogram analysis and b) estimation [2]. The first step is identification and modeling of spatial structure of petrophysical data by using variogram. The second step is estimation of petrophysical properties by using interpolation methods such as kriging. This step is dependent on the characteristics of selected variogram in the first step [3]. Incorrect selection of variogram model will be affected next steps.
3.1. Best Variogram Model
The variogram is applied to represent the spatial variation. In other words, the variogram describes geological continuity of variables within relatively homogeneous layers [2]. The experimental variogram is defined as:
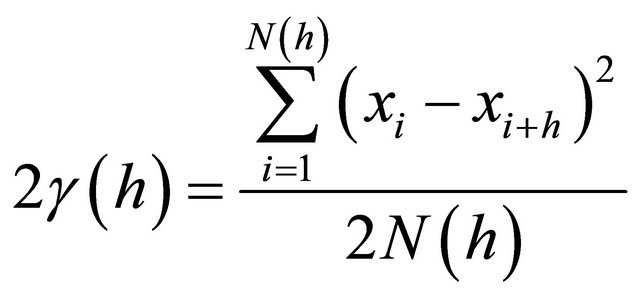 (1)
(1)
where 2γ(h): variogram, xi + h, xi: variables x at location i and i + h, h: lag vector, N(h): number of pairs.
The variogram starts from zero at the origin h = 0 and reaches to a constant value (sill: C) at certain distance that is termed range or correlation length (a) [2]. The range indicates the correlation of data along various directions. Outside the range, the data are independent of each other and have no spatial structure [4].
Theoretically, the variogram should be reduced to the minimum value namely zero at h = 0. However, experimental variogram do not have these conditions. The variogram value at h = 0 is termed nugget effect (C0) [2]. Therefore the experimental variogram is not sufficient for variogram analysis and appropriate theoretical models should be fitted on it. There are several theoretical models to fit on the experimental variogram that most common of them include: exponential, gaussian and spherical [3].
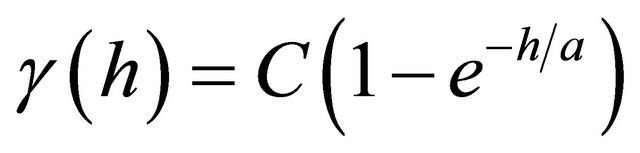 (2)
(2)
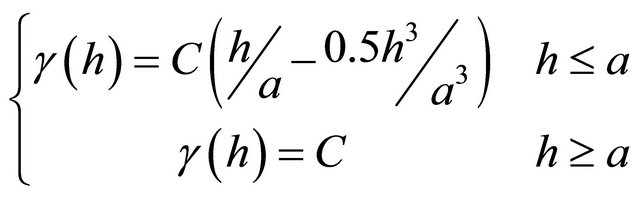 (3)
(3)
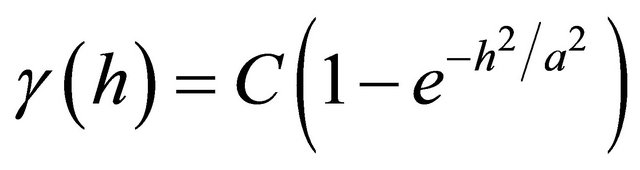 (4)
(4)
Isotropic variogram has the same range and sill in all directions and shows the homogeneity of studied variable in the entire reservoir. However, anisotropic variogram shows different spatial continuities in the various directions. The most common types of anisotropy are geometric and zonal anisotropies. The geometric anisotropy shows the similar sill and the different range in the directions of maximum (X) and minimum continuity (Y). However, the zonal anisotropy is observed where the variogram has the different sill in the directions of maximum and minimum continuity. In the 2D space, tolerance angle (θ) should be defined between the vector h and maximum direction of continuity [4].
The experimental variogram not only is a profitable tool for identification of spatial structure and indication of variations of studied variable but also has an effective role in data purification. Two important criteria that show consistency of spatial structure are the range and the relative nugget effect (nugget effect/sill: C0/C). Therefore, the variogram is more appropriate that has greater range and smaller nugget effect. It is achieved by a correct selection of the lag numbers [5]. It is noteworthy that all parameters must be considered for selecting an appropriate model.
The experimental variograms often continuously increase with lag distance; however, the variogram is not restricted to such monotonic form and decreasing segments or cyclicity can be observed. Non-monotonic variogram structures or cyclic variograms are identified as hole effect structures (Figure 2) [6].
Geological features such as lithology, sedimentary environments, and tectonic structures mainly cause this effect. Multiple structures of some variables such as porosity is another important factor that can cause the hole effect. Origin of porosity that may be primary or secondary can cause multiple structures. Consequently, the resulted variogram will be the cyclic variogram. The most important tectonic structures that cause disorganization and non-uniformity of rock mass include folds, faults, fractures, and joints.
Because increasing radius search can increase the range of variogram, in non-uniform structure, the experimental variogram becomes cyclic with the increasing of search radius. It is noteworthy that increasing number of lags can also increase the hole effect [6].
3.2. Estimating Using Kriging Method
Kriging is a geostatistical estimation method that can be considered as the best-unbiased estimator. This estimator not only has least estimation variance but also ensures unbiasedness of estimations. The kriging is a geostatistical estimator that is based on the weighted moving average [2].
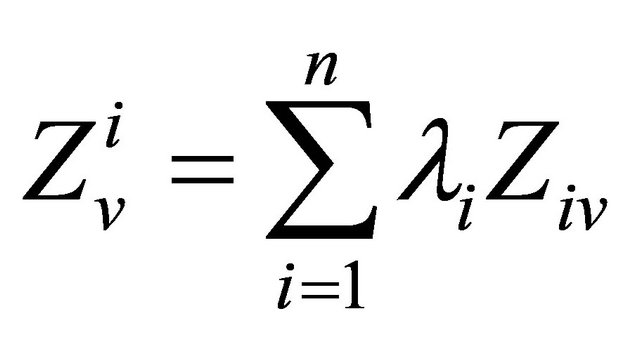 (5)
(5)
where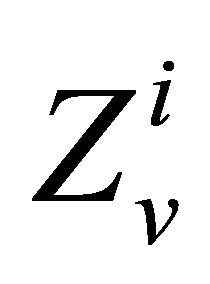 : grade estimation, λi: weight or importance of the value Ziv: the grade of ith sample.
: grade estimation, λi: weight or importance of the value Ziv: the grade of ith sample.
Equation (5) shows a linear kriging. To apply this estimator, a distribution of variable (petrophysical data) should be normally. Otherwise, non-linear kriging should be applied, or first a transformation should be found that transforms the distribution of variable to normal, and then the linear kriging be applied on transformed data [7].
The parameters of estimation should be determined according to data distribution, spatial structure, and estimation strategy. Increasing distance among points (data) makes weaker spatial structure. The points that their distances are greater than range have practically no effect on estimation [5]. In this case, removing these points from estimates would be better. Number of involved points is a criterion to confirm about validity of the estimate.
4. Methodology
For 3D modeling of static parameters of oil and gas reservoirs, one model must firstly be built from the positions of faults and horizons. This model termed a structural and reservoir framework is usually made based on seismic data and well markers. The second step is building a 3D grid from the previous structural framework with an appropriate scale [2]. It does not appear that the
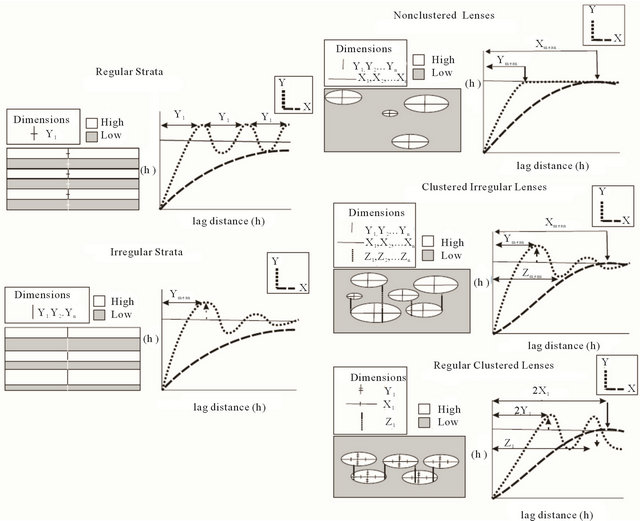
Figure 2. Types of hole effect [6].
faults have played a significant role in the development of the studied field; only the 3D model of the Ilam and Sarvak Formation tops was prepared using seismic data.
In this study, for built the 3D model, position and trajectory of 41 wells were applied to building the structural models. Then the variogram of each parameter was determined. The best variogram of all parameters is exponential (Figures 3, 4). The linear kriging method was used to estimate the 3D distribution of petrophysical parameters. As previously mentioned, to use this method, data distribution should be normal. Therefore normal scores method was applied to normalize the data (Figure 5).
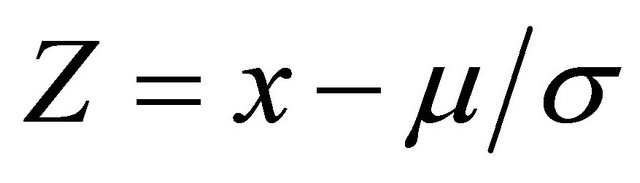 (6)
(6)
where x: a raw score to be standardized, μ: mean, σ: standard deviation.
5. Discussion and Result
The purpose of this study is to modelg the petrophysical parameters in the Ilam reservoir layer. According to resulted variogram, the spatial distributions of petrophysical parameters are anisotropic (longitudinal, lateral and in depth). This anisotropy can be caused by effect of tectonic zones and or sedimentation environments.
The hole effect is visible in all variograms (Figures 3, 4). In depth, zoning of formations that are based on the alternation of dense and porous layers is the main factor to cause this effect. The non-uniform distribution of fractures is another factor to cause the variation of porosity in the entire studied reservoir.
Laterally, structural boundaries of anticline can be identified based on its crest and limbs. These boundaries separate the low porosity zones (limbs) from high porosity zone (crest). Resulted boundaries are an important factor to cause the hole effect. Because the distribution of fractures is not constant in the entire reservoir, porosity varies in depth and lateral direction.
Lithology has clearly variations in longitudinal direction.
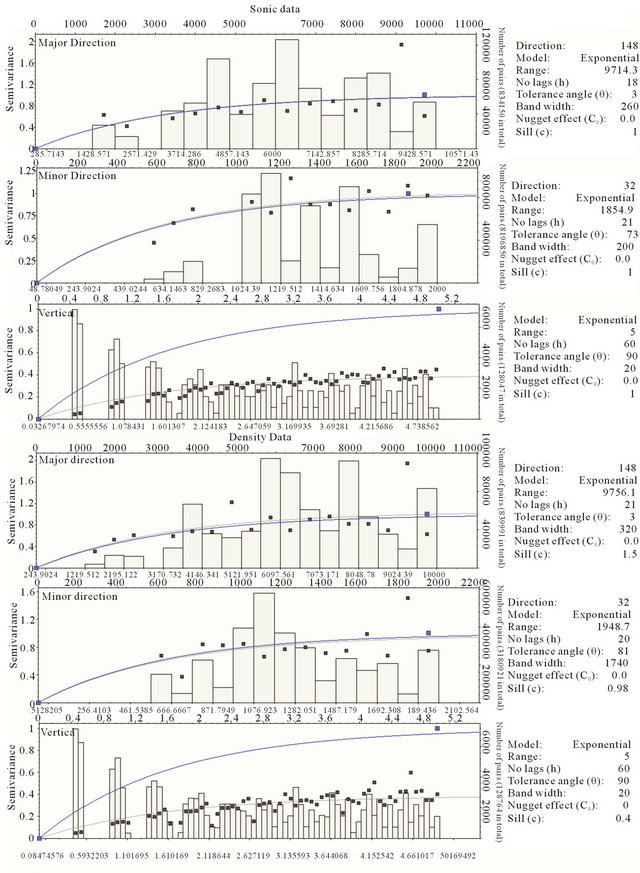
Figure 3. The variogram of sonic and density data.
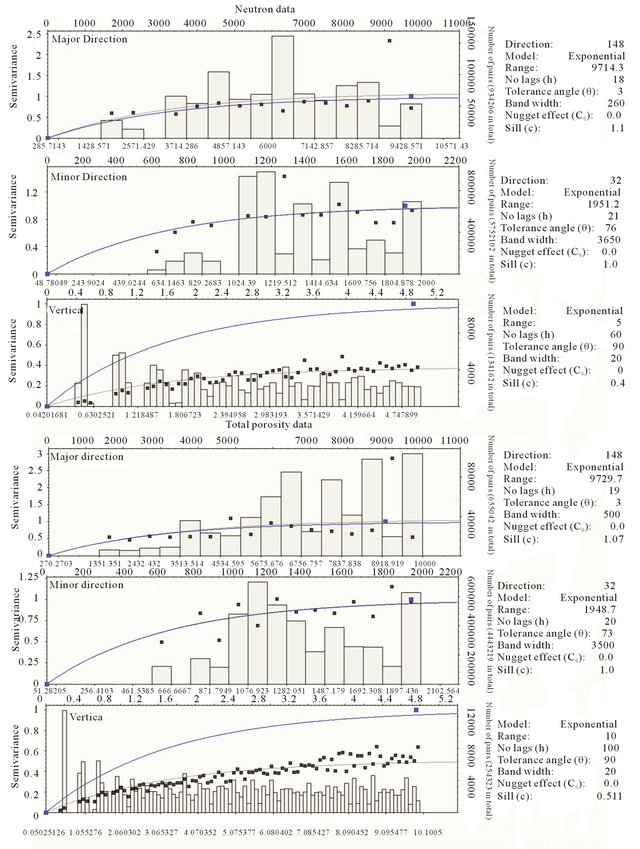
Figure 4. The variogram of neutron and porosity data.
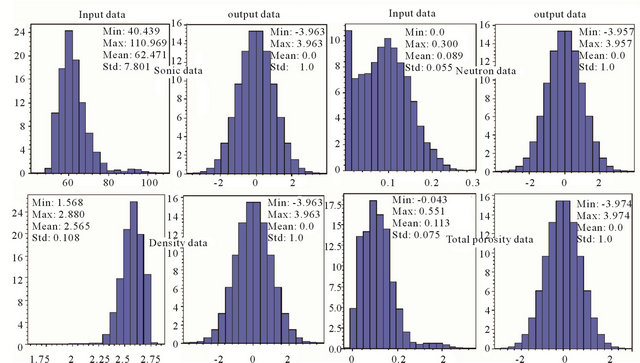
Figure 5. The normalized data.
This factor can causes the hole effect, in this direction. Because, Ilam Formation only is composed of limestone and shale, the gamma data were used to identify distribution of lithology. These data is one of the key indicators for lithology recognition, especially in sequences containing clay. In general, increasing the value of gamma ray (GR > 20 API) shows an increasing the clay content. Gamma ray more than 70 represents 100 percent clay content. Clay content in the south of reservoir is over the north parts (Figure 6).
The 3D petrophysical models clearly show the variation of petrophysical parameters and consequently the porosity variation (Figure 7). Because the inter layers of shale are existed at the beginning of the Ilam Formation (Zone 1), the petrophysical parameters in this depth is clearly different from the other depths. In this zone, the porosity is higher than the other zones (Figures 1 and 8). Considering that the effective porosity of shale layer is low, this zone can not act as reservoir. Based on the porosity percentage, Zone 2 is in the second order. This zone is known as reservoir zone. In this reservoir, Zone 3 has minimum porosity (Figure 1).
In depth, more variation is observed at the north part of reservoir (Figure 7). Longitudinally, the results of model show that sonic and neutron models increase to the north part of reservoir. However, density model shows opposite condition (Figures 9 and 10). Laterally, the porosity of west limb is higher than east limb, as presented in Figure 11.
To confirm the validity, the data of one well was removed from the model. Then, the results of estimation were compared with the actual data. This comparison showed that the estimated results have a relatively acceptable accord with the real data (Figure 12). The errors seen in some depths are mainly due to two factors that are: a) low number and unsuitable distribution of wells to build the model and b) unsuitable networking of structural framework. An unbiased data and abnormal distribution of data are other important factors that can cause the error. However, in studied reservoir, the first factor does not exist and second factor was refined using the normalized data.
6. Conclusions
In this study, the petrophysical data were applied to prepare the 3D model for the Bangestan oil reservoir in southwest of Iran. The variogram of each parameter was determined to specify the spatial correlation of geomechanical parameters. The range of resulted variogram in various directions is not similar for all parameters. This difference represents the anisotropy of studied reservoir. All resulted variogram show hole effect. The porosity and lithology variations are main causes for this effect.
The 3D models that based on kriging method clearly show the variation of petrophysical data in all studied reservoir. Laterally, the north part of reservoir shows higher variation than south part. The sonic and neutron
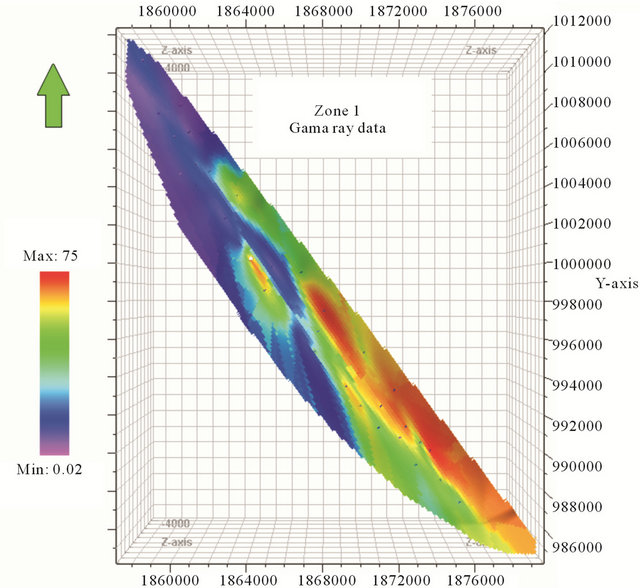
Figure 6. The longitudinal variation of gama ray data in Zone 1.
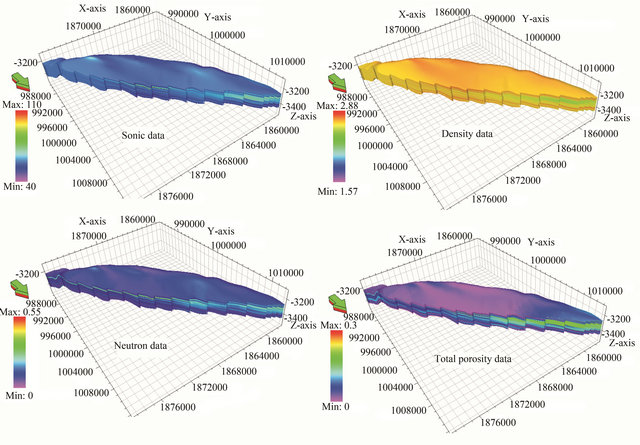
Figure 7. The 3D model of petrophysical data.
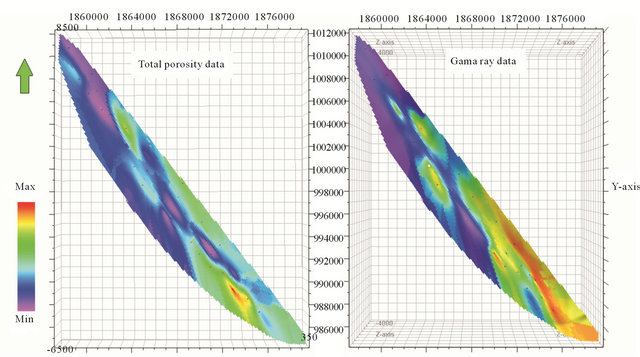
Figure 8. Comparing the gama ray and porosity data.
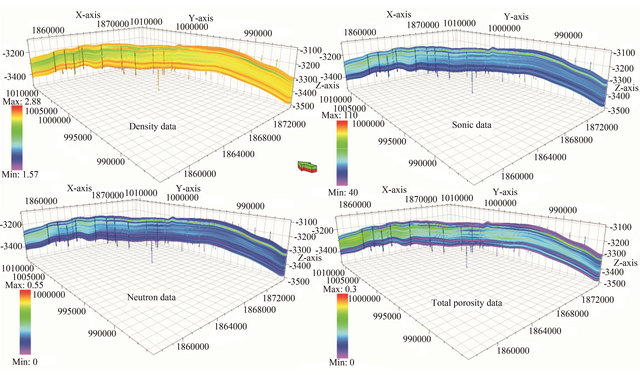
Figure 9. The longitudinal variation of petrophysical data in axis of structure.
data increase toward north part whereas the density data decrease. The west limbs of reservoir shows higher porosity than east limb. In depth, Zone1 and then Zone 2 showed higher porosity than Zone 3.
To verify the results, the real data of one well was compared with estimated data using the model. This comparison showed that the real and estimated data are very similar. This similarity of data confirms that
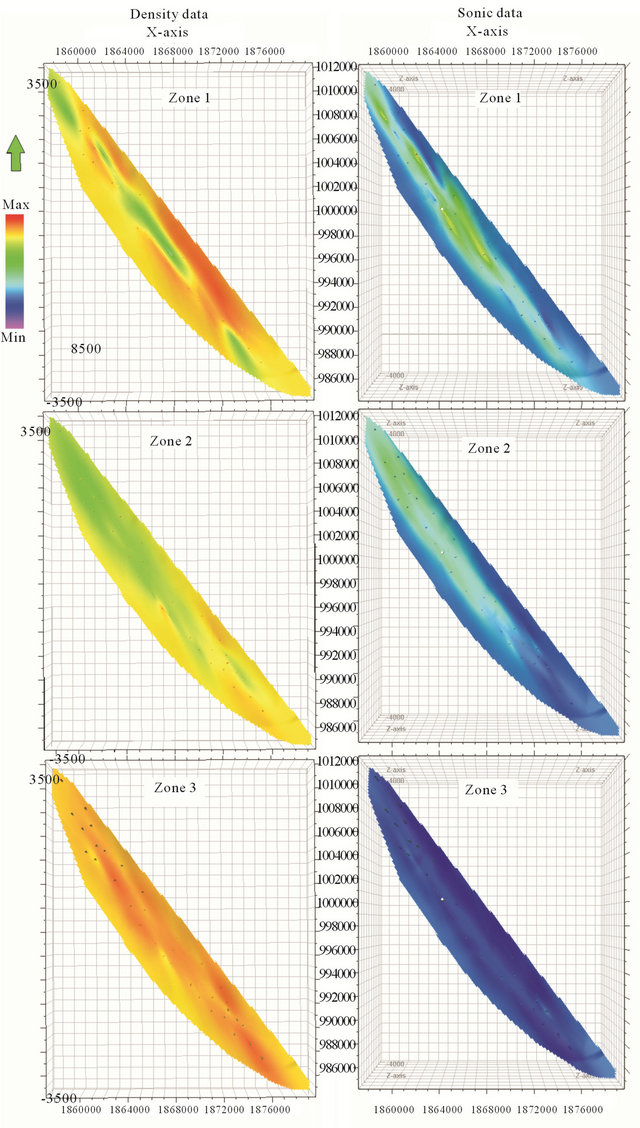
Figure 10. The comparison longitudinal of sonic and porosity data in different zones.
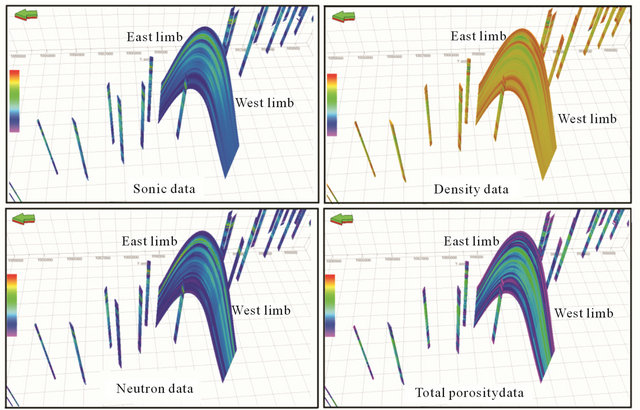
Figure 11. The lateral variation of petrophysical data.
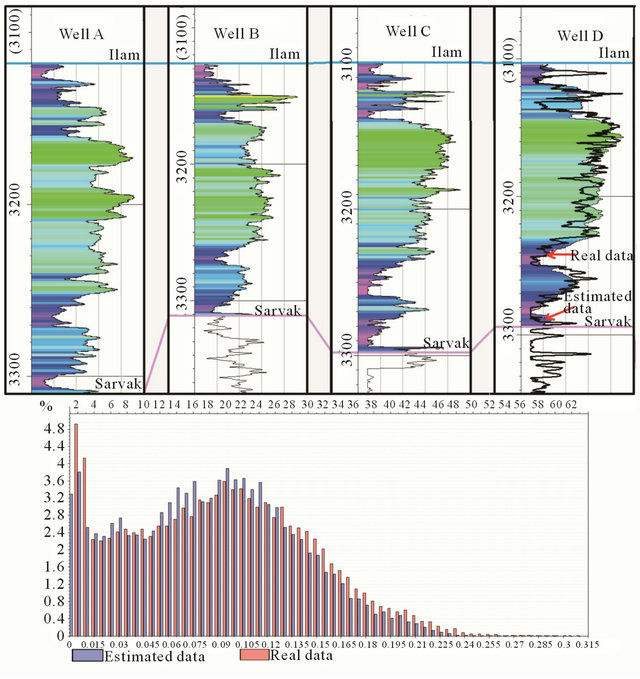
Figure 12. (a) Correlation between real and estimated data of some wells. The data of wells A, B, and C are used to build the 3D model; and the well D shows comparing the real data with the estimated data. (b) The histogram of real and estimated data.
geostatistical methods are appropriate tools for 3D modeling of petrophysical parameters in oil and gas reservoirs.
7. Acknowledgements
Authors thank National Iranian South Oilfields Company (NISOC) for their help and financial support for any data and software.
REFERENCES
- J. H. Doveton, “Geologic Log Analysis Using Computer Methods: Computer Application in Geology,” American Association of Petroleum Geologists, Tulsa, 1994.
- J. Caers, “Petroleum Geostatistics,” Society of Petroleum Engineers: SPE, 2005.
- A. G. Journel and C. Huijbregts, “Mining Geostatistics,” Academic Press, Waltham, 1978.
- C. V. Deutch, “Geostatistical Reservoir Modeling,” Oxford University Press, Oxford, 2002.
- A. A. Hassani Pak and M. Sharafaddin, “Exploration Data Analysis,” 2001. (in Persian)
- M. J. Pyrcz and C. V. Deutsch, “The Whole Story on the Hole Effect,” Centre for Computational Geostatistics, University of Alberta, Edmonton, 2003.
- A. A. Hassani Pak, “Geostatistics,” 2007. (in Persian)
NOTES
*Corresponding author.

