ABSTRACT

The polynomial $x^4+1$ is irreducible in $\mathbb{Z}\left[x\right]$ but is locally reducible, that is, it factors modulo p for all primes p. In this paper we investigate this phenomenon and prove that for any composite natural number N there are monic irreducible polynomials in $\mathbb{Z}\left[x\right]$ which are reducible modulo every prime.

Keywords:

Irreducible Polynomial, Reducible Polynomial, Galois Theory

1. Introduction

The polynomials of the title of this article have been discussed by Brandl [1] , and Guralnick et al. [2] . Brandl’s paper excludes those N which are such that $\left(N,\phi \left(N\right)\right)=1$. These are precisely the composite integers N for which there is only one abstract group of order N. The paper by Guralnick et al. does show the existence of such polynomials for all composite N’s. Our proof of the same is different, more elementary, and in some cases even constructive.

We shall first enumerate the known results which we shall use in this article. Several of these results are true more generally but we shall state them as needed in this article.

1) Let $f\left(x\right)\in \mathbb{Q}\left[x\right]$ be a non-constant polynomial. Then the Galois group of f(x) over $\mathbb{Q}$ acts transitively on its roots if and only if f(x) is a power of an irreducible polynomial over $\mathbb{Q}$.

2) Let ${\mathbb{K}}_1/\mathbb{Q},{\mathbb{K}}_2/\mathbb{Q}$ be finite normal extensions that is, splitting fields of some polynomial. Let ${\mathbb{K}}_1{\mathbb{K}}_2$ denote the compositum of the fields ${\mathbb{K}}_1,{\mathbb{K}}_2$ , that is, the smallest subfield of containing ${\mathbb{K}}_1,{\mathbb{K}}_2$. Then $\mathbb{K}$ is a normal extension of $\mathbb{Q}$ and if $\left[{\mathbb{K}}_1:\mathbb{Q}\right]$ and $\left[{\mathbb{K}}_2:\mathbb{Q}\right]$ are coprime. Then

$Aut\left(\mathbb{K}/\mathbb{Q}\right)=Aut\left({\mathbb{K}}_1/\mathbb{Q}\right)\times Aut\left({\mathbb{K}}_2/\mathbb{Q}\right)$

3) Every finite solvable group can be realized as a Galois group of some polynomials over $\mathbb{Q}$. Same is true of the symmetric groups $S_n$ and alternating groups $A_n$. We shall only need this result for cyclic groups, Frobenius groups and for the groups $S_n$ and $A_n$ [3] [4] and [5] .

4) Let $f\left(x\right)\in \mathbb{Q}\left[x\right]$ be an irreducible polynomials of degree n. Let ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n$ be its roots. Let r be an integer, $1<r<n-1$ and $C_n^r=m$. Let $f_r\left(x\right)$ denote the polynomial whose roots are all sums of r different ${\alpha }_1$. Then $f_r\left(x\right)\in \mathbb{Q}\left[x\right]$ and $f\left(x\right)$ and $f_r\left(x\right)$ have the same splitting field [6] .

5) Let $f\left(x\right)\in \mathbb{Z}\left[x\right]$ be a monic irreducible polynomial of degree n and p a prime which does not divide the discriminant of f(x). Let $G=Gal\left(f\right)$ be the Galois group of $f\left(x\right)$ over $\mathbb{Q}$. Suppose that modulo p the polynomial $f\left(x\right)$ factors into irreducible polynomials of degrees $n_1,n_2,\cdots ,n_t$ so $n_1+n_2+\cdots +n_t=n$. Then there is $\sigma \in G$ such that as a permutation on the n roots of $f\left(x\right)$ , $\sigma ={\sigma }_1{\sigma }_2\cdots {\sigma }_t$ , where ${\sigma }_i$ is acyclic permutation of length $n_i$ for $1\le i\le n$. See [7] .

6) Let N be any composite natural number and $f\left(x\right)\in \mathbb{Z}\left[x\right]$ be a monic irreducible polynomial of degree N whose Galois group over $\mathbb{Q}$ does not have any element of order N. Then $f\left(x\right)$ is reducible modulo every prime. This is an immediate consequence of (5) above.

2. Theorem and Proof

Theorem: For every composite natural number N there is a monic irreducible polynomial $f\left(x\right)\in \mathbb{Z}\left[x\right]$ of degree N which is reducible modulo every prime.

Case I N is not square-free

We write $N=p^{t}m$ where $t>1$ and p is a prime which does not divide m. Let $G_1$ be any non-cyclic group of order $p^t$ and $G_2$ a cyclic group of order m. Let $f_1\left(x\right)\in \mathbb{Z}\left[x\right]$ be an irreducible polynomial of degree $p^t$ with Galois group isomorphic to $G_1$ and $f_2\left(x\right)\in \mathbb{Z}\left[x\right]$ be an irreducible polynomial of degree m with Galois group isomorphic to $G_2$. Let ${\mathbb{K}}_1$ and ${\mathbb{K}}_2$ be splitting fields of $f_1\left(x\right)$ and $f_2\left(x\right)$ respectively. Let $\mathbb{K}={\mathbb{K}}_1{\mathbb{K}}_2$ be the compositum of the fields ${\mathbb{K}}_1$ and ${\mathbb{K}}_2$. Then $\mathbb{K}$ is of degree N over $\mathbb{Q}$ and $G=Aut\left(\mathbb{K}/\mathbb{Q}\right)$ is isomorphic to $G_1\times G_2$ and so it does not have any element of order N. Let α be any algebraic integer such that $\mathbb{K}=\mathbb{Q}\left(\backslash \alpha \right)$. Let $f\left(x\right)$ be the minimum polynomial of α. Then $f\left(x\right)\in \mathbb{Z}\left[x\right]$ is a monic irreducible polynomial of degree N and its Galois group does not have any element of order N and therefore $f\left(x\right)$ has the desired property.

Case II N is square-free and gcd(N, φ(N)) > 1

In this case we can write $N=pqm$ where p, q are primes, p divides $q-1$ and $\gcd \left(pq,m\right)=1$. Let $G_1$ be a non-abelian group of order pq and $G_2$ a cyclic group of order m. Just as in the previous case we get a monic irreducible polynomial in $\mathbb{Z}\left[x\right]$ of degree N whose Galois group does not contain an elementof order N.

Case III, N is square-free and gcd(N, φ(N)) = 1

In this case N is necessarily odd. First we assume that N is a product of just two primes. So let $N=pq$ , where p and q are distinct primes, $p<q$ and p does not divide $q-1$. Let t be the order of p modulo q. So $t>1$ is the smallest integer such that $p^t\equiv 1\left(\mathrm{mod}q\right)$. Let $G_1$ be an elementary Abelian p-group of order $p^t$ and $G_2$ be a group of order q. We note that $Aut\left(G_1\right)$ is isomorphic to $GL\left(t,p\right)$ and so its order is divisible by q. Let $G=G_1\times G_2$ be the semi-direct product of $G_1$ by $G_2$. Evidently G is not a direct product of $G_1$ and $G_2$. Therefore $G_2$ is not a normal subgroup of G. We claim that $G_2$ is its own normalizer in G. For otherwisethe index of the normalizer of $G_2$ in G would be $p^r$ , for some r, 1 ≤ r < t which would contradict the fact that t is the smallest integer satisfying $p^t\equiv 1\left(\mathrm{mod}q\right)$. Since $G_2$ has prime order q it is disjoint from its conjugates. Therefore G is a Frobenius group of order $p^t,q$ and every non-identity element of $G_2$ induces a fixed-point-free automorphism of $G_1$.

Let $\mathbb{K}$ be a normal extension of $\mathbb{Q}$ with Galois group isomorphic to G. Then $\left[\mathbb{K}:\mathbb{Q}\right]=p^{t}q$. Let H be a subgroup of G of order $p^{t-1}$ and let $\mathbb{F}\subseteq \mathbb{K}$ be its fixed subfield.

Then by FTGT ({Fundamental Theorem of Galois Theory}) the field $\mathbb{F}$ is of degree pq over $\mathbb{Q}$. We also note that as H is not a normal subgroup of G, $\mathbb{F}$ is not a normal extension of $\mathbb{Q}$. Let α be an algebraic integer such that $\mathbb{F}=\mathbb{Q}\left(\alpha \right)$ and let $f\left(x\right)$ be its minimal polynomial over $\mathbb{Q}$. Then $f\left(x\right)\in \mathbb{Z}\left[x\right]$ is irreducible of degree pq.

We claim that $\mathbb{K}$ is the splitting field of $f\left(x\right)$ (i.e. it is the normal closure of the field $\mathbb{F}$ ) and G is its Galois group over $\mathbb{Q}$.

If the normal closure of $\mathbb{F}$ were a proper subfield of $\mathbb{K}$ then it would imply that G has a proper normal subgroup of order $p^r$ where $r<t$ , but this is not possible, as G is a Frobenius group. So $f\left(x\right)\in \mathbb{Z}\left[x\right]$ is a monic irreducible polynomials of degree $N=pq$ and its Galois group over $\mathbb{Q}$ does not have any element of order $N=pq$.

Finally assume that N and $\phi \left(N\right)$ are coprime and N is a product of more than two primes. We write $N=pqm$ , where p, q are primes and $\gcd \left(pq,m\right)=1$. Let t = order of p modulo q. As discussed in the previous case let $f_1\left(x\right)\in \mathbb{Z}\left[x\right]$ be a monic irreducible polynomial of degree pq whose Galois group is the semi-direct product of an elementary group of order $p^t$ by a cyclic group of order q and is a Frobenius group.

Let $G_1$ denote this Frobenius group of order $p^{t}q$ and ${\mathbb{K}}_1$ denote the splitting field of $f_1\left(x\right)$. Let $G_2$ be a cyclic group of order m and $f_2\left(x\right)\in \mathbb{Z}\left[x\right]$ be a monic irreducible polynomialof degree m whose splitting field is ${\mathbb{K}}_2$ and Galois group over $\mathbb{Q}$ is $G_2$.

Let $\mathbb{K}={\mathbb{K}}_1{\mathbb{K}}_2$ be the compositum of the fields ${\mathbb{K}}_1$ and ${\mathbb{K}}_2$. Let $pq=n$ and

$f_1\left(x\right)={{{\displaystyle \prod }}^{\text{}}}_{i=1}^n\left(x-{\alpha }_i\right)$

$f_2\left(x\right)={{{\displaystyle \prod }}^{\text{}}}_{j=1}^m\left(x-{\beta }_j\right)$

$f\left(x\right)={{{\displaystyle \prod }}^{\text{}}}_{j=1}^m{{{\displaystyle \prod }}^{\text{}}}_{i=1}^n\left(x-{\alpha }_i{\beta }_j\right)$

We note the following:

1) $\left[{\mathbb{K}}_1:\mathbb{Q}\right]=p^{t}q,\left[{\mathbb{K}}_2:\mathbb{Q}\right]=m,\left[\mathbb{K}:\mathbb{Q}\right]=p^{t}qm$ ;

2) ${\mathbb{K}}_1=\mathbb{Q}\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n\right)$ ;

3) ${\mathbb{K}}_2=\mathbb{Q}\left({\beta }_1,{\beta }_2,\cdots ,{\beta }_m\right)$ ;

4) $\mathbb{K}=\mathbb{Q}\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n,{\beta }_1,{\beta }_2,\cdots ,{\beta }_m\right)$ ;

5) $G=Aut\left(\mathbb{K}/\mathbb{Q}\right)$ is a group of order $p^{t}qm$ isomorphic to the direct product of aFrobenius group of order $p^{t}q$ and a cyclic group of order . Therefore it does not have an element of order $N=pqm$. Note that this Frobenius groupdoes not have any subgroup of order pq.

6) The group G transitively permutes the nm algebraic numbers ${\alpha }_i{\beta }_j,1\le i\le n,1\le j\le m$. So $f\left(x\right)\in \mathbb{Z}\left[x\right]$ is an irreducible polynomial of degree $N=pqm$ , whose Galois group does not have any element of order N. This completes the proof of our theorem.

3. Alternate Methods

As we noticed the construction of irreducible polynomials in $\mathbb{Z}\left[x\right]$ of odd composite degree N where $\gcd \left(N,\phi \left(N\right)\right)=1$ , and whose Galois group does not contain an element of order N is not so straight forward. In some case such as $N=15$ or $N=35$ there is another interesting method of construction of such polynomials. In fact it works for most N’s (with very few exceptions) which are such that $C_n^r=N$ for some n and r such that $1<r<n-1$. The method we are about to describe fails in cases where $C_n^r=N$ but the symmetric group $S_n$ does have an element of order N, as it happens when $n=15,r=2$ and $N=105$.

As the symmetric group on 15 letters does have an element of order $105=C_{15}^2$ , namely a permutation which is a product of 3, 5 and a 7-cycle. Let $f\left(x\right)\in \mathbb{Z}\left[x\right]$ be a monic irreducible polynomial of degree $n>4$ whose Galois group is isomorphic to either $A_n$ or $S_n$. Let r be such that $1<r<n-1$ and $C_n^r=N$. Further assume that $S_n$ does not have any element order N. We know that $S_n$ is n-transitive and $A_n$ is $\left(n-2\right)$ -transitive on n letters. Let $f_r\left(x\right)$ denote a polynomial of degree $N=C_n^r$ whose roots are sum of all r different roots of $f\left(x\right)$. Let the roots of $f_r\left(x\right)$ be ${\beta }_i$ , where 1 ≤ i ≤ N. The polynomials $f\left(x\right)$ and let $f_r\left(x\right)$ have the same splitting field. Since both $S_n$. and $A_n$ transitively permute the N, roots of Let $f_r\left(x\right)$ this polynomial is irreducible. So the polynomial let $f_r\left(x\right)$ is the required polynomial of degree N, whose Galois group does not have any element of order N.

4. Examples

1) The first interesting case is for $N=15$. Let $f\left(x\right)\in \mathbb{Z}\left[x\right]$ be an irreduciblemonic polynomial of degree six whose Galois group over $\mathbb{Q}$ is isomorphic to symmetric oralternating group on five or six letters. Then $f_2\left(x\right)\in \mathbb{Z}\left[x\right]$ is an irreducible monic polynomial whose Galois group is the same as that of $f\left(x\right)$ and so does not have any element of order 15. Therefore $f_2\left(x\right)$ is reducible modulo every prime. For instance let $f\left(x\right)=x^6+24x-20$ whose discriminant is $2^{16}\cdot 3^6\cdot 5^6$. We note that

$f\left(x\right)\equiv \left(x+3\right)\left(x^5+4x^4+2x^3+x^2+4x+5\right)\left(\mathrm{mod}7\right)$

$f\left(x\right)\equiv \left(x+7\right)\left(x+12\right)\left(x+21\right)\left(x^3+6x^2+13x+16\right)\left(\mathrm{mod}23\right)$

$f\left(x\right)\equiv \left(x^2+26x+10\right)\left(x^4+3x^3+28x^2+25x+27\right)\left(\mathrm{mod}29\right)$

It follows that $f\left(x\right)$ is irreducible over 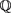and its Galois group G over 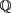is 2-transitive on its roots and has a 3-cycle. Therefore G is isomorphic to 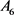the alternating group on six letters [8] . We know that 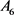is 4-transitive on six letters. Let 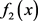represent the polynomial of degree 15 whose 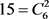roots are the sumsof the roots of 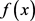taken two at a time. This polynomial turns out to be

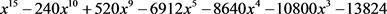
The Galois group of this polynomial is the same as that of 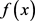and so is isomorphic to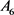. As 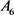has no element of order 15 this polynomial is reducible modulo every prime.

2) The second example is for. As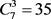, we start with a some monic polynomial 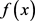of degree 7 with Galois group isomorphic to or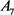. The polynomial of degree 35 whose roots are the sums of three different roots of is the required polynomial whose Galois group (being isomorphic to or) does not have any element of order 35. To illustrate this we begin with the polynomial of degree 7. We observe that the discriminant of the polynomial is and is irreducible modulo 5. Also

So is an irreducible polynomial of degree 7 whose discriminant is a square and Galois group G has a 3-cycle. So G is isomorphic to [8] .

Suppose that the roots of are. The polynomial of degree whose roots are, is

This polynomial is irreducible over. As its Galois group is isomorphic to which does not have any element of order 21 this polynomial is reducible modulo every prime.

The polynomial of degree whose roots are , is

This polynomial is irreducible over and its Galois group is isomorphic to. As does not have any element of order 35 this polynomial is reducible modulo every prime. Its discriminant is the following 311-digit number

Note: The composite natural numbers N below 100 which are such that are

Among these numbers the method described above works for N = 15, 35 and 91. This is so because, , and. As starting with a polynomial of degree 7 with Galois group isomorphic to or, we constructed an irreducible polynomial of degree 35 which is reducible modulo every prime, likewise starting with a polynomial of degree14 with Galois group isomorphic to or we can construct an irreducible polynomial of degree 91 which is reducible modulo every prime.

3) The method discussed in the previous examples above does not work for. For this we proceed as in the proof of our theorem. As the order of 11 modulo 3 is 2 we construct a Frobenius group G of order which is a semi-direct product of by a group of order 3. More specifically we extend the group by the group of order three where is the automorphism of given by. It is easily seen that this automorphism has order three and is fixed-point-free.The resulting group, the semi-direct product of by is a Frobenius group of order 363 having the subgroup as its kernel and the group as its complement.

This Frobenius group of order 363 does not have any subgroup of order 33. Let be a normal extension whose Galois group is isomorphic to G.

Let H be a subgroup of G of order 11 and be its fixed subfield. By FTGT (Fundamental Theorem of Galois Theory) the field has degree 33 over. Let α be an algebraic integer such that and let be its minimum polynomial. As proved in the theorem this polynomial has degree 33 and its Galois group is a Frobenius group of order which does not have any subgroup of order 33 andtherefore the irreducible polynomials is reducible modulo every prime.

5. Construction of the Polynomials

It remains to be seen that given a degree n polynomial how we can compute the polynomial, for. This can be done with thehelp of the concept of the resultant of two polynomials. Let

be polynomials of degree and respectively (so) with coefficients in a field. Let be the zeros of and in some extension of. Writing and as simply f and g, and resultant simply as Res we have

As this resultant is equal to the following determinant of order, its value can be computed with the help of any symbolic computation package such as MATHEMATICA.

In this determinant all the missing entries are zeros. The entries in the first m rows are the coefficients of and those in the last n rows are the coefficients of. If f and g are polynomials in two variables x and y then we can determine their resultant with respect to any of the variable. For the discussion of the calculation of for a given polynomial it will be convenient to deal with monic polynomials. Let be a polynomial of degree n with zeros. The polynomial can be regarded as a monic polynomial of degree n in y with coefficientsin the polynomial ring. As a polynomial in y its n zeros are. We note that

This observation and (and similar ones) will be used repeatedly in what follows. As before we let denote the monic polynomial of degree with zeros where.

We shall show how to find for. The method discussed can be easily generalized to larger values of r.

5.1. Computation of f₂(x)

Let

Then is a polynomial of degree with zeros. So the zeros of are and, each appearing twice. Let

Then is a monic polynomial of degree n with zeros. Therefore, is a polynomial of degree, with zeros, each zeroappearing twice. Therefore,

is a polynomial of degree with zeros.

5.2. Computation of f₃(x)

We first note that, as a polynomial in y, has degree and has roots for. In other words we can write

Let

Then is a polynomial of degree whose zeros are of following types.

, each appearing three times.

We check that the total number adds up to the right degree, namely

We shall now find a polynomial with zeros. Let

Here as before we have multiplied by to ensure that the first polynomial in the argument of is monic. We note that as a polynomial in y the roots of are, for. Also is a polynomial of degree. In fact

So the zeros of are and. Let

So is a monic polynomial with zeros and is a monic polynomial of degree with zeros,. We also note that

is a polynomial of degree with zeros, each repeated three times. Therefore

is the required polynomial of degree.

6. Addendum

Bernard Dominique [9] sent us a list of following eighteen irreducible polynomials of degree 33 and informed us that these are reducible for all primes.

If the Galois group of any of these polynomials regarded as a permutation on its 33 roots had a 33-cycle then according to Cebotarev Density Theorem the density of primes p for which any of these polynomials is irreducible should be [10] . As there is no such prime we believe that these polynomials are reducible for all primes. However, in the absence of any information about their Galois group we do not have a proof that any of these polynomials is locally reducible for all primes.

7. Conclusion

In this paper we have shown that for any composite natural number N there are polynomials of degree N with integer coefficients which are irreducible in but which are reducible modulo p for every prime p and we have given method of construction of such polynomials for various values of N.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

Cite this paper

Gupta, S. (2019) Irreducible Polynomials in ℤ[x] That Are Reducible Modulo All Primes. Open Journal of Discrete Mathematics, 9, 52-61. https://doi.org/10.4236/ojdm.2019.92006

References