ABSTRACT

It is hard to compute the competition number for a graph in general and characterizing a graph by its competition number has been one of important research problems in the study of competition graphs. Sano pointed out that it would be interesting to compute the competition numbers of some triangulations of a sphere as he got the exact value of the competition numbers of regular polyhedra. In this paper, we study the competition numbers of several kinds of triangulations of a sphere, and get the exact values of the competition numbers of a 24-hedron obtained from a hexahedron by adding a vertex in each face of the hexahedron and joining the vertex added in a face with the four vertices of the face, a class of dodecahedra constructed from a hexahedron by adding a diagonal in each face of the hexahedron, and a triangulation of a sphere with $3n\left(n\ge 2\right)$ vertices.

Keywords:

Competition Graph, Competition Number, Edge Clique Cover, Vertex Clique Cover, Triangulation of a Sphere

1. Introduction and Preliminary

Let $G=\left(V,E\right)$ be a graph in which $V$ is the vertex set and $E$ the edge set. We always use $\left|V\right|$ and $\left|E\right|$ to denote the vertex number and the edge number of $G$ , respectively. The notion of competition graph was introduced by Cohen [1] in connection with a problem in ecology. Let $D=\left(V,A\right)$ be a digraph in which $V$ is the vertex set and $A$ the set of directed arcs. The competition graph $C\left(D\right)$ of $D$ is the undirected graph $G$ with the same vertex set as $D$ and with an edge $uv\in E\left(G\right)$ if and only if there exists some vertex $x\in V\left(D\right)$ such that $\left(u,x\right),\left(v,x\right)\in A\left(D\right)$ . We say that a graph $G$ is a com- petition graph if there exists a digraph $D$ such that $C\left(D\right)=G$ .

Roberts [2] observed that every graph together with sufficiently many isolated vertices is the competition graph of an acyclic digraph. The competition number $k\left(G\right)$ of a graph $G$ is defined to be the smallest number $k$ such that $G$ together with $k$ isolated vertices added is the competition graph of an acyclic digraph. It is difficult to compute the competition number of a graph in general as Opsut [3] has shown that the computation of the competition number of a graph is an NP-hard problem. But it has been one of important research problems in the study of competition graphs to characterize a graph by its competition number. Recently, many papers related to graphs’ competition numbers have appeared. Kim, et al., [4] studied the competition numbers of connected graphs with exactly one or two triangles. Sano [5] studied the competition numbers of regular polyhedra. Kim, et al., [6] studied the competition numbers of Johnson graphs. Park and Sano [7] [8] studied the competition numbers of some kind of Hamming graphs. Kim, et al., [9] studied the competition numbers of the complement of a cycle. Furthermore, there are some papers (see [10] [11] [12] [13] [14] ) focused on the competition numbers of the complete multipartite graphs, and some papers (see [15] - [23] ) concentrated on the relationship between the competition number and the number of holes of a graph. A cycle of length at least 4 of a graph as an induced subgraph is called a hole of the graph. We use $I_r$ to denote the graph consisting only of $r$ isolated vertices, and $G\cup I_r$ the disjoint union of $G$ and $I_r$ . The induced subgraph $G\left[S\right]$ of $G$ is a subgraph of $G$ whose vertex set is $S$ and whose edge set is the set of those edges of $G$ that have both ends in $S$ .

All graphs considered in this paper are simple and connected. For a vertex $v$ in a graph $G$ , let the open neighborhood of $v$ be defined by

$N_G\left(v\right)=\left\{u|u\text{isadjacentto}v\right\}$ . For any set $U$ of vertices in $G$ , we define the neighborhood of $U$ in $G$ to be the set of all vertices adjacent to vertices in $U$ , this set is denoted by $N_G\left(U\right)$ . Let $N_G\left[U\right]=N_G\left(U\right)\cup U$ and

$E_G\left[U\right]=\left\{e\in E\left(G\right)|e\text{hasanendpointin}U\right\}$ . We denote by the same symbol $N_G\left[U\right]$ the subgraph of $G$ induced by $N_G\left[U\right]$ . Note that $E_G\left[U\right]$ is con- tained in the edge set of the subgraph $N_G\left[U\right]$ .

A subset $U$ of the vertex set of a graph $G$ is called a clique of $G$ if $G\left[U\right]$ is a complete graph. For a clique $U$ of a graph $G$ and an edge $e$ of $G$ , we say $e$ is covered by $U$ if both of the endpoints of $e$ are contained in $U$ . An edge clique cover of a graph $G$ is a family of cliques such that each edge of $G$ is covered by some clique in the family. The edge clique cover number ${\theta }_e\left(G\right)$ of a graph $G$ is the minimum size of an edge clique cover of $G$ . A vertex clique cover of a graph $G$ is a family of cliques such that each vertex of $G$ is contained in some clique in the family. The vertex clique cover number ${\theta }_v\left(G\right)$ of a graph $G$ is the minimum size of a vertex clique cover of $G$ .

Let $G$ be a graph and $F\subseteq E\left(G\right)$ be a subset of the edge set of $G$ . An edge clique cover of $F$ in $G$ is a family of cliques of $G$ such that each edge in $F$ is covered by some clique in the family. The edge clique cover number ${\theta }_e\left(F;G\right)$ of $F\subseteq E\left(G\right)$ in $G$ is defined as the minimum size of an edge clique cover of $F$ in $G$ , i.e.,

${\theta }_e\left(F;G\right)=\min \left\{\left|U\right||U\text{isanedgecliquecoverof}F\text{in}G\right\}.$ Note that the edge clique cover number ${\theta }_e\left(E\left(G\right);G\right)$ of $E\left(G\right)$ in a graph $G$ is equal to the edge clique cover number ${\theta }_e\left(G\right)$ of the graph $G$ .

Opsut [3] gave the following two lower bounds for the competition number of a graph.

Theorem 1 (Opsut [3] ). For any graph $G$ , $k\left(G\right)\ge {\theta }_e\left(G\right)-\left|V\left(G\right)\right|+2$ .

Theorem 2 (Opsut [3] ). For any graph $G$ , $k\left(G\right)\ge \min \left\{{\theta }_v\left(N_G\left(v\right)\right)|v\in V\left(G\right)\right\}$ .

Recently, Sano [24] gave a generalization of the above two lower bounds as follows:

Theorem 3 (Sano [24] ). Let $G=\left(V,E\right)$ be a graph. Let $m$ be an integer such that $1\le m\le \left|V\right|$ . Then

$k\left(G\right)\ge \underset{U\in \left(\begin{array}{c}V\\ m\end{array}\right)}{\min }{\theta }_e\left(E_G\left[U\right];N_G\left[U\right]\right)-m+1,$

where $\left(\begin{array}{c}V\\ m\end{array}\right)$ denotes the set of all $m$ -subsets of $V$ .

The following results from [25] will be used in this paper.

Theorem 4 (Harary et al. [25] ). Let $D=\left(V,A\right)$ be a digraph. Then $D$ is acyclic if and only if there exists an ordering of vertices, $\sigma =\left[v_1,v_2,\cdots ,v_n\right]$ , such that one of the following two conditions holds:

1) For all $i,j\in \left\{1,2,\cdots ,n\right\}$ , $\left(v_i,v_j\right)\in A$ implies that $i<j$ ;

2) For all $i,j\in \left\{1,2,\cdots ,n\right\}$ , $\left(v_i,v_j\right)\in A$ implies that $i>j$ .

Sano [5] pointed out that it would be interesting to compute the competition numbers of some triangulations of a sphere as he obtained the exact value of the competition numbers of regular polyhedra. In this paper we try to study the competition numbers of several kinds of triangulations of a sphere. In Section 2, we study the competition number of a 24-hedron constructed from a hexahedron by adding a vertex in each face of the hexahedron and joining the vertex added in a face with the four vertices of the face. In Section 3, we study the competition numbers of a class of dodecahedra obtained from a hexahedron by adding a diagonal in each face of the hexahedron. In Section 4, we study the competition number of a triangulation of a sphere with $3n\left(n\ge 2\right)$ vertices.

In the following, “ $S\to v$ ” means that we make an arc from each vertex in $S$ to the vertex $v$ .

2. A 24-Hedron

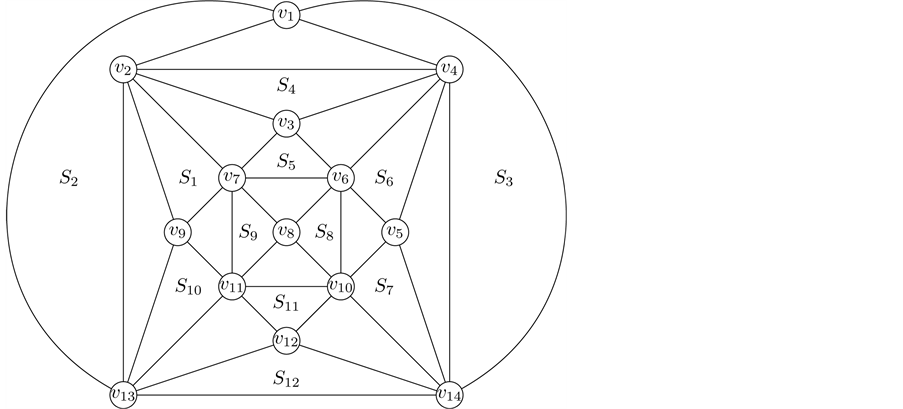
In this section we study the competition number of a 24-hedron obtained from a hexahedron by adding a vertex in each face of the hexahedron and joining the vertex added in a face with the four vertices of the face. See Figure 1.

Theorem 5. Let $\mathbb{T}$ be the 24-hedron shown in Figure 1(b). Then $k\left(\mathbb{T}\right)=3$ .

Proof. Let $V\left(\mathbb{T}\right)=\left\{v_1,v_2,\cdots ,v_{14}\right\}$ and suppose that the adjacencies between two vertices are given as Figure 2. Let

$\begin{array}{l}{S}_1=\left\{v_2,v_7,v_9\right\},S_2=\left\{v_1,v_2,v_{13}\right\},S_3=\left\{v_1,v_4,v_{14}\right\},S_4=\left\{v_2,v_3,v_4\right\},\\ S_5=\left\{v_3,v_6,v_7\right\},S_6=\left\{v_4,v_5,v_6\right\},S_7=\left\{v_5,v_{10},v_{14}\right\},S_8=\left\{v_6,v_8,v_{10}\right\},\\ S_9=\left\{v_7,v_8,v_{11}\right\},S_{10}=\left\{v_9,v_{11},v_{13}\right\},S_{11}=\left\{v_{10},v_{11},v_{12}\right\},S_{12}=\left\{v_{12},v_{13},v_{14}\right\}.\end{array}$

Then the family $\left\{S_1,S_2,\cdots ,S_{12}\right\}$ is an edge clique cover of $\mathbb{T}$ .

Now, we define a digraph $D$ as follows. Let

$V\left(D\right)=V\left(\mathbb{T}\right)\cup \left\{a,b,c\right\},$

$\begin{array}{l}{S}_1\to a,S_2\to b,S_3\to c,S_4\to v_1,S_5\to v_2,S_6\to v_3,\\ S_7\to v_4,S_8\to v_5,S_9\to v_6,S_{10}\to v_7,S_{11}\to v_8,S_{12}\to v_9,\end{array}$

where $a,b$ and $c$ are new added vertices. Then by Theorem 4 the digraph $D$ is acyclic and $C\left(D\right)=\mathbb{T}\cup \left\{a,b,c\right\}$ . Hence we have

$k\left(\mathbb{T}\right)\le 3.$ (1)

On the other hand, by Theorem 3 with $m=2$ , we have

$k\left(\mathbb{T}\right)\ge \underset{U\in \left(\begin{array}{c}V\\ 2\end{array}\right)}{\min }{\theta }_e\left(E_{\mathbb{T}}\left[U\right];N_{\mathbb{T}}\left[U\right]\right)-1.$

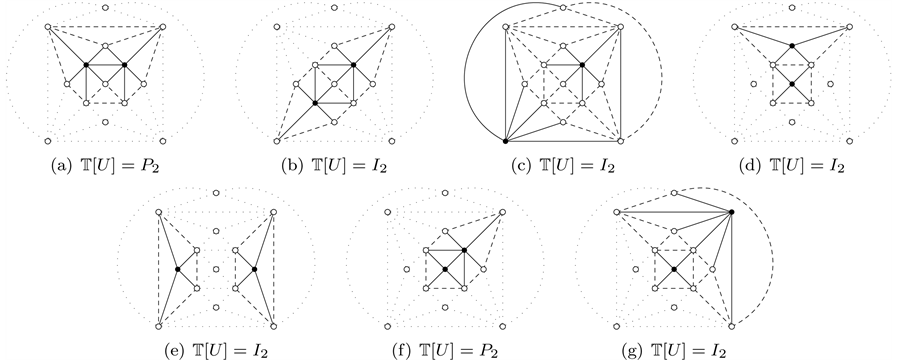
There are 7 different cases for the set $E_{\mathbb{T}}\left[U\right]$ of edges in the subgraph

$N_{\mathbb{T}}\left[U\right]$ , where $U\in \left(\begin{array}{c}V\\ 2\end{array}\right)$ (see Figure 3):

1) If $\mathbb{T}\left[U\right]=P_2$ , then ${\theta }_e\left(E_{\mathbb{T}}\left[U\right];N_{\mathbb{T}}\left[U\right]\right)=5;$

2) If $\mathbb{T}\left[U\right]=I_2$ , then ${\theta }_e\left(E_{\mathbb{T}}\left[U\right];N_{\mathbb{T}}\left[U\right]\right)=6;$

3) If $\mathbb{T}\left[U\right]=I_2$ , then ${\theta }_e\left(E_{\mathbb{T}}\left[U\right];N_{\mathbb{T}}\left[U\right]\right)=6;$

4) If $\mathbb{T}\left[U\right]=I_2$ , then ${\theta }_e\left(E_{\mathbb{T}}\left[U\right];N_{\mathbb{T}}\left[U\right]\right)=4;$

5) If $\mathbb{T}\left[U\right]=I_2$ , then ${\theta }_e\left(E_{\mathbb{T}}\left[U\right];N_{\mathbb{T}}\left[U\right]\right)=4;$

6) If $\mathbb{T}\left[U\right]=P_2$ , then ${\theta }_e\left(E_{\mathbb{T}}\left[U\right];N_{\mathbb{T}}\left[U\right]\right)=4;$

7) If $\mathbb{T}\left[U\right]=I_2$ , then ${\theta }_e\left(E_{\mathbb{T}}\left[U\right];N_{\mathbb{T}}\left[U\right]\right)=5.$

Thus it holds that

$\underset{U\in \left(\begin{array}{c}V\\ 2\end{array}\right)}{\min }{\theta }_e\left(E_{\mathbb{T}}\left[U\right];N_{\mathbb{T}}\left[U\right]\right)=4.$

Hence we have

$k\left(\mathbb{T}\right)\ge 3.$ (2)

Combining inequalities (1) and (2) we have $k\left(\mathbb{T}\right)=3$ .

3. A Class of Dodecahedra

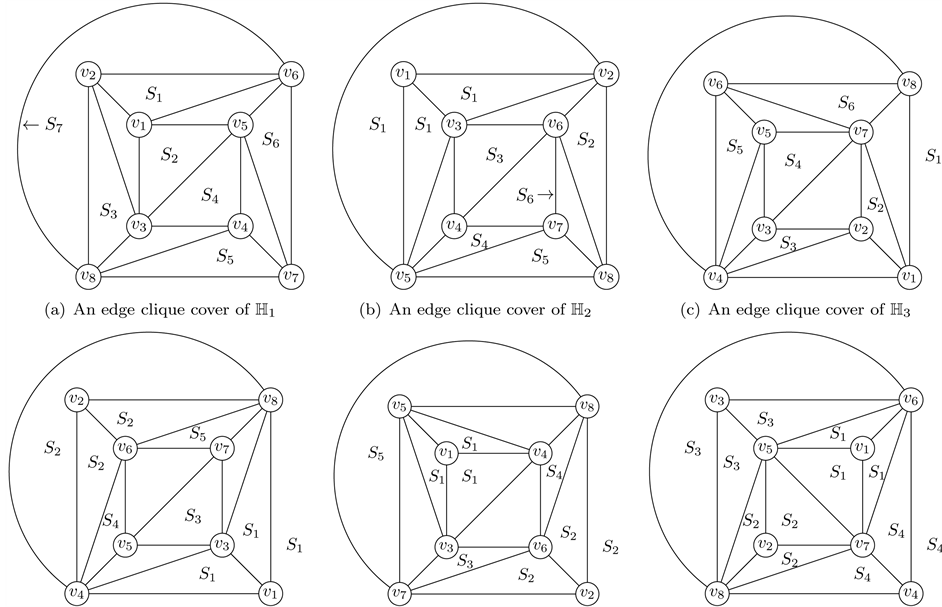
In this section we study the competition numbers of a class of dodecahedra constructed from a hexahedron by adding a diagonal in each face of the hexahedron. It is not difficult to see that there are 6 nonisomorphic such dodecahedra. Denote the 6 different dodecahedra by ${ℍ}_1$ , ${ℍ}_2$ , ${ℍ}_3$ , ${ℍ}_4$ , ${ℍ}_5$ and ${ℍ}_6$ , respectively. See Figure 4.

Theorem 6. $k\left({ℍ}_i\right)=\{\begin{array}{ll}2,\hfill & i=1,3;\hfill \\ 1,\hfill & i=2,4,5,6.\hfill \end{array}$

Proof. Let $V\left({ℍ}_i\right)=\left\{v_1,v_2,\cdots ,v_8\right\}$ and suppose that the adjacencies between two vertices are given as Figure 5, where $i=1,2,\cdots ,6$ . Now we define digraphs $D_1,D_2,\cdots ,D_6$ , respectively.

1) $D_1$ .

Let $V\left(D_1\right)=V\left({ℍ}_1\right)\cup \left\{a_1,b_1\right\}$ , and $A\left(D_1\right)$ be defined as follows:

$\begin{array}{l}{S}_1=\left\{v_1,v_2,v_6\right\}\to a_1,S_2=\left\{v_1,v_3,v_5\right\}\to b_1,S_3=\left\{v_2,v_3,v_8\right\}\to v_1,\\ S_4=\left\{v_3,v_4,v_5\right\}\to v_2,S_5=\left\{v_4,v_7,v_8\right\}\to v_3,S_6=\left\{v_5,v_6,v_7\right\}\to v_4,\\ S_7=\left\{v_6,v_8\right\}\to v_5,\end{array}$

where $a_1$ and $b_1$ are new added vertices. Note that the family $\left\{S_1,S_2,\cdots ,S_7\right\}$ is an edge clique cover of ${ℍ}_1$ .

2) $D_2$ .

Let $V\left(D_2\right)=V\left({ℍ}_2\right)\cup \left\{a_2\right\}$ , and $A\left(D_2\right)$ be defined as follows:

$\begin{array}{l}{S}_1=\left\{v_1,v_2,v_3,v_5\right\}\to a_2,S_2=\left\{v_2,v_6,v_8\right\}\to v_1,S_3=\left\{v_3,v_4,v_6\right\}\to v_2,\\ S_4=\left\{v_4,v_5,v_7\right\}\to v_3,S_5=\left\{v_5,v_7,v_8\right\}\to v_4,S_6=\left\{v_6,v_7\right\}\to v_5,\end{array}$

where $a_2$ is a new added vertex. Note that the family $\left\{S_1,S_2,\cdots ,S_6\right\}$ is an edge clique cover of ${ℍ}_2$ .

3) $D_3$ .

Let $V\left(D_3\right)=V\left({ℍ}_3\right)\cup \left\{a_3,b_3\right\}$ , and $A\left(D_3\right)$ be defined as follows:

$\begin{array}{l}{S}_1=\left\{v_1,v_4,v_8\right\}\to a_3,S_2=\left\{v_1,v_2,v_7\right\}\to b_3,S_3=\left\{v_2,v_3,v_4\right\}\to v_1,\\ S_4=\left\{v_3,v_5,v_7\right\}\to v_2,S_5=\left\{v_4,v_5,v_6\right\}\to v_3,S_6=\left\{v_6,v_7,v_8\right\}\to v_4,\end{array}$

where $a_3$ and $b_3$ are new added vertices. Note that the family $\left\{S_1,S_2,\cdots ,S_6\right\}$ is an edge clique cover of ${ℍ}_3$ .

4) $D_4$ .

Let $V\left(D_4\right)=V\left({ℍ}_4\right)\cup \left\{a_4\right\}$ , and $A\left(D_4\right)$ be defined as follows:

$\begin{array}{l}{S}_1=\left\{v_1,v_3,v_4,v_8\right\}\to a_4,S_2=\left\{v_2,v_4,v_6,v_8\right\}\to v_1,S_3=\left\{v_3,v_5,v_7\right\}\to v_2,\\ S_4=\left\{v_4,v_5,v_6\right\}\to v_3,S_5=\left\{v_6,v_7,v_8\right\}\to v_4.\end{array}$

where $a_4$ is a new added vertex. Note that the family $\left\{S_1,S_2,\cdots ,S_5\right\}$ is an edge clique cover of ${ℍ}_4$ .

5) $D_5$ .

Let $V\left(D_5\right)=V\left({ℍ}_5\right)\cup \left\{a_5\right\}$ , and $A\left(D_5\right)$ be defined as follows:

$\begin{array}{l}{S}_1=\left\{v_1,v_3,v_4,v_5\right\}\to a_5,S_2=\left\{v_2,v_6,v_7,v_8\right\}\to v_1,S_3=\left\{v_3,v_6,v_7\right\}\to v_2,\\ S_4=\left\{v_4,v_6,v_8\right\}\to v_3,S_5=\left\{v_5,v_7,v_8\right\}\to v_4,\end{array}$

where $a_5$ is a new added vertex. Note that the family $\left\{S_1,S_2,\cdots ,S_5\right\}$ is an edge clique cover of ${ℍ}_5$ .

6) $D_6$ .

Let $V\left(D_6\right)=V\left({ℍ}_6\right)\cup \left\{a_6\right\}$ , and $A\left(D_6\right)$ be defined as follows:

$\begin{array}{l}{S}_1=\left\{v_1,v_5,v_6,v_7\right\}\to a,S_2=\left\{v_2,v_5,v_7,v_8\right\}\to v_1,S_3=\left\{v_3,v_5,v_6,v_8\right\}\to v_2,\\ S_4=\left\{v_4,v_6,v_7,v_8\right\}\to v_3,\end{array}$

where $a_6$ is a new added vertex. Note that the family $\left\{S_1,S_2,S_3,S_4\right\}$ is an edge clique cover of ${ℍ}_6$ .

By Theorem 4, each $D_i$ is acyclic and

$C\left(D_i\right)=\{\begin{array}{ll}{ℍ}_i\cup \left\{a_i,b_i\right\},\hfill & i=1,3;\hfill \\ {ℍ}_i\cup \left\{a_i\right\},\hfill & i=2,4,5,6.\hfill \end{array}$

Hence we have

$k\left({ℍ}_i\right)\{\begin{array}{ll}\le 2,\hfill & i=1,3;\hfill \\ \le 1,\hfill & i=2,4,5,6.\hfill \end{array}$ (3)

On the other hand, we note that

・ $\delta \left({ℍ}_1\right)=\delta \left({ℍ}_3\right)=4$ and there is no clique with more than 3 vertices in ${ℍ}_1$ and ${ℍ}_3$ , respectively;

・ $N_{{ℍ}_2}\left(v_1\right)=\left\{v_2,v_3,v_5\right\}$ is covered by the clique $S_1=\left\{v_1,v_2,v_3,v_5\right\}$ in ${ℍ}_2$ ;

・ $N_{{ℍ}_4}\left(v_1\right)=\left\{v_3,v_4,v_8\right\}$ is covered by the clique $S_1=\left\{v_1,v_3,v_4,v_8\right\}$ in ${ℍ}_4$ ;

・ $N_{{ℍ}_5}\left(v_1\right)=\left\{v_3,v_4,v_5\right\}$ is covered by the clique $S_1=\left\{v_1,v_3,v_4,v_5\right\}$ in ${ℍ}_5$ ;

・ $N_{{ℍ}_6}\left(v_1\right)=\left\{v_5,v_6,v_7\right\}$ is covered by the clique $S_1=\left\{v_1,v_5,v_6,v_7\right\}$ in ${ℍ}_6$ .

Then we have

${\theta }_v\left(N_{{ℍ}_i}\left(v\right)\right)\ge 2,v\in V\left({ℍ}_i\right),\text{where}i=1,3,$

and

${\theta }_v\left(N_{{ℍ}_i}\left(v_1\right)\right)=1,\text{where}i=2,4,5,6.$

By Theorem 2

$k\left({ℍ}_i\right)\ge \min \left\{{\theta }_v\left(N_{{ℍ}_i}\left(v\right)\right)|v\in V\left({ℍ}_i\right)\right\}\ge \{\begin{array}{ll}2,\hfill & i=1,3;\hfill \\ 1,\hfill & i=2,4,5,6.\hfill \end{array}$ (4)

Combining inequalities (3) and (4) we have

$k\left({ℍ}_i\right)=\{\begin{array}{ll}2,\hfill & i=1,3;\hfill \\ 1,\hfill & i=2,4,5,6.\hfill \end{array}$

4. Triangulation $G\left(n\right)$ of a Sphere

In this section we study a graph $G\left(n\right)=\left(V,E\right)$ with $3n\left(n\ge 2\right)$ vertices, where

$V={\displaystyle \underset{i=1}{\overset{n}{\cup }}}\left\{x_i,y_i,z_i\right\}$

and

$E={\displaystyle \underset{i=1}{\overset{n}{\cup }}}\left\{x_i{y}_i,y_i{z}_i,x_i{z}_i\right\}\cup {\displaystyle \underset{i=1}{\overset{n-1}{\cup }}}\left\{x_i{x}_{i+1},x_i{z}_{i+1},y_i{y}_{i+1},y_i{z}_{i+1},z_i{x}_{i+1},z_i{y}_{i+1}\right\}.$

An example $G\left(3\right)$ is shown in Figure 6(a). In fact, we can draw $G\left(n\right)$ in the plane by the following way. First we draw the triangles $\Delta x_i{y}_i{z}_i\left(i=1,2,\cdots ,n\right)$ such that $\Delta x_{i+1}{y}_{i+1}{z}_{i+1}$ includes $\Delta x_i{y}_i{z}_i$ , and $x_i,y_i,z_i$ are in clockwise order if $i$ is even, or in counter-clockwise order if $i$ is odd, respectively. Then we draw the other edges. It is easy to see that each face of $G\left(n\right)$ is a triangle. So for each $n\ge 2$ , $G\left(n\right)$ is a triangulation of a sphere.

Theorem 7. For each $n\ge 2$ , $k\left(G\left(n\right)\right)=2$ .

Proof. Let $\sigma$ be a vertex ordering of $G\left(n\right)$ such that $\sigma \left(x_i\right)=v_{3i-2}$ ,

$\sigma \left(y_i\right)=v_{3i-1}$ and $\sigma \left(z_i\right)=v_{3i}$ , where $i=1,2,\cdots ,n$ . Let

$\begin{array}{l}{S}_1=\left\{v_1,v_2,v_3\right\},\\ S_{3i-1}=\left\{v_{3i-2},v_{3i+1},v_{3i+3}\right\},\\ S_{3i}=\left\{v_{3i-1},v_{3i+2},v_{3i+3}\right\}\text{and}\\ S_{3i+1}=\left\{v_{3i},v_{3i+1},v_{3i+2}\right\},\text{where}i=1,\cdots ,n-1.\end{array}$

Then the family $\left\{S_1,S_2,\cdots ,S_{3n-2}\right\}$ is an edge clique cover of $G\left(n\right)$ . An edge clique cover of $G\left(3\right)$ is shown in Figure 6(b).

Now, we define a digraph $D$ by the following:

$\begin{array}{l}V\left(D\right)=V\left(G\left(n\right)\right)\cup \left\{a,b\right\},\\ S_1=\left\{v_1,v_2,v_3\right\}\to v_4,\\ S_{3i-1}=\left\{v_{3i-2},v_{3i+1},v_{3i+3}\right\}\to v_{3i+4},\\ S_{3i}=\left\{v_{3i-1},v_{3i+2},v_{3i+3}\right\}\to v_{3i+5},\text{and}\\ S_{3i+1}=\left\{v_{3i},v_{3i+1},v_{3i+2}\right\}\to v_{3i+3},\text{where}i=1,\cdots ,n-1.\end{array}$

Note that $v_{3n+1}=a,v_{3n+2}=b$ are new vertices. Then by Theorem 4 the digraph $D$ is acyclic and $C\left(D\right)=G\left(n\right)\cup \left\{a,b\right\}$ . Hence we have

$k\left(G\left(n\right)\right)\le 2.$ (5)

On the other hand, since $\delta \left(G\left(n\right)\right)=4$ and there is no clique with more than 3 vertices in $G\left(n\right)$ , then by Theorem 2

$k\left(G\left(n\right)\right)\ge \min \left\{{\theta }_v\left(N_{G\left(n\right)}\left(v\right)\right)|v\in V\left(G\left(n\right)\right)\right\}\ge 2.$ (6)

Combining inequalities (5) and (6) we have $k\left(G\left(n\right)\right)=2$ .

5. Closing Remarks

In this paper, we provide the exact values of the competition numbers of a 24-hedron, a class of dodecahedra and a triangulation of a sphere with

$3n\left(n\ge 2\right)$ vertices. It would be interesting to compute the competition numbers of some other triangulations of a sphere.

For a digraph $D=\left(V,A\right)$ , if we partition $V$ into $k$ types, then we may construct a undirected graph $C^k\left(D\right)=\left(V,E\right)$ of $D$ as follows:

1) $uv\in E$ if and only if there exists some vertex $x\in V$ such that

$\left(u,x\right),\left(v,x\right)\in A$ and $u\mathrm{,}v$ are of the same type, or

2) $uv\in E$ if and only if there exists some vertex $x\in V$ such that

$\left(u,x\right),\left(v,x\right)\in A$ and $u\mathrm{,}v$ are of different types.

It is easy to see that $C^1\left(D\right)=C\left(D\right)$ for a given digraph $D$ , and we note that multitype graphs can be used to study the multi-species in ecology and have been deeply studied (see [26] [27] ). So these generalizations of competition graphs may be more realistic and more interesting.

Acknowledgements

We thank the editor and the referee for their valuable comments. The work was supported in part by the Natural Science Foundation of Hebei Province of China under Grant A2015106045, and in part by the Institute of Applied Mathematics of Shijiazhuang University.

Cite this paper

Zhao, Y.Q., Fang, Z.M., Cui, Y.G., Ye, G.Y. and Cao, Z.J. (2017) Competition Numbers of Several Kinds of Triangulations of a Sphere. Open Journal of Discrete Mathematics, 7, 54-64. https://doi.org/10.4236/ojdm.2017.72006

References