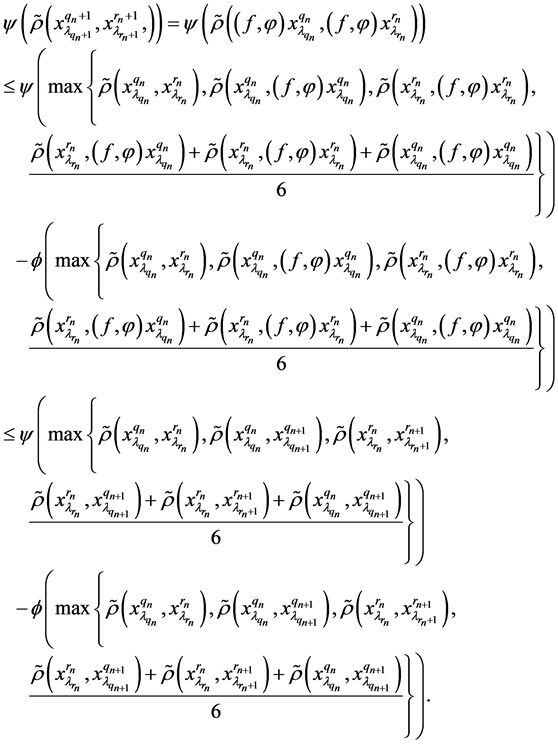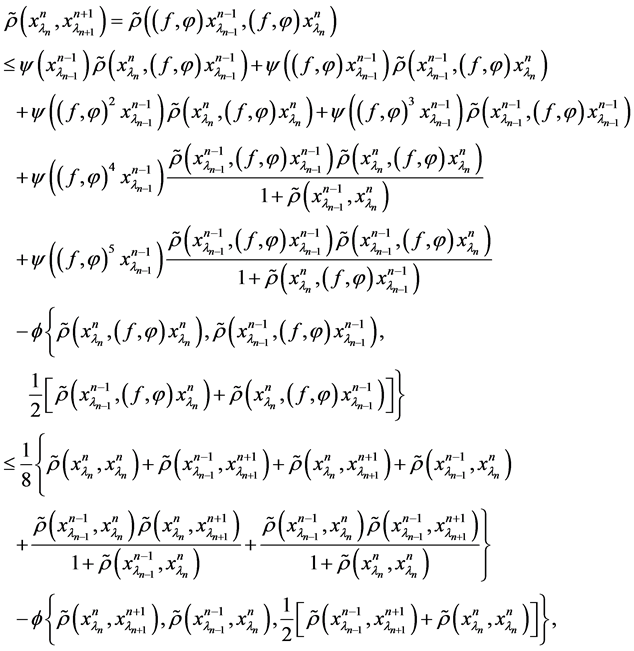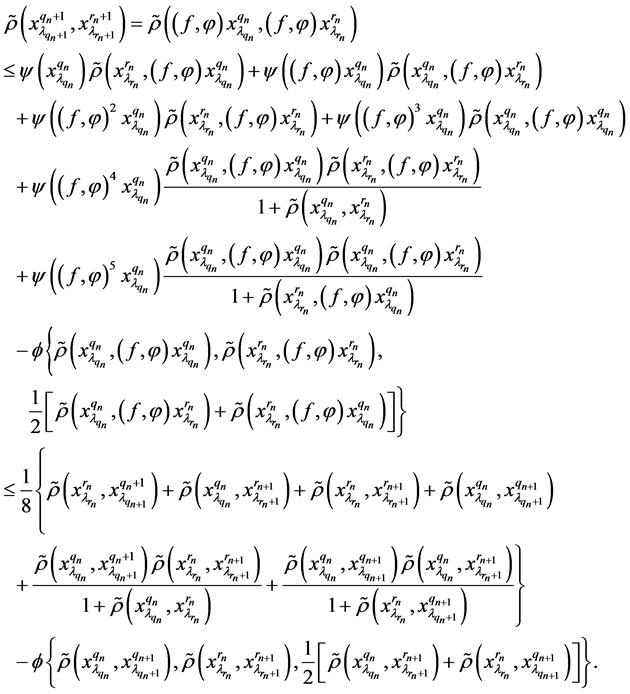Open Journal of Discrete Mathematics
Vol.07 No.03(2017), Article ID:76939,26 pages
10.4236/ojdm.2017.73012
Dislocated Soft Metric Space with Soft Fixed Point Theorems
Balaji Raghunath Wadkar1, Vishnu Narayan Mishra2,3*, Ramakant Bhardwaj4, Basant Singh1
1Department of Mathematics, AISECT University, Bhopal, India
2Applied Mathematics & Humanities Department, S.V. National Institute of Technology, Surat, India
3Department of Mathematics, Indira Gandhi National Tribal University, Amarkantak, India
4Department of Mathematics, TIT Group of Institutes, Bhopal, India
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 21, 2016; Accepted: June 13, 2017; Published: June 16, 2017
ABSTRACT
In the present paper, we define Dislocated Soft Metric Space and discuss about the existence and uniqueness of soft fixed point of a cyclic mapping in soft dislocated metric space. We also prove the unique soft fixed point theorems of a cyclic mapping in the context of dislocated soft metric space. Examples are given for support of the results.
Keywords:
Soft Set, Soft Fixed Point, Soft Point of Soft Mapping, Soft Metric Space, Dislocated Soft Metric Space

1. Introduction
The soft set theory is one of the branches of mathematics, which aims to describe phenomena and concepts of an ambiguous, undefined vague and imprecise meaning, which was initiated by Molodtsov [1] . This theory is applicable where there are no clearly defined mathematical models. Recently many papers concerning soft sets have been published (see [2] - [8] ). In many aspects of Mathematics, fixed point theory has wonderful applications. Shabir and Naz [9] presented soft topological spaces and they investigated some properties of soft topological spaces. Later many researchers were studied about soft topological spaces. In these studies, concepts of soft fixed point are expressed by different approaches. Das and Samanta [10] [11] introduced a different notion of soft metric space by using different concept of soft point and investigated some basic properties of these. In 2000, Hitzler and Seda [12] introduced the notion of dislocated metric space, in which self distance of a point need not be equal to zero. Aage and Salunke [13] established some important fixed point theorem in single and pair of mappings in dislocated metric space. Later Karapnar and Salimi [14] discussed the existence and uniqueness of fixed point of a cyclic mapping in the context of metric like space. The study of common fixed point of mapping in dislocated metric space satisfying certain contractive condition has been at the Centre of vigorous research activity (see [15] [16] [17] [18] ). Dislocated metric space plays very important role in topology, logical programming and in electronic engineering. Recently Wadkar et al. [19] , Mishra et al. [20] [21] [22] [23] , Deepmala and pathak [24] , Wadkar et al. [25] , [26] discussed and proved fixed point theorems by employing different concepts.
In the present paper, we discuss about the investigations concerning the existence and uniqueness of soft fixed point of a cyclic mapping in soft dislocated metric space. We also prove the unique soft fixed point theorems of a cyclic mapping in the context of dislocated metric space. To check the validity of the result we give the examples. Before starting to prove main result, some basic definitions are required.
Definition 1.1: Let X and E are respectively an initial inverse set and a parameter set. A soft set over X is pair denoted by (Y, E) if and only if Y is a mapping from E into the set of all subsets of the set X, i.e. Y: E → P(x), where P(x) is the power set of X.
Example of Soft Set: Let
be soft set, which describes the Nature of workers at Industry. Suppose that
, i.e. universe of four workers. Let a set of decision parameters be
. Now
stand for the parameters: high working speed, slow working speed, average working speed, work delay working speed and no working speed properly respectively.
Now consider
,
,
,
and
. By consisting of the following collection of approximations, the soft set
can be viewed.
Definition 1.2: The intersection of two soft sets
and
over X is a soft set over X denoted by
and is given by
, where
and
,
Definition 1.3: The union of two soft sets
and
over X is the soft set
, where
and for all k in C,
This relationship is denoted by
Definition 1.4: A soft set (Y, A) over X is said to be a null soft set if
, for all k in A and is denoted by
.
Definition 1.5: For all
, if
then
is called an absolute soft set over X.
Definition 1.6: The difference of two soft sets
and
over X is a soft set
over X, denoted by
and is defined as
,
.
Definition 1.7: The complement of soft set
is denoted by
and is defined as
, where
is a mapping given by
, for all
.
Definition 1.8: Let B(R) be the collection of all non-empty bounded subsets of R and E taken as a set of parameters. Then the mapping
is called a soft real set. It is denoted by (Y, E).
Definition 1.9: For two soft real numbers
and
the following conditions holds:
(i)
if
, for all
;
(ii)
if
, for all
;
(iii)
if
, for all
;
(iv)
if
, for all
.
Definition 1.10: A soft set (P, E) over X is said to have a soft point if there is exactly one
such that
, for some
, also
,
. It will be denoted by
.
Definition 1.11: Two soft points
,
are said to be equal if
and
i.e. x = y. Hence
or
.
Definition 1.12: A mapping
is soft metric on soft set
with following properties.
SM1. for all
SM2.
, if and only if
SM3. for all
SM4. for all
The soft set
with a soft metric
defined on
is called a soft metric space and denoted by
.
Definition 1.13: Let us consider a soft metric
and
be a non-negative soft real number. The soft open ball with center at
and radius
is given by
and the soft closed ball with center at
and radius
is given by
Definition 1.14: A sequence
of soft points in soft metric space
is said to be convergent in
if there is a soft point
such that
as
that is for every
there is a natural number
such that
, whenever
Definition 1.15: Let
be a soft metric space, then the sequence
of soft points in
is said to be a Cauchy sequence in
if corresponding to every
there exist
such that
i.e.
as
Definition 1.16: The soft metric space
is called complete, if every Cauchy sequence in
converges to some point of
.
Definition 1.17: Let
be a soft metric space. A function
is called a soft contraction mapping if there is a soft real number
such that for every point
we have
.
Definition 1.18: A mapping
is said to be dislocated soft metric on the soft set
if
satisfies the following conditions:
(d1)
then
(d2)
, for all
(d3)
, for all
The soft set
with soft dislocated metric
defined on
is called a dislocated soft metric space and denoted by
.
2. Main Results
Theorem 2.1: Let A and B be two non-empty closed subsets of a complete dislocated soft metric space
. Suppose
is cyclic and satisfy the following:
(c) There exist a constant
such that
for all
,
Then
has a unique soft fixed point that belongs to
.
Definition 2.2: Let
be dislocated soft metric space and U be a subset of
. We say that U is
-open subset of X if
there exists r > 0 such that
Also,
is a
-closed subset of
if
is
-open subset of
.
Lemma 2.3: Let
be dislocated soft metric space and V be a
- closed subset of X. Let
be a sequence in V. If
as
then
Proof: Let
by definition 2.2,
is a
-open set then there exist r > 0 such that
On the other hand, we have
, Since
as
So there exist
such that
for all
. Hence we conclude that
for all
. This is contradiction since
for all n in N.
Lemma 2.4: Let
be dislocated soft metric space and
be a sequence in
such that
as
and
Then
, for all
.
Lemma 2.5: If
be soft dislocated metric space, then the following conditions holds
A. If
then
B. If
be a sequence such that
then we have
C. If
then
holds for all
where
.
D. At first we define the class of Ф and Ψ by the following ways:
and
.
Definition 2.6: Let
be a soft dislocated metric space,
, let
be
-closed non empty subsets of
and let
. We say that
is a cyclic generalized
contractive mapping if
i.
is a cyclic representation of
with respect to
ii.
for all
and
or
and
(1)
for any
, where
and
Let
be a non-empty set and
be given map. The set of all soft fixed points of
will be denoted by
i.e.
.
Theorem 2.7: Let
be a complete dislocated soft metric space,
, let
be non-empty
-closed subsets of
and
let
. Suppose that
is a cyclic generalized
con-
tractive mapping. Then
has fixed point in
. Moreover if
for all
, then
has a unique fixed point in
Proof: Let
be an arbitrary point of
so there exists some
such
that
We know that
we conclude that
Thus there exist
in
such that
Recursive
where
Hence for
there exist
such that
. In case
for some
, then it is clear that
is a soft fixed point of
. Now assume that
for all n. Hence by lemma 2.5(c) we have
for all n. We shall show that the sequence
is non-in- creasing, where
. Assume that there exists some
such that
Hence we get
(2)
Set
Using conditions (1) together with (2), we get
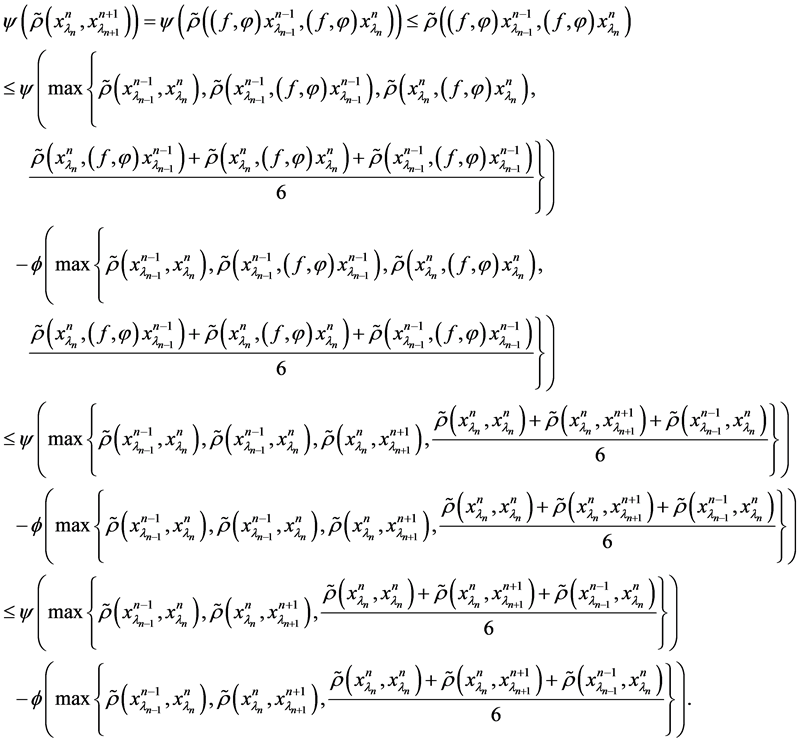 (3)
(3)
On the other hand, from lemma 2.5(D) we have
and
That is
Therefore from (3) we get
Now, if
then
.
This is contradiction. Hence we have
(4)
for all
. By taking
and
in (4) and keeping (2) in
mind, we deduce that
.
This is a contradiction. Hence we conclude that
i.e.
hold for all
. Thus there exist
such that
. We shall show that
by the method of
reductio ad absurdum. For this purpose, we assume that
. By (4) together with the property of
and
we have
.
This yields that
. This is contradiction. Hence we obtain that
. (5)
We shall show that
is a
-Cauchy sequence. To reach this goal, first we prove the followings claim:
(k) For every
there exists
such that if
with
then
.
Suppose, on the contrary that there exist
such that for any
, we can find
with
satisfying
. (6)
Now we consider
Then, corresponding to
, we can choose
in such a way that it is the smallest integer with
satisfying
and
Therefore
. By using
triangular inequality, we obtain
.
Passing to the limit as
in the last inequality and taking (5) into account, we obtain that
. (7)
Again by (d3) we derive that
Taking (5) and (7) in account we get
. (8)
By (
) we have the following inequality
(9)
and
. (10)
Letting
in (9) and (10), we have
. (11)
Again by (
) we have
(12)
and
. (13)
Letting
in (12) and (13), we derive that
. (14)
Since
and
lie in different adjacently labeled sets
and
for certain
. By using (5), (7), (8), (11) and (14) together with the fact that
is a generalized cyclic
contractive mappings, we find that
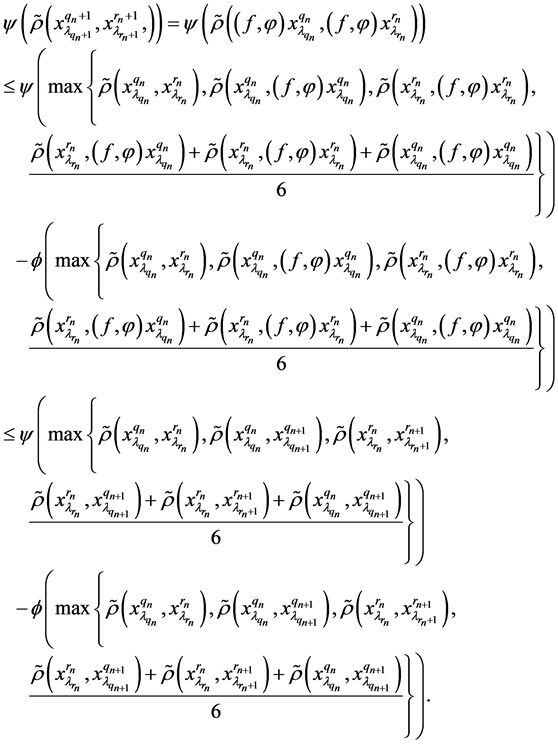
Regarding the property of
and
in the last inequality, we obtain that
, which is a contradiction. Hence the condition (k) is a satisfied. Fix
By the claim we find
such that if
with
,
. (15)
Since
, we also find
such that
(16)
for any
. Suppose that
and
. There exist
such that
Therefore
, for
So we have for
and
.
By (15) & (16) and from the last inequality, we get
.
This proves that
is a
-Cauchy sequence. Since
is arbitrary,
is a Cauchy sequence. Since Y is
-closed in
, then
is also complete, there exists
such that
in
; equivalently
. (17)
In what follows, we prove that
is a soft fixed point of
. In fact,
since
and
is a cyclic representation of Y with respect to
. The sequence
has infinite terms in each
for
. Suppose that
and we take a subsequence
of
with
(the existence of this subsequence is guaranteed by above- mentioned comment). By using the contractive condition we can obtain
Passing to the limit as
and using
, lower semi-continuity of
we have
.
So,
Therefore
is a soft fixed point of
. Finally to prove the uniqueness of soft fixed point, suppose that
are two distinct soft fixed points of
. The cyclic character of
and the fact that
are soft fixed points of
implies that
. Suppose that
and for all
. Using the contractive condition, we obtain
Then we have
.
This is a contradiction. Thus we derive that
Hence proved.
In the theorem 2.7, if we take
, for all
then we deduce the following theorem.
Theorem 2.8: Let
be a complete soft dislocated metric space and
be self map on
. Assume that there exist
,
such that
, for all
, where
Then
has a soft fixed point. Moreover if
for all
then
has a unique soft fixed point.
If in theorem (2.7) we take
and
where
then we deduce the following corollary.
Corollary 2.9: Let
be a complete soft dislocated metric space,
, let
be non empty
-closed subsets of
and let
. Suppose that
is an operator such that
i.
is a cyclic representation of
with respect to
ii. there exist
such that
for any
and
,
. Where
, then
has a soft fixed point
. Moreover if
for all
then
has a unique soft fixed point.
Example 2.10: Let X = R with soft dislocated metric
, for all
. Suppose
,
&
. Define
by
It is clear that
is a cyclic representation of Y with respect to
.
Let
and
then
and so
Hence the condition of corollary (2.9) (theorem 2.7) holds and
has a fixed point in
. Here
is a fixed point of
.
Example 2.11: Let X = R with soft dislocated metric
, for all
. Suppose
and
&
we define
by
It is clear that
is a cyclic representation of Y with respect to
. Let
and
, then
Hence the condition of corollary (2.9) (theorem 2.7) holds and
has a soft fixed point in
. Here
is a soft fixed point of
.
In the above corollary we take
for all
, then we deduce the following corollary.
Corollary 2.12: Let
be a complete soft dislocated metric space and let
be a self map on X. Assume that there exist
such that
holds for all
. Then
has a soft fixed point. More- over if
for all
, then
has a unique soft fixed point.
Example 2.13: Let X = R with soft dislocated metric space and
. For any
let
be defined by
Proof: To show that the existence and uniqueness of soft point of
, we need to consider the following cases
Let
then
.
Let
then
Let
then
.
Let
and
then
.
Let
and
then
.
Let
and
then
.
and so
Hence we conclude that all the condition of corollary (2.12) (theorem 2.7) holds and
has a soft fixed point in
. By corollary 2.9 we deduce the following result.
Corollary 2.14: Let
be a complete soft dislocated metric,
, let
be non empty
-closed subsets of X and
. Suppose that
is an operator such that
i.
is a cyclic representation of
with respect to
.
ii. there exist
such that
where
for any
,
, where
and
be Lebesgue-
integrable mapping satisfying
for
. Then
has a fixed point
. Moreover if
for all
, then
has a unique soft fixed point.
Definition 2.15: Let
with
and
. A mapping
is said to be a
sub admissible soft mapping if
for
.
Example 2.16: Let
and
be defined by
and
then
is a
sub admissible mapping, where
, indeed if
then
.
Hence
and
.
Let
be the class of all the functions
that are a continuous with the property:
if and only if
.
Definition 2.17: Let
be a soft dislocated metric space,
, let
be
-closed non empty subsets of
and let
. Assume that
is g-ψ-sub admissible mapping, where
Then
is called ψ-cyclic generalized weakly C-contraction if
i.
is a cyclic representation of Y with respect to
(18)
for any
,
,
and
and
.
Theorem 1.18: Let
be a complete soft dislocated metric space,
, let
, be
-closed non-empty subsets of
and let
. Assume that
is a ψ-cyclic generalized weakly C-
contraction. If there exists
such that
then
has a soft fixed point
Moreover if
then
is unique.
Proof: Let
be such that
. Since
is a sub ψ-ad- missible mapping with respect to
, then
for all
. Also, there exist some i0 such that
Now
implies that
Thus there exist
in
such that
. Similarly
, where
Hence for
there exist
such that
and
. In case
for some
, then it is clear that
is a fixed point of
. Now assume that
, for all n.
Since
is a cyclic generalized weak C-contraction, we have for all
we have
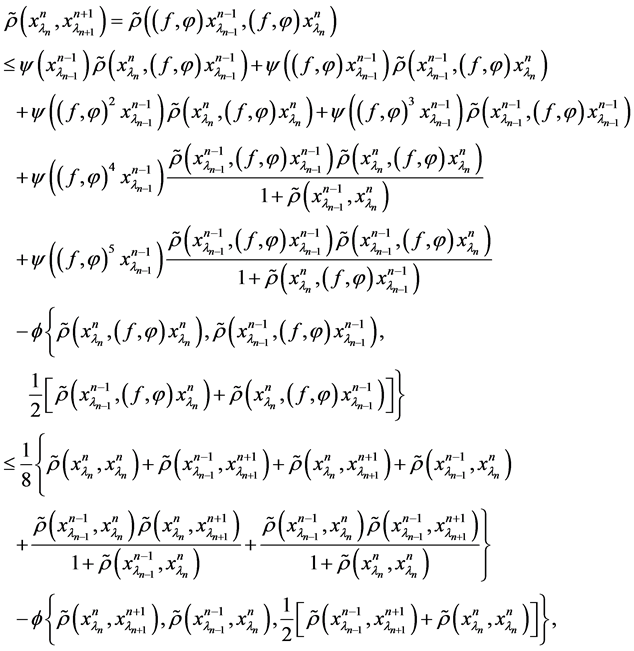
And so
(19)
On the other hand from (d3) we have
.
And by lemma (2.5D) we have
.
Also
From (19) we have
Therefore we have
. (20)
For any
, set
. On the occasion of the facts above
is a non-increasing sequence of non negative real numbers. Consequently, there exist
such that
. (21)
We shall prove that
. Since
then we get
. Similarly,
Then
.
On the other hand, by taking limit as
in (19), we have,
,
This implies
.
Hence
Now from (18) we have
By taking limit as
in the above inequality, we deduce that,
.
So
since
we get
.
Due to
and
we have
. (22)
We shall show that
is a
-Cauchy sequence. At first, we prove the following fact:
(K) for every
, there exist
such that if
with
then
Suppose to the contrary that there exist
, such that for any n in N, we can find
with
satisfying
(23)
Following the related lines of the proof of theorem (1.8) we have
and
(24)
Since
&
lie in different adjacently labeled sets Ai and Ai+1, for a certain
. Using the fact that
is ψ-cyclic generalized weakly C- contraction, we have
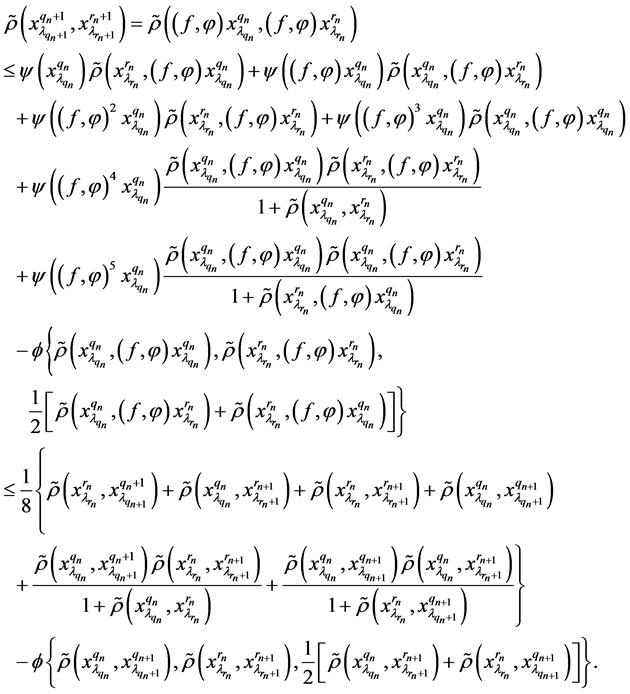
Now, by taking limit as
in the above inequality, we derive that
.
This is a contradiction. Hence condition (k) holds. We are ready to show that the sequence
is a Cauchy. Fix
By the claim, we find
such that if
with
then
. (25)
Since
, we find
such that
(26)
for any
Suppose that
with
. Then there exist
such that
. Therefore,
, for
.
So we have, for
,
.
By (25) and (26) and from the last inequality, we get
.
This proves that
is a
-Cauchy sequence.
Since Y is
-closed in
then
is also complete, there
exists
such that
in
, equivalently
. (27)
In what follows, we prove that
is a soft fixed point of
. In fact,
since
and as
is cyclic representation of Y with respect to
, the sequence
has infinite terms in each
for
. Suppose that
and we take a subsequence
of
with
(the existence of this subsequence is
guaranteed by the above mentioned comment). By using the contractive condition, we can obtain
Passing to the limit as
and using
lower semi-conti- nuity of
, we have
So
and therefore
is fixed point of
.
Finally to prove the uniqueness of soft fixed point theorem, suppose that
are soft fixed points of
. The cyclic character of
and the fact that
are soft fixed points of
implies that
. Also suppose that
. By using contrac-
tive condition we derive that
This gives us
that is
. This finishes the proof.
Corollary 2.19: Let
be a complete soft dislocated metric space,
, let
be non empty
-closed subsets of
and
let
. Suppose that
is an operator such that
i)
is cyclic representation of
with respect to
;
ii) there exist
such that
(28)
for any
,
,
, where
. Then
has fixed point
.
Example 2.20: Let
with soft dislocates metric space
, for any
suppose
and
&
we define
by
It clear that
is cyclic representation of Y with respect to
.
Proof: Let
and
Hence the condition of corollary (2.19) (theorem 2.18) holds and
has a soft fixed point in
. Here
is a soft fixed point of
.
In the above theorem 2.18, if we take
for all
then we deduce the following theorem.
Theorem 2.21: Let
be a complete soft dislocated metric space and
be a sub ψ-admissible mapping such that
for any
, where
,
. Then
has unique soft fixed point in
.
Corollary 2.22: Let
be a complete soft dislocated metric space and
be a sub ψ-admissible mapping such that
for any
, where
. Then
has unique soft
fixed point in
.
Example 2.23: Let
with soft dislocated metric space
, for any
. Let
be defined by
Proof: To show the existence and uniqueness soft point of
, we investigate the following cases
Let
then
Let
then
Let
and
then
.
Hence
Hence all the condition of corollary (2.22) (theorem 2.21) are satisfied. Thus
has a unique soft fixed point in
indeed 0 is the unique soft fixed point of
.
Corollary 2.24: Let
be a complete soft dislocated metric space,
, let
be non empty
-closed subsets of
and let
. Suppose that
is an operator such that
i)
is cyclic representation of
with respect to
ii)
where
for any
,
. Where
and
is
Lebsegue-integrable mapping satisfying
, for
and the constant
Then
has unique soft fixed point
In corollary 2.24, if we take
, for
. We obtain the following result.
Theorem 2.25: Let
be a complete soft dislocated metric space and
be a mapping such that for any
then
where
Let
is Lebsegue-integrable mapping satisfying
for
and the constant
Then
has unique soft fixed point.
3. Conclusion
In this paper, the investigations concerning the existence and uniqueness of soft fixed point of a cyclic mapping in soft dislocated metric space are established. Examples are given in the support of established results. These results can be extended to any directions, and can also be extended to fixed point theory of non-expansive multivalued mappings. These proved results lead to different directions and aspect of soft metric fixed point theory.
Acknowledgements
The authors would like their sincere thanks to the editor and the anonymous referees for their valuable comments and useful suggestions in improving the article.
Cite this paper
Wadkar, B.R., Mi- shra, V.N., Bhardwaj, R. and Singh, B. (2017) Dislocated Soft Metric Space with Soft Fixed Point Theorems. Open Journal of Discrete Mathematics, 7, 108-133. https://doi.org/10.4236/ojdm.2017.73012
References
- 1. Molodtsov, D. (1999) Soft Set-Theory-First Results. Computers & Mathematics with Applications, 37, 19-31. https://doi.org/10.1016/S0898-1221(99)00056-5
- 2. Ali, M.I., Feng, F., Liu, X., Min, W.K. and Shabir, M. (2011) On Some New Operations in Soft Set Theory. Computers & Mathematics with Applications, 62, 351-358.
- 3. Chen, D. (2005) The Parameterization Reduction of Soft Sets and Its Applications. Computers & Mathematics with Applications, 49, 757-763. https://doi.org/10.1016/j.camwa.2004.10.036
- 4. Gunduz, C., Sonmez, A. and Çakalli, H. (2013) On Soft Mappings. arXiv:1305.4545v1 [math.GM]
- 5. Hussain, S. and Ahmad, B. (2011) Some Properties of Soft Topological Spaces. Computers and Math with Applications, 62, 4058-4067. https://doi.org/10.1016/j.camwa.2011.09.051
- 6. Maji, P.K., Roy, A.R. and Biswas, R. (2002) An Application of Soft Sets in a Decision Making Problem. Computers & Mathematics with Applications, 44, 1077-1083. https://doi.org/10.1016/S0898-1221(02)00216-X
- 7. Maji, P.K., Biswas, R. and Roy, A.R. (2003) Soft Set Theory. Computers and Mathematics with Applications, 45, 555-562. https://doi.org/10.1016/S0898-1221(03)00016-6
- 8. Majumdar, P. and Samanta, S.K. (2010) On Soft Mappings. Computers and Mathematics with Applications, 60, 2666-2672. https://doi.org/10.1016/j.camwa.2010.09.004
- 9. Shabir, M. and Naz, M. (2011) On Soft Topological Spaces. Computers and Mathematics with Applications, 61, 1786-1799. https://doi.org/10.1016/j.camwa.2011.02.006
- 10. Das, S. and Samanta, S.K. (2012) Soft Real Sets, Soft Real Numbers and Their Properties. Journal of Fuzzy Mathematics, 20, 551-576.
- 11. Das, S. and Samanta, S.K. (2013) On Soft Metric Spaces. The Journal of Fuzzy Mathematics, 21, 207-213.
- 12. Hitzler, P. and Seda, A.K. (2000) Dislocated Topologies. Journal of Electrical Engineering, 51, 3-7.
- 13. Aage, C.T. and Salunke, J.N. (2008) Some Results of Fixed Point Theorem in Dislocated Quasi-Metric Spaces. Bulletin of the Marathwada Mathematical Society, 9, 1-5.
- 14. Karapinar, E. and Salimi, P. (2013) Dislocated Metric Space to Metric Space with Some Fixed Point Theorem. Fixed Point Theory and Application, 2013, 222.https://doi.org/10.1186/1687-1812-2013-222
- 15. Bayramov, S. and Gunduz, C. (2013) Soft Locally Compact and Soft Para Compact Spaces. Journal of Mathematics and System Science, 3, 122-130.
- 16. Rhoades, B.E. (1977) A Comparison of Various Definitions of Contractive Mappings. Transactions of the American Mathematical Society, 266, 257-290. https://doi.org/10.1090/S0002-9947-1977-0433430-4
- 17. Huang, L.-G. and Zhang, X. (2007) Cone Metric Spaces and Fixed Point Theorems of Contractive Mappings. Journal of Mathematical Analysis and Applications, 332, 1468-1476. https://doi.org/10.1016/j.jmaa.2005.03.087
- 18. Yazar, M.I., Gunduz, C. and Bayramov, S. (2013) Fixed Point for Soft Contractive Mappings. Cornell University Library, Thurston Ave Ithaca, NY.
- 19. Wadkar, B.R., Bhardwaj, R.K. and Singh, B. (2012) A Common Fixed Point Theorem in Dislocated Metric Space. International Journal of Engineering Research and Development, 10, 14-17.
- 20. Mishra, L.N., Mishra, V.N., Khatri, K. and Deepmala (2014) On the Trigonometric Approximation of Signals (Functions) Belonging to Generalized Weighted Lipschitz Class by Matrix Operator of Conjugate Series of Its Fourier Series. Applied Mathematics and Computation, 237, 252-263. https://doi.org/10.1016/j.amc.2014.03.085
- 21. Mishra, V.N., Khatri, K. and Mishra, L.N. (2013) Using Linear Operator to Approximate Signal of Class. Filomat, 27, 355-365.https://doi.org/10.2298/FIL1302353M
- 22. Mishra, L.N., Tiwari, S.K., Mishra, V.N. and Khan, I.A. (2015) Unique Fixed Point Theorems for Generalized Contractive Mappings in Partial Metric Spaces. Journal of Function Spaces, 2015, Article ID: 960827, 8 p.https://doi.org/10.1155/2015/960827
- 23. Mishra, L.N., Tiwari, S.K. and Mishra, V.N. (2015) Fixed Point Theorems for Generalized Weakly S-Contractive Mappings in Partial Metric Spaces. Journal of Applied Analysis and Computation, 5, 600-612.
- 24. Deepmala and Pathak, H.K. (2013) A Study on Some Problems on Existence of Solutions for Nonlinear Functional-Integral Equations. Acta Mathematica Scientia, 33, 1305-1313. https://doi.org/10.1016/S0252-9602(13)60083-1
- 25. Wadkar, B.R., Bhardwaj, R., Mishra, V.N. and Singh, B. (2017) Coupled Fixed Point Theorems in Soft Metric and B-Soft Metric Space. Ser. A: Appl. Math. Inform. And Mech., 9, 59-73. http://www.np.ac.rs/downloads/publications/vol9_br_1/rad6.pdf
- 26. Wadkar, B.R., Bhardwaj, R., Singh, B. and Mishra, V.N. (2017) Coupled Fixed Point Theorems with Monotone Property in Soft Metric and Soft B-Metric Space. International Journal of Mathematical Analysis, 11, 363-375. https://doi.org/10.12988/ijma.2017.7222




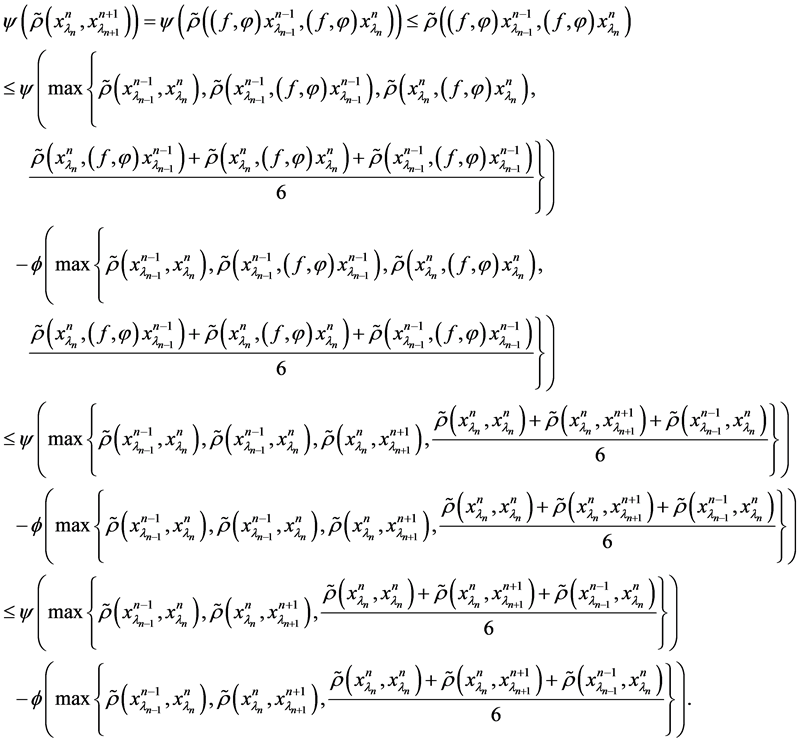 (3)
(3)