ABSTRACT

G. C. Ying, Y. Y. Meng, B. E. Sagan, and V. R. Vatter [1] found the maximum number of maximal independent sets in connected graphs which contain at most two cycles. In this paper, we give an alternative proof to determine the largest number of maximal independent sets among all connected graphs of order n ≥ 12, which contain at most two cycles. We also characterize the extremal graph achieving this maximum value.

Keywords:

Maximal Independent Set, Connected Graph Having at Most Two Cycles

1. Introduction

Let 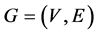be a simple undirected graph. An independent set is a subset S of V such that no two vertices in S are adjacent. A maximal independent set is an independent set that is not a proper subset of any other independent set. The set of all maximal independent sets of a graph G is denoted by 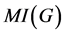and its cardinality by.

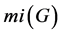The problem of determining the largest value of 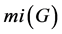in a general graph of order n and those graphs achieving the largest number was proposed by Erdös and Moser, and solved by Moon and Moser [2] . It was then extensively studied for various classes of graphs in the literature, including trees, forests, (connected) graphs with at most one cycle, bipartite graphs, connected graphs, k-connected graphs, (connected) triangle-free graphs; for a survey see [3] . Recently, Jin and Li [4] determined the second largest number of maximal independent sets among all graphs of order n.

There are results on independent sets in graphs from a different point of view. The Fibonacci number of a graph is the number of independent vertex subsets. The concept of the Fibonacci number of a graph was introduced in [5] and discussed in several papers [6] [7] . In addition, Jou and Chang [8] showed a linear-time algorithm for counting the number of maximal independent sets in a tree.

Jou and Chang [9] determined the largest number of maximal independent sets among all graphs and connected graphs of order n, which contain at most one cycle. Later B. E. Sagan and V. R. Vatter [10] found the largest number of maximal independent sets among all graphs of order n, which contain at most r cycles. In 2012, Jou [11] settled the second largest number of maximal independent sets in graphs with at most one cycle. G. C. Ying, Y. Y. Meng, B. E. Sagan, and V. R. Vatter [1] found the maximum number of maximal independent sets in connected graphs which contain at most two cycles. In this paper, we give an alternative proof to determine the largest number of maximal independent sets among all connected graphs of order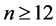, which contain at most two cycles. We also characterize the extremal graph achieving this maximum value.

For a graph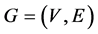, the cardinality of 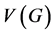is called the order, and it is denoted by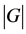. The neighborhood 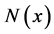of a vertex 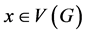is the set of vertices adjacent to x in G and the closed neighborhood 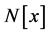is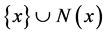. The degree of x is the cardinality of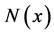, and it is denoted by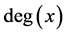. A vertex x is said to be a leaf if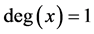. For a set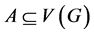, the deletion of A from G is the graph 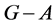obtained from G by removing all vertices in A and their incident edges. Two graphs and are disjoint if. The union of two disjoint graphs and is the graph with vertex set and edge set. If a graph G is isomorphic to another graph H, we denote. Denote a complete graph of order n and a cycle of order n. The join of two disjoint graphs and is the graph with vertex set and edge set . The star-product of two disjoint graphs and is the graph with vertex set and edge set, where is a vertex with maximum degree in for.

2. Preliminary

The following results are needed.

Lemma 1. ( [12] [13] ) For any vertex x in a graph G, the following hold.

1).

2) If x is a leaf adjacent to y, then.

Lemma 2. ( [13] ) If G is the union of two disjoint graphs and, then.

Lemma 3. Let be integers such that and let.

Then.

Proof. The derivative of is

So for any and for any. Then is decreasing on and is increasing on. Hence.

□Theorem 1. ( [9] ) If T is a tree with vertices, then, where

Furthermore, if and only if, wherewhere

is the set of batons, which are the graphs obtained from a basic path P of vertices by attaching paths of length two to the endpoints of P in all possible ways (see Figure 1).

Theorem 2. ( [9] ) If F is a forest with vertices, then, where

Furthermore, if and only if, where

where.

Theorem 3. ( [9] ) If G is a graph of order vertices with at most one cycle, then, where

Furthermore, if and only if, where

Theorem 4. ( [11] ) If G is a graph of order with at most one cycle such that, then, where

Furthermore, if and only if, where

Theorem 5. ( [9] ) If H is a connected graph of order with at most one cycle, then, where

Furthermore, if and only if (see Figure 2), where

3. The Alternative Proof

In this section, we give an alternative proof to determine the largest number of maximal independent sets among all connected graphs of order, which contain at most two cycles. We also characterize the extremal graph achieving this maximum value.

Theorem 6. If H is a connected graph of order with at most two cycles, then, where

Furthermore, if and only if, where

A unicyclic graph is a connected graph having one cycle. The order of a unicyclic graph is at least three. The following lemmas will be needed in the proof of main theorem.

Lemma 4. Suppose that is the union of a tree T and a unicyclic graph H, where. Then. The equality holds if and only if

or.

Proof. Let. Note that H has one cycle, then. We consider two cases.

Case 1. is even.

By Lemma 2, Theorem 1 and Theorem 5, we have

If the equality holds, then or.

Hence the equality holds if and only if or.

Case 2. is odd.

By Lemma 3 and since,

for.

By Theorem 1 and Theorem 5, we have

If the equality holds, then. Hence the equality holds if and only if.

By case 1 and case 2, we have that. The equality holds if and

only if or. □

Lemma 5. Suppose that F is a forest of order having at most two components. Then and the equality holds if and only if or

.

Proof. Let F be a forest of order having at most two components such that as large as possible. Then. If F has one component, then F is a tree and, by Theorem 1,. Then

n is odd and. By Theorem 1,. Now we assume that F

have two components. Let and be the components of F, where. We consider two cases.

Case 1. is even.

By Lemma 3, for

. By Lemma 2 and Theorem 1, then

The equalities hold and. By Theorem 1,. The equality holds if and only if.

Case 2. is odd.

Then F has exactly one even component, we assume that is even. By Theorem 1, then

. The

equalities hold and. The equality holds if and only if. □

The following is the proof of Theorem 6.

Proof. Let H be a connected graph of order with at most two cycles such that as large as possible. Then. Since , by Theorem 5, H have at least two cycles. That means that H have exactly two cycles and. Let v be a vertex lying on some cycle such that is as large as possible. Since, we can see that. The graph is a graph of order with at most one cycle. We consider two cases.

Case 1..

Then or. Since H is connected, this means

that v connects to every component of. Then has at most one edge, then. So we have

Then and is even. So. Note that H has two cycles, hence for even.

Case 2..

Let. Then the subgraph is a graph of order having at most one cycle. By Theorem 3,. By Theorem 4,. By Lemma 1 and Theorem 4, then

Then

Claim..

Suppose that, then n is even. By Theorem 3,

and.

By Theorem 2, is not a forest and has one cycle. Let be the component of having one cycle and, where. Note that H has two cycles and v is lying on some cycle. Thus v has two edges incident to some component of. Since, the number of the components of is at most three. Thus F is either a tree or the union of two trees. By Lemma 5,. By Lemma 3,

for. By

Theorem 5,. Note that. By Lemma 2 and

Lemma 5,

where. This is a contradiction, so.

By Claim,. Note that H has two cycles and v is lying on some cycle. Thus v has two edges incident to some component of. Since, the number of the components of is at most two. Thus, where T is a tree and is a unicyclic graph. By Lemma 4 and Theorem 3, then and . So

The equalities hold. Then and, by Lemma 4,

or. If, then n is odd and. That is, this is a contra-

diction. Thus. If n is even, where, then

and

. Then, there exists a vertex lying on

some cycle such that. This contradicts to the claim, so n is odd. Thus and

. Hence

for odd. □

Acknowledgements

The authors are grateful to the referees for the helpful comments.

Cite this paper

Jou, M.-J. and Lin, J.-J. (2016) An Alternative Proof of the Largest Number of Maximal Independent Sets in Connected Graphs Having at Most Two Cycles. Open Journal of Discrete Mathematics, 6, 227-237. http://dx.doi.org/10.4236/ojdm.2016.64019

References