Open Journal of Discrete Mathematics
Vol.06 No.02(2016), Article ID:65254,29 pages
10.4236/ojdm.2016.62005
On the Number of Cycles in a Graph
Nazanin Movarraei, Samina A. Boxwala
Department of Mathematics, University of Pune, Pune, India
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
Received 7 October 2015; accepted 28 March 2016; published 31 March 2016
ABSTRACT
In this paper, we obtain explicit formulae for the number of 7-cycles and the total number of cycles of lengths 6 and 7 which contain a specific vertex vi in a simple graph G, in terms of the adjacency matrix and with the help of combinatorics.
Keywords:
Adjacency Matrix, Cycle, Graph Theory, Path, Subgraph, Walk
1. Introduction
In a simple graph G, a walk is a sequence of vertices and edges of the form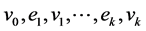 
such that the edge 
has ends 
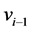and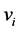
. A walk is called closed if
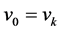. In graph theory, a path in a graph is a finite or infinite sequence of edges which connect a sequence of vertices which, are all distinct from one another. A closed path (with the common end points) is called a cycle.
It is known that if a graph G has adjacency matrix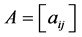
, then for 
the ij-entry of 
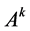is the number of 
walks of length k in G. It is also known that 
is the sum of the diagonal entries of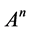 
and 
is the degree of the vertex
.
In 1971, Frank Harary and Bennet Manvel [1] , gave formulae for the number of cycles of lengths 3 and 4 in simple graphs as given by the following theorems:
Theorem 1. [1] If G is a simple graph with adjacency matrix A, then the number of 3-cycles in G is
. (It is known that
).
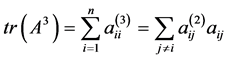Theorem 2. [1] If G is a simple graph with adjacency matrix A, then the number of 4-cycles in G is
, where q is the number of edges in G. (It is obvious that the above formula is also equal to
)
Theorem 3. [1] If G is a simple graph with n vertices and the adjacency matrix
, then the number
of 5-cycles in G is
In 2003, V. C. Chang and H. L. Fu [2] , found a formula for the number of 6-cycles in a simple graph which is stated below:
Theorem 4. [2] If G is a simple graph with adjacency matrix A, then the number of 6-cycles in G is
Their proofs are based on the following fact:
The number of n-cycles (
in a graph G is equal to 
where x is the number of
closed walks of length n, which are not n-cycles.
In 1997, N. Alon, R. Yuster and U. Zwick [3] , gave number of 7-cyclic graphs. They also gave some for- mulae for the number of cycles of lengths 5, which contains a specific vertex 
in a graph G.
In [3] - [9] , we have also some bounds to estimate the total time complexity for finding or counting paths and cycles in a graph.
In our recent works [10] [11] , we obtained some formulae to find the exact number of paths of lengths 3, 4 and 5, in a simple graph G, given below:
Theorem 5. [11] Let G be a simple graph with n vertices and the adjacency matrix
. The number of
paths of length 3 in G is
.
Theorem 6. [11] Let G be a simple graph with n vertices and the adjacency matrix
. The number of
paths of length 4 in G is
.
Theorem 7. [11] Let G be a simple graph with n vertices and the adjacency matrix
. The number of
paths of length 3 in G, each of which starts from a specific vertex 
is
.
Theorem 8. [11] Let G be a simple graph with n vertices and the adjacency matrix
. The number of paths of length 4 in G, each of which starts from a specific vertex 
is
.
Theorem 9. [10] Let G be a simple graph with n vertices and the adjacency matrix
. The number of
.
Theorem 10. [10] If G is a simple graph with n vertices and the adjacency matrix
, then the number
of 4-cycles each of which contains a specific vertex 
of G is
.
In [3] we can also see a formula for the number of 5-cycles each of which contains a specific vertex 
but, their formula has some problem in coefficients. In [12] we gave the correct formula as considered below:
Theorem 11. [12] If G is a simple graph with n vertices and the adjacency matrix
, then the number of 5-cycles each of which contains a specific vertex 
of G is
.
In this paper, we give a formula to count the exact number of cycles of length 7 and the number of cycles of lengths 6 and 7 containing a specific vertex 
in a simple graph G, in terms of the adjacency matrix of G and with the help of combinatorics.
2. Number of 7-Cycles
In 1997, N. Alon, R. Yuster and U. Zwick [3] , gave number of 7-cyclic graphs. The n-cyclic graph is a graph that contains a closed walk of length n and these walks are not necessarily cycles. In this section we obtain a formula for the number of cycles of length 7 in a simple graph G with the helps of [3] .
Method: To count N in the cases considered below, we first count 
for the graph of first con- figuration. This will give us the number of all closed walks of length 7 in the corresponding graph. But, some of these walks do not pass through all the edges and vertices of that configuration and to find N in each case, we have to include in any walk, all the edges and the vertices of the corresponding subgraphs at least once. So, we delete the number of closed walks of length 7 which do not pass through all the edges and vertices. To find these kind of walks we also have to count 
for all the subgraphs of the corresponding graph that can contain a closed walk of length 7.
Theorem 12. If G is a simple graph with n vertices and the adjacency matrix
, then the number of
7-cycles in G is
, where x is equal to 
in the cases that are considered below.
Proof: The number of 7-cycles of a graph G is equal to
, where x is the number of closed
walks of length 7 that are not 7-cycles. To find x, we have 11 cases as considered below; the cases are based on the configurations-(subgraphs) that generate all closed walks of length 7 that are not 7-cycles.
In each case, N denotes the number of closed walks of length 7 that are not 7-cycles in the corresponding subgraph, M denotes the number of subgraphs of G of the same configuration and
, (
) denote the total number of closed walks of length 7 that are not cycles in all possible subgraphs of G of the same configurations. However, in the cases with more than one figure (Cases 5, 6, 8, 9, 11), N, M and 
are based on the first graph in case n of the respective figures and 
denote the number of subgraphs of G which don’t have the same configuration as the first graph but are counted in M. It is clear that 
is equal to
. To find N in each case, we have to include in any walk, all the edges and the vertices of the corresponding subgraphs at least once.
Case 1: For the configuration of Figure 1, 
, 
and
. (See Theorem 1)
Figure 1. Closed walks of length 7 type 1.
Case 2: For the configuration of Figure 2, 
, 
and
.
Figure 2. Closed walks of length 7 type 2.
Case 3: For the configuration of Figure 3, 
, 
and
.
Figure 3. Closed walks of length 7 type 3.
Case 4: For the configuration of Figure 4, 
, 
and
.
Figure 4. Closed walks of length 7 type 4.
Case 5: For the configuration of Figure 5(a), 
,
. Let 
denote the number of
subgraphs of G that have the same configuration as the graph of Figure 5(b) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the graph
of Figure 5(b) and 6 is the number of times that this subgraph is counted in M. Let 
denote the number of subgraphs of G that have the same configuration as the graph of Figure 5(c) and are counted in M.
Thus
, where 
is the number of subgraphs of G that have the same configuration as the
graph of Figure 5(c) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of subgraphs of G that have the same configuration as the graph of Figure 5(d) and are counted in M.
Thus
, where 
is the number of subgraphs of G that have the same configuration as
the graph of Figure 5(d) and 4 is the number of times that this subgraph is counted in M. Consequently,
.
Figure 5. Closed walks of length 7 type 5.
Case 6: For the configuration of Figure 6(a),
,
. Let 
denote the
number of subgraphs of G that have the same configuration as the graph of Figure 6(b) and are counted in M.
Thus
, where 
is the number of subgraphs of G that have the same configuration as
the graph of Figure 6(b) and 2 is the number of times that this subgraph is counted in M. Consequently,
.
Figure 6. Closed walks of length 7 type 6.
Case 7: For the configuration of Figure 7, 
, 
(see Theorem 3) and
.
Figure 7. Closed walks of length 7 type 7.
Case 8: For the configuration of Figure 8(a), 
, 
(see Theorem 5).
Let 
denote the number of subgraphs of G that have the same configuration as the graph of Figure 8(b) and
are counted in M. Thus
, where 
is the number of subgraphs of G that have the same
configuration as the graph of Figure 8(b) and 4 is the number of times that this subgraph is counted in M.
Consequently,
.
Figure 8. Closed walks of length 7 type 8.
Case 9: For the configuration of Figure 9(a), 
,
(see Theorem 11). Let 
denote the number
of subgraphs of G that have the same configuration as the graph of Figure 9(b) and are counted in M. Thus
, where 
is the number subgraphs of G that have the same configuration as the graph of
Figure 9(b) and 2 is the number of times that this subgraph is counted in M. Consequently,
.
Figure 9. Closed walks of length 7 type 9.
Case 10: For the configuration of Figure 10, 
, 
and
.
Figure 10. Closed walks of length 7 type 10.
Case 11: For the configuration of Figure 11(a), 
,
. Let 
denote the number
of subgraphs of G that have the same configuration as the graph of Figure 11(b) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the graph
of Figure 11(b) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of subgraphs of G that have the same configuration as the graph of Figure 11(c) and are counted in M.
Thus
, where 
is the number of subgraphs of G that have the same configuration as
the graph of Figure 11(c) and 6 is the number of times that this subgraph is counted in M. Let 
denote the number of subgraphs of G that have the same configuration as the graph of Figure 11(d) and are
counted in M. Thus
, where 
is the number of subgraphs of G that have the same
configuration as the graph of Figure 11(d) and 6 is the number of times that this subgraph is counted in
M. Consequently,
.
Figure 11. Closed walks of length 7 type 11.
Now, we add the values of 
arising from the above cases and determine x. By putting the value of x in
we get the desired formula. □
Example 1. In
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
and
. So 
and
by Theorem 12, the number of cycles of length 7 in 
is
.
3. Number of Cycles Passing the Vertex vi
In this section we give formulae to count the number of cycles of lengths 6 and 7, each of which contain a specific vertex 
of the graph G.
Theorem 13. If G is a simple graph with n vertices and the adjacency matrix
, then the number of
6-cycles each of which contains a specific vertex 
of G is
, where x is equal to 
in the
cases that are considered below.
Proof: The number of 6-cycles each of which contain a specific vertex 
of the graph G is equal to
, where x is the number of closed walks of length 6 form the vertex 
to 
that are not 6-cycles.
To find x, we have 17 cases as considered below; the cases are based on the configurations-(subgraphs) that generate 
walks of length 6 that are not cycles. In each case, N denotes the number of walks of length 6 from 
to 
that are not cycles in the corresponding subgraph, M denotes the number of subgraphs of G of the same configuration and
, (
) denote the total number of 
walks of length 6 that are not cycles in all possible subgraphs of G of the same configuration. However, in the cases with more than one figure (Cases 11, 12, 13, 14, 15, 16, 17), N, M and 
are based on the first graph of the respective figures and 
denote the number of subgraphs of G which don’t have the same configuration as the first graph but are counted in M. It is clear that 
is equal to
. To find N in each case, we have to include in any walk, all the edges and the vertices of the corresponding subgraphs at least once.
Case 1: For the configuration of Figure 12, 
, 
and
.
Figure 12. 
walks of length 6 type 1.
Case 2: For the configuration of Figure 13, 
, 
and
.
Figure 13. 
walks of length 6 type 2.
Case 3: For the configuration of Figure 14, 
, 
and
.
Figure 14. 
walks of length 6 type 3.
Case 4: For the configuration of Figure 15, 
, 
and
. (See Theorem 7)
Figure 15. 
walks of length 6 type 4.
Case 5: For the configuration of Figure 16, 
, 
and
.
Figure 16. 
walks of length 6 type 5.
Case 6: For the configuration of Figure 17, 
, 
and
.
Figure 17. 
walks of length 6 type 6.
Case 7: For the configuration of Figure 18, 
, 
and
.
Figure 18. 
walks of length 6 type 7.
Case 8: For the configuration of Figure 19, 
, 
and
.
Figure 19. 
walks of length 6 type 8.
Case 9: For the configuration of Figure 20, 
, 
and
.
Figure 20. 
walks of length 6 type 9.
Case 10: For the configuration of Figure 21, 
, 
and
.
Figure 21. 
walks of length 6 type 10.
Case 11: For the configuration of Figure 22(a), 
,
. Let 
denote the
number of all subgraphs of G that have the same configuration as the graph of Figure 22(b) and are counted in
M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the
graph of Figure 22(b) and this subgraph is counted only once in M. Consequently,
.
Figure 22. 
walks of length 6 type 11.
Case 12: For the configuration of Figure 23(a), 
,
. Let 
denote the number
of all subgraphs of G that have the same configuration as the graph of Figure 23(b) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the graph
of Figure 23(b) and 2 is the number of times that this subgraph is counted in M. Consequently,
.
Figure 23. 
walks of length 6 type 12.
Case 13: For the configuration of Figure 24(a), 
,
. Let 
denote the number
of all subgraphs of G that have the same configuration as the graph of Figure 24(b) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the graph
of Figure 24(b) and this subgraph is counted only once in M. Consequently,
.
Figure 24. 
walks of length 6 type 13.
Case 14: For the configuration of Figure 25(a), 
,
. Let 
denote the number
of all subgraphs of G that have the same configuration as the graph of Figure 25(b) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the graph of Figure 25(b) and this subgraph is counted only once in M. Consequently,
.
Figure 25. 
walks of length 6 type 14.
Case 15: For the configuration of Figure 26(a), 
,
. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 26(b) and are
counted in M. Thus
, where 
is the number of subgraphs of G that have the same
configuration as the graph of Figure 26(b) and 2 is the number of times that this subgraph is counted in M. Consequently,
.
Figure 26. 
walks of length 6 type 15.
Case 16: For the configuration of Figure 27(a), 
,
. Let 
denote the number of
all subgraphs of G that have the same configuration as the graph of Figure 27(b) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the graph of
Figure 27(b) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 27(c) and are counted in
M. Thus
, where 
is the number of subgraphs of G that have the same configuration as
the graph of Figure 27(c) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 27(d) and are
counted in M. Thus
, where 
is the number of subgraphs of G that have the same
configuration as the graph of Figure 27(d) and 2 is the number of times that this subgraph is counted in
M. Consequently,
.
Figure 27. 
walks of length 6 type 16.
Case 17: For the configuration of Figure 28(a), 
,
. Let 
denote the number of all
subgraphs of G that have the same configuration as the graph of Figure 28(b) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the graph of Figure 28(b) and this subgraph is counted only once in M. Consequently,
.
Figure 28. 
walks of length 6 type 17.
Now we add the values of 
arising from the above cases and determine x. Substituting the value of x in
and simplifying, we get the number of 6-cycles each of which contains a specific vertex 
of G. □
Example 2. In the graph of Figure 29 we have,
. So, we have
. Consequently, by Theorem 13, the number of 6-cycles each of which contains the vertex 
in the graph of Figure 29 is 60.
Figure 29. Complete graph with 7 vertices.
Theorem 14. If G is a simple graph with n vertices and the adjacency matrix
, then the number of
7-cycles each of which contains a specific vertex 
of G is
, where x is equal to 
in the
cases that are considered below.
Proof: The number of 7-cycles each of which contains a specific vertex 
of the graph G is equal to
, where x is the number of closed walks of length 7 form the vertex 
to 
that are not 7-cycles.
To find x, we have 30 cases as considered below; the cases are based on the configurations-(subgraphs) that generate 
walks of length 7 that are not cycles. In each case, N denotes the number of walks of length 7 from 
to 
that are not cycles in the corresponding subgraph, M denotes the number of subgraphs of G of the same configuration and
, (
) denote the total number of 
walks of length 7 that are not cycles in all possible subgraphs of G of the same configuration. However, in the cases with more than one figure (Cases 9, 10, ∙∙∙, 18, 20, ∙∙∙, 30), N, M and 
are based on the first graph of the respective figures and 
denote the number of subgraphs of G which do not have the same configuration as the first graph but are counted in M. It is clear that 
is equal to
. To find N in each case, we have to include in any walk, all the edges and the vertices of the corresponding subgraphs at least once.
Case 1: For the configuration of Figure 30, 
, 
and
.
Figure 30. 
walks of length 7 type 1.
Case 2: For the configuration of Figure 31, 
, 
and
.
Figure 31. 
walks of length 7 type 2.
Case 3: For the configuration of Figure 32, 
, 
and
.
Figure 32. 
walks of length 7 type 3.
Case 4: For the configuration of Figure 33, 
, 
and
.
Figure 33. 
walks of length 7 type 4.
Case 5: For the configuration of Figure 34, 
, 
and
.
Figure 34. 
walks of length 7 type 5.
Case 6: For the configuration of Figure 35, 
, 
and
.
Figure 35. 
walks of length 7 type 6.
Case 7: For the configuration of Figure 36, 
, 
and
.
Figure 36. 
walks of length 7 type 7.
Case 8: For the configuration of Figure 37, 
, 
,
.
Figure 37. 
walks of length 7 type 8.
Case 9: For the configuration of Figure 38(a), 
,
. Let 
denote the
number of all subgraphs of G that have the same configuration as the graph of Figure 38(b) and are counted in
M. Thus
, where 
is the number of subgraphs of G that have the same configuration as
the graph of Figure 38(b) and this subgraph is counted only once in M. Consequently,
.
Figure 38. 
walks of length 7 type 9.
Case 10: For the configuration of Figure 39(a), 
,
. Let 
denote the
number of all subgraphs of G that have the same configuration as the graph of Figure 39(b) and are counted in
M. Thus
, where 
is the number of subgraphs of G that have the same configuration as
the graph of Figure 39(b) and this subgraph is counted only once in M. Consequently,
.
Figure 39. 
walks of length 7 type 10.
Case 11: For the configuration of Figure 40(a), 
,
. Let 
denote the number of all
subgraphs of G that have the same configuration as the graph of Figure 40(b) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the graph
of Figure 40(b) and 2 is the number of times that this subgraph is counted in M. Consequently,
.
Figure 40. 
walks of length 7 type 11.
Case 12: For the configuration of Figure 41(a), 
,
. Let 
denote the number of all
subgraphs of G that have the same configuration as the graph of Figure 41(b) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the graph
of Figure 41(b) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 41(c) and are counted in
M. Thus
, where 
is the number of subgraphs of G that have the same configuration as
the graph of Figure 41(c) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 41(d) and are
counted in M. Thus
, where 
is the number of subgraphs of G that have the same
configuration as the graph of Figure 41(d) and 2 is the number of times that this subgraph is counted in
M. Consequently,
.
Figure 41. 
walks of length 7 type 12.
Case 13: For the configuration of Figure 42(a), 
,
. Let 
denote the
number of all subgraphs of G that have the same configuration as the graph of Figure 42(b) and are counted in
M. Thus
, where 
is the number of subgraphs of G that have the same configuration as
the graph of Figure 42(b) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 42(c) and are
counted in M. Thus
, where 
is the number of subgraphs of G that have the same
configuration as the graph of Figure 42(c) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure
42(d) and are counted in M. Thus
, where 
is the number of subgraphs of G that have
the same configuration as the graph of Figure 42(d) and 2 is the number of times that this subgraph is
counted in M. Consequently,
.
Figure 42. 
walks of length 7 type 13.
Case 14: For the configuration of Figure 43(a), 
,
. Let 
denote the number of all
subgraphs of G that have the same configuration as the graph of Figure 43(b) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the graph
of Figure 43(b) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 43(c) and are counted in
M. Thus
, where 
is the number of subgraphs of G that have the same configuration as
the graph of Figure 43(c) and this subgraph is counted only once in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 43(d) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the graph
of Figure 43(d) and 2 is the number of times that this subgraph is counted in M.
Consequently,
.
Figure 43. 
walks of length 7 type 14.
Case 15: For the configuration of Figure 44(a), 
,
. Let 
denote the number
of all subgraphs of G that have the same configuration as the graph of Figure 44(b) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the graph
of Figure 44(b) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 44(c) and are counted in
M. Thus
, where 
is the number of subgraphs of G that have the same configuration as
the graph of Figure 44(c) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 44(d) and are
counted in M. Thus
, where 
is the number of subgraphs of G that have the same
configuration as the graph of Figure 44(d) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure
44(e) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the
same configuration as the graph of Figure 44(e) and 1 is the number of times that this subgraph is counted in
M. Consequently,
.
Figure 44. 
walks of length 7 type 15.
Case 16: For the configuration of Figure 45(a), 
,
. Let 
denote the
number of all subgraphs of G that have the same configuration as the graph of Figure 45(b) and are counted in
M. Thus
, where 
is the number of subgraphs of G that have the same configuration as
the graph of Figure 45(b) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 45(c) and are
counted in M. Thus
, where 
is the number of subgraphs of G that have the same
configuration as the graph of Figure 45(c) and 1 is the number of times that this subgraph is counted in M.
Consequently,
.
Figure 45. 
walks of length 7 type 16.
Case 17: For the configuration of Figure 46(a), 
,
. Let 
denote the
number of all subgraphs of G that have the same configuration as the graph of Figure 46(b) and are counted in
M. Thus
, where 
is the number of subgraphs of G that have the same configuration as
the graph of Figure 46(b) and 2 is the number of times that this subgraph is counted in M. Consequently,
.
Figure 46. 
walks of length 7 type 17.
Case 18: For the configuration of Figure 47(a), 
,
. Let 
denotes the number of all subgraphs of G that have the same configuration as the graph of Figure 47(b) and are
counted in M. Thus
, where 
is the number of subgraphs of G that have the same
configuration as the graph of Figure 47(b) and 1 is the number of times that this subgraph is counted in M.
Consequently,
.
Figure 47. 
walks of length 7 type 18.
Case 19: For the configuration of Figure 48, 
,
(see Theorem 11) and
.
Figure 48. 
walks of length 7 type 19.
Case 20: For the configuration of Figure 49(a), 
, 
(see
Theorem 5). Let 
denote the number of all subgraphs of G that have the same configuration as the graph of
Figure 49(b) and are counted in M. Thus
, where 
is the number of subgraphs of G that
have the same configuration as the graph of Figure 49(b) and 2 is the number of times that this subgraph is
counted in M. Consequently,
.
Figure 49. 
walks of length 7 type 20.
Case 21: For the configuration of Figure 50(a), 
, 
(see Theorem 7).
Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 50(b)
and are counted in M. Thus
, where 
is the number of subgraphs of G that have the
same configuration as the graph of Figure 50(b) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 50(c)
and are counted in M. Thus
, where 
is the number of subgraphs of G that have
the same configuration as the graph of Figure 50(c) and 2 is the number of times that this subgraph is counted in M.
Consequently,
.
Figure 50. 
walks of length 7 type 21.
Case 22: For the configuration of Figure 51(a), 
, 
(see Theorem
7). Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure
51(b) and are counted in M. Thus
, where 
is the number of subgraphs of G that have
the same configuration as the graph of Figure 51(b) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of
Figure 51(c) and are counted in M. Thus
, where 
is the number of subgraphs of G that
have the same configuration as the graph of Figure 51(c) and 6 is the number of times that this subgraph is counted in M. Let 
denotes the number of all subgraphs of G that have the same configuration as the graph
of Figure 51(d) and are counted in M. Thus
, where 
is the number of subgraphs of G
that have the same configuration as the graph of Figure 51(d) and 1 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph
of Figure 51(e) and are counted in M. Thus
, where 
is the number of subgraphs of G
that have the same configuration as the graph of Figure 51(e) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the
graph of Figure 51(f) and are counted in M. Thus
, where 
is the number of subgraphs
of G that have the same configuration as the graph of Figure 51(f) and 1 is the number of times that this subgraph is counted in M. Consequently,
.
Figure 51. 
walks of length 7 type 22.
Case 23: For the configuration of Figure 52(a), 
,
(See Theorem 11).
Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 52(b)
and are counted in M. Thus
, where 
is the number of subgraphs of G that have the
same configuration as the graph of Figure 52(b) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 52(c)
and are counted in M. Thus
, where 
is the number of subgraphs of G that have
the same configuration as the graph of Figure 52(c) and 1 is the number of times that this subgraph is counted in M. Consequently,
.
Figure 52. 
walks of length 7 type 23.
Case 24: For the configuration of Figure 53(a), 
,
(See Theorem 11). Let 
denote the number of all subgraphs of G that have the same configuration as thegraph of Figure 53(b) and are counted in M. Thus
, where 
is the number of subgraphsof G that have the same configuration as the graph of Figure 53(b) and 1 is the number of times that this figure is counted in M. Consequently,
Figure 53. 
walks of length 7 type 24.
Case 25: For the configuration of Figure 54(a), 
,
(See Theorem 8). Let 
denote
the number of all subgraphs of G that have the same configuration as the graph of Figure 54(b) and are counted
in M. Thus
, where 
is the number of subgraphs of G that have the same configuration as
the graph of Figure 54(b) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number all subgraphs of G that have the same configuration as the graph of Figure 54(c) and are counted
in M. Thus
, where 
is the number of subgraphs of G that have the same configuration
as the graph of Figure 54(c) and 1 is the number of times that this subgraph is counted in M. Consequently,
Figure 54. 
walks of length 7 type 25.
Case 26: For the configuration of Figure 55(a), 
,
. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 55(b) and are
counted in M. Thus
, where 
is the number of subgraphs of G that have the same
configuration as the graph of Figure 55(b) and 1 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure
55(c) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the
same configuration as the graph of Figure 55(c) and 1 is the number of times that this subgraph is counted in M. Consequently,
Figure 55. 
walks of length 7 type 26.
Case 27: For the configuration of Figure 56(a), 
,
. Let 
denote the
number of all subgraphs of G that have the same configuration as the graph of Figure 56(b) and are counted in
M. Thus
, where 
is the number of subgraphs of G that have the same configuration as
the graph of Figure 56(b) and 1 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 56(c) and are
counted in M. Thus
, where 
is the number of subgraphs of G that have the same
configuration as the graph of Figure 56(c) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure
56(d) and are counted in M. Thus
, where 
is the number of subgraphs of G that have
the same configuration as the graph of Figure 56(d) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of
Figure 56(e) and are counted in M. Thus
, where 
is the number of subgraphs of G that
have the same configuration as the graph of Figure 56(e) and 2 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph
of Figure 56(f) and are counted in M. Thus
, where 
is the number of subgraphs of G
that have the same configuration as the graph of Figure 56(f) and 2 is the number of times that this
subgraph is counted in M. Consequently, 
Figure 56. 
walks of length 7 type 27.
Case 28: For the configuration of Figure 57(a), 
,
. Let 
denote the number
of all subgraphs of G that have the same configuration as the graph of Figure 57(b) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the graph
of Figure 57(b) and 1 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 57(c) and are counted in
M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the graph of Figure 57(c) and 1 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 57(d) and are
counted in M. Thus
, where 
is the number of subgraphs of G that have the same
configuration as the graph of Figure 57(d) and 3 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure
57(e) and are counted in M. Thus
, where 
is the number of subgraphs of G that have
the same configuration as the graph of Figure 57(e) and 2 is the number of times that this subgraph is
counted in M. Consequently, 
Figure 57. 
walks of length 7 type 28.
Case 29: For the configuration of Figure 58(a), 
,
. Let 
denote
the number of all subgraphs of G that have the same configuration as the graph of Figure 58(b) and are counted
in M. Thus
, where 
is the number of subgraphs of G that have the same configuration
as the graph of Figure 58(b) and 1 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 58(c) and are
counted in M. Thus
, where 
is the number of subgraphs of G that have the same
configuration as the graph of Figure 58(c) and 4 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure
58(d) and are counted in M. Thus
, where 
is the number of subgraphs of G that have
the same configuration as the graph of Figure 58(d) and 4 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of
Figure 58(e) and are counted in M. Thus
, where 
is the number of subgraphs of G that
have the same configuration as the graph of Figure 58(e) and 1 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph
of Figure 58(f) and are counted in M. Thus
, where 
is the number of subgraphs of G
that have the same configuration as the graph of Figure 58(f) and 2 is the number of times that this subgraph is counted in M. Consequently,
Figure 58. 
walks of length 7 type 29.
Case 30: For the configuration of Figure 59(a), 
,
. Let 
denote the number of
all subgraphs of G that have the same configuration as the graph of Figure 59(b) and are counted in M. Thus
, where 
is the number of subgraphs of G that have the same configuration as the graph of
Figure 59(b) and 1 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 59(c) and are counted in M.
Thus
, where 
is the number of subgraphs of G that have the same configuration as the
graph of Figure 59(c) and 1 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 59(d) and are counted
in M. Thus
, where 
is the number of subgraphs of G that have the same configuration
as the graph of Figure 59(d) and 3 is the number of times that this subgraph is counted in M. Let 
denote the number of all subgraphs of G that have the same configuration as the graph of Figure 59(e) and are
counted in M. Thus
, where 
is the number of subgraphs of G that have the same
configuration as the graph of Figure 59(e) and 2 is the number of times that this subgraph is counted in
M. Consequently, 
Figure 59. 
walks of length 7 type 30.
Now, we add the values of 
arising from the above cases and determine x. Substituting the value of x in
and simplifying, we get the number of 7-cycles each of which contains a specific vertex 
of G. □
Example 3 In the graph of Figure 29 we have,
. So, we have
. Consequently, by Theorem 14, the number of 7-cycles each of which contains the vertex 
in the graph of Figure 29 is 0.
Cite this paper
Nazanin Movarraei,Samina A. Boxwala, (2016) On the Number of Cycles in a Graph. Open Journal of Discrete Mathematics,06,41-69. doi: 10.4236/ojdm.2016.62005
References
- 1. Harary, F. and Manvel, B. (1971) On the Number of Cycles in a Graph. Mat. Casopis Sloven. Akad. Vied, 21, 55-63.
- 2. Chang, Y.C. and Fu, H.L. (2003) The Number of 6-Cycles in a Graph. Bulletin of the ICA, 39, 27-30.
- 3. Alon, N., Yuster, R. and Zwick, U. (1997) Finding and Counting Given Length Cycles. Algorithmica, 17, 209-223.
http://dx.doi.org/10.1007/BF02523189 - 4. Bjorklund, A., Husfeldt, T., Kaski, P. and Koivisto, M. (2009) Counting Paths and Packing in Halves. Lecture Notes in Computer Science, 5757, 578-586.
http://dx.doi.org/10.1007/978-3-642-04128-0_52 - 5. Bjorklund, A., Husfeldt, T., Kaski, P. and Koivisto, M. (2008) The Fast Intersection Transform with Applications to Counting Paths, CoRR, abs/0809.2489.
- 6. Chen, J., Lu, S., Sze, S.H. and Zhang, F. (2007) Improved Algorithms for Path, Matching and Packing Problems. 18th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA 2007), Philadelphia, 298-307.
- 7. Koutis, I. (2008) Faster Algebraic Algorithm for Path and Packing Problems. CALP, LNCS 5125, 575-586. Springer, Berlin.
- 8. Kroese, D.P. and Roberts, B. (2007) Estimating the Number of s-t Paths in a Graph. Journal of Graph Algorithms and Applications, 11, 195-214.
http://dx.doi.org/10.7155/jgaa.00142 - 9. Williams, R. (2009) Finding a Path of Length k in O*(2K)Time. Information Processing Letters, 109, 315-318.
http://dx.doi.org/10.1016/j.ipl.2008.11.004 - 10. Boxwala, S.A. and Movarraei, N. (2015) On the Number of Paths of Length 5 in a Graph. International Journal of Applied Mathematical Research, 4, 30-51.
http://dx.doi.org/10.14419/ijamr.v4i1.3874 - 11. Movarraei, N. and Shikare, M.M. (2014) On the Number of Paths of Lengths 3 and 4 in a Graph. International Journal of Applied Mathematical Research, 3, 178-189.
- 12. Boxwala, S.A. and Movarraei, N. (2015) On the Number of Paths of Length 6 in a Graph. International Journal of Applied Mathematical Research, 4, 267-280.
http://dx.doi.org/10.14419/ijamr.v4i2.4314