Received 14 January 2015; accepted 14 December 2015; published 17 December 2015

ABSTRACT

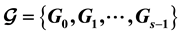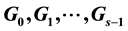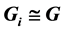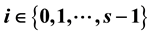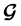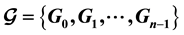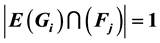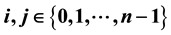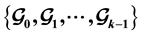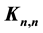A decomposition of a graph H is a partition of the edge set of H into edge- disjoint subgraphs. If for all, then is a decomposition of H by G. Two decompositions and of the complete bipartite graph are orthogonal if, for all. A set of decompositions of is a set of k mutually orthogonal graph squares (MOGS) if 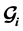and 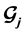are orthogonal for all 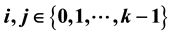and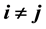. For any bipartite graph G with n edges, denotes the maximum number k in a largest possible set of MOGS of by . Our objective in this paper is to compute where is a path of length d with d + 1 vertices (i.e. Every edge of this path is one-to-one corresponding to an isomorphic to a certain graph F).

Keywords:

Orthogonal Graph Squares, Orthogonal Double Cover

1. Introduction

In this paper we make use of the usual notation: for the complete bipartite graph with partition sets of sizes m and n, for the path on n + 1 vertices, for the disjoint union of D and F, for the union of D and F with (set of vertices) that belong to each other (i.e. union of D and F with common vertices of the set belong to F and D), for the complete graph on n vertices, for an isolated vertex. The other terminologies not defined here can be found in [1] .

A decomposition of a graph H is a partition of the edge set of H into edge-disjoint subgraphs. If for all, then is a decomposition of H by G. Two decompositions and of the complete bipartite graph are or-

thogonal if, for all. Orthogonality requires that

for all. A set of decompositions of is a set of k mutually orthogonal graph squares (MOGS) if and are orthogonal for all and. We use the notation for the maximum number k in a largest possible set of MOGS of by G, where G is a bipartite graph with n edges.

If two decompositions and of by G are orthogonal, then is an orthogonal double cover of by G. Orthogonal decompositions of graphs and orthogonal double covers (ODC) of graphs have been studied by several authors; see the survey articles [2] [3] .

It is well-known that orthogonal Latin squares exist for every. A family of k-orthogonal Latin squares of order n is a set of k Latin squares any two of which are orthogonal. It is customary to denote be the maximal number of squares in the largest possible set of mutually orthogonal Latin squares MOLS of side n. A decomposition of by is equivalent to a Latin square of side n; two decompositions and of by are orthogonal if and only if the corresponding Latin squares of side n are orthogonal; and thus. The computation of is one of the most difficult problems in combinatorial designs; see the survey articles by Abel et al. [4] and Colbourn and Dinitz in [5] . Since is a natural extension of, the study of for general graphs is interesting.

El-Shanawany [6] establishes the following: i); ii) and

; iii) let be a prime number, then; iv) let p be a prime

number, then. Based on ii), El-Shanawany [6] proposed:

Conjecturer 1. Let p be a prime number. Then

Sampathkumar et al. [7] have proved El-Shanawany conjectured. In the following section, we present another technique to prove this conjecture as in Theorem 8.

The two sets and denote the vertices of the partite sets of. The

length of the edge of is defined to be the difference, where. Note that sums and differences are carried over in (that is, sums and differences are carried modulo n). Let G be a subgraph of without isolated vertices and let. The a-translate of G, denoted by, is the edge- induced subgraph of induced by. A subgraph G of is half-starter

if and the lengths of all edges in G are mutually different.

Lemma 2 (see [8] ). If G is a half-starter, then the union of all translates of G forms an edge decomposition of (i.e.).

In what follows, we denote a half-starter G by the vector,

where and can be obtained from the unique edge of length i in G.

Theorem 3 (see [8] ). Two half-starters and are orthogonal if.

If two half-starters and are orthogonal, then the set of translates of G and the set of translates of F are orthogonal.

A set of decompositions of } is a set of k mutually or-

thogonal graph squares (MOGS) if and are orthogonal for all and.

Note that

In the following, we define a G-square over additive group.

Definition 4 (see [6] ). Let G be a subgraph of A square matrix of order n is called an G-square if every element in occur exactly n times, and the graphs, with are isomorphic to graph G.

We have already from Lemma 2 and Definition 4 that every half starter vector and its translates are equivalent to G-square. For more illustration, the first matrix in equation (1) is equivalent to the first row in Figure 3, which represented by the half starter vector and its translates.

Definition 5. Two squares matrices and of order n are said to be orthogonal if for any ordered pair, there is exactly one position for and.

Now, we shall derive a class of mutually orthogonal subgraphs of by a given graph G as follow.

Definition 6. A set of matrices of is called a set of k mutually orthogonal graph squares (MOGS) if and are orthogonal for all and.

Definition 7 (see [9] ). Let F be a certain graph, the graph F-path denoted by, is a path of a set of vertices and a set of edges if and only if there exists the following two bijective mappings:

1) defined by, where is a collection of d graphs, each one is isomorphic to the graph F.

2) defined by, where is a class of disjoint sets of vertices (i.e., decomposed into disjoint sets such that no two vertices within the same set are adjacent).

As a special case if the given graph F is isomorphic to then, is the natural path that is,.

For more illustration, see Figure 1, Figure 2.

Consider paths of length, all attached to the same vertex (root vertex). This tree will be called. Clearly, is the star with s edges and is the path with k edges. Define as a set of all leaves of i.e. and.

In the following section, we will compute where such that as in theorem 8 and as in theorem 11.

2. Mutually Orthogonal Graph-Path Squares

The following result was shown in [7] . Here we present another technique for the proof.

Theorem 8. Let q be a prime number. Then

Proof. Let be a subgraph of with q edges; for fixed and, define the q half- starter vectors as follows, our task is to prove the orthogonality of those q half-stater vectors in mutually. Let us define the half starter vector as for all. Then for all two different elements, we have

, then, are mutually orthogonal half-starter

vectors of graphs and of respectively iff. It remains to prove the isomorphism of half starter graphs of for all. Let , and therefore. Furthermore, if

, then, since (orthogonality

of and), and therefore. Moreover, for any the graph isomorphic to has the edges: ■

An immediate consequence of the Theorem 8 and Conjecture 1 is the following result.

Example 9. The three mutually orthogonal decompositions (MOD) of by given in Figure 3 are associated with the three mutually orthogonal -squares as in Equation (1):

(1)

Note that, every row in Figure 3 represents edge decompositions of by.

The following result is a generalization of the Theorem 8.

Theorem 10. Let n be a prime power such that with integer power of a prime number q and G be a subgraph of. Then

Proof. For fixed and, define the q half-starter vectors as follows,

(2)

Our task is to prove the orthogonality of those q half-starter vectors in mutually. Let us define the half starter vector as for all. Then for all two different elements, we

have, and then, are mutually orthogonal

half-stater vectors of graphs and of respectively iff. It remains to prove the isomorphism of half starter graphs of for all. Let , and therefore. Furthermore, if

, then, since (orthogonality

of and), and therefore. Moreover, for any the graph isomorphic to G has the edges:

(3)

■

Note that, in the special case the Theorem 10 proved El-Shanawany conjecture; also, in the case, and, Theorem 10 constructed an orthogonal double cover of by G.

Furthermore, we can construct the following result using Theorem 10 in case and.

Theorem 11. Let be a positive integer such that and be a subgraph

of. Then

Proof. The result follows from the vector in Equation (2) and its edges in Equation (3) with

such that, imply that which define the

number of graphs isomorphic to F. As a direct application of Theorem 11; see Figure 4. ■

Conjecture 12. if q is a prime number with an integer power.

Conjecture 13. if q is a prime number with an integer power and are positive integers.

Cite this paper

RamadanEl-Shanawany, (2016) On Mutually Orthogonal Graph-Path Squares. Open Journal of Discrete Mathematics,06,7-12. doi: 10.4236/ojdm.2016.61002

References