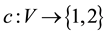Received 30 July 2014; revised 25 August 2014; accepted 20 September 2014
ABSTRACT
We prove that a random labeled (unlabeled) tree is balanced. We also prove that random labeled and unlabeled trees are strongly 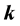 -balanced for any
-balanced for any . Definition: Color the vertices of graph
. Definition: Color the vertices of graph 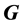 with two colors. Color an edge with the color of its endpoints if they are colored with the same color. Edges with different colored endpoints are left uncolored.
with two colors. Color an edge with the color of its endpoints if they are colored with the same color. Edges with different colored endpoints are left uncolored. 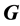 is said to be balanced if neither the number of vertices nor and the number of edges of the two different colors differs by more than one.
is said to be balanced if neither the number of vertices nor and the number of edges of the two different colors differs by more than one.
Keywords:
Random Trees, Balance, Equicolorable Graphs

1. Introduction
The notion of a balanced graph is defined [1] as follows:
Definition 1.1 Let 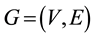 be a finite simple graph,
be a finite simple graph, 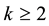 be an integer,
be an integer, 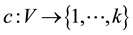 be a map.
be a map.
For all , we write
, we write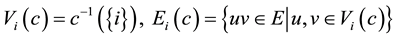 . We also write
. We also write 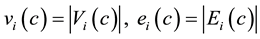 . The map
. The map 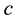 is called a coloring.
is called a coloring.
The case of 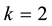 is especially interesting. In this case, the sets
is especially interesting. In this case, the sets 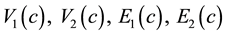 are called the sets of black vertices, white vertices, black edges, and white edges respectively. If the coloring
are called the sets of black vertices, white vertices, black edges, and white edges respectively. If the coloring 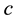 is fixed we may drop it in the notation.
is fixed we may drop it in the notation.
Definition 1.2 A finite simple graph 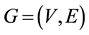 is called balanced if there exists a coloring
is called balanced if there exists a coloring 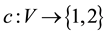
such that ![]() and
and![]() . A map
. A map ![]() satisfying this condition is called a balanced coloring.
satisfying this condition is called a balanced coloring.
The graph in Figure 1 is balanced since we have shown a balanced coloring of it.
It is not difficult to see that:
![]()
Figure 1. With the given coloring, the graph has 4 black and 3 white vertices; it also has 2 white edges (labeled with a “W”) and 1 black edge (labeled with a “B”).
1) The complete graph ![]() is balanced if and only if
is balanced if and only if ![]() or
or ![]() is even.
is even.
2) The star ![]() is balanced if and only if
is balanced if and only if![]() ; see Figure 2 for a balanced coloring of
; see Figure 2 for a balanced coloring of![]() .
.
3) The double star ![]() is balanced if and only if
is balanced if and only if![]() . (The double star
. (The double star ![]() is a connected graph where some two adjacent vertices have degree
is a connected graph where some two adjacent vertices have degree ![]() and
and![]() , and all other vertices have degree 1).
, and all other vertices have degree 1).
In [2] , the author introduces a somewhat similar notion of a cordial graph, a generalization of both graceful and harmonious graphs. It has been conjectured by A. Rosa, G. Ringel and A. Kotzig that every tree is graceful (Graceful Tree Conjecture, [3] ), and it has been conjectured by R. Graham and N. Sloane that every tree is harmonious (see [4] ). While these conjectures are still open, in [5] it is proved that every tree is cordial.
Not every tree is balanced; in this paper, we will be interested in the property of being balanced for a random labeled and unlabeled tree, as well as for random labeled graphs.
The main results of the paper are Theorem A and Theorem B, stated below.
Theorem A A random labeled (unlabeled) tree is balanced; more precisely, if ![]() denotes the number of all labeled (unlabeled) trees on
denotes the number of all labeled (unlabeled) trees on ![]() vertices, and
vertices, and ![]() denotes the number of all balanced labeled (unla-
denotes the number of all balanced labeled (unla-
beled) trees on ![]() vertices, then
vertices, then ![]() and
and![]() .
.
Remark 1.3 In this paper, for simplicity, we consider only uniform models of random graphs and random trees. The results can be extended to a large class of non-uniform models as well. Note that ![]() (see [6] or [7] ) and
(see [6] or [7] ) and ![]() for some positive constants
for some positive constants ![]() and
and ![]() (see [8] ).
(see [8] ).
We also would like to introduce the notion of ![]() -balanced graphs.
-balanced graphs.
Definition 1.4 Let![]() . A finite simple graph
. A finite simple graph ![]() is called
is called ![]() -balanced if there exists a coloring
-balanced if there exists a coloring ![]() such that
such that ![]() and
and ![]() for all distinct
for all distinct![]() . The map
. The map ![]() will be called a
will be called a ![]() -balanced coloring.
-balanced coloring.
Definition 1.5 Let![]() . A finite simple graph
. A finite simple graph ![]() is called strongly
is called strongly ![]() -balanced if there exists a coloring
-balanced if there exists a coloring ![]() such that
such that![]() , and
, and ![]() for all distinct
for all distinct![]() . The map
. The map ![]() will be called a strongly
will be called a strongly ![]() -balanced coloring.
-balanced coloring.
In more popular terms, a finite simple graph is strongly ![]() -balanced if and only if it is
-balanced if and only if it is ![]() -equitably colorable. In Section 5 we study some basic properties of
-equitably colorable. In Section 5 we study some basic properties of ![]() -balanced graphs. We prove the following theorem.
-balanced graphs. We prove the following theorem.
Theorem B. For all![]() , a random (labeled) tree is strongly
, a random (labeled) tree is strongly ![]() -balanced.
-balanced.
Remark 1.6 Let us emphasize that Theorem B is originally due to B. Bollobás and R. Guy (see [9] ). Our proof in this paper is very different with some ingredients which might be interesting independently.
Remark 1.7 It has been proved by I. Ben-Eliezer and M. Krivelevich (see [10] ) that a random graph is balanced. For![]() , it seems quite plausible that a random graph is indeed
, it seems quite plausible that a random graph is indeed ![]() -balanced. However, notice that the clique number of a random graph on
-balanced. However, notice that the clique number of a random graph on ![]() vertices is at least
vertices is at least ![]() (see [11] ) thus a random graph is not strongly
(see [11] ) thus a random graph is not strongly ![]() -balanced.
-balanced.
Acknowledgement: We would like to thank to B. Gittenberger for the discussion and for bringing the reference [12] to our attention; to I. Pak for his comments; to M. Krivelevich for bringing [9] to our attention. We also would like to extend our gratitude to the anonymous referee for many helpful remarks, and for pointing out a flaw in the proof of Lemma 5.3.
Notes:
1) For any finite simple graph![]() , we will denote the maximum degree of
, we will denote the maximum degree of ![]() by
by![]() .
.
2) A vertex of degree one will be called a leaf vertex or simply a leaf. A non-leaf vertex ![]() is called a pre- leaf vertex if it is adjacent exactly to
is called a pre- leaf vertex if it is adjacent exactly to ![]() leaves where
leaves where![]() . A pre-leaf vertex of degree two is called special.
. A pre-leaf vertex of degree two is called special.
3) For![]() , there exists a unique tree up to isomorphism with
, there exists a unique tree up to isomorphism with ![]() vertices and maximum degree at most two; we will call this tree a path on
vertices and maximum degree at most two; we will call this tree a path on ![]() vertices, and denote it with
vertices, and denote it with![]() .
.
4) For a finite simple graph ![]() and for a subset
and for a subset![]() , the induced subgraph
, the induced subgraph ![]() will be called the full subgraph of
will be called the full subgraph of ![]() on
on![]() .
.
5) For a tree ![]() and a non-leaf vertex
and a non-leaf vertex![]() , a subset
, a subset ![]() will be called a branch of
will be called a branch of ![]() with respect to
with respect to ![]() if
if ![]() is a maximal subset such that the full subgraph
is a maximal subset such that the full subgraph ![]() is connected and
is connected and ![]() where
where ![]() denotes the distance in the tree
denotes the distance in the tree![]() .
.
2. Characterization of Balanced Graphs
In this section we observe some basic facts on balanced and ![]() -balanced graphs. Let us first prove a very simple lemma which provides a necessary and sufficient condition for a graph to be balanced.
-balanced graphs. Let us first prove a very simple lemma which provides a necessary and sufficient condition for a graph to be balanced.
Lemma 2.1 Let ![]() be a finite simple graph with
be a finite simple graph with ![]() vertices, and degrees
vertices, and degrees![]() .
. ![]() is balanced if and only if there exists a partition
is balanced if and only if there exists a partition ![]() such that
such that
1) ![]()
2) ![]()
Proof. Let![]() .
.
Assume ![]() is balanced with a balanced coloring
is balanced with a balanced coloring![]() .
.
Let![]() .
.
Since ![]() is a balanced coloring, we get
is a balanced coloring, we get ![]() so condition 1) is satisfied.
so condition 1) is satisfied.
For every![]() , we denote
, we denote
![]()
and for every![]() , we denote
, we denote
![]()
Then![]() . On the other hand, since
. On the other hand, since ![]() is balanced, we have
is balanced, we have ![]() .
.
Then![]() . Thus condition 2) is also satisfied.
. Thus condition 2) is also satisfied.
To prove the converse, assume conditions 1) and 2) are satisfied. We define the coloring ![]() as follows: for every
as follows: for every ![]() we set
we set ![]() and for every
and for every ![]() we set
we set![]() .
.
Then we have![]() .
.
On the other hand,
![]()
Then by condition 2), we get![]() .
. ![]()
Corollary 2.2 It is proved in [1] that an ![]() -regular finite simple graph with
-regular finite simple graph with ![]() vertices is balanced if and only if
vertices is balanced if and only if ![]() is even or
is even or![]() . This fact also follows immediately from Lemma 2.1. In [13] , the authors deduce the same fact from their characterization of balanced graphs.
. This fact also follows immediately from Lemma 2.1. In [13] , the authors deduce the same fact from their characterization of balanced graphs.
Lemma 2.1 shows that the balancedness of a graph completely depends on the degree sequence of it. This is no longer the case for ![]() -balanced graphs for
-balanced graphs for![]() . In fact, the trees
. In fact, the trees ![]() and
and ![]() in Figure 3 have the same degree sequence
in Figure 3 have the same degree sequence![]() , and it is not difficult to see that
, and it is not difficult to see that ![]() is 3-balanced while
is 3-balanced while ![]() is not.
is not.
The fact that, for![]() , the
, the ![]() -balancedness is not determined by the degree sequence causes difficulties in proving that random graphs are
-balancedness is not determined by the degree sequence causes difficulties in proving that random graphs are ![]() -balanced. It also seems plausible that, generically,
-balanced. It also seems plausible that, generically, ![]() -balancedness is a weaker condition than balancedness, although it does not seem easy to describe (with a good sufficient condition) when exactly is this true. It is useful to point out the following simple fact.
-balancedness is a weaker condition than balancedness, although it does not seem easy to describe (with a good sufficient condition) when exactly is this true. It is useful to point out the following simple fact.
Proposition 2.3 For all distinct ![]() there exists a finite simple graph which is
there exists a finite simple graph which is ![]() -balanced but not
-balanced but not ![]() -balanced.
-balanced.
Proof. Let ![]() be a prime number such that
be a prime number such that![]() .
.
Let us first assume that![]() . If
. If ![]() divides
divides![]() , then the graph
, then the graph ![]() is
is ![]() -balanced but not
-balanced but not ![]() -balanced. If
-balanced. If ![]() does not divide
does not divide ![]() then the graph
then the graph ![]() is
is ![]() -balanced but not
-balanced but not ![]() -balanced.
-balanced.
Now assume that![]() . Then the graph
. Then the graph ![]() is
is ![]() -balanced but not
-balanced but not ![]() -balanced.
-balanced. ![]()
3. Combinatorial Lemmas
Let![]() . The elements of
. The elements of ![]() consist of sequences of positive integers of length
consist of sequences of positive integers of length ![]() such that no term is bigger than
such that no term is bigger than![]() . We denote
. We denote![]() .
.
Now we introduce the notion of balanced sequences:
Definition 3 A sequence (an element) ![]() is called balanced if and only if there exists a partition
is called balanced if and only if there exists a partition ![]() such that
such that
1) ![]()
2) ![]()
The partition ![]() will be called a balanced partition.
will be called a balanced partition.
In these new terms, Lemma 2.1 states that a graph is balanced if and only if its degree sequence is balanced.
When the sequence is not balanced, we would like to measure how far it is from being balanced.
Definition 3.1 Let ![]() be any finite sequence of non-negative integers. The quantity
be any finite sequence of non-negative integers. The quantity
![]()
will be called the balance of![]() .
.
Remark 3.2 By Lemma 2.1, a sequence ![]() is balanced if and only if
is balanced if and only if![]() . The quantity
. The quantity![]() , somewhat roughly, measures how far the sequence is from being balanced. For an example, let
, somewhat roughly, measures how far the sequence is from being balanced. For an example, let ![]()
and ![]() be a sequence of length 8. It is easy to see
be a sequence of length 8. It is easy to see ![]() .
.
The following easy lemma will be useful:
Lemma 3.3 Let ![]() be any finite sequence of non-negative integers. Then
be any finite sequence of non-negative integers. Then![]() .
.
Proof. We will present a constructive proof.
Without loss of generality, we may assume that![]() . First, let us assume that
. First, let us assume that ![]() is even, so let
is even, so let![]() . We will build two subsets
. We will build two subsets ![]() of
of ![]() inductively such that
inductively such that![]() ,
, ![]() and
and
![]() .
.
We divide the sequence into pairs![]() , and we will abide by the rule that exactly one element of each pair belongs to
, and we will abide by the rule that exactly one element of each pair belongs to ![]() and the other element belongs to
and the other element belongs to![]() . We start by letting
. We start by letting ![]() . Assume now we have built the subsets
. Assume now we have built the subsets ![]() such that
such that ![]() and
and ![]() for all
for all![]() .
.
Let![]() . If
. If ![]() then we let
then we let ![]() but if
but if ![]() then we let
then we let ![]() , and we proceed by induction. Then we let
, and we proceed by induction. Then we let![]() . Clearly, we have
. Clearly, we have![]() .
.
If ![]() is odd, then we may replace
is odd, then we may replace ![]() by
by ![]() and apply the previous argument.
and apply the previous argument. ![]()
We will need the following notations
Definition 3.4 Let![]() . We will denote
. We will denote
![]()
Lemma 3.5 Let ![]() such that
such that ![]() and
and![]() . Then
. Then ![]() is balanced.
is balanced.
Proof. Let![]() . Without loss of generality we may assume that
. Without loss of generality we may assume that
![]() . If
. If ![]() then
then ![]() is clearly balanced so let
is clearly balanced so let ![]() and let
and let
![]() .
.
By Lemma 3.3, ![]() hence there exists a partition
hence there exists a partition ![]() such that
such that ![]() and
and![]() . Then there exists a partition
. Then there exists a partition ![]() such that
such that ![]() and
and![]() . By letting
. By letting ![]() we obtain that
we obtain that ![]() ,
, ![]() , and
, and![]() .
. ![]()
4. Proof of Theorem A
First, we will discuss the case of labeled trees. The following theorem of J. W. Moon will play a crucial role.
Theorem 4.1 (see [14] ) If ![]() is a fixed positive constant, then in a random labeled tree
is a fixed positive constant, then in a random labeled tree ![]() with
with ![]() vertices, the maximum degree
vertices, the maximum degree ![]() satisfies the following inequality
satisfies the following inequality
![]()
Remark 4.2 By choosing ![]() we obtain that
we obtain that
![]()
in a random tree with ![]() vertices.
vertices.
We will use only the upper bound in the inequality of Remark 4.2. Besides the upper bound on the maximum degree in random trees, we also need a lower bound on the number of vertices with degree 1, and with degree 2. Notice that, since the sum of degrees of a tree with ![]() vertices is exactly
vertices is exactly![]() , at least half of the vertices have degree either 1 or 2. However, we need a linear lower bound for the number of vertices of degree 1 and for the number of vertices of degree 2 separately.
, at least half of the vertices have degree either 1 or 2. However, we need a linear lower bound for the number of vertices of degree 1 and for the number of vertices of degree 2 separately.
Let ![]() be the random variable which denotes the number of vertices of degree
be the random variable which denotes the number of vertices of degree ![]() in a labeled tree
in a labeled tree ![]() with
with ![]() vertices. Also let
vertices. Also let![]() . It has been proved by A. Rényi (see [15] ) that the asymptotic distribution of random variable
. It has been proved by A. Rényi (see [15] ) that the asymptotic distribution of random variable ![]() is normal with mean
is normal with mean ![]() and variance
and variance![]() . A similar result has been proved for the random variable
. A similar result has been proved for the random variable![]() , by A. Meir and J. W. Moon (see [16] ), namely, that the asymptotic distribution of the random variable
, by A. Meir and J. W. Moon (see [16] ), namely, that the asymptotic distribution of the random variable ![]() is normal with mean
is normal with mean ![]() and variance
and variance![]() . Combining these two results we can state the following theorem (due to A. Rényi and A. Meir-J.W. Moon)
. Combining these two results we can state the following theorem (due to A. Rényi and A. Meir-J.W. Moon)
Theorem 4.3 Let ![]() be fixed real numbers,
be fixed real numbers,![]() ; and for
; and for![]() , let
, let ![]() denotes the probability that
denotes the probability that![]() . Then
. Then
![]()
We need the following immediate corollary of this theorem
Corollary 4.4 In a random labeled tree with ![]() vertices, for all
vertices, for all![]() ,
,![]() .
.
Now, in the case of random labeled trees, Theorem A immediately follows from Theorem 4.1, Corollary 4.4, and Lemma 3.5.
The case of unlabeled trees: We will use the results analogous to Theorem 4.1 and Theorem 4.3. The analogue of Theorem 4.1 is proved by W. Goh and E. Schmutz:
Theorem 4.5 (see [12] ) There exists positive constants ![]() such that in a random unlabeled tree
such that in a random unlabeled tree ![]() with
with ![]() vertices, the maximum degree
vertices, the maximum degree ![]() satisfies the inequality
satisfies the inequality![]() .
.
Now, for any ![]() let the random variable
let the random variable ![]() denotes the number of vertices of degree
denotes the number of vertices of degree ![]() in a random unlabeled tree with
in a random unlabeled tree with ![]() vertices. The following theorem is due to M. Drmota and B. Gittenberger; in the case of
vertices. The following theorem is due to M. Drmota and B. Gittenberger; in the case of
![]() , as a special case, it provides an analogue of Theorem 4.3.
, as a special case, it provides an analogue of Theorem 4.3.
Theorem 4.6 (see [17] ) For arbitrary fixed natural![]() , there exist positive constants
, there exist positive constants ![]() and
and ![]() such that the limiting distribution of
such that the limiting distribution of ![]() is normal with mean
is normal with mean ![]() and variance
and variance![]() .
.
Corollary 4.7 For all ![]() and
and![]() , in a random unlabeled tree with
, in a random unlabeled tree with ![]() vertices
vertices![]() .
.
Now, in the case of unlabeled trees, the claim of Theorem A follows from Theorem 4.5, Lemma 3.5, and Corollary 4.7.
5. ![]() -Balanced Trees: Proof of Theorem B
-Balanced Trees: Proof of Theorem B
In this section we will assume that![]() . The fact that the
. The fact that the ![]() -balancedness is not determined by the degree sequence causes significant difficulties in proving that random graphs are balanced. We nevertheless prove that random trees are strongly
-balancedness is not determined by the degree sequence causes significant difficulties in proving that random graphs are balanced. We nevertheless prove that random trees are strongly ![]() -balanced by more careful study of
-balanced by more careful study of ![]() -balancedness.
-balancedness.
First, we need to prove the following technical lemma.
Lemma 5.1 Let ![]() be a tree and
be a tree and ![]() be distinct vertices of
be distinct vertices of ![]() with degree at least
with degree at least![]() . If
. If ![]() are distinct pre-leaf vertices of
are distinct pre-leaf vertices of ![]() then there exists a strongly 3-balanced coloring
then there exists a strongly 3-balanced coloring ![]() of
of ![]() such that
such that ![]() and
and![]() .
.
Proof. The proof is by induction on![]() . For
. For ![]() the claim is obvious (since, in this case,
the claim is obvious (since, in this case, ![]() will be isomorphic either to a path or to the double star
will be isomorphic either to a path or to the double star![]() ), so we will assume that
), so we will assume that ![]() and the claim holds for all trees of order less than
and the claim holds for all trees of order less than![]() .
.
Assume that at least one of the following two conditions holds:
(c1) there exists ![]() such that
such that![]() ;
;
(c2) there exists a leaf vertex not adjacent to any of the vertices![]() .
.
Then there exists a leaf ![]() such that if
such that if ![]() is a full subgraph on
is a full subgraph on![]() , then, in the tree
, then, in the tree![]() , we have
, we have![]() , and
, and ![]() are still pre-leaf vertices.
are still pre-leaf vertices.
By inductive hypothesis, there exists a strongly 3-balanced coloring ![]() of
of ![]() such that
such that ![]() and
and![]() . Let
. Let ![]() be the unique vertex of
be the unique vertex of ![]() adjacent to
adjacent to![]() . Without loss of generality, we may assume that
. Without loss of generality, we may assume that ![]() and
and![]() .
.
If ![]() then we let
then we let ![]() thus extending
thus extending ![]() to a strongly 3-balanced coloring
to a strongly 3-balanced coloring ![]() of
of ![]() such that
such that ![]() and
and![]() .
.
If, however, ![]() then there exists
then there exists ![]() such that
such that![]() ; also, since
; also, since![]() ,
,
there exists a branch ![]() of
of ![]() with respect to
with respect to ![]() which is disjoint from
which is disjoint from![]() . Let
. Let ![]() be a leaf vertex in
be a leaf vertex in![]() . Then
. Then ![]() and
and![]() . We define
. We define ![]() as follows:
as follows:
![]()
Notice that because of the inequality![]() , we have
, we have ![]() and
and![]() . Then the map
. Then the map ![]() is a strongly 3-balanced coloring.
is a strongly 3-balanced coloring.
Now, suppose that neither of the conditions (c1) and (c2) hold. Let ![]() be the path in
be the path in ![]() starting at
starting at ![]() and ending at
and ending at ![]() (it may possibly consist of just the vertices
(it may possibly consist of just the vertices ![]() and
and![]() ). Then the tree
). Then the tree ![]() satisfies the following conditions: there exists two vertices
satisfies the following conditions: there exists two vertices ![]() in
in ![]() and paths
and paths ![]() starting at
starting at ![]() respectively such that any vertex of
respectively such that any vertex of ![]() either belongs to one of the paths
either belongs to one of the paths ![]() or it is a leaf vertex adjacent to one of the vertices
or it is a leaf vertex adjacent to one of the vertices![]() . Then it is straightforward to build a strongly 3-balanced coloring
. Then it is straightforward to build a strongly 3-balanced coloring ![]() satisfying the conditions
satisfying the conditions ![]() and
and![]() .
. ![]()
The following proposition is interesting in itself; it will also play a key role in proving Theorem B.
Proposition 5.2 If ![]() is a tree with
is a tree with ![]() then
then ![]() is strongly
is strongly ![]() -balanced. Moreover, for
-balanced. Moreover, for
any two distinct pre-leaf vertices ![]() and
and ![]() of
of ![]() there exists a strongly 3-balanced coloring
there exists a strongly 3-balanced coloring ![]() such that
such that![]() .
.
Proof. The proof will be by induction on![]() . For
. For ![]() we have
we have ![]() hence
hence ![]() is isomorphic to a path. Thus, the claim is obvious. Let us now assume that
is isomorphic to a path. Thus, the claim is obvious. Let us now assume that![]() , and the claim holds for all trees
, and the claim holds for all trees ![]() of
of
order less than ![]() with
with![]() .
.
Let ![]() and
and![]() . We will consider the following three cases separately:
. We will consider the following three cases separately:
Case 1.![]() .
.
Let ![]() be a leaf of
be a leaf of![]() ,
, ![]() , and let
, and let ![]() be the full subgraph of
be the full subgraph of ![]() on
on![]() . Then we have
. Then we have
![]()
By inductive hypothesis, there exists a strongly 3-balanced coloring ![]() of
of![]() .
.
On the other hand, ![]() is adjacent to exactly one vertex in
is adjacent to exactly one vertex in![]() ; let
; let ![]() be this vertex. Let
be this vertex. Let ![]() be any element of
be any element of![]() . We extend the coloring
. We extend the coloring ![]() of
of ![]() to a strongly 3-balanced coloring
to a strongly 3-balanced coloring ![]() by defining
by defining![]() .
.
Case 2.![]() .
.
Let ![]() be distinct leaves and
be distinct leaves and ![]() be the only vertices of
be the only vertices of ![]() adjacent to
adjacent to ![]() respectively (
respectively (![]() and
and ![]() are not necessarily distinct). Let also
are not necessarily distinct). Let also ![]() be the full subgraph of
be the full subgraph of ![]() on the set
on the set![]() . Then we still have the inequality
. Then we still have the inequality![]() . Hence, by inductive assumption, there exists a strongly 3-balanced coloring
. Hence, by inductive assumption, there exists a strongly 3-balanced coloring ![]() of
of![]() .
.
Then there exist distinct ![]() such that
such that ![]() and
and![]() . Thus we can extend
. Thus we can extend ![]() to a strongly 3-balanced coloring of
to a strongly 3-balanced coloring of ![]() by defining
by defining ![]() and
and![]() .
.
Case 3.![]() .
.
The major difference in this case compared with the previous two cases is that when we obtain ![]() by deleting some arbitrary three leaves
by deleting some arbitrary three leaves ![]() from
from![]() , we may lose the inequality
, we may lose the inequality![]() . (Notice that
. (Notice that ![]() possesses three leaf vertices unless it is isomorphic to a path). Suppose
possesses three leaf vertices unless it is isomorphic to a path). Suppose ![]() are the vertices adjacent to
are the vertices adjacent to ![]() respectively. Note that
respectively. Note that ![]() are not necessarily distinct. If we have the inequality
are not necessarily distinct. If we have the inequality ![]() then by inductive assumption we would have a strongly 3-balanced coloring
then by inductive assumption we would have a strongly 3-balanced coloring![]() . However, if
. However, if ![]() then it becomes problematic to extend
then it becomes problematic to extend ![]() to a strongly 3-balanced coloring
to a strongly 3-balanced coloring![]() . Thus we need to employ different and more careful tactics.
. Thus we need to employ different and more careful tactics.
We will prove the following lemma which suffices for the proof of Proposition 5.2 in the case![]() .
.
Lemma 5.3 Let ![]() be a tree with
be a tree with ![]() vertices where
vertices where![]() . If
. If ![]() are distinct pre-leaf vertices of
are distinct pre-leaf vertices of ![]() then there exists a strongly 3-balanced coloring
then there exists a strongly 3-balanced coloring ![]() such that
such that![]() .
.
Proof. The proof of the lemma will be again by induction on![]() . The “
. The “![]() part” of the claim will be needed to make the step of the induction. For
part” of the claim will be needed to make the step of the induction. For![]() , the graph
, the graph ![]() is isomorphic to a path thus the claim is obvious. For
is isomorphic to a path thus the claim is obvious. For ![]() it can be seen by a direct checking. (We leave this to a reader as a simple exercise.) Thus let us assume that
it can be seen by a direct checking. (We leave this to a reader as a simple exercise.) Thus let us assume that![]() .
.
Let![]() . Let also
. Let also![]() . We will consider the following cases (the notations in each case will be independent of the notations of other cases):
. We will consider the following cases (the notations in each case will be independent of the notations of other cases):
Case A: The vertices ![]() and
and ![]() are the only pre-leaf vertices of
are the only pre-leaf vertices of![]() .
.
The claim is obvious when![]() , so we may assume that
, so we may assume that![]() . We will consider two sub- cases:
. We will consider two sub- cases:
Sub-case 1:![]() .
.
Then there exist leaves ![]() such that
such that ![]() is adjacent to
is adjacent to ![]() and
and ![]() are adjacent to
are adjacent to![]() . Let
. Let ![]() be the full subgraph of
be the full subgraph of ![]() on
on![]() . Notice that
. Notice that ![]() and
and ![]() are still pre-leaf vertices of
are still pre-leaf vertices of![]() . By the inductive hypothesis,
. By the inductive hypothesis, ![]() has a strongly 3-balanced coloring
has a strongly 3-balanced coloring ![]() such that
such that![]() . We may assume that
. We may assume that![]() . Then we extend
. Then we extend ![]() to a strongly 3-balanced coloring
to a strongly 3-balanced coloring ![]() by letting
by letting![]() .
.
Sub-case 2:![]() .
.
In this case there exists a path ![]() in
in ![]() where
where ![]() is a leaf,
is a leaf, ![]() are vertices of degree two, and
are vertices of degree two, and
![]()
where ![]() are the leaves adjacent to
are the leaves adjacent to![]() . Then we have the inequalities
. Then we have the inequalities ![]() and
and![]() . We will construct the required strongly 3-balanced coloring explicitly as follows.
. We will construct the required strongly 3-balanced coloring explicitly as follows.
First, for all ![]() we let
we let ![]() when
when ![]() is odd, and
is odd, and ![]() when
when ![]() is even. We also let
is even. We also let ![]() and
and![]() .
.
Now we need to define the coloring on the remaining set
![]()
Let ![]() where
where ![]() for all
for all![]() . (Thus we are reorder the elements of the set
. (Thus we are reorder the elements of the set ![]() from closest to the farthest from the leaf
from closest to the farthest from the leaf![]() .) Then, for all
.) Then, for all![]() , we let
, we let ![]() when
when ![]() is odd, and
is odd, and ![]() when
when ![]() is even.
is even.
For the rest of the proof we will assume that ![]() has more than two pre-leaf vertices.
has more than two pre-leaf vertices.
Case B: ![]() and
and ![]() is not special.
is not special.
Let ![]() be distinct leaves such that
be distinct leaves such that ![]() is adjacent to
is adjacent to![]() ,
, ![]() is adjacent to
is adjacent to![]() , and
, and ![]() is adjacent to a vertex
is adjacent to a vertex ![]() distinct from
distinct from ![]() and
and![]() . We let
. We let ![]() be the full subgraph on
be the full subgraph on![]() . Then
. Then ![]() and we have
and we have![]() . By inductive hypothesis, there exists a strongly 3-balanced coloring
. By inductive hypothesis, there exists a strongly 3-balanced coloring ![]() such that
such that![]() . Without loss of generality we may assume that
. Without loss of generality we may assume that![]() . Then we extend
. Then we extend ![]() to a strongly 3-balanced coloring
to a strongly 3-balanced coloring ![]() as follows: if
as follows: if ![]() then we let
then we let![]() ; and if
; and if ![]() then we let
then we let![]() .
.
Case C: ![]() and
and ![]() is special.
is special.
Let ![]() be the only leaf adjacent to
be the only leaf adjacent to![]() ,
, ![]() be the unique non-leaf vertex adjacent to
be the unique non-leaf vertex adjacent to![]() ,
, ![]() be a leaf vertex not adjacent to
be a leaf vertex not adjacent to![]() , and
, and ![]() be the unique vertex adjacent to
be the unique vertex adjacent to![]() . We let
. We let ![]() be the full subgraph on
be the full subgraph on![]() . Then
. Then ![]() and
and![]() . By inductive hypothesis, there exists a strongly 3-balanced coloring
. By inductive hypothesis, there exists a strongly 3-balanced coloring![]() . Then we extend
. Then we extend ![]() to a strongly 3-balanced coloring
to a strongly 3-balanced coloring ![]() as follows: we let
as follows: we let ![]() such that
such that ![]() is distinct from
is distinct from ![]() and
and![]() . Then we define
. Then we define ![]() such that
such that ![]() is distinct from
is distinct from ![]() and
and![]() . Finally we let
. Finally we let ![]() such that
such that ![]() is distinct from
is distinct from ![]() and
and![]() . Notice also that we obtain
. Notice also that we obtain![]() .
.
Case D: ![]() and there exists a leaf vertex adjacent to
and there exists a leaf vertex adjacent to![]() .
.
This case is similar to Case B. Since ![]() and
and![]() , we have
, we have![]() . If
. If![]() , we let
, we let ![]() be leaves adjacent to
be leaves adjacent to ![]() respectively; and if
respectively; and if![]() , we let
, we let ![]() be leaves adjacent to
be leaves adjacent to ![]() respectively, and
respectively, and ![]() be a leaf not adjacent to either of the vertices
be a leaf not adjacent to either of the vertices![]() . We define
. We define ![]() be the full subgraph on
be the full subgraph on![]() . Then
. Then ![]() hence
hence ![]() admits a strongly 3-balanced coloring
admits a strongly 3-balanced coloring ![]() such that
such that![]() . We extend
. We extend ![]() to a strongly 3-balanced coloring to
to a strongly 3-balanced coloring to ![]() as in Case B.
as in Case B.
Case E:![]() ,
, ![]() is special and there exists a leaf vertex adjacent to
is special and there exists a leaf vertex adjacent to![]() .
.
This case is similar to Case C. Let ![]() be the only leaf adjacent to
be the only leaf adjacent to![]() ,
, ![]() be the unique non-leaf vertex adjacent to
be the unique non-leaf vertex adjacent to![]() ,
, ![]() be a leaf vertex adjacent to
be a leaf vertex adjacent to![]() . We let
. We let ![]() be the full subgraph on
be the full subgraph on![]() . Then
. Then ![]() and
and![]() . By inductive hypothesis, there exists a strongly 3-balanced coloring
. By inductive hypothesis, there exists a strongly 3-balanced coloring![]() . Then we extend
. Then we extend ![]() to a strongly 3-balanced coloring
to a strongly 3-balanced coloring ![]() as follows: we let
as follows: we let ![]() such that
such that ![]() is distinct from
is distinct from ![]() and
and![]() . Then we define
. Then we define ![]() such that
such that ![]() is distinct from
is distinct from ![]() and
and![]() . Finally we let
. Finally we let ![]() such that
such that ![]() is distinct from
is distinct from ![]() and
and![]() .
.
Case F:![]() , and there is no leaf vertex adjacent to
, and there is no leaf vertex adjacent to![]() .
.
Since![]() , there exists a special vertex
, there exists a special vertex ![]() adjacent to
adjacent to![]() . Let
. Let ![]() be the unique leaf adjacent to
be the unique leaf adjacent to![]() . Let also
. Let also ![]() be a leaf not adjacent to any of the vertices
be a leaf not adjacent to any of the vertices ![]() (such a leaf exists because
(such a leaf exists because![]() ), and let
), and let ![]() be the unique vertex adjacent to
be the unique vertex adjacent to![]() .
.
We define ![]() to be the full subgraph on
to be the full subgraph on![]() . By inductive assumption, there exists a strongly 3-balanced coloring
. By inductive assumption, there exists a strongly 3-balanced coloring![]() , moreover, if
, moreover, if ![]() then
then![]() .
.
If![]() , then we let
, then we let ![]() be any element of
be any element of ![]() distinct from
distinct from![]() . Then we let
. Then we let ![]() be any element of
be any element of ![]() distinct from
distinct from ![]() and
and![]() . Finally, we let
. Finally, we let ![]() be any element of
be any element of ![]() distinct from
distinct from ![]() and
and![]() . Thus we have extended
. Thus we have extended ![]() to a strongly 3-balanced coloring
to a strongly 3-balanced coloring ![]() such that
such that![]() .
.
If ![]() then
then ![]() and we may assume that
and we may assume that![]() . Then we let
. Then we let ![]()
be any element of ![]() distinct from
distinct from ![]() and
and![]() ; then we let
; then we let ![]() be any element of
be any element of ![]() distinct from
distinct from ![]() and
and![]() ; finally we let
; finally we let ![]() be any element of
be any element of ![]() distinct from
distinct from ![]() and
and![]() .
.
Case G:![]() .
.
In this case the claim follows immediately from Lemma 5.1. ![]()
Now we can prove an analogous result for ![]() -balanced graphs.
-balanced graphs.
Proposition 5.4 Let ![]() be a tree with
be a tree with ![]() vertices where
vertices where ![]() and
and![]() . Then
. Then ![]() is strongly
is strongly ![]() -balanced.
-balanced.
Proof. The proof is by induction on![]() . For
. For![]() , the claim is true by Proposition 5.2.
, the claim is true by Proposition 5.2.
Assume now![]() . The tree
. The tree ![]() has
has ![]() vertices
vertices ![]() such that
such that![]() . Moreover, for all distinct
. Moreover, for all distinct![]() , the vertices
, the vertices ![]() and
and ![]() are not connected by an edge. Let also
are not connected by an edge. Let also![]() , and
, and ![]() be a full subgraph on the subset
be a full subgraph on the subset![]() . Then
. Then ![]() is a forest with
is a forest with ![]() vertices but with
vertices but with![]() . This implies that
. This implies that ![]() is a subgraph of a tree
is a subgraph of a tree ![]() with
with ![]() vertices where
vertices where![]() .
.
Then![]() . By inductive hypothesis, we obtain that
. By inductive hypothesis, we obtain that ![]()
is strongly ![]() -balanced, hence
-balanced, hence ![]() is strongly
is strongly ![]() -balanced. Since no two elements of
-balanced. Since no two elements of ![]() are adjacent, we obtain that
are adjacent, we obtain that ![]() is strongly
is strongly ![]() -balanced.
-balanced. ![]()
Now, for random labeled trees, Theorem B follows immediately from Theorem 4.1 and Proposition 5.4; and for random unlabeled trees, it follows immediately from Theorem 4.5 and Proposition 5.4.
References
- Lee, S.-M., Liu, A. and Tan, S.K. (1992) On Balanced Graphs. Congressus Numerantium, 87, 59-64.
- Cahit, I. (1987) Cordial Graphs: A Weaker Version of Graceful and Harmonious Graphs, Ars Combinatoria, 23, 201- 207.
- Gallian, J.A. (2009) A Dynamical Survey of Graph Labeling. The Electronics Journal of Combinatorics, Dynamic Survey 6, 43 p. (electronic).
- Graham, R. and Sloane, N. (2009) On Additive Bases and Harmonious Graphs. SIAM Journal of Algebraic and Discrete Mathematics, 1, x382-x404. http://dx.doi.org/10.1137/0601045
- Cahit, I. (1990) On Cordial and 3-Equitable Graphs, Utilitas Mathematica, 37, 189-198.
- Cayley, A. (1889) A Theorem on Trees. The Quarterly Journal of Mathematics, 23, 376-378.
- West, D.B. (2001) Introduction to Graph Theory. 2nd Edition, Prentice-Hall, Inc., Upper Saddle River, 82-83.
- Otter, R. (1948) The Number of Trees. Annals of Mathematics, 49, 583-599.
- Bollobás, B. and Guy, R. (1983) Equitable and Proportional Coloring of Trees. Journal of Combinatorial Theory, Series B, 34, 177-186.
- Ben-Eliezer, I. and Krivelevich, M. (2009) Perfectly Balanced Partitions of Smoothed Graphs. Electronic Journal of Combinatorics, 16, Note N14.
- Bollobás, B. (2001) Random Graphs. Cambridge Studies in Advanced Mathematics (Book 73). 2nd Edition, Cambridge University Press, Cambridge.
- Goh, W. and Schmutz, E. (1994) Unlabeled Trees: Distribution of the Maximum Degree. Random Structures and Algorithms, 5, 13-24.
- Kong, M.C., Lee, S.-M., Seah, E. and Tang, A. (2008) A Complete Characterization of Balanced Graphs (English Summary). Journal of Combinatorial Mathematics and Combinatorial Computing, 66, 225-236.
- Moon, J.W. (1968) On the Maximum Degree in a Random Tree. The Michigan Mathematical Journal, 15, 429-432.
- Rényi, A. (1959) Some Remarks on the Theory of Trees. Magyar Tud. Akad. Mat. Kutat Int. Kzl, 4, 73-85.
- Meir, A. and Moon, J.W. (1968) On Nodes of Degree Two in Random Trees. Mathematika, 15, 188-192. http://dx.doi.org/10.1112/S0025579300002552
- Drmota, M. and Gittenberger, B. (1999) Distribution of Nodes of Given Degree in Random Trees. Journal of Graph Theory, 31, 227-253. http://dx.doi.org/10.1002/(SICI)1097-0118(199907)31:3<227::AID-JGT6>3.0.CO;2-6



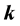 -balanced for any
-balanced for any . Definition: Color the vertices of graph
. Definition: Color the vertices of graph 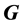 with two colors. Color an edge with the color of its endpoints if they are colored with the same color. Edges with different colored endpoints are left uncolored.
with two colors. Color an edge with the color of its endpoints if they are colored with the same color. Edges with different colored endpoints are left uncolored. 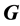 is said to be balanced if neither the number of vertices nor and the number of edges of the two different colors differs by more than one.
is said to be balanced if neither the number of vertices nor and the number of edges of the two different colors differs by more than one.
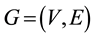 be a finite simple graph,
be a finite simple graph, 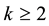 be an integer,
be an integer, 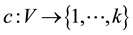 be a map.
be a map. , we write
, we write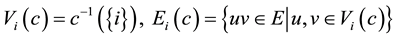 . We also write
. We also write 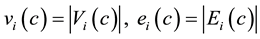 . The map
. The map 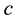 is called a coloring.
is called a coloring.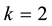 is especially interesting. In this case, the sets
is especially interesting. In this case, the sets 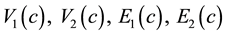 are called the sets of black vertices, white vertices, black edges, and white edges respectively. If the coloring
are called the sets of black vertices, white vertices, black edges, and white edges respectively. If the coloring 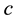 is fixed we may drop it in the notation.
is fixed we may drop it in the notation.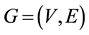 is called balanced if there exists a coloring
is called balanced if there exists a coloring