Open Journal of Discrete Mathematics
Vol.4 No.1(2014), Article ID:42401,3 pages DOI:10.4236/ojdm.2014.41002
The Number of Digraphs with Cycles of Length k
Chuanlong Wang1, Mudaster Sidik2, Xuerong Yong3
1Department of Mathematics, Taiyuan Normal University, Taiyuan, China
2Department of Mathematics, Yili Normal University, Yili, China
3Department of Mathematical Sciences, University of Puerto Rico, Mayaguez, USA
Email: clwang218@126.net, sidik571013@163.com, xryong@dimacs.rutgers.edu
Copyright © 2014 Chuanlong Wang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Chuanlong Wang et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received April 17, 2013; revised May 13, 2013; accepted June 5, 2013
ABSTRACT
In this note, we show that the number of digraphs with n vertices and with cycles of length k, 0 ≤ k ≤ n, is equal to the number of n × n (0,1)-matrices whose eigenvalues are the collection of copies of the entire kth unit roots plus, possibly, 0’s. In particular, 1) when k = 0, since the digraphs reduce to be acyclic, our result reduces to the main theorem obtained recently in [1] stating that, for each n = 1, 2, 3, …, the number of acyclic digraphs is equal to the number of n × n (0,1)-matrices whose eigenvalues are positive real numbers; and 2) when k = n, the digraphs are the Hamiltonian directed cycles and it, therefore, generates another well-known (and trivial) result: the eigenvalues of a Hamiltonian directed cycle with n vertices are the nth unit roots [2].
Keywords: Acyclic Digraph; Eigenvalue; Power Digraph; (0,1)-Matrix
1. Introduction
A digraph 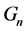 of n vertices
of n vertices 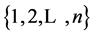 is a directed graph whose edges are oriented from vertex i to vertex j,
is a directed graph whose edges are oriented from vertex i to vertex j,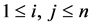 . In this note, the digraphs to be considered are with loops or cycles, but parallel edges are forbidden. An acyclic digraph is a digraph that has no cycles of any length. Let
. In this note, the digraphs to be considered are with loops or cycles, but parallel edges are forbidden. An acyclic digraph is a digraph that has no cycles of any length. Let 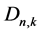 be a digraph of
be a digraph of 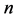 vertices with cycles of length
vertices with cycles of length 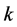 plus, possibly, an acyclic digraph with
plus, possibly, an acyclic digraph with  vertices, where
vertices, where 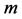 is the number of cycles, and where
is the number of cycles, and where  is fixed,
is fixed, . Then it is seen that the cycles in
. Then it is seen that the cycles in 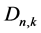 are disjoined (therefore all the cycles that it has are simple) and if
are disjoined (therefore all the cycles that it has are simple) and if 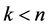 the digraph is not strongly connected. And, in particular,
the digraph is not strongly connected. And, in particular,  is a Hamiltonian directed cycle of size
is a Hamiltonian directed cycle of size 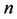 and
and 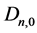 is an acyclic digraph of
is an acyclic digraph of 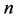 vertices, respectively.
vertices, respectively.
The acyclic directed graphs have been considered by several authors in the past decades. A first related result appeared in the literature seems to be the one described in [2]. It says that a digraph ![]() contains no cycle if and only if all eigenvalues of its adjacency matrix are 0. Subsequently, to the best of our knowledge, Robinson [3,4] and Stanley [5] counted the acyclic digraphs independently and showed that if
contains no cycle if and only if all eigenvalues of its adjacency matrix are 0. Subsequently, to the best of our knowledge, Robinson [3,4] and Stanley [5] counted the acyclic digraphs independently and showed that if 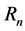 stands for the number of acyclic digraphs of
stands for the number of acyclic digraphs of 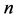 vertices then
vertices then
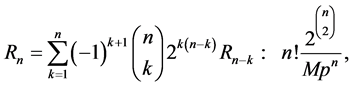
where , and
, and![]() . Later, in [6,7], Bender et al. considered the asymptotic number of acyclic digraphs with q edges, and subsequently, Gessel counted the acyclic digraphs by their sources and sinks in [8]. Most recently, E. Weisstein of Wolfram Research Inc. calculated the number,
. Later, in [6,7], Bender et al. considered the asymptotic number of acyclic digraphs with q edges, and subsequently, Gessel counted the acyclic digraphs by their sources and sinks in [8]. Most recently, E. Weisstein of Wolfram Research Inc. calculated the number,  , of
, of 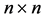
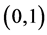 - matrices with real positive eigenvalues and showed that for
- matrices with real positive eigenvalues and showed that for 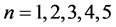 the numbers
the numbers 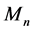 are
are
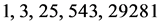
because the numbers were observed to coincide with the first five values of the sequence of the number of acyclic digraphs with n vertices that is obtained by Sloane in [9]. Weisstein conjectured that the two sequences are identical. The conjecture has recently been proven in [1].
Motivated by the above literature, we extend the acyclic digraphs to consider the digraphs 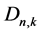 with cycles of length k in this note, where
with cycles of length k in this note, where . Our theorem established in the next section indicates that similar counting theorem holds for more general graphs.
. Our theorem established in the next section indicates that similar counting theorem holds for more general graphs.
2. The Main Results
Let us first prove the following lemma.
Lemma 1 Given a positive integer , and a nonnegative integer k with
, and a nonnegative integer k with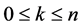 , the eigenvalues of the adjacency matrix
, the eigenvalues of the adjacency matrix  of
of 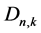 are copies of the entire kth unit roots plus, possibly, 0’s. Conversely, if B is an
are copies of the entire kth unit roots plus, possibly, 0’s. Conversely, if B is an 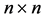
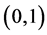 -matrix whose eigenvalues are copies of the entire kth unit roots plus, possibly, 0’s then its digraph
-matrix whose eigenvalues are copies of the entire kth unit roots plus, possibly, 0’s then its digraph 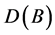 is isomorphic to
is isomorphic to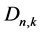 , if ignoring the acyclic parts in the two digraphs.
, if ignoring the acyclic parts in the two digraphs.
Proof. Assume that 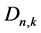 has m cycles of length k. We show that the eigenvalues of A are m copies of the entire kth unit roots plus
has m cycles of length k. We show that the eigenvalues of A are m copies of the entire kth unit roots plus 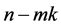 0’s. Since relabeling the vertices of a graph does not change the eigenvalues of its adjacency matrix, and since the m cycles of length k are disjoined, we may number the vertices consistently with the partial order so that A has the upper block-triangular as follows:
0’s. Since relabeling the vertices of a graph does not change the eigenvalues of its adjacency matrix, and since the m cycles of length k are disjoined, we may number the vertices consistently with the partial order so that A has the upper block-triangular as follows:
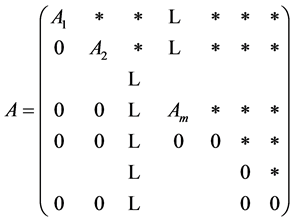
where each![]() ,
, 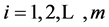 , is the adjacency matrix of a (directed simple) cycles of length k, and where ‘*’ is either a block matrix of 0, 1, or 1, or 0’s. From linear algebra, it can be easily proven that, for any i (
, is the adjacency matrix of a (directed simple) cycles of length k, and where ‘*’ is either a block matrix of 0, 1, or 1, or 0’s. From linear algebra, it can be easily proven that, for any i (![]() ), the characteristic polynomial of
), the characteristic polynomial of ![]() is
is![]() . So the eigenvalues of
. So the eigenvalues of ![]() are the kth unit roots. Since the eigenvalues of A are collection of the eigenvalues of these
are the kth unit roots. Since the eigenvalues of A are collection of the eigenvalues of these ![]() and
and 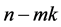 0’s, its eigenvalues are
0’s, its eigenvalues are 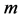 copies of the entire kth unit roots plus
copies of the entire kth unit roots plus 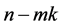 zeroes.
zeroes.
Conversely, if B is an 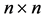
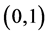 -matrix whose eigenvalues are
-matrix whose eigenvalues are  copies of the entire kth unit roots plus
copies of the entire kth unit roots plus 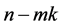 0’s, then its graph
0’s, then its graph 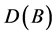 is a digraph and, for any
is a digraph and, for any , the ith eigenvalues of
, the ith eigenvalues of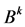 ,
, 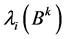 , is either 1 or 0. We now consider the power digraphs of
, is either 1 or 0. We now consider the power digraphs of  with adjacency matrix B. Since for all
with adjacency matrix B. Since for all  \
\
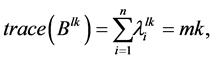
the number of closed walks of length l in the kth power graph 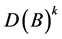 of
of 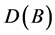 is
is . Since the eigenvalues of
. Since the eigenvalues of 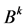 are either 1 or 0, the diagonal elements of
are either 1 or 0, the diagonal elements of 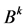 must be 1 or 0. In fact, from Perron-Frobenius theory (e. g., [10], p. 28, (1,6) Corollary (a)), we have
must be 1 or 0. In fact, from Perron-Frobenius theory (e. g., [10], p. 28, (1,6) Corollary (a)), we have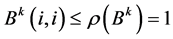 ,
, 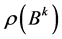 is the largest eigenvalue of
is the largest eigenvalue of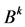 , which implies
, which implies ![]() or 0, and
or 0, and 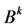 has exactly
has exactly 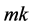 1’s on its diagonal. Thus, counting all the closed walks in the kth power graph
1’s on its diagonal. Thus, counting all the closed walks in the kth power graph  we conclude that
we conclude that  is a digraph with m disjoined cycles of length k plus an acyclic graph with
is a digraph with m disjoined cycles of length k plus an acyclic graph with  vertices. Putting the thing back to B implies that B is the adjacency matrix of a digraph with m cycles of length k plus, possibly, an acyclic digraph with
vertices. Putting the thing back to B implies that B is the adjacency matrix of a digraph with m cycles of length k plus, possibly, an acyclic digraph with 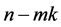 vertices. The proof is complete.
vertices. The proof is complete.
For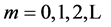 , counting the number of the digraphs and the
, counting the number of the digraphs and the 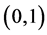 -matrices in the above lemma, we immediately have the following Theorem 1 For each
-matrices in the above lemma, we immediately have the following Theorem 1 For each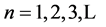 , and nonnegative integer k,
, and nonnegative integer k,  , the number of digraphs
, the number of digraphs 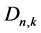 with cycles of length
with cycles of length 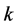 is equal to the number of
is equal to the number of 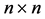
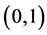 -matrices whose eigenvalues are the collection of copies of the entire kth unit roots plus, possibly, 0’s.
-matrices whose eigenvalues are the collection of copies of the entire kth unit roots plus, possibly, 0’s.
Note that when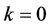 , because of the one to one corresponding, this leads to an alternative proof of the above conjecture (the main theorem of [1]). That is, for each
, because of the one to one corresponding, this leads to an alternative proof of the above conjecture (the main theorem of [1]). That is, for each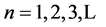 , the number of acyclic digraphs
, the number of acyclic digraphs 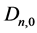 is equal to the number of
is equal to the number of 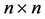
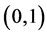 -matrices whose eigenvalues are 0’s --- from linear algebra, which is equivalent to saying that, for each
-matrices whose eigenvalues are 0’s --- from linear algebra, which is equivalent to saying that, for each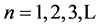 , the number of acyclic digraphs
, the number of acyclic digraphs 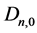 is equal to the number of
is equal to the number of
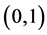 -matrices whose
-matrices whose 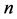 eigenvalues are equal to 1 --- and from [1], which is also equivalent to saying that, for each
eigenvalues are equal to 1 --- and from [1], which is also equivalent to saying that, for each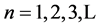 , the number of acyclic digraphs
, the number of acyclic digraphs  is equal to the number of
is equal to the number of 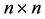
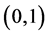 -matrices whose eigenvalues are positive real numbers.
-matrices whose eigenvalues are positive real numbers.
Corollary 1 If a digraph ![]() has cycles of lengths
has cycles of lengths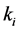 ,
,  , and the cycles are piecewise disjoined then the eigenvalues of its adjacency matrix
, and the cycles are piecewise disjoined then the eigenvalues of its adjacency matrix 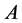 are collection of the entire kith unit roots,
are collection of the entire kith unit roots, 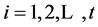 , plus 0’s. And vice versa.
, plus 0’s. And vice versa.
Funding
This research is supported partially by The Shanxi Beiren Jihua Projects of China, DIMACS (NSF center at Rutgers, The State University of New Jersey) and The University of Puerto Rico at Mayaguez.
[1] REFERENCES
[2] B. McKay, F. Oggier, G. Royle, N. Sloane, I. Wanless and H. Wilf, “Acyclic Digraphs and Eigenvalues of (0,1)-Matrices,” Journal of Integer Sequences, Vol. 7, 2004, #04.3.3.
[3] D. Cvetkovic, M. Doob and H. Sachs, “Spectra of Graphs,” 3rd Edition, Johann Ambrosius Barth Verlag, Leipzig, 1995.
[4] R. Robinson, “Enumeration of Acyclic Digraphs,” In: R. C. Bose, et al., Eds., Proceedings of 2nd Chapel Hill Conference on Combinatorial Mathematics and Its Applications, Chapel Hill, Orange County, 1970, pp. 391-399.
[5] R. Robinson, “Counting Labeled acyclic Digraphs,” In: F. Harary, Ed., New Directions in the Theory of Graphs, Academic Press, New York, 1973, pp. 239-273.
[6] R. Stanley, “Acyclic Orientations of Graphs,” Discrete Mathematics, Vol. 5, No. 2, 1973, pp. 171-178. http://dx.doi.org/10.1016/0012-365X(73)90108-8
[7] E. Bender, L. Richmond, R. Robinson and N. Wormald, “The Asymptotic Number of Acyclic Digraphs (I),” Combinatorica, Vol. 6, No. 1, 1986, pp. 15-22. http://dx.doi.org/10.1007/BF02579404
[8] E. Bender and R. Robinson, “The Asymptotic Number of Acyclic Digraphs (II),” Journal of Combinatorial Theory, Series B, Vol. 44, No. 3, 1988, pp. 363-369. http://dx.doi.org/10.1137/1.9781611971262
[9] I. Gessel, “Counting the Acyclic Digraphs by Sources and Sinks,” Discrete Mathematics, Vol. 160, No. 1-3, 1996, pp. 253-258. http://dx.doi.org/10.1016/0012-365X(95)00119-H
[10] N. J. Sloane, “The On-Line Encyclopedia of Integers Sequences,” 1996-2003.
[11] A. Berman and R. J. Plemmons, “Nonnegative Matrices in the Mathematical Sciences,” 2nd Edition, Academic, New York, 1994.

