Open Journal of Discrete Mathematics
Vol.2 No.2(2012), Article ID:18867,7 pages DOI:10.4236/ojdm.2012.22009
Some Results on Vertex Equitable Labeling
1Research Centre, Department of Mathematics, Govindammal Aditanar College for Women, Tiruchendur, India
2Department of Mathematics, Kamaraj College of Engineering and Technology, Virudhunagar, India
Email: jeyajeyanthi@rediffmail.com, bala_nithin@yahoo.co.in
Received December 15, 2011; revised January 23, 2012; accepted February 18, 2012
Keywords: Vertex equitable labeling; vertex equitable graph
ABSTRACT
Let G be a graph with p vertices and q edges and let 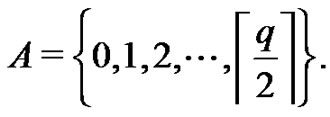 A vertex labeling
A vertex labeling 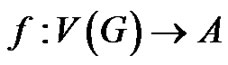 is said to be a vertex equitable labeling of G if it induces an edge labeling
is said to be a vertex equitable labeling of G if it induces an edge labeling  given by
given by 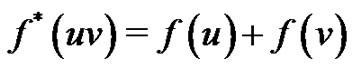 such that
such that 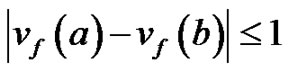 and
and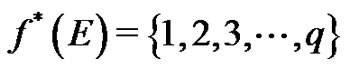 , where
, where 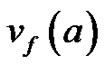 is the number of vertices v with
is the number of vertices v with 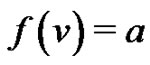 for
for 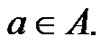 A graph G is said to be a vertex equitable graph if it admits vertex equitable labeling. In this paper, we establish the vertex equitable labeling of a Tp-tree,
A graph G is said to be a vertex equitable graph if it admits vertex equitable labeling. In this paper, we establish the vertex equitable labeling of a Tp-tree, 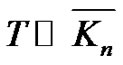 where T is a Tp-tree with even number of vertices, bistar
where T is a Tp-tree with even number of vertices, bistar 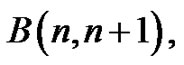 the caterpillar
the caterpillar 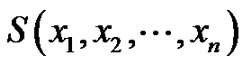 and crown
and crown 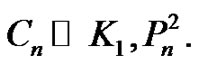
1. Introduction
All graphs considered here are simple, finite, connected and undirected. We follow the basic notations and terminologies of graph theory as in [1]. The symbols 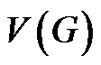 and
and  denote the vertex set and the edge set of a graph G. Let
denote the vertex set and the edge set of a graph G. Let  be a graph with
be a graph with  vertices and
vertices and 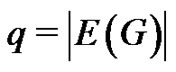 edges. A labeling f of a graph G is a mapping that assigns elements of a graph to the set of numbers (usually to positive or non-negative integers). If the domain of the mapping is the set of vertices (the set of edges) then we call the labeling vertex labeling (edge labeling). The labels of the vertices induce labels of the edges. There are several types of labeling. A detailed survey of graph labeling can be found in [2]. A vertex labeling f is said to be difference labeling if it induces the label
edges. A labeling f of a graph G is a mapping that assigns elements of a graph to the set of numbers (usually to positive or non-negative integers). If the domain of the mapping is the set of vertices (the set of edges) then we call the labeling vertex labeling (edge labeling). The labels of the vertices induce labels of the edges. There are several types of labeling. A detailed survey of graph labeling can be found in [2]. A vertex labeling f is said to be difference labeling if it induces the label 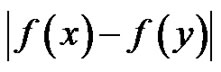 for each edge xy which is called as weight of the edge xy.
for each edge xy which is called as weight of the edge xy.
A difference labeling f of a graph G is said to be k-equitable if for each weight induced by f on the edges of G appears exactly k times. If a graph G has a k-equitable labeling then G is said to be k-equitable. Equitable labeling of graphs was introduced by Bloom and Ruiz in [3]. A brief summary of definitions which are useful for the present study is given below.
Definition 1.1 [4] Let T be a tree and u0 and  be two adjacent vertices in T. Let u and v be two pendant vertices of T such that the length of the path u0-u is equal to the length of the path
be two adjacent vertices in T. Let u and v be two pendant vertices of T such that the length of the path u0-u is equal to the length of the path 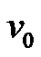 -v. If the edge
-v. If the edge 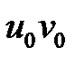 is deleted from T and u and v are joined by an edge uv, then such a transformation of T is called an elementary parallel transformation (or an ept, for short) and the edge
is deleted from T and u and v are joined by an edge uv, then such a transformation of T is called an elementary parallel transformation (or an ept, for short) and the edge 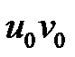 is called transformable edge.
is called transformable edge.
If by a sequence of ept’s, T can be reduced to a path, then T is called a Tp tree (transformed tree) and such sequence is regarded as a composition of mappings (ept’s) denoted by P, is called a parallel transformation of T. The path, the image of T under P is denoted as P(T).
A Tp tree and a sequence of two ept’s reducing it to a path are illustrated in Figure 1.
Definition 1.2 The corona  of the graphs G1 and G2 is obtained by taking one copy of G1 (with p vertices) and p copies of G2 and then joining the
of the graphs G1 and G2 is obtained by taking one copy of G1 (with p vertices) and p copies of G2 and then joining the 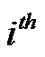 vertex of G1 to every vertex of the
vertex of G1 to every vertex of the 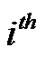 copy of G2.
copy of G2.
Definition 1.3 Caterpillar is a tree with the property that the removal of its pendant vertices leaves a path.
Definition 1.4 The square graph G2 of a graph G has the vertex set 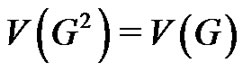 with
with  adjacent in G2 whenever
adjacent in G2 whenever 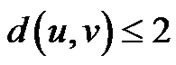 in G.
in G.
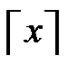 denotes the smallest integer greater than or equal to x.
denotes the smallest integer greater than or equal to x.
The concept of mean labeling was introduced by S. Somasundaram and R. Ponraj in [5] and further studied in [6-8]. A. Lourdusamy and M. Seenivasan introduced a vertex equitable labeling in [9]. In a vertex equitable labeling we use the labels 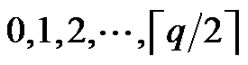 for the vertices,
for the vertices,

Figure 1. A Tp-tree and a sequence of two ept’s reducing it to a path.
the number of times the different vertex labels appear cannot differ by more than one. The induced edge labels are defined as the sum of the incident vertex labels. They proved that the graphs like path, bistar  combs
combs 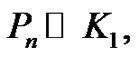 bipartite complete
bipartite complete 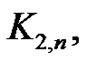 friendship graph
friendship graph 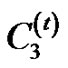 for
for 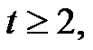 quadrilateral snake,
quadrilateral snake,
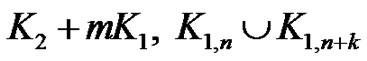
if and only if  ladder graph
ladder graph  arbitrary super division of a path and cycle
arbitrary super division of a path and cycle  with
with 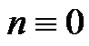 or
or  are vertex equitable. Also they proved that the graph
are vertex equitable. Also they proved that the graph 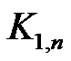 if
if 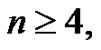 Eulerian graph with n edges where
Eulerian graph with n edges where  or
or 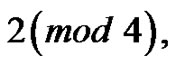 the wheel
the wheel 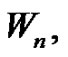 the complete graph
the complete graph 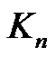 if
if 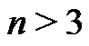 and triangular cactus with q edges where
and triangular cactus with q edges where 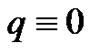 or 6 or 9
or 6 or 9 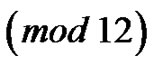 are not vertex equitable. Moreover they proved that if G is a graph with p vertices and q edges, q is even and
are not vertex equitable. Moreover they proved that if G is a graph with p vertices and q edges, q is even and 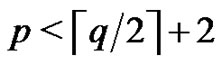 then G is not vertex equitable.
then G is not vertex equitable.
Definition 1.5 [9] Suppose G is a graph with p vertices and q edges. Let 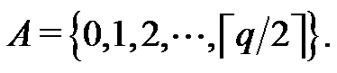 A vertex labeling
A vertex labeling 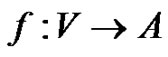 induces an edge labeling
induces an edge labeling 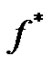 defined by
defined by 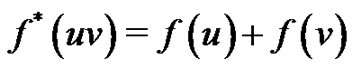 for all edges uv. For
for all edges uv. For 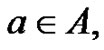 let
let 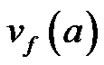 be the number of vertices v with
be the number of vertices v with 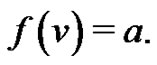 A graph G is vertex equitable if there exists a vertex labeling f such that for all a and b in A,
A graph G is vertex equitable if there exists a vertex labeling f such that for all a and b in A,
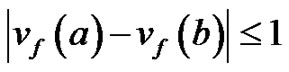
and the induced edge labels are 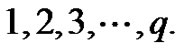
P. Jeyanthi and A. Maheswari proved in [10,11] that tadpoles, Cm  Cn, armed crowns, [Pm;
Cn, armed crowns, [Pm;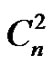 ] and,
] and, 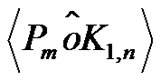 , the graphs obtained by duplicating an arbitrary vertex and an arbitrary edge of a cycle Cn, total graph of Pn, splitting graph of Pn and fusion of two edges of a cycle Cn are vertex equitable graphs. In this paper, we establish the vertex equitable labeling of a Tp-tree,
, the graphs obtained by duplicating an arbitrary vertex and an arbitrary edge of a cycle Cn, total graph of Pn, splitting graph of Pn and fusion of two edges of a cycle Cn are vertex equitable graphs. In this paper, we establish the vertex equitable labeling of a Tp-tree, 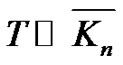 where T is a Tp-tree with even number of vertices, the bistar
where T is a Tp-tree with even number of vertices, the bistar  the caterpillar
the caterpillar 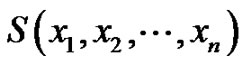 and the crown
and the crown 
2. Main Results
Theorem 2.1 Let 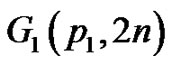 and
and 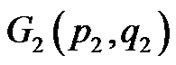 be any two vertex equitable graphs with equitable labeling f and g respectively. Let u and v be the vertices of G1 and G2 respectively such that
be any two vertex equitable graphs with equitable labeling f and g respectively. Let u and v be the vertices of G1 and G2 respectively such that 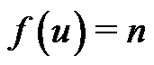 and
and  Then the graph
Then the graph  obtained from G1 and G2 by identifying the vertices u and v is a vertex equitable graph.
obtained from G1 and G2 by identifying the vertices u and v is a vertex equitable graph.
Proof. Clearly 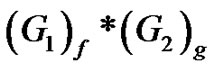 has
has  edges and
edges and 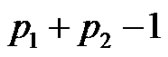 vertices. Let
vertices. Let
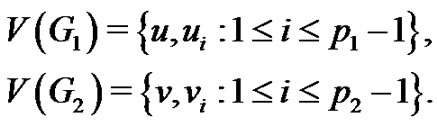
Define 
by  for
for 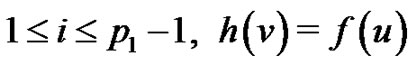 and
and 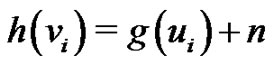 for
for 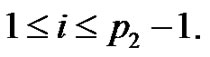 Clearly,
Clearly,
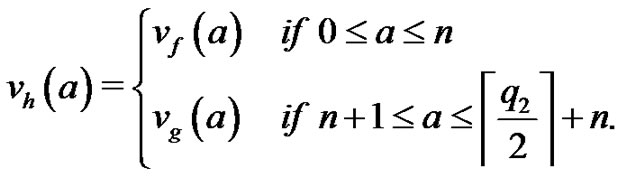
Therefore,  and the labels of the edges of the copy of G1 are
and the labels of the edges of the copy of G1 are  and the labels of the edges of the copy of G2 are
and the labels of the edges of the copy of G2 are  Hence,
Hence,  is a vertex equitable graph.
is a vertex equitable graph.
Theorem 2.2 Let 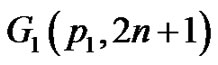 and
and 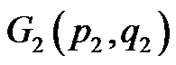 be any two vertex equitable graphs with equitable labeling f and g respectively. Let u and v be the vertices of G1 and G2 respectively such that
be any two vertex equitable graphs with equitable labeling f and g respectively. Let u and v be the vertices of G1 and G2 respectively such that  and
and 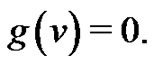 Then the graph G obtained by joining u and v by an edge is vertex equitable.
Then the graph G obtained by joining u and v by an edge is vertex equitable.
Proof. Clearly G has 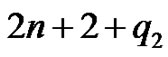 edges and
edges and 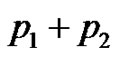 vertices. Let
vertices. Let

Define 
by 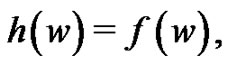 if
if  if
if 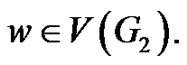 The labels of the edges of the copy of G1 are
The labels of the edges of the copy of G1 are 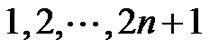 and the labels of the edges of the copy of G2 are
and the labels of the edges of the copy of G2 are 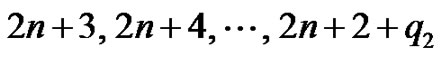 and
and
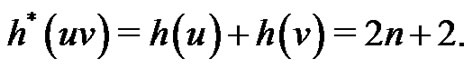
Hence, G is a vertex equitable graph.
Theorem 2.3 Every Tp-tree is a vertex equitable graph.
Proof. Let T be a Tp-tree with n vertices. By the definition of a transformed tree there exists a parallel transformation P of T such that for the path 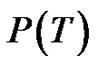 we have 1)
we have 1)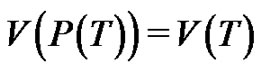 , 2)
, 2) 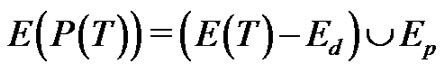 where
where  is the set of edges deleted from T and
is the set of edges deleted from T and  is the set of edges newly added through the sequence
is the set of edges newly added through the sequence 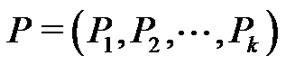 of the epts P used to arrive the path
of the epts P used to arrive the path 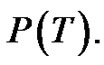 Clearly,
Clearly,  and
and  have the same number of edges.
have the same number of edges.
Now denote the vertices of 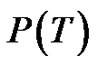 successively as
successively as 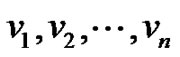 starting from one pendant vertex of
starting from one pendant vertex of 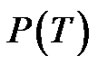 right up to the other.
right up to the other.
For 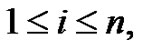 define the labeling f as
define the labeling f as
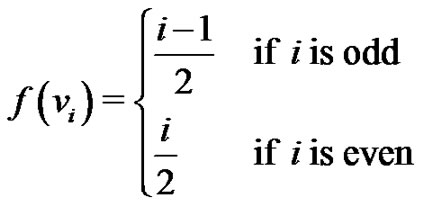
Then f is a vertex equitable labeling of the path 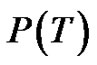
Let 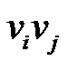 be any edge of T with
be any edge of T with  and
and 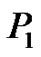 be the ept that deletes this edge and add the edge
be the ept that deletes this edge and add the edge 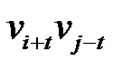 where t is the distance of
where t is the distance of 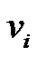 from
from 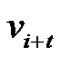 and also the distance of
and also the distance of 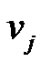 from
from 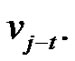 Let P be a parallel transformation of T that contains
Let P be a parallel transformation of T that contains 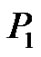 as one of the constituent epts.
as one of the constituent epts.
Since 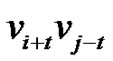 is an edge of the path
is an edge of the path 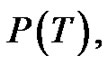 it follows that
it follows that 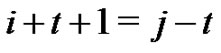 which implies
which implies 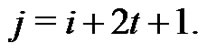 Therefore
Therefore 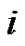 and
and 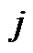 are of opposite parity.
are of opposite parity.
The induced label of the edge  is given by
is given by
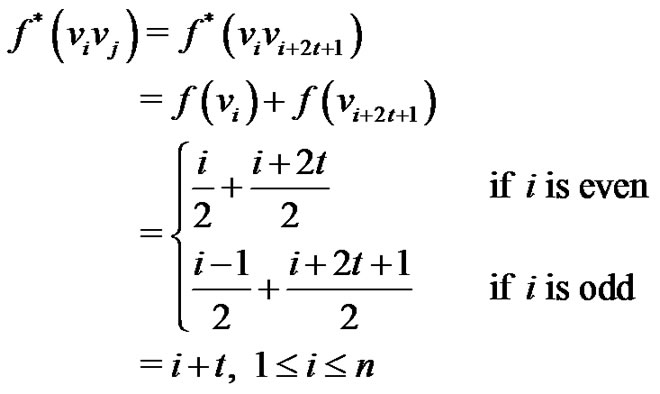
Now
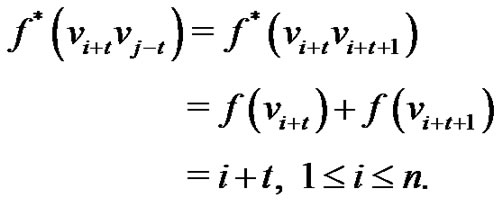
Therefore, we have  and hence f is a vertex equitable labeling of the Tp-tree T.
and hence f is a vertex equitable labeling of the Tp-tree T.
An example for the vertex equitable labeling of a Tp- tree with 12 vertices is given in Figure 2.
Theorem 2.4 Let T be a Tp-tee with even number of vertices. Then the graph 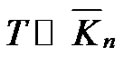 is a vertex equitable graph for all
is a vertex equitable graph for all 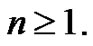
Proof. Let T be a Tp-tree of even order m and the vertex set 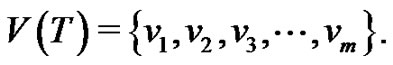 Let
Let 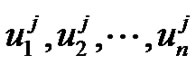 be the pendant vertices joined with
be the pendant vertices joined with  by an edge. Then
by an edge. Then
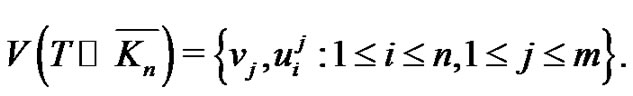
By the definition of a Tp-tree, there exists a parallel transformation P of T such that for the path  we have 1)
we have 1)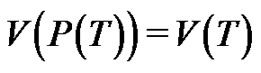 , 2)
, 2) 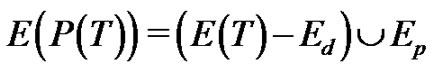 where
where  is the set of edges deleted from T and
is the set of edges deleted from T and 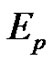 is the set of edges newly added through the sequence
is the set of edges newly added through the sequence  of the epts P used to arrive the path
of the epts P used to arrive the path  Clearly,
Clearly, 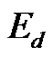 and
and  have the same number of edges.
have the same number of edges.
Now denote the vertices of  successively as
successively as 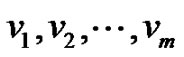 starting from one pendant vertex of
starting from one pendant vertex of 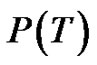 right up to the other. The labeling f defined by
right up to the other. The labeling f defined by
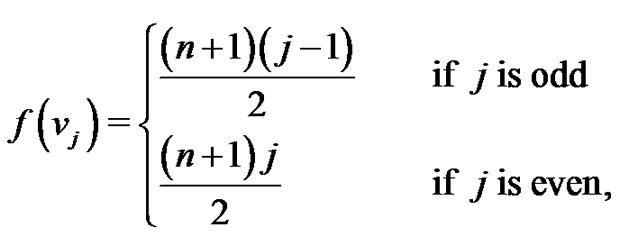
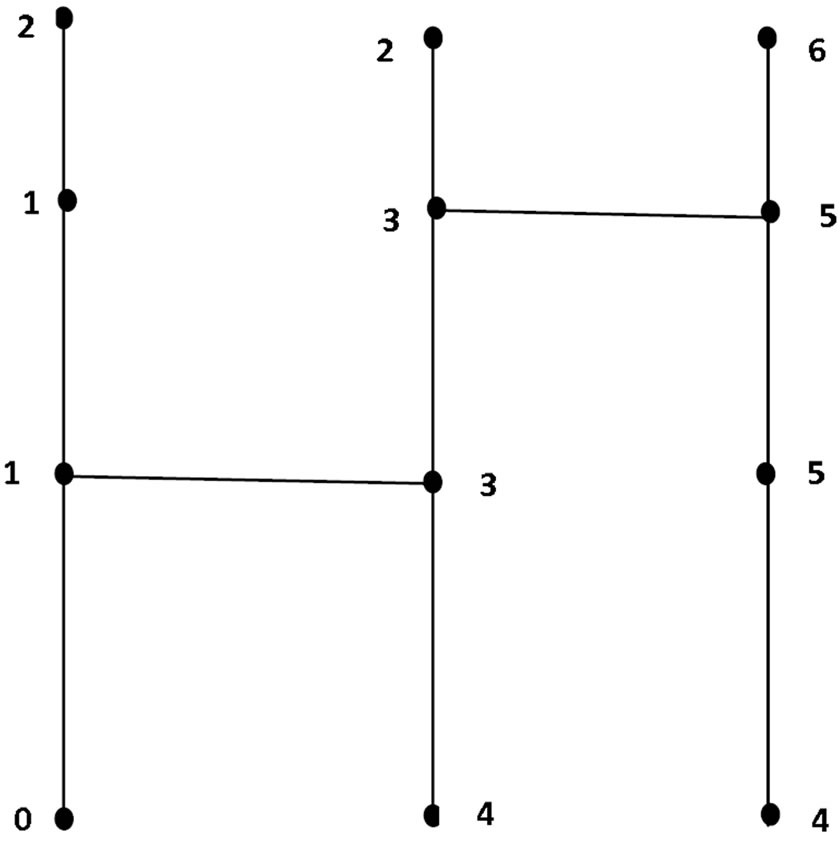
Figure 2. Vertex equitable labeling of a Tp-tree with 12 vertices.

is a vertex equitable labeling graph.
Let 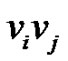 be any edge of T with
be any edge of T with 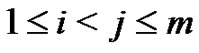 let
let 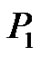 be the ept that deletes this edge and adds the edge
be the ept that deletes this edge and adds the edge 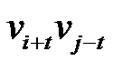 where t is the distance of
where t is the distance of 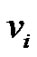 from
from 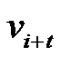 and also the distance of
and also the distance of 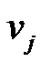 from
from 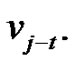 Let P be a parallel transformation of T that contains
Let P be a parallel transformation of T that contains 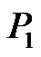 as one of the constituent epts.
as one of the constituent epts.
Since 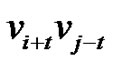 is an edge in the path
is an edge in the path 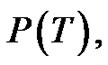 it follows that
it follows that 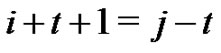 which implies
which implies 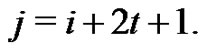 Therefore i and j are of opposite parity.
Therefore i and j are of opposite parity.
The induced label of the edge 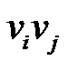 is given by
is given by
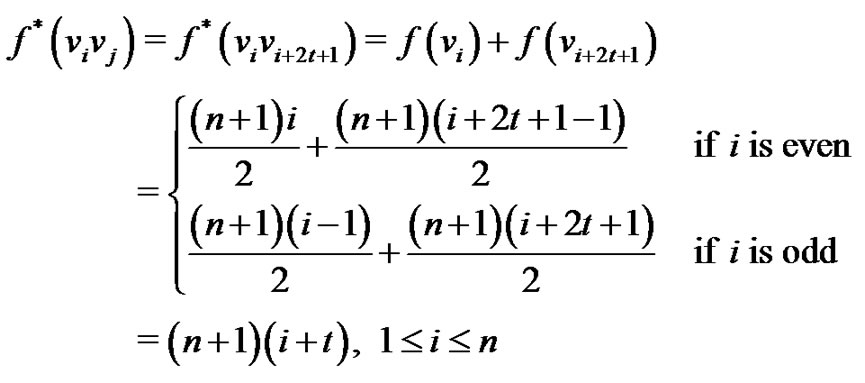
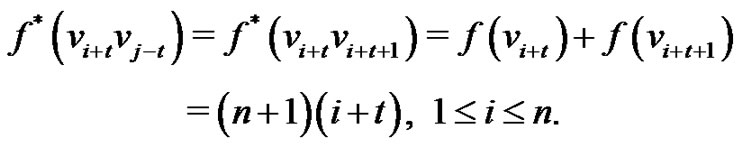
Therefore, we have 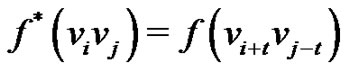 and thus f is a vertex equitable labeling of
and thus f is a vertex equitable labeling of 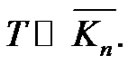
An example for the vertex equitable labeling of 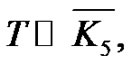 where T is a Tp-tree with 12 vertices is shown in Figure 3.
where T is a Tp-tree with 12 vertices is shown in Figure 3.
Let  be a graph obtained from
be a graph obtained from 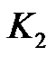 by attaching n pendant edges at one vertex and
by attaching n pendant edges at one vertex and 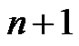 pendant edges at the other vertex.
pendant edges at the other vertex.
Theorem 2.5 The bistar 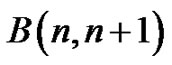 is a vertex equitable graph.
is a vertex equitable graph.
Proof. Let 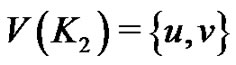 and
and  and
and 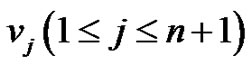 be the vertices adjacent to u and v respectively. Now,
be the vertices adjacent to u and v respectively. Now, 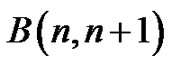 has
has  edges and
edges and 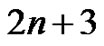 vertices. Define
vertices. Define
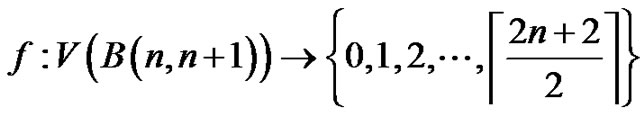
by 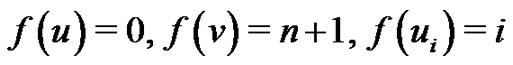 if
if 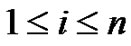 and
and 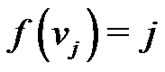 if
if 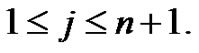 Then f is a vertex equitable labeling of
Then f is a vertex equitable labeling of 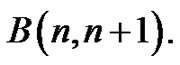
Theorem 2.6 Let 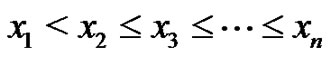 and
and

Then 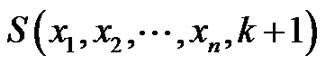 is a vertex equitable graph.
is a vertex equitable graph.
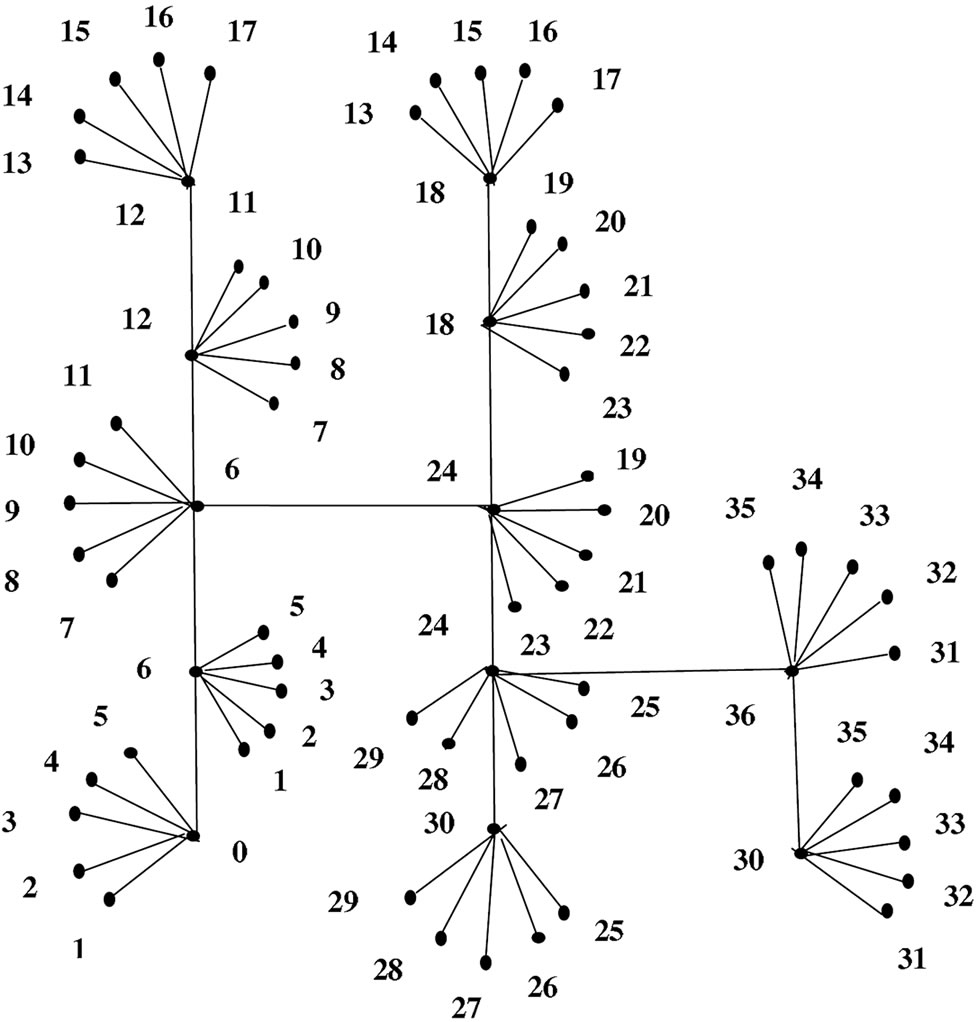
Figure 3. Vertex equitable labeling of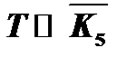 .
.
Proof. By Theorem 2.5, 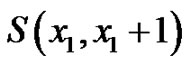 is a vertex equitable graph. Let
is a vertex equitable graph. Let  be the corresponding vertex equitable labeling of
be the corresponding vertex equitable labeling of 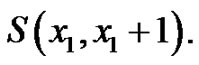 Let
Let 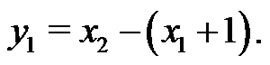 Since
Since 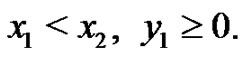 Consider the graphs
Consider the graphs 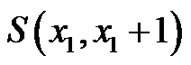 and
and 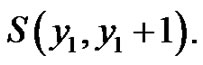 The number of edges of the graph
The number of edges of the graph 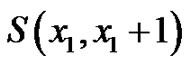 is
is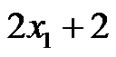 .
.
Now, 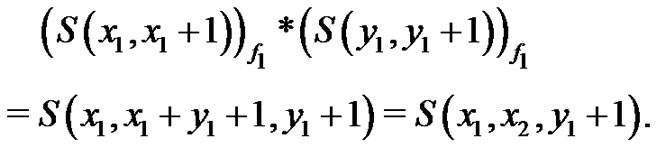
Therefore, by Theorem 2.1, 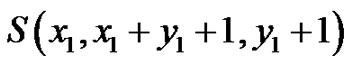 is a vertex equitable graph. Let
is a vertex equitable graph. Let 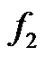 be the corresponding vertex equitable labeling of
be the corresponding vertex equitable labeling of 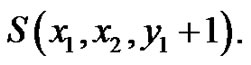 Again the number of edges of
Again the number of edges of 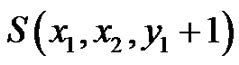 is even.
is even.
Now take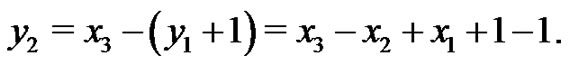 Hence
Hence 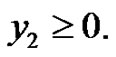 Also
Also

Therefore, by Theorem 2.1, 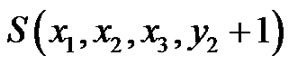 is a vertex equitable graph and the number of edges is even. Proceeding like this, at the
is a vertex equitable graph and the number of edges is even. Proceeding like this, at the 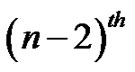 step we get
step we get 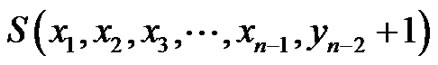 is a vertex equitable graph where
is a vertex equitable graph where

Let 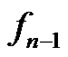 be the corresponding vertex equitable labeling of
be the corresponding vertex equitable labeling of  Take
Take
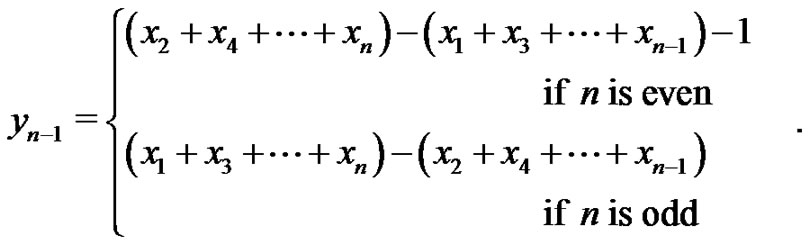
Clearly 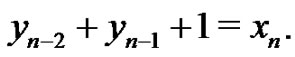 Now,
Now,
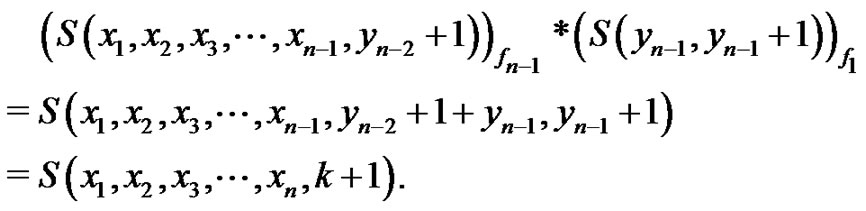 Therefore,
Therefore, 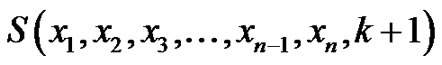 is a vertex equitable graph.
is a vertex equitable graph.
An example for the vertex equitable labeling of  if n is odd is given in Figure 4.
if n is odd is given in Figure 4.
An example for the vertex equitable labeling of  if n is even is given in Figure 5.
if n is even is given in Figure 5.
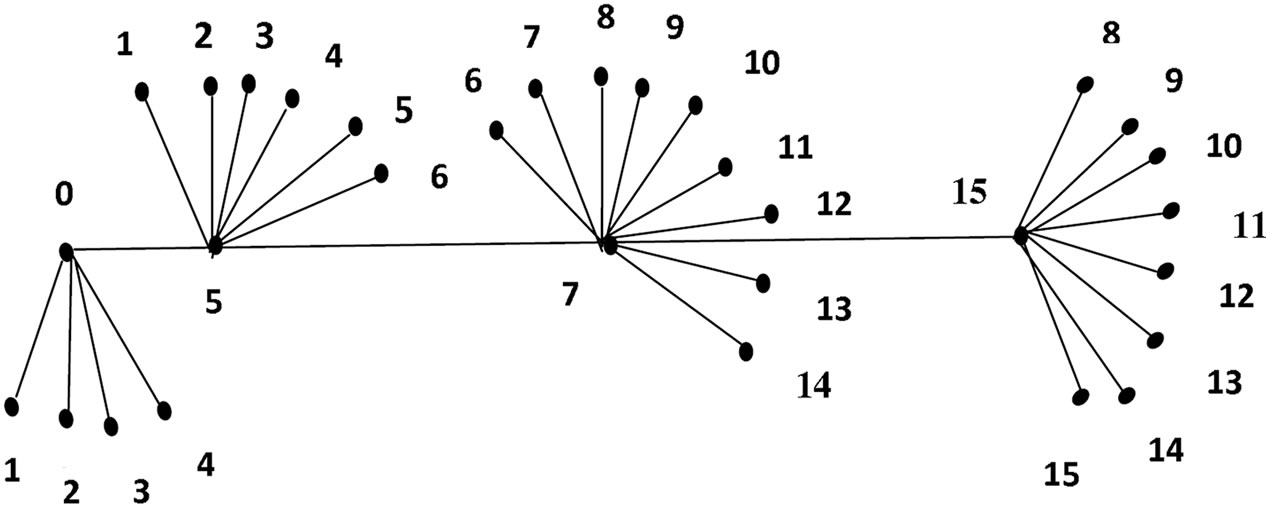
Figure 4. Vertex equitable labeling of S (4, 6, 9, 7 + 1).

Figure 5. Vertex equitable labeling of S (5, 7, 9, 10, 2 + 1).
Theorem 2.7 The crown 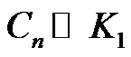 is a vertex equitable graph.
is a vertex equitable graph.
Proof: Let 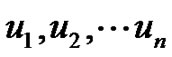 be the vertices of the cycle Cn and let vi be the vertex adjacent to ui for
be the vertices of the cycle Cn and let vi be the vertex adjacent to ui for  Then the vertex set
Then the vertex set 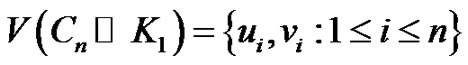 and the edge set
and the edge set . Define
. Define 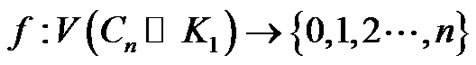 for the following cases:
for the following cases:
Case 1. 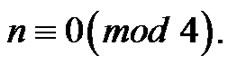
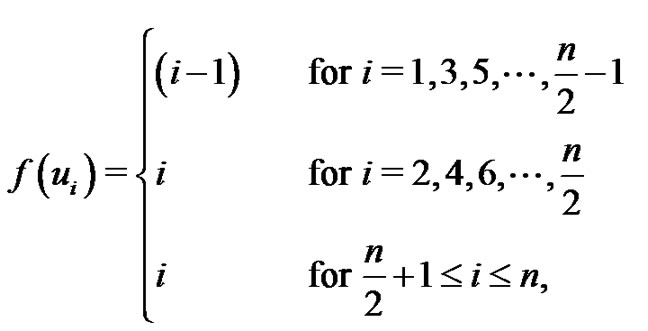
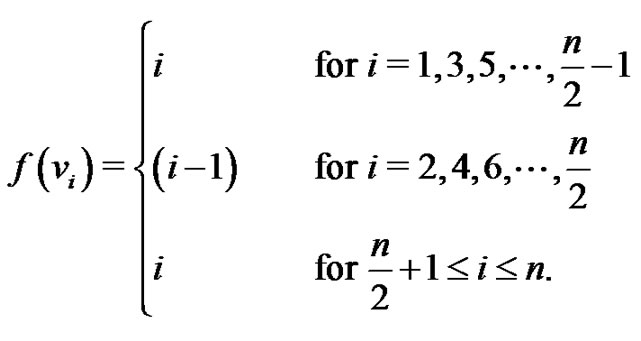
Case 2. 
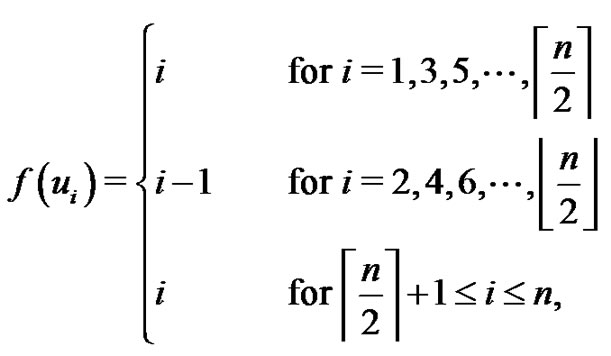
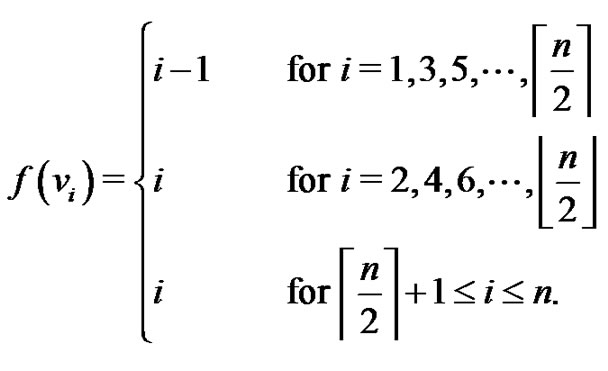
Case 3. 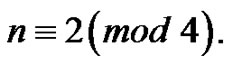


Figure 6. Vertex equitable labeling of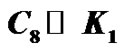 .
.
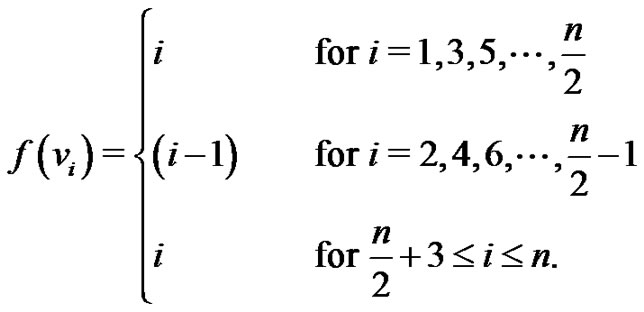
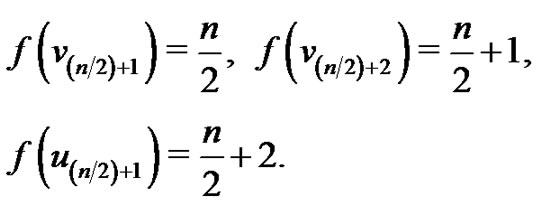
Case 4. 
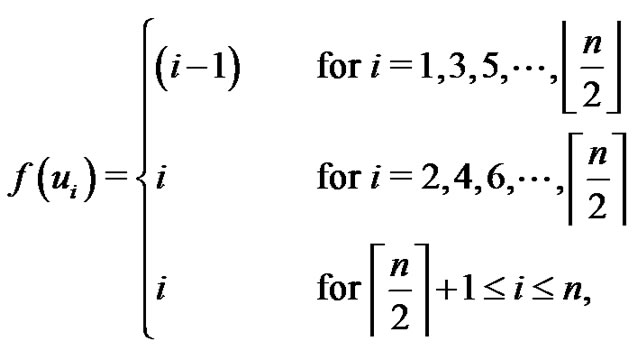
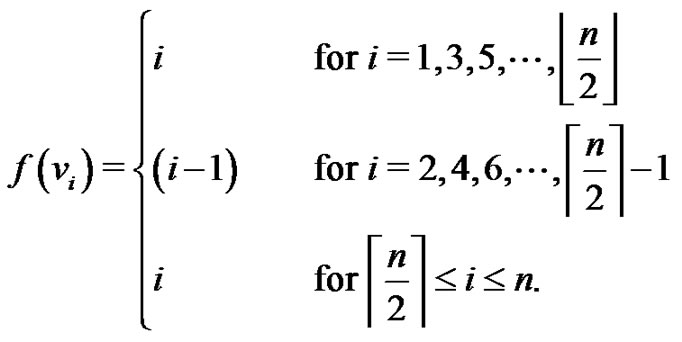
In all the above cases, f is a vertex equitable labeling. Hence 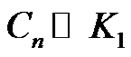 is a vertex equitable graph.
is a vertex equitable graph.
An example for the vertex equitable labeling of 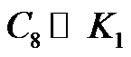 is shown in Figure 6.
is shown in Figure 6.
Theorem 2.8 The graph 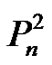 is a vertex equitable graph.
is a vertex equitable graph.
Proof. Let 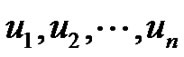 be the path
be the path 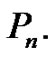 Clearly,
Clearly,  has n vertices and
has n vertices and 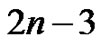 edges. Define
edges. Define
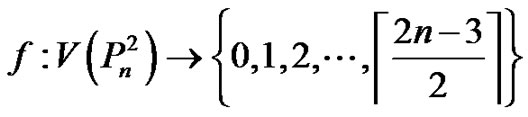
by 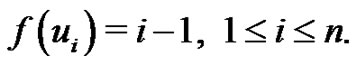 Evidently,
Evidently, 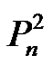 is a vertex equitable graph.
is a vertex equitable graph.
REFERENCES
- F. Harary, “Graph Theory,” Addison Wesley, Massachusetts, 1972.
- J. A. Gallian, “A Dynamic Survey of Graph Labeling,” The Electronic Journal of Combinatorics, Vol. 18, 2011, Paper #DS6.
- G. Bloom and S. Ruiz, “Decomposition into Linear Forest and Difference Labelings of Graphs,” Discrete Applied Mathematics, Vol. 49, 1994, pp. 61-75. doi:10.1016/0166-218X(94)90201-1
- S. M. Hegde and S. Shetty, “On Graceful Trees,” Applied Mathematics E-Notes, Vol. 2, 2002, pp. 192-197.
- R. Ponraj and S. Somasundram, “Mean Labeling of Graphs,” National Academy Science Letters, Vol. 26, 2003, pp. 210-213.
- R. Ponraj and S. Somasundram, “Non-Existence of Mean Labeling for a Wheel,” Bulletin of Pure and Applied Sciences (Mathematics & Statistics), Vol. 22E, 2003, pp. 103-111.
- R. Ponraj and S. Somasundram, “Some Results on Mean Graphs,” Pure and Applied Mathematical Sciences, Vol. 9, 2004, pp. 47-58.
- R. Ponraj and S. Somasundram, “Further Results on Mean Graphs,” Proceedings f SACOEFERENCE, National Level Conference, Dr. Sivanthi Aditanar College of Engineering, 2005, pp. 443-448.
- M. Seenivasan and A. Lourdusamy, “Vertex Equitable Labeling of Graphs,” Journal of Discrete Mathematical Sciences & Cryptography, Vol. 11, No. 6, 2008, pp. 727- 735.
- P. Jeyanthi and A. Maheswari, “On Vertex equitable labeling,” Preprint.
- P. Jeyanthi and A. Maheswari, “Vertex Equitable Labeling of Cycle and Path Related Graphs,” Utilitas Mathematica, Article in Press.

