Open Journal of Discrete Mathematics
Vol.2 No.1(2012), Article ID:17153,6 pages DOI:10.4236/ojdm.2012.21002
Bounds for Domination Parameters in Cayley Graphs on Dihedral Group
Department of Mathematics, Manonmaniam Sundaranar University, Tirunelveli, India
Email: tamche59@gmail.com
Received November 3, 2011; revised December 18, 2011; accepted December 25, 2011
Keywords: Cayley graph; Dihedral group; Domination; Total domination; Connected domination; Efficient domination
ABSTRACT
In this paper, sharp upper bounds for the domination number, total domination number and connected domination number for the Cayley graph G = Cay(D2n, Ω) constructed on the finite dihedral group D2n, and a specified generating set Ω of D2n. Further efficient dominating sets in G = Cay(D2n, Ω) are also obtained. More specifically, it is proved that some of the proper subgroups of D2n are efficient domination sets. Using this, an E-chain of Cayley graphs on the dihedral group is also constructed.
1. Introduction and Notation
Design of interconnection networks is an important integral part of any parallel processing of distributed system. There has been a strong interest recently in using Cayley graphs as a model for developing interconnection networks for large interacting arrays of CPU’s. An excellent survey of interconnection networks based on Cayley graphs can be found in [1]. The concept of domination for Cayley graphs has been studied by various authors [2-7]. I. J. Dejter and O. Serra [3] obtained efficient dominating sets for Cayley graphs constructed on a class of groups containing permutation groups. The efficient domination number for vertex transitive graphs has been obtained by Jia Huang and Jun-Ming Xu [4]. A necessary and sufficient condition for the existence of an independent perfect domination set in Cayley graphs has been obtained by J. Lee [5]. Total domination in graphs was introduced by Cockayne, Dawes, and Hedetniemi [2] and is now well studied in graph theory. T. Tamizh Chelvam and I. Rani [6-8] have obtained bounds for various domination parameters for a class of Circulant graphs.
Let Γ be a finite group. Let Ω be a generating set of Γ satisfying e Ï Ω and a Î Ω implies a−1 Î Ω. The Cayley graph corresponding to Γ is the graph G = (V, E), where V(G) = Γ and E(G)={(x, xa): x Î V(G), a Î Ω} and it is denoted by G = Cay(Γ, Ω). Let G= (V, E), be a finite, simple and undirected graph. We follow the terminology of [9]. A set S Í V of vertices in a graph G is called a dominating set if every vertex v Î V is either an element of S or adjacent to an element of S. A dominating set S is a minimal dominating set if no proper subset of S is a dominating set. The domination number g(G) of a graph G is the minimum cardinality of a dominating set in G and the corresponding dominating set is called a g-set. A set S Í V is called a total dominating set if every vertex v Î V is adjacent to an element u (¹v) of S. The total domination number gt(G) equals the minimum cardinality among all the total dominating sets in G and the corresponding total dominating set is called a gt-set. A dominating set S is called a connected dominating set if the induced subgraph áSñ is connected. The connected domination number gc(G) of a graph G equals the minimum cardinality of a connected dominating set in G and a corresponding connected dominating set is called a gc-set. A set S Í V is called an efficient dominating set (E-set) if for every vertex v Î V, |N[v]∩S|=1.
An E-chain is a countable family of nested graphs, each of which has an E-set. We say that a countable family of graphs G = {Gi, i ³ 1} with each Gi has an E-set Si is an inclusive E-chain if for every i ³ 1, there exists a surjective map fi: Gi+1 ® Gi such that 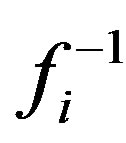 (Si) Ì Si+1. And also we define that a finite family of graphs G = {Gi, i ³ 0} is an inductive E-chain if every Gi+1 is a spanning subgraph of Gi and each Gi has an E-set Si. Let V(Gi) be any finite group and if, for each i ³ 0, there exists a bijective map zi: V(Gi) ® V(Gi+1) such that zi(Si ) Í Si+1 and Si is the subgroup of V(Gi) then we say that G is an inductive subgroups E-chain.
(Si) Ì Si+1. And also we define that a finite family of graphs G = {Gi, i ³ 0} is an inductive E-chain if every Gi+1 is a spanning subgraph of Gi and each Gi has an E-set Si. Let V(Gi) be any finite group and if, for each i ³ 0, there exists a bijective map zi: V(Gi) ® V(Gi+1) such that zi(Si ) Í Si+1 and Si is the subgroup of V(Gi) then we say that G is an inductive subgroups E-chain.
A graph 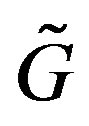 is called a covering of G with projection
is called a covering of G with projection 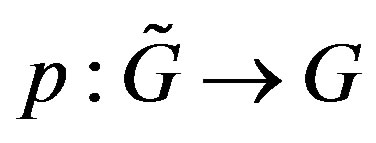 if there is a surjection
if there is a surjection 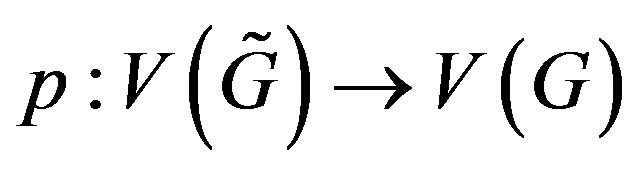 such that
such that 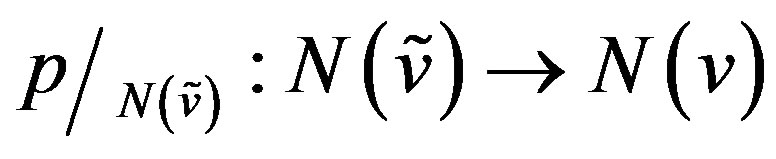 is a bijection for any vertex
is a bijection for any vertex 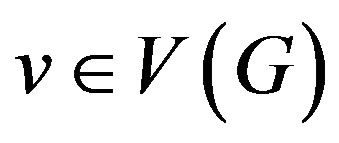 and
and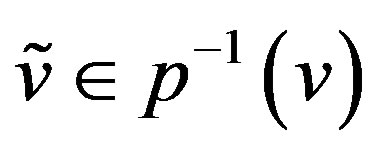 . We use the covering function to show the inclusive E-chain.
. We use the covering function to show the inclusive E-chain.
In this paper, we obtain upper bounds for domination number, total domination number and connected domination number in a Cayley graph 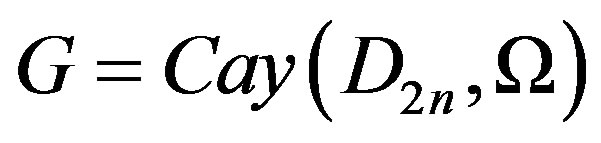 constructed on the dihedral group
constructed on the dihedral group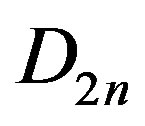 , for
, for 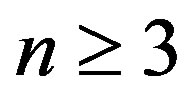 and a generating set
and a generating set . Further, we obtain some E-sets in
. Further, we obtain some E-sets in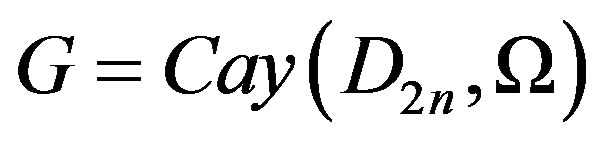 . Note that the dihedral group
. Note that the dihedral group 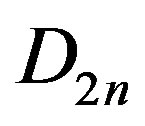 with identity e is the group generated by two elements r and s with
with identity e is the group generated by two elements r and s with 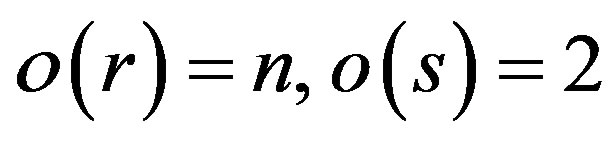 and
and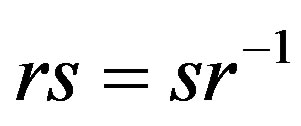 . From these defining relations, one can take
. From these defining relations, one can take
 and
and
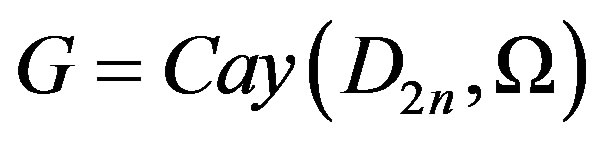 , where
, where  is a generating set of
is a generating set of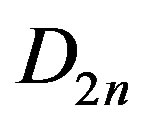 . Throughout this paper,
. Throughout this paper, 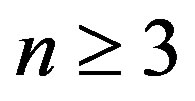 be an integer,
be an integer, 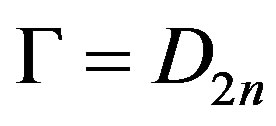 ,
,
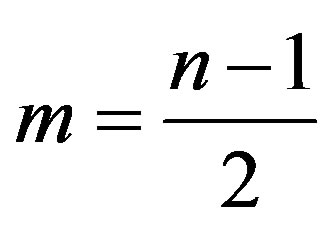 and k, t be integers such that
and k, t be integers such that 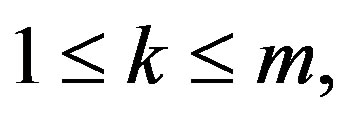
 . We take the generating set
. We take the generating set  in the form that
in the form that
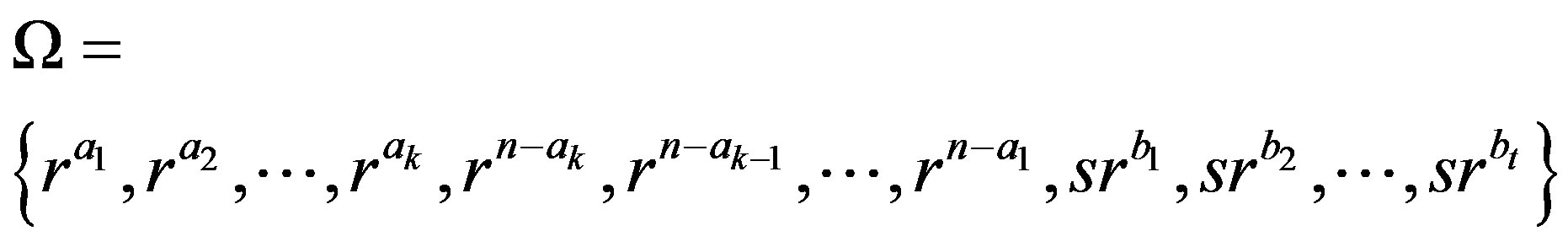 where
where  and
and 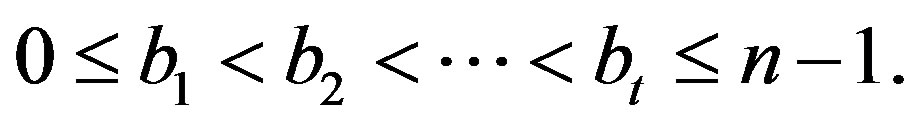 Let
Let 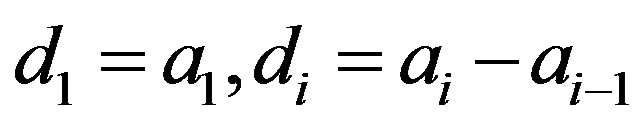 for
for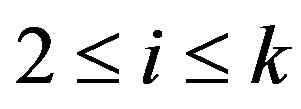 ,
, 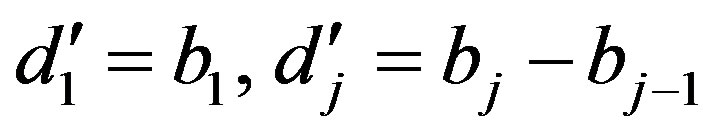 for
for 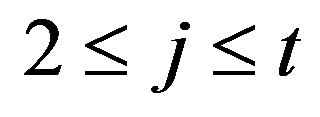 and
and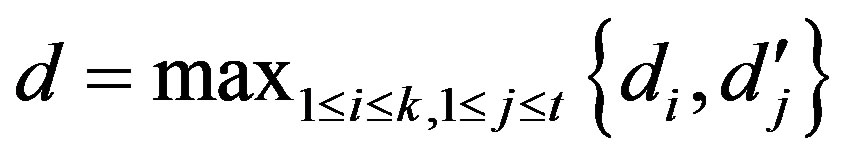 . Some of the results are listed below for further reference.
. Some of the results are listed below for further reference.
Theorem 1 [4] Let G be a k-regular graph. Then
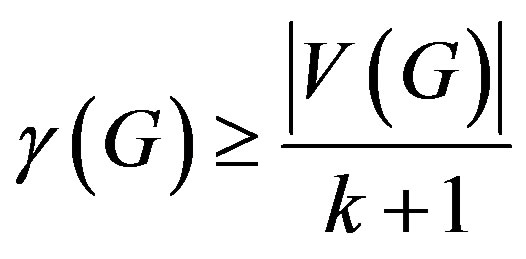 , with the equality if and only if G has an efficient dominating set.
, with the equality if and only if G has an efficient dominating set.
Theorem 2 [5] Let  be a covering and let S be a perfect domination set of G. Then
be a covering and let S be a perfect domination set of G. Then  is a perfect domination set of
is a perfect domination set of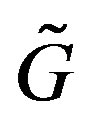 . Moreover, if S is independent, then
. Moreover, if S is independent, then 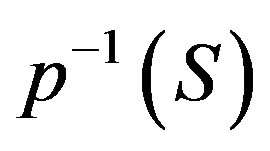 is independent.
is independent.
Theorem 3 [10] Every subgroup of the dihedral group  is cyclic or dihedral. A complete listing of the subgroups is as follows:
is cyclic or dihedral. A complete listing of the subgroups is as follows:
1) cyclic subgroups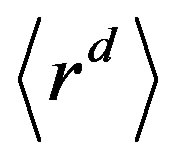 , where d divides n, with index 2d.
, where d divides n, with index 2d.
2) dihedral subgroups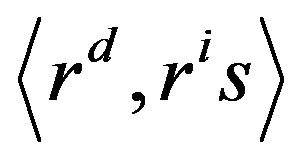 , where d divides n and
, where d divides n and 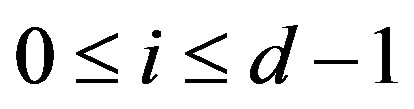 with index d. Every subgroup of
with index d. Every subgroup of 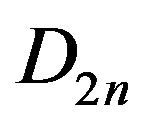 occurs exactly once in this listing.
occurs exactly once in this listing.
2. Domination, Total Domination and Connected Domination Numbers
In this section, we obtain upper bounds for the domination number, total domination number and connected domination number of graph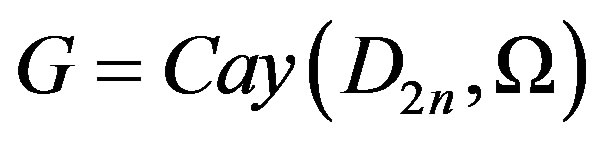 . Also whenever the equality occurs we give the corresponding sets.
. Also whenever the equality occurs we give the corresponding sets.
Lemma 4 Let 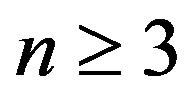 be an integer,
be an integer, 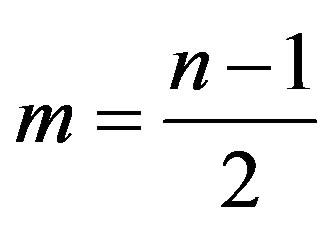 and kt are integers such that
and kt are integers such that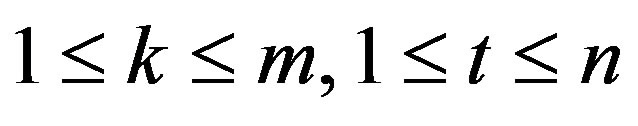 . Let
. Let
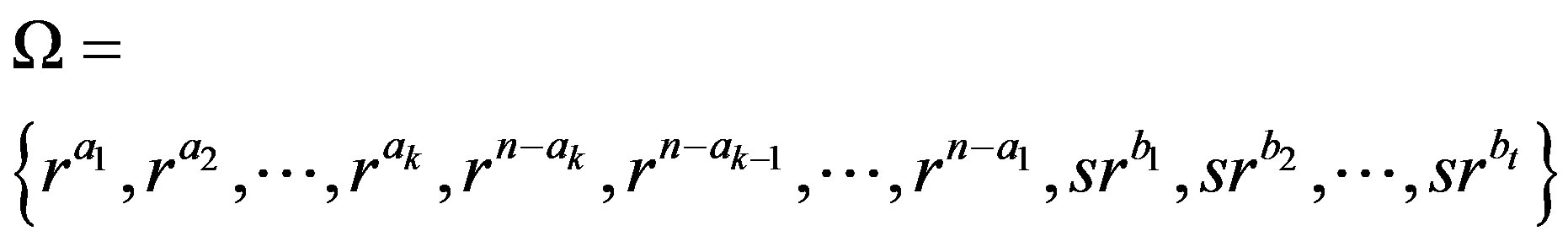
and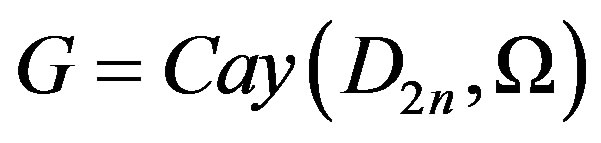 . If
. If 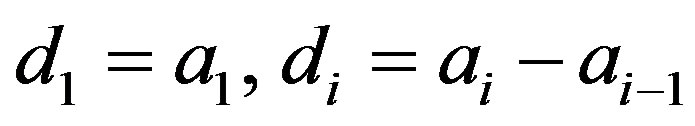 for
for  ,
, 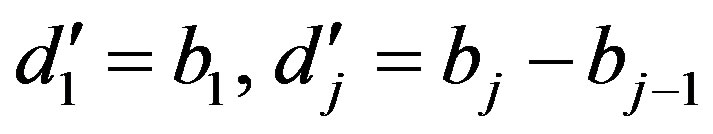 for
for 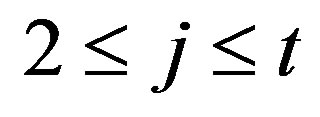 and
and 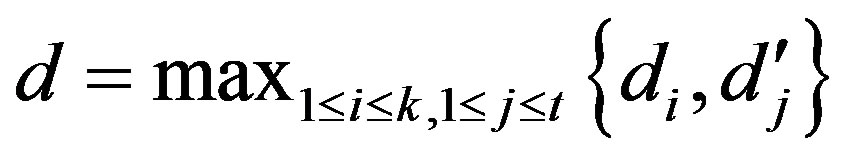 , then
, then
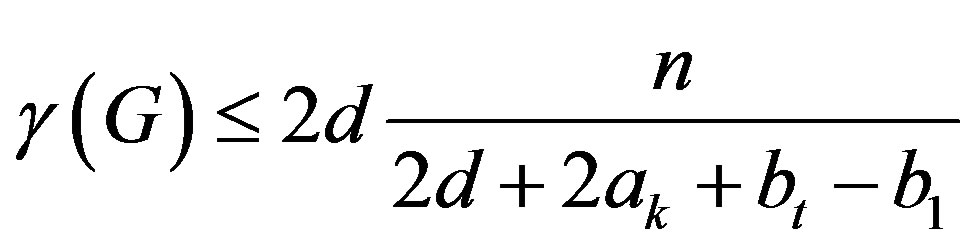 .
.
Proof. Let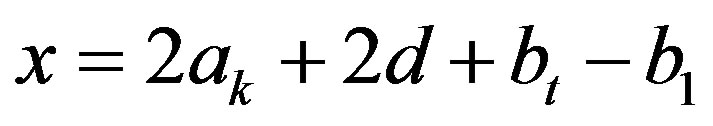 and
and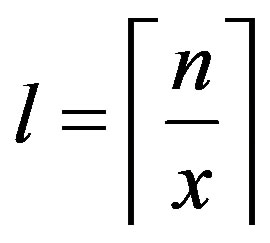 . Consider the set
. Consider the set
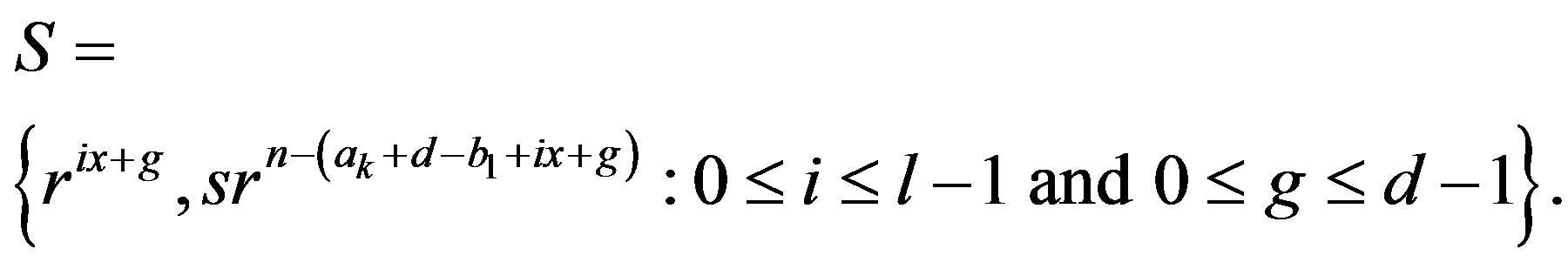
Clearly 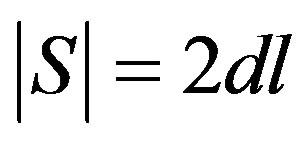 and
and
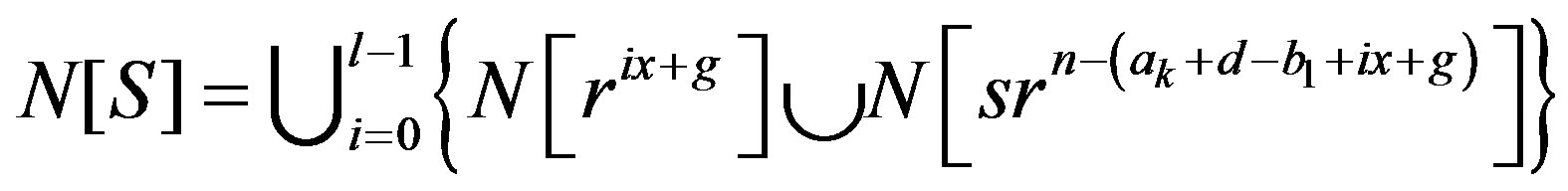 where
where 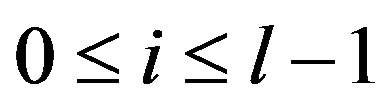 and
and  We have to prove that
We have to prove that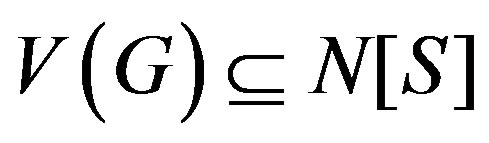 . If
. If , then we can write
, then we can write 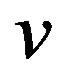 as either one vertex of the form
as either one vertex of the form 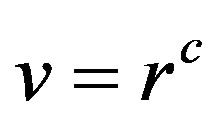 or
or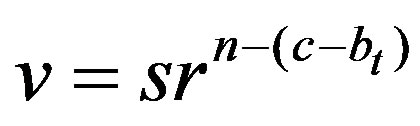 , where
, where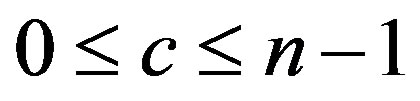 . By the division algorithm,
. By the division algorithm, 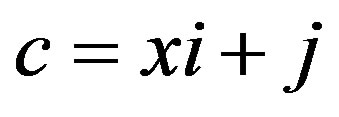 , where
, where 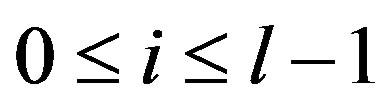 and
and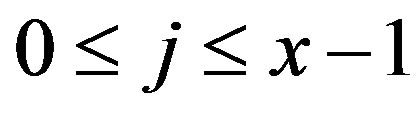 .
.
Suppose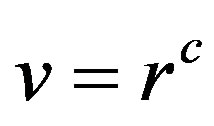 . We have the following cases:
. We have the following cases:
Case 1. Suppose 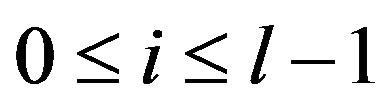 and
and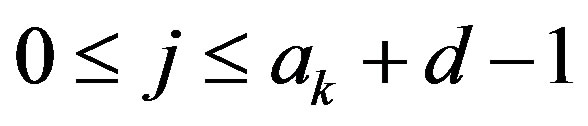 .
.
Subcase 1.1 If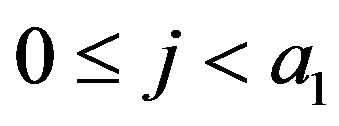 , then by the definition of
, then by the definition of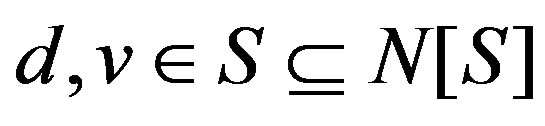 .
.
Subcase 1.2 If , for some integers m, g with
, for some integers m, g with 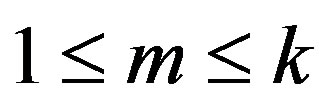 and
and 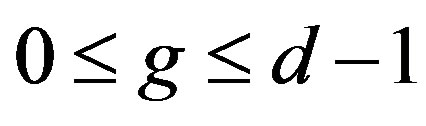 then
then 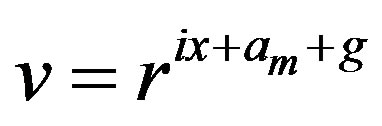 whereas
whereas 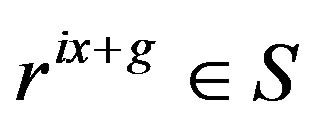 and so
and so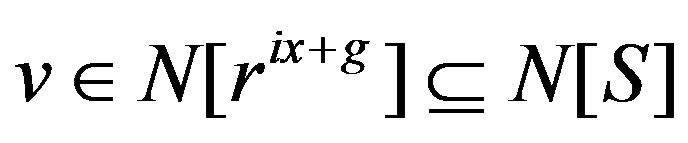 .
.
Case 2. Suppose  and
and 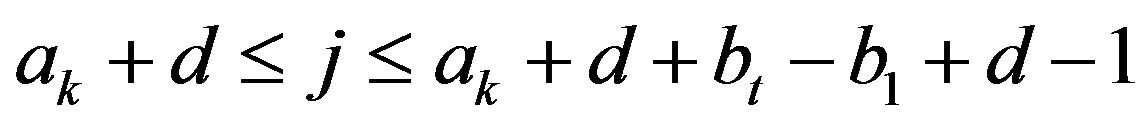 . In this case, there exists an integer h with
. In this case, there exists an integer h with 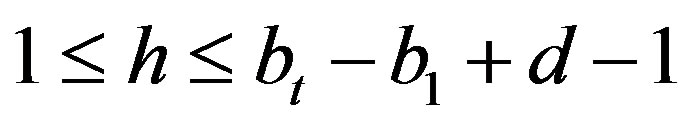 such that
such that 
Subcase 2.1 If 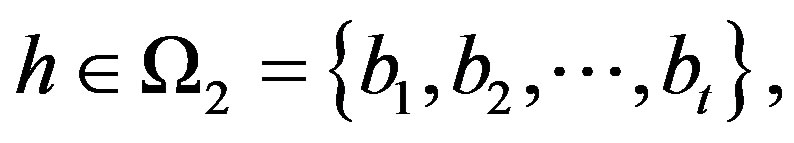 then
then 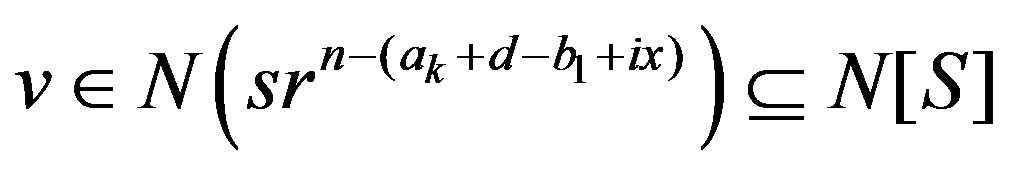
Subcase 2.2 Suppose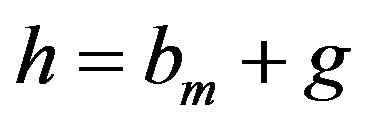 , for some integers m, g with
, for some integers m, g with  and
and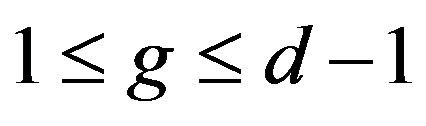 . In this case,
. In this case, 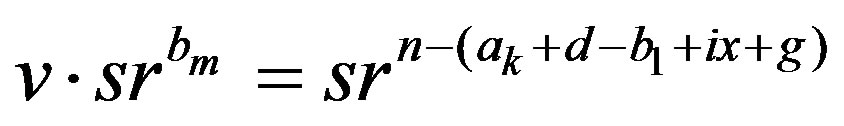 , which means that
, which means that 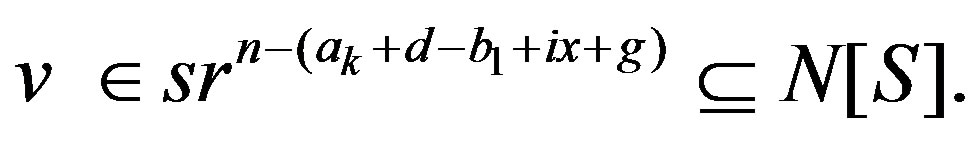
Case 3. Suppose 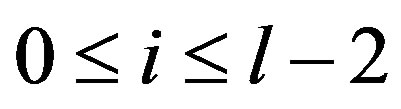 and
and
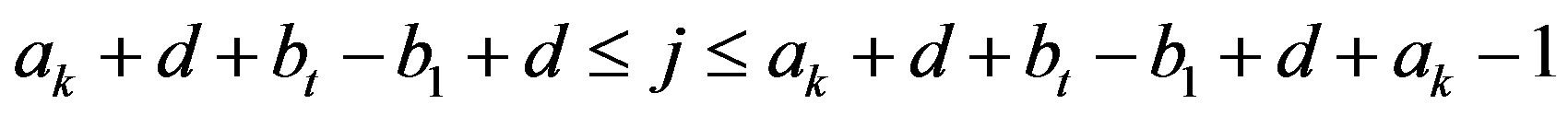 .
.
In this case, there exists an integer h with 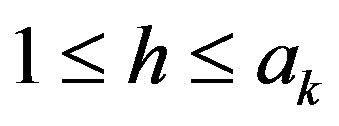 such that
such that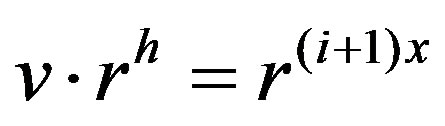 .
.
Subcase 3.1 If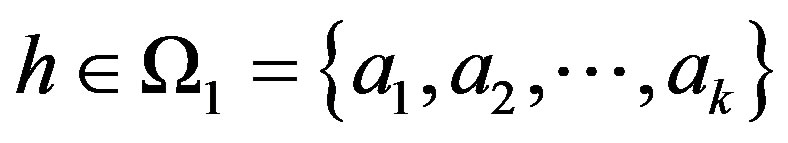 , then
, then 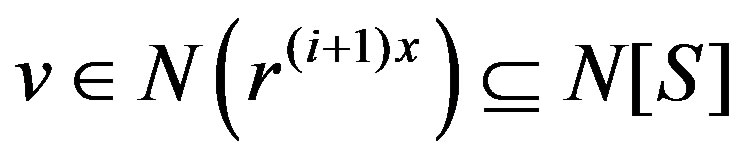 .
.
Subcase 3.2 Suppose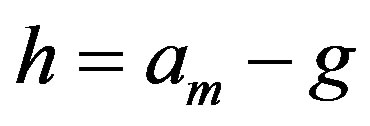 , for some integers m, g, with
, for some integers m, g, with 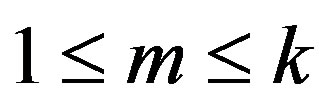 and
and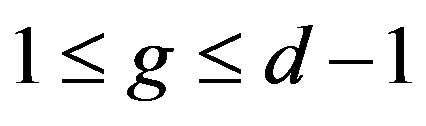 . In this case,
. In this case, 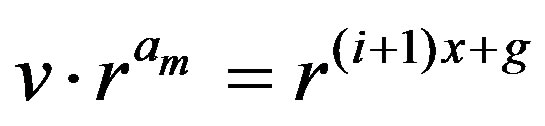 , which means that
, which means that 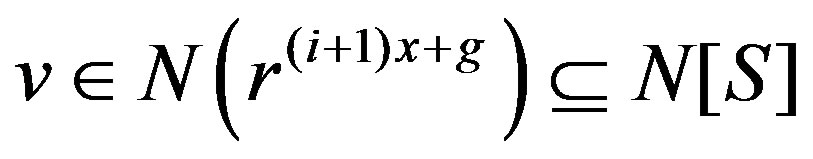 .
.
Case 4. Suppose 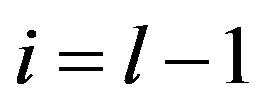 and
and
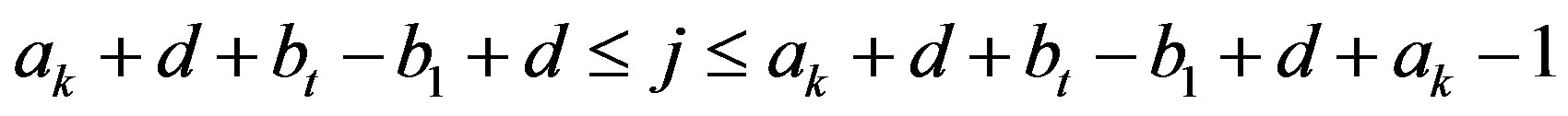 .
.
Then there exists an integer h with 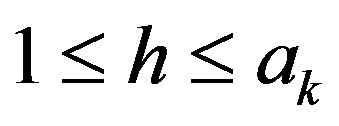 such that
such that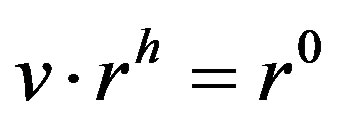 .
.
Subcase 4.1 If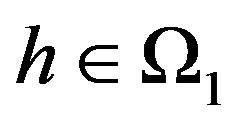 , then
, then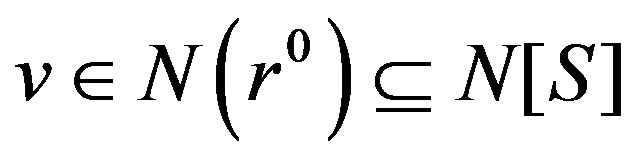 .
.
Subcase 4.2 Suppose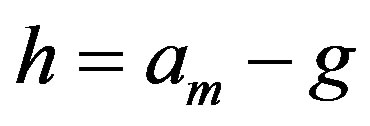 , for some integers m, g with
, for some integers m, g with  and
and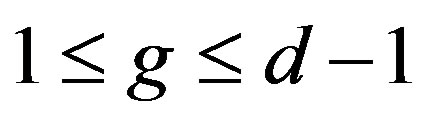 . In this case,
. In this case, 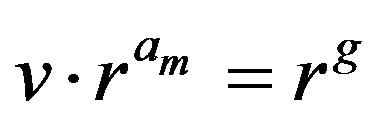 which means that
which means that .
.
Suppose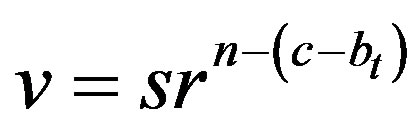 . We have the following cases:
. We have the following cases:
Case 1. Suppose 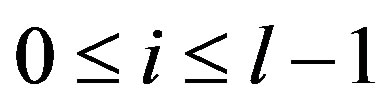 and
and 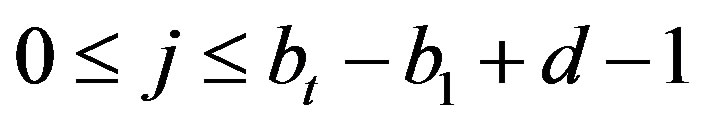 . In this case, there exists an integer h with
. In this case, there exists an integer h with 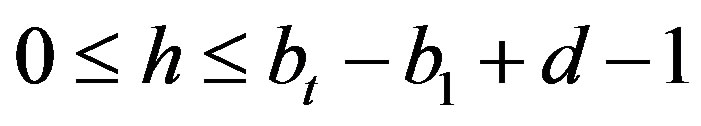 such that
such that 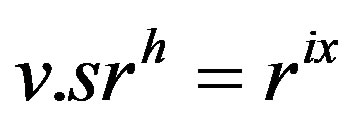
Subcase 1.1 If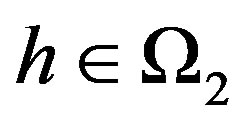 , then
, then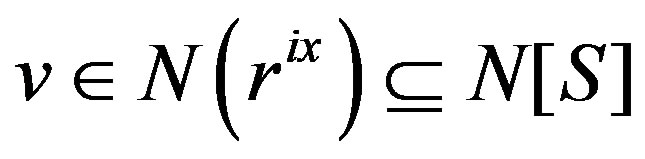 .
.
Subcase 1.2 Suppose , for some integers m, g with
, for some integers m, g with 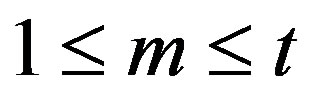 and
and . In this case,
. In this case, 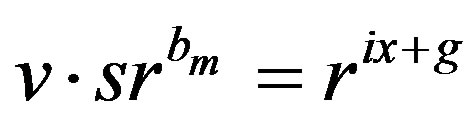 , which means that
, which means that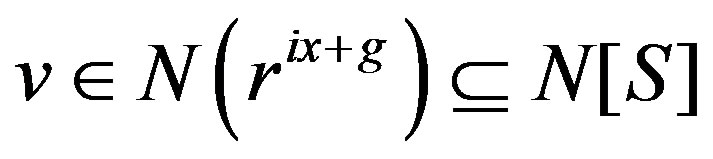 .
.
Case 2. Suppose 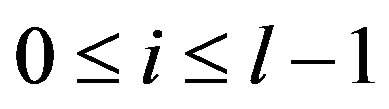 and
and 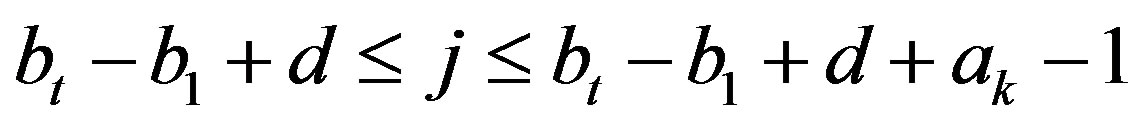 . In this case, there exists an integer h with
. In this case, there exists an integer h with 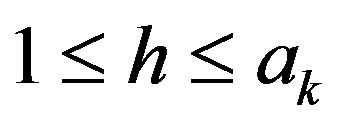 such that
such that 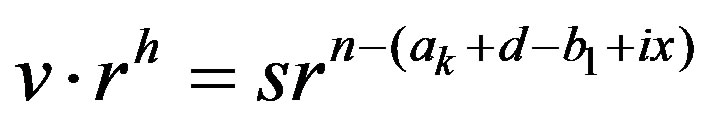 .
.
Subcase 2.1 If 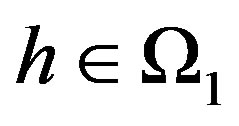 then
then 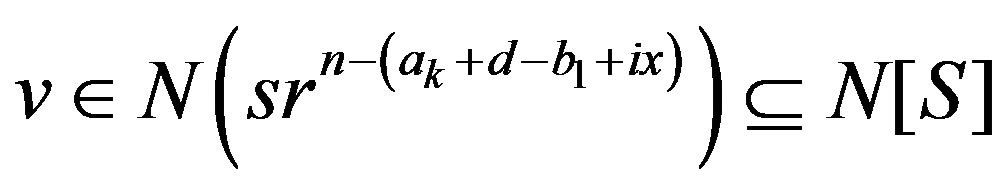 .
.
Subcase 2.2 Suppose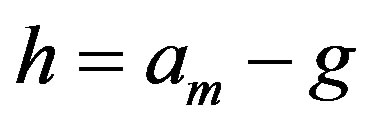 , for some integers m, g with
, for some integers m, g with 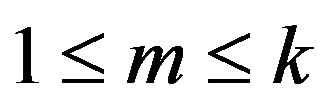 and
and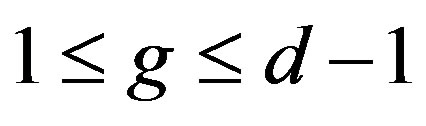 . In this case,
. In this case, 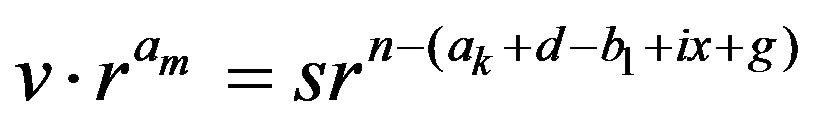 , which means that
, which means that 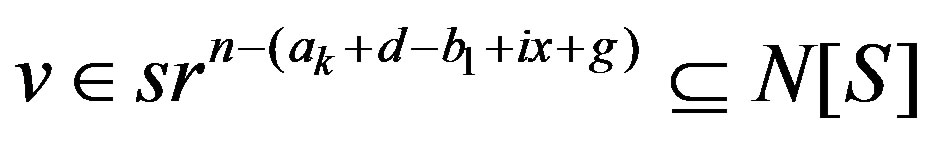 .
.
Case 3. Suppose  and
and  . In this case, there exists an integer h with
. In this case, there exists an integer h with 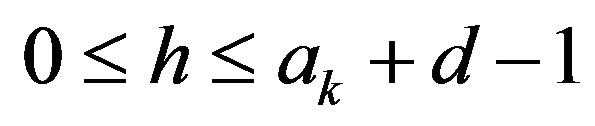 such that
such that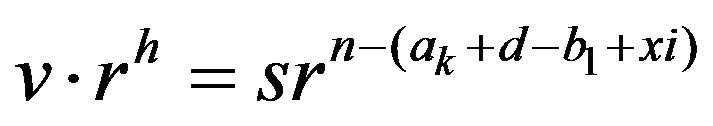 .
.
Subcase 3.1 If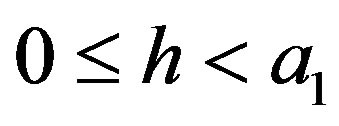 , then by the definition of
, then by the definition of 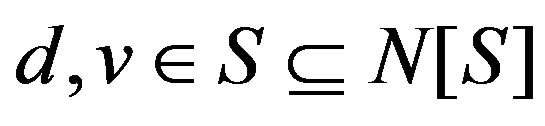 .
.
Subcase 3.2 Suppose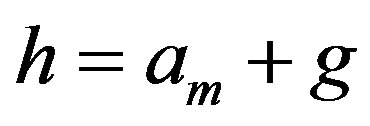 , for some integers m, g with
, for some integers m, g with  and
and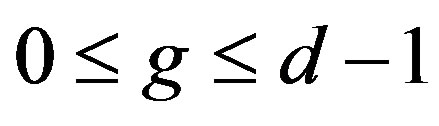 . In this case,
. In this case,  , which means that
, which means that 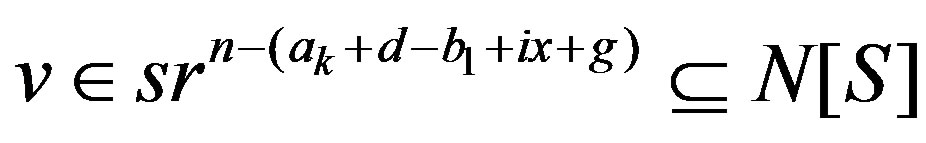 .
.
Thus S is a dominating set of G.
The following lemma provides an upper bound for the total domination number in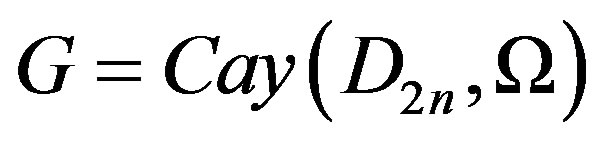 .
.
Lemma 5 Let  be an integer,
be an integer, 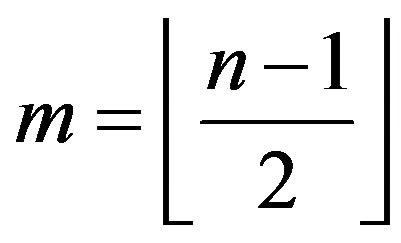 and k, t be integers such that
and k, t be integers such that . Let
. Let
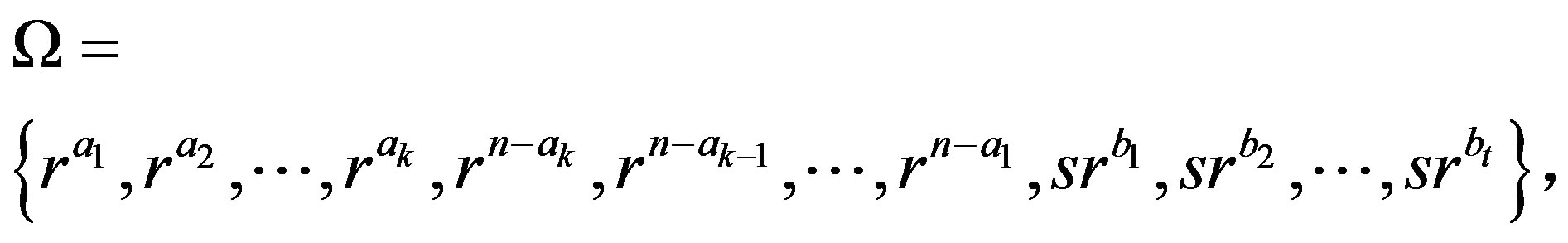
and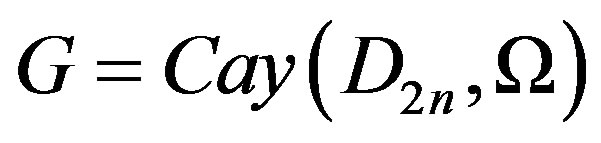 . If
. If 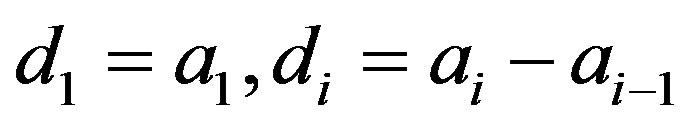 for
for
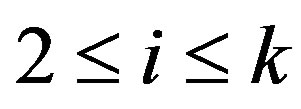 ,
, 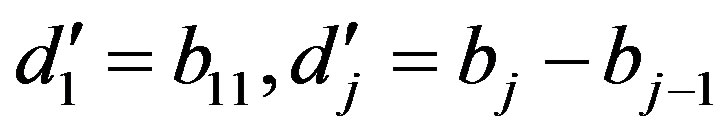 for
for  and
and
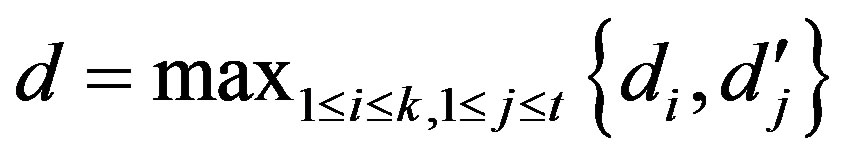 , then
, then .
.
Proof. Let 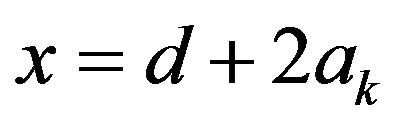 and
and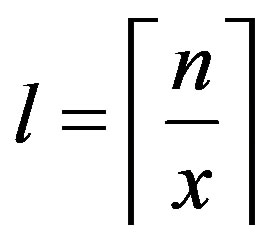 . Consider the set
. Consider the set
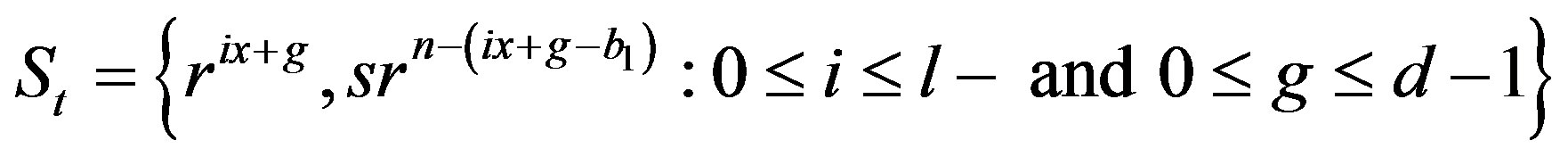 .
.
Clearly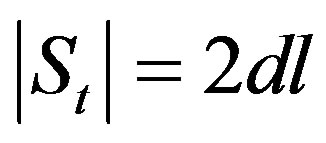 . We have to prove that
. We have to prove that 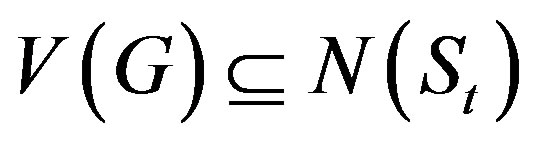 If
If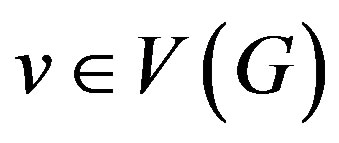 , then we can write
, then we can write 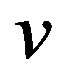 as either one vertex of the form
as either one vertex of the form 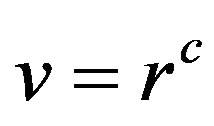 or
or , where
, where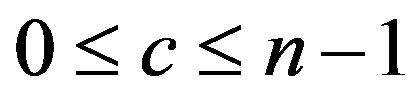 . By the division algorithm,
. By the division algorithm, 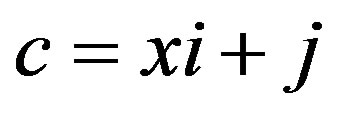 , where
, where 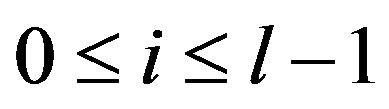 and
and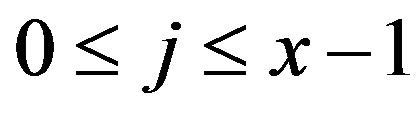 . We have the following cases:
. We have the following cases:
Case 1. Suppose 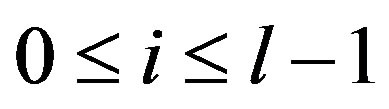 and
and . For some integer g with
. For some integer g with 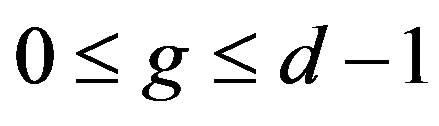 and by the definition of d, if
and by the definition of d, if , then
, then  or if
or if
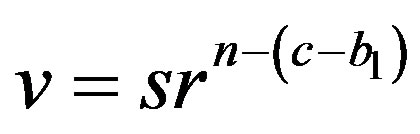 , then
, then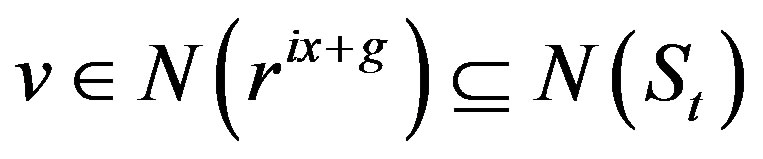 .
.
Case 2. Suppose 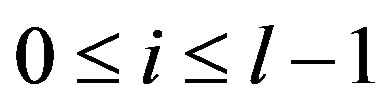 and
and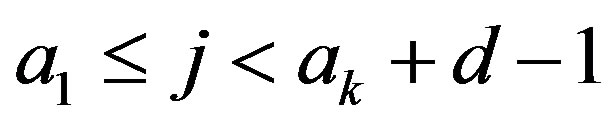 . We can write
. We can write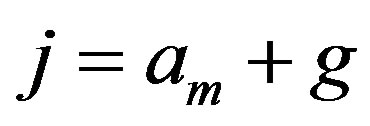 , for some integers m, g with
, for some integers m, g with 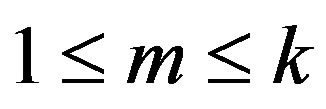 and
and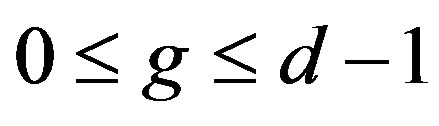 . If
. If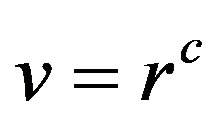 , then
, then 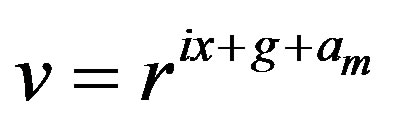 whereas
whereas 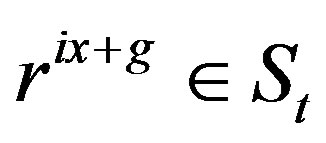 and so
and so 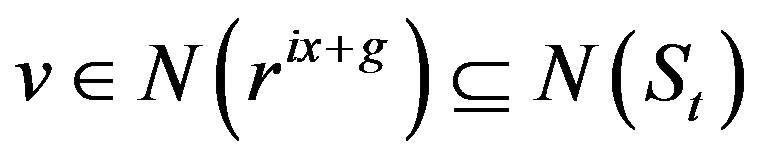 or if
or if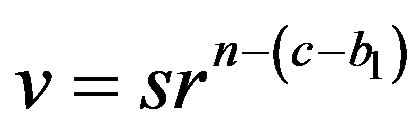 , then
, then
 whereas
whereas 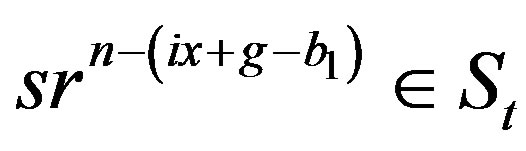 and so
and so
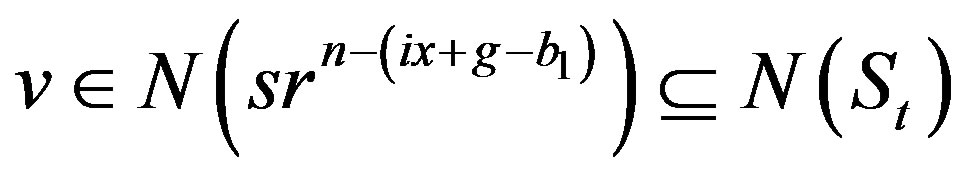 .
.
Case 3. Suppose 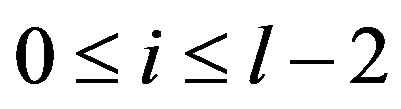 and
and
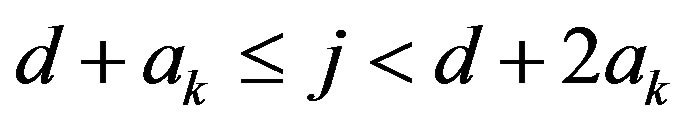 . In this case, there exists an integer h with
. In this case, there exists an integer h with  such that
such that 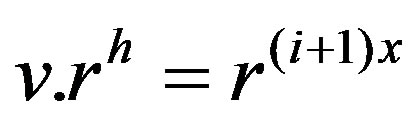 or
or
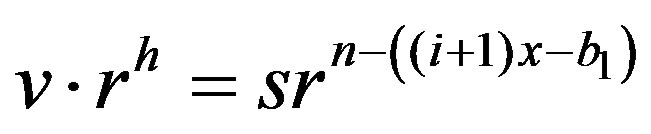 .
.
Subcase 3.1 Suppose 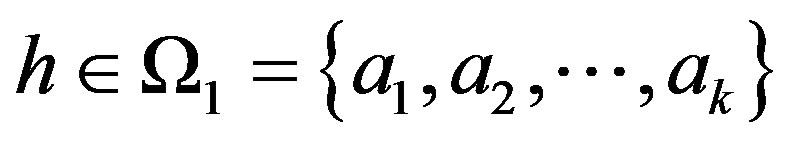 and if
and if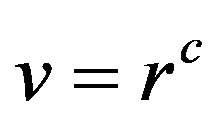 , then
, then 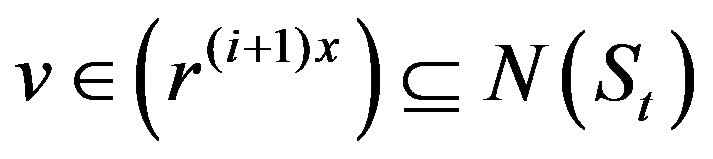 or if
or if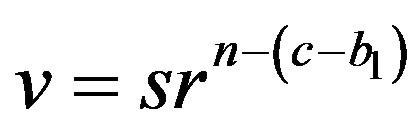 then
then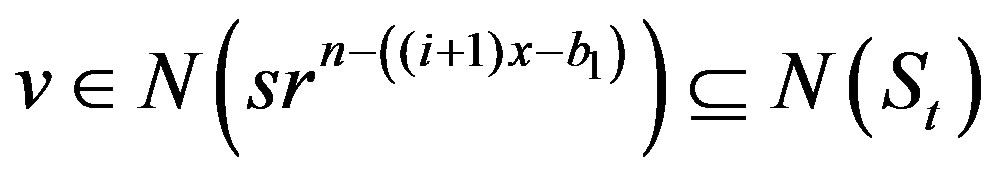 .
.
Subcase 3.2 Suppose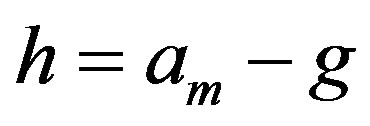 , for some integers m, g with
, for some integers m, g with 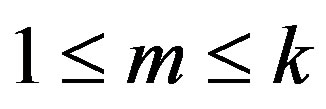 and
and . In this case, if
. In this case, if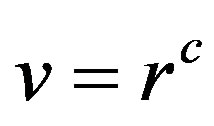 , then
, then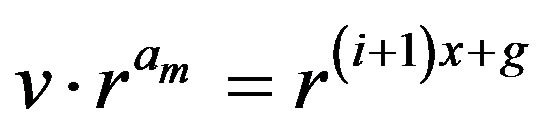 , which means that
, which means that
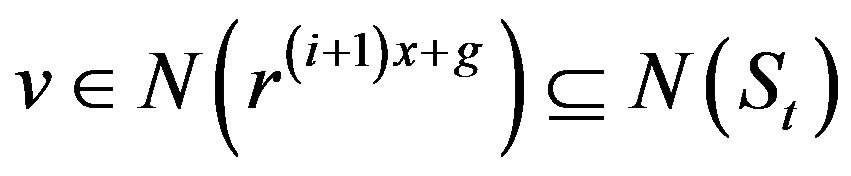 or if
or if , then
, then
 , which implies that
, which implies that 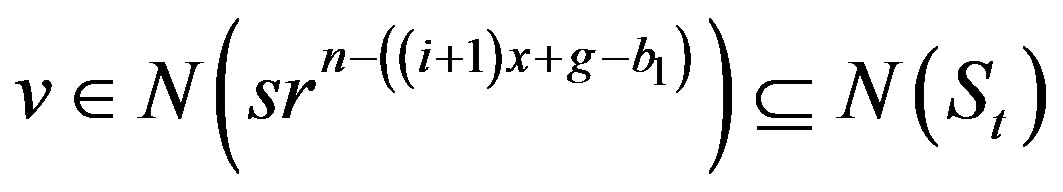 .
.
Case 4. Suppose 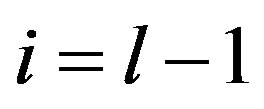 and
and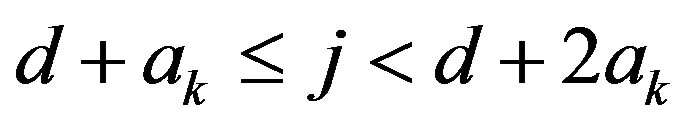 . Then there exists an integer h with
. Then there exists an integer h with 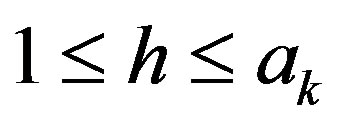 such that
such that 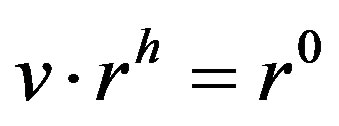 or
or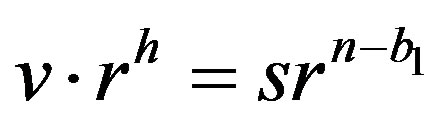 .
.
Subcase 4.1 When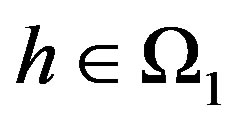 , and if
, and if , then
, then 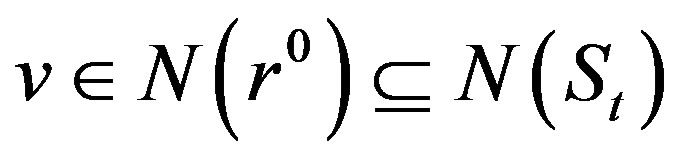 or if
or if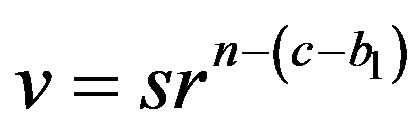 , then
, then
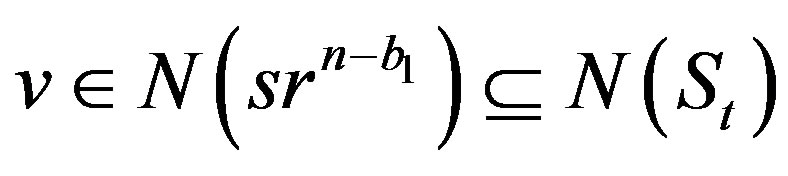 .
.
Subcase 4.2 Suppose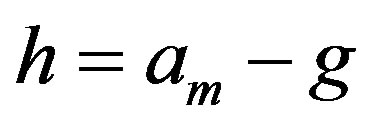 , for some integers m, g with
, for some integers m, g with  and
and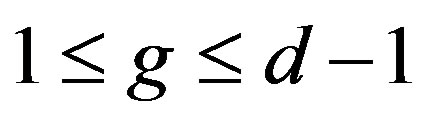 . In this case, if
. In this case, if 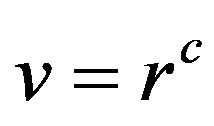 and
and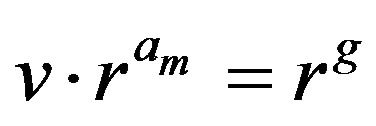 , which means that
, which means that
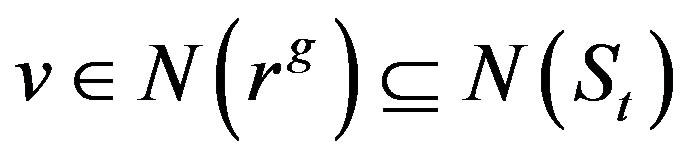 or if
or if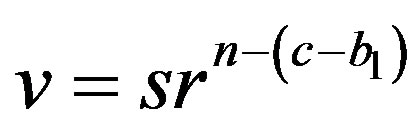 , then
, then
 , which means that
, which means that 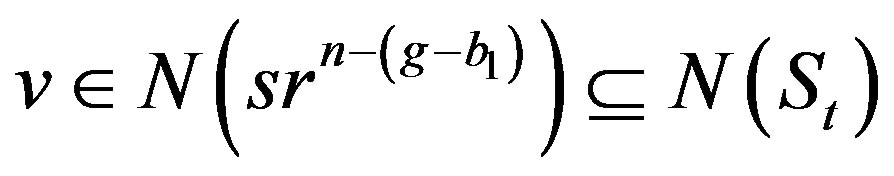 .
.
Thus 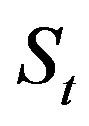 is a total dominating set of G.
is a total dominating set of G. 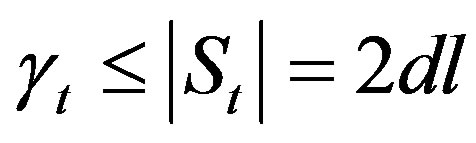 .
.
Now we obtain an upper bound for the connected domination number.
Lemma 6 Let 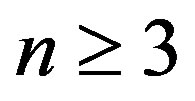 be an integer,
be an integer, 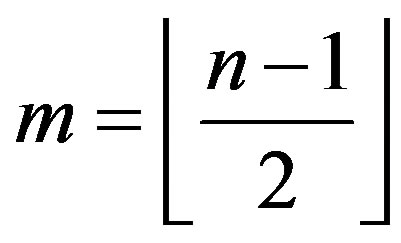 and k, t be integers such that
and k, t be integers such that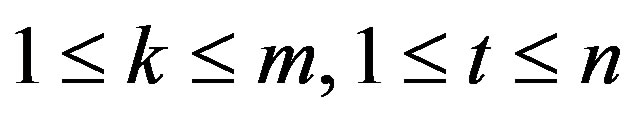 . Let
. Let

and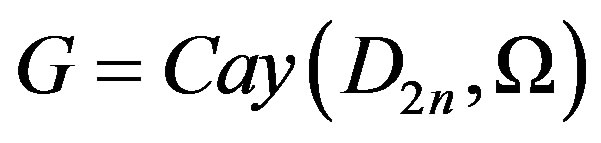 . If
. If 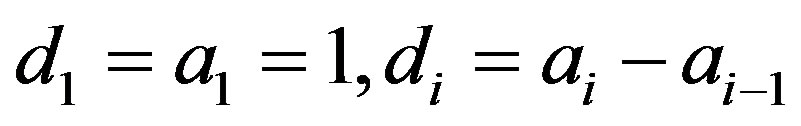 for
for ,
, 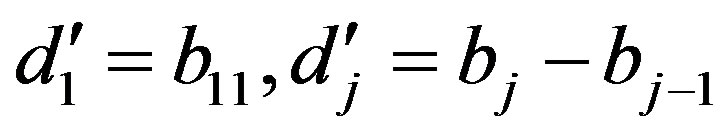 for
for  and
and
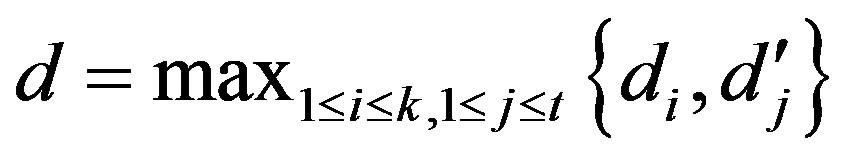 , then
, then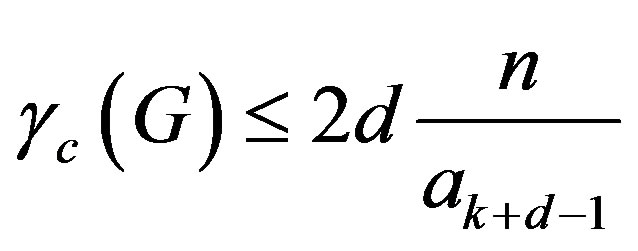 .
.
Proof. Let 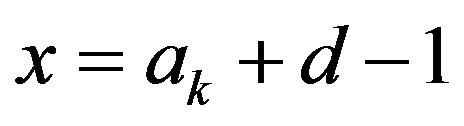 and
and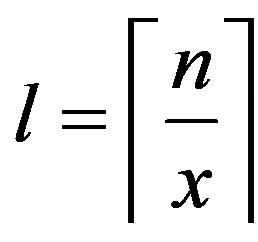 . Consider the set
. Consider the set
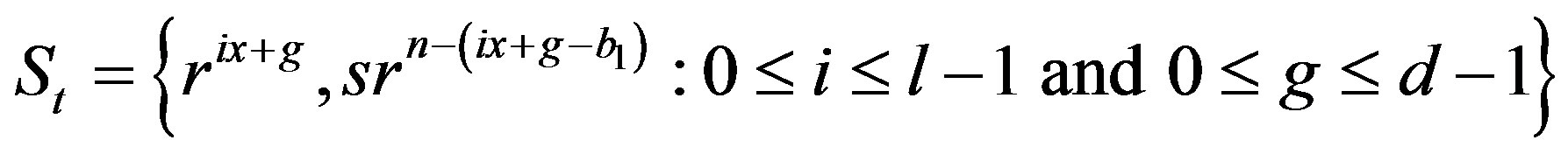 .
.
In the notation of Lemma 5, a1 = 1 and  and
and  is a total dominating set. Since
is a total dominating set. Since  and for each
and for each  with
with , we have paths
, we have paths
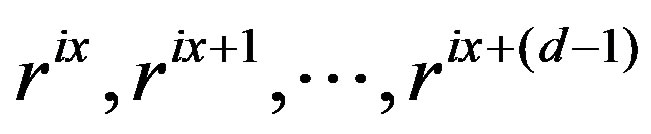 and
and 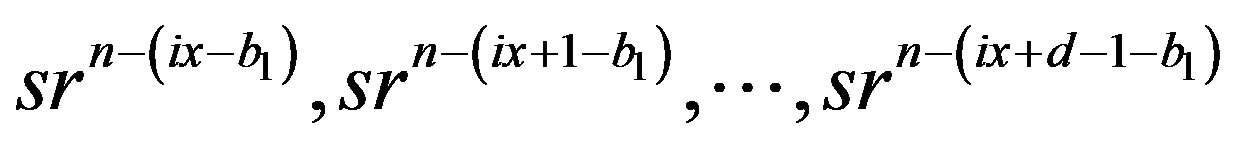 . Also note that
. Also note that  and
and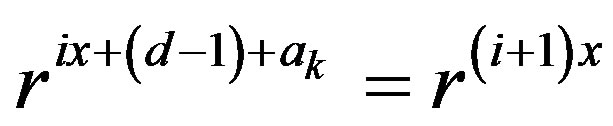 ,
, 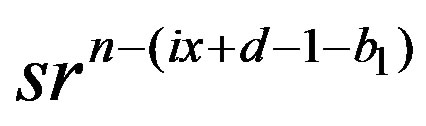 and
and 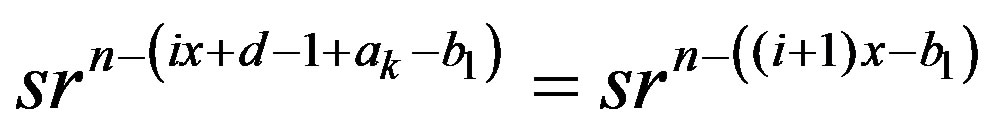 are connected. Hence the induced subgraph
are connected. Hence the induced subgraph  is connected.
is connected.
3. Subgroups as Efficient Domination Sets
In this section, we obtain some E-sets in 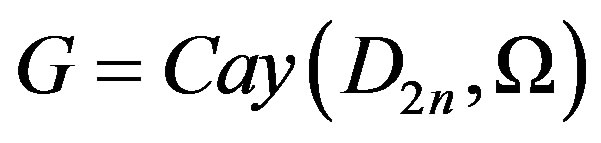 . Moreover we have identified certain subgroups of
. Moreover we have identified certain subgroups of 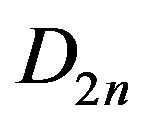 which are also efficient domination sets in
which are also efficient domination sets in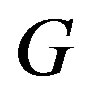 .
.
Theorem 7 Let 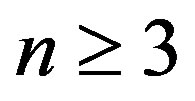 be an integer,
be an integer, 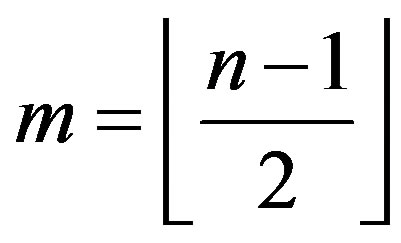 and k, t be integers such that
and k, t be integers such that 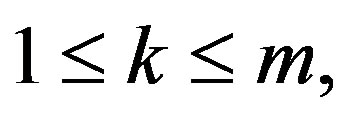
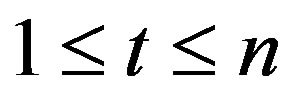 and d is an integer such that
and d is an integer such that 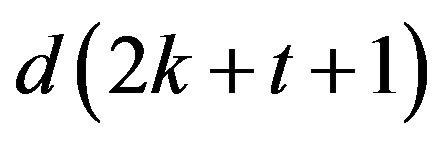 divides n. Let
divides n. Let
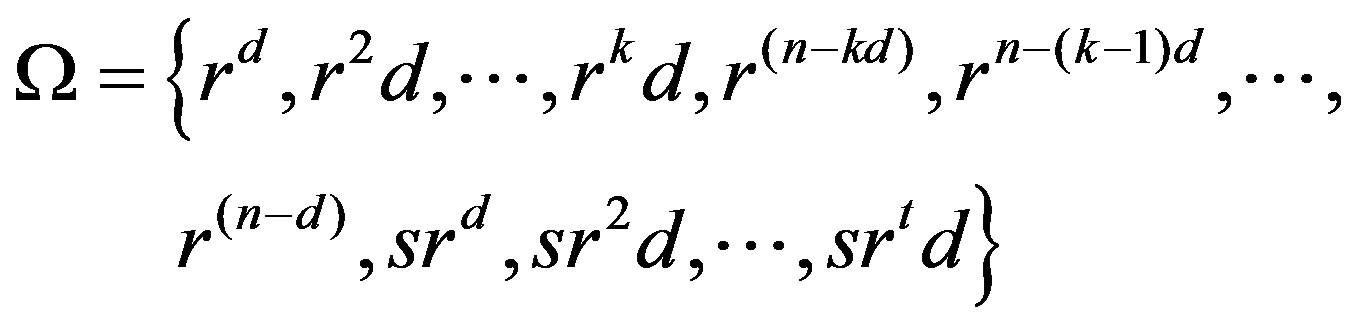
and . Then
. Then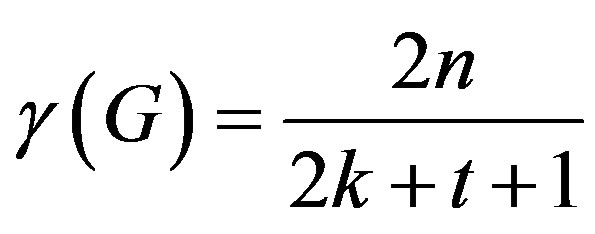 . In this case,
. In this case,  has an E-set.
has an E-set.
Proof. Let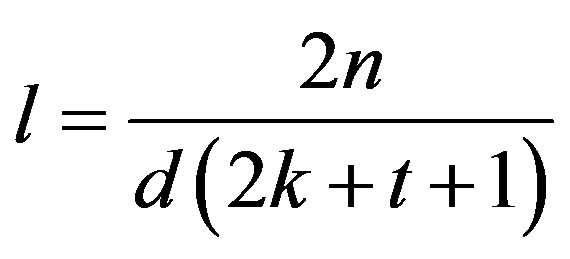 and
and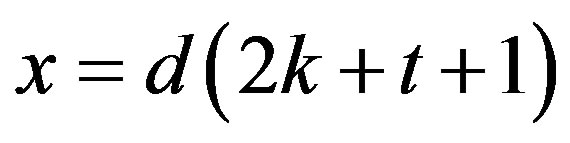 . In the notation of Lemma 4,
. In the notation of Lemma 4,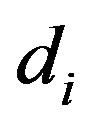 ’s and
’s and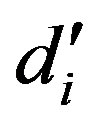 ’s are same,
’s are same, 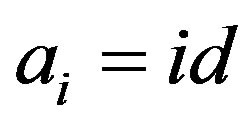 for all
for all 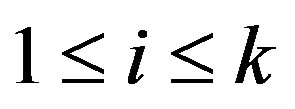 and
and  for all
for all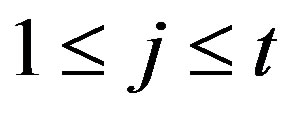 .
.
Let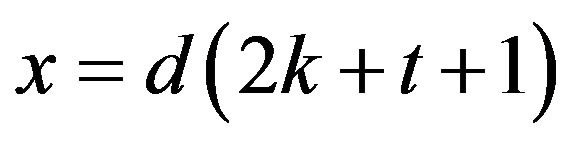 and
and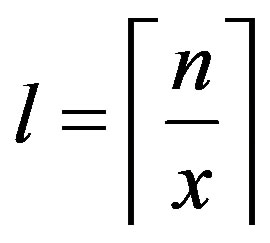 . By Lemma 4,
. By Lemma 4,

is a dominating set and hence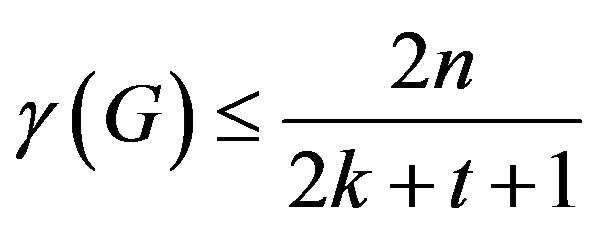 . Since
. Since
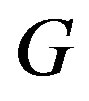 is
is  regular, by Theorem 1, one can conclude that
regular, by Theorem 1, one can conclude that 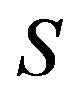 is an E-set in
is an E-set in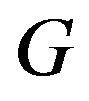 .
.
Remark 8 Note that Theorem 3 identifies all subgroups of the dihedral group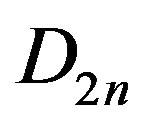 . Now we us identify some of the subgroups as efficient dominating sets.
. Now we us identify some of the subgroups as efficient dominating sets.
Theorem 9 Let 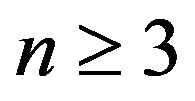 be an integer,
be an integer, 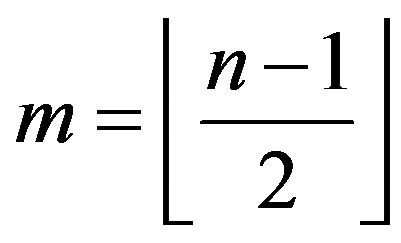 and k, t be integers such that
and k, t be integers such that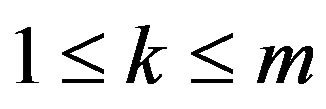 ,
, 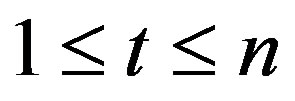 and
and 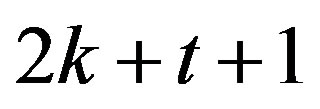 divides
divides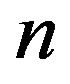 . Let
. Let 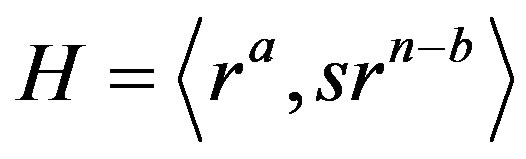 be a subgroup of the dihedral group
be a subgroup of the dihedral group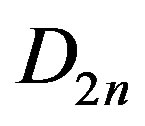 , where
, where 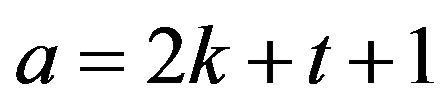 and
and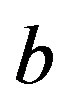 ,
,  Then, there exists a generating set
Then, there exists a generating set  of
of 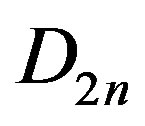 such that H is an efficient dominating set for the Cayley graph
such that H is an efficient dominating set for the Cayley graph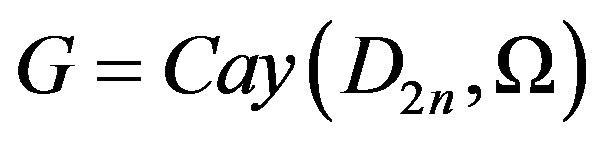 .
.
Proof. Let
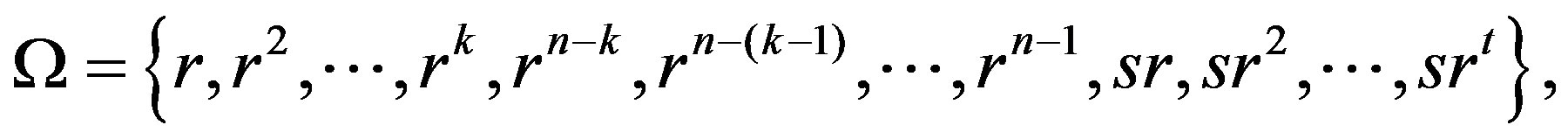
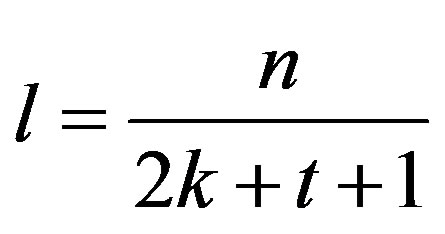 and
and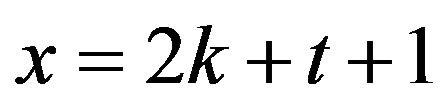 . By taking
. By taking 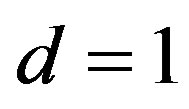 in Theorem 7,
in Theorem 7,

is an efficient dominating set of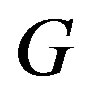 .
.
Remark 10 Under the assumptions of Theorem 9,  is an efficient dominating set for the Cayley graph
is an efficient dominating set for the Cayley graph  for all
for all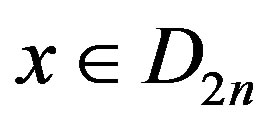 .
.
4. E-Chains in Cayley Graphs
Theorem 7 and 9 provide a tool to produce E-sets and visualize some of the subgroups as E-sets in  . We use this tool to obtain an inclusive E-chain and inductive subgroups E-chain of Cayley graphs on the dihedral group.
. We use this tool to obtain an inclusive E-chain and inductive subgroups E-chain of Cayley graphs on the dihedral group.
Theorem 11 Let 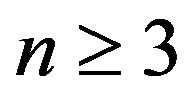 be an integer,
be an integer, 
and k be an integers such that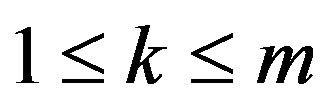 ,
, 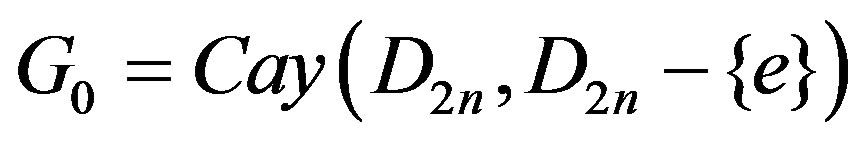 ,
,

and 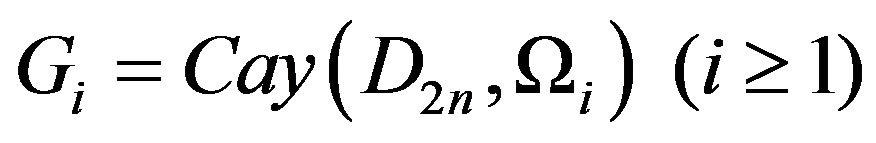 Assume that
Assume that 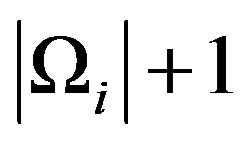 divides
divides 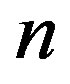 and
and 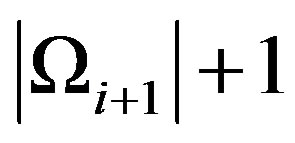 divides
divides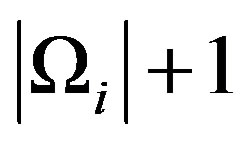 . Then the finite family of graphs
. Then the finite family of graphs 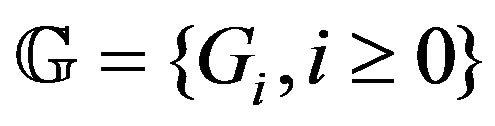 is inductive subgroups E-chain.
is inductive subgroups E-chain.
Proof. Let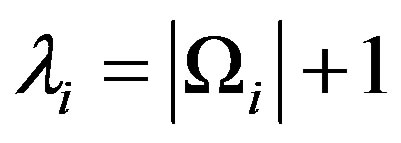 . By the assumption
. By the assumption . divides
. divides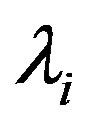 . Define the map
. Define the map 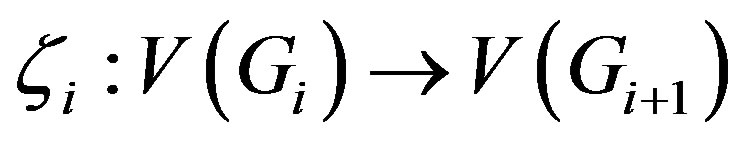 by
by 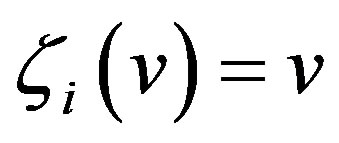 for all
for all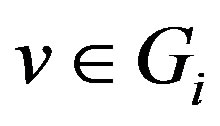 . By Theorem 9,
. By Theorem 9, 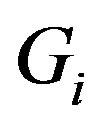 has an efficient dominating set and it is of the form
has an efficient dominating set and it is of the form
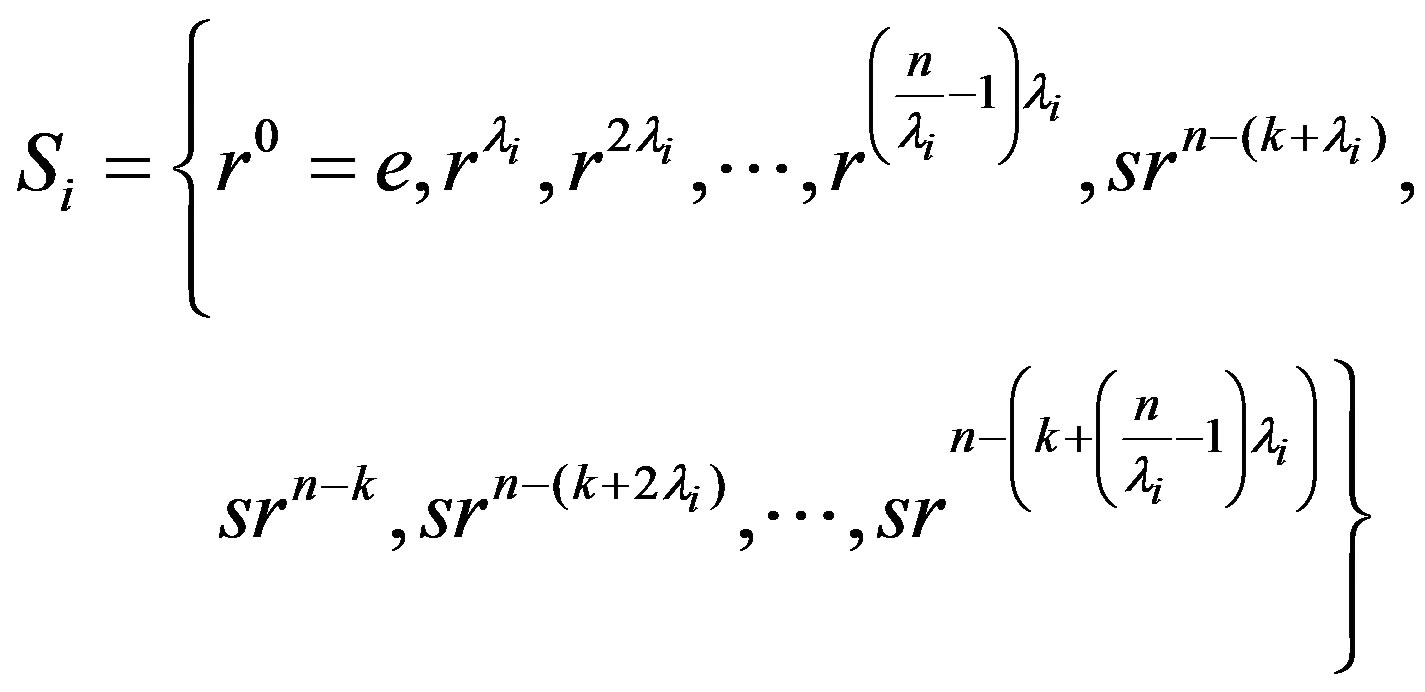
and also ’s are subgroups. It implies that
’s are subgroups. It implies that  for every
for every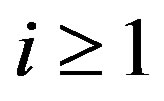 . Hence the family of graphs
. Hence the family of graphs  is inductive subgroups E-chain.
is inductive subgroups E-chain.
The construction of an inclusive E-chain of Cayley graphs is based on the following lemma.
Lemma 12 Let 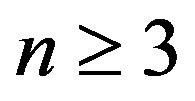 be an integer,
be an integer, 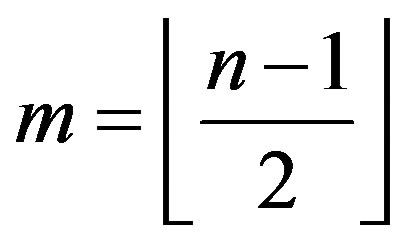 , k, t be integers such that
, k, t be integers such that ,
,  and d is an integer such that
and d is an integer such that 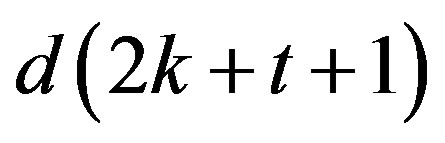 divides
divides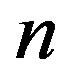 . For
. For , let
, let
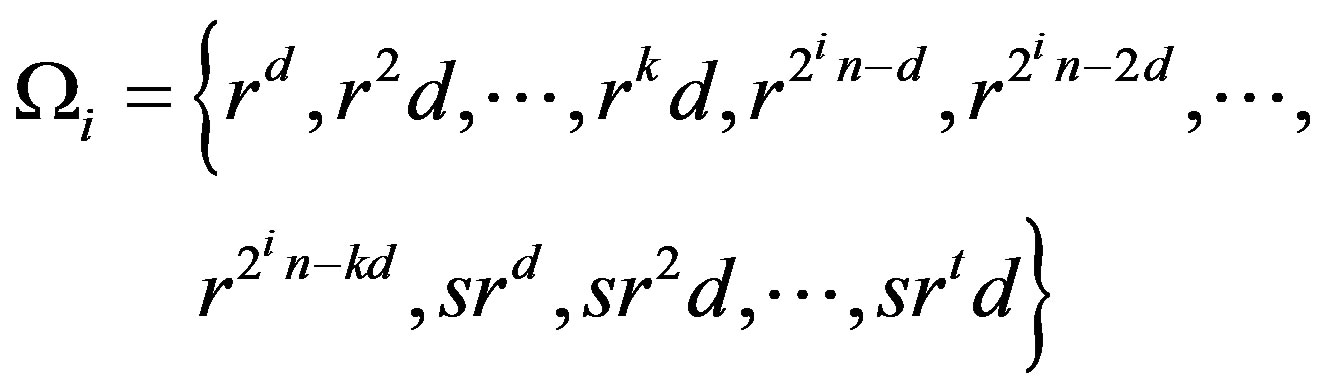
and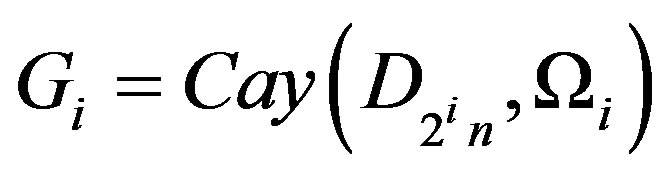 . Then
. Then  is a covering of
is a covering of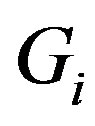 .
.
Proof. Define the surjective map
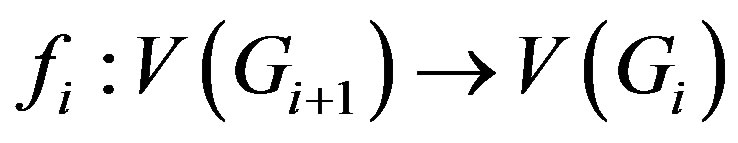 by
by  and
and
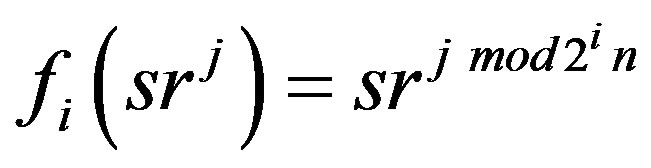 for all j, where
for all j, where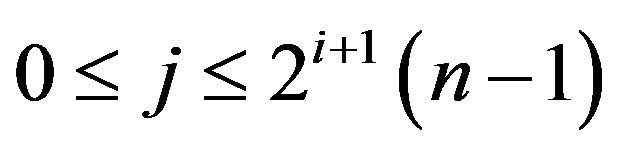 . Note that
. Note that 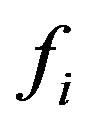 is a group homomorphism from
is a group homomorphism from 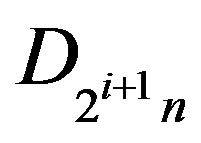 onto
onto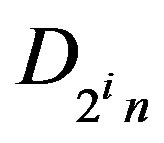 . Let
. Let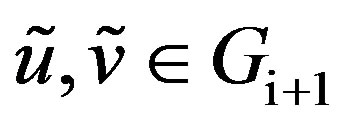 . Suppose
. Suppose 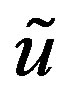 and
and  are adjacent in
are adjacent in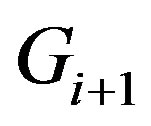 . Then, there exists
. Then, there exists  with
with
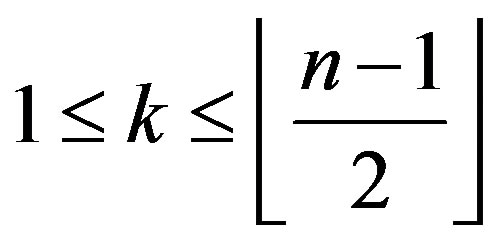 or
or 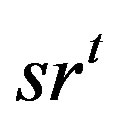 with
with 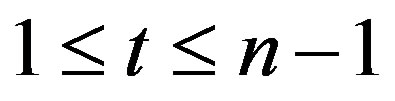 such that
such that
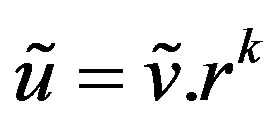 or
or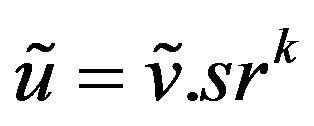 . Since
. Since 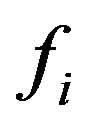 is a group homomorphism and
is a group homomorphism and
 , we have
, we have 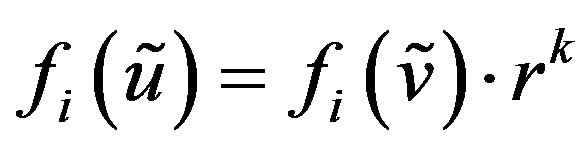 or
or 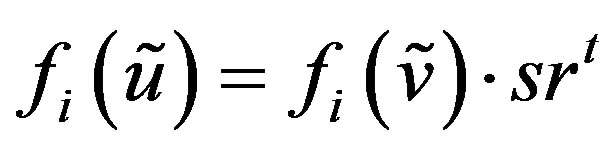 and so
and so 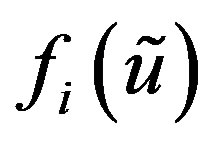 and
and  are adjacent in
are adjacent in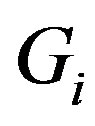 . Consider the map
. Consider the map 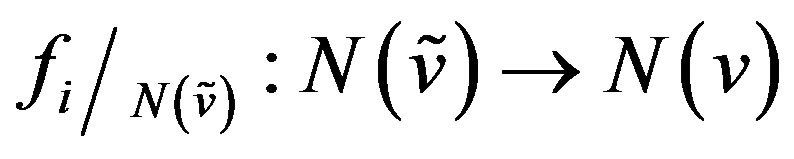 for any vertex
for any vertex 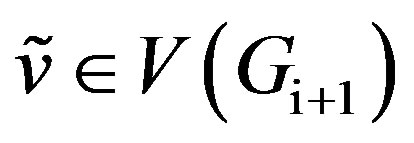 and
and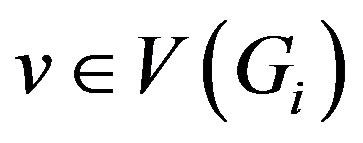 . Claim
. Claim 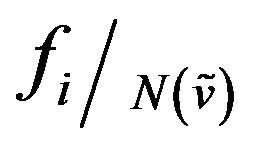 is bijection. Any element
is bijection. Any element 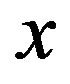 in
in 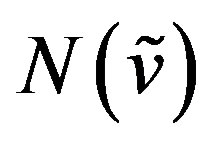 as either one vertex of the form
as either one vertex of the form 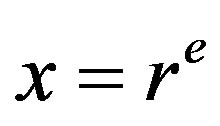 or
or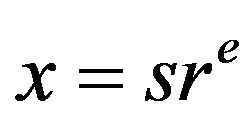 , where
, where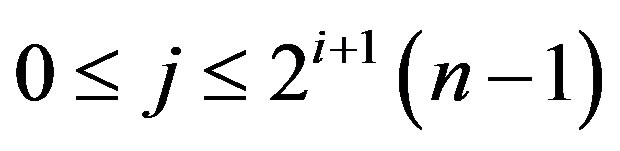 . Let
. Let 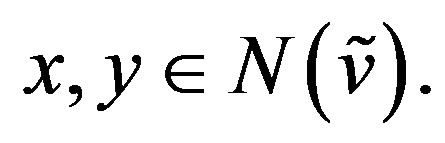 Then we have following three cases:
Then we have following three cases:
Case 1. Let  and
and 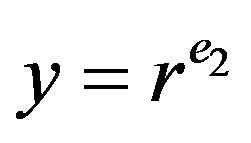 with
with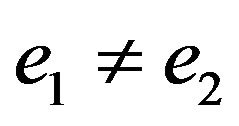 . Suppose
. Suppose , i.e.
, i.e. 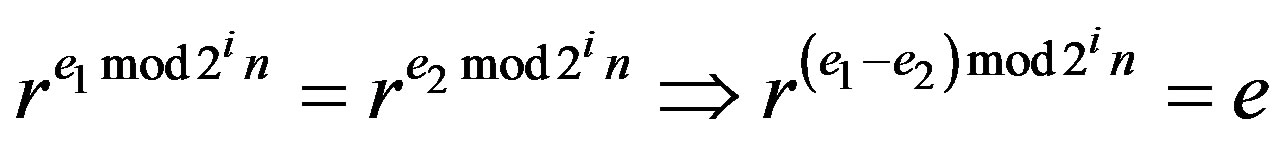 . i.e.
. i.e. 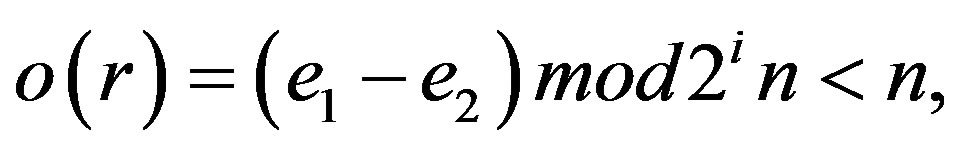 which is a contradiction to
which is a contradiction to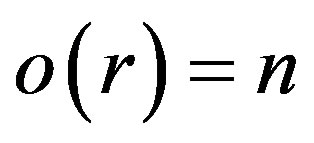 . Therefore
. Therefore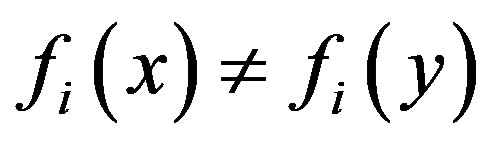 .
.
Case 2. Let 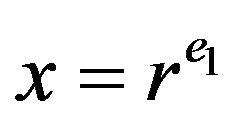 and
and . Suppose
. Suppose
 , i.e.
, i.e. 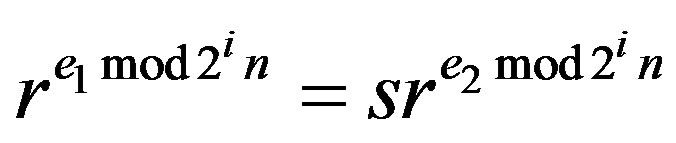 This means
This means
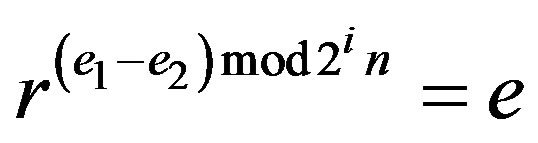 or
or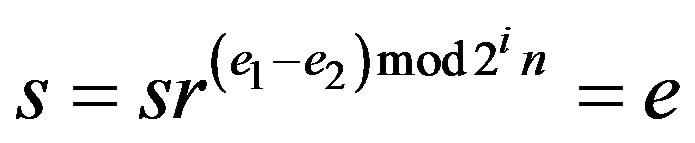 , which is a contradiction. Therefore
, which is a contradiction. Therefore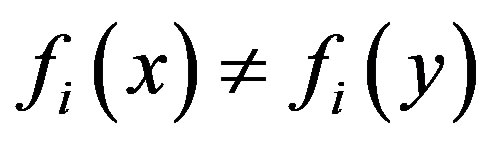 .
.
Case 3. Let  and
and 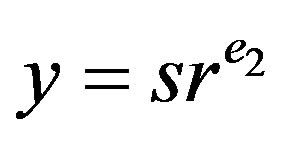 with
with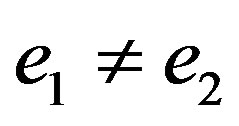 . Suppose
. Suppose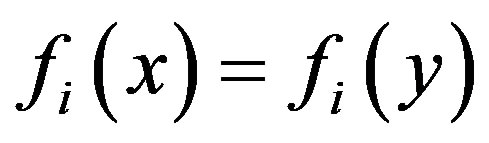 , i.e.
, i.e.
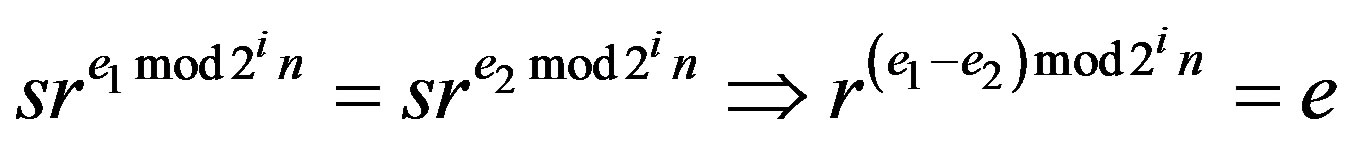 . i.e.
. i.e.
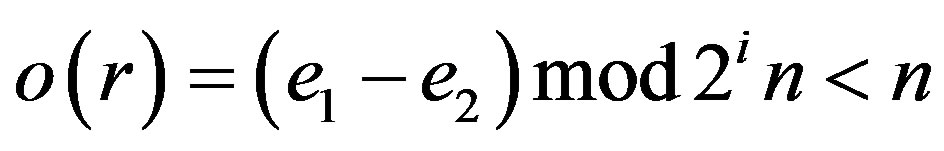 which is a contradiction. Therefore
which is a contradiction. Therefore 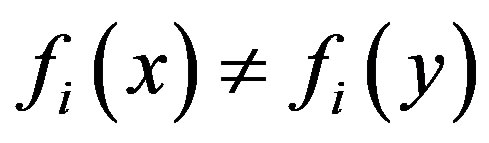 . Hence distinct elements of
. Hence distinct elements of 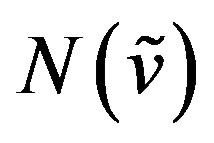 are distinctly mapped onto
are distinctly mapped onto  and so
and so 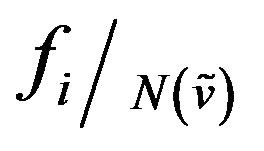 is a required bijection.
is a required bijection.
Theorem 13 Let 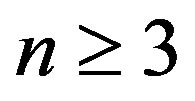 be an integer,
be an integer, 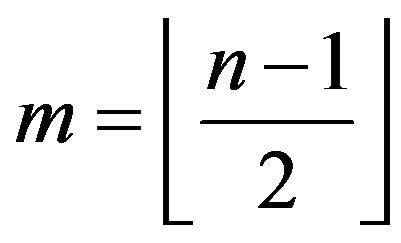 k, t, be integers such that
k, t, be integers such that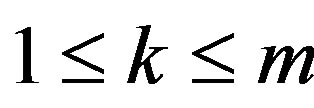 ,
, 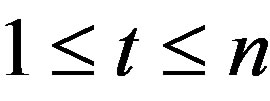 and d is an integer such that
and d is an integer such that 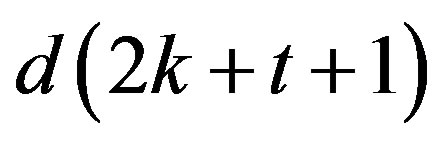 divides
divides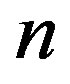 . For
. For 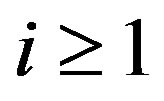 let
let

and . Let
. Let 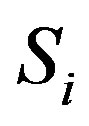 be an efficient dominating set for
be an efficient dominating set for . Then the finite family of graphs
. Then the finite family of graphs 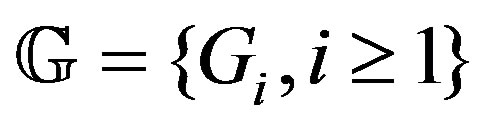 is an inclusive E-chain.
is an inclusive E-chain.
Proof. Since by above Lemma, 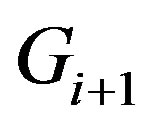 is a covering of
is a covering of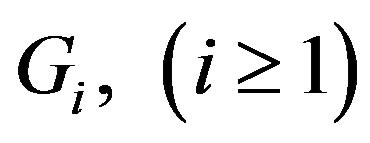 . Since by Theorem 2,
. Since by Theorem 2,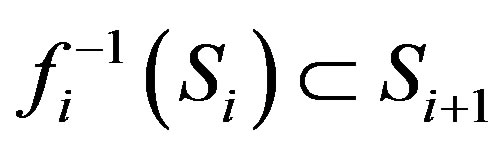 . Hence the finite family of graphs
. Hence the finite family of graphs 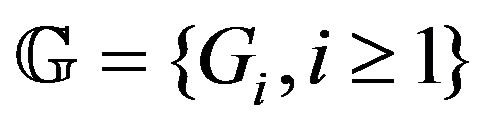 is an inclusive E-chain.
is an inclusive E-chain.
5. Acknowledgements
The work reported here is supported by the Special Assistance Programme (F510-DRS-I/2007) of University Grants Commission, India awarded to the Department of Mathematics, Manonmaniam Sundaranar University for the period 2007-2012.
REFERENCES
- S. Lakshmivarahan, J. S. Jwo and S. K. Dhall, “Symmetry in Interconnection Networks Based on Cayley Graphs of Permutation Groups: A Survey,” Parallel Computing, Vol. 19, No. 4, 1993, pp. 361-407. doi:10.1016/0167-8191(93)90054-O
- E. J. Cockayne, R. M. Dawes and S. T. Hedetniemi, “Total Domination in Graphs,” Networks, Vol. 10, No. 3, 1980, pp. 211-219. doi:10.1002/net.3230100304
- I. J. Dejter and O. Serra, “Efficient Dominating Sets in Cayley Graphs,” Discrete Applied Mathematics, Vol. 129, No. 2-3, 2003, pp. 319-328. doi:10.1016/S0166-218X(02)00573-5
- R. J. Huang and J.-M. Xu, “The Bondage and Efficient Domination of Vertex Transitive Graphs,” Discrete Mathematics, Vol. 308, No. 4, 2008, pp. 571-582. doi:10.1016/j.disc.2007.03.027
- J. Lee, “Independent Perfect Domination Sets in Cayley Graphs,” Journal of Graph Theory, Vol. 37, No. 4, 2000, pp. 219-231.
- T. Tamizh Chelvam and I. Rani, “Dominating Sets in Cayley Graphs on Zn,” Tamkang Journal of Mathematics, Vol. 37, No. 4, 2007, pp. 341-345.
- T. Tamizh Chelvam and I. Rani, “Independent Domination Number of Cayley Graphs on Zn,” The Journal of Combinatorial Mathematics and Combinatorial Computing, Vol. 69, 2009, pp. 251-255.
- T. Tamizh Chelvam and I. Rani, “Total and Connected Domination Numbers of Cayley Graphs on Zn,” Advanced Studies in Contemporary Mathematics, Vol. 20, 2010, pp. 57-61.
- T. W. Haynes, S. T. Hedetniemi and P. J. Slater, “Fundamentals of Domination in Graphs,” Marcel Dekker, New York, 1998.
- K. Conrad, “Dihedral Groups II,” 2009. http://www.math.uconn.edu/~kconrad/blurbs/grouptheory/dihedral2.pdf

