Open Journal of Discrete Mathematics
Vol.1 No.2(2011), Article ID:5765,7 pages DOI:10.4236/ojdm.2011.12006
Computing Recomposition of Maps with a New Sampling Asymptotic Formula
1Departamento de Análisis Económico y Finanzas, Universidad de Castilla-La Mancha, Cuenca (Castilla-La Mancha), Spain
2Departamento de Matemática Aplicada y Estadstica, Universidad Politécnica de Cartagena, Cartagena (Región de Murcia), Spain
3Departamento de Matemáticas, Universidad de Castilla-La Mancha, Cuenca (Castilla-La Mancha), Spain
E-mail: almudena.antuna@uclm.es, juan.garcia@upct.es, mangel.lopez@uclm.es
Received April 6, 2011; revised May 5, 2011; accepted May 21, 2011
Keywords: Band-limited signal, Shannon’s sampling theorem, Approximation theory
Abstract
The aim of the present paper is to state an asymptotic property 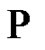 of Shannon’s sampling theorem type, based on normalized cardinal sines, and keeping constant the sampling frequency of a not necessarilly bandlimited signal. It generalizes in the limit the results stated by Marvasti, et al. [7] and Agud, et al. [1]. We show that
of Shannon’s sampling theorem type, based on normalized cardinal sines, and keeping constant the sampling frequency of a not necessarilly bandlimited signal. It generalizes in the limit the results stated by Marvasti, et al. [7] and Agud, et al. [1]. We show that  is fulfilled for any constant signal working for every given sampling frequency. Moreover, we conjecture that Gaussian maps of the form
is fulfilled for any constant signal working for every given sampling frequency. Moreover, we conjecture that Gaussian maps of the form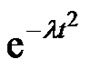 ,
, 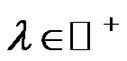 , hold
, hold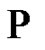 . We support this conjecture by proving the equality given by
. We support this conjecture by proving the equality given by 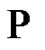 for the three first coefficients of the power series representation of
for the three first coefficients of the power series representation of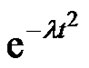 .
.
1. Introduction and Statement of the Main Results
A central result of the signal theory in engineering is the well-known Shannon-Whittaker-Kotel’nikov’s theorem (see for instance [9] or [11]) working for band-limited maps of 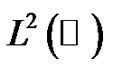 (i.e., for Paley-Wiener signals), and based on the normalized cardinal sinus map
(i.e., for Paley-Wiener signals), and based on the normalized cardinal sinus map  defined by
defined by
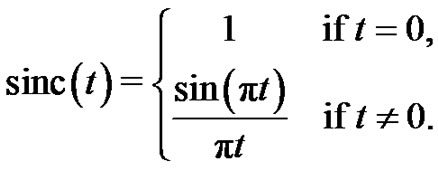
Another philosopher’s stone of the signal processing theory is the Middleton’s sampling theorem for band step functions (see [8]). This result was one of the first modifications of the classic Sampling theorem (see [10]) which only works for band-limited maps. After this starting point many different extensions and generalizations of this theorem appeared in the literature trying to obtain approximations of non band-limited signals (see for instance [2] or [4]). Good surveys on these extensions are [3] or [11].
In this paper we follow the spirit of the previous results in the sense of trying to obtain approximations of non band-limited signals by using band-limited ones by increasing the band size. But our approach is completely different to the previous ones in the sense that we keep constant the sampling frequency generalizing in the limit the results of Marvasti et al. [7] and Agud et al. [1] .
In this setting, we state the following asymptotic property of Shannon’s sampling theorem type where the convergence is considered in the Cauchy’s principal value for the series and pointwise for the limit.
Property 1 Let 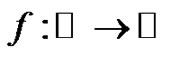 be a map and
be a map and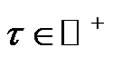 . We say that
. We say that  holds the property
holds the property  for
for 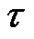 if
if
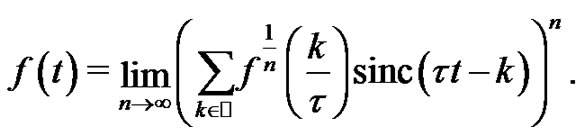 (1)
(1)
The statement of the main results is:
Theorem 1 Every constant signal holds property 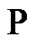 for every given
for every given .
.
Conjecture 1 The Gaussian maps, i.e. maps of the form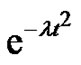 ,
, 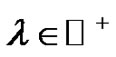 hold property
hold property 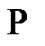 for every given
for every given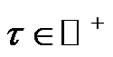 .
.
To support our feeling on the truth of the Conjecture 1 we prove, without loss of generality for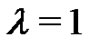 , that the Gaussian map
, that the Gaussian map 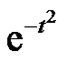 holds expression (1) for the three first coefficients of the power series representation of
holds expression (1) for the three first coefficients of the power series representation of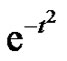 . Note that since the Gaussian map is analytical, for proving formula (1) is enough to show the equality between the coefficients of the power series representation of the Gaussian map and the coefficients of the series stated in the second member of (1) after proving the analitycity of the second member of (1). The statement of our result is the following:
. Note that since the Gaussian map is analytical, for proving formula (1) is enough to show the equality between the coefficients of the power series representation of the Gaussian map and the coefficients of the series stated in the second member of (1) after proving the analitycity of the second member of (1). The statement of our result is the following:
Theorem 2 Let 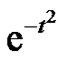 be a Gaussian map. Then the three first coefficients of the power series representation of
be a Gaussian map. Then the three first coefficients of the power series representation of 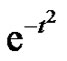 are equal to the three first ones of the second member of expression (1).
are equal to the three first ones of the second member of expression (1).
The paper is divided into three sections. In Section 2 we present the ideas and results that have inspired us to formulate property 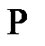 and Conjecture 1. Section 3 is devoted to prove Theorem 1 and in Section 4 is proved Theorem 2.
and Conjecture 1. Section 3 is devoted to prove Theorem 1 and in Section 4 is proved Theorem 2.
2. On the Property 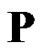 and Conjecture 1
and Conjecture 1
We state as a property  an approximation in the limit, through potentials of band-limited maps of the original signal, based on [1] and [7].
an approximation in the limit, through potentials of band-limited maps of the original signal, based on [1] and [7].
In [1] is proven that given a sequence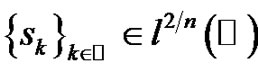 ,
, 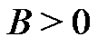 ,
,  and
and 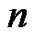 odd, there exist exactly
odd, there exist exactly 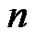 band-limited signals
band-limited signals 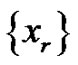 with bandwidth equal to
with bandwidth equal to 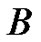 such that
such that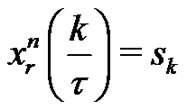 . Moreover, is shown that
. Moreover, is shown that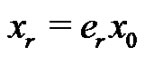 , where
, where 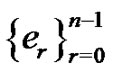 are the roots of unity of order
are the roots of unity of order 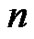 and
and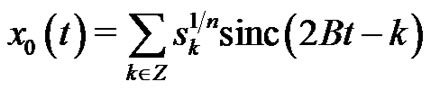 .
.
From this is directly deduced that if we consider an odd number 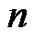 and a band-limited signal
and a band-limited signal  with bandwidth
with bandwidth 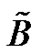 such that the sequence of coefficients
such that the sequence of coefficients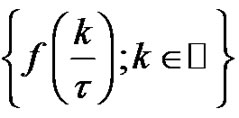 with
with 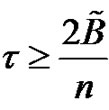 holds the properties stated in [1], then the signal admits a recomposition of Shannon type in the form
holds the properties stated in [1], then the signal admits a recomposition of Shannon type in the form
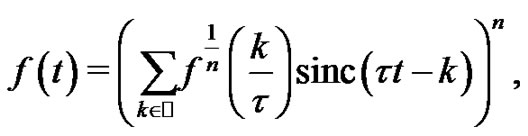 (2)
(2)
where clearly the sampling frequency can be choosen bigger than the Nyquist one.
Our aim is to provide a method for approximating non band-limited signal by band-limited ones and keeping the frequency of the sampling constant. And our idea is to take limits in (2) obtaining an equality of the form
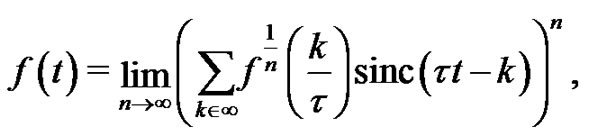 expressed as a property
expressed as a property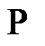 .
.
In Section 3 we prove that property  is held by any constant map for every
is held by any constant map for every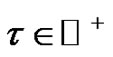 . Thus, the universe of non-trivial signals which hold the conjecture is nonempty (note that
. Thus, the universe of non-trivial signals which hold the conjecture is nonempty (note that 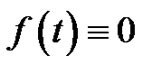 holds
holds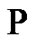 ). Our feeling is that there are a big number of representative signals in engineering processes which satisfy property
). Our feeling is that there are a big number of representative signals in engineering processes which satisfy property .
.
We state as Conjecture 1 to prove that any signal of Gaussian type holds the statement. Note that the Gaussian map, which is mathematically important in itself, plays an important role in the signal theory because the Gaussian map is the unique function which reachs the minimum of the product of the temporal and frecuential width. This minimum is given by the Uncertainty Principle, see [6]. We believe in the working of Conjecture 1 and we support it through Theorem 2 where we show the equality between the three first coefficients of the power series representation of the Gaussian map and property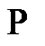 . For proving completely the conjecture, by the analyticity of the Gaussian map, is enough to prove that expression
. For proving completely the conjecture, by the analyticity of the Gaussian map, is enough to prove that expression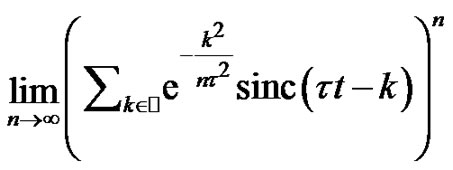 defines an analytical map and to show that the equality works for the rest of coefficients.
defines an analytical map and to show that the equality works for the rest of coefficients.
3. Proof of Theorem 1
The following lemma will play a key role in the proof of Theorem 1.
Lemma 3  for every
for every .
.
Proof. First of all we shall show that the result works for every . Indeed, if
. Indeed, if , the result is straight because of
, the result is straight because of
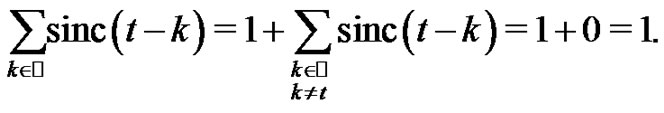
Therefore, from now on we assume that . Taking simetric terms in the series we obtain
. Taking simetric terms in the series we obtain
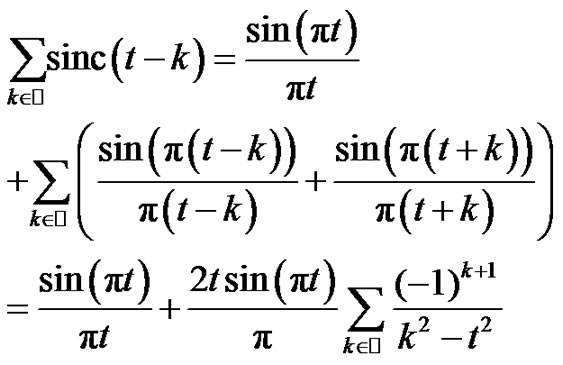 (3)
(3)
On the other hand, for a given 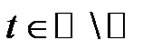 is known that
is known that
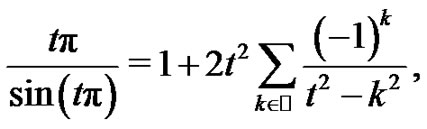
and therefore
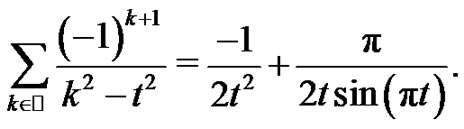 (4)
(4)
Finally, replacing (4) in expression (3) the proof is over for every real number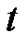 .
.
The prove of the result for complex numbers is a consequence of the use of the Analytic Prologation Principle. For applying it, is enough to prove that the series  is an analytic function. Indeed, by (3) the series can be written in the form
is an analytic function. Indeed, by (3) the series can be written in the form

Obviously, the first term of the previous sum is an analytic map. For proving the analyticity of the second term of the sum we shall prove that the series uniformly converges on every compact set
uniformly converges on every compact set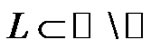 . In fact, let
. In fact, let 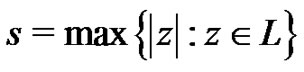 and
and 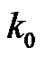 be such that
be such that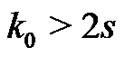 , then for every
, then for every 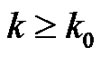 is
is 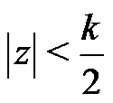 for every
for every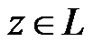 . Therefore,
. Therefore,
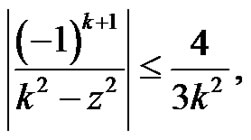
which guarantees the uniformly convergency of the series in  and the proof is over.
and the proof is over.
Remark 4 We underline that the fact of the series 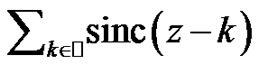 defines an analytic function is a direct consequence of the application of the Uniform Convergence Principle for cardinal Series, see [5, pag. 70] or [11, pag. 22] for a more up-to-date reference. We present a direct approach in the proof of Lemma 3 for completness of the arguments.
defines an analytic function is a direct consequence of the application of the Uniform Convergence Principle for cardinal Series, see [5, pag. 70] or [11, pag. 22] for a more up-to-date reference. We present a direct approach in the proof of Lemma 3 for completness of the arguments.
Proof of Theorem 1. Let 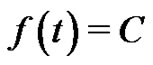 be a constant signal and
be a constant signal and . By Lemma 3 we have
. By Lemma 3 we have

Thus, is shown that  holds property
holds property  ending the proof.
ending the proof.
4. Proof of Theorem 2
In the sequel we denote by 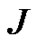 a set of consecutive natural numbers in the form
a set of consecutive natural numbers in the form 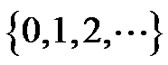 which eventually can be
which eventually can be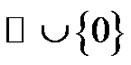 . By
. By 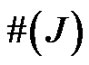 we denote the cardinal of the set
we denote the cardinal of the set 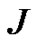 and we assume the arithmetic of the infinity (i.e.,
and we assume the arithmetic of the infinity (i.e., ), therefore by
), therefore by 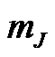 we denote
we denote .
.
Given a sequence 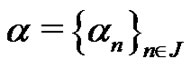 of real numbers, by
of real numbers, by 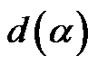 we denote the diameter of the sequence
we denote the diameter of the sequence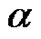 , i.e.,
, i.e.,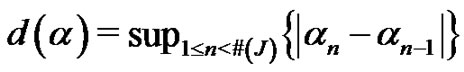 . As usual by
. As usual by  we denote the integer part.
we denote the integer part.
Lemma 5 Let  be an increasing bounded sequence of real numbers holding the following conditions:
be an increasing bounded sequence of real numbers holding the following conditions:
1)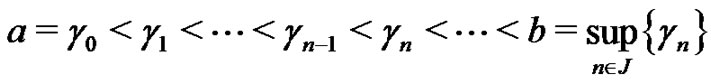 2)
2) 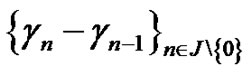 is monotonic.
is monotonic.
Let  be a continuous map of constant sign on
be a continuous map of constant sign on , eventually
, eventually 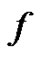 can be equal to zero. Then for every sequence
can be equal to zero. Then for every sequence 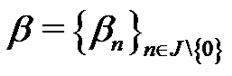 such that
such that
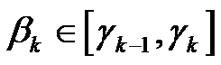 and for every
and for every 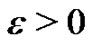 there exists
there exists 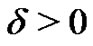 such that if
such that if 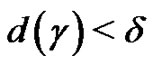 then
then
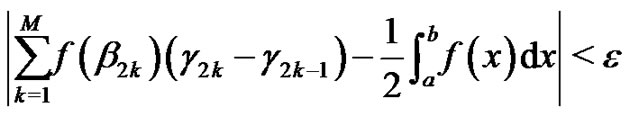 (5)
(5)
and
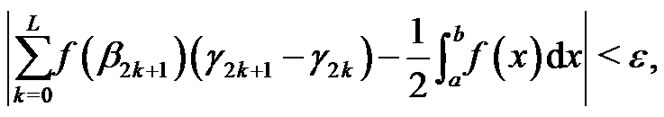 (6)
(6)
where 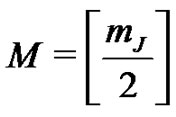 and
and .
.
Proof. For proving (5) we assume, without loss of generality, that  and
and 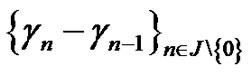 is a decreasing sequence. We shall use the following notation
is a decreasing sequence. We shall use the following notation
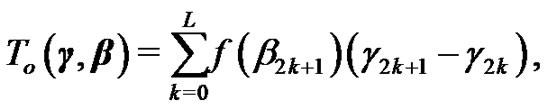
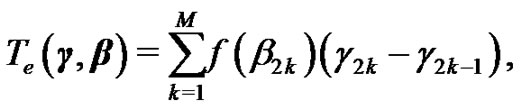

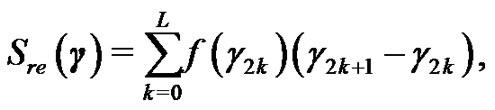
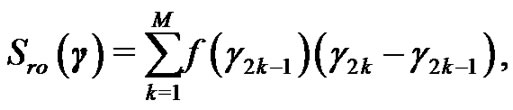
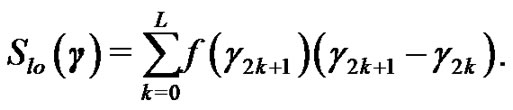
For a given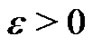 , since
, since 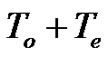 is a Riemann sum of
is a Riemann sum of  on
on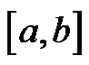 , there exists
, there exists 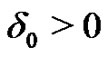 such that if
such that if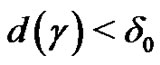 , then
, then
 (7)
(7)
Taking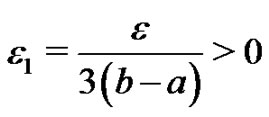 , since the map
, since the map 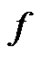 is uniformly continuous on the interval
is uniformly continuous on the interval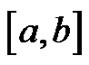 , then there exists
, then there exists 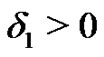 such that if
such that if 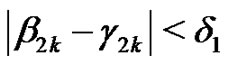 then
then
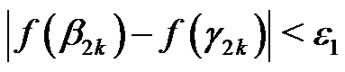 and consequently if
and consequently if 
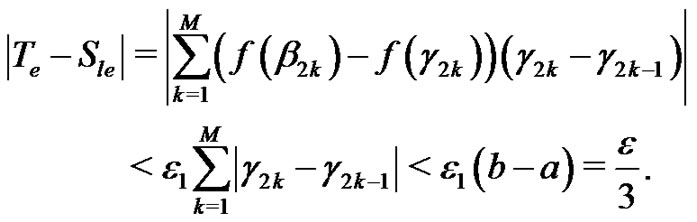 (8)
(8)
Proceeding in a similar way
 (9)
(9)
Now, it is easily deduced that
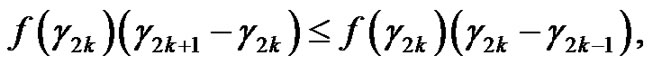
and
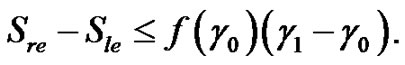
So, taking 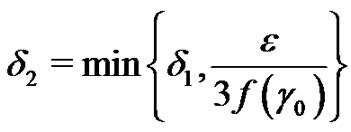 if
if 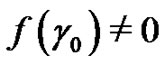 and
and
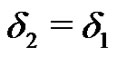 in other case, if
in other case, if  then
then
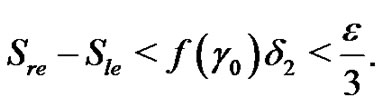
Using the previous inequality, 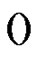 and
and 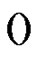 we have that
we have that
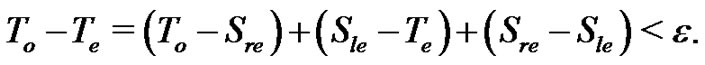 (10)
(10)
On the other hand, it is clear that
 (11)
(11)
and so, using 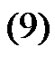 and
and 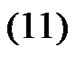
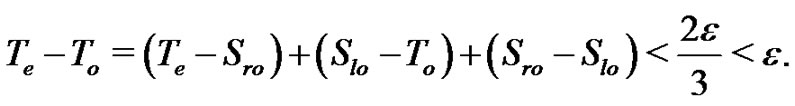
From here and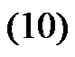 , if
, if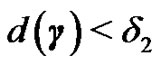 ,
,

So, taking 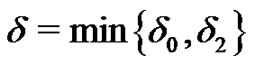 and using the previous inequality and (7), if
and using the previous inequality and (7), if 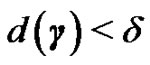 then
then
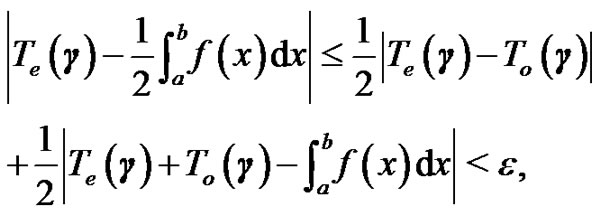
which is just 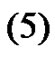 as we want to show.
as we want to show.
The proof of (6) follows in an analogous way.
Lemma 6 Let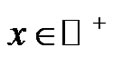 ,
,  and
and
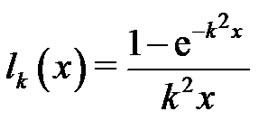 . Then for every
. Then for every 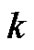 is
is
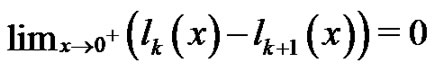 uniformly in
uniformly in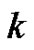 .
.
Proof. Note that for every 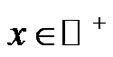 and every
and every ,
, 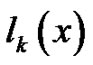 is decreasing in
is decreasing in .
.
We fixed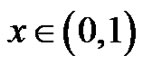 . For a given
. For a given  there exist
there exist 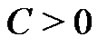 holding
holding 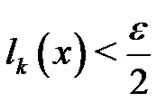 for any
for any 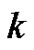 such that
such that
 and consequently
and consequently
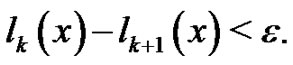 (12)
(12)
On the other hand, using the power series representation of the exponential function and the Newton’s binomial,
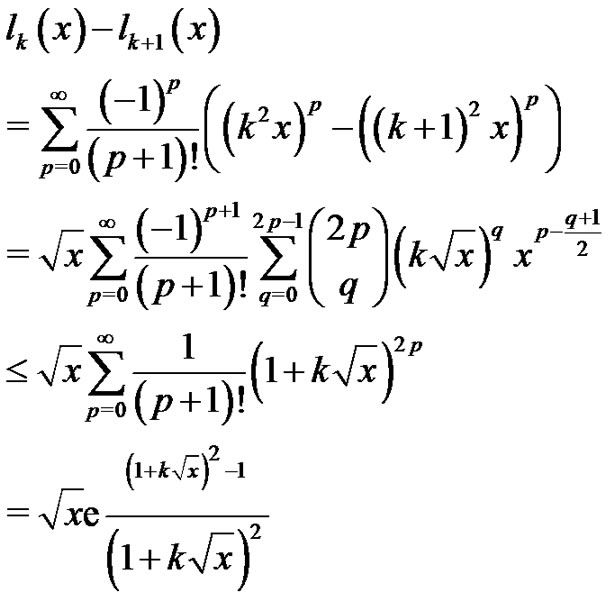
and if 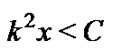 we have the following inequality
we have the following inequality
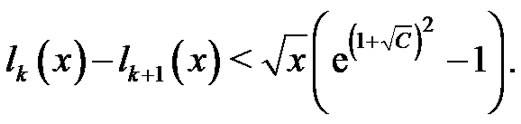
Since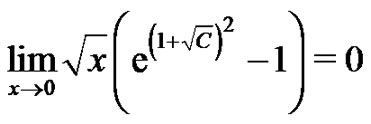 , using the last inequality and
, using the last inequality and  the proof is over.
the proof is over.
The following proposition will play a key role in the proof of Theorem 2.
Proposition 7 Let 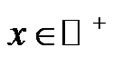 and
and  . Then is held
. Then is held

Proof. We consider the functions 
on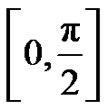 . Let
. Let  fixed. We note that
fixed. We note that 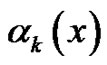 is a decreasing sequence on
is a decreasing sequence on . It is easily deduced that using the Intermediate Value Theorem
. It is easily deduced that using the Intermediate Value Theorem

and therefore
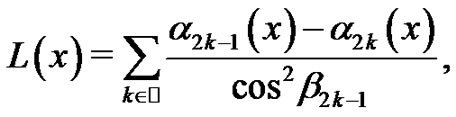 (13)
(13)
for suitable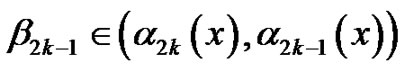 .
.
Note that 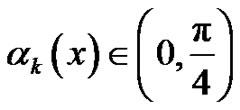 for all
for all  and consequently
and consequently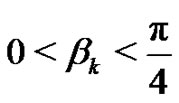 . Thus,
. Thus,
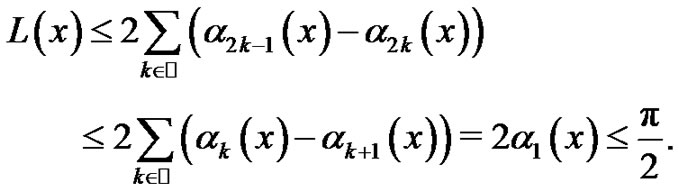
Since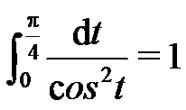 , then
, then
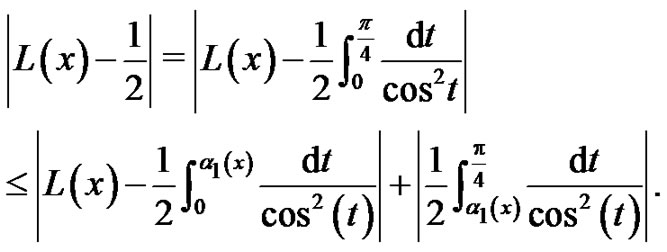 (14)
(14)
On the one hand, given 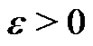 clearly there exists
clearly there exists 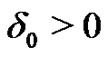 such that if
such that if 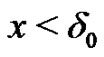 then
then
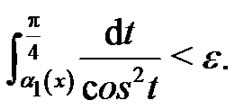 (15)
(15)
On the other hand, using Lemma 5 for
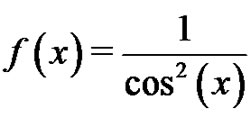 ,
, 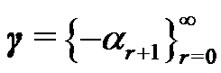 ,
, 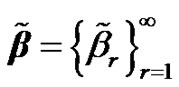 such that
such that
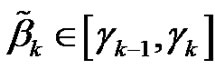 ,
, 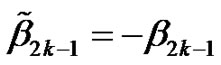 ,
, 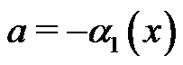 and
and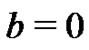 , there exists
, there exists 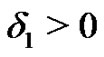 such that if
such that if 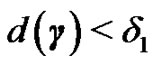 then
then
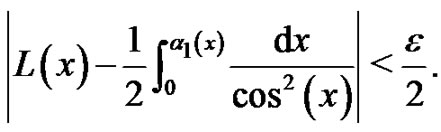 (16)
(16)
Since arctan  is a continuous map on
is a continuous map on , for
, for 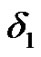 by Lemma 6 there exists
by Lemma 6 there exists 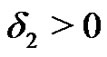 such that if
such that if 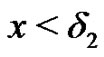 then
then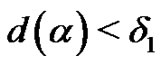 .
.
Therefore, taking , and replacing
, and replacing 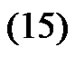 and
and 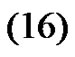 in
in 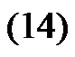 we obtain
we obtain
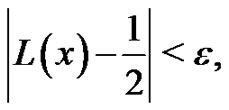
finishing the proof.
Proof of Theorem 2. The aim of the proof is to show that the limit of the three first nonzero coefficients of the power series representations of
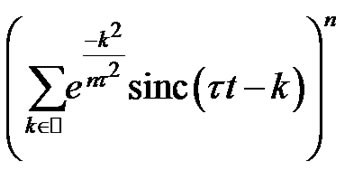
and 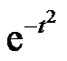 are equal for every
are equal for every  and
and  given. Indeed, for every
given. Indeed, for every 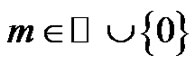 and
and 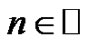 we fix the following notation
we fix the following notation
 (17)
(17)
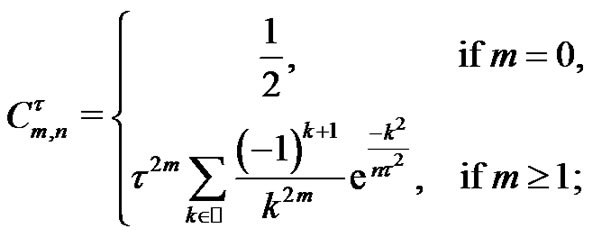 (18)
(18)
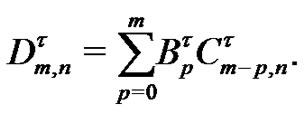 (19)
(19)
Let
Note that by the analitycity is enough to consider pointwise convergence for all . Now, using expressions
. Now, using expressions ,
,  ,
,  and the power series of the sine function, the map
and the power series of the sine function, the map 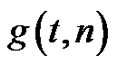 can be written in the form
can be written in the form
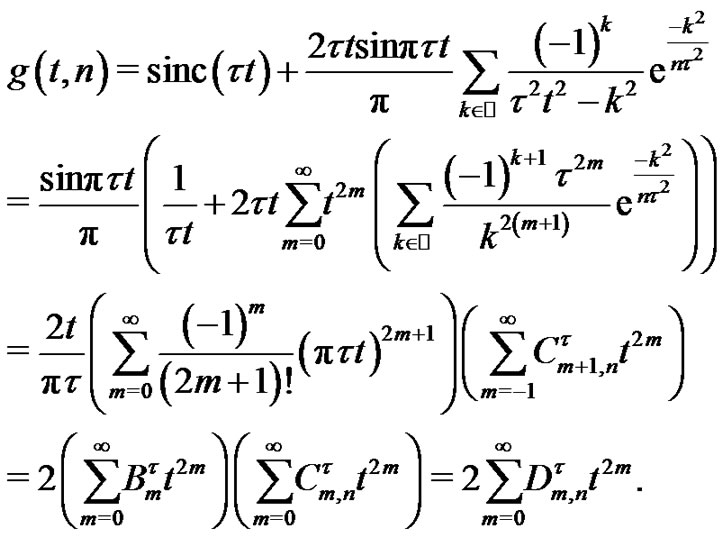
and therefore

For  it is clear that
it is clear that
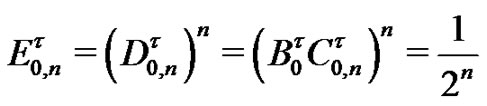 and hence
and hence

For 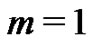 is
is

So, using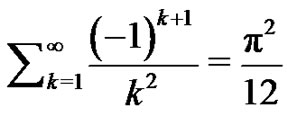 ,
,
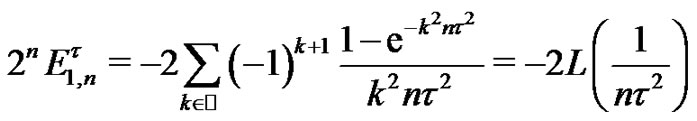
where 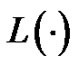 is introduced in Proposition 7 and now by such result we obtain
is introduced in Proposition 7 and now by such result we obtain
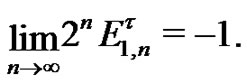 (20)
(20)
For 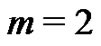 it follows that
it follows that
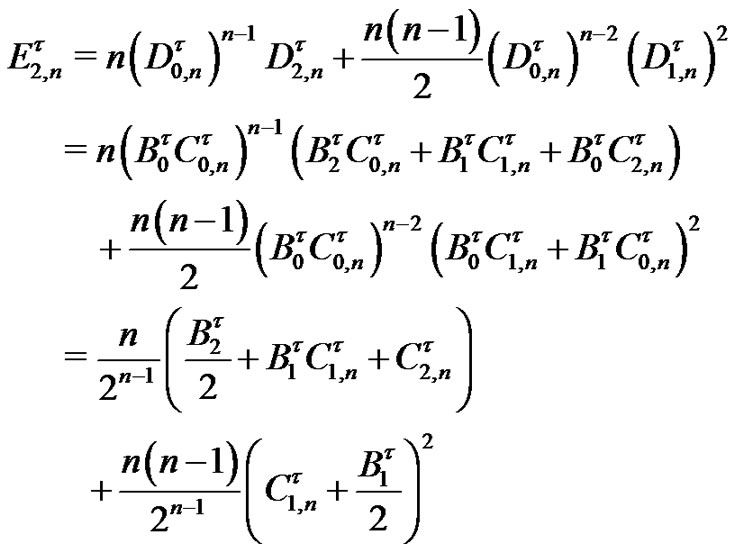
Therefore
 (21)
(21)
where


We will take the limit in each part separately. Since
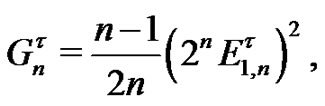
from 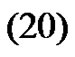 we obtain
we obtain
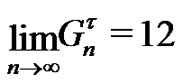 (22)
(22)
To determine the limit of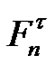 , replacing each
, replacing each  and
and 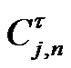 by
by  and
and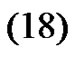 , we get
, we get
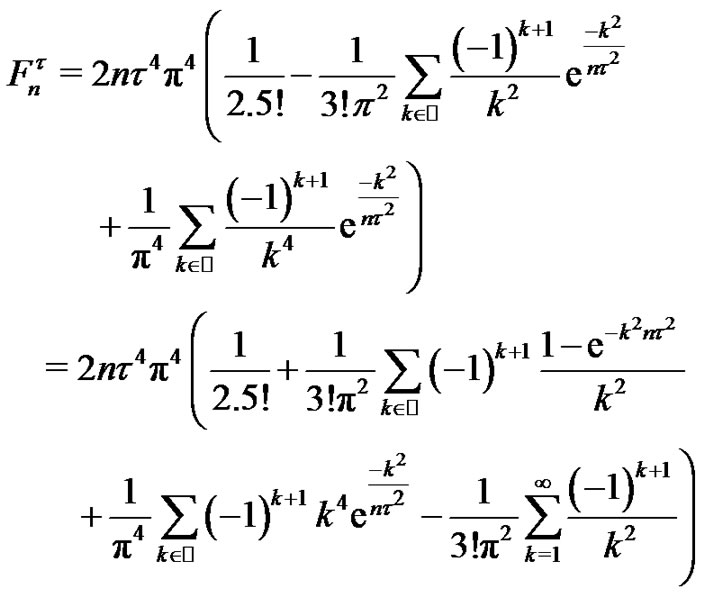
Using again 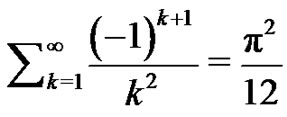 and applying
and applying
 , the above expression becomes
, the above expression becomes
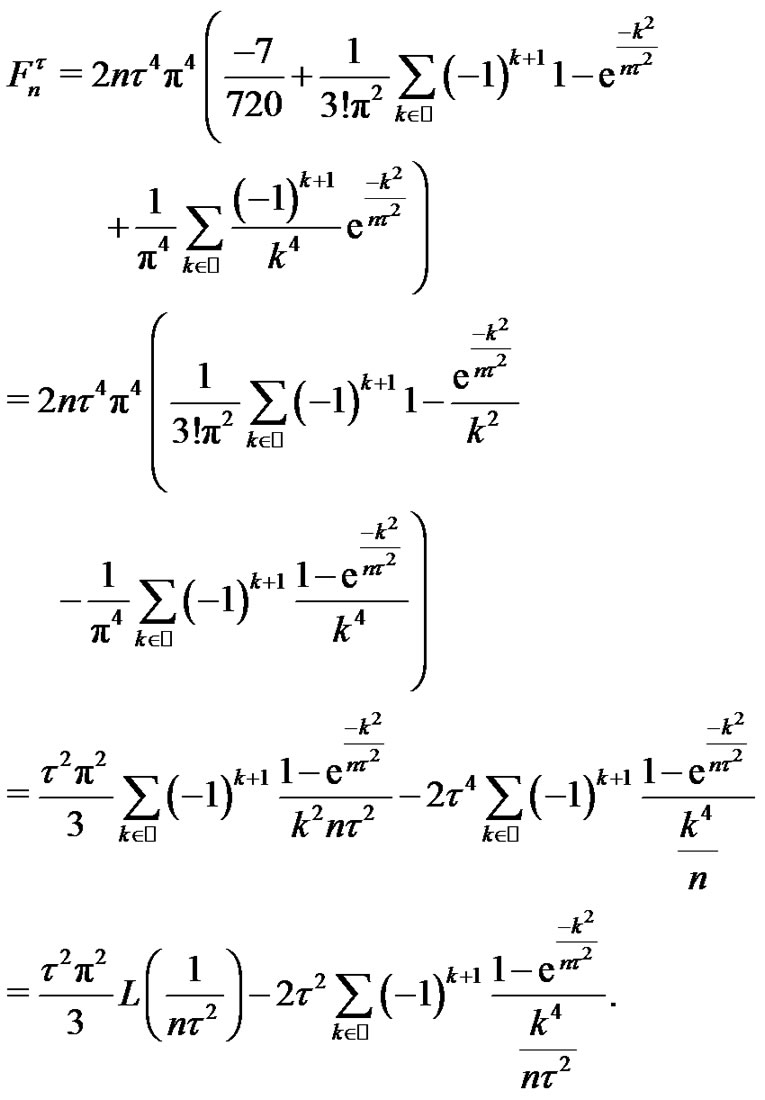
Therefore, since
 using Proposition 7 is
using Proposition 7 is
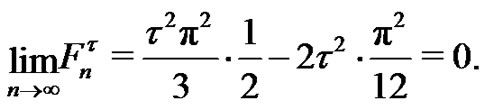
So, from here and , taking limits in
, taking limits in 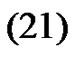 we get
we get
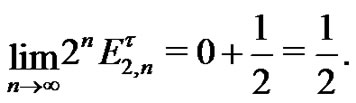
Note that from the results obtained for 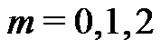 is stated that the limit of the three first nonzero coefficients of the power series representations of
is stated that the limit of the three first nonzero coefficients of the power series representations of
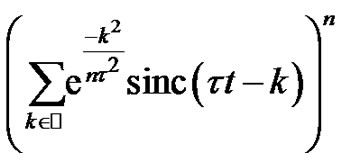
are equal to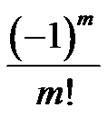 , coefficients of the power series representation of
, coefficients of the power series representation of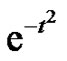 , ending the proof.
, ending the proof.
5. Conclusions
By stating property 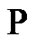 a new method for computing reconstructions of a given non--band limited signal is presented. The formula is closed and stable from a numerical point view which allow to implement and do empirical experiment for other kind of signals. Our feeling is that with this approach a new frame to compute approximations of signal is opened.
a new method for computing reconstructions of a given non--band limited signal is presented. The formula is closed and stable from a numerical point view which allow to implement and do empirical experiment for other kind of signals. Our feeling is that with this approach a new frame to compute approximations of signal is opened.
6. Acknowlegments
The authors want to thank to Professors J. Garay and R. G. Cataln for their value comments formulated in a constructive spirit.
7. References
[1] L. Agud and R. G. Cataln, “New Shannon’s Sampling Recomposition,” Revista de la Academia de Ciencias Zaragoza, Vol. 56, 2001, pp. 45-48.
[2] P. L. Butzer, S. Ries and R. L. Stens, “Approximation of Continuous and Discontinuous Functions by Generalized Sampling Series,” Journal of Approximation Theory, Vol. 50, No. 1, 1987, pp. 25-39. doi:10.1016/0021-9045(87)90063-3
[3] P. L. Butzer and R. L. Stens, “Sampling Theory for not Necessarily Band-Limited Functions: A Historical Overview,” SIAM Review, Vol. 34, No. 1, 1992, pp. 40-53. doi:10.1137/1034002
[4] J. A. Gubner, “A New Series for Approximating Voight Functions,” Journal of Physics A: Mathematical and General, Vol. 27, No. 19, 1994, pp. L745-L749. doi:10.1016/0021-9045(87)90063-3
[5] J. R. Higgings, “Five Short Stories about the Cardinal Series,” Bulletin of the American Mathematical Society, Vol. 12, 1985, pp. 45-89. doi:10.1090/S0273-0979-1985-15293-0
[6] H. J. Landau and H. O Pollak, “Prolate Spheroidal Wave Functions, Fourier Analysis and Uncertainly,” Bell System Technical Journal, Vol. 40, No. 1, 1961, pp. 65-84.
[7] F. Marvasti and A. K. Jain, “Zero Crossing Bandwidth Compression, and Restoration of Nonlinearly Distorted Band-Limited Signals,” Journal of the Optical Society of America, Vol. 3, No. 5, 1986, pp. 651-654. doi:10.1364/JOSAA.3.000651
[8] D. Middleton, “An Introduction to Statistical Communication Theory,” McGraw-Hill, New York, 1960.
[9] C. E. Shannon, “Communication in the Presence of Noise,” Proceedings of the Institute of Radio Engineers, Vol. 137, 1949, pp. 10-21.
[10] E. T. Whittaker, “On the Functions Which are Represented by the Expansions of the Interpolation Theory,” Proceedings of the Royal Society, Vol. 35, 1915, pp. 181-194.
[11] A. I. Zayed, “Advances in Shannon’s Sampling Theory,” CRC Press, Florida, 1993.
NOTES
*This work has been partially supported by MCI (Ministerio de Ciencia e Innovación) and FEDER (Fondo Europeo Desarrollo Regional), grant number MTM2008--03679/MTM, Fundación Séneca de la Región de Murcia, grant number 08667/PI/08 and JCCM (Junta de Comunidades de Castilla-La Mancha), grant number PEII09-0220-0222.

