Optics and Photonics Journal
Vol.07 No.11(2017), Article ID:80289,14 pages
10.4236/opj.2017.711020
Photonic Crystal Fiber Based Sensor for Detecting Binary Liquid Mixture
Md. Faizul Huq Arif1*, Md. Jaminul Haque Biddut2, Md. Shaiful Islam Babu3, H M Mostafizur Rahman4, Md. Mahbubur Rahman1, Busrat Jahan5, Moshrefa Sultana Chaity6, Shah Mostafa Khaled1
1Institute of Information Technology (IIT), University of Dhaka, Dhaka, Bangladesh
2Automation and Robotics, Faculty of Electrical Engineering and Information Technology (EEIT), TU Dortmund University, Dortmund, Germany
3Department of Computer Science and Engineering, World University of Bangladesh, Dhaka, Bangladesh
4School of Information Technology, BAC International Study Centre, Dhaka, Bangladesh
5Department of Computer Science and Engineering, Feni University, Feni, Bangladesh
6Institute of Information Technology (IIT), Jahangirnagar University, Dhaka, Bangladesh
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 5, 2017; Accepted: November 11, 2017; Published: November 14, 2017
ABSTRACT
Detection of liquid mixture of different volume ratio is very important in industrial purposes. The paper reports a sensing mechanism of binary liquid mixture for different volume fraction, based on the measurement of refractive index of the mixture. Here, a highly sensitive liquid filled core Photonic Crystal Fiber structure has been proposed to detect liquid mixture solution. Numerical investigation of the proposed structure is carried out by employing full vectorial Finite Element Method (FEM).
Keywords:
Binary Liquid Mixture, Photonic Crystal Fiber, Refractive Index, Sensitivity, Confinement Loss

1. Introduction
Fiber optic technology was developed primarily for telecommunication and medical science. However, the recent advances of fiber optic technology with its widespread of applications lead extensive interests to the researchers. The emergence of Photonic Crystal Fiber (PCF) was a breakthrough in the fiber optic technology. Since the invention of PCF using 2D photonic crystal, in 1992 [1] , the fiber optic researchers have been engaged on Research and Development (R & D) with this type of fiber.
PCF is an optic based technology which offers wondering features over conventional optical fibers. It has remarkable characteristics such as small size, free from electrical interference, geometric versatility, improved sensitivity and inherent compatibility with respect to fiber optic telecommunications making it outstanding for opto-devices [2] [3] . PCFs can be used for variety of sensing applications such as, physical sensor, gas sensor, chemical sensor, liquid sensor, electrical and magnetic field sensor, humidity, temperature, pressure sensor, biomedical properties sensor and so on [3] .
Since the last decade, optical techniques have been developing widely in the field of analytical chemistry for chemical and biochemical analysis [4] . The field of Optofluidics is emerging because of the development in optics and microfluidics in lab-on-a-chip microsystems [5] [6] [7] [8] . PCFs have recently been integrated in lab-on-a-chip systems for sensing applications.
Recently, several studies [9] [10] [11] [12] [13] have suggested microstructure optical fiber for liquid sensing applications since detection of liquid chemical efficiently is one of the most challenging tasks for industrial production management. Most of the industries use various types of liquid and they need to be sensed smartly for safety issues.
Previously, several researches already have been done in the prospect of sensing different liquids in terms of vapor sensing. J. Park et al. [14] proposed a hollow core Photonic Crystal Fiber for chemical sensing application using the absorption method. In recent years, liquid filled core PCFs has received a great attention due to the highly interaction of light and the sample to be sensed. A large number of articles have described infiltrated PCFs with different components as a promising field. The articles [9] [10] [11] [12] [13] reported that microstructured core PCF filled with different chemical substances, which show the enhancement of the evanescent field interaction in case of liquid sensing. However, the introduction of liquid filled hollow-core led to abundant demonstrations of thermally and electrically tunable fibers [15] [16] [17] . Recently, the article [3] describes that infiltrated hollow-core shows better sensing property and it is simple in design. However, all above the articles [9] [10] [11] [12] [13] describe the sensitivity characteristics in terms of pure compounds.
A vast amount of literature has been surveyed on various types of industrial chemicals and bio-chemicals. The literature survey indicates that industrial chemicals are the mixture of two or more fundamental liquids. Binary solution is one of the widely used chemical in industry. Therefore, to identify binary liquid mixture of different volume fractions is a challenging task. Generally, different chemical reagents are added to detect it. However, these techniques are time consuming and costly too. To detect the binary mixture smartly, various sensing mechanisms has also been surfed. The article [18] introduced fiber optic sensor for detecting liquid mixtures. In this study Photonic Crystal Fiber (PCF) based detection mechanism has been proposed. In addition, a precise study has been done to detect binary liquid mixtures in terms of different volume fractions using our proposed PCF.
In this article, we have introduced our proposed architecture for smart detection of liquid chemicals in industrial purposes. We considered the potentiality of using our proposed liquid filled hollow core PCF as an optical instrument of a chemical industry to detect necessary liquid mixtures.
2. Methodology
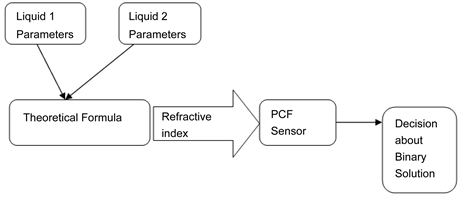
The composition of binary liquid mixtures can be determined by refractive indices measurements since the refractive index is the function of the composition of binary mixtures [19] [20] . The articles [21] [22] [23] describe the estimation of refractive indices of some binary mixtures and their mixing properties. To determine the refractive index of binary liquid mixtures the most extensively used methods are Arago-Biot [24] , Lorentz-Lorentz [25] , Weiner [26] , Heller [27] and Gladstone-Dale [28] . We can use any above mentioned relationship in the theoretical formula of our proposed simple block diagram of smart detection procedure of binary mixture through the refractive index values, which has been presented in Figure 1. The equations have been expressed in following:
Arago-Biot:
(1)
Lorentz-Lorentz:
(2)
Weiner:
(3)
Heller:
(4)
Gladstone-Dale:
Figure 1. Block diagram of smart detection procedure of binary mixture.
(5)
where, n = Refractive index of mixture,
n1 and n2=Refractive index of two pure compounds,
y1 and y2 = Volume fractions.
Refractive index of mixture is obtained by taking input values of two pure chemicals at a certain temperature. However, in this study, we have selected Arago-Biot equation for investigation since it is very simple. Here, extensive investigations have been done for Ethanol-Water and Benzene-Toluene mixtures. The refractive indices of the input pure components have been taken at different wavelength of light (0.5 µm to 1.5 µm) for extensive investigation; all values have been calculated using Sellmeier formula. Table 1 shows refractive indices of Ethanol, Water, Benzene and Toluene for different wavelengths of light at room temperature 293.15 k.
We have calculated the refractive index of the binary mixture varying volumes of 1 to 0 ml, 0.8 to 2 ml, 0.6 to 0.4 ml, 0.4 to 0.6 ml, 0.2 to 0.8 ml and 0 to 1 ml. Moreover, calculated data using Arago-Biot equation for different volume fractions of the two binary mixtures have been given in Table 2 and Table 3.
To focus on efficient sensing we have proposed a highly sensitive Photonic Crystal Fiber (PCF) structure with low confinement loss.
3. Proposed PCF Structure
Several issues are faced like maintaining fiber’s integrity and practical feasibility to design such a photonic waveguide in which the core region is made of liquids. However, the research articles [29] shows that liquid insertion at the central hole is permitted and it allows the incident light to propagate directly through the liquid due to the effective index guidance. Moreover, this type of PCF structure can be interfaced with existing technologies without any difficulty [30] [31] [32] .
Table 1. Wavelength dependent refractive index values of ethanol, water, benzene and toluene at a temperature of 293.15 k.
Table 2. Calculated value of refractive indices of the ethanol-water mixture for different volume fractions.
Table 3. Calculated value of refractive indices of the benzene-toluene mixture for different volume fractions.
The cross section of the proposed PCF structure is shown in Figure 2. Air holes in the cladding are arranged in four regular hexagonal rings which has six air holes in the first ring and six added air holes in every added ring. Air filling ratio of the cladding holes (d/Ʌ) of the optimized structure was kept fixed at 0.79 where, d is the diameter of cladding air holes and the symbol Ʌ denotes the distance between two adjacent air holes. However, the diameter of hollow core (red circle) dc is slightly greater than the cladding air holes diameter d. The pure silica has been utilized as the background material. The central core hole is filled with the targeted material. Refractive indices of all materials are obtained using the following Sellmeier equation [33] .
Figure 2. Cross section of the proposed photonic crystal Fiber.
(6)
where, n is the wavelength dependent refractive index and the symbol λ represents the operating wavelength. and are Sellmeier coefficients of the material.
The cross section of the proposed PCF is divided into triangular homogeneous sub-spaces using mesh analysis. For each sub-spaces the wave equation is solved. Using Perfectly Matched Layer (PML) as the boundary condition the optical properties and propagation characteristics of leaky mod are measured. Thickness of the PML is set to 10% of the radius of the cross section for efficient calculation of confinement loss [34] [35] .
In order to fulfill the ever increasing demands for PCF based chemical sensors, a novel PCF structure is need to be developed to overcome the critical trade-off between relative sensitivity and confinement loss in prior PCFs. However, by calibrating the design parameters of our proposed PCF, we can achieve a higher relative sensitivity and lower confinement loss simultaneously.
4. Simulation and Principle of Operation
To simulate the guiding properties of our proposed PCF structure, a full vectorial Finite Element Method (FEM) is applied for solving Maxwell’s equation due to its well-known reliability in case of solving very complex structure [36] [37] [38] [39] [40] . The FEM formulation for modal analysis based on the Perfectly Matched Layer (PML) is capable of handling analyze leaky mode.
Using Circular PML as the boundary condition, propagation characteristics and optical properties can be evaluated efficiently. The modal analyses have been performed on the cross section in the x-y plane of the PCF as the wave propagates through z direction. Using anisotropic PML the following vectorial equation with a magnetic field formulation can be derived from Maxwell’s equation [41] [42] [43] .
(7)
where, is the magnetic field, is the relative dielectric permittivity and is the permeability. The symbol K0 (=2π/λ) represents the wave-number in the vacuum at the operating wavelength λ.
As the electromagnetic radiation passes through the PCF, a small portion of energy is leaking from the core to the exterior matrix material. This leakage is known as confinement loss. However, this leakage can be eliminated by taking infinite number of air holes in the cladding. But, in practical structure, the number of air holes is finite. Therefore, the modes of PCFs are inherently leaky. It is measured from the imaginary part of the complex effective index using the following equation [44] .
[dB/m] (8)
where, Im (neff) is the imaginary part of effective index [45] . The legibility of the method depends on the accuracy of the value of the imaginary part. The accuracy of Im (neff) can be increased by using larger computational window and a finer mesh [46] .
The evanescent field interaction between light and the material to be sensed can be measured by the relative sensitivity coefficient. According to the Beer-Lambert law, the relative sensitivity coefficient can be defined as [47] :
(9)
where, nr represents the refractive index of the material to be sensed, and ne is the modal effective index. Here, f is the fractional power located in the air holes which can be defined as [42] :
(10)
The transverse electric and magnetic fields of the guided mode are respectively introduced by Ex, Ey, and Hx, Hy. Using FEM, the effective index mode neff is calculated by solving Maxwell’s equation. FEM based simulation tool COMSOL Multiphysics is used to find the guided modes. During simulation, the cross section is divided into 15,778 triangular elements with 110,803 degrees of freedom for the employed elements.
5. Numerical Results and Discussion
The proposed PCF structure has a liquid filled hollow core which operates in the near-infrared region (NIR). We have presented our simulated result between the wavelength range 0.8 to 1.5 µm. In this study, we have analyzed the sensing performance of our proposed PCF for two different binary liquid mixtures (Ethanol-Water, and Benzene-Toluene). The designed structure of PCF supports the fundamental mode and some higher-order modes. In this study, we have considered the fundamental modes. Figure 3 shows the 2D and 3D views of fundamental optical field distribution of our proposed PCF structure when core was filled with Ethanol-Water mixture at an operating wavelength of 1.3 µm.
It is clearly seen from the Figure 3 that the mode field is tightly confined in the core region. Hence, there is highly interaction between light and the material inserted in the hollow core.
Figure 4 illustrates the wavelength dependence effective refractive index profile. It is clear from the Figure 4 that the effective indices decrease linearly with an increase in wavelength. It is also evidently seen that effective index values are higher when the core is filled with higher indexed liquid mixture.
Figure 5 depicts the wavelength dependent confinement loss with the same parameters. It is clear from the curves that confinement loss is declining when the operating wavelength of light is increasing.
Initially to investigate the relative sensitivity we have calculated the performance of our proposed PCF filling different pure liquids over the refractive index range 1.35 to 1.50. We have observed that sensitivity increases with wavelength when the refractive index of the core material is less than the silica background (~1.45). On the contrary, sensitivity decreases when the refractive index of the core material is greater than 1.45. Figure 6 shows the relative sensitivity curves of our proposed PCF as a function of wavelength. It is observed from the Figure 6 that the relative sensitivity increases with wavelength when the core of the PCF is infiltrated with Ethanol-Water mixture and it shows the vice-versa, when the core was filled with Benzene-Toluene mixture.


Figure 3. Mode field pattern of the proposed PCF for x polarization at λ = 1.3 µm: (a) 2D view; (b) 3D view.


Figure 4. Wavelength versus effective refractive index curves of our proposed PCF structure; infiltrated the hollow core with different volume fraction of (a) ethanol-water mixture, and (b) benzene-toluene mixture.


Figure 5. Wavelength versus confinement loss curves of our proposed PCF structure; infiltrated the hollow core with different volume fraction of (a) ethanol-water mixture, and (b) benzene-toluene mixture.
After presenting the relative sensitivity and confinement loss curves, we have checked the accuracy for both of the properties of the proposed PCF. The convergence error of the structure due to defective modes is very low about 5.8 × 10−7. In a standard fiber draw, ±1% changing in fiber global parameter may occur during the fabrication process [48] . However, in [49] it has been described that sol-gel technique shows a variation in air hole size less than 3% over 2 km spans for the fabrication of PCF. Therefore, to consider this structural variation, the global parameter has been varied up to ±5% from their optimum values. Table 4 presents the variation of relative sensitivity and confinement loss of our designed structure due to the changes in global parameters. Our proposed structure is designed to get a good tolerance of fabrication error.


Figure 6. Wavelength versus sensitivity curves of our proposed PCF structure; infiltrated the hollow core with different volume fraction of (a) ethanol-water mixture, and (b) benzene-toluene mixture.
Table 4. Variation of relative sensitivity and confinement loss of the proposed PCF for the changes in global parameters at λ = 1.30 µm; volume fraction of the both mixtures: y1 = 0.4, y2 = 0.6.
In case of the fabrication issue of our proposed structure, it is important to discuss the robustness of the structure. The studies [50] show that low air-filling ratio of air holes makes a fiber robust. In our optimized structure, air filling ratio of the cladding holes is set to 0.79 which is tolerable for fabrication.
To show the significance of our proposed structure with more evidence we need to compare the sensing performance with the prior works. The article [11] presents a simulation based study for Formalin (mixture of Formaldehyde and Water) detection through PCF. In the usual sense, Formalin is not treated as a binary solution, since it may contain 10% - 12% Methanol with various metallic impurities. However, we have calculated the sensing performance for the binary Formaldehyde-Water mixture (volume ratio: 4:6). It is expected, in case of the presence of all elements of Formalin, our proposed PCF will show near the same result also. It can be estimated that our proposed structure is approximately 40% higher sensitive than the structure proposed in [11] .
6. Conclusions
In conclusion, this paper reports a framework for binary liquid mixture sensing application using the theoretical mixing rules. In addition, for more accuracy, wavelength dependent refractive indices of the mixture have been studied. The behavior of the proposed PCF structure has also been investigated for different volume fraction of the analyte to be detected. However, the drawback of this research is that all data is calculated at a fixed temperature 293.15 k.
The mechanism can also easily be extended to other liquid mixtures (e.g. Formalin). Therefore, it is expected that the proposed framework will add a new window of research in the field of chemical engineering. Moreover, our proposed PCF structure exhibits high relative sensitivity and low confinement loss simultaneously. Therefore, the designed structure can effectively overcome the critical trade-off between confinement loss and sensitivity.
Acknowledgements
This research is supported by the fellowship from ICT division, Ministry of posts, Telecommunications and Information Technology, Bangladesh. No-56.00.000.028. 33.073.16-50, Date: 16.04.2017. Moreover, the authors are grateful to those who participated in this research work.
Cite this paper
Arif, M.F.H., Biddut, M.J.H., Babu, M.S.I., Rahman, H.M.M., Rahman, M.M., Jahan, B., Chaity, M.S. and Khaled, S.M. (2017) Photonic Crystal Fiber Based Sensor for Detecting Binary Liquid Mixture. Optics and Photonics Journal, 7, 221-234. https://doi.org/10.4236/opj.2017.711020
References
- 1. Buczynski, R. (2004) Photonic Crystal Fibers. Acta Physica Polonica Series A, 106, 141-168. https://doi.org/10.12693/APhysPolA.106.141
- 2. Ademgil, H. and Haxha, S. (2015) PCF Based Sensor with High Sensitivity, High Birefringence and Low Confinement Losses for Liquid Analyte Sensing Applications. Sensors, 15, 31833-31842. https://doi.org/10.3390/s151229891
- 3. Arif, M.F.H., Ahmed, K., Asaduzzaman, S. and Azad, M.A.K. (2016) Design and Optimization of Photonic Crystal Fiber for Liquid Sensing Applications. Photonic Sensors, 6, 279-288. https://doi.org/10.1007/s13320-016-0323-y
- 4. Mortensen, N.A., Xiao, S. and Pedersen, J. (2008) Liquid-Infiltrated Photonic Crystals: Enhanced Light-Matter Interactions for Lab-on-a-Chip Applications. Microfluidics and Nanofluidics, 4, 117-127. https://doi.org/10.1007/s10404-007-0203-2
- 5. Verpoorte, E. (2003) Chip Vision-Optics for Microchips. Lab on a Chip, 3, 42N-52N.
- 6. Mogensen, K.B., Klank, H. and Kutter, J.P. (2004) Recent Developments in Detection for Microfluidic Systems. Electrophoresis, 25, 3498-3512.https://doi.org/10.1002/elps.200406108
- 7. Balslev, S., Jorgensen, A.M., Bilenberg, B., Mogensen, K.B., Snakenborg, D., Geschke, O., Kutter, J.P. and Kristensen, A. (2006) Lab-on-a-Chip with Integrated Optical Transducers. Lab on a Chip, 6, 213-217. https://doi.org/10.1039/B512546D
- 8. Choi, C.J. and Cunningham, B.T. (2006) Single-Step Fabrication and Characterization of Photonic Crystal Biosensors with Polymer Microfluidic Channels. Lab on a Chip, 6, 1373-1380. https://doi.org/10.1039/b603514k
- 9. Asaduzzaman, S., Arif, M.F.H., Ahmed, K. and Dhar, P. (2015) Highly Sensitive Simple Structure Circular Photonic Crystal Fiber Based Chemical Sensor. IEEE International WIE Conference on Electrical and Computer Engineering (WIECON-ECE), Dhaka, 19-20 December 2015, 151-154. https://doi.org/10.1109/WIECON-ECE.2015.7443884
- 10. Arif, M.F.H., Asaduzzaman, S., Ahmed, K. and Morshed, M. (2016) High Sensitive PCF Based Chemical Sensor for Ethanol Detection. 5th International Conference on Informatics Electronics and Vision (ICIEV), Dhaka, 13-14 May 2016, 6-9.https://doi.org/10.1109/ICIEV.2016.7760031
- 11. Arif, M.F.H., Biddut, M.J.H., Ahmed, K. and Asaduzzaman, S. (2016) Simulation Based Analysis of Formalin Detection through Photonic Crystal Fiber. 5th International Conference on Informatics Electronics and Vision, Dhaka, 776-779. https://doi.org/10.1109/ICIEV.2016.7760106
- 12. Asaduzzaman, S., Ahmed, K., Arif, M.F.H. and Morshed, M. (2015) Proposal of a Simple Structure Photonic Crystal Fiber for Lower Indexed Chemical Sensing. 18th International Conference on Computer and Information Technology, Dhaka, 127-131. https://doi.org/10.1109/ICCITechn.2015.7488055
- 13. Ahmed, K. and Morshed, M. (2016) Design and Numerical Analysis of Microstructured-Core Octagonal Photonic Crystal Fiber for Sensing Applications. Sensing and Bio-Sensing Research, 7, 1-6.
- 14. Park, J., Lee, S., Kim, S. and Oh, K. (2011) Enhancement of Chemical Sensing Capability in a Photonic Crystal Fiber with a Hollow High Index Ring Defect at the Center. Optics Express, 19, 1921-1929. https://doi.org/10.1364/OE.19.001921
- 15. Larsen, T., Bjarklev, A., Hermann, D. and Broeng, J. (2003) Optical Devices Based on Liquid Crystal Photonic Bandgap Fibres. Optics Express, 11, 2589-2596. https://doi.org/10.1364/OE.11.002589
- 16. Du, F., Lu, Y.Q. and Wu, S.T. (2004) Electrically Tunable Liquid-Crystal Photonic Crystal Fiber. Applied Physics Letters, 85, 2181-2183. https://doi.org/10.1063/1.1796533
- 17. Wolinski, T.R., Szaniawska, K., Ertman, S., Lesiak, P., Domanski, A.W., Dabrowski, R., Nowinowski-Kruszelnicki, E. and Wojcik, J. (2006) Influence of Temperature and Electrical Fields on Propagation Properties of Photonic Liquid-Crystal Fibres. Measurement Science and Technology, 17, 985. https://doi.org/10.1088/0957-0233/17/5/S08
- 18. Zhou, B., Venart, J.E.S. and Hinata, S. (1992) Fiber Optic Sensor for Liquid Mixture Composition. Fluid Phase Equilibria, 79, 175-185.
- 19. Mehra, R. (2003) Application of Refractive Index Mixing Rules in Binary Systems of Hexadecane and Heptadecane with n-Alkanols at Different Temperatures. Proceedings Indian Academy of Sciences Chemical Sciences, 115, 147-154. https://doi.org/10.1007/BF02716982
- 20. Martincek, I., Pudis, D., Kacik, D. and Schuster, K. (2010) Volume Fraction Determination of Binary Liquid Mixtures by Measurement of the Equalization Wavelength. Sensors, 10, 7082-7088. https://doi.org/10.3390/s100807082
- 21. Sharma, S., Patel, P.B., Patel, R.S. and Vora, J.J. (2007) Density and Comparative Refractive Index Study on Mixing Properties of Binary Liquid Mixtures of Eucalyptol with Hydrocarbons at 303.15, 308.15 and 313.15 K. Journal of Chemistry, 4, 343-349.
- 22. Roy, M.N., Das, R.K. and Chanda, R. (2010) Study on Solution Properties of Binary Mixtures of Some Industrially Important Solvents with Cyclohexylamine and Cyclohexanone at 298.15 K. International Journal of Thermophysics, 31, 535-545. https://doi.org/10.1007/s10765-010-0752-6
- 23. Isehunwa, S.O., Olanisebe, E.B., Ajiboye, O.O. and Akintola, S.A. (2015) Estimation of the Refractive Indices of Some Binary Mixtures. African Journal of Pure and Applied Chemistry, 10, 58-64. https://doi.org/10.5897/AJPAC2015.0613
- 24. Arago, D.F.J. and Biot, J.B. (1806) Mémoires de l’Académie des sciences de l’Institut de France, Vol. 1806, 7.
- 25. Lorentz, H.A. (1906) Theory of Electrons. (In Leipzig)
- 26. Weiner, O. (1910) Berichte. Vol. 62, 256. (In Leipzig)
- 27. Heller, W. (1945) The Determination of Refractive Indices of Colloidal Particles by Means of a New Mixture Rule or from Measurements of Light Scattering. Physical Review, 68, 5. https://doi.org/10.1103/PhysRev.68.5
- 28. Dale, D. and Gladstone, F. (1858) On the Influence of Temperature on the Refraction of Light. Philosophical Transactions, 148, 887. https://doi.org/10.1098/rstl.1858.0036
- 29. Yiou, S., Delaye, P., Rouvie, A., Chinaud, J., Frey, R., Roosen, G., Viale, P., Février, S., Roy, P., Auguste, J.L. and Blondy, J.M. (2005) Stimulated Raman Scattering in an Ethanol Core Microstructured Optical Fiber. Optics Express, 13, 4786-4791. https://doi.org/10.1364/OPEX.13.004786
- 30. Huang, Y., Xu, Y. and Yariv, A. (2004) Fabrication of Functional Microstructured Optical Fibers through a Selective-Filling Technique. Applied Physics Letters, 85, 5182-5184. https://doi.org/10.1063/1.1828593
- 31. Luo, M., Liu, Y.G., Wang, Z., Han, T., Wu, Z., Guo, J. and Huang, W. (2013) Twin-Resonance-Coupling and High Sensitivity Sensing Characteristics of a Selectively Fluid-Filled Microstructured Optical Fiber. Optics Express, 21, 30911-30917. https://doi.org/10.1364/OE.21.030911
- 32. Gerosa, R.M., Spadoti, D.H., de Matos, C.J., Menezes, L.D.S. and Franco, M.A. (2011) Efficient and Short-Range Light Coupling to Index-Matched Liquid-Filled Hole in a Solid-Core Photonic Crystal Fiber. Optics Express, 19, 24687-24698. https://doi.org/10.1364/OE.19.024687
- 33. Ghosh, G. (1997) Sellmeier Coefficients and Dispersion of Thermo-Optic Coefficients for Some Optical Glasses. Applied Optics, 36, 1540-1546. https://doi.org/10.1364/AO.36.001540
- 34. Morshed, M., Hasan, M.I. and Razzak, S.A. (2015) Enhancement of the Sensitivity of Gas Sensor Based on Microstructure Optical Fiber. Photonic Sensors, 5, 312-320. https://doi.org/10.1007/s13320-015-0247-y
- 35. Asaduzzaman, S. and Ahmed, K. (2016) Proposal of a Gas Sensor with High Sensitivity, Birefringence and Nonlinearity for Air Pollution Monitoring. Sensing and Bio-Sensing Research, 10, 20-26.
- 36. Ademgil, H. (2014) Highly Sensitive Octagonal Photonic Crystal Fiber Based Sensor. Optik International Journal for Light and Electron Optics, 125, 6274-6278.
- 37. Monro, T.M., Belardi, W., Furusawa, K., Baggett, J.C., Broderick, N.G.R. and Richardson, D.J. (2001) Sensing with Microstructured Optical Fibres. Measurement Science and Technology, 12, 854. https://doi.org/10.1088/0957-0233/12/7/318
- 38. Hoo, Y.L., Jin, W., Ho, H.L., Wang, D.N. and Windeler, R.S. (2002) Evanescent-Wave Gas Sensing using Microstructure Fiber. Optical Engineering, 41, 8-9. https://doi.org/10.1117/1.1429930
- 39. Kuhlmey, B.T., Eggleton, B.J. and Wu, D.K. (2009) Fluid-Filled Solid-Core Photonic Bandgap Fibers. Journal of Lightwave Technology, 27, 1617-1630. https://doi.org/10.1109/JLT.2009.2021142
- 40. Vieweg, M., Gissibl, T., Pricking, S., Kuhlmey, B.T., Wu, D.C., Eggleton, B.J. and Giessen, H. (2010) Ultrafast Nonlinear Optofluidics in Selectively Liquid-Filled Photonic Crystal Fibers. Optics Express, 18, 25232-25240. https://doi.org/10.1364/OE.18.025232
- 41. Saitoh, K., Koshiba, M., Hasegawa, T. and Sasaoka, E. (2003) Chromatic Dispersion Control in Photonic Crystal Fibers: Application to Ultra-Flattened Dispersion. Optics Express, 11, 843-852. https://doi.org/10.1364/OE.11.000843
- 42. Selleri, S., Vincetti, L., Cucinotta, A. and Zoboli, M. (2001) Complex FEM Modal Solver of Optical Waveguides with PML Boundary Conditions. Optical and Quantum Electronics, 33, 359-371. https://doi.org/10.1023/A:1010886632146
- 43. Akowuah, E.K., Gorman, T., Ademgil, H., Haxha, S., Robinson, G.K. and Oliver, J.V. (2012) Numerical Analysis of a Photonic Crystal Fiber for Biosensing Applications. IEEE Journal of Quantum Electronics, 48, 1403-1410. https://doi.org/10.1109/JQE.2012.2213803
- 44. Ademgil, H. and Haxha, S. (2011) Bending Insensitive Large Mode Area Photonic Crystal Fiber. Optik International Journal for Light and Electron Optics, 122, 1950-1956.
- 45. Saitoh, K. and Koshiba, M. (2003) Leakage Loss and Group Velocity Dispersion in Air-Core Photonic Bandgap Fibers. Optics Express, 11, 3100-3109. https://doi.org/10.1364/OE.11.003100
- 46. Uranus, H.P. and Hoekstra, H.J.W.M. (2004) Modelling of Microstructured Waveguides using a Finite-Element-Based Vectorial Mode Solver with Transparent Boundary Conditions. Optics Express, 12, 2795-2809. https://doi.org/10.1364/OPEX.12.002795
- 47. Cordeiro, C.M., Franco, M.A., Chesini, G., Barretto, E.C., Lwin, R., Cruz, C.B. and Large, M.C. (2006) Microstructured-Core Optical Fibre for Evanescent Sensing Applications. Optics Express, 14, 13056-13066. https://doi.org/10.1364/OE.14.013056
- 48. Poletti, F., Finazzi, V., Monro, T.M., Broderick, N.G., Tse, V. and Richardson, D.J. (2005) Inverse Design and Fabrication Tolerances of Ultra-Flattened Dispersion Holey Fibers. Optics Express, 13, 3728-3736. https://doi.org/10.1364/OPEX.13.003728
- 49. Bise, R.T. and Trevor, D. (2005) Solgel-Derived Microstructured Fibers: Fabrication and Characterization. In: Optical Fiber Communication Conference, Optical Society of America, OWL6.
- 50. Pottage, J.M., Bird, D.M., Hedley, T.D., Birks, T.A., Knight, J.C., Russell, P.S.J. and Roberts, P.J. (2003) Robust Photonic Band Gaps for Hollow Core Guidance in PCF Made from High Index Glass. Optics Express, 11, 2854-2861. https://doi.org/10.1364/OE.11.002854