ABSTRACT

Static fracture toughness characteristics are traditionally determined in tests of standard notched specimens using a P-V curve, where P is the load and V is the notch- opening displacement. This curve has a characteristic point Q. At the load P_Q corresponding to this point, the crack starts to propagate. For this load, the fracture toughness characteristics are then calculated. In brittle (elastic) fracture, the P-V curve at the onset of crack propagation has an extremum (or a local extremum), from whose ordinate P_Q is determined with sufficient accuracy. In ductile and elastic-ductile fracture, P-V curves are monotonically increasing, and P_Q is calculated using the 5% secant offset method without taking into account the characteristics of the material, so that the P_Q is determined inaccurately. To improve the accuracy of P_Q determination, we propose a thermographic method for determining the fracture toughness of metals. This method involves plotting the load P against the temperature change ∆Т over a relatively short period of time at the notch tip. This plot is then transformed to a P-ΔS curve, where ΔS is the specific entropy increment at the notch tip, which is calculated through ∆Т. This thermodynamic diagram has a characteristic step at the beginning of crack propagation, and from the ordinate of this step, P_Q can be determined much more accurately. Furthermore, in the thermographic method, the preparation of test specimens can be simplified by replacing the process of growing a fatigue crack at the tip of a notch by making a sharp cut, which provides significant time savings. Statistical processing and comparison of test results of steel 20 specimens using the conventional and thermographic methods have shown the advantages of the thermographic method in accuracy and complexity.

Keywords:

Crack Resistance, Stress Intensity Factor, Temperature, Entropy, Specified Load, Incision, Cut, Crack Motion

1. Introduction

Optics-mechanical devices, being used in modern machines, might be exploited in extreme conditions under significant external loading. That is why the power components of these instruments must possess adequate strength characteristics.

This work considers a new (designed by the authors) thermographic method for definition of static crack resistance characteristics of materials.

These characteristics are defined experimentally on special samples with an incision (cut) created in advance. We use either flat samples with a crack in the center or in the edge, or cylinder samples with a ring crack. Before the test it is necessary to extend the cut by fatigue crack with the length not less than 1.5 mm.

At standard testing [1] the diagrams “P-V” are built, where Р―applied force, V― crack sides shift. The purpose of this testing is fixation of the moment of crack initiation. This moment corresponds to nominal load P_Q, on the basis of which all the crack resistance parameters are then calculated.

In case of brittle destruction nominal load is equal to either maximal, or local maximal of loading, i.e. crack initiation is managed to be fixed pretty exactly. Diagrams “P-V”, representing visco-elastic or viscous destruction, are characterized by the absence local maximums of loading, which makes it difficult to fix nominal load. For this purpose, it is recommended to make the following―to draw 5 % secant line, and nominal load P_Q is defined as the ordinate of this secant line crossing the curve “P-V” [1] [2] . By drawing this 5% secant line they try to separate geometrical non-linearity, defining 2% crack growing, after which, as it is considered, starts the crack movement, from physical non-linearity, connected with development of intensive plastic defor- mation in the tip of the crack.

However at such traditional approach, the nominal load P_Q is not defined with enough accuracy, because individual features of tested materials are not taken into account, and also drawing a 5% secant line is rather difficult. Besides, when preparing the samples for test, it is necessary to make fatigue cracks 0.3 mm deep, which appears to be rather difficult an operation.

2. Objectives and Methods of Research

The objectives of this research were: the improvement of determination accuracy of crack resistance parameter in case of visco-elastic and viscous destruction; decreasing labour intensity when preparing samples for experiment. The research was conducted on flat samples from steel 20.

For more precise fixation of nominal load we used thermographic parameter - temperature change in the crack tip during rather short time period. The tests were conducted on sixteen flat samples (Figure 1) with central cracks of normal fracture according to model I of linear fracture mechanics [1] [3] [4] [5] . Together with traditional diagrams ”P-V”, we drew diagrams “P-ΔT”, which then were redrawn into diagrams “P-ΔS”, where -increment of specific entropy in plastic zone of crack development.

By comparison of these two thermodynamic diagrams with diagram “P-V” the correlation between their characteristic points was determined.

The sample sizes were chosen according to the recommendations in [1] [3] . On the half of samples (1 group), as it is required in standard method, before the tests were created fatigue cracks from the crack tips, on the rest of samples (2 group) fatigue cracks were replaced by sharp thin saw cuts. The fatigue crack was created from initial incision at coefficient of asymmetry of loading cycle R = 0.1.

Crack resistance (fracture viscosity) parameters were determined on the results of single static tests of given samples on the universal hydraulic machine “УГ-20”. The temperature in the crack tip was fixed with help of thermo vision device“Aga-750” [6] [7] , having sensitivity 0.1˚C when the scanner mechanism is in operation. When observing the point the scanner mechanism was switched off, and sensitivity of thermo vision device increased significantly.

Figure 2 shows the scheme of the equipment used in the experiment.

In testing the samples in crack tips occur elastic-plastic deformations with big plastic zone formation. In such cases as the most reliable crack resistance parameters are accepted: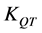―critical SIF (Stress Intensity Factor) for the sample of given thickness,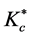―conditional critical SIF, corresponding to quasi brittle destruction,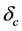―divergence in crack tip at maximal loading.

3. Results of Experiments

Figure 3 shows the diagrams “P-V”, “P-ΔT” for one of the 1 group samples. The second diagram was then redrawn into the diagram “P-ΔS” on formula [8] :

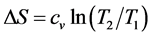(1)

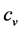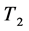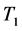Here,―specific heat capacity of material; and―temperatures in the crack tip in the end and in the beginning of the given time period. It is necessary to note, that in the formula (1)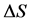―that part of entropy stream that only heats up the deformation centre, but it is the stream that is adequate to the given task, as during plastic deformation practically all the energy turns to heat.

Figure 4 shows similar diagrams, but obtained at 2 group sample testing. Saw cuts were made with sharpened hacksaw 0.3 mm wide. We note that for the other tested samples the diagrams have similar view.

Let us discuss the obtained results. First of all we will note that the diagram “-V” for the 2 group samples (Figure 4) is inappropriate for defining crack resistance parameters. This was, generally speaking, the thing that had to be expected, because these samples’ pre-test preparation was not conducted in approved strongly regulated technology [1] [3] ―fatigue crack was not made. And diagrams “P-ΔT” and “P-ΔS” [9] for both sample groups turned out to be nearly identical.

Let us also note, that diagrams “P-ΔT” and “P-ΔS” have three clearly defined zones [7] [9] , having obvious physical sense: at first (1-st zone) there is some decrease in temperature, connected with Thomson effect, then warming of the material by means of micro plastic deformation compensates Thomson effect and temperature stabilizes (2-nd zone) and, at last, there starts the sharp rise of temperature by means of energy release at plastic deformation (3-rd zone).

And the very important thing is, that certain points of these diagrams correlate with certain points on diagram ”P-V”: ordinates of the point on the boundary between 1-st and 2-nd zones practically correspond with the ordinate of the point Q on diagram “P-V”, and points С, denoting maximal loads, are practically equal.

Then with the standard method all necessary crack resistance parameters for 1-st group samples were defined on the obtained in experiment reference points, taken from diagram “P-V”, and thermodynamic diagram “P-ΔS” defined the parameters for all the samples of both groups.

And in conclusion calculated parameters were statistically processed, and as a result were defined confidence intervals and average square errors of crack resistance parameters, obtained from diagrams ”P-V” and “P-ΔS”.

4. Analysis of the Results and Conclusions

1) Fracture toughness characteristics are fairly accurately determined by the conventional method (based on P-V curves) in brittle (elastic) fracture. In tests of steel 20 specimens, ductile fracture was observed. Due to the complex nature of the crack initiation phenomenon in ductile fracture, it cannot be detected directly from P-V curves. Hellan [2] notes that the conventional 5% secant offset method for determining the onset of crack propagation, which does not take into account the individual characteristics of test specimens, is a source of uncertainty in the results. Because cracks can propagate within the material, it is impossible to use some alternative methods, for example, optical processes. The mere detection of fracture may be difficult because the damage at the crack front increases gradually through the growth and coalescence of micropores. The conventional method involves an error which may be substantial. Therefore, Hellan and other researchers [2] [3] [10] [11] [12] highlight the need to develop new experimental methods for calculating fracture toughness characteristics in ductile fracture. The thermographic method may be regarded as a step in this direction.

2) From the calculated confidence intervals, it can be seen that the fracture toughness characteristics calculated by the P-ΔS curve are more concentrated than the characteristics calculated from the P-V curve, suggesting that the accuracy of their determination is higher. This result can be explained by the fact that the P-ΔS curve has a sharp break near the calculated point, from which this point is easy to determine. This break has a clear physical interpretation -it corresponds to the onset of intense plastic deformation, which, as noted in the literature and observed in our experiments, occurs suddenly [1] [3] . It is at this point that crack propagation begins, which should be detected in tests.

3) The finding that P-∆Т and P-∆S curves do not depend on the type of specimen allows the time-consuming process of growing a fatigue crack in the preparation of test specimen to be replaced by the simple process of making a sharp cut from the top of a notch. This also suggests that thermodynamic diagrams accurately reflect the properties of the test material.

The list of comments and concerns on the use of the thermodynamic approach in static fracture toughness tests can be continued. However, it is undeniable that in the viscoelastic fracture tests of steel 20 specimens, P-∆S diagrams provided a more accurate and rapid determination of the load at the onset of crack propagation, which can then be used to calculate fracture toughness characteristics [1] [3] .

Cite this paper

Kurilenko, G.A. and Ayrapetyan, V.S. (2016) Determination of the Fracture Toughness of Optomechanical Devices. Optics and Photonics Journal, 6, 298-304. http://dx.doi.org/10.4236/opj.2016.611030

References