Optics and Photonics Journal
Vol.05 No.12(2015), Article ID:62236,10 pages
10.4236/opj.2015.512033
Radiation Forces on a Dielectric Sphere Produced by Finite Olver-Gaussian Beams
Salima Hennani, Lahcen Ez-zariy*, Abdelmajid Belafhal*
Laboratory of Nuclear, Atomic and Molecular Physics Department of Physics, Faculty of Sciences, Chouaïb Doukkali University, El Jadida, Morocco

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 October 2015; accepted 21 December 2015; published 25 December 2015
ABSTRACT
In this work, we use the analytical expression of the propagation of Finite Olver-Gaussian beams (FOGBs) through a paraxial ABCD optical system to study the action of radiation forces produced by highly focused FOGBs on a Rayleigh dielectric sphere. Our numerical results show that the FOGBs can be employed to trap and manipulate particles with the refractive index larger than that of the ambient. The radiation force distribution has been studied under different beam widths. The trapping stability under different conditions is also analyzed.
Keywords:
Finite Olver-Gaussian Beams, Radiation Forces, Scattering Force, Gradient Force, Rayleigh Dielectric Sphere

1. Introduction
In recent years, the accelerating finite Airy beam has been introduced within the framework of laser optics field by Siviloglou et al. [1] [2] , on the basis of the result published by Berry and Balzas [3] , in the context of the quantum mechanics, whose have introduced the Airy wave packet function as a solution of the Schrödinger equation in 1979. This new laser beams family exhibits many important characteristics, which permit them good candidates in several applications such as manipulating, trapping and transport of particles. It has an intensity profile that tends to be accelerated transversely during propagation. This leads to its experimental realization where most of the interesting properties were observed directly in many configurations [2] , and the study of its ballistic dynamics shows that these waves follow parabolic trajectories similar to these of projectiles moving under the action of uniform gravitational field [4] [5] . This can absolutely help in handling micron particles. This topic was discussed in the literature first by Ashkin [6] and demonstrated how to manipulate three-dime- nsional trapping of a dielectric particle by using a highly focused laser beam thanks to their wide applications in manipulating various particles such as neutral atoms [7] , molecules [8] , micron-sized dielectric particles [9] , DNA molecules [10] and living biological cells [11] -[13] . The optical traps or tweezers have also attracted attention in many literature works [14] - [18] . The radiation forces explained by scattering and gradient forces are generated by the exchange of momentum and energy between photons and particles.
As known, the first conventional optical trap is constructed by the fundamental Gaussian beams because it has a Gaussian peak in the cross profile and it is suitable for trapping the particle with the index of refraction higher than that of ambient [7] . However, many researchers have demonstrated that other beams are also useful in trapping particles such as doughnut laser beams including Bessel beams which are more available in the trapping and manipulation of process [19] - [21] . The trapping characteristics of different beams, such as Laguerre-Gaus- sian [22] , hollow-Gaussian [23] , Bessel-Gaussian [24] , cylindrical vector [25] , Gaussian Schell model [26] and flat-topped-Gaussian beams [27] , have been studied.
The “non-diffracting” Airy beam has also attracted attention for its use in trapping particles because of its potential applications in several domains of the same context, such as: guidance plasma [28] , acceleration of electrons in vacuum [29] , production of three optical bullets dimensions [30] and optical micromanipulation [31] [32] . Opposed to other laser beams, the Airy family beam can transport microparticles along curved self- healed paths, and remove particles or cells from a section of a sample chamber [33] . Its novelty is that the trapping potential landscape tends to freely self-bend during propagation, and also its bend degree can be controlled, and the direction of acceleration can be switched by a nonlinear optical method [33] , and the micromanipulation by Airy beam reported to date is related to Mie particles [31] [32] whose radii are larger than the wavelength. All these tunable properties make the Airy beam as a versatile and powerful tool for many optical manipulations. Our work done in this review is based on the above cited theoretical studies dealing the radiation force on spherical particles [8] - [10] [33] - [37] . Of these, we cite the theoretical analysis of the radiation pressure force of laser light on a dielectric sphere in the Rayleigh regime developed by Harada and Asakura [33] , the method proposed by Rohrbach and Stelzer [34] , to calculate the forces trapping dielectric particles and the investigation made by Zemánek et al. [35] about the rule of Gaussian beams in optical trapping of Rayleigh particles. Yet, Cheng et al. [36] have developed an analysis of optical trapping and propulsion of Rayleigh particles using the ordinary Airy beam. And in Ref. [37] , Svoboda and Block have discussed some biological applications of optical forces.
In this paper, we consider a theoretical description of the radiation forces produced by the Finite Olver- Gaussian beam in Rayleigh scattering regime when the radius of particles is much smaller than the wavelength. Note that the new beams family, called “Finite Olver-Gaussian beams”, is introduced within the optic field and their characteristics and propagation properties in aligned and misaligned optical systems are studied and examined for the first time by our research group [37] - [39] .
2. Fields of Finite Olver-Gaussian Beams through an ABCD Optical System
The electrical field of FOG Bs at the input plane (z = 0) is defined by Belafhal et al. [38] as
 (1)
(1)
where 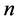 is the order of FOGBs. For
is the order of FOGBs. For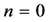 , we will treat the ordinary finite Airy beam with
, we will treat the ordinary finite Airy beam with 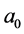 is the truncation coefficient and
is the truncation coefficient and 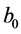 is a coefficient to be equal to 1 or 0, depend that the incident beam is modulated by a Gaussian envelope or not, respectively. Due to the special properties of Airy Beam, it can absolutely be used to guide and trap neutral particles.
is a coefficient to be equal to 1 or 0, depend that the incident beam is modulated by a Gaussian envelope or not, respectively. Due to the special properties of Airy Beam, it can absolutely be used to guide and trap neutral particles.
Under the paraxial approximation, the electrical field of FOGBs beam passing via any ABCD optical system can be expressed as [39] .
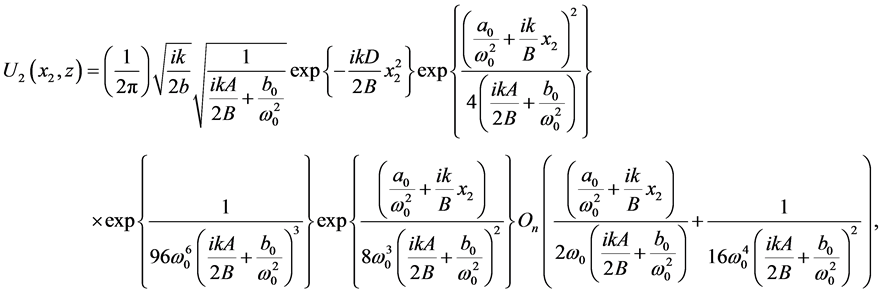 (2)
(2)
where 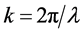 is the wave number and
is the wave number and 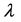 being the wavelength. A, B, C and D are the transfer matrix elements of the paraxial optical system. z is the distance between the input and the output planes. Consider now the FOGBs propagates through a free space described by the following transfer matrix
being the wavelength. A, B, C and D are the transfer matrix elements of the paraxial optical system. z is the distance between the input and the output planes. Consider now the FOGBs propagates through a free space described by the following transfer matrix
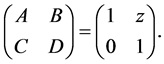 (3)
(3)
Substituting Equation (3) in Equation (2), one obtains the intensity distribution of the FOGBs through a free space.
3. Theory of the Radiation on a Dielectric Sphere
Assume that the particle is sufficiently small compared to the wavelength of the laser beam i.e.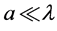 , where a is the radius of the particle and
, where a is the radius of the particle and 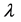 is the wavelength of the incident beam. So, in the Rayleigh scattering the particle could be treated as a point dipole. Two types of radiation forces can be examined: the scattering force and the gradient one. The electric field is polarized in the x -direction. The center of the particle is located at the position (x, z). The physical quantities of the field vectors of the electromagnetic wave are real functions of time and space given by [33]
is the wavelength of the incident beam. So, in the Rayleigh scattering the particle could be treated as a point dipole. Two types of radiation forces can be examined: the scattering force and the gradient one. The electric field is polarized in the x -direction. The center of the particle is located at the position (x, z). The physical quantities of the field vectors of the electromagnetic wave are real functions of time and space given by [33]
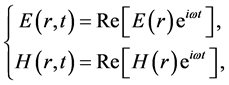 (4)
(4)
with 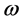 is the temporal angular frequency of the laser beam. The instantaneous energy flux crossing an area per time unit in the beam propagation direction corresponding to the propagation vector is given by [33]
is the temporal angular frequency of the laser beam. The instantaneous energy flux crossing an area per time unit in the beam propagation direction corresponding to the propagation vector is given by [33]
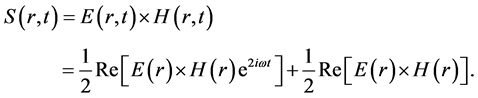 (5)
(5)
The measurable physical quantity which evaluates the radiation force, of the light, is the beam intensity at the position 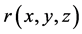 which is defined as
which is defined as
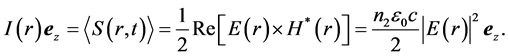
In the last equation, 
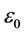
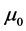
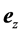
The radiation pressure force exerted on the particle in the Rayleigh regime is described by two components actions on the dipole. One of these forces is the scattering force. As known, the electric field oscillates harmonically in time, and the induced point dipole follows with synchronization the electric field which gives that the particle acts as an oscillating electric dipole which radiates secondary or scattered waves in all directions. The scattering force is given and discussed in [37]
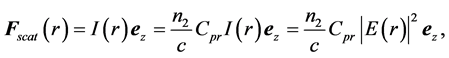
where 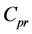
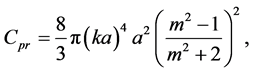
with 

The other component is a gradient force due to the Lorentz force acting on the dipole induced by the electromagnetic field [37] . The instantaneous gradient force is defined by [37]
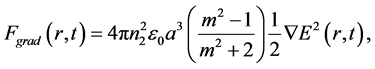
where 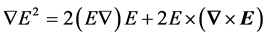

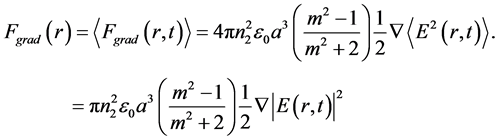
with
4. Numerical Simulations and Results Discussions
By the use of the theory of the radiation on a dielectric sphere, exposed in the previous section, we will prove numerically that the considered beams family drags particles into their intensity peaks. The parameters chosen in the calculations are: the radius of the particle is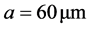
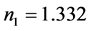
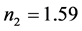
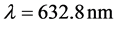
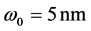
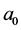
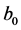
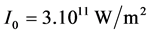

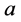
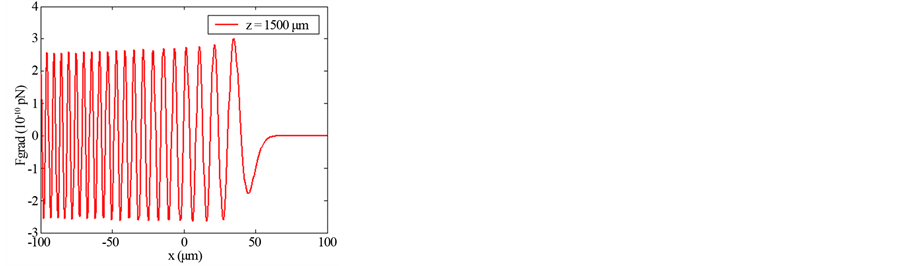
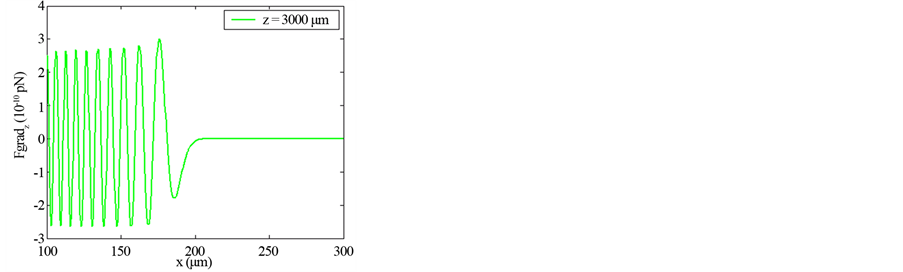
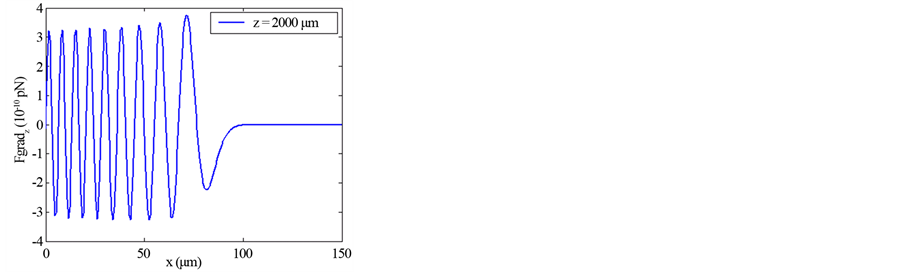
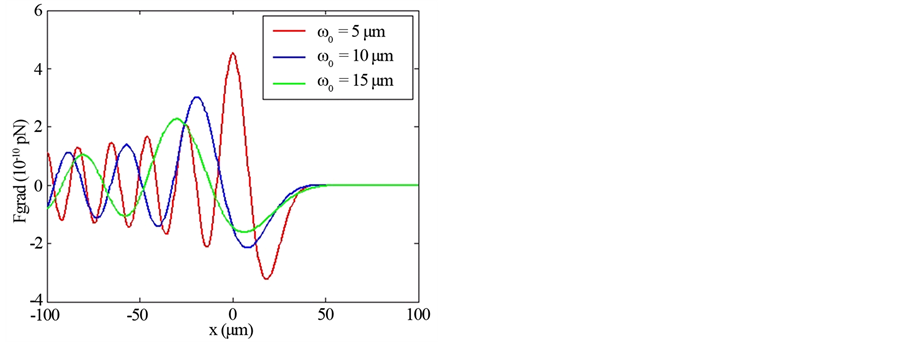
Figures 1-4 show the transverse gradient force along x-axis for the various orders n = 0, 1 and 2 at different axial positions z and with different values of the beam size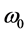
Figure 1. Transverse gradient force of finite zeroth-order Olver-Gaussian beam versus x for different values of ω0 and for z = 500 μm.
Figure 2. Transverse gradient force of finite zeroth-order of Olver-Gaussian beam versus x for different propagation distances z and ω0 = 5 μm.
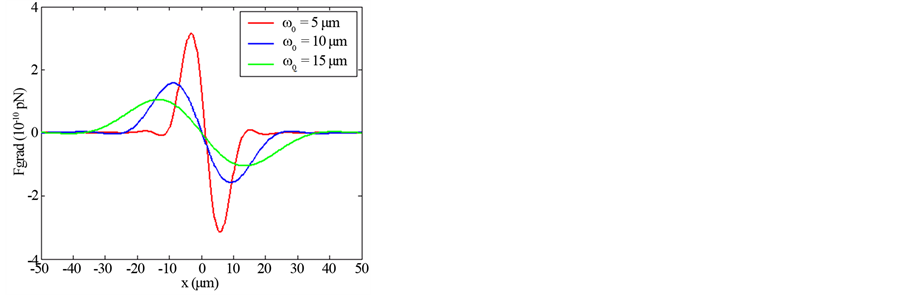
Figure 3. Transverse gradient force of Finite Olver-Gaussian beam of second order (n = 2) versus x for different: (a) Propag- ation distances z, (b) Beam width size.
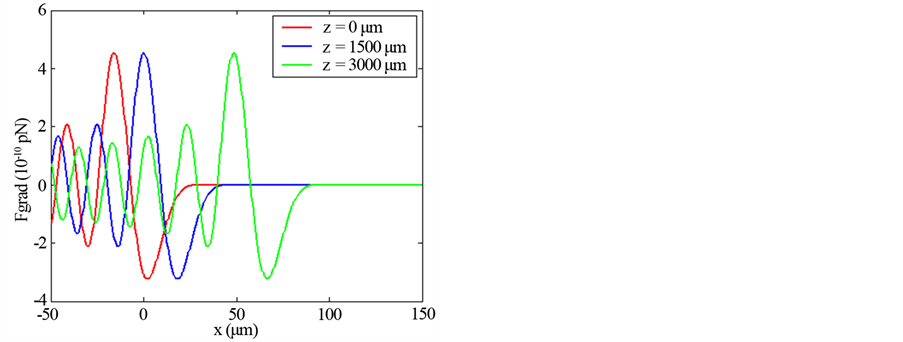
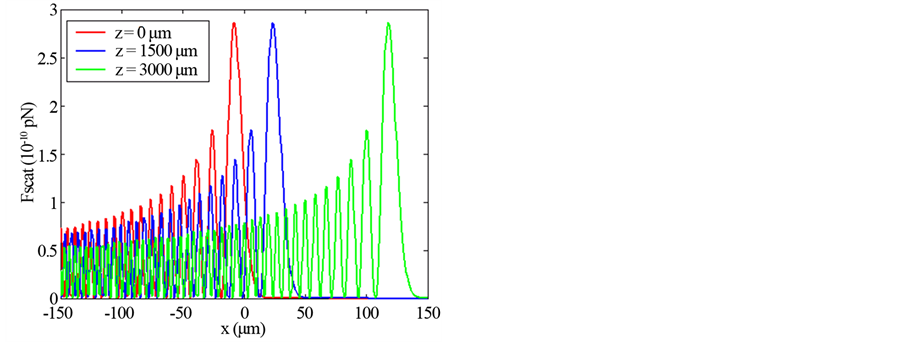
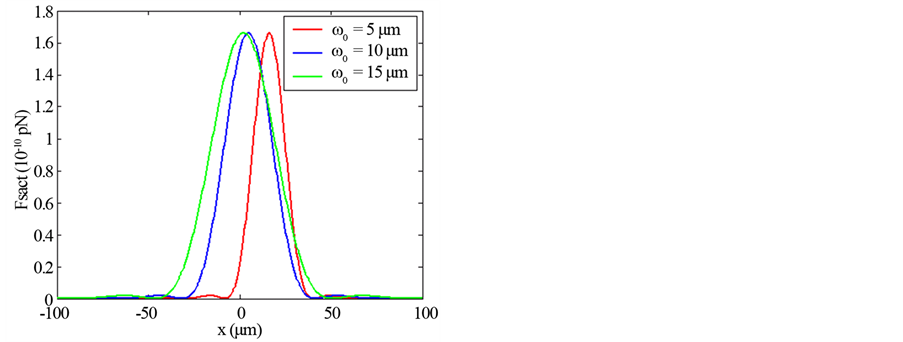
Figure 4. Scattering force of Finite Olver-Gaussian beam of first order (n = 1) versus x for different: (a) Propaga- tion distance z (ω0 = 5 μm), (b) Beam witdth size ω0 (z = 500 μm).
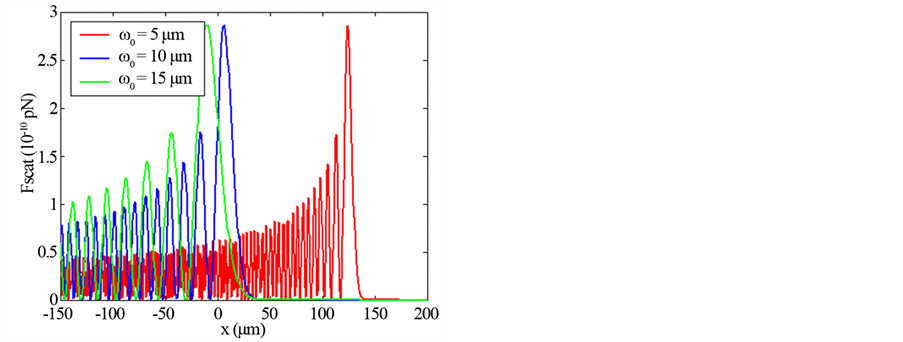
Figure 5. Transverse gradient force of Finite Olver-Gaussian beam of first order (n = 1) versus x for different: (a) Propagation distances z (ω0 = 5 μm), (b) Beam witdth size ω0 (z = 500 μm).
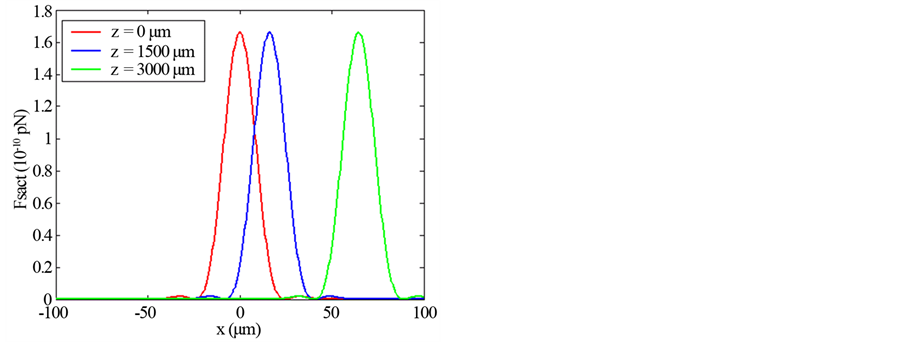
Figure 6. Scattering force of finite zeroth-order Olver-Gaussian beam versus x for different: (a) Propagation distances z (ω0 = 5 μm), (b) Beam witdth size ω0 (z = 500 μm).
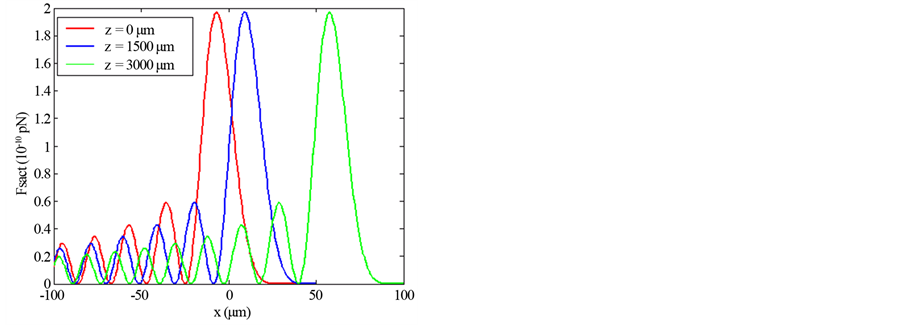
Figure 7. Scattering force of Finite Olver-Gaussian beam of second order (n = 2) versus x for different: (a) propaga- tion distances z (ω0 = 5 μm), (b) Beam witdth size ω0 (z = 500 μm).

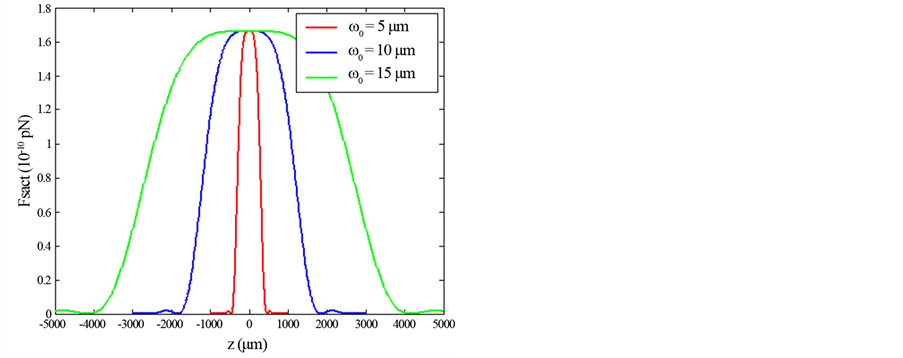
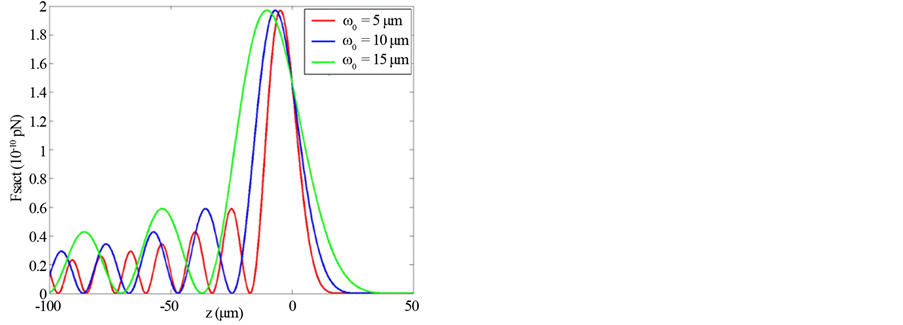
Figure 8. Example of a scattering force of Finite Olver-Gaussian beam at varying z planes for different beam width size ω0 (z = 500 μm). for: (a): zeroth order (n = 0), (b): first order (n = 1) and (c): second order (n = 2).
Illustrations of Figures 1-4 show that as far as the propagation distance z increases as much as the number of oscillations of the gradient force increases and the zeros of the central lobe and sidelobes move towards the positive x. However, the maxima of the lobes decrease insignificantly with the increase of z. Yet, the gradient force reaches less of zeros and the lobes maximums decrease with the increase of the waist size of the incident Gaussian envelope. The decrease of the maximums lobes with the waist is very significant. In Figures 5-7, we plot the scattering force of the various orders n of the Finite Olver-Gaussian beam versus x for different propagation distances z and different beam width sizes ω0.
As the same as in Figures 1-4 concern the gradient force, from the plots of Figure 5 and Figure 7 about the scattering force, it is pointed that the same remarks are repeated in this case. Figure 8, shows the scattering force of the Finite Olver-Gaussian beam for different orders n along z-axis and with different values of beam size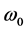
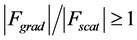
5. Conclusion
We have investigated the radiation force exerted on a dielectric particle in the Rayleigh scattering regime illuminated by FOGBs with different beams order n. Several numerical simulations are carried out in the work, in order to study and analyze the effects of some parameters on the radiation gradient and transverse forces, for instance, the parameters of the laser beam illuminate the dielectric sphere and the propagation distance. The numerical results show that the Finite Olver-Gaussian beams could drag particles by the peaks of intensity and could transport and manipulate them in the inter-lobes. Finally, we conclude that Finite Olver-Gaussian beams may be used in many practical applications of nanotechnology and biotechnology.
Cite this paper
SalimaHennani,LahcenEz-zariy,AbdelmajidBelafhal, (2015) Radiation Forces on a Dielectric Sphere Produced by Finite Olver-Gaussian Beams. Optics and Photonics Journal,05,344-353. doi: 10.4236/opj.2015.512033
References
- 1. Siviloglou, G.A. and Christodoulides, D.N. (2007) Accelerating Finite Energy Airy Beams. Optics Letters, 32, 979-981.
http://dx.doi.org/10.1364/OL.32.000979 - 2. Siviloglou, G.A., Broky, J., Dogariu, A. and Christodoulides, D.N. (2007) Observation of Accelerating Airy Beams. Physical Review Letters, 99, 213901.
http://dx.doi.org/10.1103/PhysRevLett.99.213901 - 3. Berry, M.V. and Balazs, N.L. (1979) Nonspreading Wave Packets. American Journal of Physics, 4, 264-267.
http://dx.doi.org/10.1119/1.11855 - 4. Siviloglou, G.A., Broky, J., Dogariu, A. and Christodoulides, D.N. (2008) Ballistic Dynamics of Airy Beams. Optics Letters, 33, 207-209.
http://dx.doi.org/10.1364/OL.33.000207 - 5. Besieris, I.M. and Shaarawi, A.M. (2007) A Note on an Accelerating Finite Energy Airy Beam. Optics Letters, 32, 2447-2449.
http://dx.doi.org/10.1364/OL.32.002447 - 6. Ashkin, A. (1970) Atomic-Beam Deflection by Resonance-Radiation Pressure. Physical Review Letters, 25, 1321.
http://dx.doi.org/10.1103/PhysRevLett.25.1321 - 7. Yavuz, D.D., Kulatunga, P.B., Urban, E., Johnson, T.A., Proite, N., Henage, T., Saffman, M., et al. (2006) Fast Ground State Manipulation of Neutral Atoms in Microscopic Optical Traps. Physical Review Letters, 96, 063001.
http://dx.doi.org/10.1103/PhysRevLett.96.063001 - 8. Calander, N. and Willander, M. (2002) Optical Trapping of Single Fluorescent Molecules at the Detection Spots of Nanoprobes. Physical Review Letters, 89, 143603.
http://dx.doi.org/10.1103/PhysRevLett.89.143603 - 9. Taguchi, K., Ueno, H. and Ikeda, M. (1997) Rotational Manipulation of a Yeast Cell Using Optical Fibres. Electronics Letters, 33, 1249-1250.
http://dx.doi.org/10.1049/el:19970827 - 10. Day, C. (2006) Optical Trap Resolves the Stepwise Transfer of Genetic Information from DNA to RNA. Physics Today, 59, 26-27.
http://dx.doi.org/10.1063/1.2180165 - 11. Mao, F.L., Xing, Q.R., Wang, K., Lang, L.Y., Wang, Z., Chai, L. and Wang, Q.Y. (2005) Optical Trapping of Red Blood Cells and Two-Photon Excitation-Based Photodynamic Study Using a Femtosecond Laser. Optics Communications, 256, 358-363.
http://dx.doi.org/10.1016/j.optcom.2005.06.076 - 12. Chang, Y.R., Hsu, L. and Chi, S. (2005) Optical Trapping of a Spherically Symmetric Rayleigh Sphere: A Model for Optical Tweezers upon Cells. Optics Communications, 246, 97-105.
http://dx.doi.org/10.1016/j.optcom.2004.10.066 - 13. Xie, C.G. and Li, Y.Q. (2003) Confocal Micro-Raman Spectroscopy of Single Biological Cells Using Optical Trapping and Shifted Excitation Difference Techniques. Journal of Applied Physics, 93, 2982-2986.
http://dx.doi.org/10.1063/1.1542654 - 14. Neuman, K.C. and Block, S.M. (2004) Optical Trapping. Review of Scientific Instruments, 75, 2787-2809.
http://dx.doi.org/10.1063/1.1785844 - 15. Furst, E.M. (2003) Interactions, Structure, and Microscopic Response: Complex Fluid Rheology Using Laser Tweezers. Soft Materials, 1, 167-185.
http://dx.doi.org/10.1081/SMTS-120022462 - 16. Ashkin, A. (1992) Forces of a Single-Beam Gradient Laser Trap on a Dielectric Sphere in the Ray Optics Regime. Biophysical Journal, 61, 569-582.
http://dx.doi.org/10.1016/S0006-3495(92)81860-X - 17. Ashkin, A. (2000) History of Optical Trapping and Manipulation of Small-Neutral Particle, Atoms, and Molecules. IEEE Journal of Selected Topics in Quantum Electronics, 6, 841-856.
http://dx.doi.org/10.1109/2944.902132 - 18. Grzegorczyk, T.M., Kemp, B.A. and Kong, J.A. (2006) Stable Optical Trapping Based on Optical Binding Forces. Physical Review Letters, 96, 113903.
http://dx.doi.org/10.1103/PhysRevLett.96.113903 - 19. O’Neil, A.T. and Padgett, M.J. (2000) Three-Dimensional Optical Confinement of Micron-Sized Metal Particles and the Decoupling of the Spin and Orbital Angular Momentum within an Optical Spanner. Optics Communications, 185, 139-143.
http://dx.doi.org/10.1016/S0030-4018(00)00989-5 - 20. Kuga, T., Torii, Y., Shiokawa, N., Hirano, T., Shimizu, Y. and Sasada, H. (1997) Novel Optical Trap of Atoms with a Doughnut Beam. Physical Review Letters, 78, 4713.
http://dx.doi.org/10.1103/PhysRevLett.78.4713 - 21. Gahagan, K.T. and Swartzlander, G.A. (1996) Optical Vortex Trapping of Particles. Optics Letters, 21, 827-829.
http://dx.doi.org/10.1364/OL.21.000827 - 22. Dienerowitz, M., Mazilu, M., Reece, P.J., Krauss, T.F. and Dholakia, K. (2008) Optical Vortex Trap for Resonant Confinement of Metal Nanoparticles. Optics Express, 16, 4991-4999.
http://dx.doi.org/10.1364/OE.16.004991 - 23. Zhao, C.L., Wang, L.G. and Lu, X.H. (2007) Radiation Forces on a Dielectric Sphere Produced by Highly Focused Hollow Gaussian Beams. Physics Letters A, 363, 502-506.
http://dx.doi.org/10.1016/j.physleta.2006.11.028 - 24. Zhao, C., Wang, L. and Lu, X. (2008) Radiation Forces of Highly Focused Bessel-Gaussian Beams on a Dielectric Sphere. Optik-International Journal for Light and Electron Optics, 119, 477-480.
http://dx.doi.org/10.1016/j.ijleo.2006.11.013 - 25. Zhan, Q.W. (2003) Radiation Forces on a Dielectric Sphere Produced by Highly Focused Cylindrical Vector Beams. Journal of Optics A: Pure and Applied Optics, 5, 229.
http://dx.doi.org/10.1088/1464-4258/5/3/314 - 26. Wang, L.G. and Zhao, C.L. (2007) Dynamic Radiation Force of a Pulsed Gaussian Beam Acting on Rayleigh Dielectric Sphere. Optics Express, 15, 10615-10621.
http://dx.doi.org/10.1364/OE.15.010615 - 27. Zhao, C., Cai, Y., Lu, X. and Eyyuboglu, H.T. (2009) Radiation Force of Coherent and Partially Coherent Flat-Topped Beams on a Rayleigh Particle. Optics Express, 17, 1753-1765.
http://dx.doi.org/10.1364/OE.17.001753 - 28. Polynkin, P., Kolesik, M., Moloney, J.V., Siviloglou, G.A. and Christodoulides, D.N. (2009) Curved Plasma Channel Generation Using Ultraintense Airy Beams. Science, 324, 229-232.
http://dx.doi.org/10.1126/science.1169544 - 29. Li, J.X., Zang, W.P. and Tian, J.G. (2010) Vacuum Laser-Driven Acceleration by Airy Beams. Optics Express, 18, 7300-7306.
http://dx.doi.org/10.1364/OE.18.007300 - 30. Chong, A., Renninger, W.H., Christodoulides, D.N. and Wise, F.W. (2010) Airy-Bessel Wave Packets as Versatile Linear Light Bullets. Nature Photonics, 4, 103-106.
http://dx.doi.org/10.1038/nphoton.2009.264 - 31. Baumgartl, J., Mazilu, M. and Dholakia, K. (2008) Optically Mediated Particle Clearing Using Airy Wavepackets. Nature Photonics, 2, 675-678.
http://dx.doi.org/10.1038/nphoton.2008.201 - 32. Baumgartl, J., Hannappel, G.M., Stevenson, D.J., Day, D., Gu, M. and Dholakia, K. (2009) Optical Redistribution of Microparticles and Cells between Microwells. Lab on a Chip, 9, 1334-1336.
http://dx.doi.org/10.1039/b901322a - 33. Harada, Y. and Asakura, T. (1996) Radiation Forces on a Dielectric Sphere in the Rayleigh Scattering Regime. Optics Communications, 124, 529-541.
http://dx.doi.org/10.1016/0030-4018(95)00753-9 - 34. Rohrbach, A. and Stelzer, E.H. (2001) Optical Trapping of Dielectric Particles in Arbitrary Fields. Journal of Optics A: Pure and Applied Optics, 18, 839-853.
http://dx.doi.org/10.1364/JOSAA.18.000839 - 35. Zemánek, P., Jonás, A., Srámek, L. and Liska, M. (1998) Optical Trapping of Rayleigh Particles Using a Gaussian Standing Wave. Optics Communications, 151, 273-285.
http://dx.doi.org/10.1016/S0030-4018(98)00093-5 - 36. Cheng, H., Zang, W., Zhou, W. and Tian, J. (2010) Analysis of Optical Trapping and Propulsion of Rayleigh Particles Using Airy Beam. Optics Express, 18, 20384-20394.
http://dx.doi.org/10.1364/OE.18.020384 - 37. Svoboda, K. and Block, S.M. (1994) Biological Applications of Optical Forces. Annual Review of Biophysics and Biomolecular Structure, 23, 247-285.
http://dx.doi.org/10.1146/annurev.bb.23.060194.001335 - 38. Belafhal, A., Ez-Zariy, L., Hennani, S. and Nebdi, H. (2015) Theoretical Introduction and Generation Method of a Novel Nondiffracting Waves: Olver Beams. Optics and Photonics Journal, 5, 234-246.
http://dx.doi.org/10.4236/opj.2015.57023 - 39. Hennani, S., Ez-zariy, L. and Belafhal, A. (2015) Propagation Properties of Finite Olver-Gaussian Beams Passing through a Paraxial ABCD Optical System. Optics and Photonics Journal, 5, 273-294.
http://dx.doi.org/10.4236/opj.2015.59026
NOTES
*Corresponding author.