Received 19 August 2015; accepted 23 October 2015; published 26 October 2015

ABSTRACT

The solar grating spectrometer is an essential tool to study the thermodynamics properties of the solar atmosphere with different height distributions, but its imaging performance will be degraded by the wavefront aberration generalized by the atmospheric turbulence. On the other hand, the narrow slit of the grating spectrometer will filter the wavefront aberration to some extent. The influence of the filter slit on the wavefront aberration and the correction requirement of the adaptive optics are analyzed theoretically and experimentally. We demonstrate that the influence of filter slit on the different types and magnitudes of wavefront aberration is different, and the RMS value of the wavefront aberration less than 0.3λ is down to below almost 60% after the filter slit, and it can lower the correction range requirement of the adaptive optics. The numerical simulation and experiment results show that: after the adaptive optics correction, the influence of the wavefront aberration on the spectral resolution is neglected, and the energy utilization is considerably improved; both numerical simulation and experiment results are in good agreement.

Keywords:

Solar Atmosphere, Aberration, Adaptive Optics, Prototype, Spectral Resolution

1. Introduction

It is well known that the evolving magnetic field causes the solar atmosphere eruption, and it produces most of the sometimes spectacular visible phenomena, such as the sunspots, prominences, flares, coronal mass ejections and so on [1] [2] . Real-time observation and forecast of the solar atmosphere activities are very important since the violent activities of the solar atmosphere and period variation will influence the living environment of human being, and the imaging grating spectrometer is an important tool to achieve this goal [3] -[5] . It not only can perform the imaging observation, but also can perform the spectral observation and identify the thermodynamics parameters of the solar atmosphere by the spectral information, such as the magnetic field, pressure and element abundance. As a result, the imaging grating spectrometer is broadly applied in the solar atmosphere observation.

However, the imaging performance of the grating spectrometer installed in the ground-based solar telescope is limited by the wavefront aberration [6] [7] , i.e. the dynamic wavefront aberration generalized by the atmospheric turbulence and the static wavefront aberration of the optical system. The wavefront aberration not only will degrade the spatial resolution, but also will degrade the spectral resolution and energy utilization. Fortunately, after development for several years, Adaptive Optics (AO) technique has made great progress, and it has become an important tool to reduce the influence of the atmospheric aberration and static aberration [8] -[10] . Therefore, the Adaptive Optics system is integrated in the solar telescope to compensate the atmospheric turbulence influence on the imaging performance of the solar telescope.

On the other hand, unlike the general optical system, the used slit of the grating spectrometer is narrow enough, and it will filter the wavefront aberration to some extent. Quantitatively studying the influence of the filter slit on the wavefront aberration with different types and magnitudes becomes a necessity. Since the filter slit will filter the wavefront aberration, the traditional AO system cannot be directly applied to compensate the wavefront aberration. Our goal is to demonstrate the influence of the filter slit on the wavefront aberration and the influence of the Adaptive Optics theoretically and experimentally. To the best of our knowledge, it is an innovative work.

This paper is organized as follows: in Section 2, the influence factors of the imaging grating spectrometer are analyzed; in Section 3, the numerical simulation is performed and is validated experimentally; in Section 4, the conclusions are summarized.

2. The Influence Factors on the Imaging Performance of the Grating Spectrometer

The spectral resolution and energy utilization are the key parameters of the imaging grating spectrometer, and they are mainly influenced by the wavefront aberration, slit width and the spectral sampling of the CCD camera. Among them, the influence of the slit width and the spectral sampling of the CCD camera on the spectral resolution cannot be avoided, and can be represented by the net spectral resolution [4] . On the other hand, the quantitative influence of the filter slit on the spectral resolution and energy utilization of the grating spectrometer is still rare understood, and we will discuss it in the following paragraphs.

The optical layout of the grating spectrometer is depicted in the Figure 1. The field of view of the imaging grating spectrometer is limited by the slit since the slit is the field stop. Generally, the slit is rectangle, and the slit length is long enough. Hence, the field of view is limited by the slit width.

The spectral purity [4] is used to represent the influence of the slit width on the spectral resolution, given by

(1)

where the 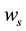is the slit width of the grating spectrometer, α is the incidence angle of the grating, m is the diffraction order, f is the focal length of the collimator, d is grating constant.

After considering the influence of the slit width, the spectral resolution [4] is given by

(2)

where

(3)

where the 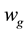and the 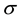is the illuminated width and the groove density of the grating, respectively.

It is apparent that the energy utilization increases with the slit width, but at the cost of the spectral resolution based on Equation (2). When the slit width is equal to the airy disk diameter of the solar telescope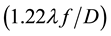, the influence of the slit width on the spectral resolution is minimized, and the energy utilization is maximized [7] .

Actually, the real spectral resolution 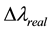often is determined by the Rayleigh Criterion [11] [12] . That is, the spectral line s1 and s2 with equal intensity can be distinguished, when is equal to the full width at half maximum (FWHM) of the spectral line (s1 or s2). On the other hand, the spectral resolution will be degraded by the aberration, and the s1 and s2 cannot be identified as distinct spectral line again, as depicted in the Figure 2.

In order to directly measure the relative spectral resolution degradation, the is given by

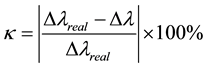(4)

where the is the real spectral resolution influenced by the aberration, and 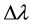is the spectral resolution without the influence of the aberration. The 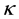represents the variable of the 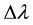caused by the aberration.

For the point source, the energy utilization is given by

(5)

where the φ is the wavefront aberration, the and are the point spread function

with and without the influence of the aberration, respectively.

The observed spectral line [11] is given by

(6)

where the O(λ) is the observed spectral line, I(λ) is the real spectral line, the PSF(λ) denotes the modulation of the system, and the denotes the convolution operator.

Unlike the general optical system, the slit of the grating spectrometer will filter the wavefront aberration to some extent. According to the optics theory, the point spread function after the filter slit is given by

(7)

where the and are the slit width and length, respectively; The is the modulation of the solar telescope and the atmospheric turbulence, given by

where the FFT{●} denotes the Fourier transform operator, the is the wavefront aberration of the solar telescope and the atmospheric turbulence, the is the wavefront aberration of the optical system of the grating spectrometer. The and is given by

It can be inferred from the Equation (7) that the slit will filter the wavefront aberration due to the diffraction of the slit, and the high frequencies of the wavefront aberration will be blocked by the slit.

The point spread function at the focal plane of the grating spectrometer is given by

(8)

where the is the modulation of the grating spectrometer, given by

Supposing the dispersion direction is along the x-axis, according to the linear dispersion definition [12] , the relation between the spatial coordinate x and the spectral coordinate λ is given by

(9)

where the β is the diffraction angle of the grating.

And the is given by

(10)

Substituting the Equation (10) into the Equation (6), the observed spectral line is given by

(11)

Supposing the value P is the maximum value of the observed spectral line, and the spectral resolution influenced by the wavefront aberration can be obtained by solving the equation O(λ) = 0.5P. Assuming the λ₊ and λ₋ are the real solutions, and λ₊ > λ₋, hence the real spectral resolution influenced by the wavefront aberration is given by

(12)

And the relative spectral resolution K can be expressed as follows:

(13)

3. Numerical Simulation and Experiment Validation

3.1. System Description

The AO system is integrated in the solar grating spectrometer, and it consists of a Hartmann Shack Wavefront sensor (HS WFS) and an electrically addressed phase-only liquid-crystal spatial light modulator (LC SLM), as depicted in the Figure 3. The polarized HeNe laser with 632.8 nm wavelength is used as the light source for all the experiments, its FWHM is 1 pm. Our goal is to demonstrate the influence of the wavefront aberration on the spectral resolution, hence the experiment conclusions are also validated for the broad solar spectrum.

The RMS value of the initial wavefront aberration of the optical elements is 0.15λ, detected by the HS WFS with 28 × 28 sub-apertures. After the AO correction, the RMS value of the residual wavefront aberration is roughly 0.025λ, and a nearly diffration-limited focal spot is attained, the result of the experiment is as depicted in the Figure 4.

In the following experiments, an original wavefront aberration will firstly be generated by the LC SLM and will exist throughout the whole correction procedure. The generated aberration will be detected by the HS WFS. Based on the reconstructed wavefront generalized by the HS WFS, the control computer calculates the conjugated wavefront at each position with the response matrix, and it is applied to control the corresponding pixel of the LC SLM and then the aberrated wavefront is corrected. In the experiment, the tiny slit widths we used are 50 μm and 100 μm, respectively, which are roughly equal to one airy disk diameter of the optical system and two airy disk diameter, respectively, where f is the focal length of L1, is the wavelength, D is the input aperture diameter.

3.2. The Influence of the Filter Slit on the Wavefront Aberration

To demonstrate the influence of the filter slit on the wavefront aberration with different types and magnitudes,

the experiment validation is performed. The wavefront aberrations described by the Zernike polynomials with order number from 3^rd to 15^th. After the initial aberration of the optical system is corrected by the AO, and a new wavefront aberration is superimposed in the initial wavefront aberration. The RMS values of the wavefront aberrations are 0.1λ, 0.2λ and 0.3λ, which is generalized by the LC SLM. Zernike tip and tilt terms have been eliminated. To directly demonstrate the influence of the filter slit, is given by

(14)

where, the RMS and RMS_s represent the RMS value before and after the filter slit, respectively. The bigger the is, the stronger the influence of filter slit on the wavefront aberration is. The experimental results are illustrated in Figure 5.

We demonstrate that: when the same slit is used, the influence of the filter slit on the different order Zernike aberration is different. The bigger the magnitude of the Zernike aberration is, the stronger the influence of the filter slit on the wavefront aberration is. On the other hand, to the same Zernike aberration, the smaller the slit is, the stronger the influence of the filter slit on the wavefront aberration is. Generally, when the wavefront aberration less than 0.3λ, the is attained after the filter slit. It is apparent that the wavefront aberration needed to be corrected becomes smaller after the filter slit, hence the filter slit can lower the requirement of the AO correction.

3.3. Single Zernike Order Aberration Correction

To investigate the influence of the Adaptive Optics on the κ and η, a series of closed-loop corrections of aberrated wavefronts described by Zernike polynomials with order number from 3^rd to 15^th are carried out. Since the residual wavefront aberration of the optical system roughly is 0.025λ after the AO correction, then a new wavefront aberration is superimposed into the corrected wavefront aberration. The RMS value of the wavefront aberration is 0.2λ, which is generalized by the LC SLM. Zernike tip and tilt terms are eliminated. Close-loop correction example for the 9^th order Zernike aberrations is illustrated in the Figure 6. Apparently, a nearly diffraction focal spot is obtained after the AO correction. The influence of the AO correction on the κ and η is depicted in the Figure 7. The results show an effective wavefront correction, the κ is less than 2%, and η is better than 95%.

3.4. Kolmogorov Phase Screen Correction

The validation experiments of the influence of AO correction on the κ and η are performed. The atmospheric phase screen is consistent with Kolmogorov’s theory. The phase screen consists of 3^rd to 15^th Zernike orders, and the D/ro = 5, D/ro = 7 and D/ro = 10 are used, where the D is the input aperture diameter, and ro is the Fried parameter. Close-loop correction examples for the D/ro = 5 is illustrated in the Figure 8. The influence of the AO correction on the κ and η is illustrated in the Figure 9. The numerical simulation and experiment results show that an effective wavefront correction is obtained. The influence of the wavefront aberration generalized by the atmospheric turbulence on the κ and η can be neglected after the AO correction. The κ is less than 2%, and the energy utilization η is considerably improved, better than 95%.

4. Conclusions

The solar grating spectrometer with high spectral resolution is an important tool to study the characteristics of the solar atmosphere. Otherwise, the energy utilization is import to the signal-to-noise and temperal resolution. However, the spectral resolution and energy utilization will be influenced by the wavefront aberration. Unlike the general optics system, the slit of the grating spectrometer is narrow enough, and it will filter the wavefornt aberration to a certain extent. Hence, when the AO system is applied to compensate the wavefront aberration, the influence of the filter slit on the wavefront aberration should be considered.

In this paper, the influence of the filter slit on the wavefront aberration is analyzed theoretically and experimentally. The results show that the RMS value of the aberration less than 0.3λ is down to below almost 60% after the filter slit. It is apparent that the wavefront aberration needed to be corrected becomes smaller after the filter slit. Besides, the closed-loop of the AO corrections is conducted. We demonstrate that diffraction-limited focal spot is attained. The influence of the residual wavefront aberration on the spectral resolution is neglected,

and the energy utilization is considerably improved.

Acknowledgements

This work was funded by the Joint Funds of the National Natural Science Foundation of China under No. 11178004.

Cite this paper

LianhuiZheng,ChanghuiRao,NaitingGu,QiQiu, (2015) The Influence of Filter Slit on the Imaging Performance of the Solar Grating Spectrometer Based on Adaptive Optics. Optics and Photonics Journal,05,303-311. doi: 10.4236/opj.2015.510028

References