Optics and Photonics Journal
Vol.05 No.03(2015), Article ID:54857,11 pages
10.4236/opj.2015.53007
Self-Absorption Effects on Electron Temperature-Measurements Utilizing Laser Induced Breakdown Spectroscopy (LIBS)-Techniques
Shawqi A. M. Mansour
Ministry of Education and Higher Education, Accreditation and Quality Authority, Gaza, Palestine
Email: dr_shmansour@yahoo.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 March 2015; accepted 19 March 2015; published 20 March 2015
ABSTRACT
In the present work, we have studied the temporal evolution of aluminum alloy plasma produced by the fundamental (1064 nm) of a Q-switched Nd:YAG laser by placing the target material in air at atmospheric pressure. The four Al I-neutral lines at 308.21, 309.27, 394.40 and 369.15 nm as well as Al II-ionic lines at 281.61, 385.64 and 466.30 nm are used for the determination of the electron temperature Te using Saha-Boltzmann plot method. The neutral aluminum lines were found to suffer from optical thickness which manifested itself on the form of scattered points around the Saha-Boltzmann line. The isolated optically thin hydrogen Hα-line at 656.27 nm appeared in the spectra under the same experimental conditions was used to correct the Al I-lines which contained some optical thickness. The measurements were repeated at different delay times ranging from 1 to 5 µs. The comparison between the deduced electron temperatures from aluminum neutral lines before correction against the effect self-absorption to that after correction revealed a precise value in temperature. The results sure that, in case of the presence of self-absorption effect the temperature varies from (1.4067 - 1.2548 eV) as the delay time is varied from 0 to 5 µs. Whereas, in the case of repairing against the effect, it varies from (1.2826 - 0.8961 eV) for the same delay time variation.
Keywords:
Laser Induces Breakdown Spectroscopy (LIBS), Self-Absorption (SA), Saha-Boltzmann Plot, Delay Time (Td), Electron Number Density (Ne), Plasma Temperature (Te)

1. Introduction
The laser induced breakdown spectroscopy (LIBS) is a useful technique for elemental analysis of the materials in the form of solids, liquids and gases. It has a variety of applications like material analysis, environmental monitoring, determination of soil contamination, and biomedical studies, etc. [1] -[3] . It employs a low-energy pulsed laser and a focusing lens to generate plasma on the surface of a target. The spectrum of the plasma plume is the signature of the chemical species in the sample, and its analysis yields their composition and relative abundance. It depends on several parameters, including target features (physical and chemical), ambient medium properties (plus-width), wavelength, spot size, and laser energy [4] [5] . In general, aluminum metal is the most coast-effective and widely used in various industries. It is the third most common element after oxygen and alloyed with other material, usually iron, silicon, zinc and magnesium, to create metals with different properties. Due to its importance and wide utility, aluminum has become the material of choice for a diverse range of applications and remained a subject of interest for many researchers [6] -[12] . Recently, Sun and Yu [13] proposed a simplified procedure for correcting self-absorption effect by laser-ablated aluminum target in air. El Sherbini et al. [14] utilized the diode laser atomic absorption spectroscopy (DLAAS) technique to assess the degree of optical opacity of plasmas at the wavelength of the Hα-line by focusing a 6 ns Nd:YAG laser pulse at 1064 nm on different solid targets material including aluminum target.
In this paper, we report the spectroscopic studies of the plasma generated at the surface of alumina (Al) by the fundamental (1064 nm) of a Q-switched Nd:YAG laser. We have studied the transitions at 256.87, 257.59, 265.32, 266.12, and 394.51 nm, and the resonance line at 396.26 nm of neutral aluminum. These transitions have been used to study the temporal behavior by estimating the plasma temperature Te and the electron number density Ne.
2. Experimental Setup
The experimental setup is shown in Figure 1. Briefly we used a Q-Switched Nd:YAG (Quintal, model Brilliant B) pulsed laser having a pulse duration of 6ns and a 10-Hz repetition rate which capable of delivering 600 mJ at 1064 nm. An absolutely calibrated power-meter (Ophier, model 1z02165) was used in measuring the fraction of the laser light reflected from a quartz beam splitter to monitor the incident laser energy. The laser beam was focused on the target (certified aluminum based alloy with traces of Mg 1.16%) using a convex lens with a 10cm focal length. The target was mounted on a 3-D sample stage, which was rotated to avoid the non-uniform pitting of the target. The distance between the focusing lens and the sample was kept less than the focal length of the lens to prevent any breakdown of the ambient air in the front of the target. The spectra were obtained by aver- aging three data of single shot under identical experimental conditions. The radiation emitted by the plasma was
Figure 1. Schematic diagram of the experimental set up.
collected by a quarts fiber optics (25 µm diameter) positioned at a distance of 12.5 mm and normal to the direction of the laser beam. The optical fiber was connected with Echelle type spectrograph (type catalina, model SE 200) with resolving power of 2400 and equipped with a time gated ICCD Camera (1064 × 1064 pix with 13 µm × 13 µm pixel size at a binning mode of 1 × 1 (type Andor, model iStar DH 737-18F). The wavelength scale was calibrated using a low pressure Hg-lamp (type Ocean optics). The instrumental bandwidth was measured from the FWHM of the Hg lines and was found to be 0.12 ± 0.02 nm. The experimental setup was absolutely calibrated using a deuterium tungsten halogen lamp (type Ocean optics, model DH 2000 Cal.). The gain of the camera was kept at constant level of 200. The gate time was adjusted at a gate time of 2 µs while we have scanned the different delay times from 1 to 5 µs to measure the temporal variation of the plasma parameters at different delay times after the laser pulse.
3. Results and Discussions
3.1. Emission Studies
In the first set of this experimental work, we have recorded the plasma emission generated by the fundamental (1064 nm) of a Nd:YAG laser. The laser was focused by a quarts lens with a focal length of 10 cm. Aluminum plasma was recorded at different delay times ranging from 1 to 5 µs along the direction of the propagation of the plasma. Figure 2 represents the window of emission spectrum of aluminum plasma covering the spectrum region from 200 to 400 nm which consists of the neutral aluminum spectral lines that we used for the determination of the electron temperature, while the small window in the same diagram shows the whole spectrum. The ionic aluminum emission spectral lines at 281.61, 358.64, 466.30 nm and the neutral lines at 308.21, 309.27, 394.40, 396.15 nm were selected for the determination of electron number density (Ne) and the electron temperature (Te) respectively, and are listed with related details [15] in Table 1. A couple of lines belonging to magnesium lines (Mg II, I) at 285.21, 279.54 and 280.26 nm respectively have also been detected in the emission spectra. We can observed clearly that the lines spectra are superimposed on a large continuum component. This continuum is mainly results from free-free (Bremsstrahuling process) and the free-bound transitions. This continuum should be removed before proceeding in the spectral line shape analysis.
3.2. Determination of the Electron Density
During the evaluation of laser induced plasma (LIP), excitation and ionization of the evaporated material occur. It is important to determine the thermodynamic parameters of LIP such as the electron number density and the
Figure 2. The emission spectrum of neutral aluminum plasma produced by 1064 nm wavelength of the Nd:YAG laser target whereas, the small window represents the whole spectra including the Hα-line at the wavelength 656.27 nm.
Table 1. Spectroscopic parameters of the spectral lines used for estimating electron temperature.
electron temperature. One of the most reliable techniques to determine the electron number density is from the measured Stark broadened line profile of an isolated line of either neutral atom or single charge ion. The electron number density (Ne), related to the full width at half of maximum (FWHM) of the Stark broadening lines given by the following relation [16] :
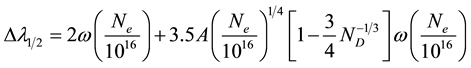 (1)
(1)
where,  is the electron impact width parameter, A is the ion broadening parameter, Ne is the electron number density and ND is the number of particles in the Debye sphere. The first term in Equation (1) refers to the broadening due to the electron contribution while, the second term is attributed to the ion broadening. Since the contribution of the ionic broadening is normally very small, therefore, it can be neglected. The electron number densities have been determined from the line profiles of the isolated aluminum neutral lines using Equation (1) by neglecting the contribution of the ion impact broadening and Doppler broadening to become in a new Equation:
is the electron impact width parameter, A is the ion broadening parameter, Ne is the electron number density and ND is the number of particles in the Debye sphere. The first term in Equation (1) refers to the broadening due to the electron contribution while, the second term is attributed to the ion broadening. Since the contribution of the ionic broadening is normally very small, therefore, it can be neglected. The electron number densities have been determined from the line profiles of the isolated aluminum neutral lines using Equation (1) by neglecting the contribution of the ion impact broadening and Doppler broadening to become in a new Equation:
 (2)
(2)
where, Δλ is the Lorentzian FWHM of the line, and is the Stark broadening parameter, which can be found in [17] , Nr is the reference electron density which equal to 1016 (cm−3) for neutral atoms and 1017 (cm−3) for singly charged ions [18] [19] .
In the special case of the hydrogen Hα-line, the electron density can be related to the Lorentzian half width at the half of the maximum Δλ1/2 through the relation [20] :
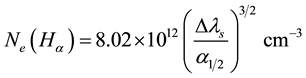 (3)
(3)
where, Δλs is the intrinsic full width at half of maximum (FWHM) of the spectral line in Angstrom, and α1/2 is the half width of the reduced Stark profiles in Angstrom. Precise values of α1/2 for the Balmer series can be found in [17] . However, when the laser beam is focused on the target, the ablation of the target takes place, and due to the density gradient, the plasma rapidly expands. Figure 3 shows the results of the best fitting to the different spectral lines at an arbitrary delay times of 1, 3, 5 µs and at a fixed gate time of 2 µs. The full width half maximum (FWHM) of the spectra are used to estimate the electron number density. The temporal behavior of the electron number density in the plume is determined using Equation (2) for Al II, I lines and Equation (3) for hydrogen line at the wavelength 656.27 nm. It is evident that, the deviation of the measured electron density calculated from the aluminum resonance lines with respect to that estimated from the optically thin Hα-line indicates the existence of self-absorption while, the aluminum ionic lines exhibits a good agreement with Hα-line reminiscent of free from self-absorption as shown in Figure 4 and Figure 5 respectively.
3.3. Determination of Self-Absorption Coefficients
The process of re-absorption of the plasma to the light photons in their path to outside the plasma active volume
Td = 1 µs Td = 2 µs Td = 3 µs
Figure 3. Represents examples of the Voigt fitting to different arbitrary spectral lines at 656.27 nm (Hα-line), 281.61 nm (Al II), 308.21 nm (Al I), and the Al I at 394.40 nm at three different delay times of 1, 3, 5 µs, respectively.
is called the self-absorption. It is well known that this process affecting the spectral line shape i.e. the line intensity decreases and its full width at half maximum (FWHM) increases [21] -[24] . El Sherbini et al. [25] have been developed a new method in order to quantify the effect of self-absorption to the emitted lines in terms of what is known as the coefficient of self-absorption, depending on the suggestion of Kunze [26] in the definition of the coefficient of self-absorption that given by the expression:

where, k(λo)l is the optical depth of the plasma at the line center. Similarly, they suggested that the same amount (SA) can be expressed on the form of relative spectral line widths of Lorentzian components of the same line in a two different situations of self-absorbed line given by [25] :
Figure 4. Represents the temporal variation of the measured electron density using the Hα-line (Black solid squares) and the Al I lines at 308.21 nm, (red solid diamond), 309.27 nm, (blue solid triangles), 394.40 nm (magenta solid circle), and 396.15 nm (cyan solid pentagram).
Figure 5. Represents the temporal variation of the measured electron density using the Hα-line (Black solid squares) and the Al II lines at 281.61 nm, (red solid right triangle), 309.27 nm, (blue solid triangles), 394.40 nm (green solid diamond).

where, α = 0.56, Δλo is the intrinsic FWHM of the Lorentzian component of the spectral line if the line is optically thin and Δλ is the distorted Lorentizian of the same line which resulted from the effect of the self-absorp- tion. The Equation (5) can be modified to expressed in terms of the ratio of two electron density values as [25] :

where, ne (line) is the electron density of the line which suffering from self-absorption effect and ne(Hα) is the electron density of Hα-line free from self-absorption. Hence, we utilized Equation (6) in order to calculate the amount of absorption (SA), and then used Equation (4) to get the corrected value of the spectral line intensity Io(λo). The self-absorption coefficients were calculated using Equation (6) to the four resonance aluminum lines (Al I) at 308.21, 309.27, 394.40 and 396.15 nm. Figure 6 shows algorithmic decreases in the SA values, indicating an increase of the optical depth of the lines with delay time. This means that as the plasma became cooler with the delay time (as a result of expansion) the population of the atoms in the lower state becomes higher and hence the more the absorption.
3.4. Determination of the Electron Temperature
The excitation temperature (T) of a given species is in general retrieved using the well known Boltzmann plot method [27] . Assuming the LTE is established within the plasma, the population in different levels governed by the Boltzmann distribution. The line intensity Iji (of a transition from an upper level j to a lower level i) is thus related to the energy of the upper level Ej by the relation:

where, λ is the wavelength of the transition, Aji and gj are the transition probability and the statistical weight of the upper level, k and h are the Boltzmann and Plank constants, c is the velocity of the light, N and U(T) are the number density and the partition function of the considered species, respectively. This relation leads to a linear plot against Ej if several transitions of the same species are considered. The temperature of this species can thus be deduced from the slope of such a plot. In order to increase the accuracy of the calculation, the range of Ej should be as large as possible. For this reason, a more precise method consists of representing the emissions from the different ionized states of the same element in the same plot. This method, called the Saha-Boltzmann plot allows a significant extension of the range of Ej and therefore an increase in the accuracy of the temperature determination [28] . The validation of this method implies however that the species of different ionization degrees of a given element are in thermodynamic equilibrium with the same temperature. In this way, the Boltz- mann and Saha equations are supposed to be verified with a single temperature. We get in this case an expression similar to case of the Boltzmann plot [27] :
Figure 6. A demonstration to the variation of the coefficients of self- absorption for the Al I lines at 308.21 nm, (red solid diamond), 309.27 nm, (blue solid triangles), 394.40 nm (magenta solid circle), and 396.15 nm (cyan solid pentagram).

where the superscript z represents the type of species (z = 0 for neutral atom, z = 1 for single ionized specie, etc). This relation is similar to Equation (7) as mentioned. However for ionized species (z ≥ 1) the quantities marked with the superscript * must be replaced by the following expressions (only z = 1 is considered in our work for simplicity):


Obviously for z = 0, Equation (8) become identical to Equation (7). In Equation (9), m refers to the mass of electron. In Equation (10), Eion and 
3.5. Validity of the Local Thermodynamic Equilibrium (LTE)
The use of the emission spectroscopy for the determination of the plasma temperature and the electron number density requires optically thin plasma spectral lines. The self-absorption depends on the oscillator strength, level energies degeneracy, broadening parameters and also on the plasma parameters. The condition that the atomic states should be populated and depopulated predominantly by electron collisions, rather than by radiation, requires an electron density which is sufficient to ensure the high collision rate. The corresponding lower limit of the electron density is given by McWhirter criterion, which is the necessary (but not sufficient condition) for attaining the minimum number density to check the validity of LTE [29] :

where, ΔEji is the largest energy transition for which the condition holds and Te is the plasma temperature in electron volts [30] . At T ~12421 K, Equation (11) yields:
Before correction against (SA) After correction against (SA)
Figure 7. Saha-Boltzmann plot for the neutral aluminum lines at 308.21 nm, (red solid diamond), 309.27 nm, (blue solid triangles), 394.40 nm (magenta solid circle), and 396.15 nm (cyan solid pentagram) as well as ionized lines (Black solid square) emitted by the laser induced plasma from the target at a delay times ranging from 1 to 5 µs (from top to bottom) respectively, and a gate time of 2 µs before and after the correction against self-absorption.
Figure 8. Variation of the electron temperature with delay time utilizing Saha-Boltzmann (black solid circle-before correction) and (red solid square-after the correction against self-absorption effect).
4. Conclusion
The LIBS method has been successfully applied as an analytical technique for the analysis of aluminum plasma using the fundamental (1064 nm) Nd:YAG laser. The optical emission spectrum of the aluminum plasma reveals transitions of neutral and singly ionized spectral lines. The effects of the self-absorption on Al lines at 308.21, 309.27, 394.40 and 396.15 nm were quantified utilizing simple formulas based on the measurement of the ratio of the apparent electron density from the lines of interest to that derived from the optically thin Hα-line. The spectral line intensities were then corrected. In the comparative study of the effect self-absorption, we have observed enhanced temperatures in the case of correction against self-absorption as compare to that before correction. The results show that the atomic aluminum lines (Al I) appeared in LIBS spectrum are good candidate for measuring the temperature of the plasma in LIBS experiments, especially after correction against self-absorption effect.
Acknowledgements
The author is thankful to laboratory of lasers and new materials (LINM) in Cairo University in Egypt for the encouragement in terms of provision of time and moral support to carryout research work. Beside, express his gratitude to the valuable discussions with Prof. Th. M. El Sherbini, Prof. S. H. Allam and Dr. A. M. El Sherbini.
References
- Cardi, F., Torrisi, L. and Giuffrid, L. (2010) Comparison of pd Plasma Produced at 532nm and 1064nm by a Nd:YAG Laser Ablation. Nuclear Instruments and Methods in Physics Research Section B, 268, 499-505.
- Samad, R.E., Vidal, J.T., de Rossi, W. and Vieira, N.D. (2010) Determination of Molybdenum Ablation Threshold for Ultra Short Pulses in Atmosphere and Vacuum Using the Diagonal Scan Technique. Optical Society of America (OSA)/Latin America Optics and Photonics (LAOP) Conference, Recife, 27-30 September 2010, 1-3.
- Aryal, K., Hatri, H., Collins, R.W. and Marsillac, S. (2012) In Situ and Ex Situ Studies of Molybdenum Thin Films Deposited by RF and DC Magnetron Sputtering as a Back Contact for CIGS Solar Cells. International Journal of Photo Energy, 2012, Article ID: 723714.
- Russo, R.E., Mao, X.L., Liu, H.C., Yoo, J.H. and Mao, S.S. (1999) Time-Resolved Plasma Diagnostics and Mass Removal Durin Single-Pulse Laser Ablation. Applied Physics A, 69, S887-S894. http://dx.doi.org/10.1007/s003390051553
- Chang, J.J. and Warmer, B.E. (1996) Laser-Plasma Interiaction during Visible-Laser Ablation of Metals. Applied Physics Letter, 69, 473-475. http://dx.doi.org/10.1063/1.118144
- Lu, Y., Tao, Z. and Hong, M. (1999) Characteristics of Excimer Laser Induced Plasma from an Aluminum Target. Japanese Journal of Applied Physics, 38, 2958-2963. http://dx.doi.org/10.1143/JJAP.38.2958
- Colon, C., Hatem, G., Verdugo, E., Ruiz, P. and Campos, J. (1993) Measurement of the Stark Broadening and Shift Parameters for Several Ultraviolet Lines of Singly Ionized Aluminum. Journal of Applied Physics, 73, 4752-4758. http://dx.doi.org/10.1063/1.353839
- Body, D. and Chadwick, B.L. (2001) Optimization of the Spectral Data Processing in a LIBS. Review Scientific Instruments, 72, 1625-1629. http://dx.doi.org/10.1063/1.1338486
- Kim, D.E., Yoo, K.J., Park, H.K., Oh, K.J. and Kim, D.W. (1997) Quantitative Analysis of Aluminum Impurities in Zinc Alloy. Applied Spectroscopy, 51, 22-29. http://dx.doi.org/10.1366/0003702971938920
- Handoko, A.D., Lee, P.S., Lee, P., Mohanty, S.R. and Rawat, R.S. (2006) Time Resolved Emission Spectroscopy. Journal of Physics: Conference Series, 28, 100-104.
- Ying, M., Xia, Y., Sun, Y., Zaho, M., Ma, Y., Liu, X., Li, Y. and Hou, X. (2003) Plasma Properties of a Laser-Ablated Aluminum Target in Air. Laser and Particle Beams, 21, 97-101. http://dx.doi.org/10.1017/S0263034603211186
- De Giacomo, A., Dell’Aglio, M., Gaudiuso, R., Cristoforetti, G., Legnaioli, S., Palleschi, V. and Tognoni, E. (2008) Spatial Distribution of Hydrogen and Other Emitters in Aluminum Laser-Induced Plasma in Air and Consequences on Spatially Integrated Laser-Induced Breakdown Spectroscopy Measurements. Spectrochimica Acta Part B, 63, 980-987. http://dx.doi.org/10.1016/j.sab.2008.06.010
- Sun, L. and Yu, H. (2002) Correction of Self-Absorption Effect in Calibration-Free Laser Induced Breakdown Spectroscopy by Induced Reference Method. Talanta, 79, 388-395. http://dx.doi.org/10.1016/j.talanta.2009.03.066
- El Sherbini, A.M., Aboulfotouh, A.M., Allam, S.H. and El Sherbini, Th.M. (2010) Diode Laser Absorption Measurements at the Hα-Transition in Laser Induced Plasmas on Different Targets. Spectrochimica Acta Part B, 65, 1041-1046. http://dx.doi.org/10.1016/j.sab.2010.11.004
- NIST, Handbook of Basic Atomic Spectroscopic Data. Kurucz Output Atomic Spectral Lines Data Base from Kuruz’s RL. CD-ROM 28, Gaithersburg.
- Griem, H.R. (1997) Principles of Plasma Spectroscopy. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511524578
- Kepple, P. and Griem, H.R. (1968) Improved Stark Profile Calculations for Hydrogen Lines: Hα, Hβ, Hγ and Hδ. Physical Review, 173, 317-325. http://dx.doi.org/10.1103/PhysRev.173.317
- Konjevic, N., Lesage, A., Fuhr, J.R. and Wiese, W.L. (2002) Experimental Stark Width and Shifts for Spectral Lines of Neutral and Ionized Atoms (A Critical Review of Selected Data for the Period 1989 through 2000). Journal of Physical and Chemical Reference Data, 31, 819. http://dx.doi.org/10.1063/1.1486456
- Konjevic, N. (2003) Plasma Broadening and Shifting of Non-Hydrogenic Spectral Lines: Present Status and Applications. Physics Reports, 316, 339-401. http://dx.doi.org/10.1016/S0370-1573(98)00132-X
- Griem, H.R. (1964) Spectral Line Broadening by Plasmas. Academic Press, New York.
- Bulajic, D., Corsi, M., Cristoforetti, G., Legnaioli, S., Palleschi, V., Salvetti, A. and Tognoni, E. (2002) A Procedure for Correcting Self-Absorption in Calibration Free-Laser Induced Breakdown Spectroscopy. Spectrochimica Acta Part B, 57, 339-353. http://dx.doi.org/10.1016/S0584-8547(01)00398-6
- Amamoua, H., Pois, A., Ferhat, B., Redon, R., Rossetto, B. and Matheron, P. (2002) Correction of Self-Absorption Spectral Line and Ratios of Transition Probabilities for Homogenous and LTE Plasma. Journal of Quantitative Spectroscopy and Radiative Transfer, 75, 747-763. http://dx.doi.org/10.1016/S0022-4073(02)00040-7
- Amamoua, H., Boisa, A., Ferhatb, B., Redona, R., Rossettoa, B. and Riperta, M. (2003) Correction of the Self-Absorption for Reversed Spectral Lines: Application to Two Resonance Lines of Neutral Aluminum. Journal of Quantitative Spectroscopy and Radiative Transfer, 77, 365-372. http://dx.doi.org/10.1016/S0022-4073(02)00163-2
- Bredice, F., Borges, F.O., Sobra, H., Villagran-Munze, M., Di Rocco, H.O., Cristoforetti, G., Legnaioli, S., Palleschi, V., Pardini, L., Salvetti, A. and Tognoni, E. (2006) Evaluation of Self-Absorption of Manganese Emission Lines in Laser Induced Breakdown Spectroscopy Measurements. Spectrochimica Acta Part B, 61, 1294-1303. http://dx.doi.org/10.1016/j.sab.2006.10.015
- EL Sherbini, A.M., EL Sherbini, Th.M., Hegazy, H., Cristoforetti, G., Legnaiol, S., Palleschi, V., Pardini, L., Salvetti, A. and Tognoni, E. (2005) Evaluation of Self-Absorption Coefficients of Aluminum Emissions Lines in Laser-Induced Breakdown Spectroscopy (LIBS)-Measurements. Spectrochimica Acta Part B, 60, 1573-1579.
- Kunze, H.J. (2009) Introduction to Plasma Spectroscopy. Springer Series on Atomic, Optical and Plasma Physics, Vol. 56, Springer, New York.
- Aragon, C. and Aguilera, J.A. (2008) Characterization of Laser Induced Plasma by Optical Emission Spectroscopy: A Review of Experiments and Methods. Spectrochimica Acta Part B, 63, 893-916. http://dx.doi.org/10.1016/j.sab.2008.05.010
- Yalcin, S., Crosley, D.R., Smith, G.P. and Faris, G.W. (1999) Influence of Ambient Conditions on the Laser Air Spark. Applied Physics B: Laser and Optics, 68, 121-130. http://dx.doi.org/10.1007/s003400050596
- McWhirter, R.W.P. (1965) In: Huddleston, R.H. and Leonard, S.L., Eds., Plasma Diagnostics Techniques, Chap. 5, Academic Press, New York, 206.
- Samek, O., Beddows, D.C.S., Kaiser, J., Kukhlevsky, S.V., Liska, M., Telle, H.H. and Young, J. (2000) Application of Laser-Induced Breakdown Spectroscopy to in Situ Analysis of Liquid Samples. Optical Engineering, 56, 865-875.






























