Optics and Photonics Journal
Vol.05 No.01(2015), Article ID:53138,8 pages
10.4236/opj.2015.51002
Encrypted Sensing Based on Digital Holography for Fingerprint Images
Masafumi Takeda1*, Kazuya Nakano2, Hiroyuki Suzuki3, Masahiro Yamaguchi4
1Graduate School of Science & Engineering, Tokyo Institute of Technology, 4259 Nagatsuta-cho, Midori-ku, Yokohama, Japan
2Nippon Sport Science University, 1221-1 Kamoshida-cho, Aoba-ku, Yokohama, Japan
3Imaging Science & Engineering Laboratory, Tokyo Institute of Technology, 4259 Nagatsuta-cho, Midori-ku, Yokohama, Japan
4Global Scientific Information and Computing Center, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo, Japan
Email: *takeda.m.ad@hotmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 November 2014; accepted 5 December 2014; published 13 January 2015
ABSTRACT
We propose a novel biometric sensing technique for personal authentication in which fingerprint images are captured using an optical encryption method. This method can reduce the risk of data theft or leakage of personal information captured by biometric sensing. This method, termed en- crypted sensing, is implemented using digital holography with double random phase encoding. We demonstrate experimentally that a fingerprint image can be captured as an optically encrypted image and can be restored correctly only when the correct cipher key is used. Moreover, we investigate experimentally the verification accuracy of the decrypted images.
Keywords:
Biometric Authentication, Digital Holography, Double Random Phase Encoding, Fingerprinting

1. Introduction
Recently, there has been a rise in the use of biometric authentication systems in a wide variety of secure interfaces, including computer logins, banking systems, automated teller machines, and building entrance management. Because biometric information represents important personal data, and because enrolled biometric information, unlike most personal authentication information such as passwords, cannot be altered, it is necessary to take great care to prevent leakage of these data. Correspondingly, template protection techniques for biometric authentication have been actively pursued through the development of cryptographic algorithms that protect raw biometric information obtained using a sensor while preserving high verification accuracy [1] -[4] . However, particular threats, such as side-channel attacks [5] occurring while raw biometric information is being transformed into a protected template, are becoming increasingly realistic. It is believed that threats such as these can be avoided by encrypting biometric images prior to image sensing, i.e., optical en- cryption.
Optical encryption techniques apply optical calculation methods such as optical wave propagation oroptical phase modulation for image encryption and decryption. These techniques are advantageous not only for rapid calculations using parallel processing, but also security enhancement due to non-electronic computation methods, because there is less risk of optical information being read, as opposed to digital data in electronic devices, which are inevitably exposed to a number of security risks. Double random phase encoding (DRPE) [6] is a well-known optical encryption method that has been studied extensively for two decades. DRPE is an optical symmetric-key encryption technique in which an optical image is encrypted by multiplying two random phase masks in the spatial and Fourier or Fresnel planes. To obtain an optically-encrypted image, digital holography (DH) [7] -[10] is commonly employed. DH makes it possible to not only capture an optical wavefront as holo- graphic data, but also to reconstruct various styles of optical wavefront computationally from the holographic data. DRPE has been implemented using DH [7] [11] , whereby the random phase masks are typically inserted into the object beam path. Suchan optical system requires precise alignment; however, it is challenging to reconstruct the object image with high quality from the DH. Tajahuerce and Javidi proposed an optical encryption system for three-dimensional (3D) objects [12] , whereby an encrypted image was obtained with simple alignment because only the reference beam was modulated using a random phase mask, and a non-modulated wave was used as the object beam. This optical arrangement could be implemented easily and can restore a clear object image from a DH. However, the encrypted image was not equivalent to DRPE because the object beam was not modulated by a random phase mask, which might decrease the security level of encryption. To obtain a fingerprint image for biometric authentication, both sufficient security to prevent data leakage and sufficient image quality for highly accurate recognition are required. Therefore, we propose an optical security system that is suitable for obtaining fingerprint images as optically encrypted holographic data. We term this system “encrypted sensing”. In addition, we also propose an image reconstruction method through which we can obtain a clear fingerprint image from the encrypted hologram. To obtain the reconstructed image with high quality, we apply speckle reduction using multiple holograms, as well as reconstruction using a phase only mask, rather than a complex amplitude mask. We demonstrate that improved recognition accuracy is obtained by applying only a phase-only mask and speckle reduction.
The remainder of the paper is organized as follows. In the following section, a theoretical description of the proposed sensing system is given. In Section 3, experiments for obtaining encrypted fingerprint images are de- scribed, together with an investigation of the quality of the decrypted fingerprint images. Conclusions are drawn in Section 4.
2. Method
2.1. User Authentication Scheme
Figure 1 shows a schematic diagram that illustrates the concept of biometric encrypted sensing proposed here. During enrollment, biometric information (i.e., a fingerprint pattern) is encrypted using the optical system within the biometric sensor, and the encrypted information is transmitted to the verification system for user authentica- tion. This encrypted biometric information is then decrypted using a corresponding decryption key and the bio- metric information is stored in the biometric template database. During verification, encrypted biometric infor- mation is also captured, and it is then sent to the verification system. Subsequently, it is also decrypted in the ve- rification system, and the biometric information and the enrolled data are verified by calculating their similarity. If both the biometric image and the encryption key are provided correctly, the user is authorized. This system makes it possible to perform two-factor authentication that will authorize users only when both biometric and the secret data are verified. The verification system, which is assumed to be a securely protected using, for ex- ample, a tamper-resistant device can be located in either a centralized server or a user device. Throughout this overall process, raw biometric information in digital form exists only in the protected verification system, and the risk of theft or leakage of biometric data is thus significantly reduced.
2.2. Encrypted Sensing Based on DRPE
In our system, optical encryption is performed via a combination of DH and DRPE. With DH, a wavefront encoding the optical information from an object wave is typically captured via interference with a reference plane wave, as shown in Figure 2. In ref. [12] , random phase-modulated light was used as the reference wave, which is used as an encryption key. In our system, both the object wave and the reference wave are modulated using diffusers, as shown in Figure 3. To capture fingerprints stably, we place a total reflection prism in the middle of the object wavepath. The resulting DH is captured using a charged coupled device (CCD) image sensor, and can be expressed as follows:
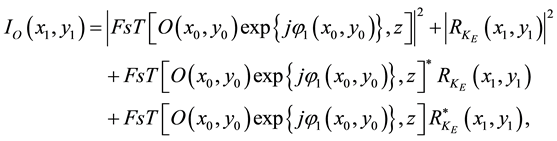 (1)
(1)
where 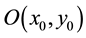 represents the fingerprint image,
represents the fingerprint image, 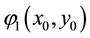 is the phase modulation by the diffuser in the object wavepath,
is the phase modulation by the diffuser in the object wavepath, 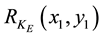 is the complex amplitude distribution of the phase-modulated reference wave on the CCD plane,
is the complex amplitude distribution of the phase-modulated reference wave on the CCD plane, 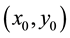 and
and 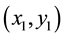 are coordinates of the object and the CCD planes, and * denotes the complex conjugate. The operator
are coordinates of the object and the CCD planes, and * denotes the complex conjugate. The operator 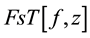 denotes a Fresnel transform in which f and z are the original wavefront and the propagation distance, respectively.
denotes a Fresnel transform in which f and z are the original wavefront and the propagation distance, respectively. 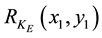 is derived as the Fresnel transform of the phase object assigned by the diffuser D2 (see Figure 3).
is derived as the Fresnel transform of the phase object assigned by the diffuser D2 (see Figure 3).
Figure 4 shows a flow chart of the Fresnel-type DRPE process. An encrypted image is obtained via two phase modulations―one in the space domain, and the other in the Fresnel domain. With the approaches described in Refs. [7] and [11] , two phase masks were inserted in the object wave path for DRPE; however, with our system,
Figure 1. Concept of the encrypted biometric sensing system. The database (DB) in the verification system represents the template database for user biometric information.
Figure 2. Typical optical system used in digital holography.
Figure 3. The optical system used with our encrypted sensing scheme. Here D1 and D2 are diffusers.
Figure 4. Schematic diagram illustrating the Fresnel-type DRPE scheme.
they are applied to the object and reference waves. The Fresnel-type DRPE uses three cipher keys: the phase distribution on the Fresnel domain, the distance of Fresnel diffraction, and the wavelength of laser; all of which that must be provided correctly to restore the plaintext image from the encrypted image. In this paper, the laser wavelength is assumed to be unique, whereas the other two components are employed as cipher keys.
Let us consider the third term of Equation (1), which is similar to DRPE. If the amplitude of 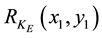 can be approximated to be constant, the third term of Equation (1) corresponds to the encrypted image of Fresnel-type DRPE. In this case,
can be approximated to be constant, the third term of Equation (1) corresponds to the encrypted image of Fresnel-type DRPE. In this case, 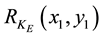 can be expressed as
can be expressed as
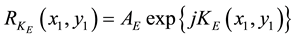 (2)
(2)
where AE is a constant amplitude and 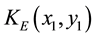 is the phase distribution of the encryption key. The encrypted image
is the phase distribution of the encryption key. The encrypted image 

where the constant AE has been omitted for clarity. The encrypted image 
For decryption, 


After this calculation, the complex amplitude image 



where 




If

From this equation, it follows that the original fingerprint image is obtained.
If the amplitude of 



If the encryption and decryption keys differ significantly, the decrypted image becomes a random pattern. The diffraction distance z can be also used as a parameter to restore the correct plaintext image.
2.3. Obtaining the Decoding Key
To implement a recording system for encrypted DH, we employ off-axis holography, in contrast to the work described in Ref. [12] , where they used in-line holography. To reconstruct a fingerprint image from an encrypted hologram, 
In the optical system shown in Figure 5, a hologram 


Where 






where 



3. Experiments
3.1. Optical System
We carried out several experiments in which holograms of encrypted fingerprint images were captured and the original fingerprint images were then numerically restored. To do this, we constructed an optical system for acquiring holograms, as shown in Figure 6, which used a He-Ne laser with a wavelength of 633 nm as a light source and a CCD image sensor with 1024 × 768 pixels that was 4.65 μm ´ 4.65 μm. A fingerprint was placed on a total reflection prism and the reflected light was focused using two lenses (L3 and L4) to form an image on the CCD image sensor.
3.2. Image Reconstruction
As discussed in Section 2.2, the decrypted images were obtained so that 



Figure 5. Optical system for obtaining decoding key.
Figure 6. Schematic diagram showing the experimental optical system. Here f1 = 0.2 m, f2 = 0.1 m, d1 = 0.056 m, and d2 = 0.2 m.


Figure 7. Experimentally obtained images (a) An encrypted hologram; (b) A decrypted fingerprint image reconstructed using a complex amplitude wave; (c) A decrypted fingerprint reconstructed using a constant-amplitude wave (i.e., our method); (d) A decrypted fingerprint using constant amplitude wave with speckle noise reduction; (e) A decrypted image with an incorrect decryption key, and (f) a decrypted image with an incorrect distance (244 mm).
component and the correct propagation distance. In this case, the fingerprint image is difficult to discern. Figure 7 (c) shows a decrypted image using the correct 

Figures 7(e) shows a decrypted image using an incorrect
3.3. Verification Accuracy
We evaluated the verification accuracy of the experimental setup described above in terms of the ability to match restored fingerprint images. Using the optical system shown in Figure 6, we captured 100 encrypted holograms of fingerprint images from 10 subjects (10 encrypted DHs per fingerprint). In these trials, five of the fingerprint images for each subject were used for enrollment and the others were used for testing; 250 genuine fingerprint trials (25 trials per subject) and 450 imposter trials (45 trials per subject) were carried out. Nonlinear correlation [16] was employed in these trials for pattern matching. The nonlinear correlation n(x,y) between two images can be expressed as follows:

Where 



As a quantitative criterion for verification, the peak-to-side-lobe ratio (PSR) [17] was calculated as follows:

where σ denotes the standard deviation of 

Using PSR as a verification score, the false rejection rate (FRR) of the genuine verification attempts and the false acceptance rate (FAR) of the imposter verification attempts were calculated. In addition, we determined a receiver operating characteristic (ROC) curve, in which each point is plotted according to the FRR (x-axis) and FAR (y-axis) for a given threshold value, as shown in Figure 9. The equal error rate (EER) of our method with speckle noise reduction was 12.4%, and that without speckle noise reduction was 35.0%. The EER obtained using a complex amplitude 
The accuracy of our system was not better than that of image verification using a conventional sensor (i.e., unencrypted sensing). However, there are a number of possible causes of image degradation: first, we did not use a guide to fix the fingerprints; and second, we did not ask the subjects to restrain the pressure that they applied. The latter issue might cause a variation in the degree of fingerprint distortion among the images. In such cases, speckle reduction via summation may not be effective. By reducing the influence of such factors, our method has potential for further improvements in verification accuracy.
4. Conclusions
We have described an encrypted sensing system for capturing fingerprint images using digital holography and


Figure 8. Nonlinear correlations. (a) Genuine (complex); (b) Genuine with speckle reduction (phase only); (c) Genuine without speckle reduction (phase only); (d) Genuine with incorrect decryption keys (phase only) and (e) Imposter (phase only).
Figure 9. ROC curves.
optical encryption. We showed experimentally that a fingerprint image could be restored correctly by decrypting an encrypted hologram with the correct key and propagation distance. The quality of the restored fingerprint im- age could be more clearly visible than that when using a conventional method by improving the calculation method for restoring a fingerprint image from an encrypted digital hologram. The verification performance of the restored fingerprint images was investigated, and we demonstrated that our method has favorable verification accuracy.
The principal advantage of the system described here is that it can enhance the security of biometric authentication by capturing optically encrypted images rather than raw fingerprints. Combining physically unclonable functions (PUFs) [18] with our system might enable the development of very secure user authentication methods. For example, the use of an encoding key provided by a diffuser as a PUF may provide a secure key based on the physical features of an individual object.
References
- Ratha, N.K., Connell, J.H. and Jain, A.K. (2001) Enhancing Security and Privacy in Biometrics-Based Authentication Systems. IBM Systems Journal, 40, 614-634. http://dx.doi.org/10.1147/sj.403.0614
- Uludag, U., Pankanti, S. and Jain, A.K. (2005) Fuzzy Vault for Fingerprints. Audio- and Video-Based Biometric Person Authentication Lecture Notes in Computer Science, 3546, 310-319. http://dx.doi.org/10.1007/11527923_32
- Soutar, C., Roberge, D., Stoianov, A., Gilroy, R. and Kumar, B.V.K.V. (1999) Biometric EncryptionTM. http://www.cse.lehigh.edu/prr/Biometrics/Archive/Papers/BiometricEncryption.pdf
- Hirata, S. and Takahashi, K. (2009) Cancelable Biometrics with Perfect Secrecy for Correlation-Based Matching. Advances in Biometrics Lecture Notes in Computer Science, 5558, 868-878. http://link.springer.com/chapter/10.1007%2F978-3-642-01793-3_88
- Clancy, T.C., Kiyavash, N. and Lin, D.J. (2003) Secure Smartcard Based Fingerprint Authentication. Proceedings of the 2003 ACM SIGMM Workshop on Biometrics Methods and Applications―WBMA, 45. https://www.cs.umd.edu/~clancy/docs/bio-wbma2003.pdf
- Refregier, P. and Javidi, B. (1995) Optical Image Encryption Based on Input Plane. Optics Letters, 20, 767-769. http://dx.doi.org/10.1364/OL.20.000767
- Javidi, B. and Nomura, T. (2000) Securing Information by Use of Digital Holography. Optics Letters, 25, 28-30. http://dx.doi.org/10.1364/OL.25.000028
- Yamaguchi, I., Yamamoto, K., Mills, G.A. and Yokota, M. (2006) Image Reconstruction Only by Phase Data in Phase- Shifting Digital Holography. Applied Optics, 45, 975-983. http://dx.doi.org/10.1364/AO.45.000975
- Javidi, B. and Nomura, T. (2000) Three-Dimensional Object Recognition by Use of Digital Holography. Optics Letters, 25, 28-30. http://dx.doi.org/10.1364/OL.25.000028
- Matoba, O., Nomura, T., Perez-Cabre, E., Millan, M.S. and Javidi, B. (2009) Optical Techniques for Information Security. Proceedings of IEEE, 97, 1128-1148. http://dx.doi.org/10.1109/JPROC.2009.2018367
- Liu, S., Guo, C.L. and Sheridan, J.T. (2014) A Review of Optical Image Encryption Techniques. Optics & Laser Technology, 57, 327-342. http://dx.doi.org/10.1016/j.optlastec.2013.05.023
- Tajahuerce, E. and Javidi, B. (2000) Encrypting Three-Dimensional Information with Digital Holography. Applied Optics, 39, 6595-6601. http://dx.doi.org/10.1364/AO.39.006595
- Takeda, M., Ina, H. and Kobayashi, S. (1982) Fourier-Transform Method of Fringe-Pattern Analysis for Computer- Based Topography and Interferometry. Journal of the Optical Society of America, 72, 156-160. http://dx.doi.org/10.1364/JOSA.72.000156
- Spagnolo, G.S. and Cozzella, L. (2012) Laser Speckle Decorrelation for Fingerprint Acquisition. Journal of Optics, 14, 094006. http://dx.doi.org/10.1088/2040-8978/14/9/094006
- Utsugi, T. and Yamaguchi, M. (2013) Reduction of the Recorded Speckle Noise in Holographic 3D Printer. Optics Express, 21, 662-674. http://dx.doi.org/10.1364/OE.21.000662
- Javidi, B. (1989) Nonlinear Joint Power Spectrum Based Optical Correlation. Applied Optics, 28, 2358-2367. http://dx.doi.org/10.1364/AO.28.002358
- Kumar, B.V.K.V., Savvides, M., Xie, C., Venkataramani, K., Thornton, J. and Mahalanobis, A. (2004) Biometric Verification with Correlation Filters. Applied Optics, 43, 391-402. http://dx.doi.org/10.1364/AO.43.000391
- Helinski, R., Acharyya, D. and Plusquellic, J. (2009) A Physical Unclonable Function Defined Using Power Distribution System Equivalent Resistance Variations. Proceedings of the 46th Annual Design Automation Conference on ZZZ-DAC’09, 676. http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=5227103&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Fabs_all.jsp%3Farnumber%3D5227103
NOTES
*Corresponding author.
















