Optics and Photonics Journal Vol.05 No.02(2015), Article ID:54336,34
pages
10.4236/opj.2015.52005
Phantom of Human Adipose Tissue and Studies of Light Propagation and Light Absorption for Parameterization and Evaluation of Noninvasive Optical Fat Measuring Devices
Stefan Hartmann1, Matthias Moschall1, Oliver Schäfer2, Frank Stüpmann1, Ulrich Timm1, David Klinger1, Jens Kraitl1, Hartmut Ewald1
1Institut für Allgemeine Elektrotechnik, Universität Rostock, Rostock, Germany
2Deutsches Elektronen-Synchrotron DESY, Hamburg, Germany
Email: matthias.moschall@uni-rostock.de
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 February 2015; accepted 25 February 2015; published 28 February 2015
ABSTRACT
A method for noninvasive determination of fat and water content in the human body is examined. A spatially resolved spectroscopy method is used which can record low intensity near infrared spectra. This novel approach is compared to other methods for the determination of fat and water content. Monte Carlo simulations of light propagation in tissue are shown and the production and characterization of optical phantoms of adipose tissue are investigated.
Keywords:
Body Fat Percentage, Noninvasive Body Fat Measurement, Spectroscopy, Optical Properties of Tissue, Optical Phantoms, Monte Carlo Simulation

1. Introduction and Overview
Adiposity (obesity) is a growing problem in the modern world, as there are many consequences that result from it [1] [2] . Both from a medical as well as from an aesthetic point of view in gyms as well as for athletes in competitive sports there is a need for methods that indicate the fitness, training, health, and nutritional status of the individual. In addition to many very elaborate measurement methods which already exist two further techniques have been developed for the determination of body fat. These are bioelectrical impedance analysis (BIA) and the optical detection, which is performed either spectroscopically or by multispectral photometry. Commercial devices already exist which exploit both methods but they suffer from considerable restrictions.
A new method for tissue measurement using spatially-resolved spectroscopic techniques was investigated. The method uses light radiation which is transmitted by infrared emitting diodes into the tissue. This radiation penetrates the tissue and is reflected, absorbed and scattered according to its optical properties. Radiation emerging from the tissue is detected by a 2D spectrometer. However, the resulting spectrum is uncalibrated.
Therefore for parameterization, verification and calibration purposes artificial phantoms based on the basis of epoxy resins with the optical characteristics of human adipose tissue were investigated. These have the advantage of long term stability of the required tissue properties as well as mechanical stability. The absorption and scattering behavior of the skin could be reproduced within one order of magnitude. Monte Carlo simulations showing the light propagation in tissue and enable the measurement strategies for determination of local subcutaneous fat to be derived. It could be shown that light of 900 nm penetrates skin with a subcutane fat layer of 15 mm. Depending on the sensitivity of the detector greater depths can be reached. Absorption profiles were obtained for light paths detected at varying distances from the irradiation point. These show, that for increasing distance between detector and light entry point the main region of absorption becomes wider and reaches greater depths.
The measurements with homogenized animal tissue samples show a clear correlation between the recorded spectra and the fat and water content of the samples. Due to the homogenization, the ratio between water and fat is constant throughout the sample and the spectroscopic measurement becomes independent of penetration depth. In skin, fat is distributed as an inhomogeneous layer. For a direct spectroscopic detection of fat, this layer should be fully penetrated, which usually only succeeds usually only for thin skin layers (e.g. biceps).
Our investigations indicate the feasibility of spectroscopic measurement of local subcutaneous fat content is feasible.
2. The Human Body Fat from a Medical Perspective
The skin (derma) essentially consists of three layers, the epidermis, the dermis and the subcutis, [3] see Figure 1. Adipose tissue is anatomically defined as subcutaneous adipose tissue (panniculus adiposus). In addition to the subcutaneous there is intramuscular and visceral fat [4] .
From a medical point of view, the adipose tissue is a special form of reticular connective tissue. Adipose tissue accounts for approximately 10% - 20% of the body weight of a normal-weight man and 15% - 25% of the body weight of a woman. The reticular connective tissue is a three-dimensional sponge-like association of reticulum and reticular fibers in whose gaps fat cells are stored. Fat cells are cells which contain a globule of fat, surrounded by cytoplasm. Chemically, fat drops are a mixture of glycerol esters (neutral fats), oleic, palmitic, stearic acids and dyes (lipochromes). There are two types of fat: white and brown. Brown adipose tissue almost
Figure 1. Illustration of the typical structure of the human skin [9] .
exclusively appears in the newborn. The brown color results from the exogenous, fat-soluble dyes such as carotenoids. In contrast to white adipose tissue, the cells of brown adipose tissue are smaller and contain instead of a larger one many of small globules of fat instead of a single large one. Recent studies predict that “at least some ten percent” of adults still have active brown fat cells [5] . White adipose tissue is subdivided into abdominal fat (visceral fat), subcutaneous fat and intramuscular fat. The intramuscular fat only makes up about 2% - 3% of the human total body fat. The abdominal fat serves as padding material, for protection of organs and tissue replacement. The subcutaneous fat is used as energy storage, as an elastic cushion under mechanical impacts and as thermal insulator to maintain the body temperature. Subcutaneous fat is mainly placed in hypodermal connective tissue and above the abdominal cavity. The abdominal fat is incorporated in the tissue of muscles and organs [6] . It is known that considered on its own an increased amount of subcutaneous fat storage is medically safe. Here the aesthetic aspects are more important [7] . Medically relevant are the storages deposits in the organ tissue, the visceral fat [7] . These generally lead to health problems. Fat cells (adipocytes) are indeed degraded by the body, but constantly replaced by new ones. Therefore, by diets and physical activity only the fat, but not the adipose tissue containing it, could be degraded [8] .
The generation and reduction of fat is largely determined by the composition and extent of food intake, as well as the degree of physical activity. Therefore, fat analyzing devices are mainly used in medical facilities, fitness centers and competitive sports.
3. State of the Art in Human Body Fat Determination
3.1. Calculation of Body Fat from Body Weight and Size
3.1.1. Broca’s Formula and Body Mass Index (BMI)
Broca’s formula [10] is a quite simple mathematical tool to determine the normal weight of the body size.
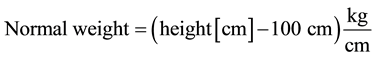
In recent years, Broca’s formula has been replaced by the formula to determine the Body Mass Index.
The Body Mass Index (BMI) is the most common method to assess the weight of a person in relation to its body size. The BMI is the ratio between weight and height of a person:

The value of “body height squared” has, however, no relation to the body surface. The calculation of BMI includes neither stature, physique, sex, nor the individual body composition of fat and muscle tissue [11] .
3.1.2. Determining the Percentage of Body Fat from BMI
By using the BMI, the body fat is solely inferred from height and weight. As a consequence the proportion of fat in individuals with a well-trained muscle tissue is overestimated, because it is heavier than fat tissue. On the other hand it is possible that people with a medically critical percentage of body fat but inferior muscular development are rated with a normal ranged BMI.
Different studies have searched for correlations between BMI and percentage of body fat [12] -[18] . As a result of these different formulas were generated. The calculated results of those are shown in Figure 2. The white symbols stands for black women and the black symbols stands for white women. It is worth noting that the variations are considerable, although rather idealized groups were used.
3.2. Additional Methods of Determining Human Body Fat
In addition to the simple methods, described above, other scientific methods are available to determine body fat in the human body. Among them are some very accurate methods, but because of the disproportionate effort or the cost they are only applied in scientific studies. These methods include:
・ Magnetic Resonance Imaging (MRI)
・ Computer Tomography (CT)
・ Hydrodensitometry by underwater weighing
・ 40K Measurements
Figure 2. Correlation of body fat percentage and BMI (kg/m2) in women ages 20 - 89 [16] .
・ Neutron Activation
・ Ultrasound imaging
・ Dual Energy X-Ray Absorptiometry (DXA or DEXA measurement)
・ Deuterium dioxide dilution method (D2O dilution) [19] .
For all of these methods very expensive equipment or specialized methodical know-how is necessary. Other disadvantages are the lack of availability of equipment, the long analysis time and, for some methods, the radiation exposure of the patient. These methods are intended for scientific and medical studies only. They mostly rely on complex four-compartment models, which decide between bone (minerals), water, protein and fat.
Because of its complexity and costs, these methods can not be used in medical facilities, gyms and sports in general, where the body fat determination becomes part of the daily routine. In this field of application other methods must be preferred. There is the skin fold measurement (antropometry) and the bioimpedance analysis (BIA). These methods are widely based on a two-compartment model, which distinguishes between fat-free mass (FFM) and fat.
3.3. Determination of the Percentage of Body Fat by NIR Measurement
On the other hand, there are optical methods using NIR photometry or spectroscopy (Lipometer [20] -[22] , FUTREX [23] -[25] , Dermalog [9] ). These popular optical fat determination systems measure the local tissue composition of water and fat under the skin and deduce the overall body fat.
The NIR method uses light which is transmitted into the skin by infrared emitting diodes. This radiation penetrates the tissue and is reflected, absorbed and scattered according to the tissue’s optical properties. Radiation emerging from the skin is detected by photo detectors of the optical measuring system and then processed.
The method of NIR measurement is easy to use, fast, noninvasive, and without radiation exposure of the subjects. The instruments provide considerable advantages in handling and preparation compared to most alternative methods [26] . There are now some of these approaches, which are also partly marketed commercially. Four such NIR measurement concepts are presented briefly. The NIR measurement is always depth-dependent.
3.3.1. FUTREX
FUTREX successively carried out two measurements at 940 nm and 950 nm [23] [25] . The FUTREX devices Figure 3 operate with 4 - 6 LEDs. Reflected light is collected by a photo diode using a diffuser and afterward the percentage of body fat is computed. It is measured at a specific point on the subject’s biceps in a sitting position.
3.3.2. Lipometer
The measurements of a Lipometer Figure 4 are carried out in a standing position on the right side of the upper
Figure 3. Futrex [24] .
Figure 4. The Lipometer device [20] .
torso. For full coverage of the subcutaneous fat, 15 representative, anatomically well-defined parts of the body should be measured [20] . The Lipometer operates withe LEDs at a wavelength of 660 nm and with a single photodiode [21] .
3.3.3. NIR Technologies
NIR Technologies uses a Fourier-Transform-NIR (FT-NIR) spectrometer, a delicate type of NIR spectroscopy. A NIR-source is used emitting a laser beam of near infrared intensity which is passed said beam through an interferometer to encode data from the whole spectral range simultaneously. The light is incident through optical fiber bundle on the earlobe, and the reflected light is taken via the optical fiber bundle to the detector. An FT-NIR spectrometer is used and can achieve a spectral resolution up to 0.3 nm [27] .
In [28] is shown that this method achieves the precision of the Dual Energy X-Ray Absorptiometry (DEXA) measurement.
3.3.4. Dermalog
The principle of Dermalog is to obtain a depth-dependent tissue measurement by evaluation of a spatially- resolved spectroscopic measurement [9] . Following this principle, a method is developed shall be obtained that is more accurate than the photometric methods of FUTREX and Lipometer and less expensive than the FT-NIR method of NIR Technologies.
The exploitation of the relationship between penetration depth and detection distance of the light reemerging from skin is very complex. As light source, a wide-band LED is used as the light source. It generates a continuous, homogeneous, intense, thermally stable light in the NIR spectral range from 800 nm up to 1000 nm. The detector is a 2D spectrometer with a slit-shaped aperture Figure 5. As Figure 6 illustrates, the emitted light is coupled into the tissue. Idealized light paths through the tissue are also shown. This is a reflective measurement. The received signals are recorded as a plurality of spectra corresponding to a plurality of pixels of the camera
Figure 5. Demonstration of the Dermalog spectrometer with light source and the entrance slit.
Figure 6. Recording unit, position of the lighting and the imaging region.
sensor used in the spectrometer along the longitudinal direction of the diaphragm. By means of multivariate data analysis, the proportion of fat can be calculated from the spectra as a function of distance from the irradiation site and accordingly as a function of depth beneath the detected skin layers [9] .
4. Simulation Tools
The understanding of propagation of light in biological tissue is a crucial point in the design of bio-optical sensors. Monte Carlo simulations help to gain insight into the processes involved. While commercial software, such as ASAP [29] , offers excellent tools for the design and investigation of bio-optical sensors and optical systems in general. However, the underlying algorithms are largely hidden from the user. So it can be difficult, therefore, to investigate fundamental phenomena in the propagation of light in tissue, especially quantitative questions concerning penetration depth and absorption profile of light. This was the motivation to implement a simpler ray tracing algorithm for arbitrarily stacked layers of material within the MATLAB framework [30] . Due to the accessible source code every part of the simulation can be adapted and data can be accessed everywhere in the program.
Despite the very diverse micro anatomy of skin, its major regions, epidermis, dermis, and subcutis as well as underlying muscle tissue can be approximated well by homogeneous material layers with distinct optical properties. By restricting the simulation to one-dimensional material stacks all three problems of modeling, intersection point calculation and administration can be greatly simplified. All material properties are stored as a vector with a layer index, and intersection points can be calculated by simple vector operations.
The design of the photon simulation is based on works of Prahl et al. [31] , but was significantly modified, as the program matured. The data of all interactions is written to a file in HDF5 format [32] . Unlike in ASAP the file format is open. The HDF5 format allows efficient, flexible storage of large amounts of data, and, by means of a generic browser, its investigation. A variety of analysis can afterward be run on those files. In this way simulated data can be reused to address various questions. Coordinates, direction of flight (unit vector corresponding to direction cosines), power of photon and a process code are stored per interaction point for each photon. The latter indicates, if the photon just started, crossed a material border, was scattered in the material or left the system borders.
In terms of physical processes, scattering is modeled using the usual Henyey-Greenstein function [33] . Absorption is calculated for every piece of the path analytically. Interface effects at the material borders, such as reflection, refraction and total internal reflection are treated taking into account absorption by using complex refractive indices, while polarization states are averaged. Diffraction, interference and quantum optical effects are not included, as they are negligible for the problems and scale addressed by the simulation. The light source is modeled as a Gaussian beam, where power, wavelength, diameter, starting position and direction are eligible. The light source’s power is distributed equally over the number of simulated “photons” (thought as fractions of transported power).
A power limit can be set, down to which the photons are being traced through the
system. For the correct termination of photons, regarding energy conservation, the
method of “Russian roulette” is applied. Statistically every
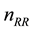 -th photon
receives
-th photon
receives
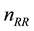 -times its
current (roughly limiting) power and will be traced further; all other photons below
limiting power will be stopped. The value of
-times its
current (roughly limiting) power and will be traced further; all other photons below
limiting power will be stopped. The value of
 commonly found in examples is 10. However, no conclusive investigation of its influence
could be found in literature. It is likely to have an influence on the geometrical
power distribution around the limiting power.
commonly found in examples is 10. However, no conclusive investigation of its influence
could be found in literature. It is likely to have an influence on the geometrical
power distribution around the limiting power.
A lower limit for choosing a sensible limiting power can be derived from the following
thoughts: The sensitivity of a sensor determines the smallest fraction of power
 that can be detected. As the initial power is split up into a number
that can be detected. As the initial power is split up into a number
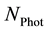 of smaller packages (photons), they could reach the sensor on different paths and
sum up to a detectable energy. In the most extreme case all simulated photons could
arrive at the sensor and their remaining power could sum up to just the smallest
detectable fraction. Thus the lowest sensible limiting power,
of smaller packages (photons), they could reach the sensor on different paths and
sum up to a detectable energy. In the most extreme case all simulated photons could
arrive at the sensor and their remaining power could sum up to just the smallest
detectable fraction. Thus the lowest sensible limiting power,
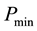 would be given
as:
would be given
as:
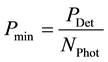
If Russian roulette is applied, the power of the discarded photons is contributed by the one surviving and amplified photon. In a way it represents the discarded photons that would have reached the same spot with a much lower energy, and which is now accumulated in one surviving photon.
As MATLAB code needs comparably high processing times, some effort was put into methods to reduce computation time and use the results in the best possible way. The simulation was implemented to use the parallel processing capabilities of MATLAB from an early stage on. For debugging purposes and single-core machines the feature is optional. Furthermore the algorithm was implemented as a function, taking material data, light source and other parameters as input argument. Thus the simulation can be operated from a graphical user interface or alternatively could be called in batch mode in another MATLAB script for mass processing. In order to maintain a small memory footprint of the simulation and analysis programs, the photons are processed in subgroups and the computation results from these groups are stored in or retrieved from the HDF5 file consecutively. The subgroup size was chosen by experiment for best processing time.
An activity diagram of the algorithm is given in Figure 7. The program consists of three nested loops. The outermost one serves the handling of the photon subgroups and stores the intermediate results in the file. For each subgroup the photons are computed in the second loop. As each photon is independent of the others these loop cycles can be computed in parallel. The tracing of each photon happens in the innermost loop. It is executed until the photon is marked as finished, that is, when it lost all its power. First the photon is initialized, depending on the settings for the light source, with a start position, power, and direction of flight. In each loop cycle the length of the photon path element is computed as a random number from the mean free path in the respective material. The next step is to check, if the border to the next material layer was crossed. In that case the path element is cut at the border and interface effects (reflection and refraction) are computed. If the photon stays within the same material layer, a new direction is determined from the scattering parameters. The absorption along the path element is calculated. From the result of these steps the next loop cycle is initialized or the photon is terminated, using the “russian roulette” method. For convenience a status bar was implemented to give an estimate of the remaining time of these time consuming calculations.
Figure 7. Algorithm of the simulation.
5. Optical Determination of Tissue Properties
Basis for the optical fat determination is a study by Conway [34] from 1984, whose results are widely recognized. In this study, the fat content was first determined spectroscopically.
Light propagation in the human skin is dominated by scattering and absorption processes.
In addition, reflection and refraction occur at boundary layers, but macroscopically
the light is diffusely distributed, due to the irregular structure of biological
surfaces. However, reflection and refraction are important when coupling light into
skin. The relatively large refractive index difference between air and tissue already
leads to partial light reflection at the skin surface. Scattering processes take
place at the boundaries of the cells, the cell nuclei, and the collagen fibers of
the connective tissue. Scattering can be described by two parameters (see [33] ),
the scattering coefficient


Both parameters are often combined into the reduced scattering coefficient:

The light emerging at various locations contains different ratio information from different depths of the tissue. For the spatially resolved spectroscopic method, it is necessary to quantify these relationships accurately.
Different evaluation methods have been published for the investigation of the depth
dependence of measurements with separated input light and the path-dependent exit
region in human tissue. A work of Cui et al. [35] relates the average depth





However, the assumption of a fixed absorption path for all measurements is not realistic
in this case, because the average path length increases in relation to the light
exit point distance. An average path length




The effective path length is increased considerably by diffuse light scattering.
Therefore, a correction factor must be used on such simplified models, to convert
between the real and the effective path length. Such a correction factor, or parametrization
for more complicated models, could be determined from the results of Monte-Carlo
simulation. Depending on the wavelength, light is absorbed by the chemical compounds
in the skin. At a certain wavelength, the respective absorption behavior is also
represented by the absorption coefficient
One assumption is that a changing of water or fat content in the skin tissue results to a variation of these maxima, which can be detected. If these variations are in a known ratio then a calculation of the proportion of fat and water can be done.
Since there is clearly a difference between fat and other tissue components such as water and RHb (deoxidized hemoglobin), a quantitative tissue analysis is possible. In Figure 8 shows the absorption curves and the second derivative of water, fat and a biceps measurement with the Dermalog spectrometer prototype are also shown.
6. Simulation of Light Propagation in Skin
In first simulations simple physical phenomena, such as reflection, refraction, and absorption, were computed
Figure 8. Absorption spectra (left) and its second derivative (right) of water (blue), fat (green) and biceps spectrum (red).
and compared with analytical calculations. They served to verify the program and showed full agreement. Further comparative studies of scattering with ASAP agreed within 20%. These deviations can be attributed to differences between the algorithm and the treatment of physical phenomena.
The models used for the simulations consist of layers described by their optical properties (absorption and scattering coefficient, refractive index and anisotropy factor). The layers can have different thickness but share a common cross-section. The latter can be freely chosen, usually such, that the cloud of photon scattering paths are fully contained within the boundaries of the model.
In a next step the basic light propagation in skin was studied. In all tissue layers forward scattering dominates with anisotropy factors of 0.7 ... 0.9. This prevents the light from direct back-scattering and allows a penetration into the skin. Figure 9 shows the number of interaction points versus depth and radial distance of photons that were detected in the specified zone, marked in white lines. Most of the interactions is arranged in a curved zone between entry and exit point. The exact shape depends on the optical properties of the tissue, but is similar for the same medium at changing detector distances. That implies greater penetration depths to be achieved with greater sensor distances, where the deepest point of the curved region is reached at roughly half the distance between entry and exit point.
In order to get a better understanding of the distribution of absorbed power, absorption profiles were calculated (Figure 10). Here each radial distance bin can be thought as a ring-shaped receiver. For each photon path that ended on the surface in such a bin, the absorbed power versus the depth of the absorption process was shown in a histogram. The values of the histogram were normalized to the entire absorbed power along the path. In a second step these relative absorption profiles for each path were averaged and sorted into the radial distance bins according to the path’s exit point. Thus, for each detection distance it can be seen how the absorbed power along the path is distributed in depth. These histograms containing depth information contribute considerably to the spectroscopic information, represented by the absorbed fraction of the light. For all absorption profiles with growing detection distance the region of maximum absorption extends to greater depth and becomes wider. This is due to the large spread of interaction events around the curved area, observed in Figure 9. If the absorption plots are created using an absolute power scale then these features are mostly hidden due to the strong superimposed signal attenuation.
With these diagrams, conceptual studies were done to investigate measurement strategies of local fat content in skin. Depending on the penetration depth two scenarios where envisaged. In the case that light of the absorption wavelength of fat (930 nm) can penetrate the entire subcutis, the tissue’s fat content can be determined as a concentration by remission spectroscopy. Alternatively, red light could be used to penetrate the layer of subcutane tissue. Due to myoglobin, red light is absorbed in the underlying muscle tissue. Used in combination with a spatially resolved spectral measurement this should allow locating the boundaries between dermis, subcutis and muscle tissue. Thus the thickness of the subcutis can be determined and the fat content derived.
For the evaluation of both scenarios, simulations were done based on optical properties of tissue from litera-
Figure 9. Number of interactions of photon paths (logarithmic scale) which ended in the respective detector region on the surface (Depth = 0), marked by vertical white lines. The model corresponds to Table 3, but the subcutis is 20 mm thick.
Figure 10. Absorption-depth profiles in a logarithmic scale vs. detection distance. Profiles for 633 nm (top) and 960 nm (bottom) are shown in a pessimistic (left) and an optimistic (right) scenario.
ture. Unfortunately such data for the exact absorption wavelengths of fat, water and myoglobin were not available. The wavelengths data for 633 nm and 900 nm, chosen instead, are close to these absorption bands and may give an overall comparative impression of the scale of light propagation and absorption phenomena (Figure 10). Additionally, optical data of tissue always depends strongly on sample preparation, measurement conditions, and method. Therefore an optimistic and a pessimistic case was constructed for both wavelengths from published data to roughly assess the range of results (Tables 1-4). The data were obtained from several sources. The refractive indices for muscle and subcutis are from [37] pp. 232/233, for dermis from [38] , and epidermis from [39] . For the optimistic case data with low absorption coefficients was chosen, for the pessimistic case data with higher ones. All values were taken from [37] , data for muscle and subcutis from page 180 for the pessimistic and
Table 1. Optical properties at 633 nm for optimistic model.
Table 2. Optical properties at 633 nm for pessimistic model.
Table 3. Optical properties at 900 nm for optimistic mode.
Table 4. Optical properties at 900 nm for pessimistic model.
179 for the optimistic case (forearm, 633 nm only). Data for the dermis is taken from pages 179 and 180, where the optimistic case is Caucasian and the pessimistic case negroid dermis with considerably increased absorption. Finally, the values for epidermis are from page 169 and are the same for both scenarios.
From the simulation results it can be immediately seen, that absorption events extend far deeper for 900 nm. Especially for 633 nm the absorption has two maxima, corresponding to the dermis and muscle tissue and a weaker one inside the subcutane layer. This shows the dermis and muscle tissue to both absorb strongly at that wavelength. It also explains the smaller depths reached, as for red light the dermis acts as a strong filter and the light passing into the underlying layers is strong attenuated. For 900 nm the material borders are less pronounced in the absorption profile. This suggests, that the spectroscopic method at 900 nm is likely to be more suitable for measuring subcutane fat. Depending on the intensity of detected light, layers of 15 mm or more should be ascertainable. If light of absorption wavelength 930 nm is used, the assessable depth could decrease, as absorption in the subcutis will increase. Further simulations with more specialized optical tissue-data at the wavelengths of interest will be required to address questions of feasibility and sensor design in more detail.
7. Phantoms with the Optical Characteristics of Human Adipose Tissue
Optical phantoms were created to provide reliable calibration standards for the Dermalog spectrometer and possibly other optical methods. Human skin is subject to large fluctuations, from person to person and, moreover, is not sufficiently stable in its properties over a longer period to serve as a standard. Therefore for parametrization, verification and calibration of artificial phantoms with the optical characteristics of human adipose tissue would be a preferred alternative. Logically, the phantoms need to be similar in their optical behavior to human subcutaneous fat in terms of absorption and scattering. For a reproducible production it was necessary to determine a relation between the phantom’s system parameters and their optical characteristics.
The implementation of the phantoms is subject to system-related restrictions. The processes in the tissue are always a result of various influences. Affected by environmental conditions such as temperature and humidity, the blood flow within the tissue is increased or diminished. As a result, the tissue may not be identical at each time. Additionally organic structures are always different, even for the same types of tissue. These properties can not completely be recreated in phantoms. Consequently phantoms can always represent only certain aspects of the skin. The results of measurements on phantoms must be reproducible even after a longer period of time. Therefore phantoms must be stable in their properties as the quality of referencing and consequently the measurement result depends on it.
Phantoms used in optical body fat measurement should meet several requirements:
・ Reproduction of the absorption behavior of the fat and water peaks at 930 and 960 nm
・ Reproduction of the scattering behavior of the skin
・ Mechanical stability
・ Long-term stability of the properties
Consequently these essential characteristics must be emulated:
・ Absorbance, represented by the absorption coefficient
・ Scattering, represented by the scattering coefficient
・ Anisotropy, represented by the anisotropy factor
These parameters are dependent on the wavelength of the incident light and must be adjusted accordingly to the measuring range.
An assumption for the wavelength range of 900 - 1000 nm are the following values [40] :
・ Scattering coefficient
・ Absorption coefficient
・ Anisotropy factor
It should be noted, that the values of the optical properties for the wavelength range used vary greatly in literature.
7.1. Selection of Materials
Depending on the application there are various types and possibilities for implementation of solid phantoms. These consist of three basic components, as shown in Figure 11.
・ Base material
・ Scattering component
・ Absorbing dye
After extensive research and consultation with manufacturers suitable components for the first generation of solid state phantoms were selected. The base or matrix material forms the body of a phantom. It provides mechanical stability of the overall structure and determines to a high degree the production steps. In part, the following tasks, depending on the choice of the other constituents can also be fulfilled by the base material [41] :
・ Solving other components
・ Setting a base absorption
・ Adjusting the refractive index
・ Making a good optical connection to other phantoms
・ Acting as a filter for specific wavelengths
The main characteristics of the most important base materials are compared in Table 5 [42] .
Figure 11. Basic structure of a phantom.
Table 5. The properties of base materials.
Epoxy resin Epoxy Resin Robnor RX716C with accompanying hardener HX716C [43] was selected as base material. It is characterized by its excellent stability when mixed with the necessary absorber solvent, low shrinkage of 0.5% (volume), and low attenuation of light of about 4%.
7.2. Scattering Component
The scattering component is supposed to generate the scattering coefficient and the anisotropy in the phantom. For this purpose, different materials are used in the form of tiny spheres. Due to the difference in refractive index to the surrounding base material, and depending on the exact size and shape of the scattering particles, it generates the required characteristic scattering behavior. Essential properties of the scattering components which are commonly used are compared in Table 6 [44] .
Alec Tiranti “Super White” polyester pigment was chosen as scattering component.
These polyester pigments allow for a reduced scattering coefficient of

7.3. Absorber
In phantoms wide- and narrow-band absorbers with the absorption behaviors of other substances are used. These behavior patterns can be more or less well modeled. For the absorber, several products were selected [46] . The properties of the main absorbers are shown in Table 7. The positive properties are marked with (+), the negative properties are marked with (−) and the neutral properties are marked with (*).
For the fat band at 930 nm the absorber Epolin EpolightTM 3169 Near Infrared Dye [47] in powder form was chosen with an absorption maximum at 934 nm. This is a replica, which allows for a good emulation of the band. Epolin EpolightTM 3130 Near Infrared Dye [48] was chosen as absorber for the water band at 960 nm. It is also an absorber in powder form and has an absorption maximum at 950 nm. Thus, the absorption band of water can only be approximated, as it is the closest wavelength presently available. By increasing the concentration of the absorber an increase of absorption to the desired level should be possible. Both absorbers (Epolin EpolightTM 3169 and 3130) have their origin in the production of protective eye wear and are very well suited for the application in solid state phantoms due to their solubility and the possibility of embedding them in the epoxy resin carrier.
Table 6. The properties of the main scattering components.
Table 7. The properties of the main absorbers.
7.4. Prestudies for the Base of the Phantoms
In order to decide on what basis the phantoms can be produced best, preliminary investigations were made.
7.4.1. Sample Phantoms Based on Water
The first few experiments were carried out with water-based phantoms due to their immediate availability. The goal of these experiments was to learn the basic characteristics of the Dermalog spectrometer (Figure 5) in the interesting wavelength range. The second goal was the to check the reproducibility of the measurement results. Initially, only the scattering characteristics were taken into account, since it was assumed that this was the main difficulty in the implementation. This has also been confirmed in subsequent project stages. The base material was tap water and for the scattering in the phantom a 20% Intralipid solution was used. The latter is a product for artificial nutrition in the clinical area, consisting of a suspension of fine fat droplets in water. The mixture was prepared in a commercially available Petri dish (Figure 12). First, a predefined amount of water was measured. The next step was the gradual addition of Intralipid in subsequent mixing parts:
・ Water: fixed at five parts
・ Intralipid®: variation of 1...10 parts
Solution components where measured in parts not in quantity to ensure always the same liquid volume placed in the Petri dish. So the quantities vary for each measurement. To get a meaningful result and save material, water was fixed at five parts. Every concentration was mixed with new water and increasing Intralipid parts. The design and results of these first measurements are shown in the following illustrations.
The measurement was done by using the Dermalog spectrometer and the mixed solutions. A Petri dish, filled with solution, was placed on top of the spectrometer (Figure 12). This kind of measuring should been used to get first spectra from the used spectrometer. So the results are raw absorbance spectra (Figure 13), showing influence of scattering particles mixed into water by varying the concentration. To determine the absolute fat concentration in next steps the second derivation of these spectra (Figure 14) was used. It was found to be quite possible to detect concentration differences with this method.
To avoid the influence of glass thickness of Petri dish in the next step a latex sheath was used with different
Figure 12. Measurement of Intralipid in a petri dish with Dermalog spectrometer.
Figure 13. Absorbance spectrum of the Intralipid test series (Dermalog software).
Intralipid water mixtures (Figure 15). The results are shown in Figure 16 and Figure 17. First one shows the raw spectra and the second one respectively second derivation. Additional measurements were performed on filled latex sheaths with different Intralipid water mixtures (Figure 15), but the light output for unknown reasons was very low and thus an exhaustive evaluation was not possible.
Measurements are showing that 94% of the irradiation passes through the latex wall. That was the result of the examination of the transmission, but provided no clear explanation for the very low light output. A possible interpretation would be that due to the small size of the lipid droplets sufficient anisotropy is given and con- sequently too little light is re-emitted. This indicates that a large proportion of the reflection during the Petri dish measurements occurred at the glass plate surface. This would have a negative impact on the quality of the measurements.
Figure 14. Second derivative of the spectra of Intralipid measurement series (Dermalog software).
Figure 15. Latex sheaths with Intralipid-water mixtures.
This indicates that a large proportion of the reflection during the Petri dish measurements occur at the glass plate surface. This would have a negative impact on the quality of the measurements.
7.4.2. Phantom Samples on the Basis of Epoxy Resin
After the water-based phantoms, experiments were made with phantoms on the basis of epoxy resin.
To get meaningful results, the following material combinations were chosen for the investigations:
1) pure epoxy resin
2) Epoxy resin + scattering particles
3) Epoxy resin + absorber
Figure 16. Absorbance of latex sheaths with Intralipid-water mixtures.
Figure 17. Second derivative of the spectra of the latex sheaths, filled with an Intralipid water mixture.
4) Epoxy resin + scattering particles + absorber
The preparation was carried out by mixing the individual components directly in the mold.
The individual samples, as shown in Figure 18, cured for about 3 days at room temperature. Subsequently, they were analyzed visually with the naked eye, microscopically and spectrophotometrically. Various insights were gained, which contributed significantly to the improvement of subsequent processing operations.
On the one hand, all the samples showed various types of defects, including dirt, caused by insufficient purity during the mixing process and residues in the resin container. Furthermore, in all of the samples air bubbles
Figure 18. First phantoms based on epoxy resin.
formed during the curing due to the gas development in the base material Figure 19.
Additionally differences in concentration of scattering and absorption transportation particles within the phantoms occurred. In Figure 19 is shown sample 1. The picture was taken with a digital microscope. This suggests an insufficient mixing of the components Figure 20. This picture is made with sample is 3 with a digital microscope too. It can be seen that lumps have been formed due to concentration differences. Therefore at other locations, there are areas with no dye.
First phantoms were made without any recipe, just to get knowledge about material handling. In addition to characterize irregularities, build during curing, all phantoms were analyzed by a digital microscope (Figure 19 and Figure 20). The selected resin meets the requirements, because it has an attenuation of only 4%, as detected during the transmission measurement.
The obtained findings of the experiments provided the basis for the second series of samples, in which for the first time the solvent chosen for the absorber was used. Methyl-ethyl-ketone was selected, because this, unlike the other specified in [47] -[49] , has less harmful properties and thus few, requirements on the workplace had to be met. The mixing process was performed in a well ventilated room and under a fume hood. Furthermore, a desiccator was used to create a vacuum during the drying phase, which significantly curbed the formation of bubbles.
7.5. Preparation of the Phantom Based on Epoxy Resin
7.5.1. Mixing
In the preparation essentially all the findings from the prestudies for epoxy resin based phantoms were used. The phantoms were made by predefined recipes, just using base material and different concentration of scattering particles, shown beyond. For every concentration four phantoms were made, numbered by XX-Y, in which XX means used weight of scattering component and Y number of sample.
Recipe:
・ Epoxy resin and hardener (100:42): 70 g for four phantoms, same for each concentration
・ Phantom 50-1 to 50-4 50 mg scattering component (respective ratio base material to scattering component (1: 1400)
・ Phantom 60-1 to 60-4 60 mg scattering component (respective ratio base material to scattering component (1: 1166.67)
・ Phantom 70-1 to 70-4 70 mg scattering component (respective ratio base material to scattering component (1: 1000)
・ Phantom 80-1 to 80-4 60 mg scattering component (respective ratio base material to scattering component (1: 875)
・ Phantom 90-1 to 90-4 90 mg scattering component (respective ratio base material to scattering component (1:777.78)
In addition, an ultrasonic bath was employed to improve the dissolution of air bubbles, which ensured that bubbles at the bottom would ascend and could be extracted into the vacuum chamber from the mixture later. An improvement of the vacuum process was performed such that the time in the chamber is minimized in order to prevent boiling of the material, hence the formation of additional air bubbles was avoided. The mixture of the individual components was done stepwise, first the calculated amount of epoxy resin was filled into a mixing
Figure 19. Inclusions in the phantom.
Figure 20. Differences in concentration of the absorber in the phantom.
vessel and mixed with the scattering particles, followed by addition the hardener in manufacturer defined ratio (Epoxy resin:Hardener, 100:42). For realization of identical phantom samples an additional vessel was used for mixing the components four forms were cast with the resulting mixture. The mixture was prepared with a commercial hand mixer to obtain a very homogeneous structure. That method was applied to all concentrations. Curing took place at room temperature to obtain a minimum of stresses in the structure. The result is shown in Figure 21.
7.5.2. Mechanical Processing Specimens
The cast samples were not immediately usable for the determination of the previously defined optical parameters. For this reason, various methods for the preparation of the phantoms were tested. By grinding, the reflection losses on the surface could be reduced. Thus more photons reach the interior of the phantom, whereby the proportion of diffuse scattering and the transmission increased. One problem, however, has been found here: small deviations in the parallelism of top and bottom as well as local inhomogeneities in roughness and thickness caused significant variations during the measurements on the same phantom. Hence, a nearly coplanar arrangement of the surfaces was realized in further experiments using a milling machine. The processable thickness of the phantoms is limited, as the material is deformed due to the high mechanical and thermal stresses in this step. Therefore, the adjustment of thickness less than 8 mm was made in a engine lathe. In this way, phantoms of about 4 mm thickness were prepared, as shown in Figure 18.
Finally, as shown in Figure 22, one long side of the phantom was smoothed and polished to provide a very plane surface. Now the phantoms were ready for analysis and to determine the optical parameters.
7.6. Analysis of the Cast Phantoms
All produced samples were examined before further use by means of three methods. First, a visual inspection
Figure 21. Phantoms for the measurement series in the mold.
Figure 22. Phantoms prepared for measurements.
was performed to detect obvious defects. In the next step, if necessary, conspicuous structures were examined microscopically. The final spectrometric analysis formed the basis of the determination of the optical parameters of the individual phantoms by applying the IAD method, which will be explained in section §8 .
7.6.1. Visual Inspection of the Phantoms
The visual inspection of the phantoms produced was unremarkable. There were only very few recognizable inclusions. Even the air inclusions after casting have dispersed during curing. The differences in the permeability of light for different concentrations were clearly visible and the phantoms appeared very homogeneous.
7.6.2. Microscopic Examination of the Phantoms
The areas previously identified as conspicuous during the visual inspection were also examined microscopically. The knowledge gained was that introduced dirt particles fall during the curing process and thus can be mechanically removed by subsequent machining. This excludes an accelerated, high temperature curing process, which would not give the material enough time to set down. The cause of the contamination were various dirt particles in the transport vessel of the epoxy resin. During the investigation it also showed that small residual amounts of microscopic air bubbles are left in the material. Possibilities for the removal and analysis of the influence of these have to be treated in further work.
8. Determining Optical Characteristics of a Sample Using Inverse Adding Doubling (IAD)
Absorption and scattering processes occur together in the sample. Thus direct measurements are hindered. A known method to work around this is the so-called Inverse Adding Doubling (IAD) method by Scott Prahl [50] . It can be used to determine optical properties of scattering and absorbing materials. This method combines measurements using two integrating spheres combined with a few system parameters in order to calculate optical properties of the sample. Integrating spheres are coated with a diffuse reflective surface on the inside. Multiple ports can be configured for incoming or outgoing light. Diffuse reflection inside the sphere minimizes the impact of the original direction of the light. Integrating spheres are used for integral analyzes of the reflected and transmitted light of the sample, regardless of its direction. Thus, influences of surface processes that may affect the direction of the outgoing light is suppressed, and only the relevant processes in the interior of the sample are detected by the measurement. The IAD calculation is implemented in a program. The data obtained from the measurement data can be read from a file in a specific format in the IAD program. This file consists of two parts, the header and the data area.
8.1. Determining System Properties
The process begins with the question, how many integrating spheres are to be used. In principle, all measurements can be performed with a one or two sphere design. With a two sphere design, the measurement is more comfortable, since different measurements can be conducted with a single setup. This allows analyzes of time sensitive objects regarding their reflectivity and transmission. This is particularly advantageous if these material properties are variable over time or due to temperature effects. The disadvantage is the higher cost compared to a single sphere setup, as well as the greater number of system parameters to be considered (two spheres are never identical). In a first step, the spheres and the structure have to be characterized in terms of their physical properties. For this purpose, the following parameters are determined [50] :
・ Area of the spherical surface (inside)
・ Area of the input and sample ports
・ Area of the output port Ae
・ Area of detection Sports
・ Wall surface without ports

・ Area of the light beam section
・ Reflectance of the sphere coating
The determination of the reflectivity of the spheres is critical, given the effects
of incorrect entries directly on the result of the IAD and so give misinterpretations
in absorption capacity of the object to be measured.


with

By Equation (5) the areas are expressed as a fraction of the total surface of the
sphere. The determination of


The sphere is illuminated at a point between the stray light trap and the output
port with a bundle of rays as much in parallel as possible. As shown in Figure 23 the light intensity is measured at the detection
port both with open and closed (with a reflectance standard―known reflectivity



Figure 23. Measurements for determining the reflectivity of the coating on the integrating sphere.
8.2. Determining Sample Properties
Further input parameters are required for the IAD calculation:
・ Total remission MR
・ Total transmission MT
・ Collimated transmission MU
・ Refractive index n
Determining Reflectance and Transmittance
Five measurements per sample are required for calculating




The digits 1...6 represent the intensity values obtained at the respective measurement points. The measurements 3 to 6 are used to determine the system parameters (ambient light compensation, dark adjustment, reflectivity). The measurements 1 and 2 are directed towards the actual samples. This configuration allows the measurement of all the samples within a short time. All other measurements are independent of the sample and thus need to be conducted only once for each series of measurements.
In Figure 24 the measurement setup for detecting all necessary values need for MR and MT calculation is shown. The detectors marked as black cubes with a number, which respectively names the spectrometer probes.
・ Detector 1 and 2―measurement of sample
¾ Detector 1: true reflectance
¾ Detector 2: true transmittance
・ Detector 3―measurement of standards true reflectance (white reference for reflectance)
・ Detector 4―measurement of transmittance reference
・ Detector 5―measurement of reflectance dark value
・ Detector 6―measurement of transmittance dark value
8.3. Determining the Collimated Transmission
Determining the transmission of collimated MU is more complex than the previous measurements. In this measurement, only the undisturbed photons transported through the medium are to be detected. Their fraction is so
Figure 24. Measurements determining the total reflectance and transmittance of the sample.
small that the smallest influences of the measurement setup can lead to deviations by several orders of magnitude. After extensive tests the following conditions for a clean and reliable measurement result could be determined:
・ Environment is shielded from ambient light
・ The light source is very well collimated and
・ The possibility to precisely locate the sample between the light source and detector.
The individual measured values for the calculation are determined by Equation (8).

In particular the determination of


with



for
arises

By using Equation (10) the Equation (9) can be linearized. From a linear fit, the collimated transmittance can be determined. Experiments reviled fluctuations in the zero-point correction of the instrument and in the power
Figure 25. Measurements for determining the collimated transmission.
of the light source. Thus three values were recorded for each measurement. First,
the total power




The results of the calculations for

8.4. Determining the Refractive Index
The refractive index

The measurement process is quite simple with an Abbé refractometer (Figure 27). The substance to be measured is applied to the surface of the measuring prism. For measurements of solids (e.g. resin phantoms) extra work is required. Clean measuring results can be obtained only on an optically flat surface. For curved surfaces the measurement result depends on the surface angle resulting in a washed out transition region rather than a sharp boundary line. On rough surfaces, it even comes to averaging over many different exit angles and a boundary region is not visible. Furthermore, the coupling of the measuring object at the measuring prism is critical due to the very thin air gap. It can be filled with a thin layer of immersion liquid with the same refractive index as the prism measurement. Here 1-Bromnaphtalin with a refractive index of 1.657 is used as an immersion liquid.
Simulation for Phantoms
Some plausibility studies for the phantom measurements were done in simulation. For these, the models were sized like the rectangular phantoms. In that way, possible real light losses in the transversal direction could be modeled. The optical properties were taken from the measurements. The energy deposition in the experimental
Figure 26. Positioning the sample in the set-up for measurement of the collimated transmission.
Figure 27. Measuring the refractive index of the phantom at the Abbé refractometer.
setups was simulated and compared with the measured values. Simulated and measured values agreed within less than 20%.
9. Investigation of the Phantoms
In the following, the results of the measurements on the phantoms are shown. The procedure described in 8 was used. The reflectance and transmittance, the collimated transmission and the refractive index were determined.
First the untreated samples were measured by a spectrometer of the type “Jeti VS 140 (Horiba Jobin Yvon OEM)”, wavelength range: 800...1700 nm, in terms of transmission and remission using the integrating sphere system.
9.1. Reflectance and Transmittance of the Phantoms
The determination of the scattering coefficient of the reduced scattering coefficient requires the determination of the collimated transmittance. The results of calculated total reflectance and transmittance of the phantoms are shown in Figure 28.
All values are measured by using the method described in chapter 8.2.1. Just one phantom each concentration was prepared and used. The Figure 28 shows the calculated (Formula 6 and 7) total reflectance and total transmittance for phantom number 1, marked as XX M_R (total reflectance) respectively XX M_T (total transmittance).
Determining reflectance and transmittance.
9.2. Collimated Transmission of the Phantoms
The determination of the scattering coefficient of the reduced scattering coefficient requires the determination of the collimated transmittance. It was necessary to choose the configuration in that way, that the object, to be
Figure 28. Results of calculated total reflectance and transmittance of the phantoms.
measured, can be movable positioned between the detector and light source, see section 8.3.
Figure 29 shows the recorded measurements of collimated transmittance with regression line and shows the low recorded intensities.
While the total power is in the range of a few tenths of milliwatts, the values for the collimated transmission are lower by about three orders of magnitude.
9.3. Refractive Index
All the phantoms were measured with the Abb? refractometer. The determined refractive indices are shown in Table 8.
9.4. Results of IAD-Calculation
With the results of the measurements of the reflectance and transmittance, the collimated transmission, the refractive index and the constants of the measuring system, the anisotropy factor (for the used wavelength of 670 nm) was determined via the IAD calculation for all phantoms.
9.4.1. Absorption Coefficient of the Phantoms
The absorption coefficient


9.4.2. Reduced Scattering Coefficient of the Phantoms
In Figure 31 the reduced scattering coefficient

9.4.3. Anisotropy of the Phantoms
In Figure 32 is shown the calculated anisotropy

9.4.4. Scattering Coefficient of the Phantoms
The calculation of the absolute scattering coefficient

Figure 29. Results of the measurements of collimated transmittance (with regression).
Figure 30. Results of absorption coefficient of the phantom series.
Table 8. Refractive indices of phantoms.
Figure 31. Results of effective scattering coefficient of the phantom series.
Figure 32. Results of anisotropy of the phantom series.
10. Reference Measurements of Tissue Properties with 2D Spectrometer
The used spectrometer of Dermalog includes a light source. The recorded two-dimensional images in Figure 34 provide a impression of the practicality of the measurement setup.
Comparative measurements have been carried out using methods recognized in the food industry. Animal samples were investigated by Foodscan Lab [51] .
For the experiment, a piece of lean pork and a piece of pork belly fat were homogenized with a meat grinder or shredder separately. Starting from 100% pork, the belly fat percentage in the sample was increased by 5% to about 30% fat content in the following steps. For the analysis in each unit a sample plate (diameter about 12 cm, bottom of glass) was up to the bigger (about 2 cm) filled. The prepared sample was first measured in the Foodscan Lab device. Immediately followed by the examination of each sample in the dish with the Dermalog spectrometer. The run time of the device was about 1 h, adjusted at 150 mA LED current. A black reference was taken only once, a white reference on the other hand, immediately before each sample measurement. The measurement was carried out through the glass side at two different points. A resulting average spectral image was
Figure 33. Results of the scattering coefficient of the phantom series.
Figure 34. Enhanced 2D recording on the palm (right); the green curve represents the intensity distribution on the distance from the light source; the red curve is an absorbance spectrum.
stored per sample.
Figure 35 and Figure 36 showing examples of measured samples and the measurement result obtained by Foss Food Lab Scan.
For the animal tissue the measurement results of the Foodscan Labs and the spectrometer are shown in Figure 37. As expected, the uncalibrated concentration measurements show opposing trends, as expected from the systematically varied proportion of fat and water in the sample.
11. Summary
A novel approach for tissue measurement as spatially-resolved spectroscopic measurement was investigated. The method uses light radiation which is transmitted by infrared emitting diodes into the tissue. This radiation
Figure 35. Homogenized pork sample with fat content 1.79%.
Figure 36. Homogenized pork sample with fat content 32.57%.
Figure 37. 2nd derivatives for homogenized samples and their correlation for homogenized samples with values of Foodscan Lab.
penetrates the tissue and is reflected, absorbed and scattered according to its optical properties. Radiation emerging from the tissue is detected by a spatially-resolving spectrometer. The resulting spectrum is uncalibrated. Therefore optical phantoms on the basis of epoxy resin were produced as calibration standards. These have the advantage of long term stability of the properties and mechanical stability. The absorption and scattering behavior of the skin could be reproduced within one order of magnitude.
Monte Carlo simulations showing the light propagation in tissue and derive the measurement strategies for determination of local subcutane fat. It could be shown that light of 900 nm penetrates skin with a subcutane fat layer of 15 mm. Depending on the sensitivity of the detector greater depths can be reached. Absorption profiles were obtained for light paths detected at varying distances from the irradiation point. These show, that for increasing distance between detector and light entry point the main region of absorption becomes wider and reaches greater depths.
The measurements with homogenized animal tissue samples show a clear correlation between the recorded spectra and the fat and water content of the samples. Due to the homogenization, the ratio between water and fat is constant throughout the sample and the spectroscopic measurement becomes independent from penetration depth. In skin, fat is distributed as an inhomogeneous layer. For a direct spectroscopic detection of fat, this layer should be fully penetrated, which succeeds usually only for thin skin layers (e.g. biceps).
Thus, the results of the study of Conway [34] can be largely confirmed by the performed measurements and evaluations. The spectral range between 850 nm and 1000 nm, is suitable for the investigation, since the light penetrates the tissue and thus can be used to non invasively measured in vivo.
Our investigations indicate the feasibility of spectroscopic measurement of local subcutaneous fat content. The method would be easy to use, fast in the measurement, non-invasive, without radiation exposure to the subjects.
12. Outlook
Compared to other local methods (ultrasound, caliper) a spectroscopic sensor can additionally detect water and possibly other substances in the skin. Some substances are known to accumulate in the skin, indicating certain diseases that could be detected in future.
For a reliable evaluation of optical methods for determination of body fat it is desirable to have a common standard for comparison.
All natural samples show strong variation in their properties. Also they are not reproducible. In contrast, resin based phantoms are a promising way to implement such a standard, as they are reproducible, long term stable, easy to handle and can be manufactured to specific optical properties. In future, detailed optical models of the skin with epidermis, dermis and subcutaneous fat could be used.
References
- OECD (2011) Health at a Glance: OECD Indicators. OECD Publishing. http://dx.doi.org/10.1787/health_glance-2011-en
- Sassi, F. (2010) Obesity and the Economics of Prevention: Fit not Fat. OECD Publishing, Paris. http://dx.doi.org/10.4337/9781849808620
- Sams, W.M. and Lynch, P.J. (1990) Structure and Function of the Skin. In: Lynch, P.J., Ed., Principles and Practice of Dermatology, Churchill Livingstone, New York.
- Provyn, S., Clarys, J.P., Wallace, J., Scafoglieri, A. and Reilly, T. (2008) Quality Control, Accuracy, and Prediction Capacity of Dual Energy X-Ray Absorptiometry Variables and Data Acquisition. Journal of Physiological Anthropology, 27, 317-323. http://dx.doi.org/10.2114/jpa2.27.317
- Nedergaard, J., Bengtsson, T. and Cannon, B. (2007) Unexpected Evidence for Active Brown Adipose Tissue in Adult Humans. American Journal of Physiology-Endocrinology and Metabolism, 293, E444-E452. http://dx.doi.org/10.1152/ajpendo.00691.2006
- Fanghänel, J., Pera, F., Anderhuber, F. and Nitsch, R. (2003) Anatomie des Menschen. 17th Edition, Walter de Gruyter, Berlin, 1222.
- Pillmann, N., Schwinger, R.H.G. and Brixius, K. (2009) Fettstoffwechsel, Geschlecht und Sport. Blickpunkt der Mann., 7, 7-10.
- Spalding, K.L., Arner, E., Westmark, P.O., Bernard, S. and Buchholz, B.A. (2008) Dynamics of Fat Cell Turnover in Humans. Nature, 453, 783-787. http://dx.doi.org/10.1038/nature06902
- Lehmann, E., Mull, G., Hengfoss, C. and Kulcke, A. (2010) Vorrichtung und Verfahren zur Bestimmung des Fettgehaltes des menschlichen Körpers. Patent EP2382916B1.
- Flexikon (2014) Broca-Formel. http://flexikon.doccheck.com/de/Broca's_formula
- Sattar, N. and Lean, M. (2006) ABC of Obesity: Assessment of Obesity and Its Clinical Implications. BMJ, 333, 695-698. http://dx.doi.org/10.1136/bmj.333.7570.695
- Gallagher, D., Heymsfield, S.B., Heo, M., Jebb, S.A. and Murgatroyd, P.R. (2000) Healthy Percentage Body Fat Ranges: An Approach for Developing Guidelines Based on Body Mass Index. The American Journal of Clinical Nutrition, 72, 694-701.
- Jackson, A.S., Stanforth, P.R., Gagnon, J., Rankinen, T. and Leon, A.S. (2002) The Effect of Sex, Age and Race on Estimating Percentage Body Fat from Body Mass Index: The Heritage Family Study. International Journal of Obesity and Related Metabolic Disorders, 26, 789-796.
- Deurenberg, P., Weststrate, J.A. and Seidell, J.C. (1991) Body Mass Index as a Measure of Body Fatness: Age- and Sex-Specific Prediction Formulas. The British Journal of Nutrition, 65, 105-114. http://dx.doi.org/10.1079/BJN19910073
- Deurenberg, P., Yap, M. and van Staveren, W.A. (1998) Body Mass Index and Percent Body Fat. A Meta Analysis among Different Ethnic Groups. International Journal of Obesity and Related Metabolic Disorders, 22, 1164-1171. http://dx.doi.org/10.1038/sj.ijo.0800741
- Gallagher, D., Visser, M., Sepulveda, D., Pierson, R.N., Harris, T. and Heymsfield, S.B. (1996) How Useful Is Body Mass Index for Comparison of Body Fatness across Age, Sex and Ethnic Groups. American Journal of Epidemiology, 143, 228-239. http://dx.doi.org/10.1093/oxfordjournals.aje.a008733
- Jackson, A.S. (1984) Research Design and Analysis of Data Procedures for Predicting Body Density. Medicine & Science in Sports & Exercise, 16, 616-620. http://dx.doi.org/10.1249/00005768-198412000-00018
- Chathuranga, R. (2013) Relationship between Body Mass Index (BMI) and Body Fat Percentage, Estimated by Bioelectrical Impedance, in a Group of Sri Lankan Adults: A Cross Sectional Study. BMC Public Health, 13, 797. http://dx.doi.org/10.1186/1471-2458-13-797
- Malatesta, D. (2013) Gültigkeit und Relevanz des Body-Mass-Index (BMI) als Massgrösse für Übergewicht und Gesundheitszustand auf individueller und epidemiologischer Ebene. Institut des Sciences du Sport de l’Universit? de Lausanne, Faculté de biologie et de médecine―Département de physiologie. (Gesundheitsf?rderung Schweiz Arbeitspapier 8). Gesundheitsförderung Schweiz, Bern.
- Adam, A., Horejsi, R. and Möller, R. (2009) Das Lipometer® - Ein Spin-Off der Medizinischen Universität Graz Anwendungsmöglichkeiten und Entwicklungschancen. Institut für Physiologische Chemie, Medizinische Universität Graz, Graz, Österreich.
- Moeller, R., Tafeit, E., Pieber, T.R., Sudi, K. and Reibnegger, G. (2000) Measurement of Subcutaneous Adipose Tissue Topography (SAT-Top) by Means of a new Optical Device, LIPOMETER, and the Evaluation of Standard Factor Coefficients in Healthy Subjects. American Journal of Human Biology, 12, 231-239. http://dx.doi.org/10.1002/(SICI)1520-6300(200003/04)12:2<231::AID-AJHB9>3.0.CO;2-X
- Moeller, R., Giuliani, A., Mangge, H., Tafeit, E. and Glaeser, M. (2014) Android Subcutaneous Adipose Tissue Topography in Females with Polycystic Ovary Syndrome: A Visible Phenotype Even in Juveniles. http://cdn.intechopen.com/pdfs-wm/29512.pdf
- Rosenthal, R.D. (1991) The Use of Near-IR Light to Measure Body Fat. Paper Presented at Scandinavian Weight Reduction Technical Conference.
- Futrex Datenblatt (2014) http://www.zelltec.de/media/files/FUTREX_Datenblatt.pdf
- Rosenthal, R.D. (1988) Near-Infrared Apparatus and Method for Determining Percent Fat in a Body. Patent US 4928014 A.
- Tanita: Understanding Body Fat Analysis (Version 2.1) (2014) http://www.tanita.com/en/tanita-publications/
- Azizian, H., Winsborough, S., Younikian, M. and Winsborough, C. (2002) Method of In-Vivo Measurement of Fat Content of a Body and Apparatus Therefor. Patent US 7711411 B2.
- Josse, A.R., Azizian, H., French, S.B., Kramer, J.K.G. and Phillips, S.M. (2011) Body Fat Content Determination in Premenopausal, Overweight, and Obese Young Women Using DXA and FT-NIR. Obesity, 19, 1497-1502. http://dx.doi.org/10.1038/oby.2011.39
- Breault (2014) ASAP Documentation. http://www.breault.com
- MATLAB (2014) http://www.mathworks.de/products/matlab/
- Prahl, S.A., Keijzer, M., Jacques, S.L. and Welch, A.J. (1989) A Monte Carlo Model of Light Propagation in Tissue. SPIE Institute Series, IS 5, 102-111.
- HDF5 Group (2014) HDF5 Data Model, Library, and File Format for Storing and Managing Data. http://www.hdfgroup.org/HDF5/
- Henyey, L.G. and Greenstein, J.L. (1941) Diffuse Radiation in the Galaxy. Astrophysical Journal, 93, 70-83. http://dx.doi.org/10.1086/144246
- Conway, J.M., Norris, K.H. and Bodwell, C.E. (1984) A new Approach for the Estimation of Body Composition. The American Journal of Clinical Nutrition, 40, 1123-1130.
- Cui, W., Wang, N. and Chance, B. (1991) Study of Photon Migration Depths with Time-Resolved Spectroscopy. Optics Letters, 16, 1632-1634. http://dx.doi.org/10.1364/OL.16.001632
- Schmidt, W. (2000) Optische Spektroskopie: Eine Einführung. 2nd Edition, Wiley-VCH, Weinheim. http://dx.doi.org/10.1002/9783527663323
- Tuchin, V.V. (2007) Tissue Optics: Light Scattering Methods and Instruments for Medical Diagnosis. 2nd Edition, SPIE Press, Bellingham, Washington, 145-191, 227-242.
- Osterholz, J. (2002) Frequency-Domain Spektroskopie und dynamische Streulicht-Spektroskopie an biologischen Geweben. Ph.D. Thesis, Mathematisch-Naturwissenschaftliche Fakultät, Düsseldorf University, Düsseldorf, 21.
- van der Zee, P. (1992) Measurement and Modelling of the Optical Properties of Human Tissue in the Near Infrared. Ph.D. Thesis, Department of Medical Physics and Bioengineering, London University, London, 99.
- Meinke, M. (2006) Spektroskopische Bestimmung biophysikalischer Parameter humanen Blutes. Habilitationsschrift, Charité, Centrum für diagnostische und interventionelle Radiologie und Nuklearmedizin, Berlin, 14-15.
- Pogue, B.W. and Patterson, M.S. (2006) Review of Tissue Simulating Phantoms for Optical Spectroscopy, Imaging and Dosimetry. Journal of Biomedical Optics, 11, Article ID: 041102, 6-7.
- Pogue, B.W. and Patterson, M.S. (2006) Review of Tissue Simulating Phantoms for Optical Spectroscopy, Imaging and Dosimetry. Journal of Biomedical Optics, 11, Article ID: 041102, 5.
- Robnor Resins (2014) Provisional Technical Datasheet, Epoxy Resin PX716C.
- Pogue, B.W. and Patterson, M.S. (2006) Review of Tissue Simulating Phantoms for Optical Spectroscopy, Imaging and Dosimetry. Journal of Biomedical Optics, 11, Article ID: 041102, 3-4.
- Medphys (2012) http://www.medphys.ucl.ac.uk/research/borl/research/NIR_topics/phantom_recipe.htm
- Pogue, B.W. and Patterson, M.S. (2006) Review of Tissue Simulating Phantoms for Optical Spectroscopy, Imaging and Dosimetry. Journal of Biomedical Optics, 11, Article ID: 041102, 5.
- Epolin (2014) Technical Data Sheet, Epolight 3169 Near Infrared Dye. http://www.epolin.com/sites/default/files/048a%5B1%5D.pdf
- Epolin (2014) Technical Data Sheet, Epolight 3130 Near Infrared Dye. http://www.epolin.com/sites/default/files/037a%5B1%5D.pdf
- Environment Protection Agency (2014) Hazard Summary for Methyl Ethyl Ketone. http://www.epa.gov/ttnatw01/hlthef/methylet.html
- Prahl, S. (2010) Everything I Think You Should Know about Inverse Adding-Doubling. http://omlc.ogi.edu/software/iad/iad-3-9-10.zip
- Foss GmbH (2012) http://www.foss.de/industry-solution/products/foodscan-meat-analyzer
























































