Optics and Photonics Journal
Vol.04 No.11(2014), Article ID:51884,8 pages
10.4236/opj.2014.411032
Nonlinear Phase Noise Estimate Based on Electronic Orthogonal Coherent for 112 Gb/s PDM-4QAM System
Baocun Wang1, Bin Li1,2*, Fengguang Luo1, Benxiong Huang2,3, Ming Tian1, Xuecheng Zou1
1Institute of Optics and Electronic Imformation, Huazhong University of Science and Technology, Wuhan, China
2School of Electronic and Imformation Engineering, Huazhong University of Science and Technology, Wuhan, China
3National Engineering Laboratory for Next Generation Internet Acess System, Wuhan, China
Email: *libin8208@126.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 September 2014; revised 12 October 2014; accepted 8 November 2014
ABSTRACT
In this paper, we proposed a novel method of joint phase noise estimate (JPNE) for PDM-M-QAM (M = 4, 16, 32, 64, …) transmission systems, and established the theoretical model to illustrate the operation mechanism. The simulation of laser phase noise and fiber nonlinearity compensation based on the proposed JPNE method had also been demonstrated. For 112 Gb/s PDM-4QAM transmission system, the simulation results had showed that the optimum launch power increased from −4 dBm to at least 0 dBm compared with the condition of no phase noise compensation in reach of all simulation distances.
Keywords:
Joint Phase Noise Estimate, Fiber Nonlinearity, PDM-4QAM, Optimum Launch Power, Phase Noise Compensation

1. Introduction
Recently, long haul fiber optic transmission based on quadrature amplitude modulation (QAM) has drawn significant research interest [1] . Coherent detection together with the polarization division multiplexing (PDM-) QAM format has paved the way for robust transmission systems at 100 Gb/s or beyond. Indeed, these solutions benefit from the capacity of advanced digital signal processing (DSP) to compensate for linear impairments, which made the transmission system remarkable tolerance to chromatic dispersion (CD) and polarization mode dispersion (PMD). In addition, laser phase noise (LPN) can also be mitigated by feed forward carrier recovery (FFCR) techniques with penalties depending on the transmitter (TX) and receiver (RX) laser linewidth-to-sym- bol rate ratio, however, the computation complexity of FFCR scheme increases significantly for higher-order modulation formats (M-QAM, M = 16, 32, 64, …) [2] . However, nonlinear (NL) impairments caused by fiber Kerreffect are still a major problem in long-haul transmission systems since it limits the maximum launch power, which in turn reduces the maximum achievable reach. Recent years, some researchers have deeply studied on compensating both laser phase noise and nonlinear impairments. Sergejs Makovejs et al. proposed a novel digital signal processing technique for carrier phase estimation and symbol estimation in PDM-16QAM and QPSK transmission system; the obtained results demonstrated that the optimum launch power increased from −4 dBm to −1 dBm with a consequent increase in maximum reach from 1440 km to 2400 km [3] [4] . Mohamed Morsy- Osman et al. proposed and experimentally demonstrated polarization demultiplexing, frequency offset and phase noise compensation using an electrically inserted pilot for Single-Carrier Systems, and reported excellent back- to-back and transmission performances [5] - [8] . The powerful DSP capacity of coherent receiver can also be used to deal with nonlinear impairments, for example, digital inverse backward-propagation [9] - [12] . However, due to the heavy computation during algorithm processing, it’s found that the digital inverse backward-propa- gation compensation for nonlinear effects was very challenging.
In this paper, we proposed a novel monitoring and compensation method for joint phase noise which included LPN and NL phase disturbance. In transmitter, a RF pilot was inserted into monitored channel, due to that it was affected by LPN and NL as same as in-band signals during transmitting. So we can extract the phase deviation of the received RF pilot in receiver and compensate the receiving signal’s phase error based on phase rotation. The theoretical analysis and experimental results were presented. It shows that the proposed method has a significant effect on compensation of joint phase noise in 112 Gb/s PDM-4QAM system.
2. Principle of Joint Phase Deviation Estimate
The proposed model of joint phase deviation estimate is shown in Figure 1. Two-way orthogonal light were separated by the polarization diversity hybrid, at the X-polarization, the light was separated into two ways by the 90˚ phase shift, two ways light were detected by the PD and were orthogonal mixed respectively with the local RF, after, four ways mixed signals respectively get through LPF to remove the high frequency component. The
Figure 1. Architecture of Joint phase estimate. OLO: optical local oscillator; RF: radio frequence (electronic local oscillator).
outputs of LPFs were digital sampled by ADCs and feed into DSP to process based on certain algorithm, and this algorithm was expressed in this paper.
At the Y-polarization, the operating process was same as the X-polarization’s. Finally, both of the X-polari- zation and the Y-polarization signal phase deviation can be estimated respectively.
Following, we illustrate the operation process on X-polarization. The carrier of X-polarization can be given by:
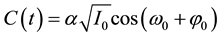 (1)
(1)
and the lower and upper sideband of the pilot at in-phase can be respectively given by:
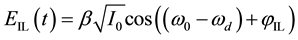 (2)
(2)
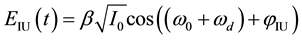 (3)
(3)
and the lower and upper sideband of the pilot at quadrature-phase can be respectively given by:
 (4)
(4)
 (5)
(5)
where 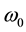 was the optical carrier frequency,
was the optical carrier frequency, 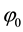 was instantaneous phase of the carrier,
was instantaneous phase of the carrier,  was the frequency of the RF pilot, both
was the frequency of the RF pilot, both 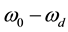 and
and 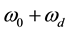 were two frequency elements of the lower and upper sideband,
were two frequency elements of the lower and upper sideband,  and
and 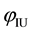 were instantaneous phase of
were instantaneous phase of  and
and 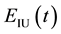 respectively,
respectively, 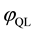 and
and 


During the transmission, the phase of RF pilot must be affected by the fiber nonlinear which contains of cross-phase modulation (XPM), self-phase modulation (SPM), besides, fiber linear impairments (some as chromatic dispersion, polarization mode dispersion) also can load some phase errors on the pilot. So we can estimate the joint phase deviation of the RF pilot to compensate M-QAM signals.
At the receiver, the received







where







The proposed architecture of joint phase estimate for PDM-M-QAM system is shown in Figure 1. As similar with coherent receiver, a coherent front-end integrates polarization beams splitters (PBSs), an optical hybrid, a local laser and balanced photodetectors (BPDs) to provide four signals corresponding to the I and Q components on both polarizations. After the square-law photodetectors and the electronic mixing, four outputs of low-pass filters (LPF) were given by:




where 








where










the phase mode values (PMVs) of in-phase and quadrature-phase can respectively be given by:


from the formulars 17, 18, 19, 20, we can known that 

3. Simulation for 112 Gb/s PDM-4QAM System
The joint phase estimate and compensation simulation configuration for 112 Gb/s PDM-4QAM system was shown in Figure 3. 213 random bits were generated, and transmitting DSP tasks was shown in Figure 4(a) that were carried out at the Nyquist rate in MATLAB R2009b, the transmitting DSP was first performed pulse
Figure 2. The sketch map of phase rotation based on PMVI + j*PMVQ coordinate.
Figure 3. The experimental architecture of joint phase estimate and compensation for 112 Gb/s PDM-4QAM system.
shaping on transmitted data symbols, a root-raised cosine (RRC) pulse shape with a roff-off factor of 0.1 was assumed throughout all simulations. After, the four 28 Gbaud I and Q signals on both polarization were upsampled to 4 samples/symbol and launched into optisystem 9.0 to simulate the optical layer of the transmission system. Note that 4 samples/symbol are used in optisystem to provide enough simulation bandwidth, also, infinite DAC resolution was assumed. At the optical layer simulation, the TX and RX lasers were assumed to have a wavelength of 1554.12 nm and a linewidth of 100 KHz respectively each, four ways RF pilots were loaded through two I-Q modulators which placed at X-pol and Y-pol respectively, and all the RF pilot with the frequency of 250 MHz. The power of the loaded RF pilot depends on the pilot-to-signal power ratio (PSPR), which was defined in [13] , clearly, there was a trade-off between increasing and decreasing PSPR. The larger PSPR, the higher accuracy for phase deviation monitoring, but if PSPR exceeds a certain value, the pilot tone maybe disturbs data signals that lead to bit error rate sharply increase, if PSPR is too small, the pilot tone could be sub- merged by ASE noise and result in phase deviation monitoring is defeated, although that barely induces disturbance to data signals. So an optimized PSPR was carried out according to [6] , and the PSPR was set at −18 dB. Finally, the hybrid modulating signal (contains PDM-4QAM signals and RF pilot tones) were respectively propagated over 10 × 80 km, 20 × 80 km, 30 × 80 km of dispersion unmanaged standard singal mode fiber (SSMF) with attenuation of 




Figure 4. DSP tasks for transmission system in X-polarization: (a) TX side; (b) RX side.
eight LPFs respectively and to extract down-mixing signals, after the signal was downsampled by ADC that processed in MATLAB also. MATLAB where they were first downsampled to their Nyquist rate and then processed Figure 5(b). Finally, a bit-error rate (BER) level of 
4. Simulation Results and Discussion
First, we performed PMV monitoring under conditions of 800 km, 1600 km, 2400 km SMF respectively, the launch powers were set at 0 dBm for three simulations, and the OSNR level of receiver was maintained at 16.5 dB through a white light adjusted noise loading. In this paper we just provided the PMV monitored results corresponding to 128 symbols that to show monitoring feature in different nonlinear strength. And the monitored PMVs corresponding to three different distances were respectively showed in Figures 5-7. The fluctuation of PMV can stand for phase noise that created by the nonlinear effect in ultra long-haul fiber links. Through comparing, the fluctuation of PMVs under the SMF distance of 800 km was smooth compared with 1600 km and 2400 km, that indicated the NL impairments was more serious along with the longer transmission distance.
Then, we performed phase noise compensation based on the proposed phase deviation monitoring technology, the operation specifics as follow: during each symbol cycle, we firstly monitored the PMVs mapping to I and Q phase in each polarizations, and calculate phase deviation for each symbol in each polarizations, after, the phase rotator performed phase rotating for each symbols according to the calculated phase deviation values to realize symbol constellation diagram phase correction, the receiving compensation process was shown in Figure 5, the CD impairments was compensated by the CD linear equalization with Viterbi and Viterbi phase estimation (VVPE) for FFCR [13] . To assess the transmission performance of 112 Gb/s PDM-4QAM system (both with and without the proposed NL phase compensation), the Q-factor was measured as a function of input power for several fixed transmission distances that were plotted in Figure 8. Figure 8(a) showed that the optimum launch power for all measured distances was approximately −4 dBm, for the low input powers the main source of degradation was OSNR degradation due to accumulated ASE noise from the EDFAs in the fiber link, while for higher input powers the performance was degraded due to in-band nonlinearity effect. Applying the proposed
Figure 5. Monitored PMVs corresponding to 128 symbols (SMF: 800 km; OSNR: 16.5 dB; Launch power: 0 dBm).
Figure 6. Monitored PMVs corresponding to 128 symbols (SMF: 1600 km; OSNR: 16.5 dB; Launch power: 0 dBm).
Figure 7. Monitored PMVs corresponding to 128 symbols (SMF: 2400 km; OSNR: 16.5 dB; Launch power: 0 dBm).

Figure 8. The system Q values versus various launch power. (a) Without NL phase compensation; (b) With NL phase compensation.
NL phase compensation that allowed for an increase in the optimum launch power by 3.5 dB for all measured distances, that was showed in Figure 8(b), it’s also observed that the increase of input launch power margin from 5 dB to 10 dB at the distance of 1200 km with the FEC limit of
Constellation diagrams in condition of back to back and after 800 km, 1600 km and 2400 km transmission (both with and without NLC) were showed in Figure 10.
5. Conclusion
In this paper, we proposed a novel method of joint phase noise estimate (JPNE) for PDM-M-QAM (M = 4, 16,
Figure 9. Performance comparison of transmission with and without NLC.
Figure 10. Simulation PDM-4QAM constellation diagrams at 112 Gbit/s. (a) Back to back without noise loading; (b) 800 km transmission without NLC at −4 dBm; (c) 800 km transmission with NLC at −4 dBm; (d) 1600 km transmission without NLC at −1 dBm; (e) 1600 km transmission with NLC at −1 dBm; (f) 2400 km transmission without NLC at −1 dBm; (g) 2400 km transmission with NLC at −1 dBm.
32, 64, …) transmission systems, and established the theoretical model to illustrate the operation mechanism. Through simulation, the random phase noise among four channels of 112 Gb/s PDM-4QAM system was moni- tored; the results indicated that the phase perturbation increased with a long distance, meanwhile, the transmis- sion performance for 112 Gb/s PDM-4QAM system with the proposed NL compensation was investigated, over the range of distances examined. The optimum launch power was found to be −4 dBm with the linear compensa- tion only. We also studied the maximum benefit available from the proposed NL compensation for single-chan- nel transmission and found an increase in optimum launch power from −4 dBm to 0 dBm, with consequent in- crease in maximum reach by 50% to 2400 km.
Acknowledgements
The work described in this paper was carried out with the support of the National Natural Science Foundation of China (61301226), and also supported by “the Fundamental Research Funds for the Central Universities”, HUST: CXY13M001.
References
- Gnauck, A.H., Winzer, P.J., Konczykowska, A., Jorge, F., Dupuy, J., Riet, M., Charlet, G., Zhu, B. and Peckham, D.W. (2012) Generation and Transmission of 21.4-Gbaud PDM 64-QAM Using a Novel High-Power DAC Driving a Single I/Q Modulator. Journal of Lightwave Technology, 30, 532-536. http://dx.doi.org/10.1109/JLT.2011.2175200
- Fatadin, I., Ives, D. and Savory, S.J. (2009) Blind Equalization and Carrier Phase Recovery in a 16-QAM Optical Coherent System. Journal of Lightwave Technology, 27, 3042-3049. http://dx.doi.org/10.1109/JLT.2009.2021961
- Makovejs, S., Millar, D.S., Lavery, D., Behrens, C., Killey, R.I., Savory, S.J. and Bayvel, P. (2010) Characterization of Long-Haul 112 Gbit/s PDM-QAM-16 Transmission with and without Digital Nonlinearity Compensation. Optics Express, 18, 12939-12947. http://dx.doi.org/10.1364/OE.18.012939
- Khairuzzaman, Md., Zhang, C., Igarashi, K., Katoh, K. and Kikuchi, K. (2010) Equalization of Nonlinear Transmission impairments by Maximum-Likelihood-Sequence Estimation in Digital Coherent Receivers. Optics Express, 18, 4776.
- Morsy-Osman, M., Zhuge, Q., Chagnon, M., Xu, X. and Plant, D.V. (2013) Time Domain Hybrid QAM Based Rate-Adaptive Optical Transmissions Using High Speed DACs. Proc. of OFC, OTu3I.6, Los Angeles.
- Morsy-Osman, M., Chen, L.R. and Plant, D.V. (2011) Joint Mitigation of Laser Phase Noise and Fiber Nonlinearity for Polarization-Multiplexed QPSK and 16-QAM Coherent Transmission Systems. Proc. ECOC Tu.3.A.3.
- Lu, G.-W., Nakamura, M., Kamio, Y. and Miyazaki, T. (2007) Ultimate Linewidth-Tolerant 20-Gbps QPSK-Homo- dyne Transmission Using a Spectrum-Sliced ASE Light Source. Optics Express, 15, 7660.
- Morsy-Osman, M., Zhuge, Q., Chen, L.R. and Plant, D.V. (2011) Feedforward Carrier Recovery via Pilot-Aided Transmission for Single-Carrier Systems with Arbitrary M-QAM Constellations. Optics Express, 19, 24331.
- Ip, E. and Kahn, J.M. (2008) Coherent Detection in Optical Fiber Systems. Journal of Lightwave Technology, 26, 3416.
- Mateo, E.F., Zhou, X. and Li, G.F. (2011) Improved Digital Backward Propagation for the Compensation of Inter- Channel Nonlinear Effects in Polarization-Multiplexed WDM Systems. Optics Express, 19, 570.
- Tanimura, T., Nölle, M., Fischer, J.K. and Schubert, C. (2012) Analytical Results on Back Propagation Nonlinear Compensator with Coherent Detection. Optics Express, 20, 28779.
- Mateo, E.F., Yaman, F. and Li, G.F. (2010) Improved Digital Backward Propagation for the Compensation of Inter- Channel Nonlinear Effects in Polarization-Multiplexed WDM Systems. Optics Express, 18, 15144.
- Viterbi, A. (1983) Nonlinear Estimation of PSK-Modulated Carrier Phase with Application to Burst Digital Transmission. IEEE Transactions on Information Theory, 29, 543-551. http://dx.doi.org/10.1109/TIT.1983.1056713
NOTES
*Corresponding author.











