Optics and Photonics Journal
Vol.04 No.09(2014), Article ID:50068,23 pages
10.4236/opj.2014.49025
Calculation of Atomic Data and Gain Coefficient for XUV & Soft X-Ray Laser Emission from Ge XXIII
Wessameldin S. Abdelaziz
National Institute of Laser Enhanced Sciences, Cairo University, Giza, Egypt
Email: wessamlaser@yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 June 2014; revised 18 July 2014; accepted 12 August 2014
ABSTRACT
Energy levels, transition probabilities, oscillator strengths, and collision strengths have been calculated for transitions in Ne-like Ge. The data refer to a 241 fine-structure levels belonging to the configurations 1s2 2s2 2p5nl, 1s2 2s1 2p6nl (n = 3, 4, 5, 6; l = s, p, d, f, g and h), which have been calculated by the fully relativistic flexible atomic code (FAC). These data are used in the determination of the reduced population for the 241 fine structure levels and gain coefficients over a wide range of electron densities (from 2 × 10+20 to 4 × 10+22 cm−3) and at various electron plasma temperatures (650, 850, 1050, 1250, 1450, 1650, 1850) eV by using the MATLAB R2013a Computer program for solving simultaneous coupled rate equations. The reduced population for the 241 fine structure levels the gain coefficients for those transitions with positive population inversion factor are determined and plotted against the electron density.
Keywords:
Energy Levels, Transition Probabilities, Oscillator Strengths, Collision Strengths

1. Introduction
The concept for x-ray lasers went back to the 1965s, when it was based on the laser-produced plasmas by electron de-excitation having a promising interest science, which was first proposed by the Soviet scientists Gudzenko and Shelepin [1] . They thought that the short wavelength laser in the x-ray region of the electromagnetic spectrum needed a large energy gap which was sustained in the highly ionized ions. After ionization, in the equilibrium plasma, ions having specific number of electrons such as 2 (helium-like), 10 (neon-like), 28 (nickel-like) and 46 (palladium-like) were relatively stable and survived in a wide range of temperature and density [2] [3] . X-ray lasers pumping methods are electron collisional excitation, photo excitation, charge transfer, electron collisional recombination and de-electronic recombination pumping using a picosecond chirped pulse amplification (CPA) pulse [4] , a capillary discharge [5] [6] and a free electron laser. However, the electron collisional excitation pumping of the inner shell and outer shell of highly ionization states have shown a more stable and a higher output [7] [8] . Thus, the electron collisional pumping proved to be the most efficient method in producing the x-ray lasers.
Experimentally there exist in the literature some studies trying to develop high-efficiency X-ray laser with significant gain, for example, [3] [9] proposed the original mechanism for demonstrating X-ray lasing by resonant photo pumping. Several authors during the past three decades [10] [11] have studied this lasing mechanism experimentally and theoretically, in the hope of developing high-efficiency X-ray laser. In another study by Qi, N. and Krishnan, M. [12] , the shortest wavelength at which the significant gain had been measured using the resonant photo pumping was in the beryllium-like carbon at 2163 Å, which was far from the X-ray spectral region.
In this paper, we calculate energy levels for 241 fine-structure states using a fully relativistic approach based on Dirac equation (see Table 1). Weighted Oscillator strengths, spontaneous radiative decay rates are calculated in the single multipole approximation (see Table 2), and Collision strengths by electron impact using the factorization-interpolation method are calculated in the distorted wave approximation. Effective collision strengths are calculated by interpolating the data from the collision strengths and integrating over Max wellian distribution at different temperatures. Rate coefficients are calculated from effective collision strengths using a formula that will be described later in this paper. Then, we predict the reduced population and gain coefficient for Ge XXIII by a steady state equation in the collisional radiative model after achieving a population inversion between the allowed transition states.
Table 1. Energy levels of Ge XXIII, and their threshold energies (in eV).
Index: Level index. State Configuration: The configuration to which the level belongs (jj-coupling). Jπ: J is the Total angular momentum, π is the Parity. FAC: Energies from the FAC code (our calculation). COWAN: Energies from the COWAN code (also calculated). NIST: National Institute of Standards and Technology, http://www.nist.gov [24] . Exp.: Energies calculated experimentally [23] . CIV3: Energies from the CIV3 code [22] . MCDF: Energies from the MCDF code [23] . RCI: Energies from the RCI code [23] .
Table 2. Comparison between some weighted oscillator strengths, and transition probabilities for E1 transitions of Ge XXIII.
i and j: The lower (i) and upper (j) levels of a transition as defined in Table 4. gf (nm) (FAC): Weighted oscillator strengths from the FAC code (our calculation). gf (nm) (COWAN): Weighted oscillator strengths from the COWAN code (also calculation). gf (nm) (CIV3): Weighted oscillator strengths from the CIV3 code [22] . gf (nm) (RCI): Weighted oscillator strengths from the RCI code [23] . Aji (s−1) (FAC): Transition probabilities (in nm) from the FAC code (our calculation). Aji (s−1) (COWAN): Transition probabilities (in nm) from the COWAN code (also calculation). Aji (s−1) (CIV3): Transition probabilities (in nm) from the CIV3 code [22] .
2. Gain Coefficient Computations
The possibility of laser emission from plasma of Ge XXIII ion via electron collisional pumping, in the XUV and soft X-ray spectral regions is investigated at different plasma temperatures and plasma electron densities. The reduced population densities are calculated by solving the coupled rate equations [13] [14] .
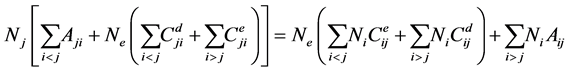 (1)
(1)
where 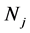 and
and 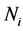 is the fractional population of level
is the fractional population of level  and
and 







where 

The electron impact excitation rates usually are expressed via the effective collision strengths 

where the values of 

The actual population density 


where 

where 



where 241 is the number of all the levels of the ion under consideration, the quantity actually obtained from Equation (1) is the fractional population




where 


where M is the ion mass 




As seen from Equation (8), the gain coefficient is expressed in terms of the upper state density

3. Results and Discussions
3.1. Energy Levels
The energy level values obtained using the fully relativistic flexible atomic code (FAC) for the 1s2 2s2 2p5nl, 1s2
Table 3. Comparison between some wavelengths (λ) for E1 transitions of Ge XXIII (in nm).
i and j: The lower (i) and upper (j) levels of a transition as defined in Table 4. λ (nm) (FAC): Transition wavelengths (in nm) from the FAC code (our calculation). λ (nm)(COWAN): Transition wavelengths (in nm) from the COWAN code (also calculation). λ (nm) (CIV3): Transition wavelengths (in nm) from the CIV3 code [22] . λ (nm) (MCDF): Transition wavelengths (in nm) from the MCDF code [23] . λ (nm) (RCI): Transition wavelengths (in nm) from the RCI code [23] . λ (nm) (Exp.): Transition wavelengths (in nm) calculated experimentally [23] .
2s1 2p6nl (n = 3, 4, 5, 6; l = s, p, d, f, g and h) configurations in Ne-like Ge ions are presented in Table 1. The main components of the computed Eigen vectors are also given in these tables in the jj-coupling schemes. For Ge XXIII, the agreement between FAC, MCDF, and other theoretical and experimental energies [19] - [23] with the values available at the National Institute of Standards and Technology (NIST) [24] and is within values less than 0.5% for a majority of levels.
3.2. Radiative Decay Rates
The oscillator strengths 


where m and e are the electron mass and charge, respectively, c is the velocity of light, 



(Dimensionless) and the line strength S (in atomic units,
The wavelengths, transition probabilities, and weighted oscillator strengths, for E1transitions calculated using the (FAC) are reported in Table 2 and Table 3 for Ge XXIII. We present a comparison between our results and other theoretical transition probabilities for allowed E1 transitions for Ge XXIII in tables respectively. It shows that our results are in a good agreement with the other theoretical and experimental results [22] [23] . Table 2 shows a comparison between the FAC, MCDF, RCI, and other theoretical weighted oscillator strength [22] [23] values for some transitions among the levels of the 1s2 2s2 2p5nl, 1s2 2s1 2p6nl (n = 3, 4, 5, 6; l = s, p, d, f, g and h) configurations for Ge XXIII. Generally, there are no discrepancies between our FAC, COWAN, CIV3, MCDF, RCI, and experimental calculations and the agreement is within ≤20% for strong transitions.
3.3. Level Population
The reduced population densities are calculated for 241 finestructure levels arising from 1s2 2s2 2p6nl, 1s2 2s2 2p5 nl, 1s2 2s1 2p6 nl (n = 3, 4, 5, 6; l = s, p, d, f, g and h) configurations that emit radiation in the XUV and soft X-ray spectral regions. The calculations were performed by solving the coupled rate Equation (1) simultaneously using MATLAB R2013acomputer program. The present calculations for the reduced populations as a function of electron densities are plotted in Figure 1 to Figure 4 for levels (5, 15, 33, 37) of the configurations [(2p1\23s1\2)1,(2p1\23p1\2)0,(2s1\23p1\2)1,(2s1\23d5\2)2] at different plasma temperatures (650, 850, 1050, 1250, 1450,
Figure 1. Reduced population of level (2p1\23s1\2)1 for Ge XXIII after electron collisional pumping as a function of the electron density at temperatures (650, 850, 1050, 1250, 1450, 1650, and 1850) eV.
Figure 2. Reduced population of level (2p1\23p1\2)0 for Ge XXIII after electron collisional pumping as a function of the electron density at temperatures (650, 850, 1050, 1250, 1450, 1650, and 1850) eV.
Figure 3. Reduced population of level (2s1\23p1\2)1 for Ge XXIII after electron collisional pumping as a function of the electron density at temperatures (650, 850, 1050, 1250, 1450, 1650, and 1850) eV.
Figure 4. Reduced population of level (2s1\23d5\2)2 for Ge XXIII after electron collisional pumping as a function of the electron density at temperatures (650, 850, 1050, 1250, 1450, 1650, and 1850) eV.
1650, and 1850) eV for Ge XXIII ion. In the calculation we took into account spontaneous radiative decay rate and electron collisional processes between all levels under the study. The behavior of level populations of the various ions can be explained as follows: in general at low electron densities the reduced population density is proportional to the electron density, where excitation to an excited state is followed immediately by radiative decay, and collisional mixing of excited levels can be ignored. This result is in agreement with that of Feldman et al. [19] - [21] . At high electron densities (Ne > 5 × 1022), the radiative decay to all the levels will be negligible compared to collisional depopulations and all the level populations become independent of the electron density and are approximately equal (see Figures 1 to 4).
3.4. Radiative Lifetime
The lifetimes are determined almost entirely from the allowed and the strong inter combination transitions. The radiative lifetime 


where the sum is extended over all the lower states which can be reached from the upper state by radiative decay.
Table 4 contains the present results of radiative lifetime for the upper and lower laser levels for the Ge XXIII.
3.5. Inversion Factor
As we mentioned before, laser amplification will occur only if there is population inversion, or in other words, for positive inversion factor F > 0. However, large amplification, the gain exceeds all losses and ensures laser emission. In order to work in the XUV and X-ray spectral regions, we have selected transitions between any two levels producing photons with wavelengths between 12 and 52 nm. The electron density at which the population reaches corona equilibrium approximately equals to A/D, where A is the radiative decay rate and D is the collisional de-excitation rate [19] [21] . The population in version is largest where the electron collisions de-excitation rate for the upper level is comparable to the radiative decay rate for this level.
3.6. Gain Coefficient
As a result of population inversion there will be positive gain in laser medium. Equation (8) has been used to calculate gain coefficient for the Doppler broadening of various transitions in the Ge XXIII ion. Our results for the maximum gain coefficient in cm−1 for those transitions having appositive inversion factor F > 0 in the case of Ge XXIII ion at different temperatures are calculated (see Table 4) and plotted against electron density in Figure 5 and Figure 6. The figures show that the population inversions occur for several transitions in the Ge
Figure 5. Gain coefficient against electron density (Ne) at different temperatures (650, 850, 1050, 1250, 1450, 1650, 1850) eV.
Figure 6. Gain coefficient against electron density (Ne) at different temperatures (650, 850, 1050, 1250, 1450, 1650, 1850) eV.
XXIII ion, however, the largest gain occurs for the Ge XXIII ion at (2s1\23d5\2)2-----(2s1\23p3\2)1 transition. These short wavelength laser transitions can be produced using plasmas created by optical lasers as the lasing medium. For Ge XXIII ion the rates for electron collisional excitation from the 1s2 2s2 2p6 ground state to the 1s22s12p63d configuration are greater than the rates for excitation from the ground state to the 1s22s12p63p state. For electron densities and electron temperatures that are typical of laboratory high-density plasma sources, such as laser produced plasmas, it is possible to create a quasi-stationary population inversion between the 2s1 2p63d and 2s1 2p63p states in Ge XXIII ion. Our calculations have shown that under favorable conditions large laser gains for this transition in the XUV and soft X-ray regions of the spectrum can be achieved in the Ge XXIII. The gain calculations were performed at electron temperatures equal to (650, 850, 1050, 1250, 1450, 1650, and 1850) eV at different electron densities. It is obvious that the gain increases with the temperature. We also find that some wavelengths for the lasing transitions in Table 4 are much closed to the values of it in the ref. [23] which give us the accurate wavelength calculated experimentally, although we Ignores some physical processes in the our rate equation.
4. Conclusions
The analysis of how the electron collisional pumping (ECP) is suitable for attaining population inversion and offering the potential for laser emission in the spectral region between 12 and 53 nm from the Ge XXIII ion.
This class of lasers can be achieved under the suitable conditions of pumping power as well as electron density. If the positive gains obtained previously for some transitions in the ions under studies (Ge XXIII ion) together with the calculated parameters can be achieved experimentally, then successful low-cost electron collisional pumping XUV and soft X-ray lasers can be developed for various applications. The results have suggested the laser transitions in the Ge XXIII plasma ion (see Table 4), as the most promising laser emission lines in the XUV and soft X-ray spectral regions.
References
- Gudzenko, L.I. and Shelepin, L.A. (1966) Amplification of Radiation in the Decay of a Maximally Ionized Plasma. Journal of Applied Mechanics and Technical Physics, 7, 82.
- Maxon, S., Hagelstein, P., Reed, K. and Scofield, J. (1985) A Gas Puff Soft X-Ray Laser Target Design. Journal of Applied Physics, 57, 971. http://dx.doi.org/10.1063/1.334700
- Vinogradov, A.V., Sobelman, I. and Yukov, E. (1977) Population Inversion of Transitions in Neon-Like Ions. Soviet Journal of Quantum Electronics, 7, 32. http://dx.doi.org/10.1070/QE1977v007n01ABEH008807
- King, R.E., Pert, G.J., McCabe, S.P., Simms, P.A., MacPhee, A.G., Lewis, C.L.S., et al. (2001) Saturated X-Ray Lasers at 196 A and 73 A Pumped by Picosecond Travelling Wave Excitation. Physical Review A, 64, Article ID: 053810. http://dx.doi.org/10.1103/PhysRevA.64.053810
- Rocca, J.J., Shlyaptsev, V., Tomasel, F.G., Cortázar, O.D., Hartshorn, D. and Chilla, J.L.A. (1994) Demonstration of a Discharge Pumped Table Top Soft X-Ray Laser. Physical Review Letters, 73, 2192. http://dx.doi.org/10.1103/PhysRevLett.73.2192
- Tomsel, F.G., Rocca, J.J., Shlyaptsev, V.N. and Macchietto, C.D. (1997) Lasing at 60.8 nm in Ne-Like Sulfur Ions in Ablated Material Excited by a Capillary Discharge. Physical Review A, 55, 1437.
- Healy, S.P., Janulewicz, K.A. and Pert, G.J. (1997) Short Wavelength Lasing on Collisionally Pumped, Highly Excited 2s Hole States of Neon Like Ions in Performed Plasmas Irradiated with Picosecond Pulses. Optics Communications, 144, 24-30. http://dx.doi.org/10.1016/S0030-4018(97)00287-3
- Simms, P.A., McCabe, S. and Pert, G.J. (1998) Comparison of Neon Like Germanium Inner Shell and Nickel Like Gadolinium at 62 A and 66 A by Picosecond Heating of a Performed Plasma. Optics Communications, 153, 164-171.
- Norton, B.A. and Peacock, N.J. (1975) Population Inversion in Laser-Produced Plasmas by Pumping with Opacity- Broadened Lines. Journal of Physics B, 8, 989. http://dx.doi.org/10.1088/0022-3700/8/6/026
- Bhagavatula, V.A. (1976) Soft X-Ray Population Inversion by Resonant Photoexcitation in Multicomponent Laser Plasmas. Journal of Applied Physics, 47, 4535. http://dx.doi.org/10.1063/1.322425
- Nilsen, J., Beiersdorfer, P., Elliott, S.R., Phillips, T.W., Bryunetkin, B.A., Dyakin, V.M., Pikuz, T.A., Faenov, A.Ya., Pikuz, S.A., von Goeler, S., Bitter, M., Loboda, P.A., Lykov, V.A. and Politov, V.Yu. (1994) article title. Physical Review A, Article ID: 502143.
- Qi, N. and Krishnan, M. (1988) Enhancement of Ultraviolet Laser Plasma Emission Produced in a Strong Static Electric Field. Optics Communications, 67, 124-128.
- Feldman, U., Bhatia, A.K. and Suckewer, S. (1983) Short Wavelength Laser Calculations for Electron Pumping in Neon-Like Krypton (Kr XXVII). Journal of Applied Physics, 54, 2188. http://dx.doi.org/10.1063/1.332371
- Feldman, U., Seely, J.F. and Bhatia, A.K. (1984) Scaling of Collisionally Pumped 3s-3p Lasers in the Neon Isoelectronic Sequence. Journal of Applied Physics, 56, 2475. http://dx.doi.org/10.1063/1.334308
- Chapline, G. and Wood, L. (1975) X-Ray Lasers. Physics Today, 28, 40. http://dx.doi.org/10.1063/1.3069004
- Vinogradov, A.V. and Shlyaptsev, V.N. (1980) Calculations of Population Inversion Due to Transitions in Multiply Charged Neon-Like Ions in the 200-2000 Å Range. Soviet Journal of Quantum Electronics, 10, 754. http://dx.doi.org/10.1070/QE1980v010n06ABEH010287
- Goldstein, W.H., Oreg, J., Zigler, A., Bar-Shalom, A. and Klapisch, M. (1988) Gain Predictions for Nickel-Like Gadolinium from a 181-Level Multiconfigurational Distorted-Wave Collisional-Radiative Model. Physical Review A, 38, 1797. http://dx.doi.org/10.1103/PhysRevA.38.1797
- Sobel’man, I.I. (1979) Introduction to the Theory of Atomic Spectra, International Series of Monographs in Natural Philosophy. Vol. 40, Pergamon Press, Oxford.
- Hagelstein, P.L. (1986) Relativistic Distorted-Wave Results for Nickel-Like Gadolinium. Physical Review A, 34, 874. http://dx.doi.org/10.1103/PhysRevA.34.874
- Zhang, H.L., Samson, D.H. and Fontes, C.J. (1991) Relativistic Distorted-Wave Collision Strengths and Oscillator Strengths for the 33 Ni-Like Ions with 60 ≤ Z ≤ 92. Atomic Data and Nuclear Data Tables, 48, 91-163. http://dx.doi.org/10.1016/0092-640X(91)90024-X
- Feldman, U., Doschek, G.A., Seely, J.F. and Bhatia, A.K. (1985) Short Wavelength Laser Calculations for Electron Pumping in Be I and B I Isoelectronic Sequences (18 ≤ Z≤ 36). Journal of Applied Physics, 58, 2909. http://dx.doi.org/10.1063/1.335838
- Hibbert, A., Ledourneuf, M. and Mohan, M. (1993) Energies, Oscillators Strengths, and Life Times for Neon-Like Ions up to Kr XXVII. Atomic Data and Nuclear Data Tables, 53, 23-112.
- Daido, H., Kodama, R., Murai, K., Yuan, G., Takagi, M., Kato, Y., Choi, I.W. and Nam, C.H. (1995) Significant Improvement in the Efficiency and Brightness of the J = 0-1 19.6-nm Line of the Germanium Laser by Use of Double-Pulse Pumping. Optics Letters, 20, 61-63.
- NIST. http:///F:/NIST/NIST%20ASD%20Levels%20Output32.htm











