Optics and Photonics Journal
Vol.4 No.6(2014), Article ID:47047,7 pages
DOI:10.4236/opj.2014.46013
Optical Fiber Torsion Sensor with Mechanically Induced Long Period Fiber Gratings in Rare-Earth Doped Fibers
Maria Pulido-Navarro1*, José Álvarez-Chávez1, Daniel Ceballos-Herrera2, Ponciano Escamilla-Ambrosio3
1Instituto Politécnico Nacional, Centro de Investigación e Innovación Tecnológica (CIITEC-IPN), Mexico City, Mexico
2Universidad Autónoma de Nuevo León (UANL), Nuevo León, Mexico
3Instituto Politécnico Nacional, Centro de Investigación en Computación (CIC-IPN), Mexico City, Mexico
Email: *mgpulido88@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 March 2014; revised 18 April 2014; accepted 12 May 2014
ABSTRACT
In this work wavelength sensitivity in mechanically induced long period fiber gratings (MLPFG) is analyzed. This analysis is first carried out both in standard single-mode fiber SMF-28 and in Er-doped fibers. The mechanical analysis for both types of fibers under different torsion conditions is presented. In order to apply the torsion one of the fiber ends is fixed while torsion is applied on the other end. A MLPFG whose period is 503 µm is used to press the fiber after torsion is applied. This allows for micro curvatures to be formed on the fiber, which in turn generates a periodical index perturbation on it. Here, it was noted that the sensitive wavelength shift of the rejection bands is bigger for Er-doped fibers. For a torsion of 6 turns applied to 10 cm of doped fiber the wavelength peaks can be moved up to 25 nm, which is longer to what was detected on standard fibers. Therefore, by using Er-doped fibers to monitor torsion on structures will give more sensitive and accurate results than using standard fibers. These results can be employed for sensing applications, especially for small to medium size structures, which can be mechanical, civil or aeronautics.
Keywords:Optical Fiber Sensors, Fiber Bragg Gratingsensors, Torsion Sensors, Rare-Earth Doped Fibers

1. Introduction
Torsion sensors are useful in the analysis of the working status of structures. Conventional torsion sensors are normally based on angle measurement devices, such as optical encoders and magnetic sensors [1] . These types of sensors have a large size and are usually difficult to be embedded into structures. The concept of smart structure is one in which the structure has been provided with a system that is capable of real time and in-situ measurement. Recently, sensors that can be embedded into structures have drawn a lot of attention because they can provide the technological basis for the development of smart structures [2] . Sensors based on optical fibers can be embedded or attached to structures allowing for higher sensitivity to external changes and thus exhibit better reliability. There are many types of sensors based on optical fibers. They are classified into three main types: interferometric, distributed and sensors based on Bragg gratings. An interferometric sensor consists of an optical cavity which goes from one end of the fiber to the surface to be analyzed. Two beams of light are employed; they travel along two different optical paths, made up of a system of mirrors that finally converge in order to form an interference pattern. The physical changes in structures are reflected by the changes in the optical phase between the interference of two lightwaves [3] . A distributed sensor refers to a kind of sensor where the optical fiber itself is the sensor, with lengths in the range of kilometers [4] . Distributed sensors are based on backscattering. They use this phenomenon as their measurement basis in order to improve sensitivity in the detection of discontinuities in structures. Scattering is divided into three phenomena: Rayleigh backscattering, Brillouin scattering and Raman, either stimulated or spontaneous [5] -[7] . Finally, Bragg gratings are periodic perturbations of the core of the fiber, where the distance between perturbations is called period (Λ). Within sensors based on Bragg gratings there are two types of gratings: short and long period fiber gratings (LPFG). Short period Bragg gratings show periodic perturbations with periodicities under 100 µm [8] . For LPFG the periodicities are from 100 µm up to 1000 µm [9] [10] . In LPFGs when light is incident into the fiber, the light couples into the co-propagating higher order modes producing, in the transmission spectrum, a series of missing bandwidths called resonance wavelengths. The resonance wavelengths depend directly on the Bragg period and the refraction index of the core of the fiber. These parameters are affected by external environmental changes such as temperature, humidity or strain. When this change occurs, the resonance wavelength shifts. By measuring this shift it is possible to relate the change in wavelength with strain, temperature or humidity. One advantage of LPFGs is that it is possible to have hundreds of sensors in the same optical fiber. LPFGs present some advantages over FBG such as simplicity of fabrication, low back reflection, low insertion loss and high sensitivity to temperature, bending and torsion [11] .
2. Long Period Fiber Gratings Fabrication Methods
Many methods have been studied and proposed for the fabrication of LPFGs. Ultraviolet (UV) laser exposure, is the preferred technique because of its ease of fabrication and mass production. With this method the amount of index change depends directly on the intensity and duration of the UV laser. The resulting index modulation is symmetrical and as a result of this, only axially symmetric cladding modes are coupled. The greatest disadvantage of this method is that the fiber needs to pass through a process of sensitization before manufacturing the gratings. Furthermore with time they tend to decay and cannot stand temperatures in the order of 600˚C [12] . Other proposed methods such as CO2 laser irradiation, mechanical pressure, etched corrugations, electric-arc discharge, ion beam implantation and femtosecond laser exposure are asymmetric techniques [13] [14] . CO2 laser irradiation at 10.6 µm produces gratings with high temperature stability. For the etched corrugation a tensile load is applied to the fiber resulting in a periodic strain variation in the fiber which causes a periodic modulation of the refractive index through the photoelastic effect. Electric-arc discharge is a method that uses a commercial fusion splicer, which has as its main advantages its simplicity and low cost. The splicer creates the index modulation on the fiber by local heating. The femtosecond technique uses pulses in the near infrared around 800nm. The irradiation causes densification of the glass and the gratings can stand temperatures up to 500˚C [15] . Compared with other methods, mechanical pressure is a flexible technique of low cost and also no previous process to prepare the fiber is required. Furthermore, this technique benefits from being a reversible process [16] , which means that once the mechanical piece is removed, the mechanical integrity of the fiber is kept. This is quite useful for research work and for field devices.
3. Theory
LPFGs contain a series of attenuation bands centered at discrete wavelengths. The attenuation is due to the coupling of light from the fundamental core mode (LP01) to selected cladding modes. The only cladding modes (LPmk o HE1k) to which the guided core mode can couple are those that exhibit azimuthally symmetric intensity profiles with central peaks, where m = 0 and k = (1, 2, 3,…). Light coupled to the cladding at specific wavelength modes is attenuated or radiated out giving as a result rejections bands in the transmission spectrum [17] . The phase-matching condition for LPFGs is [18] :
 (1)
(1)
where
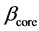 and
and
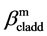 are the propagation constants of the fundamental core mode and the cladding mode,
respectively; Λ is the grating period, and m is the order of cladding modes. Therefore,
the resonance condition for coupling is given by [17]
:
are the propagation constants of the fundamental core mode and the cladding mode,
respectively; Λ is the grating period, and m is the order of cladding modes. Therefore,
the resonance condition for coupling is given by [17]
:
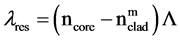 (2)
(2)
where
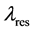 is the initial resonant wavelength,
is the initial resonant wavelength,
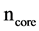 and
and
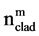 are effective indexes of the fundamental core mode and cladding mode, respectively.
are effective indexes of the fundamental core mode and cladding mode, respectively.
The minimum transmission of the attenuation band is given by [19] :
![]() (3)
(3)
where L is the length of the LPFG and κi is the coupling coefficient for the ith cladding mode.
For telecommunications purposes, low sensitivity is desired because it will minimize
the influence of environmental conditions. On the contrary, for sensors systems,
high sensitivity is seen as an advantage. An important characteristic of LPFGs is
their sensitivity, so full characterization is essential. In a natural environment,
the LPFG characteristics are affected as the external conditions change. The sensing
effects are primarily due to a differential change induced in the two modes. More
specifically, since the effective indexes
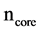 and
and
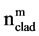 undergo dissimilar changes owing to a change in the external conditions, the difference
between the effective indexes of the two modes Δneff, is altered. What
is more, a fixed periodicity of the LPFG shrinks or stretches resulting from a change
in external conditions as well. Therefore, the resonance wavelength of the LPFG
has got to shift due to the change of Δneff and/or Λ. Consequently, the
change of external parameters such as temperature, strain, bending, torsion and
load, can be determined by measuring or calculating the resonance wavelength shift
of the LPFG.
undergo dissimilar changes owing to a change in the external conditions, the difference
between the effective indexes of the two modes Δneff, is altered. What
is more, a fixed periodicity of the LPFG shrinks or stretches resulting from a change
in external conditions as well. Therefore, the resonance wavelength of the LPFG
has got to shift due to the change of Δneff and/or Λ. Consequently, the
change of external parameters such as temperature, strain, bending, torsion and
load, can be determined by measuring or calculating the resonance wavelength shift
of the LPFG.
4. Experiment
In this section the torsion sensitivity of a Mechanical LPFG (MLPFG) on a standard single mode fiber SMF-28 and an Erbium-doped fiber is investigated. MLPFG is made up of two plates; one flat and the other grooved. For this experiment the grooved plate was done on an acrylic slab with the help of a CNC (Computer Numerical Control). In this case the change in the core refractive index of the fiber is accomplished by putting the fiber in between the two plates, and as can be appreciated from Figure 1, the fiber acquires the form of the grooved plate slots. MLPFG present the benefit of tunability; it means that the grating period can be modified by rotating the angle α between the grooved plate and the longitudinal axis of the fiber, as shown from the top view of the mechanical device in Figure 1. For our experiment a mechanical plate of 4cm length with a grooved period Λ of 503 µm is used. The grooved depth is 300 µm and its resonance wavelength and amplitude are 1530 nm and −62 dB, respectively. The length of the tested fiber is about 10 cm. The two ends of the fiber were fixed at two holders; one end of the fiber is twisted by rotating a disc attached to one of the holders by N circles. The fiber is twisted before being pressed with the grooved plate. The twist can be removed by rotating the disc in opposite direction or through releasing the fiber from the holders, which allows the fiber to recover its original mechanical properties.
A white light and a light source at 980 nm in amplified spontaneous emission (ASE) were used for the standard and the doped fibers, respectively. An optical spectrum analyzer (OSA) was used to measure the transmission spectrum as the fibers were twisted. On the other hand, by placing the mechanical induced grating at the right angle α, the peaks of the grating can be tuned until they are observed in the ASE spectrum, as can be seen
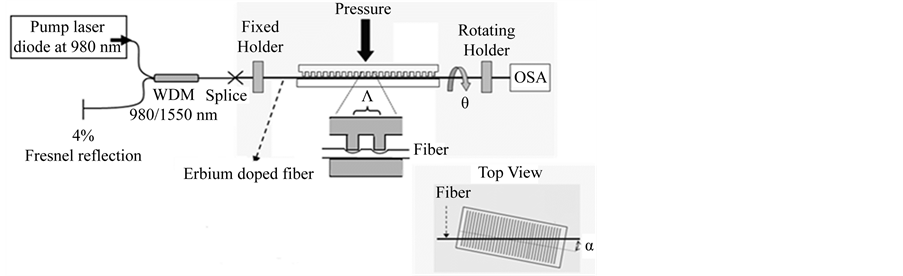
Figure 1. Experimental setup for torsion characterization of mechanically induced LPFG in Er-doped fibers.
in Figure 2 and Figure 3. What is important on this instance is to observe how the peaks are formed when the MLPFG is positioned before torsion perturbations are applied. After this step and for comparison purposes, before pressing the fiber with the grooved plate, the fiber is twisted with the rotating holder and positioned over the flat plate as can be seen in Figure 1. Subsequently, the torsion effect is shown on the four peaks of the grating. Before working on the doped fiber, experiments were carried out first on the standard SMF-28 fiber. From Figure 2, it can be observed that after 6 rotations the wavelength shifted around 3 nm, from 1223.8 nm to 1227.4 nm. After that, the laser is operated in ASE for the doped fiber. From Figure 3, four peaks are observed just before rotation is performed (1510, 1522, 1565 y 1640 nm). From Figure 4 and after torsion is applied, it is detected that the peaks shifted. This figure shows both peaks: before and after rotation, the only purpose of getting this figure is for a better analysis of the peaks position. From the results in Figure 4 it can be observed that the four peaks shift to smaller wavelengths and every peak shifts at different rate. In order to observe in a more detailed way this rate changes, the movement of the peaks for different fiber twisting are shown in the graph from Figure 5.
From Figure 5 it can be observed that the shift on the central wavelength of the peaks with different values of twisting have a linear behavior. All the measurements made in order to obtain the Figure 3 and Figure 4 were done using an OSA with a resolution of 0.2 nm. Also from Figure 5 it can be observed that for a twist of 6 laps done onto a piece of doped fiber of 10 cm length, the peaks shifted up to 25 nm. The aforementioned in particular improves what has been reported for standard fiber SMF-28. Therefore, it can be stated that Erbium doped fibers are superior on sensing twisted strain in structures.
5. Conclusion
This work was done with the idea to prove that the sensitivity of LPFGs under twisted circumstances is increased when using doped fibers instead of standard fibers. The aforementioned was corroborated; it was found that the sensitivity is highly increased when using MLPFG on doped fibers and it was observed that the peak wavelengths can shift up to 25 nm. MLPFG are easy to fabricate, cost effective and also tunable and reversible. The pressure applied on the LPFG changes the refractive index of the fiber core, thus, the grating period can be easily tuned by changing the angle α between the fiber and the grooved plate, which in turn will vary the resultant resonance wavelength. In future experiments, the resonance wavelength could be easily controlled via the grating period Λ. Furthermore, the period depth plays a role in the mode coupling efficiency. It was observed that for period depths of 300 µm and above led to stronger mode coupling. It shows deeper dips which is the result of induced higher index variation. For this work, mechanical LPFGs were used for study purposes, once the right grating period is determined, the in-fiber Bragg grating can be achieved by the traditional methods, usually by UV radiation. This work is of great importance because it showed that by using doped fibers instead of standard fibers the sensitivity is increased and for sensing purposes it is a relevant issue.
Acknowledgements
M.G. Pulido-Navarro wishes to thank CONACYT for the studentship towards her Ph.D. studies. J.A. Alvarez-
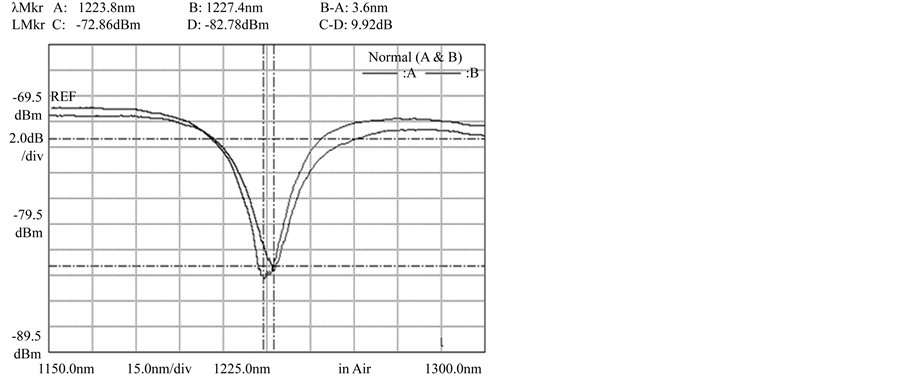
Figure 2. Wavelength shift in standard SMF-28 with MLPFG.

Figure 3. ASE Spectra of the Er-doped fiber with the mechanically induced LPFG.
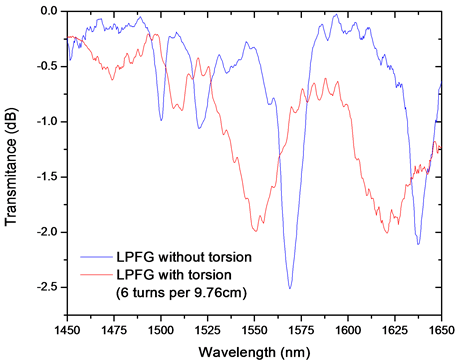
Figure 4. ASE Spectra of the Er-doped fiber with the mechanically induced LPFG under torsion.
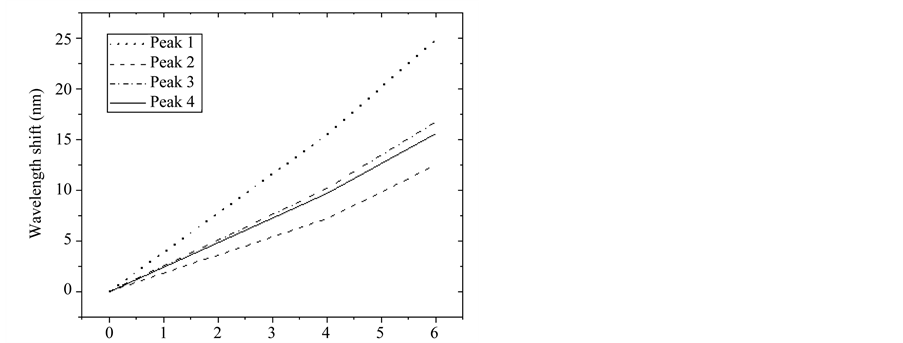
Figure 5. Wavelength shift of each peak of the LPFG at different twist rates.
Chavez would like to thank CONACYT, CIITEC-IPN and CONACYT Ciencia Basica, for the funding of his projects.
References
- Lemarquand, V. (1999) Synthesis study of Magnetic Torque Sensors. IEEE Transactions on Magnetics, 35, 4503-510. http://dx.doi.org/10.1109/20.809143
- Wang, Y. and Rao, Y. (2004) Long Period Fibre Grating Torsion Sensor Measuring Twist Rate and Determining Twist Direction Simultaneously. Electronics Letters, 40, 3.
- Pinet, E., Hamel, C., Glisic, B., Inaudib, D. and Mironic, N. (2007) Health Monitoring with optical Fiber Sensors: From Human Body to Civil Structures. SSN10 Conference Health Monitoring of Structural and Biological Systems, San Diego, 18-22.
- Hotate, K. (2012) Distributed Fiber Sensing Technology: Currents and Challenges. Optica Pura y Aplicada, 45, 63-69. http://dx.doi.org/10.7149/OPA.45.2.63
- Peled, Y., Motil, A. and Kressel, I. (2013) Monitoring the Propagation of Mechanical Waves Using an Optical Fiber Distributed and Dynamic Strain Sensor Based on BOTDA. Optics Express, 21, 10697-10705. http://dx.doi.org/10.1364/OE.21.010697
- Heiman, D., Hamilton, D. and Hellwarth, R. (1979) Brillouin Scattering Measurements on Optical Glasses. Physical Review, 19, 6583-6592. http://dx.doi.org/10.1103/PhysRevB.19.6583
- Inaudi, D. and Glisic, B. (2006) Distributed Fiber Optic Strain and Temperature Sensing for Structural Health Monitoring. The Third Int’l Conference on Bridge Maintenance, Safety and Management, Portugal, 8.
- Ladicicco, A., Paladino, D., Pilla, P., Campopiano, S., Cutolo, A. and Cusano, A. (2012) Long Period Gratings in New Generation Optical Fibers. Recent Progress in Optical Fiber Research. Dr. Moh. Yasin (Ed.), Italy, 291-326.
- Sun, L., Li, J., Jin, L. and Guan, B. (2012) Structural Microfiber Long-Period Gratings. Optics Express, 20, 18079-18084. http://dx.doi.org/10.1364/OE.20.018079
- Bhatia, V. (1999) Applications of Long-Period Gratings to Single and Multi-Parameter Sensing. Optics Express, 4, 457-466. http://dx.doi.org/10.1364/OE.20.018079
- Rao, Y. (2012) OFS Research over the Last 10 Years at CQU & UESTC. Photonic Sensors, 2, 97-117. http://dx.doi.org/10.1007/s13320-012-0057-4
- Zhang, B.W. and Kahiziri, M. (2007) High-Temperature Resistance Fiber Bragg Grating Temperature Sensor Fabrication. Sensors Journal, 7, 586-591. http://dx.doi.org/10.1109/JSEN.2007.891941
- Wang, Y., Wang, D. and Jin, W. (2006) CO2 Laser-Grooved Long Period Fiber Grating Temperature Sensor System Based on Intensity Modulation. Applied Optics, 45, 7966-7970. http://dx.doi.org/10.1364/AO.45.007966
- Vengsarkar, A., Lemaire, P., Judkins, J., Bhatia, V., Erdogan, T. and Sipe, J. (1996) Long-Period Fiber Gratings as Band-Rejection Filters. Journal of Lightwave Technology, 14, 58-65. http://dx.doi.org/10.1109/50.476137
- James, S. and Tatam, R. (2003) Optical Fibre Long-Period Grating Sensors: Characteristics and Application. Measurement Science and Technology, 14, 49-61. http://dx.doi.org/10.1088/0957-0233/14/5/201
- Ceballos-Herrera, D., Torres-Gómez, I., Martínez-Ríos, A. and Sánchez-Mondragón, J. (2009) Higher-Order Core Mode Resonances in a Mechanically Induced Long-Period Holey Fiber Grating. Optical Review, 16, 622-626. http://dx.doi.org/10.1007/s10043-009-0120-6
- MacDougall, T., Pilevar, S., Haggans, C. and Jackson, M. (1998) Generalized Expression for the Growth of Long Period Gratings. IEEE Photonics Technology Letters, 10, 1449-1451. http://dx.doi.org/10.1109/68.720290
- Zhu, T., Rao, Y., Wang, J. and Song, Y. (2007) Strain Sensor without Temperature Compensation Based on LPFG with Strongly Rotary Refractive Index Modulation. Electronics Letters, 43, 1132-1133. http://dx.doi.org/10.1049/el:20071568
- Kashyap, R. (1999) Fibre Bragg Gratings. Academic, New York.
NOTES

*Corresponding author.

