Optics and Photonics Journal
Vol.4 No.3(2014), Article ID:44245,8 pages DOI:10.4236/opj.2014.43007
Numerical Study of Transient Temperature Distribution in Passively Q-Switched Yb:YAG Solid-State Laser
Jala M. El-Azab1, Hamed M. Kandel1, Mohamed A. Khedr1, Hatem M. El-Ghandoor2
1National Institute of Laser Enhanced Sciences, Cairo University, Cairo, Egypt
2Physics Department, Faculty of Science, Ain Shams University, Cairo, Egypt
Email: hamed_kandel@niles.edu.eg
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 3 January 2014; revised 5 February 2014; accepted 4 March 2014
ABSTRACT
In this work, the thermal characterization of continuously pumped passively Q-switched laser is quantitatively represented. The system under investigation is end-pumped Yb:YAG passively Q-switched by Cr4+:YAG as saturable absorber. The rate equations describing the dynamics of laser action are numerically solved simultaneously with the temperature conductivity heat equation to depict the transient temperature distribution. The study has been performed in the cylindrical coordinates to characterize the temperature distribution in the axial and radial directions. The thermal transient time in both directions as well as the thermal focal length are calculated. The temporal behavior of the temperature distribution has been illustrated in a 3-dimensional diagram.
Keywords:Q-Switched Laser; Temperature Distribution; Thermal Lensing

1. Introduction
The thermal distribution, within the laser active medium of Q-switched solid-state lasers when subjected to optical pumping, has been studied by many authors [1] -[3] . Also, the focal length of the thermal lens has been calculated [4] -[6] .
Most of the research has dealt with the temperature distribution inside the active medium at the steady-state and only some have studied the transient behavior especially in passive Q-switched solid state lasers. During the pulse generation, the population inversion density varies with time, resulting in a variation of the absorption of optical pump power. Therefore, the temperature distribution will be altered accordingly and exhibits undulations. The population inversion density has been drawn by a sawtooth time function by Jianlang Li et al. [7] to qualitatively study the radial temperature distribution in CW end-pumped passively Q-switched laser, using MATLAB® PDE toolbox, to solve the parabolic heat equation. However, due to the repetitive thermal load of the Qswitched lasers, the quantitative study of both radial and axial temperature distributions requires solving the coupled laser rate equations simultaneously with the thermal conductivity equation which is extensively numerically complicated. Tao Li et al., [8] have studied the effect of different pumping power and repetition rate for different active media of active Q-switched lasers on the temperature distribution. Recently, Mohammadzahery et al., estimated the time dependence of the thermal power density by calculating the maximum pulse power from the laser output parameters before using MATLAB® PDE toolbox for passively Q-switched microchip Nd:YAG laser [9] .
In the present work, a numerical model for passive Q-switching lasers has been developed to quantitatively describe the temperature distribution in both axial and radial directions. This was carried out by solving the coupled laser rate equations using fourth order Runge-Kutta method in conjunction with the thermal conductivity equation using finite difference method. The model has been applied to Yb:YAG passively Q-switched by Cr4+:YAG as saturable absorber due to its simple energy level scheme, long upper laser level lifetime, low quantum defects which decrease heat generation during lasing three folds less than Nd-based laser systems [8] . The rate equations describing the Q-switched laser and the thermal behavior are given in Section 2. The results are represented and discussed in Section 3 and concluded in Section 4.
2. Thermal Theoretical Model
According to the passively Q-switched theory, the modified coupled rate equations of photon density and population inversion density of gain medium and the saturable absorber in the passively Q-switched resonator are given by [10] -[12] :
 (1)
(1)
 (2)
(2)
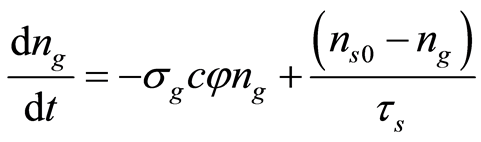 (3)
(3)
 (4)
(4)
where φ is the photon density in the laser cavityσ is the stimulated emission cross-section of the laser crystaln is the population inversion density of the gain mediumtr is the cavity round-trip time (tr = 2 l//c) of laser cavity of optical length l/σg is the absorption cross-section of ground state of the saturable absorberσe is the absorption cross-section of the excited statec is the speed of the lightls is the length of the saturable absorberng and ne are the absorber ground state and excited state population density respectivelyns0 is the total population density of the saturable absorberL is the nonsaturable intracavity round-trip dissipative optical lossR is the reflectivity of the output couplerγ is the inversion reduction factor (γ = 2 for Yb3+-doped three-level solid state lasers)Wp is the volumetric pump powert is the lifetime of the upper laser level of the gain mediumts is the excited-state lifetime of the saturable absorber.
Solving the coupled rate Equations (1) to (3), the population inversion density  as a function of time can be obtained. The absorption coefficient
as a function of time can be obtained. The absorption coefficient  is a function of population inversion density given by [7] :
is a function of population inversion density given by [7] :
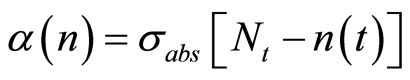 (5)
(5)
where, σabs is the absorption cross-section of the laser crystal at pump wave length and Nt is the doping concentration of the active medium. Considering the active medium as a rod of radius r0 and length l, the laser crystal is held at room temperature using a cooling heat sink at 300 K. Therefore, the temperature distribution will be radially symmetric and the temporal behavior of the thermal load of the active medium in the cylindrical coordinates can be expressed as:
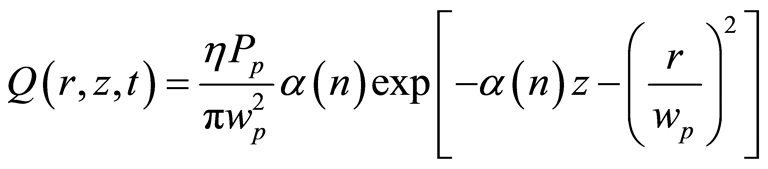 (6)
(6)
where, η is fractional thermal load and wp is the radius at the pump beam waist. While the transient temperature distribution can be obtained by solving the thermal conductivity equation described by the partial differential equation [7] :
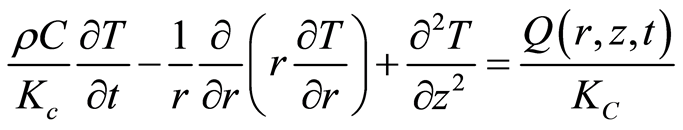 (7)
(7)
with boundary conditions
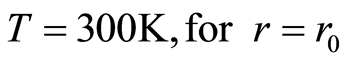 (8)
(8)
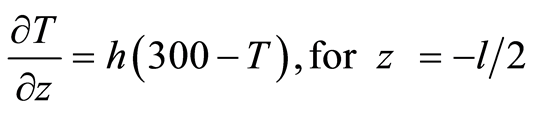 (9)
(9)
 (10)
(10)
where, ρ is the mass density, C is the specific heat of active medium, KC is the thermal conductivity, T is the temperature, r and z are the radial and axial coordinates of the points in the laser crystal, respectively and h is heat transfer coefficient between the laser crystal surface and air. The radial and axial thermal time constants are known as [13]
 (11)
(11)
The thermal relaxation time can be defined as the time at which the temperature in the center of the rod decays to 1/e of its initial value [14] .
 (12)
(12)
The temperature instability (the thermal oscillation contrast) can be calculated as following [8] :
 (13)
(13)
where, ΔT is the repetitively oscillatory amplitude, Trise is the temperature rise at the center of pump facet and Tmax and Tmin are the temperature distribution peak and valley values, respectively.
The temperature distribution in end-pumped laser may result in thermal lensing, assuming only radial heat flow in laser rod that is in contact with heat sink of fixed temperature. The focal length of thermal lens [1] for Gaussian pump beam can expressed by:
 (14)
(14)
where, α is the absorption coefficient of pump beam, Ph is the fraction of pump power that results in heating (= ηPp) and dn/dT is the change of refractive index of laser crystal with temperature.
3. Result and Discussions
The spectral and thermal parameters of Yb:YAG passively Q-switched using Cr4+:YAG used for numerical simulation are listed in Table 1 [15] .
Using the simulation parameters, the radial and axial thermal relaxation times are found to be 48 ms and 768 ms, respectively, while the focal length of thermal lens for the laser system under investigation is 14.1 cm. Since the laser rod length is 4 mm, no self-focusing will occur within the rod at the operating pump power (30 W).
In the simulation of the temperature distribution, the temporal behavior is studied for 10 ms with 50 ns time step. Due to the radial symmetry, the simulation is carried out for a cross-sectional area (r0 × l) divided into a spatial mesh of 80 × 25 nodes.
By coupling the rate equations (Equations (1)-(3)), with the thermal conductivity equation (Equation (7)), the resulting pulse repetition rate of the Q-switched laser pulse is 4.95 KHz corresponding to a period (1/PRR) of 0.2 ms. This period is very short compared to axial and radial thermal relaxation times.
The temperature distribution in the radial direction is shown in Figure 1 at different points on the pump facet; point Ar (z = 0, r = 0 mm), point Br (z = 0, r = 0.2 mm), point Cr (z = 0, r = 0.4 mm), point Dr (z = 0, r = 0.6 mm), point Er (z = 0, r = 0.8 mm) and point Fr (z = 0, r = 1 mm). It can be observed from the Figure, that the temperature distribution at each point arises to a quasi-steady state within 1.6ms. The quasi-steady state value increases as approaching to the center of the rod since the optical pump is localized in the beam waist (Tmax = 304.54 K at point Ar). The quasi-steady state indicates that an equilibrium state between the continuous heat input to the active medium and the radial heat flow from the center of the rod to its surface (and subsequently to the heat sink) has been established.
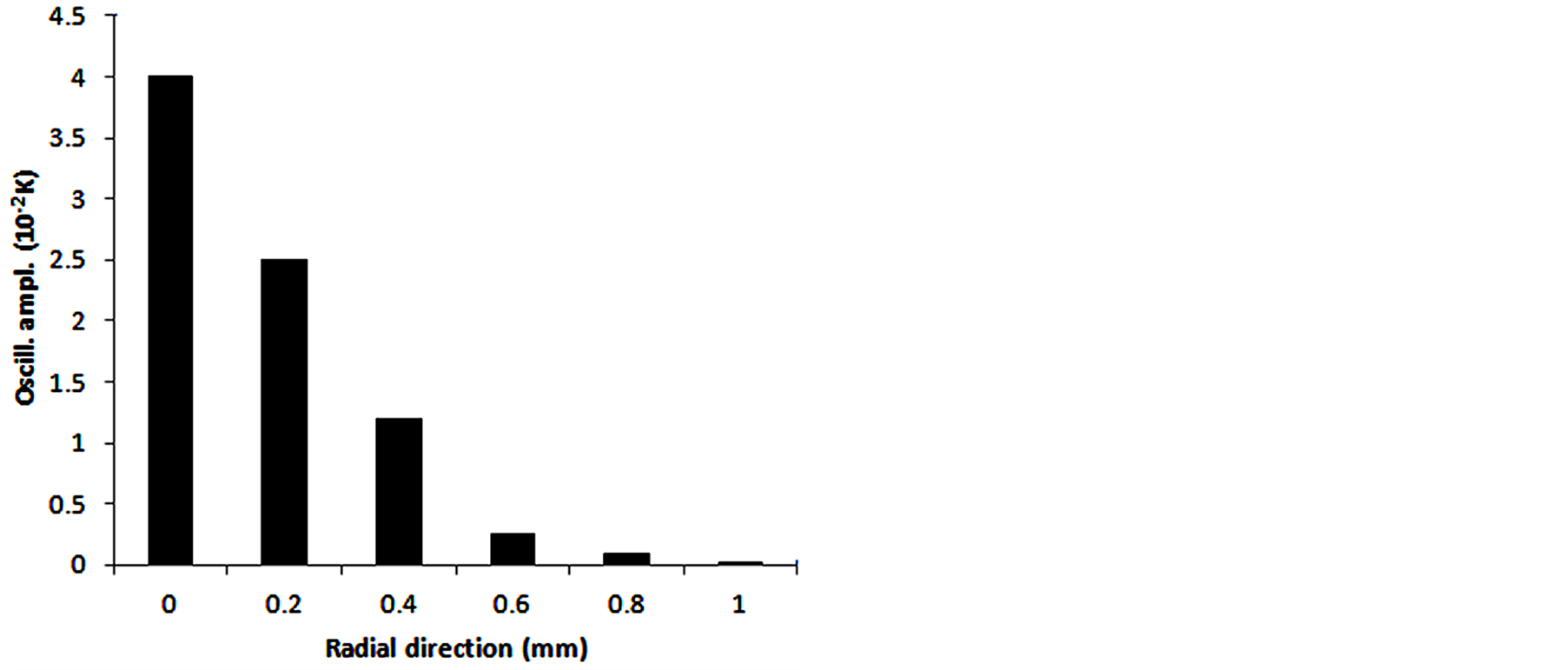
In addition, as shown in Figure 2(a), the repetitive oscillatory amplitude ΔT decreases in the radial direction. At the rod center, the amplitude is the largest (ΔT = 0.04 K at point Ar) and decreases gradually within the illuminated area of the pump beam waist (wp = 313.5 μm). Since the remaining area of the rod is not exposed to the pumping power (r > wp in Equation (6)), the thermal load is resulting from the heat conduction from the hot spot to the peripherals at constant temperature. Thence, the oscillatory amplitude decreases dramatically (ΔT = 0.0001 K at point Fr). The corresponding temperature instability ζ is calculated from Equation (13) and it decreases from 9% at point Ar to 0.08% at point Fr as shown in Figure 2(b).
By observing the repetitively oscillatory amplitude, it can be seen that the frequency of the oscillation is synchronized with the pulse repetition rate as shown in Figure 3. Also, it can be noticed that the oscillation is asymmetric as the rising edge is sharper than the falling one in the area which is exposed to the optical pumping (r < wp). Outside the optically pumped area (r > wp), the oscillation becomes symmetric and a phase shift occurs (Figure 4). The asymmetry of the oscillation can be explained as within the area exposed to optical radiation, the portion of energy gained and converted into heat (ηPp) is high until this amount is transferred by conduction to the neighbor points in the direction of the outer surface (r = r0). Thus, the rate of increase of temperature due
Table 1. Thermal parameters used in thermal model.
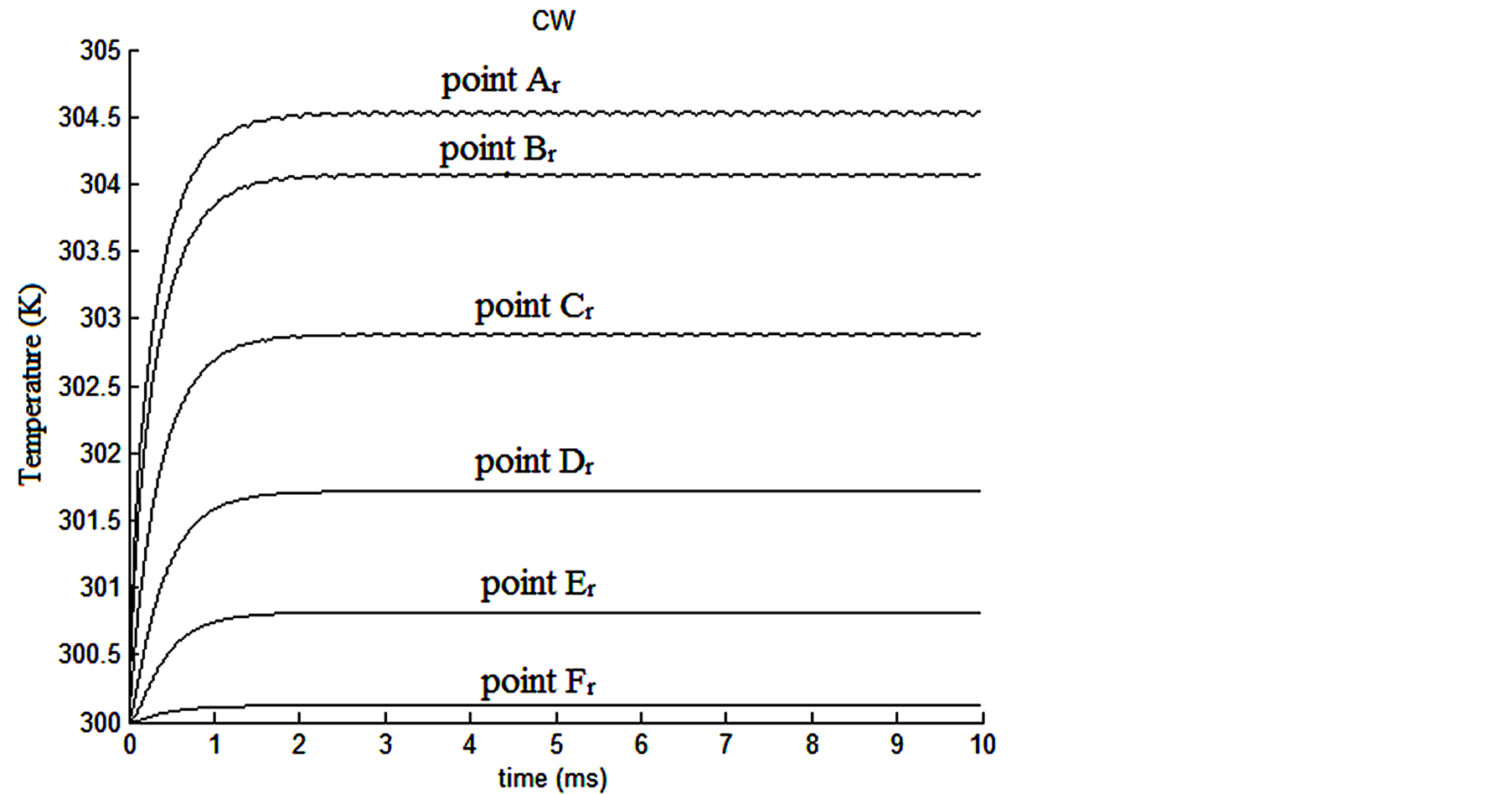
Figure 1. The temperature distribution of Yb:YAG rod in the radial direction.
 (a)
(a)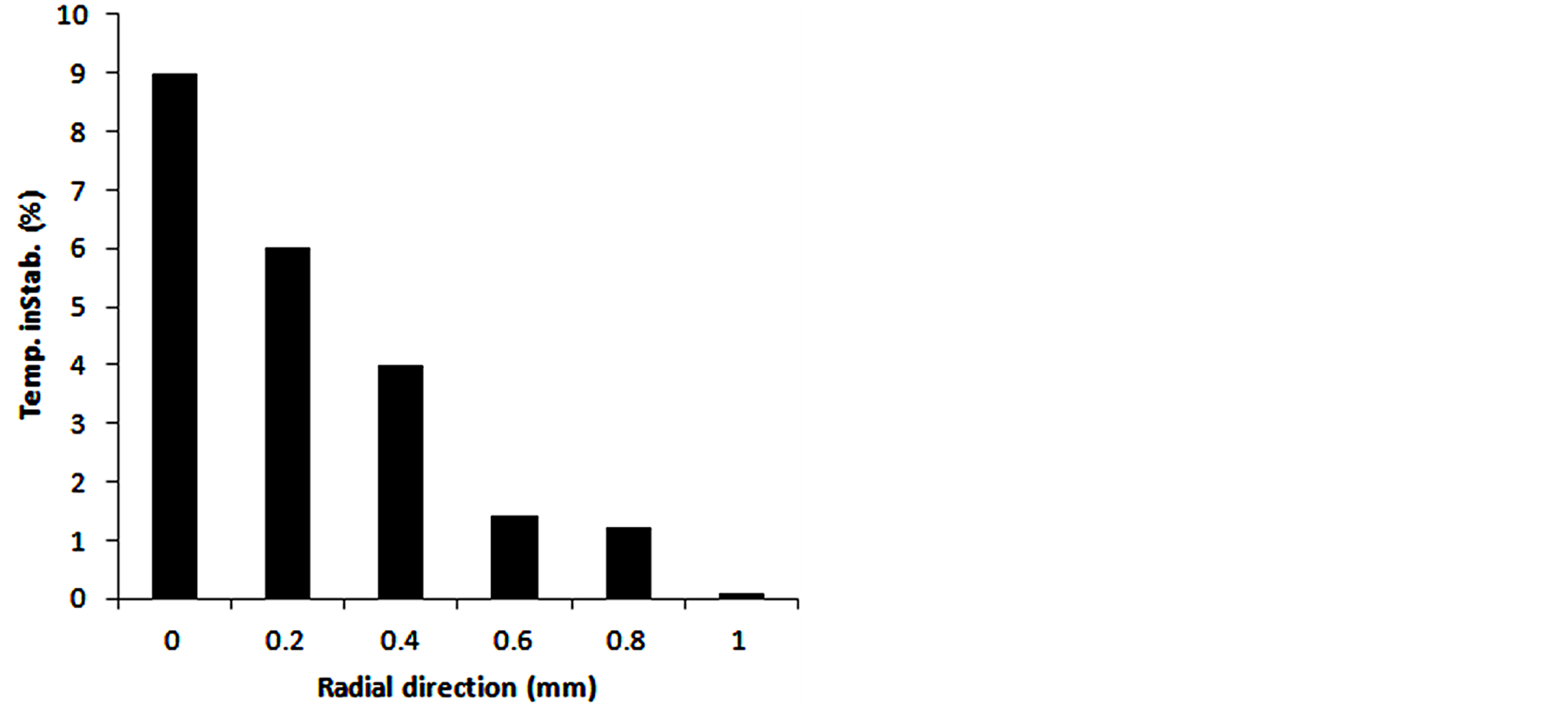 (b)
(b)
Figure 2. (a) The oscillatory amplitude DT and; (b) The temperature instability in the radial direction.
to the optical radiation is faster than the rate of its release due to conduction. At radii larger than the area of radiation area (r > wp), the heat transfer is due to the conduction only. Consequently, each point is receiving energy from its preceding point then delivers this energy to the proceeding point in approximate same rate which results in more symmetry in the oscillation.
The time required to transfer the heat from the center of the rod to its peripheral yields phase shift shown in Figure 4.
The temperature distribution is also studied along the rod length, at pump facet point Al (z = 0, r = 0 mm), point Bl (z = 1, r = 0 mm), point Cl (z = 2, r = 0 mm), point Dl (z = 3, r = 0 mm) and point El (z = 4, r = 0 mm). As shown in Figure 5, the temperature distribution in the axial direction shows a similar behavior as the one of the radial direction. However, the oscillatory amplitude decreases in the axial faster than the radial one, which can be expected due to the absorption of the pumping light along the axial direction, i.e. the contribution of the optical energy into the temperature distribution is decreased with the length (Equation (6)).

Figure 3. The synchronization between n (t) and the temperature distribution at pump facet point Ar.

Figure 4. The temperature distribution at the pumping facet at points Ar and Fr.
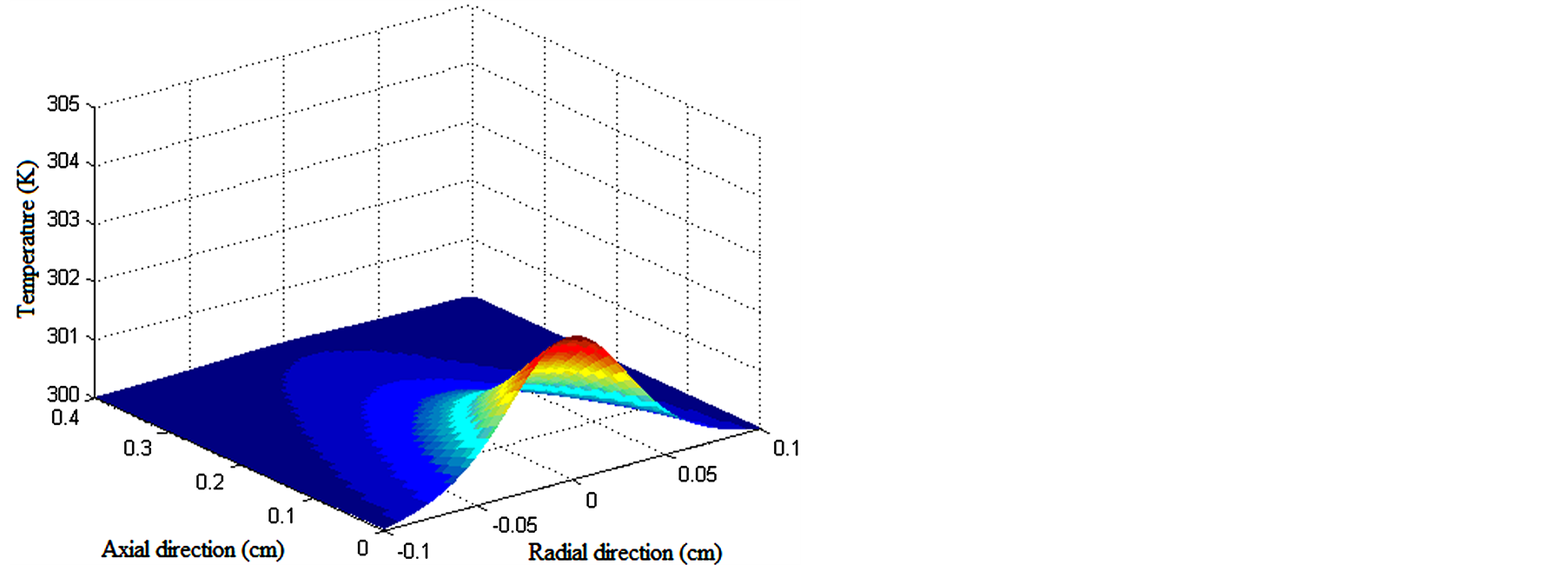
By studying the temperature distribution in the axial and radial directions, the results can be combined in a 3D diagram which illustrates the temperature variation in both directions (Figure 6). Figure 6 shows the evolution of the temperature distribution at the start of the optical pumping and at quasi-steady state. The highest temperature is in dark red and the lowest temperature is in dark blue. It can be seen that the temperature variation in the radial direction is stronger than that in the axial direction. The hot spot is at the center of the front facet of the rod and increases until steady state to 304.54 K (Figure 6(b)) at 1.6 ms.
4. Conclusions
The thermal behavior of the active medium of passively Yb:YAG Q-switched laser has been numerically investigated in both the axial and radial directions. For a laser rod of 2 × 4 mm2, it was found that the thermal focal length was longer than the length of the rod. The radial and axial thermal time constants are much longer than the period of Q-switched pulse. The temperature distribution exhibits a repetitive oscillatory behavior synchronized with the repetition rate of the Q-switched pulses.
For further work, the temperature distribution can be studied for pulsed pumping in order to investigate the

Figure 5. The temperature distribution of Yb:YAG rod in the axial direction.
 (a)
(a)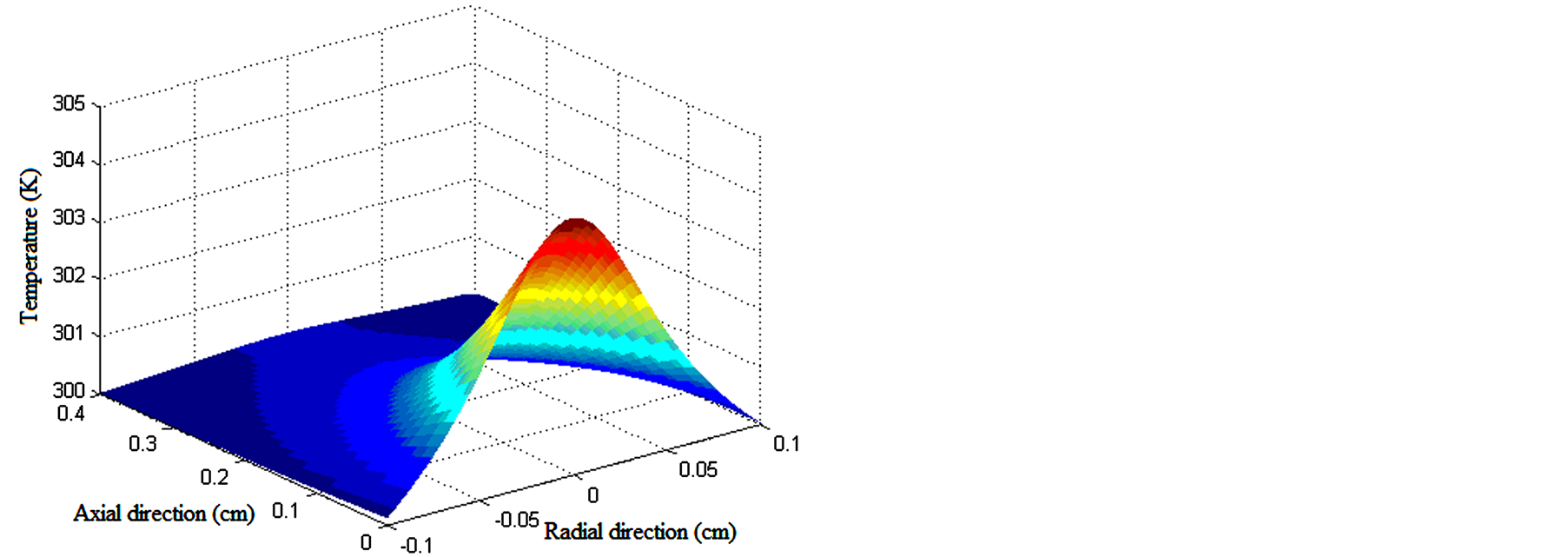 (b)
(b)
Figure 6. The overall temperature distribution inside the laser rod at: (a) 0.2 ms and (b) 1.6 ms respectively.
effect of discontinuity of pumping on the thermal load. In addition, the reciprocal effect between the temperature and the population inversion density can be considered within the rate equations of Q-switched laser system.
References
- Innocenzi, M.E., Yura, H.T., Fincher, C.L. and Fields, R.A. (1990) Thermal Modeling of Continuous-Wave EndPumped Solid-State Lasers. Applied Physics Letters, 56, 1831-1833. http://dx.doi.org/10.1063/1.103083
- Cousins, A.K. (1992) Temperature and Thermal Stress Scaling in Finite-Length End-Pumped Laser Rods. IEEE Journal of Quantum Electronics, 28, 1057-1069. http://dx.doi.org/10.1109/3.135228
- Neuenschwander, B., Weber, R. and Weber, H.P. (1995) Determination of the Thermal Lens in Solid-State Lasers with Stable Cavities. IEEE Journal of Quantum Electronics, 31, 1082-1087. http://dx.doi.org/10.1109/3.387046
- Ozygus, B. and Erhad, J. (1995) Thermal Lens Determination of End-Pumped Solid-State Lasers with Transverse Beat Frequencies. Applied Physics Letters, 67, 1361-1362. http://dx.doi.org/10.1063/1.115551
- Ozygus, B. and Zhang, Q. (1997) Thermal Lens Determination of End-Pumped Solid-State Lasers Using Primary Degeneration Modes. Applied Physics Letters, 71, 2590-2592. http://dx.doi.org/10.1063/1.119337
- Blows, J.L., Dawes, J.M. and Omatsu, T. (1998) Thermal Lensing Measurements in Line-Focus End-Pumped Neodymium Yttrium Aluminium Garnet Using Holographic Lateral Shearing Interferometry. Journal of Applied Physics, 83, 2901-2906. http://dx.doi.org/10.1063/1.367077
- Li, J., Dong, J., Mitsurua, M., Shirakawa, A. and Ueda, K. (2007) Transient Temperature Profile in the Gain Medium of CWand End-Pumped Passively Q-Switched Microchip Laser. Optics Communications, 270, 63-67. http://dx.doi.org/10.1016/j.optcom.2006.08.043
- Li, T., Zhang, S., Zhao, S., Yang, K. and Zhuo, Z. (2010) Thermal Modeling of the Continuous-Wave End-Pumped Q-Switched Lasers. Optics Communications, 283, 3070-3075. http://dx.doi.org/10.1016/j.optcom.2010.04.010
- Mohammadzahery, Z., Jandaghi, M., Alipour, S., Dadras, S. and Kazemi, S. (2012) Theoretical Study on Thermal Behavior of Passively Q-Switched Microchip Nd:YAG Laser. Optics & Laser Technology, 44, 1095-1100. http://dx.doi.org/10.1016/j.optlastec.2011.10.004
- Siegman, A.E. (1986) Lasers. University Science Books, Canada.
- Zhang, X., Zhao, S., Wang, Q., Zhang, Q., Sun, L. and Zhang, S. (1997) Optimization of Cr4+-Doped Saturable-Absorber Q-Switched Lasers. IEEE Journal of Quantum Electronics, 33, 2286-2294. http://dx.doi.org/10.1109/3.644112
- Xiao, G. and Bass, M. (1997) A Generalized Model for Passively Q-Switched Lasers Including Excited State Absorption in the Saturable Absorber. IEEE Journal of Quantum Electronics, 33, 41-44. http://dx.doi.org/10.1109/3.554875
- Koechner, W. (2005) Solid-State Laser Engineering. 6th Revised and Updated Edition.
- Clarkson, W.A., Felgate, N.S. and Hanna, D.C. (1998) Advanced Solid-State Lasers. Washington DC, 401.
- Kalisky, Y., Labbe, C., Waichman, K., Kravchik, L., Rachum, U., Deng, P., Xu, J. and Chen, W. (2002) Passively Q-Switched Diode-Pumped Yb:YAG Laser Using Cr4+-Doped Garnets. Optical Materials, 19, 403-413. http://dx.doi.org/10.1016/S0925-3467(02)00003-4


