Optics and Photonics Journal
Vol.3 No.8(2013), Article ID:41594,10 pages DOI:10.4236/opj.2013.38058
Gain Coefficient Calculation for Short Wave Laser Emission from Sodium like Co
1National Institute of Laser Enhanced Sciences, Cairo University, Cairo, Egypt
2Environmental Affairs Agency, Cairo, Egypt
3Laboratory of Lasers and New Materials, Cairo University, Cairo, Egypt
Email: wessamlaser@yahoo.com
Copyright © 2013 Wessameldin S. Abdelaziz et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Wessameldin S. Abdelaziz et al. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received October 6, 2013; revised November 4, 2013; accepted November 29, 2013
Keywords: Level Structure; Oscillator Strengths; Transition Probabilities and Radiative Life Times; Sodium like Co16+
ABSTRACT
Level structure, oscillator strengths, transition probabilities and radiative life times are evaluated for 1s2 2s2 2p63l, 4l, 5l (l = 0, 1, 2, 3, 4) states in sodium like Co16+. The calculations are carried out using COWAN code. The calculations made were compared with other results in literature where a good agreement is found. We also report on some unpublished energy values and oscillator strengths. Our results are used in the calculation of reduced population of 21 fine structure levels over a wide rang of electron density values (1018 to 1020) at various electron plasma temperature. For those transitions with positive population inversion factor, the gain coefficients are evaluated and plotted against the electron density.
1. Introduction
An important objective in the development of X-ray lasers is to deliver a coherent, saturated output at wavelengths toward the water window [1].
Such saturated X-ray lasers are required for holography [2] and microscopy [3], of biological specimens and for deflectometry [4], interferometry [5], and radiography [6] of dense plasma relevant to inertial confinement fusion and laboratory astrophysics [5]. Sodium-like ions have prominent emission lines in the UV and XUV spectrum of the sun. Highly charged sodium-like ions are observed in several types of laboratory sources such as high-voltage vacuum spark tokamak and laser-produced plasmas [1].
Spectra of these ions have a simple structure (one electron outside a closed shell); the energy levels are practically free from effects of configuration mixing and therefore they are well suited for a theoretical interpretation of line intensities and for diagnostic purposes. In recent years, there have been extensive spectroscopic studies, both experimental and theoretical, of sodium isoelectronic sequence. [7] has used multi-configuration Hartree Fock (MCHF) method and Non-Orthogonal Spline configuration interaction (CI) method to evaluate energy levels and oscillator strengths for Na-like ions up to Fe XVI. [8] have used theoretical single-configuration Dirac-Fock method to evaluate oscillator strengths for E1 transitions in the sodium isoelectronic sequence (Na I-Ca X). Large-scale calculations were undertaken within the so-called Opacity Project (OP) [8] and, as a result of broad international collaboration, a complete set of oscillator strengths was produced for all optically allowed transitions between states with 1 ≤ Z ≤ 14 as well as Z = 16, 18, 20, and 26 in all stages of ionization.
However, relativistic effects were also neglected in OP calculations, and LS coupling was assumed. Therefore, the OP data are available for multiplets only and not for individual fine-structure components. [9] assigned experimental wavelengths to 1086 lines which have oscillator strengths calculated in OP and added 1163 lines which have critically evaluated oscillator strengths. [10] and, from the US National Bureau of Standards (NBS) publications [11-13]. Experimental lifetime measurements for the 4p and 5p levels and calculation of transition probabilities in Na I have been measured using time-resolved laser induced fluorescence [14].
The purpose of this work is to present the energies of 21 fine structure levels, the oscillator strengths, the transition probabilities between them in sodium like Co16+.
The atomic data thus obtained are used to calculate reduced population of sodium like Co16+ excited levels over a wide range of electron density at various electron temperatures. The gain coefficients are also calculated.
2. Computation of Atomic Structures
2.1. Model of Central Force Field
In quantum mechanics, various physical processes can be summed by Schrödinger equation, i.e.
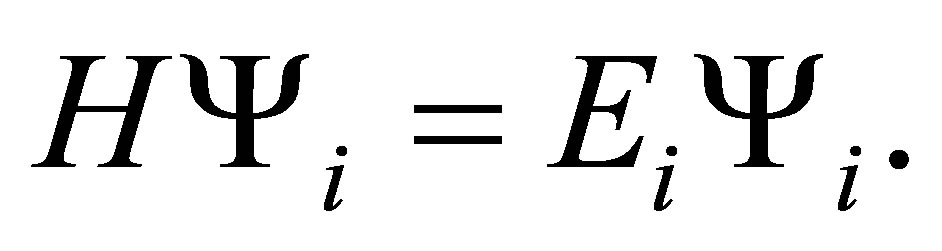 (1)
(1)
In the non-relativistic case (the influence of relativistic effect will be discussed later), the Hamiltonian of an atomic system with N electrons is [1]:
 (2)
(2)
Here Hkin, He-nuc and He-e refer, respectively, to the kinetic energy of electrons, the Coulomb potential and the energy of electrostatic interaction of electrons, ri is the distance between the i-th electron and nucleus, and ri,j = |ri – rj|.
By substituting the Hamiltonian into Schrödinger equation and solving the equation in the case of multiple electrons and multiple energy levels, the wave function is obtained. Now, due to the appearance of the term of interaction of electrons, an exact solution cannot be obtained. On the other hand, the interaction term is comparable with the Coulomb potential term, so it can by no means be ignored. An approximate solution is to adopt the method of central force field. If it is assumed that every electron moves in the central force field of the nucleus and also in the mean force field produced by other electrons, then we have the following effective Hamiltonian [1]:
 (3)
(3)
where Z is the atomic number
2.2. Method of Calculation
The key problem in the application of central field is to find an adequate potential function Veff. For this, in recent decades many effective method of calculation have been developed. Among them the more important ones are the potential model, Hartree-Fock theory, the semi-empirical methods. In the following we present a brief introduction of semi-empirical methods.
Semi-empirical methods try to calculate atomic structures via solving the simplified form of the Hartree-Fock equation. The most typical is the Hartree-Fock-Slater method.
Afterwards, Cowan et al. revised this method and developed the RCN/RCG program used in our work. The merit of the program is its extreme effectiveness, and the shortcoming is its inability to estimate the precision.
2.3. Configuration Interaction
In the above-stated model of central force field, every electron can be described with a simple wave function. The overall wave function of atoms may be expressed with the following Slater determinant [1]:
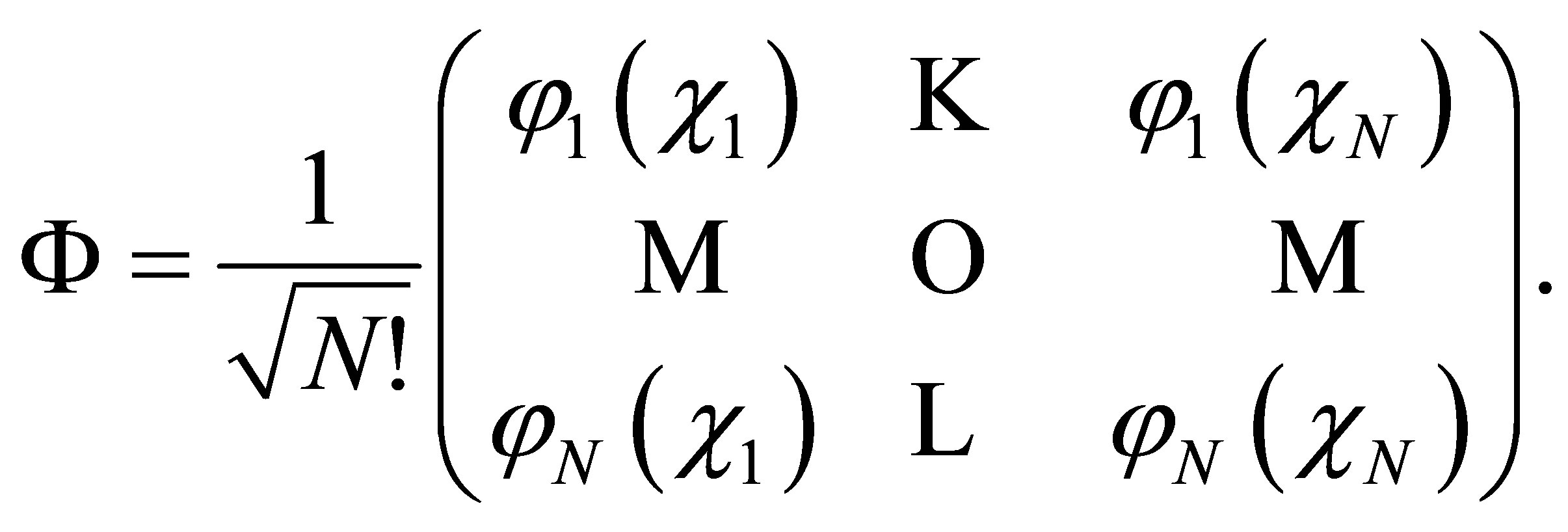 (4)
(4)
Ф: is a total function with respect to exchange of electrons.
ϕ(χ): is a single particle function or spin orbitals.
N: is a number of non-interacting electrons with no spin-orbit interaction.
In reality, such a description is not very precise. The best wave function should be a linear combination of wave functions with single configurations, and these wave functions possess the same total angular momentum and spin symmetry. This method is called the interaction of configurations. In the computation of atomic structures, consideration of the configuration interaction is the basis requirement for a program.
2.4. Relativistic Correction
In a non-relativistic system, the oscillator strengths and dipole transitions under LS-coupling can be calculated. In calculating forbidden transitions, jj-coupling must be used, and for this relativistic effects have to be taken into account. Generally speaking, the effects may be treated in two ways. One is inclusion of Breit-Pauli operator in the non-relativistic equation, and other is direct solution of the Dirac equation. For the former, a mass velocity term, the Darwin term caused by the electric moments of electrons and the spin-orbit term are added to the Hamiltonian of the model of central force field [15]. For relativistic correction, the program RCN/RCG restore to the Breit-Pauli correction.
2.5. Weighted Oscillator Strengths and Lifetimes
The oscillator strength f(γγ\) is a physical quantity related to line intensity I and transition probability W(γγ\), as given by Sobelman [16]:
 (5)
(5)
with, I α gW(γγ\) α g|f(γγ\)| = gf.
Here m = electron mass, e = electron charge, = is initial quantum state, 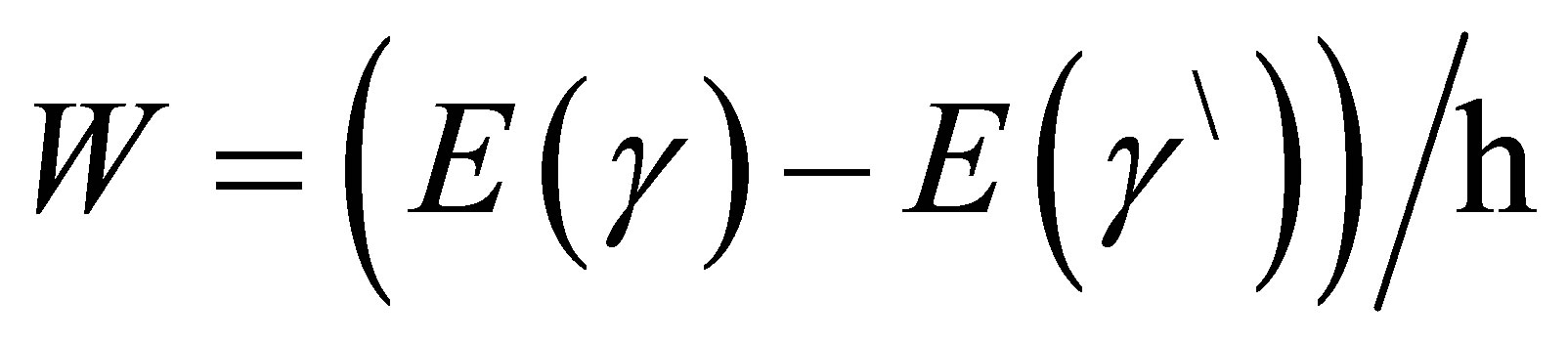 , E(γ) initial state energy, g = (2J + 1) is the number of degenerate quantum state with angular momentum J (in the formula for initial state). Quantities with primes refer to the final state.
, E(γ) initial state energy, g = (2J + 1) is the number of degenerate quantum state with angular momentum J (in the formula for initial state). Quantities with primes refer to the final state.
In the above equation, the weighted oscillator strength, gf, is given by Cowan [17]:
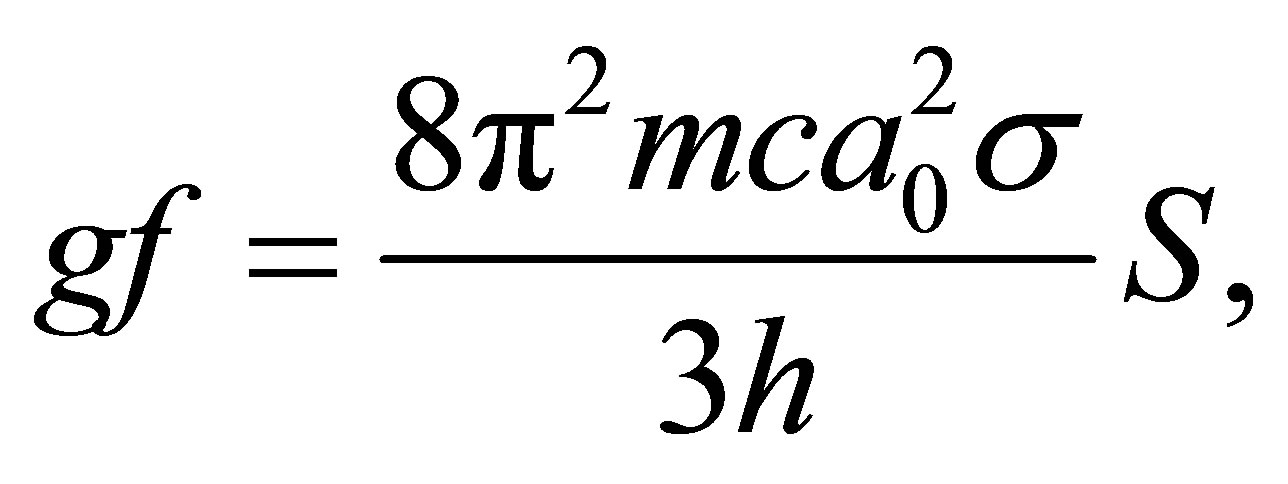 (6)
(6)
where g is the statistical weight of lower level, f is the absorption oscillator strength, 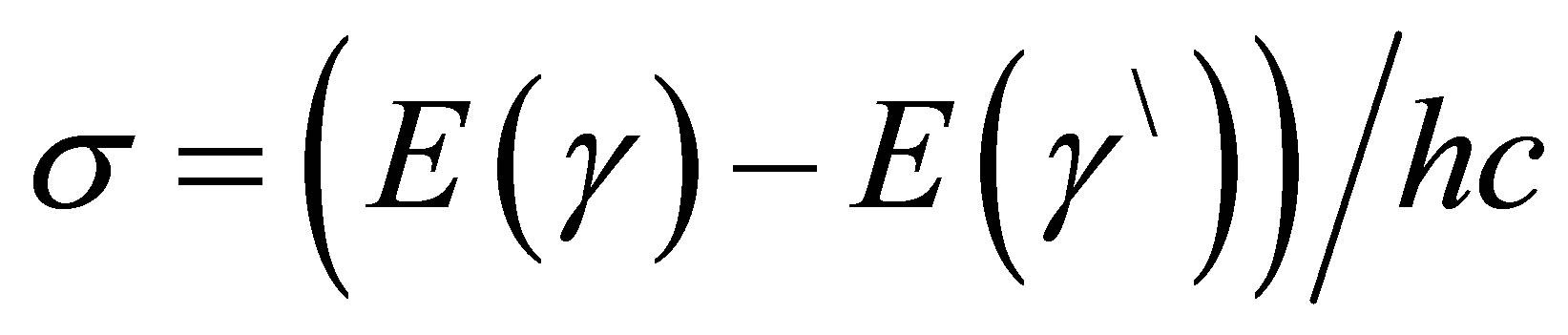 , h is planck’s constant, c = light velocity, and a0 is Bohr radius, and the electric dipole line strength is defined by:
, h is planck’s constant, c = light velocity, and a0 is Bohr radius, and the electric dipole line strength is defined by:
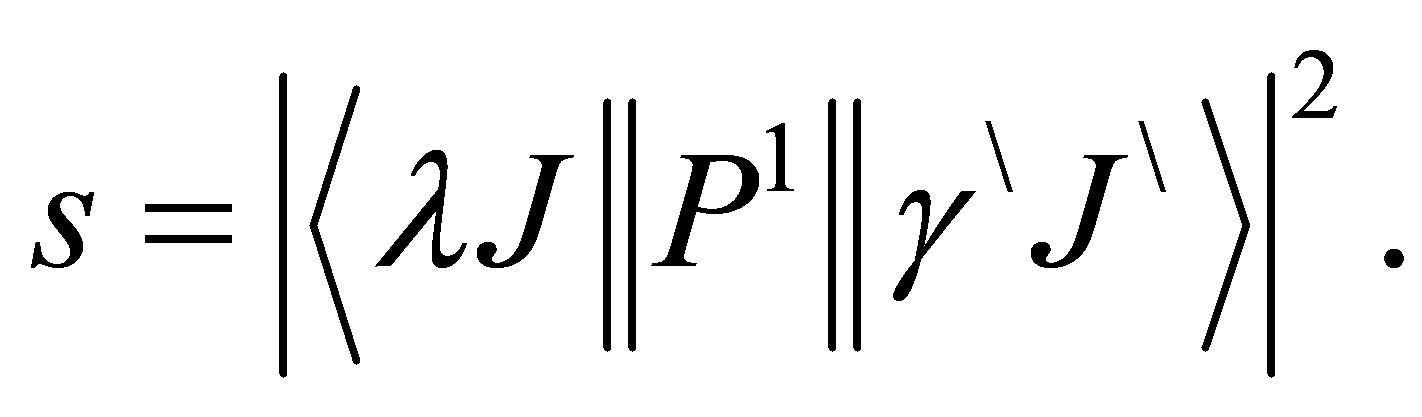 (7)
(7)
This quantity is a measure of the total strength of the spectral line, including all possible transition between m, m' for different Jz Eigen states. The tensor operator P1 (first order) in the reduced matrix element is the classical dipole moment for the atom in units of ea0.
To obtain gf, we need to calculate S first, (or its square root):
 (8)
(8)
In a multi-configuration calculation we have to expand the wave-function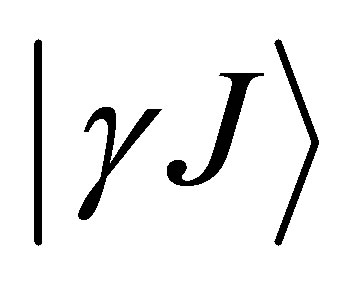 .
.
In terms of single configuration wave-functions, 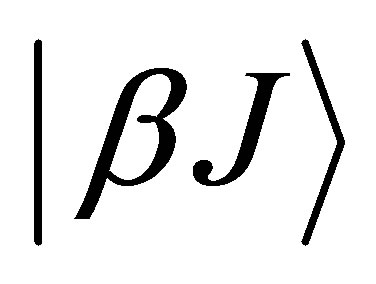 for both upper and lower levels:
for both upper and lower levels:
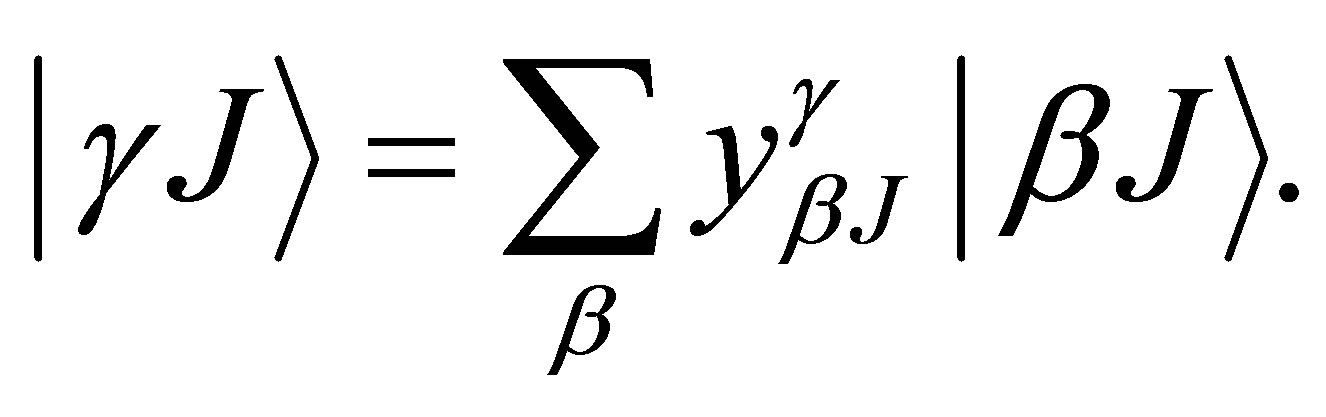 (9)
(9)
therefore, we can have the multiconfigurational expression for the square root of line strength:
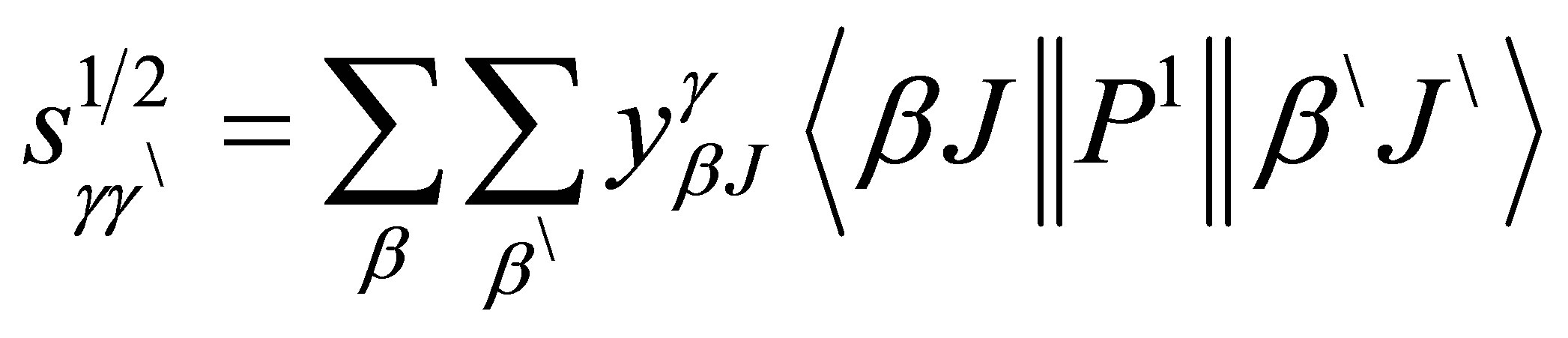 (10)
(10)
The probability per unit time of an atom in specific state 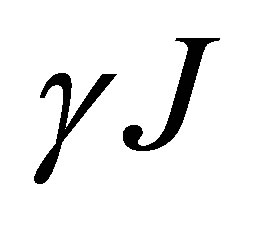 to make a spontaneous transition to any state with lower energy is
to make a spontaneous transition to any state with lower energy is
 (11)
(11)
where 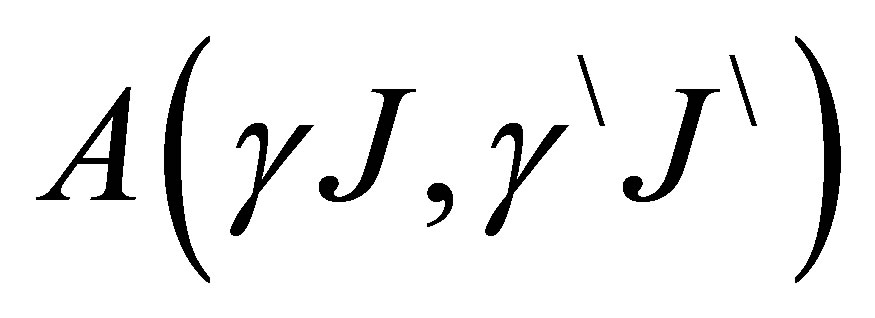 is the Einstein spontaneous emission transition probability rate, for a transition from the state.
is the Einstein spontaneous emission transition probability rate, for a transition from the state. 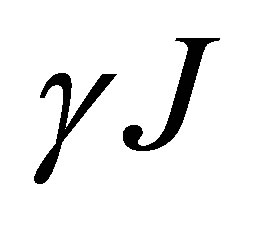 to the state
to the state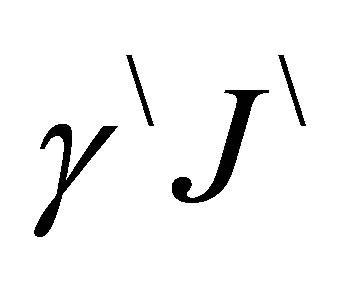 .
.
The sum is over all state 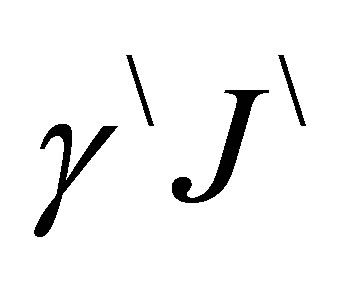 with
with 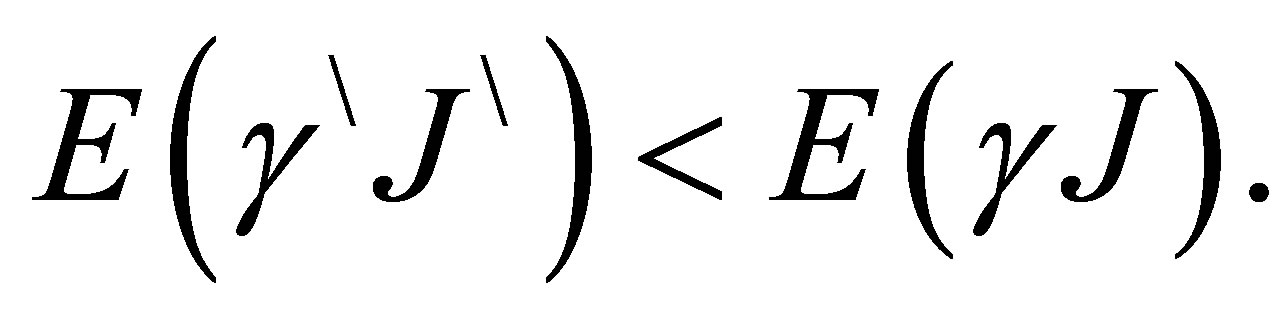
The Einstein probability rate is related to gf with the following relation by [17]:
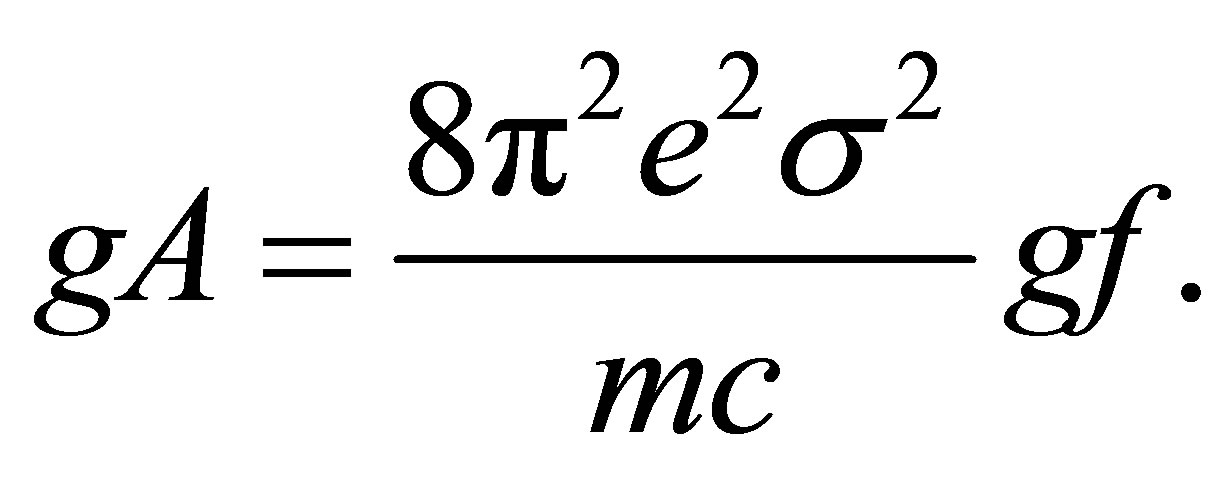 (12)
(12)
Since the natural lifetime  is the inverse of transition probability, then:
is the inverse of transition probability, then:
 (13)
(13)
which is applicable to an isolated atom.
Interaction with matter or radiation will reduce the lifetime of any state.
3. Computation of Gain Coefficient
The possibility of laser emission from plasma of ions of various members of Na like Co via electron collisional pumping, in the XUV and soft X-ray spectral regions is investigated at different plasma temperatures and plasma electron densities.
The reduced population densities are calculated by solving the coupled rate equations [18-21].
 (14)
(14)
where Nj is the population of level j, 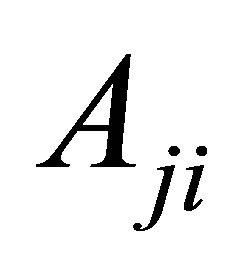 is the spontaneous decay rate from level j to level i,
is the spontaneous decay rate from level j to level i, 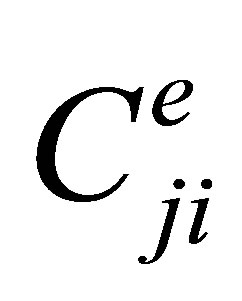 is the electron collisional excitation rate coefficient, and
is the electron collisional excitation rate coefficient, and 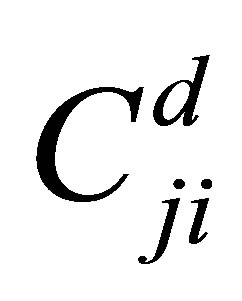 is the electron collisional de-excitation rate coefficient, which is related to electron collisional excitation rate coefficient by [22-23].
is the electron collisional de-excitation rate coefficient, which is related to electron collisional excitation rate coefficient by [22-23].
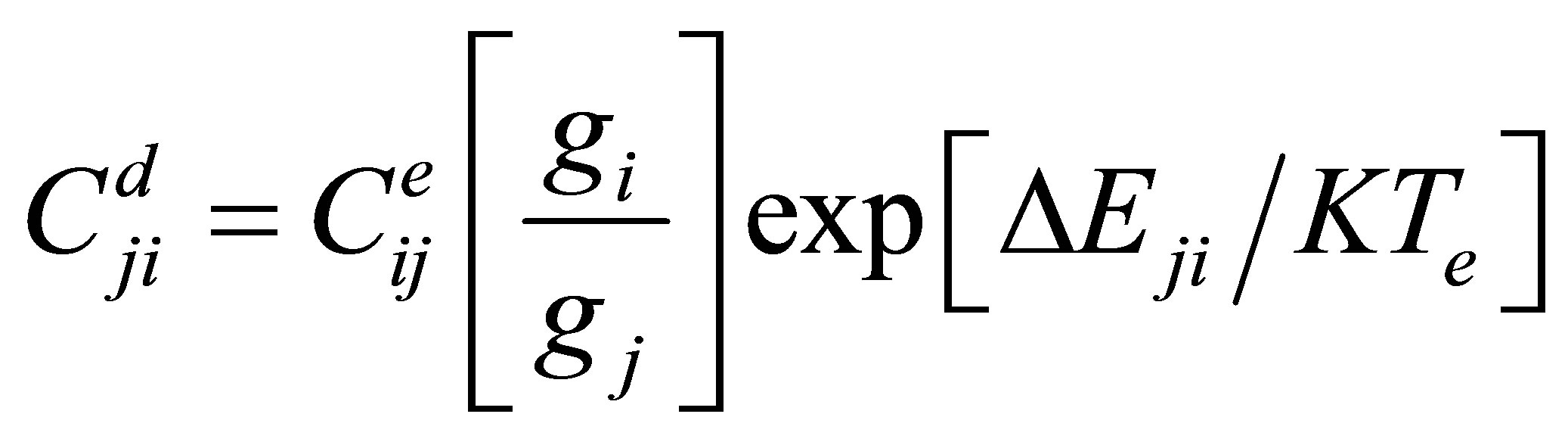 (15)
(15)
where gi and gj are the statistical weights of lower and upper levele, respectively.
The population of the j th level is obtained from the identity [19,20,24],
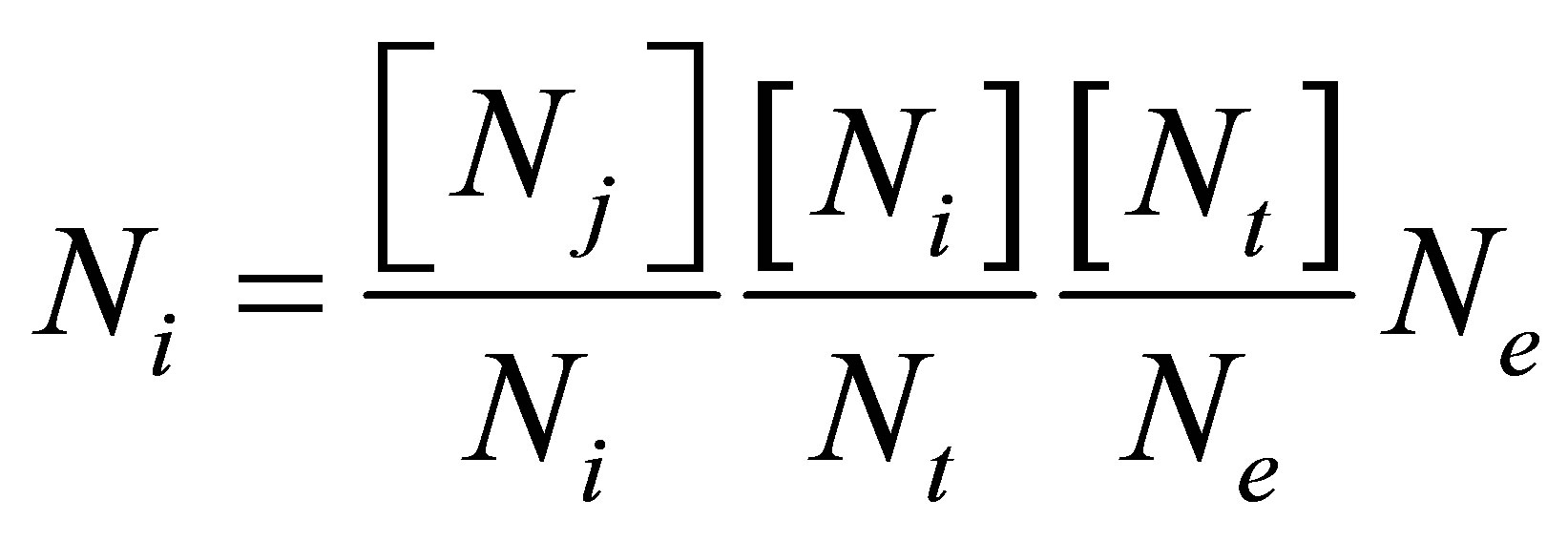 (16)
(16)
where 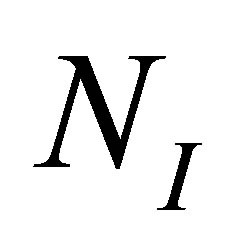 is the total number density of all levels of the ion under consideration, and Nt is the total number density of all ionization stage.
is the total number density of all levels of the ion under consideration, and Nt is the total number density of all ionization stage.
Since the populations calculated from Equation (14) are normalized such that [19,20,25]
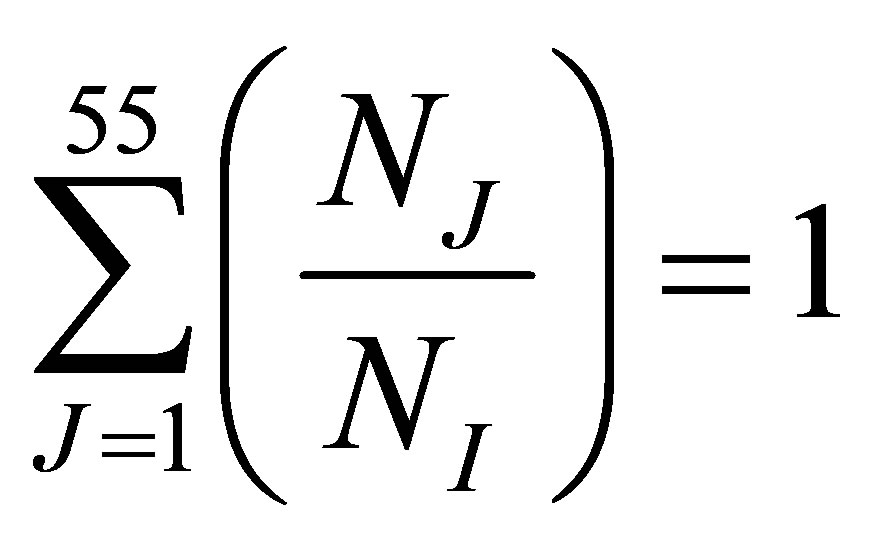 (17)
(17)
where n is the number of all the levels of the ion under consideration.
Electron collisional pumping has been applied. Collision in the lasant ion plasma will transfer the pumped quanta to other levels, and resulted in population inversions then produced between the upper and lower levels.
Once a population inversion has ensured a positive gain through F > 0 [1].
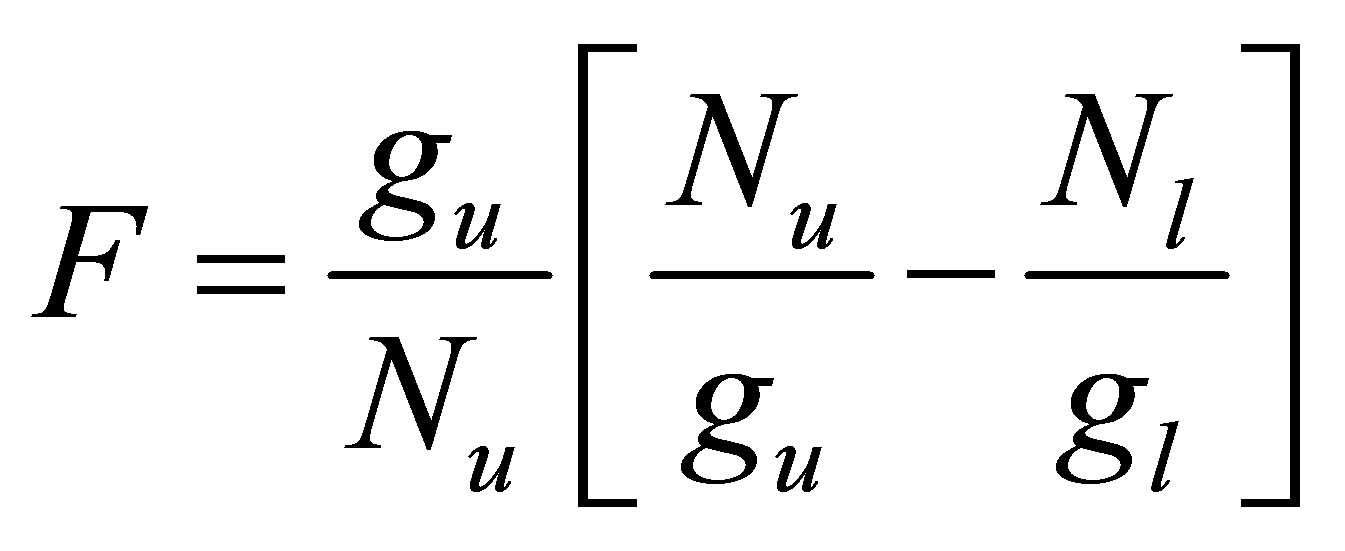 (18)
(18)
where 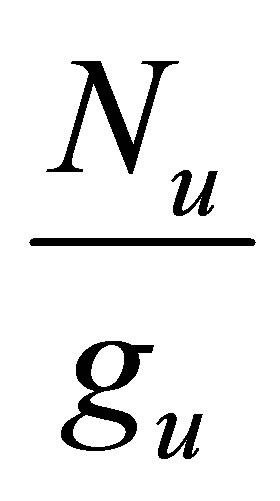 and
and 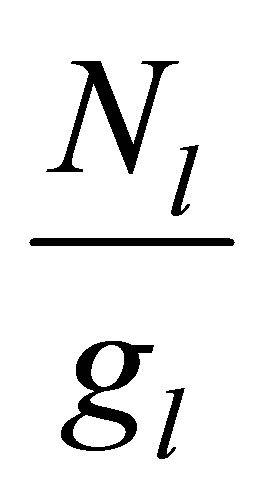 are the reduced populations of the upper level and lower level respectively. Equation (18) has been used to calculate the gain coefficient for Doppler broadening of the various transitions in the Na like Co ion.
are the reduced populations of the upper level and lower level respectively. Equation (18) has been used to calculate the gain coefficient for Doppler broadening of the various transitions in the Na like Co ion.
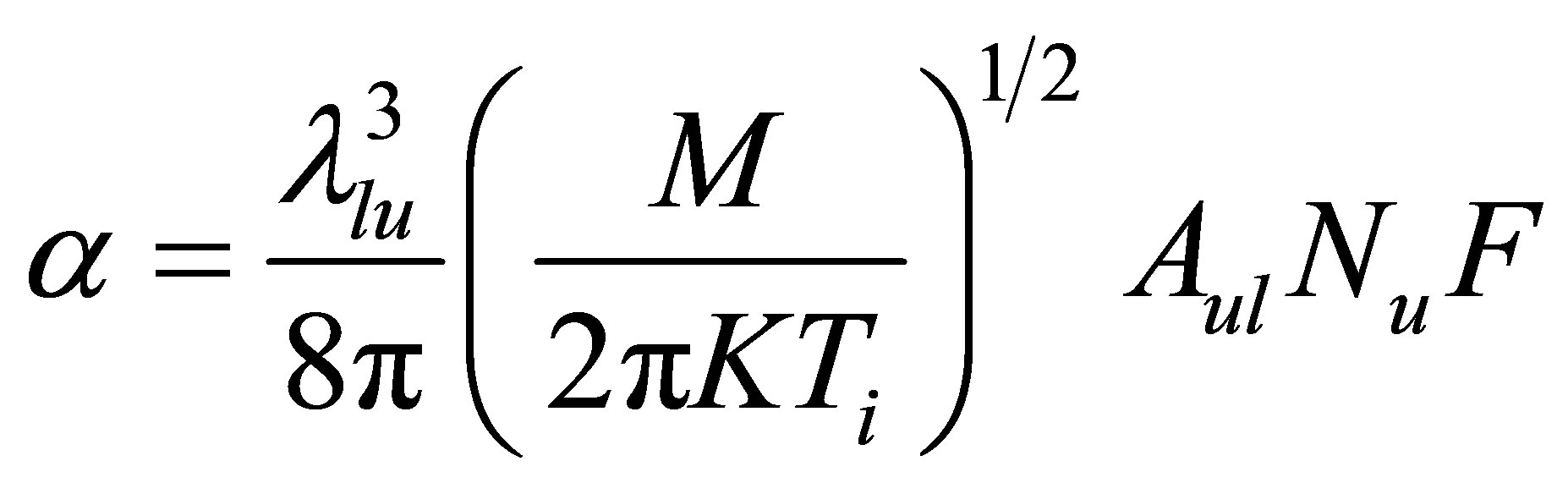 (19)
(19)
where M is the ion mass,  is the transition wavelength in cm,
is the transition wavelength in cm, 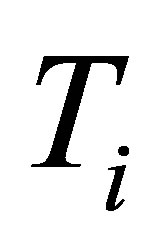 is the ion temperature in
is the ion temperature in  and u,l represent the upper and lower transition levels respectively.
and u,l represent the upper and lower transition levels respectively.
The gain coefficient is expressed in terms of the upper state density (Nu). This quantity depends on how the upper state is populated, as well as on the density of the initial source state. The source state is often the ground state for a particular ion.
4. Results and Discussions
4.1. Energy Levels
Adopting the program COWAN [17], we have computed the parameters of atomic structures of Co XVII. The energy levels considered in the calculation have 21 fine structures ranging from ground state 1s2 2s2 2p6 3s to the excited states1s2 2s2 2p6 3d, 1s2 2s2 2p6 4s, 1s2 2s2 2p6 4d, 1s2 2s2 2p6 5s, 1s2 2s2 2p6 5s, 1s2 2s2 2p6 5d, 1s2 2s2 2p6 5g even parity levels and 1s2 2s2 2p6 3p, 1s2 2s2 2p6 4p, 1s2 2s2 2p6 4f, 1s2 2s2 2p6 5p, 1s2 2s2 2p6 5f odd parity levels (Table 1).
Table 2 present energy levels and fine-structure splitting for Co16+ also presented the energy levels calculations of (Younis et al., 2006) the present calculations differ by less than 0.15% for most of the levels, they

Table 1. Calculated HFR energy levels and fine structure splitting.
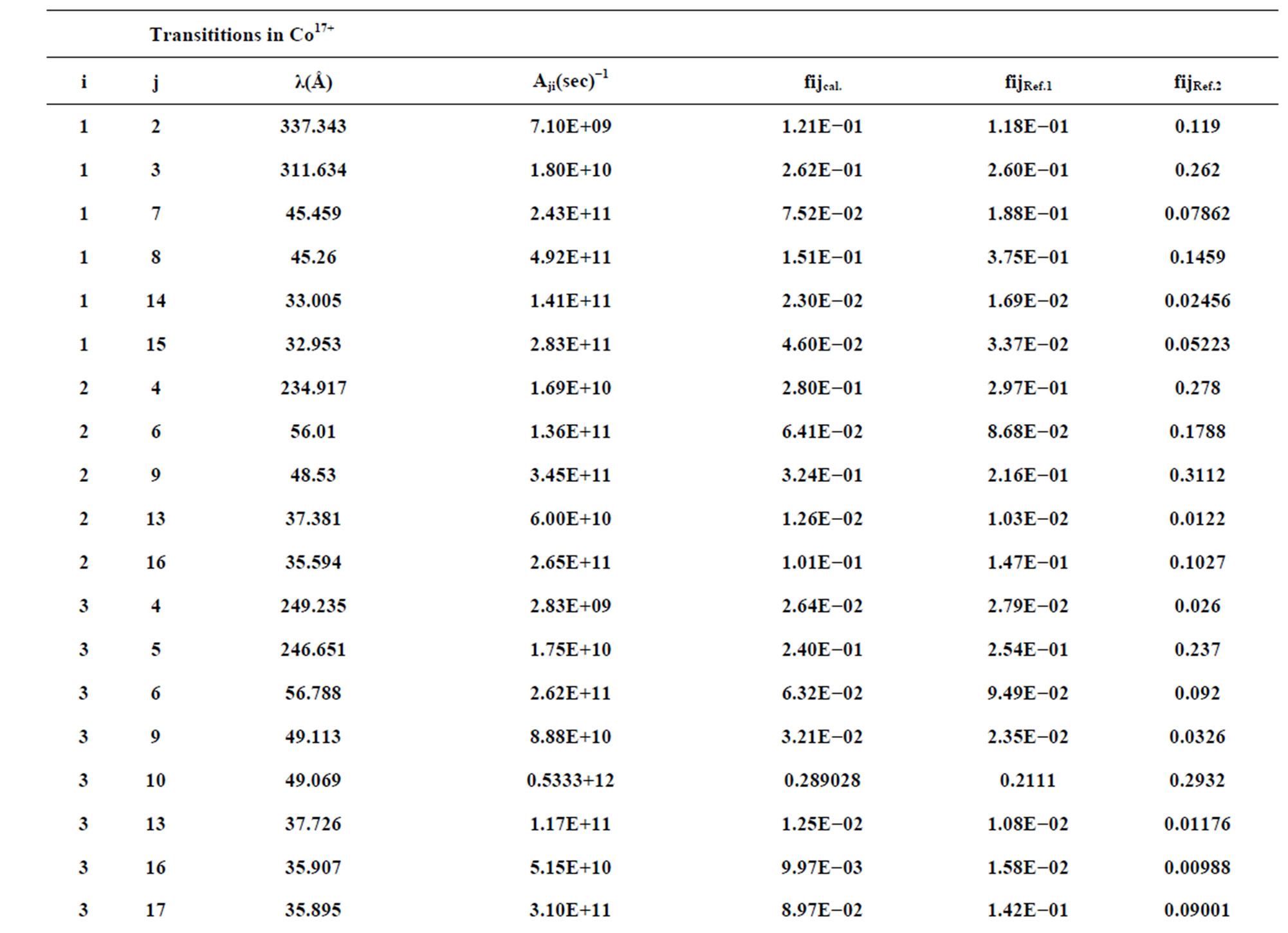
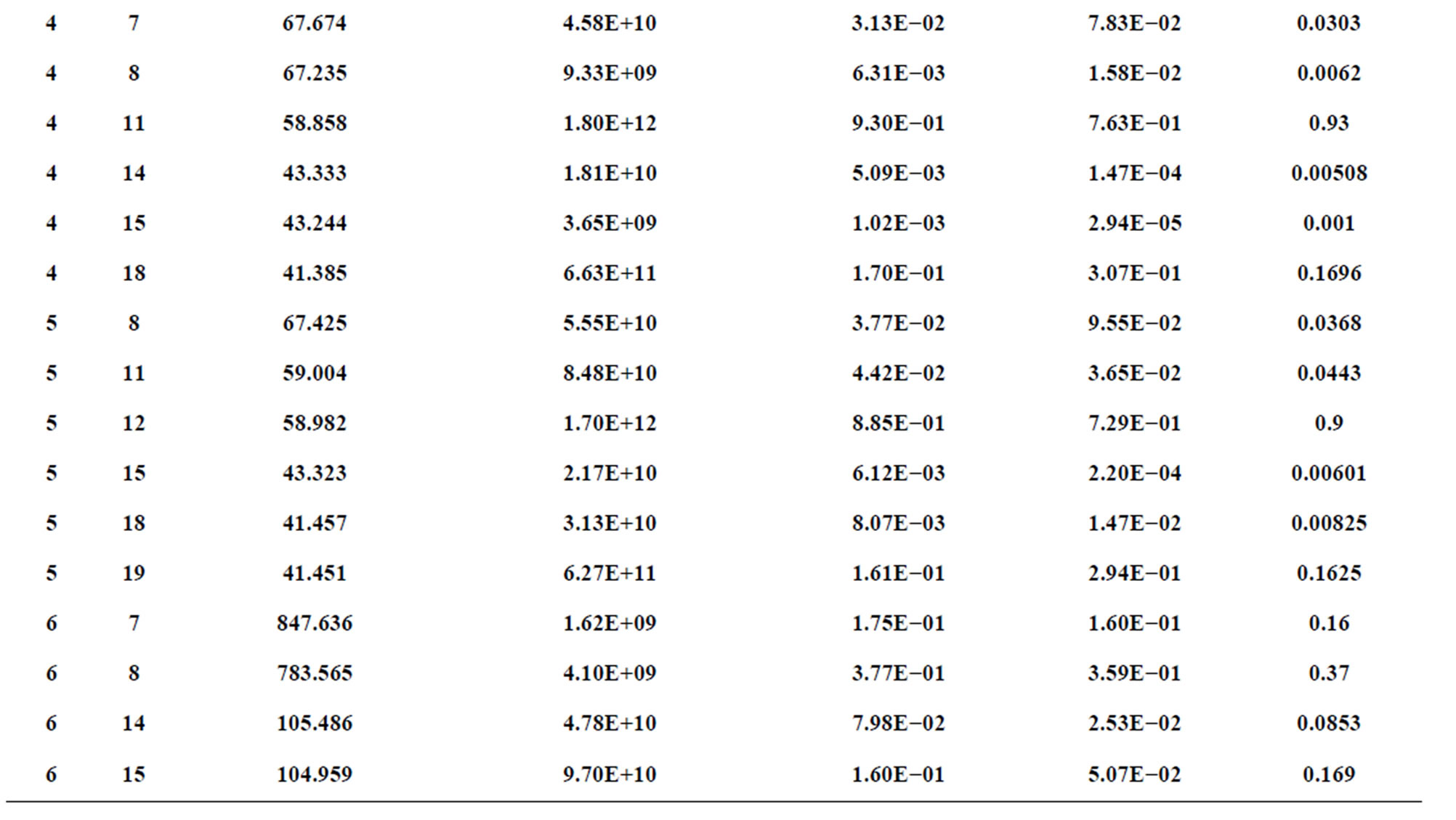


Table 2. Wavelength, oscillator strength and radiative rate for allowed.
have used Configuration–Interaction Code (CIV3).and the differ from (Nist, 2009) by less than 0.15% for most of the levels, except in some cases like the levels 2, 3, 4 and 5 in which the percentage difference between our value and the last two calculations is (0.63%, 0.64%), (−46%, 29%), (0.35%, 0.26%) and (0.27%, 0.33%) respectively, This mean that our results are in a good agreement with the theoretical and experimental value.
4.2. Oscillator Strength and Transition Probability
In the present work, we report results of oscillator strength and transition probabilities using the Cowan code taking relativistic corrections into account.
Table 3 present the wavelength, transition probability and the values of oscillator strength with a comparison against another published paper (Younis et al., 2006 [Reff.1]) and NIST. There was good agreement with (NIST, 2009 [Reff.2]) and only small differences about (0.8%) there was some similarities with the paper and high differences in some values about (85%).
4.3. Radiative Lifetime
Table 4 contains the present results of radiative lifetime for the upper and lower laser levels for the sodium-like Co.
The present calculations predict that the lifetime of the upper laser level must be longer than the lifetime of lower one to ensure the fast depletion of the population of lower level which helps the laser to sustain continuous or quasicontinuous wave operation.
4.4. Gain Distributions
4.4.1. Level Populations
The reduced population densities are calculated for 4 levels by solving the coupled rate Equations (14) using the coupled equations CRMO code [26] for solving simultaneous coupled rate equations.
Our calculations for the reduced population as a function of electron densities are plotted in Figures 1 and 2 at three different plasma temperatures (1/2, 3/4 of the ionization potential) for Na like Co.
We took into account in the calculation spontaneous radiative decay rate and electron collisional processes between all levels under study.
The behavior of level populations of the various ions can be explained as follows: in general, at low electron densities the reduced population density is proportional to the electron density, where excitation to an excited state is followed immediately by radiation decay, and collisional mixing of excited levels can be ignored.
At high densities (Ne > 1020), radiative decay to all
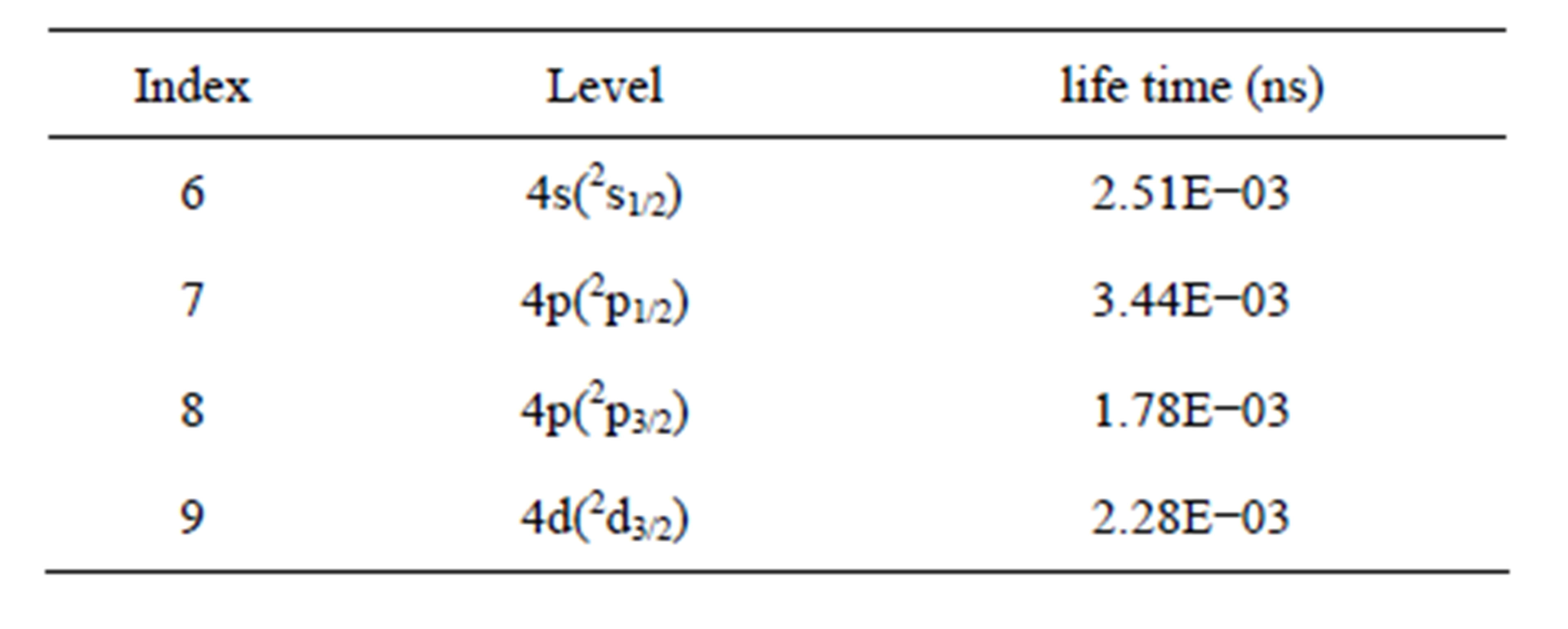
Table 3. Radiative lifetime for Co16+ laser levels.

Table 4. Parameters of the most intense laser transitions in Co16+ ion plasma.
levels will be negligible compared to collisional depopulations and all level population become independent of electron density and approximately equal (see Figures 1 and 2). The population inversion is largest where electron collisional de-excitation rate for the upper level is comparable to radiative decay for this level [21].
Form our study, it was found that the gain coefficient was very low at (1/4 ionization potential) for all elements, so the results of gain coefficient and reduced population have not been mentioned.
4.4.2. Inversion Factor
As we mentioned before, laser emission will occur only if there is population inversion or in other words for positive inversion factor F > 0. In order to work in the XUV and X-ray spectral regions, we have chosen transitions between any two levels producing photons with wavelength between 30 and 1000 Å.The electron density at which the population reaches collisional equilibrium
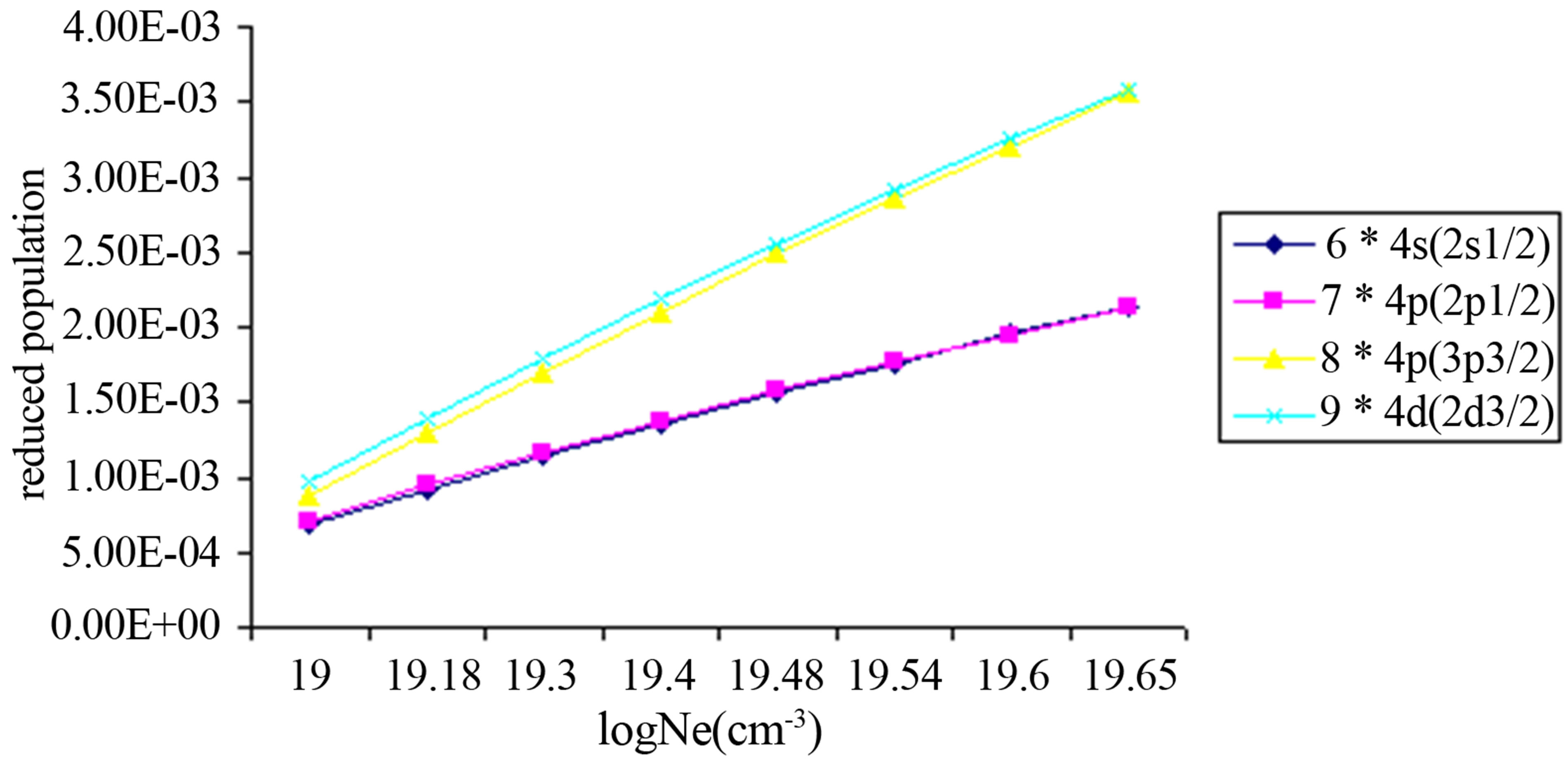
Figure 1. Reduced population of Co16+ levels after electron collisional pumping as a function of the electron density at temperature 273.29 eV.

Figure 2. Reduced population of Co16+ levels after electron collisional pumping as a function of the electron density at temperature 409.94 eV.
approximately equal to A/D, where A is radiative decay rate and D is the collisional de-excitation rate [20]. The population inversion is largest where the electron collisional de-excitation rate for the upper level is comparable to the radiative decay rate for this level.
For increasing atomic number Z, the population inversion occurs at higher electron densities, this is due to the increase in the radiative decay rate with Z and the decrease in collisional de-excitation rate coefficient with Z [27].
4.4.3. Gain Coefficient
As results of population inversion there will be positive gain in laser medium. Equation (19) has been used calculate gain coefficient for the Doppler broadening of various transitions in the Na like Co.
Our results for the maximum gain coefficient in cm−1 for those transitions having a positive inversion factor F > 0 in the case of Co16+ ion at different temperatures are calculated and plotted against electron density in Figures 3 and 4. The figures show that the population inversions occur for several transitions in the Co16+ ion, however the largest gain occurs for the Co16+ ion at 4d(2p1/2) − 4 s(2s1/2) transition.
For Na-like Co, the population inversion is due to strong monopole excitation from the 3s ground state to
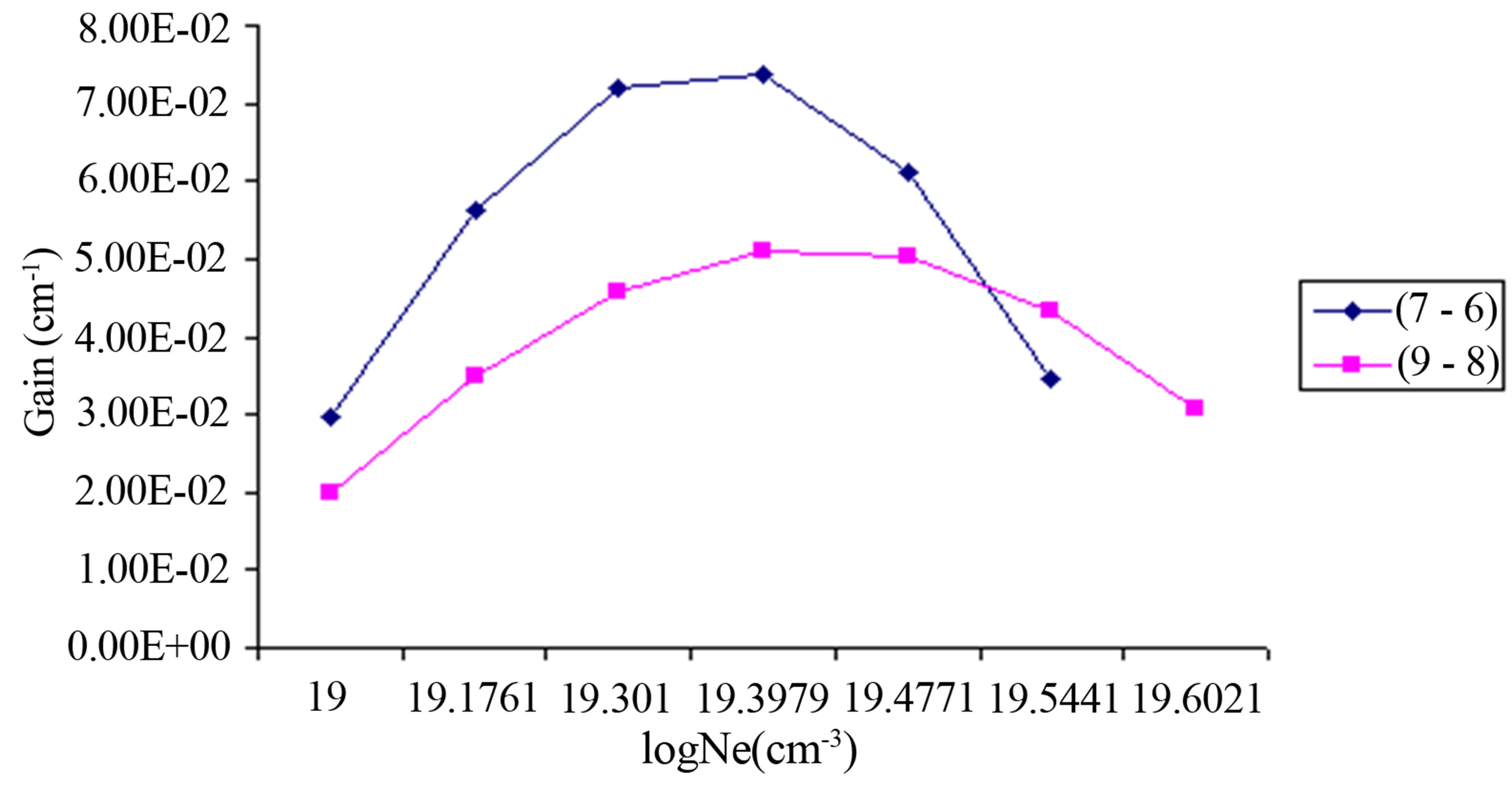
Figure 3. Gain coefficient of possible laser transitions against electron density at temperature 273.29 eV in Co16+.
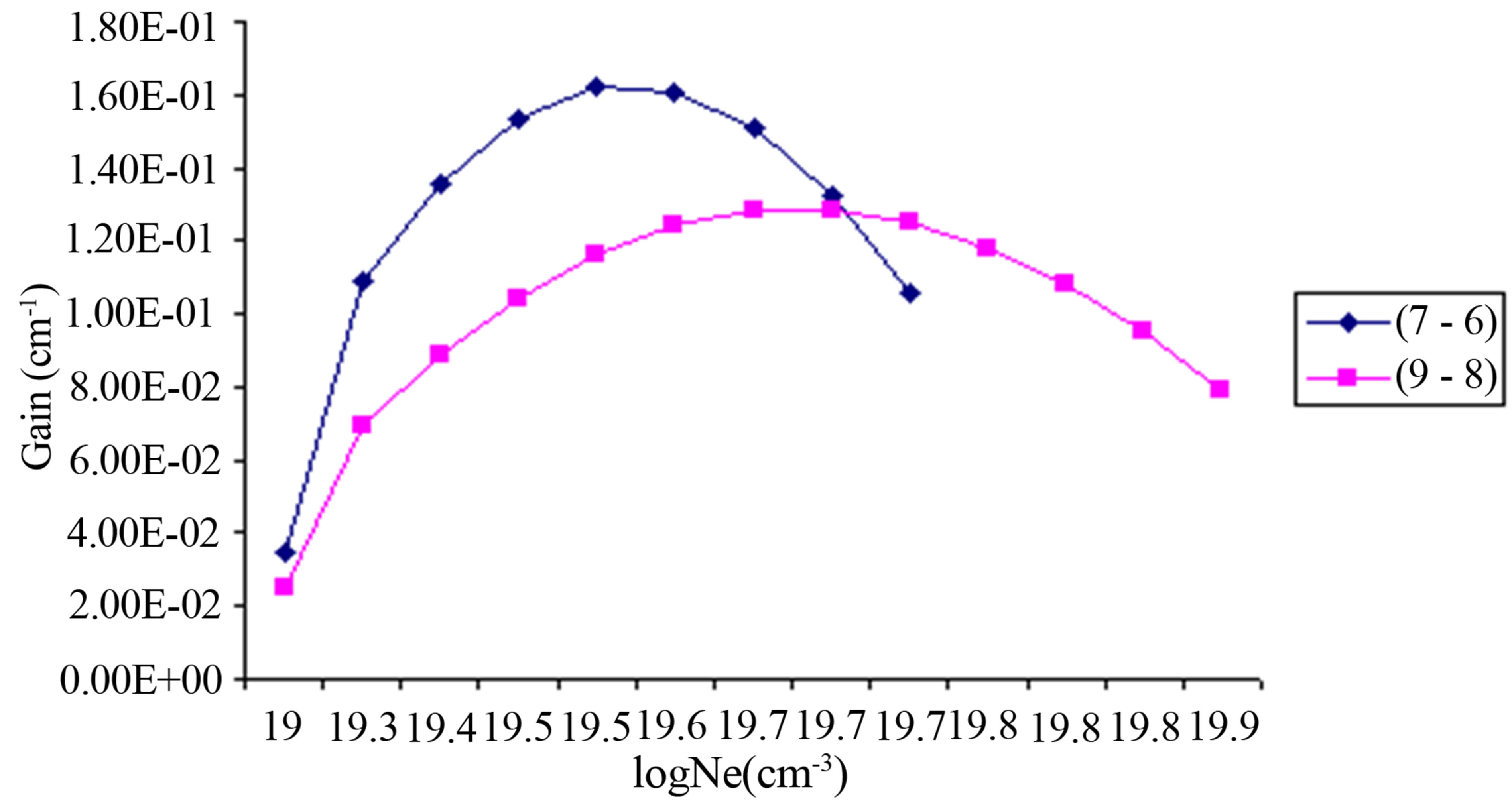
Figure 4. Gain coefficient of possible laser transitions against electron density at temperature 409.94 eV in Co16+.
the 3s 4d configuration and also the radiative decay of the 3s 4d level to the ground level is forbidden, while the 3s 4p level decays very rapidly to the ground level.
This short wavelength laser transitions was produced using plasmas created by optical lasers as the lasing medium. It is obvious that the gain increases with the temperature as the maximum gain increases with atomic number. Moreover, the peak of the gain curves shifts to higher electron densities with the increase of atomic number.
5. Conclusion
The analysis that has been presented in this work shows that electron collisional pumping (ECP) is suitable for attaining population inversion and offering the potential for laser emission in the spectral region between 50 and 1000 Å from the Na like Co. This class of lasers can be achieved under the suitable conditions of pumping power as well as electron density. If the positive gains obtained previously for some transitions in (Co16+ ion), together with the calculated parameters could be achieved experimentally, then successful low cost electron collisional pumping XUV and soft X-ray lasers can be developed for various applications. The results have suggested the following laser transitions in the Co16+ plasma ion, as the most promising laser emission lines in the XUV and soft X-ray spectral regions.
REFERENCES
- R. C. Elton, “X-Ray Lasers,” Academic Press, New York, INC, 1990.
- J. E. Trebes, S. B. Brown, et al., “Demonstration of XRay Holography with an X-Ray Laser,” Science, Vol. 238, No. 4826, 1987, pp. 517-519. http://dx.doi.org/10.1126/science.238.4826.517
- L. B. Da Silva, J. E. Trebes, et al., “X-Ray Laser Microscopy of Rat Sperm Nuclei,” Science, Vol. 258, No. 5080, 1992, pp. 269-271. http://dx.doi.org/10.1126/science.1411525
- D. Ress, L. B. Da Silva, et al., “Measurement of LaserPlasma Electron Density with a Soft X-Ray Laser Deflectometer,” Science, Vol. 265, v5171, 1994, pp. 514-517. http://dx.doi.org/10.1126/science.265.5171.514
- R. Cauble, L. B. Da Silva, et al., “Simultaneous Measurement of Local Gain and Electron Density in X-Ray Lasers,” Science, Vol. 273, No. 5278, 1996, pp. 1093-1096. http://dx.doi.org/10.1126/science.273.5278.1093
- D. H. Kalantar, M. H. Key, L. B. Da Silva, et al., “Measurement of 0.35 μm Laser Imprint in a Thin Si Foil Using an X-Ray Laser Backlighter,” Physical Review Letters, Vol. 76, 1996, 19, pp. 3574-3577. http://dx.doi.org/10.1103/PhysRevLett.76.3574
- C. F. Fischer, “Method: MCHF (ab Initio),” 2002. http://www.Vuse.Vanderbilt.Edu/~cff /mchfcollection/
- W. Siegel, J. Migdalek and Y. K. Kim, “Dirac-Fock Oscillator Strengths for E1 Transitions in the Sodium Isoelectronic Sequence (Na I-Ca X),” Atomic Data and Nuclear Data Tables, Vol. 68, No. 2, 1998, pp. 303-322. http://dx.doi.org/10.1006/adnd.1997.0769
- D. A. Verner, P. D Barthel and D. Tyther, “Atomic Data for Absorption Lines from the Ground Level at Wavelengths Greater than 228 A,” Astronomy and Astrophysics Supplement Series, Vol. 108, No. 2, 1994, pp. 287-340.
- J. R. Fuhr and W. L. Wiese, “Atomic Transition Probabilities,” In: D. R. Lide, Ed., CRC Handbook of Chemistry and Physics, 72nd Edition, CRC Press, 1991, pp. 211-213.
- W. L. Wiese, M. W. Smith and B. M. Miles, “Atomic Transition Probabilities (Na through Ca-A Critical Data Compilation),” National Standard Reference Data Series, National Bureau of Standards (US), NSRDS-NBS 22, Vol. II, 1969.
- G. A. Martin, J. R. Fuhr and W. L. Wiese, “Atomic Transition Probabilities-Scandium: Through Manganese,” Journal of Physical and Chemical Reference Data, Vol. 17, Suppl. 3, 1988,
- J. R. Fuhr, G. A. Martin and W. L. Wiese, “Atomic Transition Probabilities-Iron: Through Manganese,” Journal of Physical and Chemical Reference Data, Vol. 17, Suppl. 4, 1988, pp. 167-171.
- R. M. Lowe and E. Biemont, “Lifetime measurements for the 4p 2Po and 5p 3Po Levels and Calculation of Transition Probabilities in Na I,” Journal of Physics b-Atomic Molecular and Optical Physics, Vol. 27, No. 11, 1994, pp. 2161-2167. http://dx.doi.org/10.1088/0953-4075/27/11/012
- D. R. Hartree and E. E. Salpeter, “Quantum Mechanics of One-and Two-Electron Atoms,” Springer-Verlage, Berlin and New York, 1657.
- I. Sobelman, “Atomic Spectra and Radiative Transition,” Springer, Berlin, 1979. http://dx.doi.org/10.1007/978-3-662-05905-0
- R. D. Cowan, “The Theory of Atomic Structure and Spectra,” University of California Press, Berkeley, 1981.
- U. Feldman, A. K. Bhatia and S. Suckewer, “Short Wavelength Laser Calculations for Electron Pumping in NeonLike Krypton (Kr XXVII),” Journal of Applied Physics, Vol. 54, No. 5, 1983, pp. 2188-2197. http://dx.doi.org/10.1063/1.332371
- U. Feldman, J. F. Seely and G. A. Doschek, “3s-3p Laser Gain and x-Ray Line Ratios for the Carbon Isoelectronic Sequence,” Journal of Applied Physics, Vol. 59, No. 12, 1986, pp. 3953-3957. http://dx.doi.org/10.1063/1.336695
- U. Feldman, G. A. Doschek, J. F. Seely and A. K. Bhatia, “Short Wavelength Laser Calculations for Electron Pumping in BE I and B I Isoelectronic Sequences (18 ≤ Z ≤ 36),” Journal of Applied Physics, Vol. 58, No. 8, 1985, p. 2909. http://dx.doi.org/10.1063/1.335838
- U. Feldman, J. F. Seely and A. K. Bhatia, “Scaling of Collisionally Pumped 3s-3p Lasers in the Neon Isoelectronic Sequence,” Journal of Applied Physics, Vol. 56, No. 9, 1984, pp. 2475-2478. http://dx.doi.org/10.1063/1.334308
- G. Chapline and L. Wood, “X-Ray Lasers,” Physics Today, Vol. 28, No. 40, 1975. http://dx.doi.org/10.1063/1.3069004
- A. V. Vinogradov and V. N. Shlyaptsev, “Calculations of Population Inversion Due to Transitions in Multiply Charged Neon-Like Ions in the 200âEUR“2000 Ã… Range,” Soviet Journal of Quantum Electronics, Vol. 10, No. 6, 1980, p. 754. http://dx.doi.org/10.1070/QE1980v010n06ABEH010287
- U. Feldman, J. F. Seely and G. A. Doschek, “Short Wavelength Laser Calculations in the Be I, B I And C I Isoelectronic Sequences,” Journal de Physique Collogues, Vol. 47, No. C6, 1986, p. C6-187.
- M. J. Seaton, “Atomic Data for Opacity Calculations. I. General Description,” Journal of Physics B: Atomic and Molecular Physics, Vol. 20, No. 23, 1987, 6363.
- S. H. Allam, “CRMO Computer Code,” Private Communication, 2003.
- U. Feldman, J. F. Seely and A. K. Bhatia, “Density Sensitive x-Ray Line Ratios in the BE i, B i, and Ne i Isoelectronic Sequences,” Journal of Applied Physics, Vol. 58, No. 11, 1984, pp. 3954-3958. http://dx.doi.org/10.1063/1.335569
- W. O. Younis, S. H. Allam and Th. M. El-Sherbini, “Fine-Structure Calculations of Energy Levels, Oscillator Strengths, and Transition Probabilities for Sodium-Like Ions (Co XVII-Kr XXVI),” Atomic Data and Nuclear Tables, Vol. 92, No. 2, 2005, pp. 187-205.
- “Atomic Spectra Database Lines Form,” NIST, Physical Meats Laboratory, Vol. 11, 2009, pp. 3954-3958. http://physics.nist.gov/PhysRefData/ASD/levels_form.html
Abbreviations
Explanation of Tables
1—Table 1 gives the parameter for energy levels in units of (1000 cm−1).
2—Tables 2 gives the energy levels values in (1000 cm−1) for even levels together with the comparison of our data and those of ref.1, ref.2.
3—Tables 3 give the wavelengths in angstrom (Å), absorption oscillator strength, and transition probabilities in (sec)−1for electric dipole transition between odd lower levels and even upper levels with the comparison of our data and those of ref.1, ref.2.
4—Tables 4 give the results of radiative lifetime in (ns) for the upper and lower laser levels the energy levels.

