Optics and Photonics Journal
Vol.3 No.4(2013), Article ID:35620,9 pages DOI:10.4236/opj.2013.34042
Nonlinear Optical Properties of Two Different Nanoassemblies of Polydiacetylene (PDA): PDA Nanovesicles and PDA Nanocrystals
Department of Physics, Indian Institute of Technology, Bombay, India
Email: binaybhushan@gmail.com
Copyright © 2013 B. Bhushan et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 7, 2013; revised June 15, 2013; accepted July 20, 2013
Keywords: Third Order Nonlinear Optical Properties; Second Molecular Hyperpolarizability; Conjugated Polymers; Polydiacetylene
ABSTRACT
We have synthesized and characterized two different nanoassemblies of polydiacetylene (PDA), PDA nanovesicles and PDA nanocrystals, in order to study the influence of chain packing geometry of the two nanoassemblies on their third order nonlinear optical properties. The second molecular hyperpolarizability 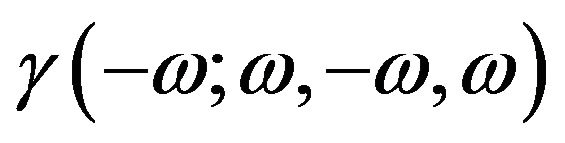 of the two samples was investigated by antiresonant ring interferometric nonlinear spectroscopic (ARINS) technique using femtosecond modelocked Ti:sapphire laser in the spectral range of 720 nm - 820 nm. The observed spectral dispersion of γ has been explained in the framework of three-essential states model involving the ground state, a one-photon excited state and a two-photon excited state. The observed optical nonlinearity has been correlated with the electronic structure of the two samples. The energy of two-photon state, transition dipole moments and line width of the transitions have been estimated. Our studies show that the arrangement of polymer chains in polydiacetylene nanocrystals is more favorable for higher nonlinearity.
of the two samples was investigated by antiresonant ring interferometric nonlinear spectroscopic (ARINS) technique using femtosecond modelocked Ti:sapphire laser in the spectral range of 720 nm - 820 nm. The observed spectral dispersion of γ has been explained in the framework of three-essential states model involving the ground state, a one-photon excited state and a two-photon excited state. The observed optical nonlinearity has been correlated with the electronic structure of the two samples. The energy of two-photon state, transition dipole moments and line width of the transitions have been estimated. Our studies show that the arrangement of polymer chains in polydiacetylene nanocrystals is more favorable for higher nonlinearity.
1. Introduction
There has been considerable scientific research on the development of efficient nonlinear optical materials with large third-order nonlinear susceptibility for photonic devices such as ultrafast optical switching, optical data storage, optical limiting etc. In this direction, conjugated polymers have been investigated extensively due to their inherently large ultrafast nonresonant nonlinearity and scope for the improvement by way of molecular engineering. Among the varieties of conjugated polymers, polydiacetylenes (PDA) exhibit large potential for photonic device applications due to the ease of processibility, variety of morphologies—crystalline or amorphous, large damage threshold and environmental as well as mechanical stability. The quasi-infinite conjugated bonding in PDA is responsible for many unique properties, such as charge transport [1], electronic absorption at long wavelengths [2] and high third-order nonlinear susceptibilities [3]. Polydiacetylenes have fully conjugated planer backbones represented by the structural formula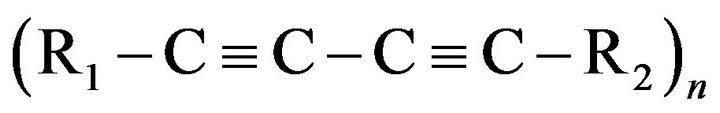 , where R1 and R2 refer to the substituent side groups. Extensive
, where R1 and R2 refer to the substituent side groups. Extensive  - electron delocalization takes place along this polymeric backbone. However, the bond alternation implies a periodic modulation of the electron charge density that produces an energy gap between a filled valence band and an empty conduction band. Therefore, PDAs are considered to be quasi 1-D semiconductors.
- electron delocalization takes place along this polymeric backbone. However, the bond alternation implies a periodic modulation of the electron charge density that produces an energy gap between a filled valence band and an empty conduction band. Therefore, PDAs are considered to be quasi 1-D semiconductors.
In polymeric system, the conjugated carbon backbone holds the key for interesting electronic and nonlinear optical properties, whereas the side groups facilitate structure control and material processing. One of the features of PDAs is the feasibility of modifying their properties to a considerable extent by introducing various substituents into the side groups. This suitability of modifying chemical structure of substituted side groups enables PDAs to be prepared in the form of single crystals, thin films and solutions. Polydiacetylenes have been extensively explored for their nonlinear optical studies. This includes PDA-PTS [3-6], PDA-3-BCMU [7], PDA- 4-BCMU [8,9], PDA-9-BCMU [10] etc. More recently, some composites of PDA have also been reported to have excellent nonlinear optical properties [11-14]. However, it is to be noted that most of these papers report the measurement of nonlinear optical response at a single resonant wavelength and hence did not offer any useful insight into the nonlinear optical properties of the given sample. On the other hand, spectral dispersion characteristic of second molecular hyperpolarizability 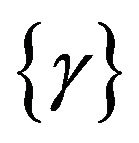 in a given spectral range is the key to understand the electronic structure-nonlinearity relationship in a given class of molecule. Moreover, the literature generally reports the investigation of nonlinearity by Z-scan technique using nanosecond pulse duration at 532 nm available from a frequency-doubled Q-switched Nd:YAG laser. However, Z-scan technique, although being very popular because of simple and single beam technique, can sometimes give misleading results because it does not differentiate between the electronic and other mechanism of nonlinearity. Also, it does not provide high enough sensitivity for the measurement of nonlinearity at moderate and safe intensity levels. On the other hand, antiresonant ring interferometric nonlinear spectroscopic (ARINS) technique reported by our group earlier [15], apart from being a highly sensitive technique, has the unique capability of discriminating electronic nonlinearity against other mechanisms of nonlinearity based on the response time of different types of nonlinear processes. In our investigation reported here, we have used transform limited, 80 fs pulses (repetition rate 100 MHz and energy per pulse 5 nJ) from a self mode-locked Ti:sapphire laser to measure the nonlinear optical response of our sample using ARINS technique. Because of use of femtosecond pulse and establishing the ARINS setup to measure nonlinearity faster than 3 ps (described below), the nonlinearity reported in this paper is purely of electronic origin. Moreover, instead of investigating the nonlinear response at a single wavelength, we have measured the third-order susceptibility in the spectral range of 720 nm - 820 nm. The subsequent spectral dispersion of second molecular hyperpolarizability has been analyzed in the framework of three-essential states model [16] and a correlation with the electronic and chemical structure of the sample has been discussed. The energy of two-photon state, transition dipole moments and the line width of transitions have also been estimated. In addition, probably for the first time to the best of our knowledge and belief, we have also explored the influence of chain coupling effects facilitated by the chain packing geometry of PDAs on their third-order optical nonlinearity. To realize this objective, we have synthesized two different types of nanoassemblies of PDA, namely, PDA nanovesicles and PDA nanocrystals in aqueous solution. The two nanoassemblies, by virtue of their basic structure, are expected to have differences in their chain packing geometry. The two samples were characterized by UV-Vis absorption spectroscopy, transmission electron microscopy (TEM) and electron diffraction (ED).
in a given spectral range is the key to understand the electronic structure-nonlinearity relationship in a given class of molecule. Moreover, the literature generally reports the investigation of nonlinearity by Z-scan technique using nanosecond pulse duration at 532 nm available from a frequency-doubled Q-switched Nd:YAG laser. However, Z-scan technique, although being very popular because of simple and single beam technique, can sometimes give misleading results because it does not differentiate between the electronic and other mechanism of nonlinearity. Also, it does not provide high enough sensitivity for the measurement of nonlinearity at moderate and safe intensity levels. On the other hand, antiresonant ring interferometric nonlinear spectroscopic (ARINS) technique reported by our group earlier [15], apart from being a highly sensitive technique, has the unique capability of discriminating electronic nonlinearity against other mechanisms of nonlinearity based on the response time of different types of nonlinear processes. In our investigation reported here, we have used transform limited, 80 fs pulses (repetition rate 100 MHz and energy per pulse 5 nJ) from a self mode-locked Ti:sapphire laser to measure the nonlinear optical response of our sample using ARINS technique. Because of use of femtosecond pulse and establishing the ARINS setup to measure nonlinearity faster than 3 ps (described below), the nonlinearity reported in this paper is purely of electronic origin. Moreover, instead of investigating the nonlinear response at a single wavelength, we have measured the third-order susceptibility in the spectral range of 720 nm - 820 nm. The subsequent spectral dispersion of second molecular hyperpolarizability has been analyzed in the framework of three-essential states model [16] and a correlation with the electronic and chemical structure of the sample has been discussed. The energy of two-photon state, transition dipole moments and the line width of transitions have also been estimated. In addition, probably for the first time to the best of our knowledge and belief, we have also explored the influence of chain coupling effects facilitated by the chain packing geometry of PDAs on their third-order optical nonlinearity. To realize this objective, we have synthesized two different types of nanoassemblies of PDA, namely, PDA nanovesicles and PDA nanocrystals in aqueous solution. The two nanoassemblies, by virtue of their basic structure, are expected to have differences in their chain packing geometry. The two samples were characterized by UV-Vis absorption spectroscopy, transmission electron microscopy (TEM) and electron diffraction (ED).
2. Experimental Procedure
Although Zhou et al. [17] have reported a methodology for the preparation of polydiacetylene nanovesicles, but we have synthesized the same by a little bit different method. First, we prepared an ethanol solution of the monomer, 10,12-pentacosadiynoic acid (PCDA) having concentration of 1.5 ´ 10−2 mol/l in a test tube. The organic solvent was then purged with N2 to give a thin film of the lipids on the glass surface of the test tube. Then deionized water was added to yield typically a total lipid concentration of 1 mM. The resulting solution was filtered through a 1.2 mm filter and the filtrate was cooled at 4˚C for 12 h. Polymerization was carried out at room temperature by irradiating the solution with 254 nm UV light (100 W) for 15 minutes to induce conjugated backbone of alternating double and triple bonds. Photopolymerization yielded deep blue colour liquid containing desired nanovesicles. Polymerization reaction got completed within 15 minutes. Exposure for very long duration (>60 minutes) or radiation more intense than 1 mW/cm2 turns the solution red presumably due to thermochromism induced by the heat generated by the absorption of radiation. A detailed explanation as well as schematic representation of the polymerization of diacetylene monomers and subsequent formation of nanovesicles has been explained in the literature [17,18].
For the synthesis of polydiacetylene nanocrystals, 2.5 ml of deionized water precooled to 20˚C was taken in a 2 cm diameter test tube and stirred with a magnetic stirrer at a speed such that a whirlpool was formed. In this stirring state of water, 1.3 ml stock solution of 10, 12 pentaco-sadiynoic acid (1.5 ´ 10−2 M) was added in the form of rapid stream using a syringe. This turned the solution milky. Next, the solution was sonicated for 20 minutes in an ultrasonic bath and then exposed to UV radiation for 15 minutes. Upon UV radiation, monomer nanoassemblies got polymerized to yield a deep blue so- lution containing PDA nanocrystals.
The two PDA nanoassemblies were characterized by UV-Vis absorption spectroscopy, transmission electron microscopy (TEM) and electron diffraction (ED). UVVis absorption spectra were taken with Jasco V-530 UV/ Vis Spectrophotometer. The absorption spectrum of PDA nanovesicles is shown in Figure 1. The absorption bands of p-conjugated polymeric diacetylene appear with main peak at 631 nm and two secondary peaks at 582 nm and 542 nm respectively. The 542 nm peak corresponds to the vibronic peak which is seen in all polydiacetylenes. The origin of the peak at 582 nm could not be ascertained. It is our conjecture that it may be arising from the splitting of absorption peak due to the chain coupling. This can be confirmed by polarization studies which are not possible in solution and hence were not pursued further.
UV-Vis absorption spectrum of PDA nanocrystals, shown in Figure 2, displays two peaks at 664 nm and 582 nm. The second peak on higher energy side is again a vibronic peak. The absorption spectrum of PDA nanocrystals is qualitatively similar to that of PDA nanovesicles except the peak in between the exciton peak and the corresponding vibronic peak observed in nanovesicles. If this peak was due to the splitting arising because of chain coupling, then it can be absent in nanocrystals due to different packing of linear array of chains. Both the exciton and vibronic peaks in PDA nanocrystals are red shifted relative to those seen in nanovesicles.
UV-Vis absorption spectrum does not reveal the differences between nanoassemblies of polymer chains in nanocrystals and those in nanovesicles. To accomplish this, the microstructure of PDA nanovesicles and nanocrystals was investigated by transmission electron microscopy (TEM). The TEM image was obtained using Philips CM200 electron microscope. The TEM image of
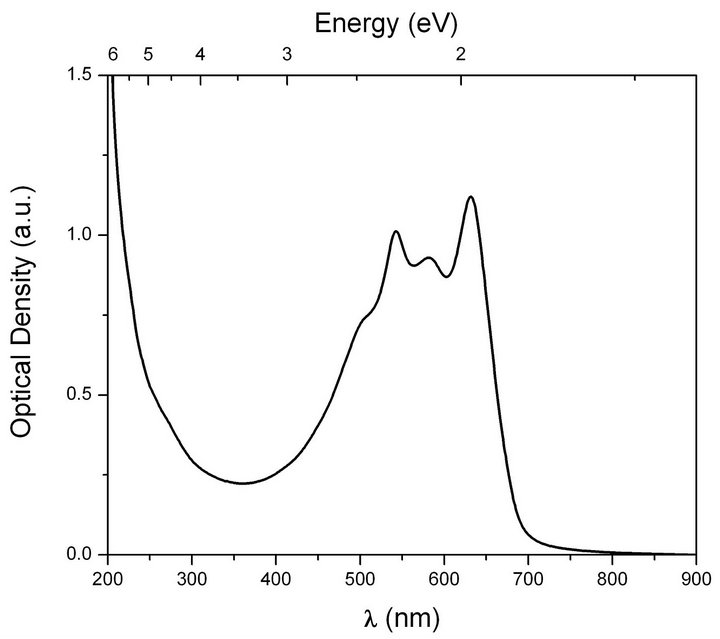
Figure 1. Linear absorption spectrum of PDA nanovesicles.
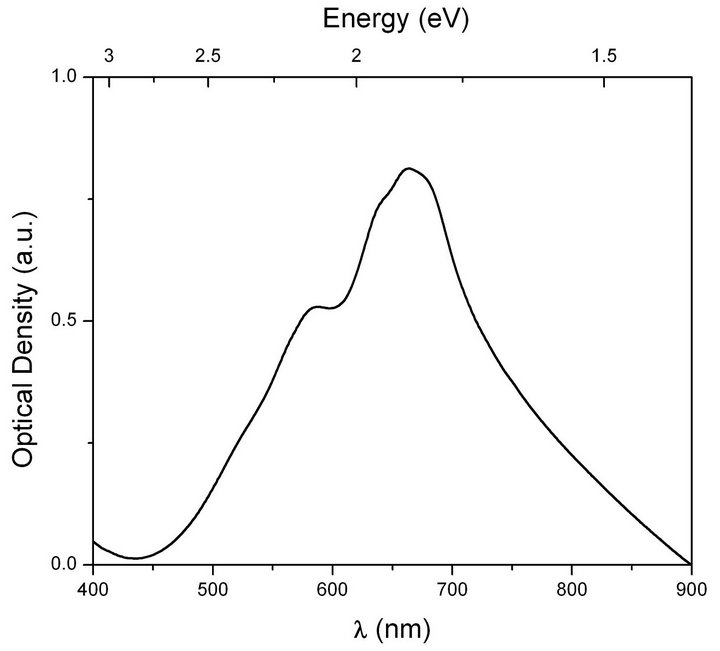
Figure 2. Linear absorption spectrum of PDA nanocrystals.
PDA nanovesicles, shown in Figure 3, shows the vesicle shell structure of about 120 nm in diameter. The thickness of the vesicle shell is about 10 nm and the core size is about 100 nm. Figure 4 shows the TEM image of PDA nanocrystals, with size ranging from 500 nm to 1.5 mm. To ascertain the crystalline nature of PDA nanocrystals, their TEM diffraction image was also recorded which is shown in Figure 5. The calculated d-spacings obtained from the diffraction pattern are 2.35 Å, 1.84 Å and 1.37 Å which are similar to that reported in the literature [19]. N. J. Poole et al [20] have also reported a similar
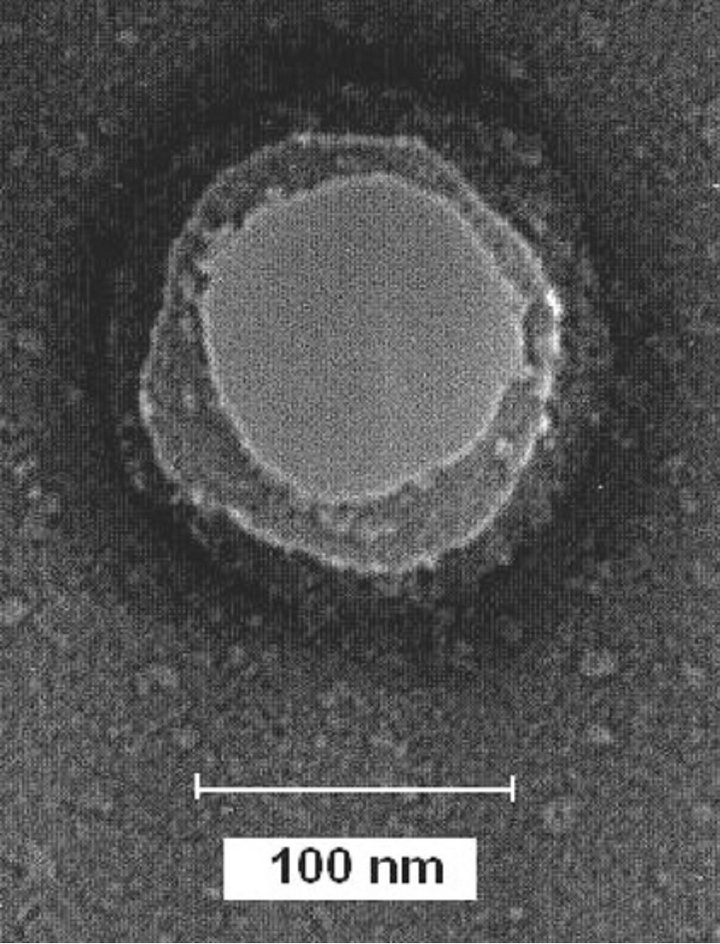
Figure 3. TEM image of PDA nanovesicle.

Figure 4. TEM image of PDA nanocrystals.

Figure 5. Electron diffraction pattern of PDA nanocrystal.
electron diffraction pattern of photooxidized polydiacetylene crystals. The TEM picture of PDA nanovesicles did not show any diffraction fringes, clearly ruling out their crystalline nature.
Third-order nonlinear optical properties of the colloidal suspensions of polydiacetylene nanovesicles and nanocrystals were investigated by antiresonant ring interfereometric nonlinear spectroscopic (ARINS) technique [15]. In this technique, a laser pulse is divided into two counter propagating, grossly unequal energy pulses by a beam splitter. These pulses after passing through the sample, placed asymmetrically in the ring, get dressed with differential nonlinear phase and interfere upon their arrival back at the beam splitter which governs the extent of the transmission through the interferometer ring. One measure the nonlinear response by its transmittance as a function of intensity. One can discriminate various mechanisms of the nonlinearity differing in their response times by simply controlling the delay in the arrival time of the two counter propagating pulses in the sample through its placement with respect to the center of the ring. In our experiment, it was set to detect nonlinearities faster than 300 fs to rule out any thermal nonlinear response.
The typical ARINS experimental setup is shown in Figure 6. Transform limited, 80 fs pulses (repetition rate 100 MHz and energy per pulse 5 nJ) from a self modelocked Ti:sapphire laser were used for the experiment. The incoming pulse beam was split by a 50 - 50 beam splitter into two counter-propagating pulses. The two counter-propagating laser pulses inside the ring were focussed inside the sample by two identical lenses of 10 cm focal length each. In order to avoid the contribution of integrating slow nonlinearities and for the measurement of fast electronic nonlinearity only, the solution sample in 1 mm path length quartz cuvette was placed inside the ring such that the intense pulse arrived earlier at the sample in order to initiate nonlinear processes.
Energy of the incident and the transmitted pulses was
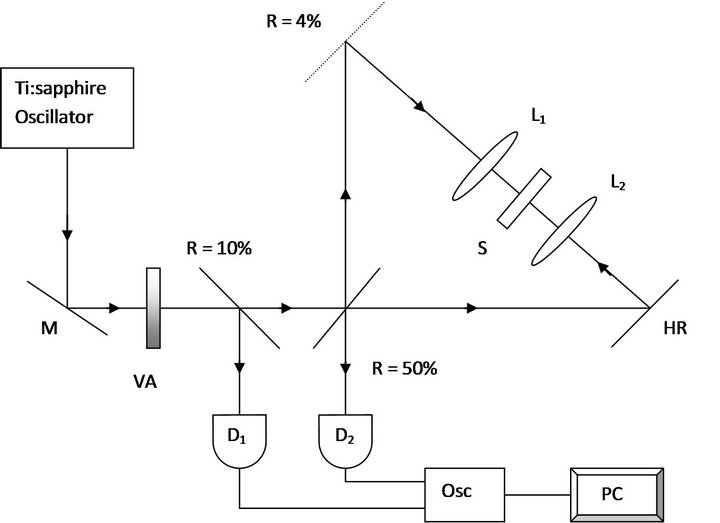
Figure 6. ARINS experimental setup. M—mirror, L1, L2—lenses, HR—high reflectivity mirror, S—sample, VA— variable attenuator, D1,D2—detectors, Osc—digital oscilloscope, PC—computer.
measured using precalibrated photodetectors. In order to avoid any misalignment due to the fluctuating air current pressure during the course of intensity scan, the experimental setup was kept inside an enclosure made of perspex. The experimental setup was standardized using toluene which yielded 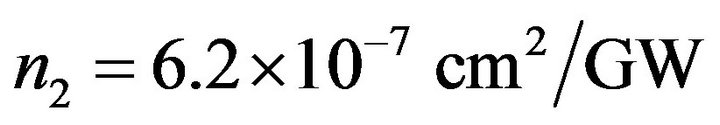 and a negligibly small value of
and a negligibly small value of 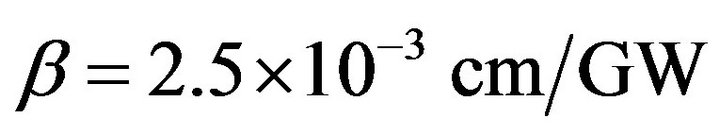 corresponding to
corresponding to 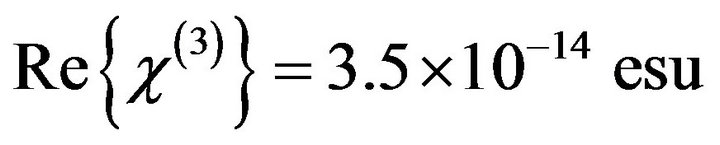 and
and
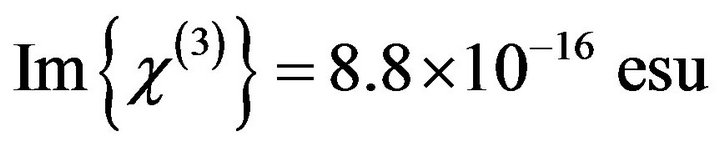 respectively. This measurement of
respectively. This measurement of  value of toluene is in excellent agreement with its earlier reported value determined by another nonlinear interferometric technique [21]. For the evaluation of the second molecular hyperpolarizability using Equation (1), nonlinear susceptibility
value of toluene is in excellent agreement with its earlier reported value determined by another nonlinear interferometric technique [21]. For the evaluation of the second molecular hyperpolarizability using Equation (1), nonlinear susceptibility  of the solvent (water) is required. ARINS intensity scans for water with available laser power did not show any measurable nonlinearity. Its value for the evaluation of
of the solvent (water) is required. ARINS intensity scans for water with available laser power did not show any measurable nonlinearity. Its value for the evaluation of 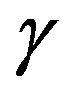 was, therefore, taken to be zero for both the real and the imaginary parts.
was, therefore, taken to be zero for both the real and the imaginary parts.
A typical transmitted intensity versus incident intensity scan of ARINS for the PDA nanovesicle at 804 nm is shown in Figure 7. Third-order nonlinear optical susceptibility of the two samples was studied over 720 nm - 820 nm spectral range. The second molecular hyperpolarizability  was evaluated using [22]
was evaluated using [22]
 (1)
(1)
based on a pairwise additive model for noninteracting molecules. Here 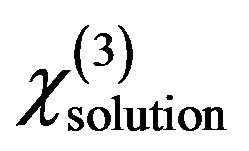 and
and 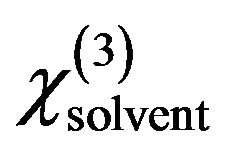 are the third-order susceptibility of solution and solvent respectively,
are the third-order susceptibility of solution and solvent respectively, 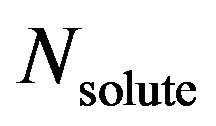
is the number density of solute, 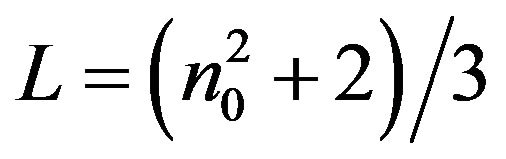 is the local field factor and
is the local field factor and 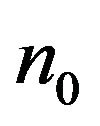 (
(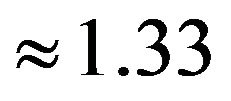 for water) is the refracttive index of the solvent.
for water) is the refracttive index of the solvent.
3. Results and Discussion
The measured  values of PDA nanovesicles and nanocrystals in the spectral range of 720 nm - 820 nm are
values of PDA nanovesicles and nanocrystals in the spectral range of 720 nm - 820 nm are
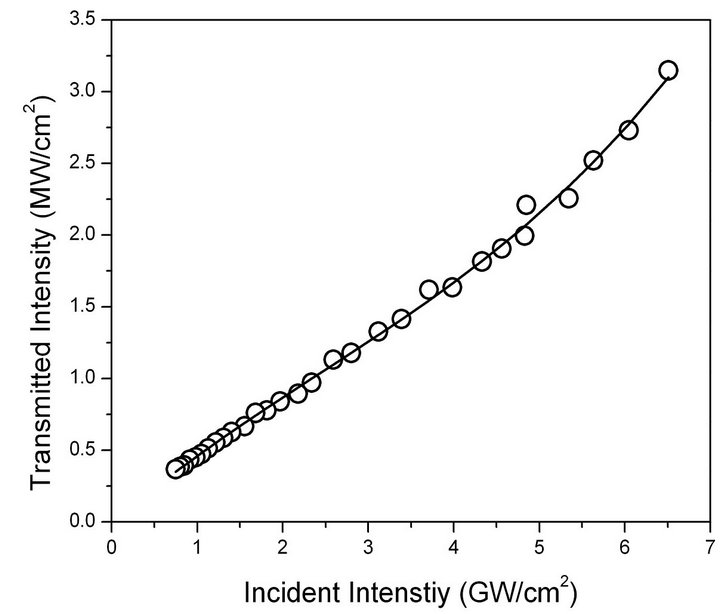
Figure 7. ARINS signal for PDA nanovesicles at 804 nm. Open circles are experimental points. Solid curve is the theoretical fit using the formulation given in Ref. [15].
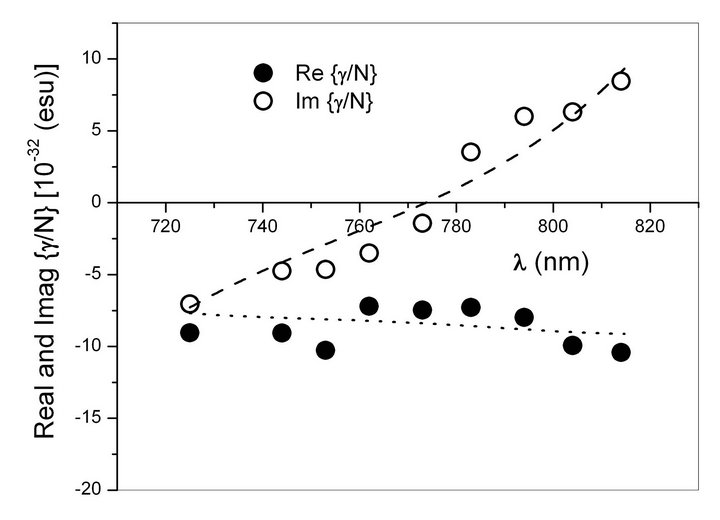
Figure 8. Three-essential states model fit to the dispersion of real and imaginary part of 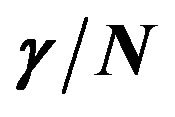 of PDA nanovesicles. Solid circles and open circles are the experimental points of
of PDA nanovesicles. Solid circles and open circles are the experimental points of 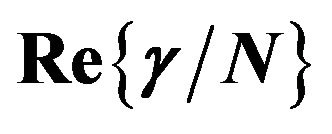 and
and  respectively. Dashed line and dotted line are their respective theoretical fits.
respectively. Dashed line and dotted line are their respective theoretical fits.
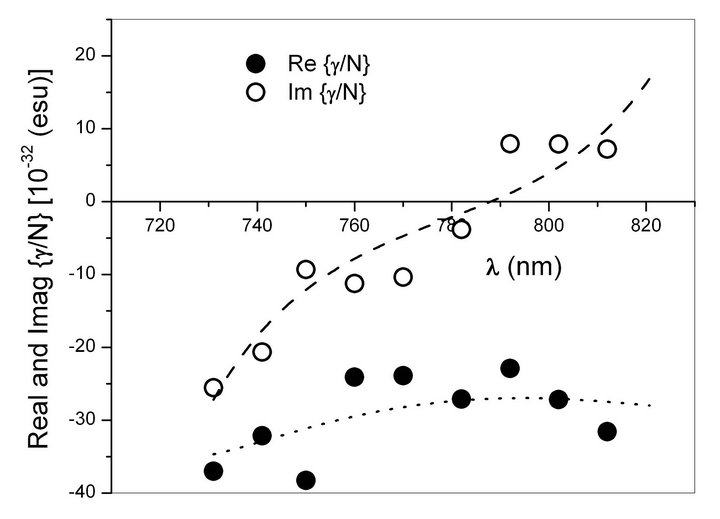
Figure 9. Three-essential states model fit to the dispersion of real and imaginary part of  of PDA nanocrystals. Solid circles and open circles are the experimental points of
of PDA nanocrystals. Solid circles and open circles are the experimental points of 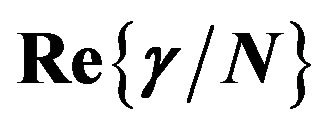 and
and 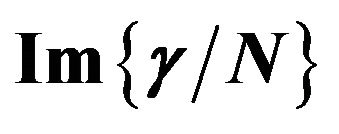 respectively. Dashed line and dotted line are their respective theoretical fits.
respectively. Dashed line and dotted line are their respective theoretical fits.
shown in Figures 8 and 9 respectively. An inspection of the imaginary part of the nonlinearity for both samples reveals that as one scans the interrogating wavelength away from one-photon resonance i.e. from 720 nm to 820 nm, magnitude of the imaginary part of the nonlinearity first decreases and then increases. On the other hand, variation of the real part is rather flat. This observed dispersion of real and imaginary parts of 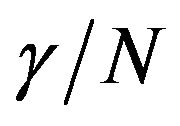 can be described in the framework of essential states model [16].
can be described in the framework of essential states model [16].
For one dimensional conjugated chains having 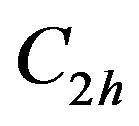 symmetry, the
symmetry, the  -electron states can be classified as even
-electron states can be classified as even 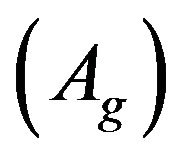 and odd
and odd  parity states [23]. One-photon transition dipole moment vanishes between states of same parity while a two-photon transition is allowed. For chains possessing
parity states [23]. One-photon transition dipole moment vanishes between states of same parity while a two-photon transition is allowed. For chains possessing 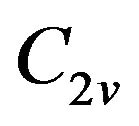 symmetry, the transition from the ground state
symmetry, the transition from the ground state 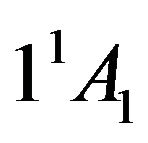 to
to 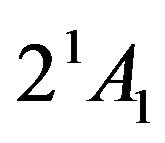 is one-photon allowed for light polarized perpendicular to the chain and to
is one-photon allowed for light polarized perpendicular to the chain and to 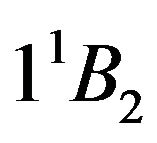 for light polarized parallel to the chain. Since for quasi 1-D chains, the component of transition dipole moment perpendicular to the chain is vanishingly small, these states can be treated analogous to
for light polarized parallel to the chain. Since for quasi 1-D chains, the component of transition dipole moment perpendicular to the chain is vanishingly small, these states can be treated analogous to  and
and 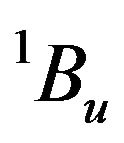 states of the
states of the 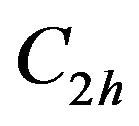 group. The electronic nonlinearity of a molecule arises from the mixing of its ground and the excited states and can be calculated within the framework of perturbation theory by summing over the response from all the states of the system. It has been shown that in organic molecules, nonlinear optical response could be adequately explained by considering only the low lying three or four states [16,24]. In the three-level model, these have been identified as the ground state
group. The electronic nonlinearity of a molecule arises from the mixing of its ground and the excited states and can be calculated within the framework of perturbation theory by summing over the response from all the states of the system. It has been shown that in organic molecules, nonlinear optical response could be adequately explained by considering only the low lying three or four states [16,24]. In the three-level model, these have been identified as the ground state  and the lowest oneand two-photon allowed states
and the lowest oneand two-photon allowed states 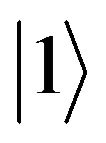 and
and  respectively. According to the perturbation expansion given by Orr and Ward [25], the second molecular hyperpolarizability in this case is given by
respectively. According to the perturbation expansion given by Orr and Ward [25], the second molecular hyperpolarizability in this case is given by
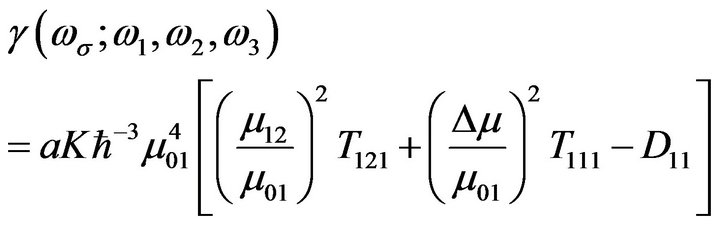 (2)
(2)
where 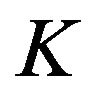 is a constant that depends on the frequency and degeneracy of a given optical process,
is a constant that depends on the frequency and degeneracy of a given optical process, 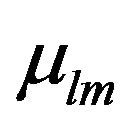 is the electronic transition dipole moment between states
is the electronic transition dipole moment between states  and
and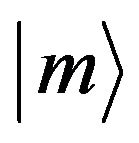 , and
, and 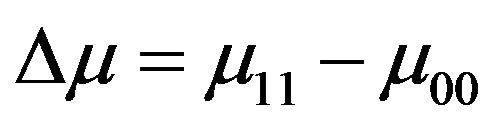 is the dipole difference,
is the dipole difference, 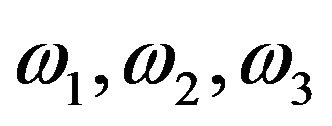 are the frequencies of the perturbing radiation fields,
are the frequencies of the perturbing radiation fields, 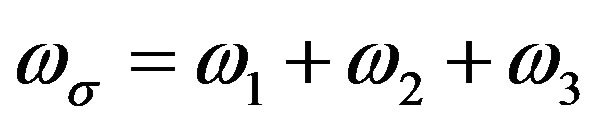 is the polarization response frequency while
is the polarization response frequency while 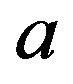 indicates the orientational average which is 1/5 for an isotropic liquid. For self–action process presented in this paper,
indicates the orientational average which is 1/5 for an isotropic liquid. For self–action process presented in this paper,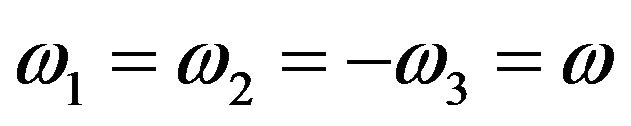 .
.
In the above equation, 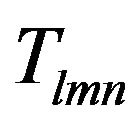 and
and 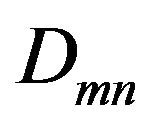 represent the triple and double sums respectively which include the damped energy dispersion terms in the denominators as in Equation (43c) of Ref. [25]. In particular,
represent the triple and double sums respectively which include the damped energy dispersion terms in the denominators as in Equation (43c) of Ref. [25]. In particular, 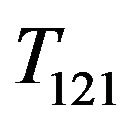 and
and 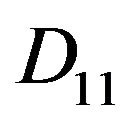 represent the contributions from the two-photon and one-photon transition channels respectively while the remaining part
represent the contributions from the two-photon and one-photon transition channels respectively while the remaining part  is nonzero only for noncentrosymmetric structures [26]. We found that the two-essential states model comprising the ground state and a onephoton state cannot describe the observed dispersion of
is nonzero only for noncentrosymmetric structures [26]. We found that the two-essential states model comprising the ground state and a onephoton state cannot describe the observed dispersion of 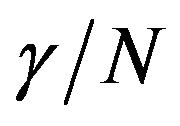 of the two PDA nanoassemblies. However, the three-essential state model involving the ground state, a one-photon excited state and a two-photon excited state describes the nature of observed dispersion satisfactorily. We have pointed out above that as the interrogating wavelength moves away from one-photon resonance i.e. from 720 nm to 820 nm, magnitude of the imaginary part of the nonlinearity first decreases and then increases. On the other hand, variation of the real part is rather flat. Such a scenario is indeed anticipated in three-essential states model when oneand two-photon channels are placed with respect to the spectral region of interest (photon energies of the exciting radiation) such that their respective negative and positive contributions to the imaginary parts of the nonlinearity interfere destructively, i.e. mutually cancel each other partially and their contributions to the real part reinforce each other to yield its rather flat dispersion. Since the one-photon channel contribution below resonance, as is the case here, will always be negative, its reinforcement by two-photon channel would mean a negative contribution from this channel as well. This would imply the two photon energy of the excitation radiation being larger than the transition energy of the two-photon channel over the entire spectral region addressed in our experiments. Considering the fact that a two-photon allowed energy state 21Ag has been observed lying above one-photon state 1Bu at ~2.85 eV in polydiacetylenes [7] and one-photon allowed state in our samples is located above the higher energy end of the spectral range of investigation (1.72 eV - 1.51 eV), the above mentioned situation is, in fact, applicable here. We, therefore, consider the three-essential states model for the quantitative description of our experimentally observed spectral dispersion characteristic of
of the two PDA nanoassemblies. However, the three-essential state model involving the ground state, a one-photon excited state and a two-photon excited state describes the nature of observed dispersion satisfactorily. We have pointed out above that as the interrogating wavelength moves away from one-photon resonance i.e. from 720 nm to 820 nm, magnitude of the imaginary part of the nonlinearity first decreases and then increases. On the other hand, variation of the real part is rather flat. Such a scenario is indeed anticipated in three-essential states model when oneand two-photon channels are placed with respect to the spectral region of interest (photon energies of the exciting radiation) such that their respective negative and positive contributions to the imaginary parts of the nonlinearity interfere destructively, i.e. mutually cancel each other partially and their contributions to the real part reinforce each other to yield its rather flat dispersion. Since the one-photon channel contribution below resonance, as is the case here, will always be negative, its reinforcement by two-photon channel would mean a negative contribution from this channel as well. This would imply the two photon energy of the excitation radiation being larger than the transition energy of the two-photon channel over the entire spectral region addressed in our experiments. Considering the fact that a two-photon allowed energy state 21Ag has been observed lying above one-photon state 1Bu at ~2.85 eV in polydiacetylenes [7] and one-photon allowed state in our samples is located above the higher energy end of the spectral range of investigation (1.72 eV - 1.51 eV), the above mentioned situation is, in fact, applicable here. We, therefore, consider the three-essential states model for the quantitative description of our experimentally observed spectral dispersion characteristic of  and
and . The respective sign of
. The respective sign of 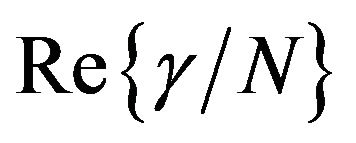 and
and 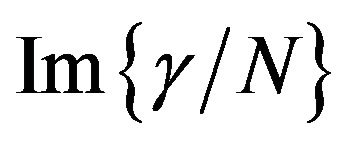 for PDA nanovesicles and nanocrystals has been assigned commensurate with the above discussion.
for PDA nanovesicles and nanocrystals has been assigned commensurate with the above discussion.
Since the photon energies in our spectral range of investigations are near to the resonance with the two channels, the dominant terms in the expression of three-essential states model of  given by Equaiton (2) will alone suffice. The resulting expression for
given by Equaiton (2) will alone suffice. The resulting expression for 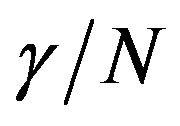 is then given by
is then given by
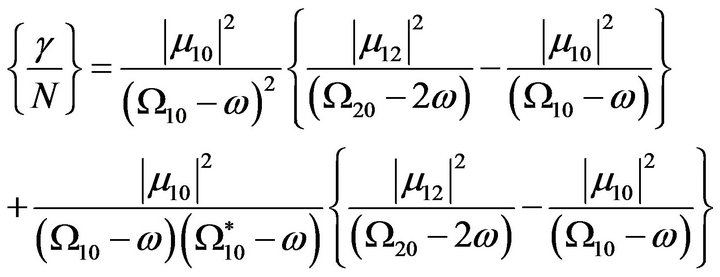 (3)
(3)
where 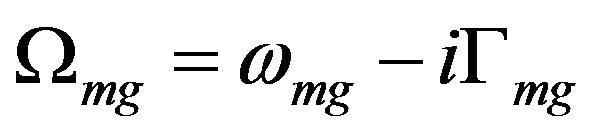 with
with 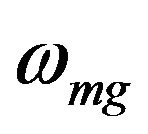 is the frequency difference between excited state m and reference state g and
is the frequency difference between excited state m and reference state g and  is the damping associated with the excited state m [25]. Resulting fits to the experimental dispersion of
is the damping associated with the excited state m [25]. Resulting fits to the experimental dispersion of 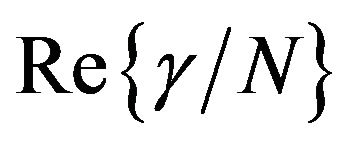 and
and 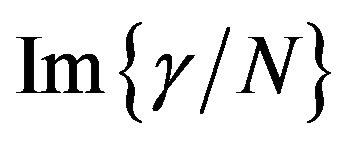 for PDA nanovesicles and nanocrystals are shown in Figures 8 and 9 respectively. It can be seen from these figures that the threeessential states model provides satisfactory description to the observed dispersion of
for PDA nanovesicles and nanocrystals are shown in Figures 8 and 9 respectively. It can be seen from these figures that the threeessential states model provides satisfactory description to the observed dispersion of 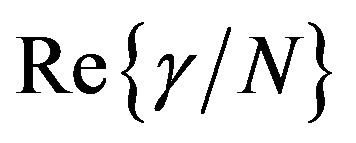 and
and 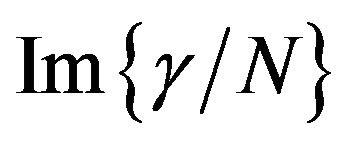 for the two samples. The three-essential state model, however, describes the nature of observed dispersion satisfactorily only when we consider a more realistic hyperbolic secant line shape instead of Lorentzian shape. This is because, the theoretical description for hyperpolarizability should take into account the inhomogeneously broadened absorption line profile of the electronic transitions of the molecules. We find that sech hyperbolic function, as suggested in Ref. [27], provides a better description for the linear absorption spectrum than the Lorentzian and hence the dispersion of the nonlinearity.
for the two samples. The three-essential state model, however, describes the nature of observed dispersion satisfactorily only when we consider a more realistic hyperbolic secant line shape instead of Lorentzian shape. This is because, the theoretical description for hyperpolarizability should take into account the inhomogeneously broadened absorption line profile of the electronic transitions of the molecules. We find that sech hyperbolic function, as suggested in Ref. [27], provides a better description for the linear absorption spectrum than the Lorentzian and hence the dispersion of the nonlinearity.
The striking feature of the dispersion characteristics of the two nanoassemblies, as shown by Figures 8 and 9, is the crossover from negative to positive values of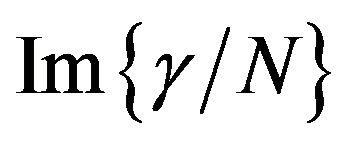 . This crossover from negative to positive values of
. This crossover from negative to positive values of  in polydiacetylene nanovesicles occurs at ~772 nm, nearly 16 nm below than that for polydiacetylene nanocrystals. As we have already pointed out above, this crossover results because of the location of oneand two-photon states with respect to the photon energies of the exciting radiation such that their respective negative and positive contributions to the imaginary parts of the nonlinearity interfere destructively and mutually cancel each other at a certain wavelength. The complete cancellation of
in polydiacetylene nanovesicles occurs at ~772 nm, nearly 16 nm below than that for polydiacetylene nanocrystals. As we have already pointed out above, this crossover results because of the location of oneand two-photon states with respect to the photon energies of the exciting radiation such that their respective negative and positive contributions to the imaginary parts of the nonlinearity interfere destructively and mutually cancel each other at a certain wavelength. The complete cancellation of 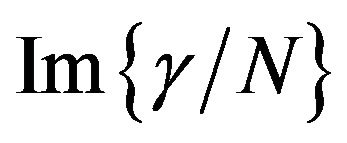 for the two PDA nanoassemblies at a particular wavelength makes both of these samples potential candidates for photonic device applications around that particular wavelength of interest.
for the two PDA nanoassemblies at a particular wavelength makes both of these samples potential candidates for photonic device applications around that particular wavelength of interest.
The best-fit parameters for the two samples are given in Table 1. It can be seen that the two-photon state in both nanoassemblies occurs at nearly same energy ~ 2.85 eV, a value in excellent agreement to the earlier reported value for the two-photon state energy in other polydiacetylenes [7,9,28]. Slightly higher values of transition dipole moments 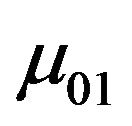 and
and  as well as of the ratio
as well as of the ratio  are predicted for nanocrystals. Polymer chains are relatively more strained in case of nanovesicles due to the positive outward pressure. This may be partly responsible for the differences in their properties of electronic structure. Higher transition moments in conjuncttion with the lower energy for the one-photon state in nanocrystals by ~0.1 eV are responsible for the higher negative value of the nonlinearity at shorter wavelengths in nanocrystals. Also, lower energy of the one-photon allowed transition increases the span of its dominance over the spectral range of interest and hence the complete cancellation of the
are predicted for nanocrystals. Polymer chains are relatively more strained in case of nanovesicles due to the positive outward pressure. This may be partly responsible for the differences in their properties of electronic structure. Higher transition moments in conjuncttion with the lower energy for the one-photon state in nanocrystals by ~0.1 eV are responsible for the higher negative value of the nonlinearity at shorter wavelengths in nanocrystals. Also, lower energy of the one-photon allowed transition increases the span of its dominance over the spectral range of interest and hence the complete cancellation of the  in nanocrystals is observed at wavelength nearly 16 nm larger than that in nanovesicles.
in nanocrystals is observed at wavelength nearly 16 nm larger than that in nanovesicles.
Comparing the values of 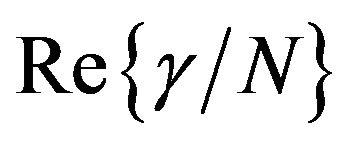 and
and 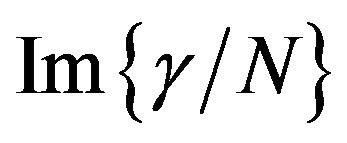

Table 1. Best-fit parameters (location of excited states, their linewidths and transition dipole moments between them) for PDA nanovesicles and PDA nanocrystals used in the three-essential states model.
for the two nanoassemblies as shown in Figures 8 and 9 respectively, we see that the PDA nanocrystals exhibit higher nonlinearities as compared to PDA nanovesicles. Here, we are offering a plausible explanation for the enhancement of nonlinearity in PDA nanocrystals. We have already stated above that the diffraction fringes in the TEM picture of PDA nanocrystals confirm their crystalline nature, indicating that the nanocrystals are having orderly arrangement of conjugated polymer chains. It has been observed that in conjugated molecules the cubic hyperpolarizability increases very rapidly with the molecular dimensions according to a power law as against that in saturated molecules with the same number of valence electrons [29]. According to the free electron model of Rustagi and Ducuing, the cubic hyperpolarizability of p conjugated molecules scales as the fifth power of the chain length [30]. Agrawal et al. calculated g for polydiacetylenes in the tight binding approximation and predicted the sixth power dependence on the chain length [31]. Since the PDA nanocrystals are having the orderly arrangement of polymer chains, the enhancement in the nonlinearity shown by them is proportionate to their chain length. On the other hand, the TEM picture of nanovesicles did not show any diffraction fringes and thus rules out their crystalline nature. This is further substantiated by the presence of third peak in between the exciton peak and the vibronic peak in nanovesicles, as compared to that of nanocrystals. We have inferred above that presence of this peak in nanovesicles might be because of splitting of chain coupling, thus preventing them from having an ordered set of polymer chains. Moreover, the strain on polymer chains due to the positive outward pressure in nanovesicles may also be contributing in disrupting the chains from making an ordered array of chains and thereby showing lower values of cubic hyperpolarizability. We can, therefore, infer that the arrangement of polymer chains in PDA nanocrystals is more favorable for higher nonlinearity than that in nanovesicles. However, it has been reported by Chen et al that the nonlinearity of PDA nanovesicles can be further enhanced by coating the outer and inner surface of the nanovesicles with silver nanoparticles [14]. They have observed the seven times enhancement in nonlinearity in the coated nanovesicles as a result of local field enhancement under the surface plasmon resonance of silver nanoparticles at the interface of PDA/Ag nanocomposites. We are of the opinion that further research in this direction may result in better understanding of the chain coupling effects of PDAs as well as the coupling between the  -electrons of the polymer and the free electrons of the metal nanoparticles in case of polymer-metal nanoparticles composites, which may lead to the development of novel, efficient and tunable nonlinear optical materials with large third-order nonlinear susceptibility.
-electrons of the polymer and the free electrons of the metal nanoparticles in case of polymer-metal nanoparticles composites, which may lead to the development of novel, efficient and tunable nonlinear optical materials with large third-order nonlinear susceptibility.
4. Conclusion
We have synthesized and studied the spectral dispersion of third-order nonlinear optical susceptibility of two different nanoassemblies of polydiacetylenes, namely PDA nanovesicles and PDA nanocrystals. Their nonlinear optical properties were investigated by the antiresonant ring interferometric nonlinear spectroscopic (ARINS) technique using femtosecond modelocked Ti:sapphire laser in the spectral range of 720 nm - 820 nm. The observed spectral dispersion characteristics of 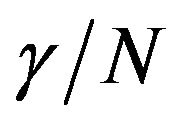 of the two samples have been analyzed in the framework of three-essential states model. While energy of the twophoton allowed state was found to be the same in both nanoassemblies, higher values of transition dipole moments for the oneand two-photon allowed channels were seen in PDA nanocrystals. Strain on polymer chains due to the positive outward pressure in nanovesicles may be partly responsible for the differences in the properties of their electronic structures. It is inferred that nanocrystals with linear arrangement of chains may be more favorable to achieve higher values of nonlinearities.
of the two samples have been analyzed in the framework of three-essential states model. While energy of the twophoton allowed state was found to be the same in both nanoassemblies, higher values of transition dipole moments for the oneand two-photon allowed channels were seen in PDA nanocrystals. Strain on polymer chains due to the positive outward pressure in nanovesicles may be partly responsible for the differences in the properties of their electronic structures. It is inferred that nanocrystals with linear arrangement of chains may be more favorable to achieve higher values of nonlinearities.
5. Acknowledgements
The corresponding author acknowledges the financial support for this research work by the University Grants Commission (UGC), Government of India (CSIR-UGC Junior Research Fellowship (JRF), Letter No 2-44/2000 (i)-EU II dated 1.2.2001).
REFERENCES
- L W. Spannring and H. Bassler, “Electron Injection into a Polydiacetylene Crystal (DCH): Determination of Electron Mobility and Energy Level Spectrum,” Chemical Physics Letters, Vol. 84, No. 1, 1981, pp. 54-58. doi:10.1016/0009-2614(81)85368-7
- D. Bloor, F. H. Preston and D. J. Ando, “Optical Properties of Fully and Partially Polymerized bis (p-Toluene Sulphonate) Diacetylene Crystals,” Chemical Physics Letters, Vol. 38, No. 1, 1976, pp. 33-36. doi:10.1016/0009-2614(76)80249-7
- C. Sauteret, J. P. Hermann, R. Frey, F. Pradere, J. Ducuing, R. H. Baughman and R. R. Chance, “Optical Nonlinearities in One-Dimensional Conjugated Polymer Crystals,” Physical Review Letters, Vol. 36, No. 16, 1976, pp. 956-959. doi:10.1103/PhysRevLett.36.956
- J. Bolger, T. G. Harvey, W. Ji, A. K. Kar, S. Molyneux, B. S. Wherrett, D. Bloor and P. Norman, “Near-Resonant Third-Order Optical Nonlinearities in P-Toluene Sulfonate Polydiacetylene,” Journal of Optical Society of America B, Vol. 9, No. 9, 1992, pp. 1552-1557. doi:10.1364/JOSAB.9.001552
- G. M. Carter, J. V. Hryniewicz, M. K. Thakur, Y. J. Chen and S. E. Meyler, “Nonlinear Optical Processes in Polydiacetylene Measured with Femtosecond Duration Laser Pulse,” Applied Physics Letters, Vol. 49, No. 16, 1986, pp. 998-1000. doi:10.1063/1.97470
- G. M. Carter, M. K. Thakur, Y. J. Chen and J. V. Hryniewicz, “Time and Wavelength Resolved Nonlinear Optical Spectroscopy of a Polydiacetylene in the Solid State Using Picosecond Dye Laser Pulses,” Applied Physics Letters, Vol. 47, No. 5, 1985, pp. 457-459. doi:10.1063/1.96146
- G. Banfi, D. Fortusini, P. Dainesi, D. Grando and S. Sottini, “Two-Photon Absorption Spectrum of 3-Butoxycarbonylmethylurethane Polydiacetylene Thin Films,” Journal of Chemical Physics, Vol. 108, No. 10, 1998, pp. 4319-4323. doi:10.1063/1.475832
- D. N. Rao, P. Chopra, S. K. Ghoshal, J. Swiatkiewicz and P. N. Prasad, “Third-Order Nonlinear Optical Interaction and Conformational Transition in poly-4-BCMU Polydiacetylene Studied by Picosecond and Subpicosecond Degenerate Four Wave Mixing,” Journal of Chemical Physics, Vol. 84, No. 12, 1986, pp. 7049-7050. doi:10.1063/1.450627
- W. E. Torruellas, K. B. Rochford, R. Zanoni, S. Aramaki and G. I. Stegeman, “The Cubic Susceptibility Dispersion of poly (4-BCMU) Thin Films: Third Harmonic Generation and Two-Photon Absorption Measurements,” Optics Communications, Vol. 82, No. 1-2, 1991, pp. 94-100. .doi:10.1016/0030-4018(91)90198-M
- S. Molyneux, A. K. Kar, B. S. Wherrett, T. L. Axon and D. Bloor, “Near-Resonant Refractive Nonlinearity in Polydiacetylene 9-BCMU Thin Films,” Optics Letters, Vol. 18, No. 24, 1993, pp. 2093-2095. doi:10.1364/OL.18.002093
- J. Tao, H. Jiang, J. Wang, G. Zou and Q. Zhang, “Tunable Nonlinear Optical Properties of PDA/Ag Composite Vesicles Based on Reversible Host-Guest Interaction,” Chemical Physics Letters, Vol. 539-540, 2012, pp. 70-73. doi:10.1016/j.cplett.2012.04.049
- X. Chen, J. Tao, G. Zou, W. Su, Q. J. Zhang and P. Wang, “Optical Nonlinearity Enhancement in Cros-Linked Polydiacetylene (PDA) Supramolecules Composited with Nanometer-Size Silver,” Current Nanoscience, Vol. 7, No. 4, 2011, pp. 556-562. doi:10.2174/157341311796196790
- X. Chen, J. Tao, G. Zou, W. Su, Q. J. Zhang and P. Wang, “Thermosensitive Silver/Polydiacetylene Nanocrystals with Tunable Nonlinear Optical Properties,” ChemPhysChem, Vol. 11, No. 17, 2010, pp. 3599-3603. doi:10.1002/cphc.201000416
- X. Chen, G. Zou, Y. Deng and Q. Zhang, “Synthesis and Nonlinear Optical Properties of Nanometer-Size Silver Coated Polydiacetylene Composite Vesicles,” Nanotechnology, Vol. 19, No. 19, 2008, pp. 195703-195703. doi:10.1088/0957-4484/19/19/195703
- P. Vasa, B. P. Singh, P. Taneja and P. Ayyub, “Antiresonant Ring Interferometry as a Sensitive Technique for Measuring Nonlinear Optical Properties of Thin Films,” Optics Communications, Vol. 233, No. 4-6, 2004, pp. 297-304. doi:10.1016/j.optcom.2004.01.051
- D. Guo, S. Mazumdar, S. N. Dixit, F. Kajzar, F. Jarka, Y. Kawabe and N. Peyghambarian, “Role of the Conduction Band in Electroabsorption, Two-Photon Absorption, and Third-Harmonic Generation in Polydiacetylenes,” Physical Review B, Vol. 48, No. 3, 1993, pp. 1433-1459. doi:10.1103/PhysRevB.48.1433
- H. S. Zhou, T. Wada, H. Sasabe and H. Komiyama, “Synthesis and Optical Properties of Nanocomposite SilverPolydiacetylene,” Synthetic Metals, Vol. 81, No. 2-3, 1996, pp. 129-132. doi:10.1016/S0379-6779(96)03754-X
- E. K. Ji, D. J. Ahn and J. M. Kim, “The Fluorescent Polydiacetylene Liposome,” Bulletin of the Korean Chemical Society, Vol. 24, No. 5, 2003, pp. 667-670. doi:10.5012/bkcs.2003.24.5.667
- R. J. Young, R. T. Read, D. Bloor and D. Ando, “Structure and Morphology of Polydiacetylene Single Crystal,” Faraday Discussions of the Chemical Society, Vol. 68, 1979, pp. 509-515. doi:10.1039/dc9796800509
- N. J. Poole, B. J. E. Smith, D. N. Batchelder, R. T. Read, R. J. Young, “Electron Microscopy of Photo-oxidized Polydiacetylene Crystals,” Journal of Materials Science, Vol. 21, No. 2, 1986, pp. 507-510. doi:10.1007/BF01145516
- N. P. Xuan, J. L. Ferrier, J. Gazengel and G. Rivoire, “Picosecond Measurements of the Third-Order Susceptibility Tensor in Liquids,” Optics Communications, Vol. 51, No. 6, 1984, pp. 433-437. doi:10.1016/0030-4018(84)90133-0
- M. T. Zhao, M. Samoc, B. P. Singh and P. N. Prasad, “Study of Third-Order Microscopic Optical Nonlinearities in Sequentially Built and Systematically Derivatized Structures,” Journal of Physical Chemistry, Vol. 93, No. 23, 1989, pp. 7916-7920. doi:10.1021/j100360a036
- J. W. Wu, J. R. Heflin, R. A. Norwood, K. Y. Wong, O. Zamani-Khamiri, A. F. Garito, P. Kalyanaraman and J. Sounik, “Nonlinear Optical Processes in Lower Dimensional Conjugated Structures,” Journal of Optical Society of America B, Vol. 6, No. 4, 1989, pp. 707-720. doi:10.1364/JOSAB.6.000707
- C. W. Dirk, Lap-Tak Cheng and M. G. Kuzyk, “A Simplified Three-Level Model Describing the Molecular Third-Order Nonlinear Optical Susceptibility,” International Journal of Quantum Chemistry, Vol. 43, No. 1, 1992, pp. 27-36. doi:10.1002/qua.560430106
- B. J. Orr and J. F. Ward, “Perturbation Theory of the Nonlinear Optical Polarization of an Isolated System,” Molecular Physics, Vol. 20, No. 3, 1971, pp. 513-526. doi:10.1080/00268977100100481
- A. V. V. Nampoothiri, P. N. Puntambekar, B. P. Singh, R. Sachdeva, A. Sarkar, Dipti Saha, A. N. Suresh and S. S. Talwar, “Spectral Dispersion of Second Molecular Hyperpolarizability of Diacetylene Derivatives: Correlation with Electronic and Chemical Structure,” Journal of Chemical Physics, Vol. 109, No. 2, 1998, pp. 685-690. doi:10.1063/1.476607
- H. Vanherzeele, J. S. Meth, S. A. Jenekhe and M. F. Roberts, “Dispersion of the Third-Order Nonlinear-Optical Properties of Poly(p-phenylene benzobisthiazole) and Its Molecular Composites with Polyamides,” Journal of Optical Society of America B, Vol. 9, No. 9, 1992, pp. 524- 533. doi:10.1364/JOSAB.9.000524
- B. Lawrence, W. E. Torruellas, M. Cha, M. L. Sundheimer, G. I. Stegeman, J. Meth, S. Etemad and G. Baker, “Identification and Role of Two-Photon Excited States in a π-Conjugated Polymer,” Physical Review Letters, Vol. 73, No. 4, 1994, pp. 597-600. doi:10.1103/PhysRevLett.73.597
- J. P. Hermann and J. Ducuing, “Third-Order Polarizabilities of Long-Chain Molecules,” Journal of Applied Physics, Vol. 45, No. 11, 1974, pp. 5100-5102. doi:10.1063/1.1663197
- K. C. Rustagi and J. Ducuing, “Third-Order Optical Polarizability of Conjugated Organic Molecules,” Optics Communications, Vol. 10, No. 3, 1974, pp. 258-261. doi:10.1016/0030-4018(74)90153-9
- G. P. Agrawal, C. Cojan and C. Flytzanis, “Nonlinear Optical Properties of One-Dimensional Semiconductors and Conjugated Polymers,” Physical Review B, Vol. 17, No. 2, 1978, pp. 776-789. doi:10.1103/PhysRevB.17.776
NOTES
1Present Address: Department of Applied Physics, Birla Institute of Technology (Mesra), Patna Campus, Near B. V. College, Patna 800014, Bihar, India.

