Optics and Photonics Journal
Vol.3 No.1(2013), Article ID:28874,5 pages DOI:10.4236/opj.2013.31002
Selective Photorefractive Light Scattering in Rh-Doped LiNbO3 Crystals
1Optic Communications Department, Far Eastern State Transport University, Khabarovsk, Russia
2Electrophysics Department, Kwangwoon University, Seoul, South Korea
Email: *krishtop@list.ru
Received November 16, 2012; revised December 17, 2012; accepted December 24, 2012
Keywords: Photorefraction Light Scattering; Lithium Niobate; Four-Wave Interaction
ABSTRACT
The photorefractive properties of lithium niobate crystals depend strongly on the kind of doping admixture. Study of LiNbO3 crystals with various doping admixtures using photorefractive light scattering allows insight into the processes taking place in the crystals. This paper presents new experimental results of non-selective and selective photorefractive light scattering investigations into rhodium-doped lithium niobate crystals and proposes a model to explain the experimental data.
1. Introduction
Photorefractive crystals, particularly lithium niobate (LiNbO3) crystals, are a prospective material for optical units for information storage and processing [1-3].
The basis for the model proposed in this study is the assumption that the volumetric phase diffraction grating that is recorded due to an interference of pumping radiation and Rayleigh primary scattering corresponds to each direction in which the photorefractive scattering is observed [1]. Volumetric phase grating is the grating of the refractive index (RI), the thickness of which is far greater than its period. The orientation and initial amplitude of each grating are determined by the direction in which the Rayleigh scattering is made. During recording such grating, Bragg diffraction of both recording beams is realized. This process is called “self-diffraction”. As a result of self-diffraction, considerable amplification of the weak beam is possible due to energy transfer from the stronger beam. In our case, the energy transfer from the pumping beam to the scattered radiation takes place equally for no all gratings. That is, based on the immediately observed pattern, it can be concluded that only for those gratings on which a diffraction of the pumping beam is performed in the directions where the photorefractive light scattering (PRLS) is recorded, a distinct amplification of the primary light noise takes place. Therefore, to creating a PRLS model we need to formulate the conditions for recording of RI gratings on which the light noise amplification is performed. Study of PRLS in LiNbO3 crystals with various doping admixtures allows insight into the processes taking place in the crystals [4-14].
Further, the results of a selective PRLS experimental investigation into rhodium-doped lithium niobate (LiNbO3: Rh) crystals are presented and the characteristic properties of the selective PRLS in rhodium (Rh)-doped crystals are observed and studied. Selective PRLS was considered a four-wave interaction. On the basis of this model, the selective PRLS indicatrix in the LiNbO3:Rh crystals was calculated.
2. Non-Selective Photorefractive Light Scattering
The experimental setup is shown in Figure 1. The PRLS of LiNbO3 crystals doped with iron (Fe) has been well researched; however, as far as the authors are aware, there are no reports on the PRLS of LiNbO3:Rh crystals. Therefore, it was considered interesting to compare the PRLS of LiNbO3:Fe with that of LiNbO3:Rh crystals.

Figure 1. Experimental setup: (1) Screen; (2) Crystal; (3) Mirrors; (4) Lens; (5) Helium-neon laser.
In the experiment, a helium-neon laser of 22 milliwatts was used. The radiation was plane polarized and the wave length was 0.6328 micrometres. The plane of polarization was parallel to the crystal optical axis. The laser beam was focused on the crystals by a lens and the PRLS patterns were observed on a screen. The PRLS patterns obtained were recorded by photograph and video. X-cut plates of the crystals were used. In the LiNbO3 crystals doped with Fe (crystal thickness 1.4 millimetres, Fe concentration 0.3%), a spot extended along the optical axis of scattering forms on the screen (see Figure 2). The central beam for the PRLS in LiNbO3:Fe was almost completely destroyed and near-complete transfer of energy from pumping beam into the scattered radiation occurred. The scattered light propagated through the crystal as an extraordinary wave. This scattering can be characterized as direct, non-selective (broad angled), polarizing isotropic (without polarization rotation). It reached the maximum angular size of ~80˚ for 2 minutes then a smooth reduction in the scattering intensity and angular dimensions took place afterwards.
In the LiNbO3 doped with Rh, the PRLS pattern has a more complex structure [3,4] (see Figure 3). The scattering pattern extends along the crystal optical axis. Near the central spot, there are areas of bright broad-angled

Figure 2. Pattern of the direct photorefractive light scattering in lithium niobate doped with Fe after 3 minutes of illumination.
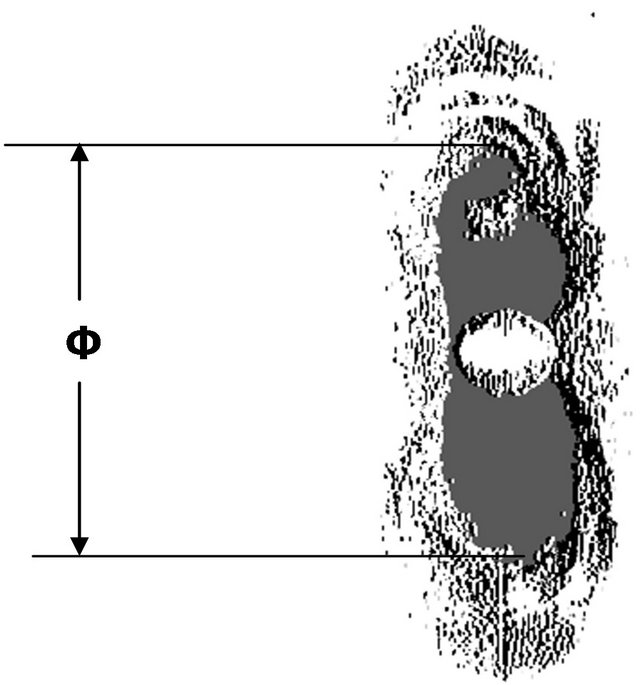
Figure 3. Pattern of the direct photorefractive light scattering in lithium niobate doped with rhodium after 15 minutes of illumination.
scattering. In addition to non-selective PRLS, selective scattering also takes place in the LiNbO3:Rh crystals. In the figure, this is represented by the arcs forming a figure of eight extending along the crystal optical axis. Above and below the central spot, three to four additional arcs are visible. Their brightness is much lower than that of the non-selective scattering. In Figure 4, the kinetics of the angle of opening, F, for the non-selective scattering in the LiNbO3:Rh crystals is shown. The maximum angle, F0, of the non-selective scattering is ~13˚. The points in the graph correspond to the experimental data. The polarization of both selective and non-selective scattering in the LiNbO3:Rh crystals coincides with that of the pumping.
We studied the kinetics of the intensity of pumping beam and scattered light in the case of the PRLS in the LiNbO3 crystals doped with Rh. Figure 5 shows the time dependence of the intensity of the laser beam passing through the crystals and Figure 6 shows the time dependence of the PRLS intensity. The integral intensity was measured within the uniform scattering area where the brightness of the PRLS pattern on the screen was maximal. As illustrated in Figures 5 and 6, the time dependence of the intensity of the central beam passing through the crystal correlates with that of the intensity of the scattered radiation. With regard to the intensity of the central beam, a sharp drop is characteristic during the first 60 seconds. It corresponds with the fast growth of
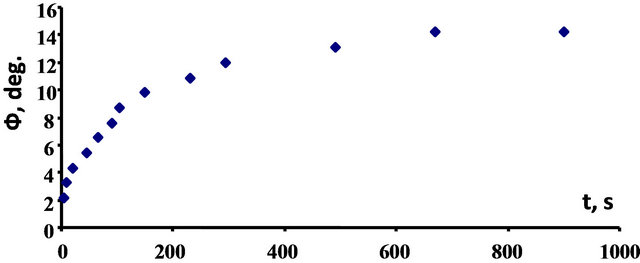
Figure 4. Angular kinetics of the nonselective photorefractive light scattering in the rhodium-doped lithium niobate crystals.

Figure 5. Kinetics of the intensity of the pumping radiation passed through the rhodium-doped lithium niobate crystals.

Figure 6. Kinetics of the scattered radiation intensity in rhodium-doped lithium niobate crystals.
the scattered radiation intensity during the same 60 seconds. Following this, the intensity of the central beam increases smoothly. Over 15 minutes of illumination, the intensity of the central beam reached a level of 0.9 of the initial one and does not changing more. The intensity of the scattered radiation for the same period decreases smoothly to 0.2 of the maximum value and no longer changes. From analysis of the above characteristics, it can be deduced that there was a non-stationary energy exchange between the pumping radiation and scattered light in the LiNbO3:Rh crystals.
Based on the two-beam model, where one beam is pumping (P is a beam or donor beam) and the second beam is scattered radiation propagating in the selected direction (S is a beam or acceptor beam), the kinetics of the energy exchange between pumping and scattered light one can be considered qualitatively. Let us consider that the intensity of the P-beam is much higher than that of the S-beam and, for simplicity, that the beams are plane waves. As stated earlier, in the area of the intersection of the beams, the interference pattern with the sinusoidal distribution of the light intensity will appear. The volume phase sinusoidal diffraction grating is then recorded. As a result of the Bragg diffraction of P-beam, a transfer of energy from the P-beam in the direction of the S-beam occurs on a grating. Correspondingly, a phase of the resulting light wave in the direction of the S-beam will change. This causes the equiphasic surfaces to turn in an interference pattern. Owing to a time lag of a medium response, the equiphasic surfaces of the refraction index are delayed and do not coincide with the interference pattern. As a result, efficient energy transfer takes place. As a turn of the refraction index grating is affected, energy exchange decreases. As soon as the equiphasic surfaces of the interference pattern and refraction index grating coincide again, the energy exchange stops. Vinetsky et al. [6] present a calculation of the time dependence of the S-beam intensity. The time dependence is expressed as follows:
 (1)
(1)
where d is the length of the non-linear interaction of the beams, D is a parameter depending on the photorefractive properties of a medium,  is time of the Maxwell relaxation. It should be noted that the non-stationary energy exchange described by Equation (1) occurs only in media with inertial local response. For the local response of a medium, the extremes of the RI grating coincide with those of the interference pattern. In the absence of the external electric field, a locality of response is determined by the photovoltaic effect. In general terms, Equation (1) correlates with the experimentally derived kinetics shown in Figure 6. This allows for the conclusion that a generalization of the two-beam model chosen for this study for the overall process of the photorefractive scattering is acceptable.
is time of the Maxwell relaxation. It should be noted that the non-stationary energy exchange described by Equation (1) occurs only in media with inertial local response. For the local response of a medium, the extremes of the RI grating coincide with those of the interference pattern. In the absence of the external electric field, a locality of response is determined by the photovoltaic effect. In general terms, Equation (1) correlates with the experimentally derived kinetics shown in Figure 6. This allows for the conclusion that a generalization of the two-beam model chosen for this study for the overall process of the photorefractive scattering is acceptable.
According to (1) the intensity of amplified beam decreases to the initial level (at Is 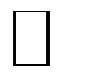 Ip, practically to zero). However in the experiment, the intensity of scattered light relaxes to some stationary level. The reason for this is the presence of the diffusion mechanism of the volume charge redistribution. The fields and, thus, the RI gratings amplitude determined by this mechanism are an order of magnitude less than those due to the photovoltaic effect [1].
Ip, practically to zero). However in the experiment, the intensity of scattered light relaxes to some stationary level. The reason for this is the presence of the diffusion mechanism of the volume charge redistribution. The fields and, thus, the RI gratings amplitude determined by this mechanism are an order of magnitude less than those due to the photovoltaic effect [1].
3. Selective Photorefractive Light Scattering
We considered the selective PRLS as the case of the four-wave interaction in photorefractive anisotropic medium (see Figure 7). The optical damage allows realizetion of the phase synchronism conditions. Our model is based on energy and momentum conservation laws for interacting waves (Equations (2) and (3)) and the equation for the Fresnel ellipsoid (Equation (5)).

Figure 7. Scheme of the four-wave interaction in the lithium niobate crystals with rhotorefraction.
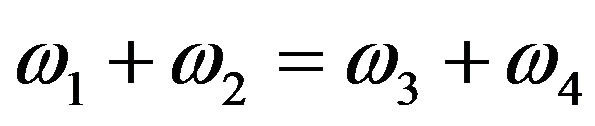 , (2)
, (2)
 , (3)
, (3)
where 1 and 2 indicate pump beams and 3 and 4 indicate scattering; w indicates a frequency of the optical waves and k indicates its wave vector. Knowing that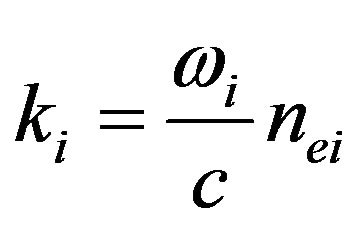 where i is 1, 2, 3, 4, right the condition (3) as a projection on the x axis (see Figure 8) and taking into account that w1 = w2 = w3 = w4:
where i is 1, 2, 3, 4, right the condition (3) as a projection on the x axis (see Figure 8) and taking into account that w1 = w2 = w3 = w4:
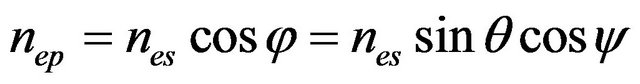 , (4)
, (4)
where 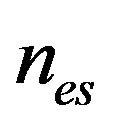 is the refraction index for scattered light, the θ and ψ angles determine the scattering light direction (see Figure 2). The refraction index for the pumping beam,
is the refraction index for scattered light, the θ and ψ angles determine the scattering light direction (see Figure 2). The refraction index for the pumping beam,  , is changed on
, is changed on  as a result of photorefractive effect:
as a result of photorefractive effect: , where
, where 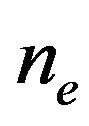 is the general refraction index for the extraordinary wave when there is no photorefractive effect and I is the pump beam intensity.
is the general refraction index for the extraordinary wave when there is no photorefractive effect and I is the pump beam intensity.
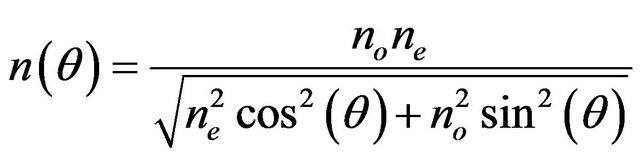 . (5)
. (5)
Further, photo-induced refraction index inhomogeneity is taken into account (Equation (7)).
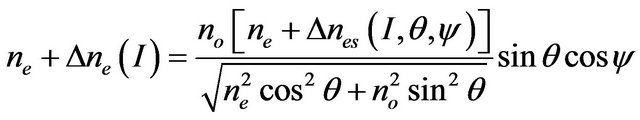 . (6)
. (6)
The equation for the angular dependence of the photoinduced refraction index changing may be correct as:
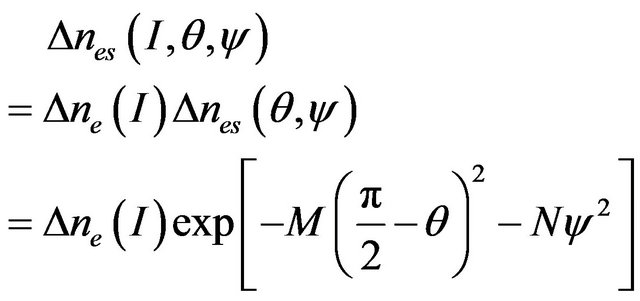 (7)
(7)
where M and N parameters determine the refraction index changing rate. Using Equation (6) with Equation (7), we calculated the phase synchronism angles q and y. The theoretical result is shown in Figure 9(a). The calculated value of the photo-induced refraction index changing in LiNbO3:Rh is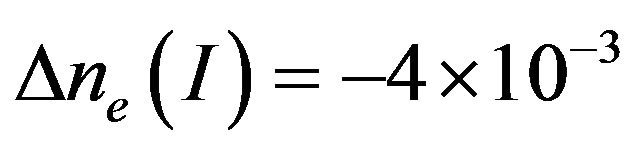 .
.
Figures 9(b) and (c) are photographs of PRLS in LiNbO3:Rh. How we can see, there is a good enough correlation between theoretical results and experimental data.
4. Conclusions
It can be argued that the proposed model is capable of describing the basic regularities of the non-selective PRLS in the LiNbO3 crystals. This proves that 1) the scattering observed is photorefractive scattering of the holographic
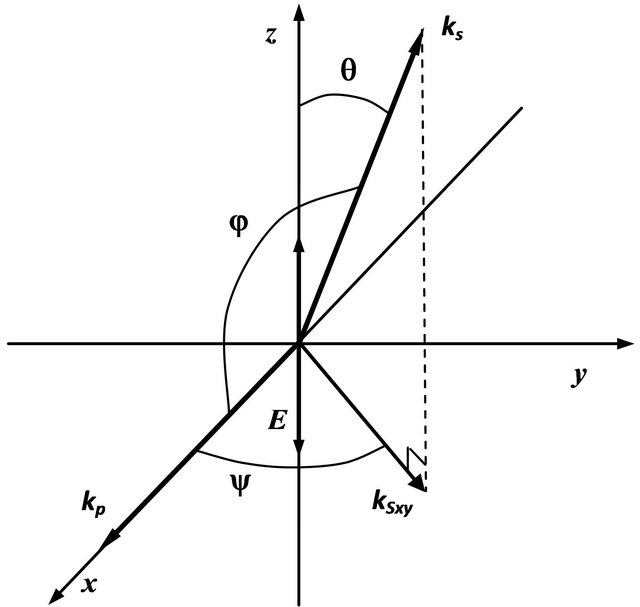
Figure 8. Coordinate system: kp is the pumping wave vector, ks is one of the scattering light wave vectors and E is field of pumping beam.
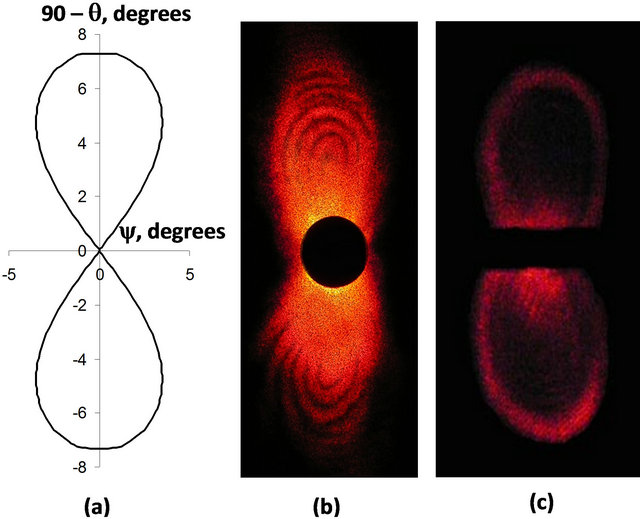
Figure 9. The selective PRLS. (a) The theoretical result; (b) Photograph of the direct PRLS; (c) Photograph of the back PRLS.
type and 2) the photovoltaic mechanism is a preferential mechanism for the redistribution of photo-generated charge carriers in LiNbO3 crystals doped with Fe or Rh. Future work will consider the introduction of a charge redistribution into the model that will allow broad-angled PRLS to be obtained closer to the experimental data. The properties of the doping admixture should also be considered. This should explain the presence of the selective scattering in LiNbO3 doped with Rh for the given geometry of the experiment.
The phase synchronism conditions for pumping and scattering waves in the case of selective PRLS of the еее-е type in LiNbO3:Rh crystals are the result of the optical anisotropy and inhomogeneous changing of the RI [7]. The experimental data for selective PRLS presented here allows the value of the maximal photo-induced refraction index changing in Rh-doped LiNbO3 crystals to be calculated.
5. Acknowledgements
The work was performed in the framework of the federal targeted program “Scientific and Pedagogical Personnel of Innovative Russia (2009-2013)”, and it has been supported by the Research Grant of Kwangwoon University in 2012-2013.
REFERENCES
- M. P. Petrov, S. I. Stepanov and A. V. Khomenko, “Photorefractive Crystals in the Coherent Optics,” Nauka, Saint-Petersburg, 1992.
- S. G. Odulov, M. S. Soskin and A. I. Khizhnyak, “Lasers on Dynamic Gratings,” Nauka, Moscow, 1990.
- K. Buse, “Light-Induced Charge Processes in Photorefractive Crystals II: Materials,” Applied Physics B, Vol. 64, No. 4, 1997, рр. 391-407. doi:10.1007/s003400050190
- Yu. M. Karpets and V. A. Maksimenko, “Photorefraction Scattering in LiNbO3 Crystals with Different Alloying Additives,” Proceedings of SPIE, Vol. 4748, 2002, рр. 211-215. doi:10.1117/12.468959
- V. A. Maksimenko, Yu. M. Karpets and E. V. Danilova, “Kinetics of Nonselective Photorefraction Light Scattering in LiNbO3:Rh Crystal,” Proceedings of SPIE, Vol. 5743, 2004, рр. 262-266. doi:10.1117/12.606302
- V. L. Vinetsky, S. G. Kukhtarev, S. G. Odulov and M. S. Soskin, “Dynamic Self-Diffraction of Coherent Light Beams,” Soviet Physics Uspekhi, Vol. 22, No. 9, 1979, рр. 113-137. doi:10.1070/PU1979v022n09ABEH005609
- Yu. M. Karpets and V. A. Maksimenko, “Photoinduced Light Scattering in LiNbO3:Rh Crystals,” Journal of Optical Technology, Vol. 71, No. 9, 2004, рр. 570-571. doi:10.1364/JOT.71.000570
- V. A. Maksimenko, Yu. M. Karpets and V. I. Stroganov, “Selective Photorefractive Scattering in LiNbO3:Rh Crystals,” Optics and Spectroscopy, Vol. 97, No. 4, 2004, рр. 588-591.
- A. V. Syui, V. I. Stroganov, V. V. Krishtop and V. V. Likhtin, “Effect of Broadband Incoherent Light on the Photoresponse of Lithium Niobate Crystals,” Optics and Spectroscopy, Vol. 104, No. 1, 2008, рр. 126-129. doi:10.1134/S0030400X08010190
- P. S. Lopatina and V. V. Krishtop, “The Influence of Electrodes Design on Optical Property of Lithium Niobate Crystal,” Journal of Optical Technology, Vol. 77, No. 6, 2010, рр. 243-245.
- N. V. Sidorov, D. V. Evstratova, M. N. Palatnikov, A. V. Syuy, A. Yu. Gaponov and E. A. Antonycheva, “Investigation of Lithium Niobate Photorefractive Properties by Photorefractive Light Scattering and Raman Spectroscopy,” Ferroelectrics, Vol. 413, No. 1, 2011, pp. 148- 155. doi:10.1080/00150193.2011.554139
- S. Fang, Y. Qiao, Y. Fu, X. Cui and Q. Jia, “Preparation and Holographic Storage Properties of Tri-Doped Mg: Mn:Fe:LiNbO3 Crystals,” Optik: International Journal for Light and Electron Optics, Vol. 122, No. 2, 2011, рр. 159-161. doi:10.1016/j.ijleo.2009.11.023
- J.-P. Liu, T.-H. Yang, H.-F. Yau and H.-Y. Lee, “Incoherent one Beam Recording in LiNbO3,” Optics Communications, Vol. 276, No. 1, 2007, pp. 67-71.
- L. S. Kokhanchik, M. V. Borodin, N. I. Burimov, S. M. Shandarov and V. V. Shcherbina, “Planar Domain Gratings Fabricated by a Set of Local E-Beam Irradiation on the Y-Cuts of LiNbO3 and the Planar Waveguide Ti: LiNbO3,” Ferroelectrics, Vol. 411, No. 1, 2010, рр. 71- 78. doi:10.1080/00150193.2010.493082
NOTES
*Corresponding author.

