Current Urban Studies
Vol.03 No.02(2015), Article ID:56507,12 pages
10.4236/cus.2015.32008
Impacts of Spatial Extend and Site Location on Calibration of Urban Growth Models
Kenneth Mubea1,2, Andreas Rienow2, Gunter Menz2,3
1Institute of Geomatics and GIS, Dedan Kimathi University of Technology, Nyeri, Kenya
2Remote Sensing Research Group (RSRG), University of Bonn, Bonn, Germany
3Centre for Remote Sensing of Land Surfaces (ZFL), University of Bonn, Bonn, Germany
Email: kpwmubea@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 March 2015; accepted 16 May 2015; published 21 May 2015
ABSTRACT
During the last decades, cities in sub-saharan Africa have undergone rapid urban growth due to increased population growth and high economic activities. This research explores the impacts of varying modelling settings including spatial extend and its location for the city of Nairobi using a cellular automata (CA) urban growth model (UGM). Our UGM used multi-temporal satellite-based data for classification of urban land-use of 1986, 2000 and 2010, road data, slope data and exclusion layer. Monte-Carlo technique was used for model calibration and Multi Resolution Validation (MRV) technique for validation. Simulation of urban land-use was done up to the year 2030 when Kenya plans to attain Vision 2030. Three spatial grid sizes varying in extent and location were applied in the UGM calibration and validation. Thus, this research explored the impacts of varying spatial extent (grid) and location on urban growth modelling and hence can contribute to an improved sustainable planning and development. This is useful for future planning as the Nairobi grows and expands into the peri-urban areas.
Keywords:
Spatial Extend and Location, Cellular Automata (CA), Nairobi, Urban Growth Model (UGM), Sustainable Development

1. Introduction
Urban growth modelling studies are currently considered as an essential component for numerous complex environmental approaches (Triantakonstantis & Mountrakis, 2012) . Tobler (1979) pioneered the use of Cellular automata (CA) in geographical modeling. Whoever, the focus was on theoretical problems such as cluster, complexity and structure formation. However, recently a couple of researchers have begun applying CA in the field of urban planning (Itami, 1994) .
Lately, CA models have been applied to model urban growth in North America (Clarke, Hoppen, & Gaydos, 1996) , South America (Leão, Bishop, & Evans, 2004) , Europe (Silva & Clarke, 2002) , Asia (Lebel, Thaitakoo, Sangawongse, & Huaisai, 2007) and Africa (Mubea, Goetzke, & Menz, 2013) . Urban models aid in making informed decisions on land-use planning in the context of future development. Additionally, urban models have been used to simulate land-use scenarios in the view of addressing plausible agenda that fosters sustainable development (Oguz, Klein, & Srinivasan, 2007 ; Mubea, Goetzke, & Menz, 2014) .
CA simulates urban growth within discrete grid space and simulates land-use state changes via rules that operate within a neighborhood that interconnects adjacent cells (Akın, Clarke, & Berberoglu, 2014) . The grid space usually has two dimensions and represents the state of land-use either as urban or non-urban in urban growth modelling. However, there has been little research on the effect of simultaneously varying the site location and size of spatial extent. Thus varying the spatial extent of a research area, such as in the case of our model city of Nairobi, we came up with a variable CA grid varying in site location. The concept of a variable grid CA has been explored in the Greater Vancouver Regional District (Vliet, White, & Dragicevic, 2009) .
In this research, three cellular automata models (UGM 1, UGM 2 & UGM 3) were used to model urban growth in Nairobi up to the year 2030 as Kenya attains Vision 2030 (Government of Kenya, 2007) . The urban land-use data for Nairobi was derived from multi-spectral Landsat imagery captured in 1986, 2000 and 2010. At the end of the research, calibration and validation of our three models were achieved.
2. The Study Area
Nairobi extends between latitudes 1˚09' and 1˚28' South, and longitude 36˚04' and 37˚10' East in Kenya, with an average altitude of 1700 meters above sea level, covering an area of 696 km2 (Figure 1). Nairobi is the capital city of Kenya. The administratively defined town has land-uses divided roughly into urban use, agriculture, rangeland, open/transitional areas, and remnants of evergreen tropical forests. Nairobi has a high growth rate per annum compared to other growth rates in Africa with 75% of urban population living in informal settlements
Figure 1. Location of the city of Nairobi within Kenya as shown in a false colour composite of LANDSAT satellite data from 30th January 2010 (path 168 row 61).
(UN-HABITAT, 2005) . From a population of 310,000 in 1960, the population reached 510,000 in 1970 (Republic
of Kenya, 1970) , 828,000 in 1979 (Republic of Kenya, 1981) , 1,321,000 in 1989 (Republic of Kenya 1994) , 2,137,000 in 1999 (Republic of Kenya, 2000) and 3,138,369 in 2009 (Republic of Kenya, 2010). The projected population in the year 2020 will be almost six million (UN-HABITAT, 2005) .
3. Modelling Nairobi’s Urban Growth
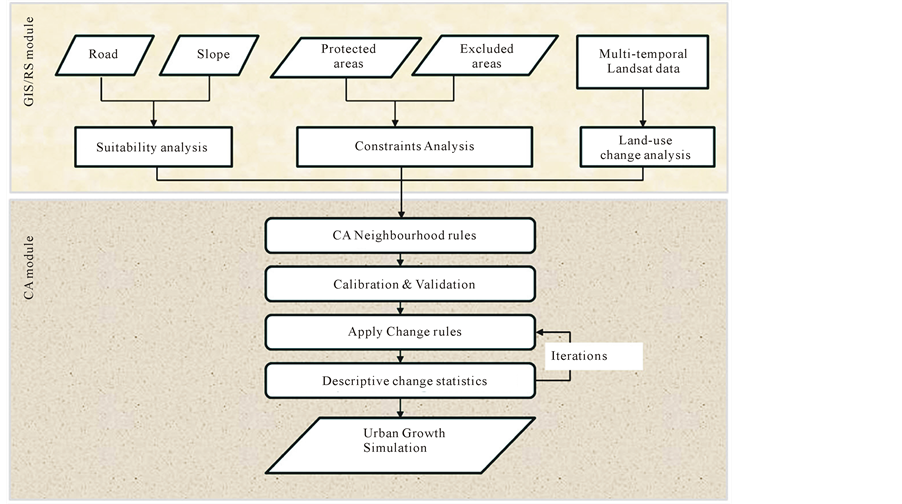
There has been growing need for accurate assessment of urban growth so as to foster sustainable urban development strategy (Han, Hayashi, Cao, & Imura, 2009) . This has resulted to development of urban growth models which are able to spatio-temporal simulate urban dynamics. Such models incorporate socio-economic and physical components at different scales so as to address challenges in urban planning and promote plausible urban development paths. Our urban growth model (UGM) was implemented in the modelling platform XULU (Extendable Unified Land Use Modelling Platform) in a modified way (Goetzke & Judex, 2011) . UGM uses cellular automata (CA) technique. CA serves as a paradigm for thinking about complex spatio-temporal phenomena and an experimental laboratory for testing ideas (Itami, 1994) .
UGM has been successful used to model urban growth in Germany (Goetzke & Judex, 2011) and in Kenya (Mubea, Goetzke, & Menz, 2013) andneeds four spatial input parameters namely: urban land-use, transportation network, slope and exclusion. The exclusion layer determines, which areas in the study area cannot be changed or converted (e.g. water bodies or protected areas) or, if not excluded, are by a certain degree resistant against urbanisation. The transportation layer represents the hierarchical road network in an area under investigation. UGM requires a land-use map for the starting year of the calibration phase and a reference land-use map at the end year. The simulated urban area of the end year is compared to the reference map using the Multiple Resolution Validation (MRV) as described in Pontius Jr. et al. (2004) . Figure 2 shows the flow chart of the major steps applied in this research.
Calibration of UGM uses Monte Carlo method in order to determine five calibration parameters (whose values range from 0 and 100) namely: 1) dispersion; 2) breed; 3) spread; 4) slope resistance and 5) road gravity. Urban growth can be classified in UGM as: a) spontaneous new growth; b) new urban centre establishment or spreading urban centre growth; c) edge growth; and, d) road influenced growth (Jantz, Goetz, Donato, & Claggett, 2010) . Table 1 illustrates the summary of growth types simulated by our UGM and illustrates the contribution of each parameter as well as when combined with others and several different growth processes (Jantz, Goetz, & Shelley, 2004) .
Figure 2. Flow chart of urban growth modelling.
Table 1. Summary of growth types simulated by the UGM model.
Several iterations of Monte-Carlo are performed in the brute-force calibration to obtain the best set of the five calibration parameters. Model evaluation involves three datasets: a reference land-use map of time 1 (t1), a reference land-use map of time 2 (t2) and a simulatedland-use map of time 2. The reference land-use map of time 1 (t1) is the initial point for modelling, that is, land-use map of 1986 and at the same time serves as a null-model, which is the assumption that no change has taken place. Therefore, the reference maps of t1 and t2 are compared. To evaluate the model result, the simulatedland-use map of t2 is compared with the classified land-use map of t2 as reference map.
We used Pontius Jr., Huffaker & Denman (2004) method to validate our results. We compared the simulation model with a null-model. The null-model obtained used the 2010 reference land-usemap as the prediction for 2010.
4. Varying Site Location and CA Grid
CAs are dynamical systems in which space and time are discrete and consists of an array of cells, each of which can be in one of a finite number of possible states, updated synchronously in discrete time steps, according to a local, identical interaction rule (Sipper, 1997; Parker, Manson, Janssen, Hoffmann, & Deadman, 2003) . The ability of CA to simulate urban growth is based on the assumption that past urban development affects future patterns through local interactions among land-uses (Santé, García, Miranda, & Crecente, 2010) . Thus, CA are able to simulate different urban growth scenarios (Mubea, Goetzke, & Menz, 2014) .
A cellular automaton consists of five basic elements namely cell space (grid), cell state, cell neighbourhood, transition rules and time. Our UGM uses two-dimensional lattice of sites or cells which is the most common form of a cellular automaton used in modelling urban growth and land-use change (Liu, 2008) . Nevertheless, most grid space is typically assumed to be homogeneous, and usually different models adopted different grid size (Barredo, Kasanko, McCormick, & Lavalle, 2003 ; Clarke, Hoppen, & Gaydos, 1997; White & Engelen, 1993) .
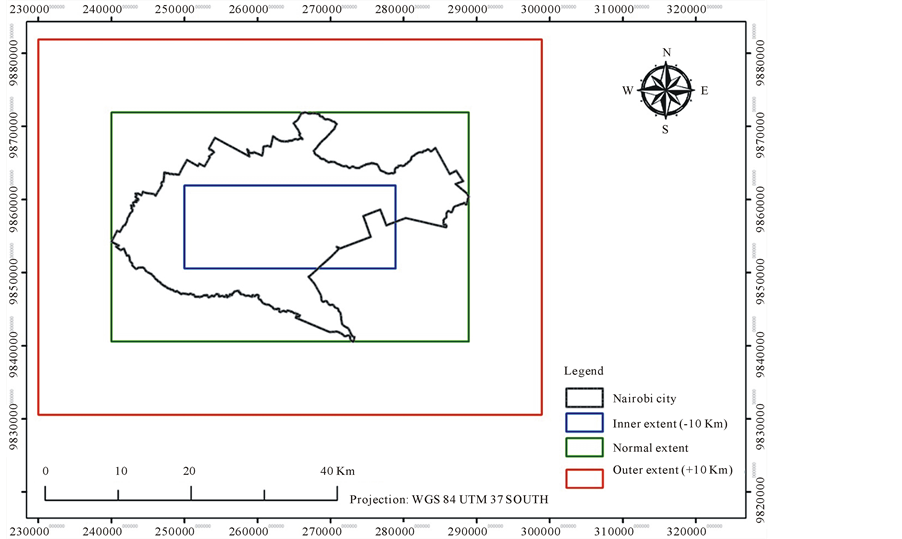
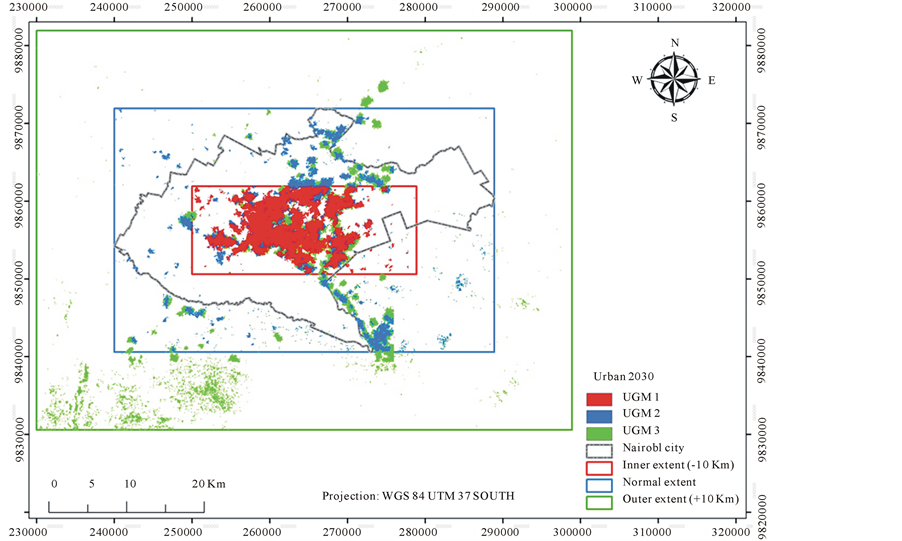
The state of each cell in CA is updated according to local rules, that is, the state of a cell at a given time depends on its own state and the states of its neighbours at the previous time step (Wolfram, 1994) . Thus by varying the delineation of the study area in our case the city limits of Nairobi, we were able to come up with three variable CA grids composed of array of cells which simulate finite state automata as shown in Figure 3 and Figure 4. Consequently, we arrived at three urban growth models translating into three approaches of urban development possibilities.
In the first model (UGM 1), we captured the central business district (CBD) of Nairobi as shown in blue in Figure 3 and Figure 4. The Nairobi CBD is composed of primarily of commercial land-uses where most companies, banks mainly operate. Government offices are also located in the CBD.
In the second model (UGM 2), we captured the city limits of Nairobi in a rectangular fashion as shown in green in Figure 3 and Figure 4. This was a variation from previous studies in which the exact polygon boundary was applied to simulate urban growth (Mubea, Goetzke, & Menz, 2013; Mubea, Goetzke, & Menz, 2014) . The region slightly captured suburban areas surrounding Nairobi.
In the third model (UGM 3), we expanded the city limits so as to capture and simulate urban growth in the
peri-urban areas neighboring Nairobi as shown in red in Figure 3 and Figure 4. This area includes high residential
Figure 3. Map of Nairobi showing the three extents for our UGM.
Figure 4. Map of location of Nairobi illustrating neighbouring towns and the three UGM extents (source: © Google Maps).
suburban areas and urban agglomerates. Some companies have expanded into the suburban areas due to availability of land, cheap labor and raw materials.
Hence, our UGM uses the concept of CA and we created three urban growth models of varying CA grid extends and locations. The variable CA grids were varied in intervals of 10 kilometers so as to simulate urban growth within the city of Nairobi, on its boundary and across the borders into the neighboring peri-urban areas. This can provide a coherent and alternate framework for the policy makers as Kenya plans to achieve Vision 2030 in the year 2030. The Government of Kenya formulated Kenya Vision 2030 (Government of Kenya, 2007) aimed at maximum protection of natural resources so as to ensure sustainable development is attained in the year 2030. Cities in Kenya have undergone rapid urbanisation as people migrate into cities in search of employment and better amenities. Thus this gave us the motivation to explorethe three urban growth approaches of varying the city limits of Nairobi.
5. Analysis
5.1. Data
Cloud-free Landsat satellite imagery for 1986, 2000 and 2010 were used to derive the land-use data layer required for the UGM. The city of Nairobi is entirely masked within Landsat TM path 168, row 61. The Landsat data sets used included TM, and ETM+ images in WGS-84 Universal Transverse Mercator (UTM), 37-South projection. Reference data were developed for each of the separate years and then randomly partitioned for classifier training and accuracy assessment. Modelling of Nairobi utilised urban extents extracted from land-use maps for 1986 and 2010 as inputs. Other layers used included slope, areas excluded from development and road network. “Ground truth” data included a topographic map which was used as locational reference data for the 1986 and 2000 classifications while GPS points served as reference data for the 2010 classification. Road network data for Nairobi and its extents were obtained from Nairobi City Council and Google map maker. An exclusion layer was obtained from Survey of Kenya and included government buildings and property as well as other land areas designated as reserved.
5.2. Land-Use Change Analysis
Land-use classification of Nairobi included six land-use classes: urban, forest/parks, urban agriculture and gardening, open/transition areas, water and rangeland (Mubea, Goetzke, & Menz, 2013) . Urban land-use included built-up areas within the study area. Forest included evergreen forest as well as high density mixed forests consisting of trees and little or no under-storey vegetation. Open/transitional areas included bare land, exposed areas, quarries and transitional areas. Water included rivers and reservoirs. The sewage treatment plant in Ruai was also included in the water class. Rangeland included bush land and ground layer covered by grass and sparsely disturbed scrub species.
Image pre-processing steps for the optical datasets included radiometric and geometric correction. GPS points were used for image to map registration. Combinations of the image reflectance spectral bands were used for classification of the 1986, 2000 and 2010 images. Training sites representing the land-use classes of interest were collected using the Region of Interest tool in ENVI 5.0. Support vector machine (SVM) classification was applied to all the data sets and its performance assessed using error matrices.
Post-classification refinements were enforced to diminish classification errors as a result of the similarities in spectral signatures of certain classes. Overall classification accuracy, user’s and producer’s accuracies, and the Kappa statistic were then derived from the error matrices.
5.3. Modelling Using UGM
Model calibration of UGM involved running the model using default parameters of slope, breed, dispersion, road and spread. The default parameter values were 1, 50 and 100. Model calibration was done iteratively in four sequences from coarse to fine calibration as the parameters were varied using Monte Carlo technique. The MRV method was used to achieve the optimal parameterisation for the UGM during the calibration phase as well as for the validation of the model results (Pontius Jr., Huffaker, & Denman, 2004) .
Three urban growth models namely: UGM 1, UGM 2 and UGM 3 were run in the modelling process. This involved varying the extents of Nairobi city so as to achieve three UGMs. In UGM 1 we used the inner extent of Nairobi city as shown in Figure 3. We obtained the region by deducting 10 kilometres from the normal extent boundary. This area amounted to 327.59 km2 and was a good representation of Nairobi’s CBD.
In UGM 2 we used the normal extent of Nairobi city as shown in Figure 3. The region was obtained from clipping the extents of the Nairobi city boundary and we ended up witha rectangular region. This area amounted to 1532.36 km2 and was a typical representation of land-uses within Nairobi city boundaries. Additionally, this area captured the peri-urban areas and suburban areas surrounding Nairobi.
In UGM 3 we used the outer extent of Nairobi city as shown in Figure 3. We obtained the region by adding 10 kilometres from the normal extent boundary. This area amounted to 3540.76 km2 and was an envisaged future representation of Nairobi as it grows absorbing neighbouring towns. We varied the extents of our UGM so as to investigate the effects on our model calibration.
6. Results and Discussion
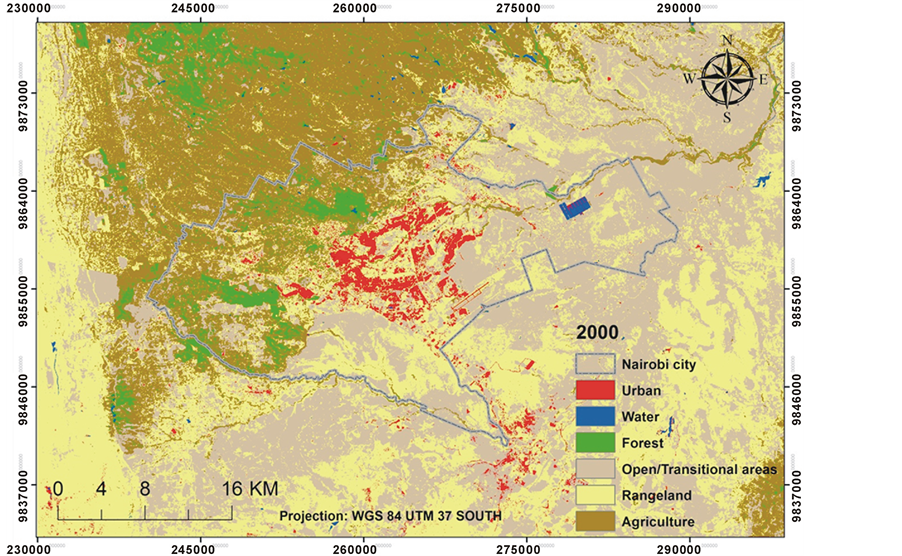
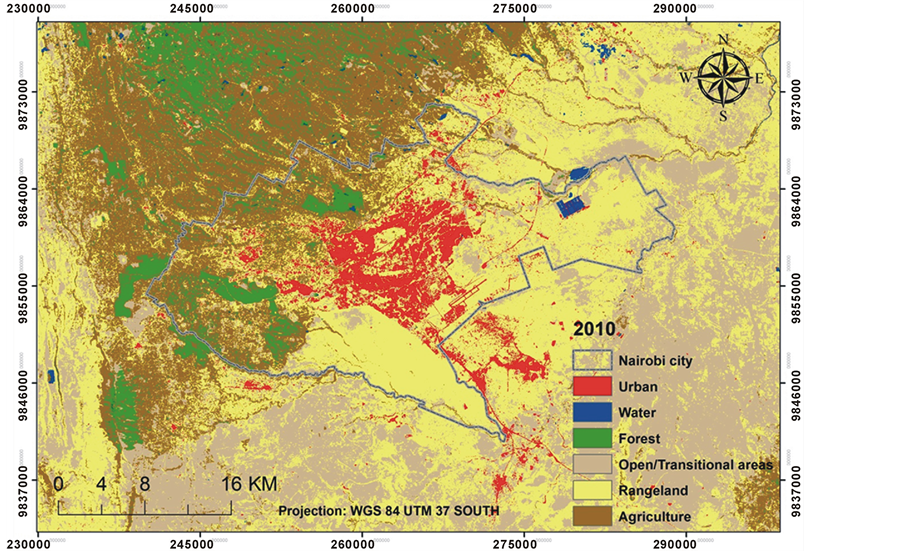
Land-use summary for Nairobiwas done for the outer limit extent covering an area of 3540.76 km2 and results tabulated in Table 2. Land-use maps for Nairobi are illustrated on Figure 5, Figure 6 and Figure 7. The
Table 2. Land-use summary and error estimates for Nairobi.
Figure 5. Land-use map for Nairobi in 1986.
Figure 6. Land-use map for Nairobi in 2000.
Figure 7. Land-use map for Nairobi in 2010.
urban/built-up areas increased from 69.77 km2 in 1986 to 75.18 km2 in 2000 and 130.45 km2 in 2010. Typical agriculture land-use include small-scale urban gardens and peri-urban agriculture for cultivation, and such land-use was converted to urban land-use namely building up of residential and commercial buildings to cater for the increased urban population in Nairobi.
The final model coefficients obtained after successful calibration of our three UGM are illustrated in Table 3. We can see the values as follows: slope at 20, spread at 10, dispersion at 1, breed at 80, road at 40, and a weighted value of 0.8960 for UGM 1; slope at 1, spread at 10, dispersion at 1, breed at 80, road at 10, and a weighted value of 0.9558 for UGM 2; and slope at 50, spread at 25, dispersion at 1, breed at 50, road at 25, and a weighted value of 0.9714 for UGM 3.
Thus, from Table 3 we can see that breed was a major contributor of urban growth in UGM 1 and UGM 2. As we can recall from Table 1 breed refers to the probability that a newly generated settlement starts its own growth and thus influenced most urban growth within the extents of Nairobi city. Dispersion was observed at 1 in all the three UGM’s and hence spontaneous growth was least likely to influence urban growth. Road was the second likely factor of urban growth in UGM 1 at 40 compared to the other UGMs since it has a high concentration of urban roads and most urban growth sprawls near road access. Slope and breed were major contributors of urban growth in UGM 3 as this region captured the peri-urban areas with relatively higher altitude. Slope least likely influenced urban growth in UGM 1 and UGM 2 as the region has a gentle slope which influences new spreading growth as it is easier to construct urban infrastructure and attracted most urban growth. Spread was a least factor influencing urban growth in our three models with low values of 10, 10 and 25 respectively for UGM 1, UGM 2 and UGM 3.
The simulated urban growth using the three models is shown in Table 4. Urban growth increased from 74.50 km2 in 2010 to 108.41 km2 in 2030 using UGM 1, 95.57 km2 in 2010 to 149.73 km2 in 2030 using UGM 2, and 142.96 km2 in 2010 to 217.70 km2 in 2030 using UGM 3. The urban growth simulation maps are shown in Figure 8 and Figure 9.
The urban growth values from Table 4 were obtained using the formula below:
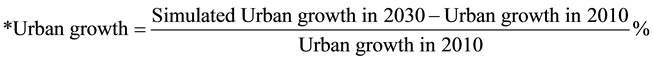
From Figure 8 and Figure 9 we can see that urban growth occurred outwards from Nairobi city mostly in the north, south-west and south-east. Thus there is likelihood of urban growth absorbing the neighbouring towns and suburban areas surrounding Nairobi.
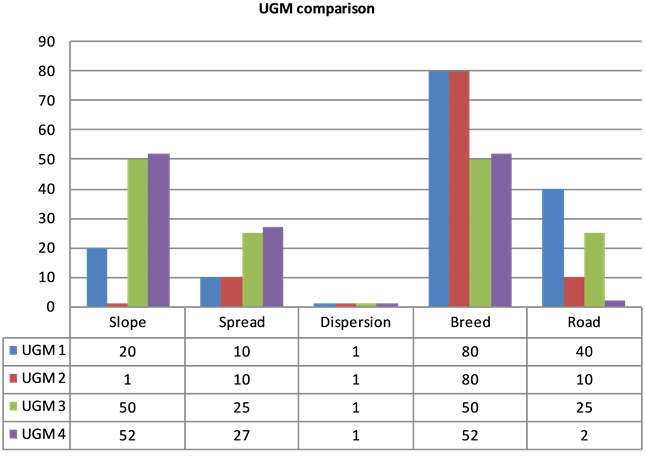
Consequently, after successfully calibrating the three models, we compared our results with our previous modelling for Nairobi city. In Mubea, Goetzke, & Menz (2014) , our modelling results were as follows (denoted as UGM 4): slope at 52, spread at 27, dispersion at 1, breed at 52, road at 2, and a weighted value of 0.9477 obtained from scenario three. Scenario three depicts a situation where we considered maximum protection of natural resources in our exclusion layer. We adopted the same approach for our three models, UGM 1, UGM 2 and UGM 3. UGM comparison from this research and our previous work is shown in Figure 10.
From Figure 10 UGM 4 represents our previous model for Nairobi city (Mubea, Goetzke, & Menz, 2014) . Here we can see that dispersion was least likely to influence urban growth in all the four models. The values of
Table 3. Best model parameters obtained in the three UGM.
Table 4. Simulated Urban Growth for Nairobi.
Figure 8. Simulated urban growth for Nairobi in 2010 using UGM 1, UGM 2 and UGM 3.
Figure 9. Simulated urban growth for Nairobi in 2030 using UGM 1, UGM 2 and UGM 3.
spread were relatively low below 30 with UGM 4 having 27. Slope and breed were greatest contributors of urban growth in UGM 3 and UGM 4. Additionally, the other model parameter values in UGM 3 and UGM 4 were slightly similar other than road.
Furthermore, we compared the weighted values for the four UGMs as shown in Figure 11. The weighted values for our four models were 0.8960 for UGM 1, 0.9558 for UGM 2, 0.9714 for UGM 3 and 0.9477 for
Figure 10. UGM comparison.
Figure 11. Weighted Value comparison.
UGM 4. From these weighted values we can conclude that the urban growth modelling resulted in simulated urban growth of 89.6 % for UGM 1, 95.6% for UGM 2, 97.1% for UGM 3 and 94.8% for UGM 4.
Thus, all the UGM were able to model urban growth in Nairobi with UGM 1 with a lowest value of 0.8960 with 89.6% of simulated urban growth. UGM 3 has the highest value of 0.9714 implying that it captures urban growth well on the outer extents of Nairobi with Nairobi city included with 97.1 % of simulated urban growth. Therefore future urban growth modelling strategies should explore urban growth on the extents of cities as plausible planning agenda. Such growth envisaged in the outer extents of Nairobi city can be attributed to high rural urban migration as new people move immigrate in search for employment, social amenities and business opportunities. Additionally, the peri-urban areas such as Athi River, Rongai, Limuru and Thika (Figure 4) are favourable for higher class income residents who prefer to commute to the Nairobi CBD for work and business.
7. Conclusions
We used Nairobi, Kenya’s capital as a case study of a fast expanding sub-saharan city model urban growth using UGM cellular automata model. Urban land-use maps from satellite image classification were used alongside other datasets in modelling urban growth in Nairobi using UGM. We explored three urban growth models for Nairobi of varying location and extent to model urban growth. We compared our modelling results with our previous urban growth model for Nairobi city.
Kenya plans to achieve Vision 2030 in the year 2030 and this can be envisaged by simulating urban growth within and the extents of Nairobi city. UGM 3 illustrates an approach in which urban growth of Nairobi will absorb neighbouring towns. Urban growth modelling is vital for guiding decision making for resource management.
Acknowledgements
The authors express their gratitude to the initiators of XULU and especially M. Schmitz, H. P. Thamm, Th. Bode and A. B. Cremers (University of Bonn, Germany). Additionally the authors are grateful to German Academic Exchange Service (DAAD) and National Council for Science and Technology (NCST in Nairobi, Kenya) for providing the stipend to facilitate this research. Likewise the authors acknowledge the contribution of the anonymous reviewers for their useful comments.
References
- Akın, A., Clarke, K., & Berberoglu, S. (2014). The Impact of Historical Exclusion on the Calibration of the SLEUTH Urban Growth Model. International Journal of Applied Earth Observation and Geoinformation, 27, 156-168. http://dx.doi.org/10.1016/j.jag.2013.10.002
- Barredo, J. I., Kasanko, M., McCormick, N., & Lavalle, C. (2003). Modelling Dynamic Spatial Processes: Simulation of Urban Future Scenarios through Cellular Automata. Landscape and Urban Planning, 64, 145-160. http://dx.doi.org/10.1016/S0169-2046(02)00218-9
- Clarke, K., Hoppen, S., & Gaydos, L. (1996). Methods and Techniques for Rigorous Calibration of Cellular Automaton Model of Urban Growth. Third International Conference/Workshop on Integrating GIS and Environmental Modeling. Santa Fe: National Center for Geographic Information and Analysis.
- Clarke, K., Hoppen, S., & Gaydos, L. (1997). A Self-Modifying Cellular Automaton Model of Historical Urbanization in the San Francisco Bay Area. Environment and Planning B: Planning and Design, 24, 247-261. http://dx.doi.org/10.1068/b240247
- Goetzke, R., & Judex, M. (2011). Simulation of Urban Land-Use Change in North Rhine-Westphalia (Germany) with the Java-Based Modelling Platform Xulu. In P. Mandl, & A. Koch (Eds.), Modeling and Simulating Urban Processes (pp. 99-116). Munster: LIT-Verlag.
- Government of Kenya (2007). Kenya Vision 2030. Nairobi: Ministry of Planning and National Development. http://www.theredddesk.org/sites/default/files/vision_2030_brochure__july_2007.pdf
- Han, J., Hayashi, Y., Cao, X., & Imura, H. (2009). Application of an Integrated System Dynamics and Cellular Automata Model for Urban Growth Assessment: A Case Study of Shanghai, China. Landscape and Urban Planning, 91, 133-141. http://dx.doi.org/10.1016/j.landurbplan.2008.12.002
- Itami, R. M. (1994). Simulating Spatial Dynamics: Cellular Automata Theory. Landscape and Urban Planning, 30, 27-47. http://dx.doi.org/10.1016/0169-2046(94)90065-5
- Jantz, A. J., Goetz, S. J., Donato, D., & Claggett, P. (2010). Designing and Implementing a Regional Urban Modeling System Using the SLEUTH Cellular Urban Model. Computers, Environment and Urban Systems, 34, 1-16. http://dx.doi.org/10.1016/j.compenvurbsys.2009.08.003
- Jantz, C. A., Goetz, S. J., & Shelley, M. K. (2004). Using the SLEUTH Urban Growth Model to Simulate the Impacts of Future Policy Scenarios on Urban Land Use in the Baltimore-Washington Metropolitan Area. Environment and Planning B: Planning and Design, 31, 251-271. http://dx.doi.org/10.1068/b2983
- Leão, S., Bishop, I., & Evans, D. (2004). Spatial-Temporal Model for Demand and Allocation of Waste Landfills in Growing Urban Regions. Computers, Environment and Urban Systems, 28, 353-385. http://dx.doi.org/10.1016/S0198-9715(03)00043-7
- Lebel, L., Thaitakoo, D., Sangawongse, S., & Huaisai, D. (2007). Views of Chiang Mai: The Contribution of Remote-Sens- ing to Urban Governance and Sustainability. In M. Netzband, W. Stefanov, & C. Redman (Eds.), Applied Remote Sensing for Urban Planning, Governance and Sustainability (pp. 221-247). Berlin: Springer. http://dx.doi.org/10.1007/978-3-540-68009-3_10
- Liu, Y. (2008). Modelling Urban Development with Geographical Information Systems and Cellular Automata (1 ed.). Boca Raton, FL: CRC Press. http://dx.doi.org/10.1201/9781420059908
- Mubea, K., Goetzke, R., & Menz, G. (2013). Simulating Urban Growth in Nakuru (Kenya) Using Java-Based Modelling Platform XULU. 2013 European Modelling Symposium (EMS), Manchester, 20-22 November 2013, 97-102.
- Mubea, K., Goetzke, R., & Menz, G. (2014). Applying Cellular Automata for Simulating and Assessing Urban Growth Scenario Based in Nairobi, Kenya. International Journal of Advanced Computer Science and Applications, 5. http://dx.doi.org/10.14569/IJACSA.2014.050201
- Oguz, H., Klein, A. G., & Srinivasan, R. (2007). Using the Sleuth Urban Growth Model to Simulate the Impacts of Future Policy Scenarios on Urban Land Use in the Houston-Galveston-Brazoria CMSA. Research Journal of Social Sciences, 2, 72-82.
- Parker, D. C., Manson, S. M., Janssen, M. A., Hoffmann, M. J., & Deadman, P. (2003). Multi-Agent Systems for the Simulation of Land-Use and Land-Cover Change: A Review. Annals of the Association of American Geographers, 93, 314-337. http://dx.doi.org/10.1111/1467-8306.9302004
- Pontius Jr., R. G., Huffaker, D., & Denman, K. (2004). Useful Techniques of Validation for Spatially Explicit Land-Change Models. Ecological Modelling, 179, 445-461. http://dx.doi.org/10.1016/j.ecolmodel.2004.05.010
- Republic of Kenya (1970). Kenya Population Census 1969. Nairobi: Government Printer.
- Republic of Kenya (1981). Kenya Population Census 1979. Nairobi: Government Printer.
- Republic of Kenya (1994). Kenya Population Census 1989. Nairobi: Government Printer.
- Republic of Kenya (2000). Economic Survey 2000. Nairobi: Government Printer.
- Republic of Kenya (2010). Economic Survey 2010. Nairobi: Government Printer.
- Santé, I., García, A. M., Miranda, D., & Crecente, R. (2010). Cellular Automata Models for the Simulation of Real-World Urban Processes: A Review and Analysis. Landscape and Urban Planning, 96, 108-122. http://dx.doi.org/10.1016/j.landurbplan.2010.03.001
- Silva, E., & Clarke, K. C. (2002). Calibration of the SLEUTH Urban Growth Model for Lisbon and Porto, Portugal. Computers, Environment and Urban Systems, 26, 525-552. http://dx.doi.org/10.1016/S0198-9715(01)00014-X
- Sipper, M. (1997). Evolution of Parallel Cellular Machines: The Cellular Programming Approach. Berlin: Springer. http://dx.doi.org/10.1007/3-540-62613-1
- Tobler, W. (1979). Cellular Geography. In S. Gale, & G. Olsson (Eds.), Philosophy in Geography (pp. 379-386). Dortrecht: Reidel.
- Triantakonstantis, D., & Mountrakis, G. (2012). Urban Growth Prediction: A Review of Computational Models and Human Perceptions. Journal of Geographic Information System, 4, 555-587. http://dx.doi.org/10.4236/jgis.2012.46060
- UN-HABITAT (2005). Regional Urban Sector Profile Study (RUSPS). Nairobi: UN-HABITAT.
- Vliet, J., White, R., & Dragicevic, S. (2009). Modeling Urban Growth Using a Variable Grid Cellular Automaton. Computers, Environment and Urban Systems, 33, 35-43. http://dx.doi.org/10.1016/j.compenvurbsys.2008.06.006
- White, R., & Engelen, G. (1993). Cellular Automata and Fractal Urban Form: A Cellular Modelling Approach to the Evolution of Urban Land-Use. Environment and Planning A, 25, 1175-1199. http://dx.doi.org/10.1068/a251175
- Wolfram, S. (1994). Cellular Automata. In A. Wesley, S. Wolfram, & M. A. Reading (Eds.), Cellular Automata and Complexity: Collected Papers. Boulder: Westview Press.