Geomaterials
Vol.1 No.2(2011), Article ID:6412,5 pages DOI:10.4236/gm.2011.12005
A New Approach to the Calculation of Work Index and the Potential Energy of a Particulate Material
Technical University of Crete, Chania, Greece
E-mail: Helistach@mred.tuc.gr
Received April 16, 2011; revised June 13, 2011; accepted June 28, 2011
Keywords: Work Index, Potential Energy, Grinding
Abstract
The work index Wi was defined by F. Bond as the specific energy (kWh/ton) required to reduce a particulate material from infinite grain size to 100 microns. The calculation is based on the size-energy relationship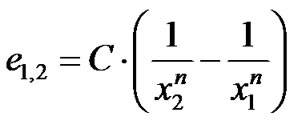 , which for n = 0.5, x1 = ∞ and x2 =100, by definition gives e∞,100 = Wi and consequently C = 10Wi. In theory, for a given material the value found for Wi should be constant regardless of the measured sizes x1 and x2 used to calculate the constant C by measuring the energy e1,2. In practice this is not so due to the fact that n ≠ 0.5 and many correction factors have been proposed to overcome this inadequacy experienced by accepting n = 0.5. The present paper proposes a simple way to calculate the appropriate exponent n using conventional grinding procedures. The same calculation can be used to calculate the true value of Wi and attribute a potential energy state to a material at any size.
, which for n = 0.5, x1 = ∞ and x2 =100, by definition gives e∞,100 = Wi and consequently C = 10Wi. In theory, for a given material the value found for Wi should be constant regardless of the measured sizes x1 and x2 used to calculate the constant C by measuring the energy e1,2. In practice this is not so due to the fact that n ≠ 0.5 and many correction factors have been proposed to overcome this inadequacy experienced by accepting n = 0.5. The present paper proposes a simple way to calculate the appropriate exponent n using conventional grinding procedures. The same calculation can be used to calculate the true value of Wi and attribute a potential energy state to a material at any size.
1. Introduction
The size-energy relationship is generally expressed by the following Equation (1),
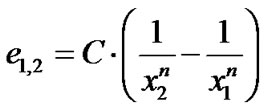 (1)
(1)
where e1,2 is the specific energy required to grind a particulate material from initial size x1 to final size x2. The parameter C is a constant and n is an exponent that according to Rittinger [1] n = 1, according to Bond [2] n = 0.5 and according to Charles [3] and Stamboliadis [4], n can take any value near these two. In the case that the initial size is infinite and the final size is 100 μm then by definition the required specific energy is called work index Wi
 (2)
(2)
The value of the constant C in (1) can be calculated using a mill of known power that enables to measure the specific energy as well as screening facilities to measure x1 and x2. By convention, the sizes x1 and x2 are the d80 ones. The constant C in (1) is related to the defined Wi and the combination of (1) and (2) gives
 (3)
(3)
and (1) can be written as follows,
 (4)
(4)
or the same
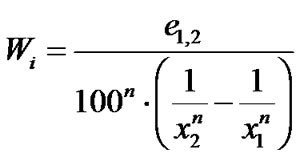 (5)
(5)
The value of the Wi in (5) can be calculated using a mill of known power that enables to measure the specific energy e1,2 as well as screening facilities to measure x1 and x2. In theory the calculated value of Wi must be constant for the same material regardless of the values of e1,2 , x1 and x2. It is a common routine to keep the feed size x1 constant, and vary the specific energy or the product size x2, depending on the experimental procedure that is kept constant during the test and calculate the value of Wi. In practice the calculated value is not constant and in general it depends on the selected values of e1,2 or x2 accordingly. To overcome this inadequacy some correction factors have been adapted by Bond [5].
The present work is an effort to show that the deviation of the Wi value is due to the assumption that the exponent n is equal to 0.5. It also indicates a different method to treat the experimental data by first calculating the actual value of the exponent n and then use this optimum value to calculate the Wi by (5).
Going a step further, the present work attributes a potential energy state, to any particulate material of known Wi, that is a function of its size only. This enables one to find a direct energy—size relationship of a material that does not depend on the initial size of the feed as it is the case of (1). Finally this work presents the results obtained for different minerals and rocks ground under different experimental conditions.
2. Experimental Procedures
The experimental procedures used are the batch process using a novel ring mill, a laboratory ball mill, a laboratory rod mill and the semi continuous process using the same rod mill as described below. In all cases the mineral sample is crushed and screened to pass a predetermined size 3.5 or 4 mm. The feed sample undergoes a wet screen analysis and a certain quantity, usually 0.5 - 1.0 kg, is used at each grinding test. The grinding products are also wet screened for their size distribution.
2.1 Ring Mill Batch Tests
The procedure is similar to the previous batch tests the difference been the mill type invented by Spitas et al. [6]. The particular mill is a high power mill made of a horizontal cylinder. Inside the mill two parallel arms are adjusted to the axis along its length with O rings hanging on the arms. During rotation the rings are directed to the cylinder, due to centrifugal forces and smash any mineral particles between the rings and the inside of the mill cylinder. The mill power is measured by an electric system based on the torsion of the axis and depends on the rotation frequency. For each batch test i the mill is loaded with a feed mass m = 1 kg and rotates for a time ti. At the end the energy Ei (Joules) is recorded and the specific energy ei = Ei/m (Joule/kg) is calculated. Dividing by 3600 the specific energy can be transformed to (kWh/ ton). Finally the product is wet screened to find the size d80.
2.2 Ball Mill Batch Process
The mill dimensions, (D × L), are 0.204 × 0.158 m and it is loaded with 6.5 kg steel balls between 25 and 32 mm in diameter. The mill rotates on rolls and its frequency is set to 70 RPM (1.667 Hertz) corresponding to 85% of the critical frequency. The mill power is P = 16.2 Watts, calculated by the formula provided by Stamboltzis [7].
 (6)
(6)
where M (kg) is the mass of balls (6.5 kg) plus the feed (0.5 kg), N (Hertz) is the rotating frequency and D (m) the mill diameter For the batch tests the mill is loaded and rotates for a time t (sec) consuming energy 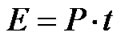 (Joules). This energy corresponds to a specific energy e = E/m (Joules/ kg), where m is the mass (kg) of the sample. Finally the product is wet screened to find the size d80.
(Joules). This energy corresponds to a specific energy e = E/m (Joules/ kg), where m is the mass (kg) of the sample. Finally the product is wet screened to find the size d80.
2.3 Rod Mill Batch Process
The mill dimensions, (D × L), are 0.204 × 0.3 m and it is loaded with 8.55 kg steel rods 14 to 20 mm diameter. The mill rotates on rolls and its frequency is set to 70 RPM corresponding to 85% of the critical frequency. The mill power is P = 22.5 Watts, calculated by (6). Finally the product is wet screened to find the size d80.
2.4 Rod Mill Semi Continuous Process
The same mill is used for the semi continuous grinding tests which is similar to the Bond test but with the existing mill of known power. After time t the mill product is wet screened at a predetermined screen size. From the weight difference of the over size before and after grinding one calculates the grinding rate. The over size (circulating load) is then dried (105˚C), returned to the mill and a mass of the feed sample equal to the under size of the screen is also added keeping the mill load constant. Using the previous grinding rate one sets the new time such as to achieve a ratio k = 2 of circulating load to new feed. The same process is repeated until the results of two successive tests differ less than 3%. The time t is registered as well as the mass m of the new feed, which is also equal to the product. The specific energy is then calculated as in the previous batch test.
3. Data Processing
3.1 Calculation of the Exponent n and the Wi
For any test the data collected is the size d80 (μm) of the feed x1 and the product x2 and the specific energy e1,2 (kWh/ton) used to achieve this size reduction. Initially the work index Wi (kWh/ton) is calculated from (5) assuming n = 0.5. As explained earlier, the calculated values should be the same since they all represent the specific energy required to grind the material from infinite size down to 100 μm. In practice these values differ and
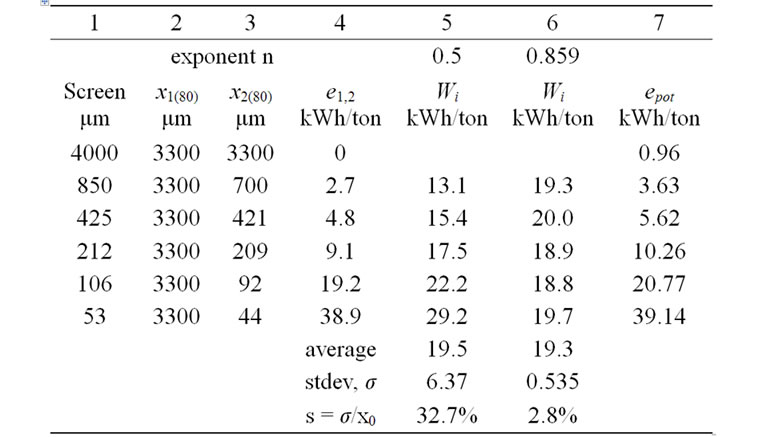
Table 1. Experimental results for quartz grinding.
they actually are higher for smaller sizes x2. To over come this theoretical deviation Bond [5] applied correction factors that depend on the size of the product and the grindability rate.
The method used here is better illustrated using a case study for quartz grinding, using the semi continuous process described above and for screens of 850, 425, 212, 106 and 53 μm. Table 1 presents the results that can be handled as follows:
The screens used are presented in column (1) and the sizes of the feed x1 and the products x2, corresponding to d80, are presented in columns (2) and (3). In column (4) are the measured specific energies used to grind quartz from size x1 to size x2. The corresponding Wi, calculated for n = 0.5, according to Bond’s theory without any correction factors, are presented in column (5). Theoretically these values should be equal within the experimental error. Their average is xo = 19.5 kWh/ton with a standard deviation σ = 6.37 that corresponds to a relative error s = σ/xo = 32.7%.
The present authors believe that the exponent in (1) is not n = 0.5 for all minerals and have developed the following procedure to calculate the optimum value of the exponent n using the existing experimental data. Assuming increasing values of n, varying from 0.1 to 1.3 by an interval of 0.1, one can calculate the work indexes for all the screens used and find the standard deviation σ of the Wi values calculated for the same n. For the present example the plot of σ versus n is presented in Figure 1 from which one can see that the minimum value for σ appears at n = 0.859.
This value can be also calculated by computer means. The calculated values of Wi for n = 0.859 are presented in column (6) of Table 1. The average value is 19.3 kWh/ton and is very close to the one calculated by the Bond theory. However in the present case σ = 0.535 and the relative error is only s = 2.8%.The plot of the Wi calculated versus product size with exponents n = 0.5 and n
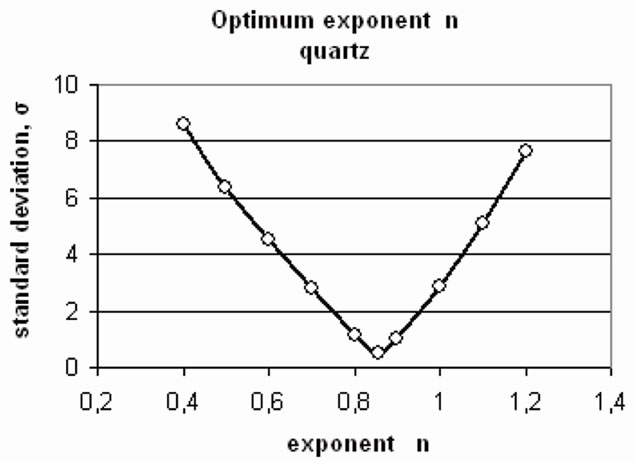
Figure 1. Standard deviation σ versus exponent n.
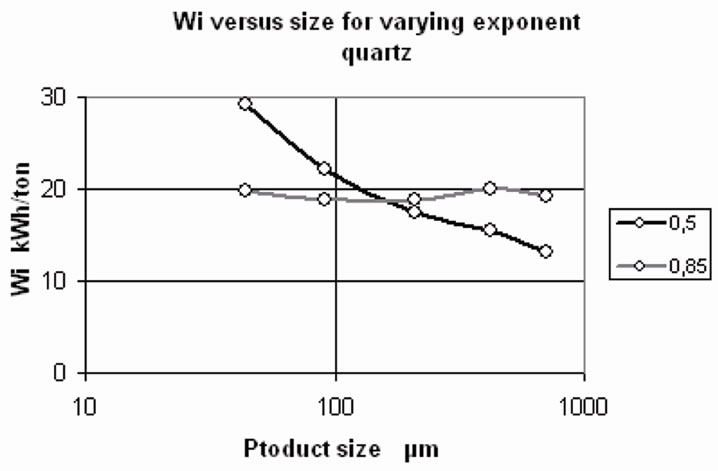
Figure 2. Wi versus size for varying exponent n.
= 0.859, is presented in Figure 2, where one can see that the values for n = 0.859 are closer to a horizontal line since the Wi is constant and independent of the screen size used for its calculation
3.2 Potential Specific Energy
Equation (4) is used to calculate the specific energy e1,2 required to grind a material from size x1 to x2 as long as the exponent n and the Wi of a material are known. Since the energy depends on these two sizes it is not possible to have a direct relationship between energy versus size. In order to reveal this relationship one has to acquire a specific energy level to any ground product that depends only on its size x regardless of the path followed. In the following this energy level will be called potential specific energy ex and can be calculated, assuming that x1 = ∞, from (4) that is reduced to (7).
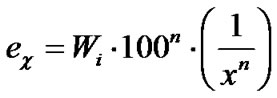 (7)
(7)
It is obvious from (7) that if x = 100 μm the potential specific energy gives the Wi that is defined as the specific energy required to reduce a material from infinite size down to 100 μm. Having determined the exponent n

Table 2. Experimental data.
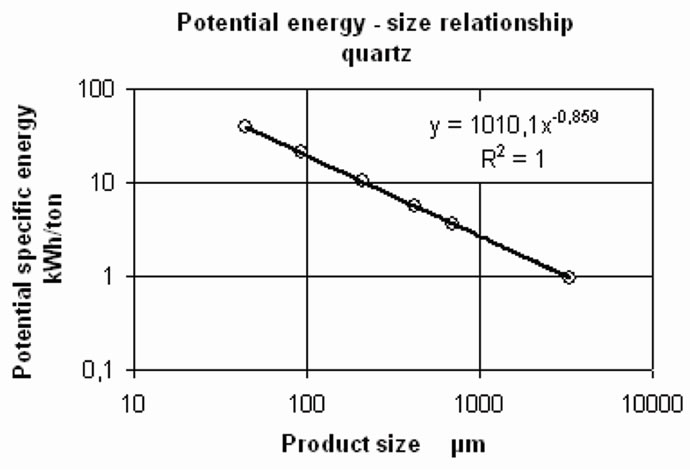
Figure 3. Specific potential energy versus product size.
from the experimental data of Table 1 one can calculate the corresponding potential specific energies, not only of the products but of the feed as well as, and present them in column (7).
The log-log plot of these data versus the material size x corresponding to x2 gives a straight line derived from (7) by taking logarithms. The slope of the line is equal to n and the plot is presented in Figure 3.
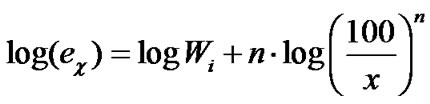 (8)
(8)
3.3 More Experimental Data
Having completed the description of data handling for the case of quartz ground in a semi continuous process, similar to the one described by F. Bond, one can provide results obtained for other minerals by one of the experimental procedures described earlier. The materials ground are cryptocrystalline limestone and magnesite, crystalline marble and quartz and serpentine with cleavage. The results are summarized in Table 2.
A close observation of Table 2 reveals the cryptocrystalline materials like limestone and magnesite as well as materials with cleavage have an exponent n at the range of 0.5, as declared by Bond, while those with big crystals that have to be broken during grinding have an exponent n greater then 0.5. The average values of Wi for different d80 of the products calculated with n = 0.5 are very close to the same average values calculated with n optimum but the error is much smaller in the later case. Consequently the potential energy versus size relationship is better described when the exponent in (8) is the optimum one.
4. Discussion and Conclusions
It is generally accepted that the specific energy required for grinding increases as the particle size becomes small and is due to three main reasons:
• The efficiency of grinding equipment diminishes as the particles become smaller.
• The intergrowth of crystals in the same particle. At sizes above the crystal size breakage occurs at the interface between crystals and the adherent energy is usually lower than the coherent energy when the crystal themselves are broken to smaller sizes [5,8].
• A part of the energy required for breakage is lost during elastic deformation of the particle before breakage and only a part of it is used to overcome the coherent energy of the particle. At fine sizes, the deformation energy becomes a greater part of the total energy and eventually it overpasses it so that a decreasing portion of the energy provided is used for breakage [9].
For all the reasons above, it is not possible to predict whether the energy consumed for grinding is proportional to the new surfaces formed or the new flaws. It appears more reasonable to accept that the net energy is proportional to the new surfaces and consequently the specific net breakage energy is proportional to the specific area that varies according to ![]() where d is the particle size. However since the energy efficiency varies according to the size one should introduce a parameter to take this into consideration. This is done by the definition of the grinding efficiency observed from the energy surface area relationship and is expressed by an exponent n that is incurporated so that in practice the specific energy is proportional to
where d is the particle size. However since the energy efficiency varies according to the size one should introduce a parameter to take this into consideration. This is done by the definition of the grinding efficiency observed from the energy surface area relationship and is expressed by an exponent n that is incurporated so that in practice the specific energy is proportional to  [10].
[10].
On the other hand Bond [5] has assumed that the specific energy required for grinding is proportional to the flaws, or the same proportional to , and to overcome the problem of the mill efficiency at various sizes has proposed a rather empirical way that incorporates the classification size in closed circuit and the grinding rate of the under size fraction.
, and to overcome the problem of the mill efficiency at various sizes has proposed a rather empirical way that incorporates the classification size in closed circuit and the grinding rate of the under size fraction.
This work proposes an easy way to determine the exponent n using several classification sizes near the product size range and determines the optimum work index Wi of the material at the working size range with an estimate of the error involved. This work also indicates how to acquire a potential energy to any material based on its Wi and its size, enabling the plot the potential energy versus the material size. Obviously the specific energy required to grind a material from one size to another is the difference of its potential specific energies at these two sizes. By definition the potential energy at size 100 μm is the work index Wi of the material.
5. References
[1] P. R. Rittinger, “Lehrbuch der Aufbereitungskunde,” Berlin, 1867.
[2] F. C. Bond, “The Third Theory of Comminution,” Transactions on AIME Mining Engineering, Vol. 193, 1952, pp. 484-494.
[3] R. J. Charles, “Energy-Size Reduction Relationships in Comminution,” Transactions on AIME Mining Engineering, Vol. 208, 1957, pp. 80-88.
[4] E. Stamboliadis, “Impact Crushing Approach to the Relationship of Energy and Particle Size in Comminution,” European Journal of Mineral Processing and Environmental Protection, Vol. 3, No. 2, 2003, pp. 160-166.
[5] F. C. Bond, “Crushing and Grinding Calculations,” British Chemical Engineering, Vol. 6, 1961, pp. 378-385.
[6] V. Spitas, P. Makris and M. Founti, “A Novel Dry Pulverizer for Low Cost Production of Powders,” Particulate Science and Technology, Vol. 17, No. 3, 1999, pp. 217- 228. doi:10.1080/02726359908906814
[7] G. Stamboltzis, “Calculation of the Net Power of Laboratory Ball Mills,” Mining and Metallurgical Annals, No. 76, 1990, pp. 47-55, in Greek Language.
[8] R. T. Hukki, “Proposal for a Solomonic Settlement between the Theories of von Rittinger, Kick and Bond,” Transactions on AIME, Vol. 220, 1961, pp. 403-408.
[9] E. Stamboliadis, “The Fracture of Brittle Materials as an Equilibrium of Surface and Cohesion Energy: The Size Effect,” Journal of the Mechanical Behavior of Materials, Vol. 16, No. 6, 2005, pp. 363-377. doi:10.1515/JMBM.2005.16.6.363
[10] E. Stamboliadis, “The Energy Distribution Theory of Comminution, Specific Surface Energy, Mill Efficiency and Distribution Mode,” Minerals Engineering, Vol. 20, No. 2, 2007, pp. 140-145. doi:10.1016/j.mineng.2006.07.009

