Received 16 April 2016; accepted 12 July 2016; published 15 July 2016

ABSTRACT

The present paper focuses an optimal policy of an inventory model for deteriorating items with generalized demand rate and deterioration rate. Shortages are allowed and partially backlogged. The salvage value is included into deteriorated units. The main objective of the model is to minimize the total cost by optimizing the value of the shortage point, cycle length and order quantity. A numerical example is carried out to illustrate the model and sensitivity analyses of major parameters are discussed.

Keywords:

EOQ, Quadratic Demand, Salvage Value, Shortage, Three-Parameter Weibull Deterioration Rate

1. Introduction

In the recent three decades, rigorous researches have come to existence on inventory models for deteriorating items. Most of the physical goods deteriorate over time. Food items, fruits, vegetables suffer from depletion by direct spoilage while stored. Highly volatile liquids such as alcohol, gasoline and turpentine undergo physical depletion over time through the process of evaporation. Electronic goods, grains, photographic films and radioactive substances deteriorate through a gradual loss of potential or utility with the passage of time. So decay or deterioration of physical items in stock is a very realistic feature and inventory researchers felt the necessary to use this factor into consideration. Generally, deterioration is defined as the natural process that occurs in most of physical items those lose their characteristic over time. It violates the assumption that goods can be held infinitely for future demand. The mathematical modeling on inventory control was started with the work of Harris [1] , who studied the classical EOQ (Economic Order Quantity) model with his implicit assumption was the stocked items have infinite shelf lives. Researches in this area were started from fashion goods. Firstly, Whitin [2] studied the deterioration on fashion goods after their valid period. After, Ghare and Schrader [3] were the first two researchers who laid the foundation of modeling inventory system of deteriorating items with help of differential equation. They studied the classical inventory model without shortage considering the constant deterioration rate. Shah and Jaiswal [4] and Aggarwal [5] developed an order level inventory models considering the constant deterioration rate. Another class of inventory models was developed on the assumptions of the time dependent deterioration rate. Firstly, Covert and Philip [6] developed an EOQ model for deteriorating items using a two-parameter Weibull distribution deterioration rate. Later, Philip [7] extended their model by considering the three-parameter Weibull distribution deterioration rate. Misra [8] first developed the production lot-size model by using both the constant and the two-parameter Weibull distribution deterioration. The review literatures on inventory modeling were given in the articles of Raafat [9] , Goyal and Giri [10] , Li et al. [11] and Bakker et al. [12] .

Besides demand and deterioration rate, other factors like allowing shortages are important for modeling of inventory. Shortages usually occur in two cases when the shortage items are totally backlogged and the other case when the items are partially backlogged. In the former case, the customers are not totally willing to accept the items while the latter case customers are only willing to accept the items which can be supplied by the whole sellers in the next period. Various types of inventory models with completely backlogging were discussed by Murdeshwar [13] , Goyal et al. [14] , Chakrabarti and Chaudhuri [15] , Salmeh et al. [16] , Zhou and Lau [17] and others.

But, in real life situation, during the shortage period, the willingness of a customer to wait for items declines with the length of the waiting time. Backlogging happens due to the lack of raw materials or work in progress or the demand is uncertain. Chang and Dye [18] were the first who studied the backlogging rate that depends on the length of the waiting time. In the real life situations, for many stocks such as fashionable commodities and high-tech products, the longer the waiting time, the smaller would be the backlogging rate. Being the backlogging rate as variable, it depends on the length of waiting time for the next replenishment. Many researchers like Papachristos and Skouri [19] , Abad [20] , Teng et al. [21] , Sana [22] , Roy et al. [23] and Singh and Pattnayak [24] studied their models with considering the partial backlogging rate.

In the classical EOQ models, the demand rate of an item was assumed as constant. However, in the real market situations, the demand rate of any item always acts as a dynamic state. In this context, Silver and Meal [25] first developed the modified EOQ model with varying demand. Many researchers like Donaldson [26] , Dave and Patel [27] , Giri et al. [28] and others worked in this direction. However, most of the above model mainly based on time-varying demands like linearly or exponential. Considering the quadratic demand as the next realistic approach, Ghosh and Chaudhuri [29] , Khanra et al. [30] and Singh and Pattnayak [31] developed their inventory models for deteriorating items. Singh et al. [32] developed an EOQ model for deteriorating items under permissible delay in payment by considering stock dependent demand.

Other category of inventory models was developed by considering the deterioration rate as the key factor. Ghare and Schrader [3] , Shah and Jaiswal [4] , Aggrawal [5] and Bhunia and Maiti [33] developed their models considering the deterioration as constant. Researchers like Covert and Philip [6] , Mishra [8] , Jalan et al. [34] , Jain and Kumar [35] and Singh and Pattnayak [36] studied their models taking two-parameter Weibull distribution deterioration. In real life situation, the two-parameter Weibull distribution deterioration may not be useful because some items start deteriorating after a certain period while storing, but not at the initial stage. Generally, when the items are kept in stock, they do not start deteriorating as soon as they are received; instead, deterioration starts after some time. For such items three-parameter Weibull distribution deterioration rate is applicable to represent the time to deterioration. The location parameter is used to describe its shelf life. Philip [7] , Chakrabarti et al. [37] and Jain and Kumar [38] studied their models considering deterioration rate as three-parameter Weibull distribution to represent the time to deterioration.

In real market situations, the sellers offer a reduced unit cost called the salvage value of the deteriorated items to the customers to motivate to buy the deteriorated units. In this context, Jaggi and Aggarwal [39] , Mishra and Shah [40] developed their models using salvage value one of costs. Recently, Annadurai [41] studied the inventory model for deteriorating items with shortages and salvage value.

In this study, an effort has been made to determine an optimal policy for deteriorating items considering quadratic demand, three parameter Weibull distribution deterioration rate and salvage value. Shortages are permitted to occur and partially backlogged. Among the different patterns of time varying demands, the most realistic approach is to consider the quadratic demand pattern because it represents both accelerated and retarded growth in demand. Quadratic demand is generally represented by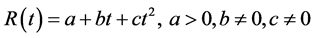. 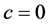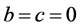When and, it represents linear and constant demand rates respectively. In real market situations, deterioration starts after some time when the items are stocked. For such items, the three-parameter Weibull distribution deterioration can be used to represent the time to deterioration. It is generally represented by 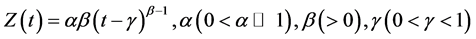where 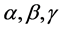and t are called scale parameter, shape parameter, location parameter and time of deterioration respectively. 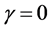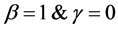When and, it represents the two-parameter Weibull and constant deterioration rate respectively.

2. Assumptions

The following assumptions are taken in developing the model.

1) A single product is considered.

2) Replenishment is instantaneous.

3) The lead time is zero.

4) The demand rate is deterministic and quadratic function of time.

5) The deterioration rate is three-parameter Weibull distribution deterioration.

6) The shortages are permitted and backlogged. It is assumed that the backlogging rate will be smaller when the waiting time is longer.

7) During the planning horizon, there is no need to replace or repair the deteriorated units.

8) The salvage value of the deteriorated units depends on the cost deterioration during the cycle time.

3. Notations

The following notations are taken in developing the model.

1)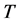: The fixed length of each ordering cycle.

2)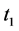: The time when the inventory level reaches zero.

3)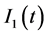: On-hand inventory at time t when.

4)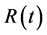: The quadratic demand rate, i.e., 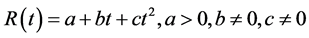where a, b and c are the initial demand rate, increasing demand rate and changing demand rate respectively.

5)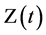: The three parameter Weibull distribution deterioration rate, i.e., . Here are called the scale parameter, the shape parameter and the location parameter respectively.

6): The backlogging rate, i.e., where is called the backlogging pa-

rameter.

7): The constant backlogging parameter where.

8): The salvage value parameter which is associated with deteriorated units during the cycle where.

9): The per cycle ordering quantity.

10): The ordering cost per order.

11): The inventory holding cost per unit.

12): The purchase cost per unit.

13): The shortage cost per unit.

14): The cost of lost sales per unit.

15): The total relevant cost per unit time.

16): The optimum length of ordering cycle.

17): The optimal shortage point of time.

18): The optimal order quantity.

19): The optimal total relevant cost.

4. Model Formulation

The inventory system goes as follow: at time, a lot size of certain units enter the system. In the interval, the inventory level gradually decreases due to demand and partly due to deterioration and it vanishes at time. Then, shortages are allowed to occur during the interval and all the demand during the shortage period is partially backlogged. Thus, the inventory level at any time t during the period can be represented by the differential equation

Using the value of where called the scale, shape and lo-

cation parameter respectively and where, the above equation is given by

(1)

Equation (1) is a linear differential equation. The integrating factor (I.F.) is.

The solution of Equation (1) with boundary condition is given by

(2)

(by neglecting the higher power of as).

The maximum positive inventory level for each cycle can be obtained by putting in Equation (2) is given by

(3)

At time, the inventory level achieves zero, then shortage is allowed to occur during the shortage interval. During this interval, the inventory level depends on demand and a fraction of demand is backlogged at

the rate. Thus, the behavior of the inventory system at any time t can be represented by

the differential equation

Using the value of where and where, the

above equation is given by

(4)

The solution of Equation (4) with boundary condition is given by

(5)

The maximum back order units are given by

(6)

Hence, the order size during the time interval is given by

(7)

Now, the total relevant cost of the model is expressed as the difference of the sum of the cost of ordering, cost of carrying inventory, cost of deterioration, cost of shortage due to backlogging and cost of opportunity due to lost sales and salvage value of the deteriorated items.

Now, the per order cost of ordering cost is

(8)

The cost of carrying inventory is

(9)

(by neglecting the higher power of as).

The cost of deterioration is

(10)

(by neglecting the higher power of as).

The cost of shortage due to backlogging

(11)

The cost of opportunity due to lost sales

(12)

The salvage value of deteriorated items per unit time

(13)

Thus, from the above arguments, the total annual cost per unit time for the retailer is

(14)

The objective of the model is to minimize the total relevant cost per unit time. The necessary

conditions for minimizing the total relevant cost per unit time are

(15)

Equation (15) implies

(16)

and

(17)

The solutions of (16) and (17) will give the optimal shortage point and the optimal cycle time. The values of and so obtained, the optimal value of the total relevant cost per unit time is determined by equation (14) provided they satisfy the sufficient conditions for minimizing are

(18)

(19)

and

(20)

at and.

If the solutions obtained from (16) and (17) do not satisfy the sufficient conditions (18), (19) and (20), the optimal solution is infeasible. In that case, either the values of parameters are consistent or there is some error in their estimations.

After obtaining the optimal values of and, the optimal order quantity and the optimal total relevant cost can be obtained from Equations (7) and (14) respectively.

5. Numerical Examples

Example 1. Let us consider the following parametric values of the inventory system as:, , , , , , , , , , & in appropriate units.

Solving the simultaneous Equations (16) and (17), the optimal shortage period and optimal cycle length are obtained as and unit time respectively. Now substituting the pair and in Equations (7) and (14), we get the optimal order quantity and average total relevant cost per unit time.

6. Sensitivity Analysis

We study the effects of changes in the parameters of the model such as, , , , , , , , , , and on the optimal shortage point, the optimal length of the cycle, the optimal order quantity and the average total relevant cost per unit time. The sensitivity analysis is performed by changing each of the parameters by −50%, −25%, +25% and +50% taking one parameter at a time while keeping others unchanged. The results are illustrated in Table 1 from Example-1.

Here “” indicates the infeasible solution.

1), , & increase with increase in the value of the parameter. Here, , & are all highly sensitive to changes in.

2) & decrease while & increase with increase in the value of the parameter. Here, , & are all moderately sensitive to changes in.

3), & decrease while increases with increase in the value of the parameter for the first two values. Here, , & are all lowly sensitive to changes in.

4), & decrease while increases with increase in the value of the parameter for the first two values. Here, , & are all lowly sensitive to changes in.

5), & increase while decreases with increase in the value of the parameter for the last two values. Here, , & are all lowly sensitive to changes in.

6), & increase while decreases with increase in the value of the parameter for the first and last values only. Here, , & are all lowly sensitive to changes in.

7), & increase while decreases with increase in the value of the parameter for the last two values. Here, , & are all lowly sensitive to changes in.

8), & decrease while increases with increase in the value of the parameter for the last two values. Here, , & are all highly sensitive to changes in.

9), & increase while decreases with increase in the value of the parameter for the last two values. Here, , & are all lowly sensitive to changes in.

10) & increase while & decrease with increase in the value of the parameter for the last two values. Here, , & are all moderately sensitive to changes in.

11) & increase while & decrease with increase in the value of the parameter for the last two values. Here, , & are all moderately sensitive to changes in.

12), & decrease while increases with increase in the value of the parameter for the last two values. Here, , & are all lowly sensitive to changes in.

13) & increase while & decrease with increase in the value of the parameter for the last two values. Here, , & are all lowly sensitive to changes in.

7. Conclusions

In the present paper, an optimal policy for deteriorating items is derived considering quadratic demand rate, a three-parameter Weibull distribution deterioration rate and salvage value. Shortages are permitted and partially backlogged. The backlogging rate is dependent on the waiting time for the next replenishment. Quadratic demand is appropriate for the seasonal fashion items, cosmetic and high-tech products. As deterioration rate starts after some time when the items are stocked. Therefore, a three-parameter Weibull distribution deterioration rate is considered for developing the model. For selling the deteriorated units, salvage value is required for the determination of optimal total cost. Finally, optimal order quantity per cycle and optimal total relevant cost is derived. Shortages are not permitted and partially backlogged. As the rate of deterioration of most items increases with time or age, i.e., the longer the item remains unused, the higher would be its failure rate. Moreover, the location parameter illustrates the shelf-life of the item in the stock. Therefore, the three-parameter Weibull distribution deterioration is suitable for items with any initial value of the rate of deterioration and for items, which start deteriorating only after a certain period of time.

The proposed model can be extended in numerous ways. Firstly, we may extend demand rate to stock dependent demand rate. Secondly, it may be extended to stochastic demand pattern. Finally, we could also extend the model by incorporating quantity discounts, inflation, a finite rate of replenishment and permissible delay in payments etc.

Cite this paper

Pandit Jagatananda Mishra,Trailokyanath Singh,Hadibandhu Pattanayak, (2016) An Optimal Policy with Quadratic Demand, Three-Parameter Weibull Distribution Deterioration Rate, Shortages and Salvage Value. American Journal of Computational Mathematics,06,200-211. doi: 10.4236/ajcm.2016.63021

References

NOTES

^*Corresponding author.