American Journal of Computational Mathematics
Vol.06 No.01(2016), Article ID:64205,6 pages
10.4236/ajcm.2016.61002
Self Similarity Analysis of Web Users Arrival Pattern at Selected Web Centers
Pushpalatha Sarla, Mallikarjuna Reddy Doodipala*, Manohar Dingari
Department of Engineering Mathematics, GITAM University Hyderabad Campus, Hyderabad, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 December 2015; accepted 1 March 2016; published 4 March 2016
ABSTRACT
The paper focuses on measuring self-similarity using few techniques by an index called Hurst index which is a self-similarity parameter. It has been evident that Internet traffic exhibits self- similarity. Motivated by this fact, real time web users at various centers considered here as traffic and it has been examined by various methods to test the self-similarity. The results from the experiments carried out verify that the traffic examined in the present study is self similar using a new method based on some descriptive measures; for example percentiles have been applied to compute Hurst parameter which gives intensity of the self-similarity. Numerical results and analysis we discussed and presented here play a significant role to improve the services at web centers in the view of quality of service (QOS).
Keywords:
Long-Range Dependence, Self-Similarity, Poisson Process, Percentiles, Hurst Parameter

1. Introduction
At present one of the major issues to know various traffic flows is in self similar nature to study and design some performance metric as that of Ethernet traffic etc. Until recently Poison approach has been used to model the road traffic irrespective of traffic intensity [1] . This was similar to the practice in the cases of Ethernet, LAN, WAN, and WWW traffic. But seminal studies [2] [3] reveal that IP packet traffic in supposed networks tends to be bursty in nature on many time scales. This burstiness of traffic can be characterized mathematically as self- similar or long-range dependence (LRD). It is clear from the work agreed [4] that Poisson process could not emulate the self-similar network traffic. Markovian arrival process (MAP) emulating self-similar traffic is fitted over desired time scales by equating second-order statistics of the counts [5] -[9] .
The idea of this paper is, we examine whether web users traffic data has the self similar property. This is to enhancement earlier results using a real time data [10] . This kind of research is useful for future studies to know the performance metrics and continuous improvement of web centers at various private and in public sector organizations. The rest of the paper has been organized as follows: Definition of self-similarity or long range dependence is given in Section II. Materials and methods are placed in Section III. In Section IV, Hurst parameter is computed using various methods. Finally, conclusions are given in Section V.
2. Long-Range Dependence and Self-Similarity
In this section we give a short description of the mathematical basis for second order self-similar processes (long-range dependence).
Exact Second-Order Self-Similar Process
The exact second-order self-similar process is defined as follows. Arrival instants are modeled as point process. Divide the time axis into disjoint intervals of unit length and let 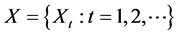 be the number of points (arrival) in the
be the number of points (arrival) in the 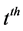 interval. Let X be a second order stationary process with variance
interval. Let X be a second order stationary process with variance 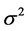 and the autocorrelation function
and the autocorrelation function 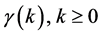 is given by
is given by
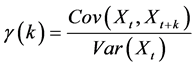 (2.1)
(2.1)
For each 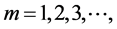 let a new time series
let a new time series 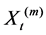 is obtained averaging the original time series X over non-overlapping blocks of size m. That is
is obtained averaging the original time series X over non-overlapping blocks of size m. That is
 (2.2)
(2.2)
This new series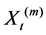 , for each m, is also a second order stationary process with autocorrelation function
, for each m, is also a second order stationary process with autocorrelation function .
.
Definition 1: The process “X” is said to be exactly second order self-similar with Hurst parameter 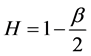
and variance  if
if
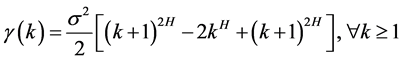 (2.3)
(2.3)
Definition 2: The process “X” is said to be asymptotically second order self-similar with Hurst parameter
 and variance
and variance 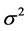 if
if

In terms of variance, self-similar process is defined as follows:
Definition 3: The process “X” is said to be exactly second order self-similar with Hurst parameter
and variance 

Now we shall differentiate long range dependence (LRD) and short range dependence (SRD) processes. For 



The series 


tive term series. Accordingly the left hand series 


they are convergent. That is, for

3. Materials and Methods
As discussed in the introduction, we are primarily interested collecting data from various sources. Real time web users data has been considered. The sample number of users logged on to an Internet server each minute over 100-minutes (see Appendix). In the study web users data can be treated as traffic and verify it is self-similar or not.
4. Methods for Estimating Hurst Parameter of Self-Similar Process
The intensity of self-similarity is given by Hurst parameter, H. The parameter H was named after the hydrologist H.E. Hurst who spent many years to investigate the problem of water storage and also to determine the level patterns of the Nile river. The parameter H has range
4.1. Periodogram Analysis
In the frequency domain, analysis of time series is merely the analysis of a stationary process by means of its spectral representation. The periodogram [11] is given by

where 





4.2. Correlogram Method
In time series analysis [12] , plot of ACF (autocorrelation function) is known as correlogram where the estimated correlation can be given in terms of auto-covariance function

It has already been observed that slow decay of correlation, which is proportional to 
indicates the long-memory process. Therefore, the plot of the sample autocorrelation should exhibit this property. A much better plot for the handling of long-range dependence is the plot of ACF in logarithmic scale. If the asymptotic decay of the correlation is hyperbolic, then the points in the plot should be approximately scattered around a straight line with a negative slope of 

Using this method, the obtained value of H in this case is 0.79.
4.3. Percentile Method
In statistical methodologies, a percentile (or centile) is the value of a variable below which a certain percent of observations fall, like partition values of a process such as quartiles and deciles. There is no exact definition of percentile [16] , however all definitions yield similar results when the number of observations is very large. One definition of percentile, often given in texts, is that the 


Given data set or time series








Using this method, the H value is computed for the data. The pertaining scattered data and trend line with the slope 
Figure 1. Percentile versus percentile number.
4.4. Math Lab Implementation Code is Linked with the Percentile Method
5. Some Conclusions
In this paper, real time web user’s data has been considered as traffic from various web centers and it has been proved to be self-similar. Various methods to test the self-similarity have been used. The obtained values of Hurst parameter h are reasonably close to each other. This kind of research is useful for future studies to know the performance metrics at web centers.
Cite this paper
PushpalathaSarla,Mallikarjuna ReddyDoodipala,ManoharDingari, (2016) Self Similarity Analysis of Web Users Arrival Pattern at Selected Web Centers. American Journal of Computational Mathematics,06,17-22. doi: 10.4236/ajcm.2016.61002
References
- 1. Perati, M.R., Raghavendra, K., Koppula, H.K.R., Doodipala, M.R. and Dasari, R. (2012) Self-Similar Behavior of Highway Road Traffic and Performance Analysis at Toll Plazas. Journal of Transportation Engineering, 138, 1233-1238.
- 2. Leland, W.E., Taqqu, M.S., Willinger, W. and Wilson, D.V. (1994) On the Self-Similar Nature of Ethernet Traffic (Extended Version). IEEE/ACM Transactions on Networking, 2, 1-15.
http://dx.doi.org/10.1109/90.282603 - 3. Crovella, M. and Bestavros, A. (1997) Self-Similarity in World Wide Web Traffic: Evidence and Possible Causes. IEEE/ACM Transactions on Networking, 5, 835-846.
http://dx.doi.org/10.1109/90.650143 - 4. Paxson, V. and Floyd, S. (1995) Wide Area Traffic: The Failure of Poisson Modeling. IEEE/ACM Transactions on Networking, 3, 226-244.
http://dx.doi.org/10.1109/90.392383 - 5. Anderson, A.T. and Nielsen, B.F. (1998) A Markovian Approach for Modeling Packet Traffic with Long Range Dependence. IEEE Journal on Selected Areas in Communications, 16, 719-732.
http://dx.doi.org/10.1109/49.700908 - 6. Yoshihara, T., Kasahara, S. and Takahashi, Y. (2001) Practical Time-Scale Fitting of Self-Similar Traffic with Markov-Modulated Poisson Process. Telecommunication Systems, 17, 185-211.
http://dx.doi.org/10.1023/A:1016616406118 - 7. Shao, S.K., Perati, M.R., Tsai, M.G., Tsao, H.W. and Wu, J. (2005) Generalized Variance-Based Markovian Fitting for Self-Similar Traffic Modeling. IEICE Transactions on Communications, E88-B, 4659-4663.
- 8. Doodipala, M.R. (2013) Second Order Statistics of Time Series of Various Real Time Problems in Conjunction with Periodogram Technique. International Journal of Latest Trends in Engineering and Technology (IJLTET), 3.
- 9. Nagatani, T. (2005) Self-Similar Behavior of a Single Vehicle through Periodic Traffic Lights. Physica A, 347, 673-682.
http://dx.doi.org/10.1016/j.physa.2004.08.007 - 10. Markidakis, S., Wheelwright, S.C. and Hydman, R.J. (1998) Forcating Methods and Applications. 3rd Edition, John Wiley & Sons. Inc., Hoboken.
- 11. Meng, Q. and Khoo, H.L. (2009) Self-Similar Characteristics of Vehicle Arrival Pattern on Highways. Journal of Transportation Engineering, 135, 864-872.
- 12. Brockwell, P.J. and Davis, R.A. (1996) An Introduction to Time Series and Fore-Casting. Springer-Verlag, New York.
http://dx.doi.org/10.1007/978-1-4757-2526-1 - 13. Sarker, M.M.A. (2007) Estimation of the Self-Similarity Parameter in Long Memory Processes. Journal of Mechanical Engineering, ME38, 32-37. Transaction of the Mech. Eng. Div., The Institution of Engineers, Bangladesh.
- 14. Beran, J., Taqqu, M.S. and Willinger, W. (2002) Long-Range Dependence in Variable Bit Rate Traffic. IEEE Transactions on Communications, 43, 1566-1579.
- 15. Beran, J. (1994) Statistics for Long-Memory Processes. Chapman and Hall.
- 16. Lane, D. Percentiles.
http://cnx.org/content/m10805/latest - 17. Web Hosting Talk Forum: 95th Percentile Billing Polling Interval.
http://www.webhostingtalk.com/showthread.php?t=579003(2008)
Appendix
The number of users logged on to an Internet server each minute over 100-minutes.
NOTES
*Corresponding author.








