American Journal of Computational Mathematics
Vol.05 No.04(2015), Article ID:61653,12 pages
10.4236/ajcm.2015.54036
Asymptotic Solutions for the Fifth Order Critically Damped Nonlinear Systems in the Case for Small Equal Eigenvalues
Md. Firoj Alam1, M. Abul Kawser1, Md. Mahafujur Rahaman2
1Department of Mathematics, Islamic University, Kushtia, Bangladesh
2Department of Computer Science & Engineering, Z. H. Sikder University of Science & Technology, Shariatpur, Bangladesh

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 October 2015; accepted 29 November 2015; published 2 December 2015
ABSTRACT
This article examines a fifth order critically damped nonlinearsystem in the case of small equal eigenvalues and tries to find out an asymptotic solution. This paper suggests that the solutions obtained by the perturbation techniques based on modified Krylov-Bogoliubov-Mitropoloskii (KBM) method is consistent with the numerical solutions obtained by the fourth order Runge-Kutta method.
Keywords:
KBM, Eigenvalues, Critically Damped System, Nonlinearity, Asymptotic Solution, Runge-Kutta Method

1. Introduction
The Krylov-Bogoliubov-Mitropoloskii ([1] [2] ) method, known as KBM method, is one of the most used methods for analysing nonlinear oscillatory and non-oscillatory differential systems with small nonlinearities. Krylov and Bogoliubov [1] first developed this method to find the periodic solutions of second order nonlinear differential systems with small nonlinearities. However, the method was later improved and justified mathematically by Bogoliubov and Mitropolskii [2] . It was then extended by Popov [3] to damped oscillatory nonlinear systems. The Popov results were rediscovered by Mendelson [4] because of the physical importance of the damped oscillatory systems. In the meantime, Murty et al. [5] developed an asymptotic method based on the theory of Bogoliubov to obtain the response of over damped nonlinear systems. Later, Murty [6] offered a unified KBM method, which was capable to cover the damped and over-damped cases. Sattar [7] also examined an asymptotic solution for a second order critically damped nonlinear system. Alam [8] proposed a new asymptotic solution for both over-damped and critically damped nonlinear systems. Akbar et al. [9] propounded an asymptotic method for fourth order over-damped nonlinear systems, which was straightforward as well as easier than the method put forward by Murty et al. [5] . Later, Akbar et al. [10] extended the method for fourth order damped oscillatory systems. Akbar et al. [11] also suggested a technique for obtaining over-damped solutions of n-th order nonlinear differential systems. Recently, Rahaman and Rahman [12] have found analytical approximate solutions of fifth order more critically damped systems in the case of smaller triply repeated roots. Besides, Rahaman and Kawser [13] have also proposed asymptotic solutions of fifth order critically damped nonlinear systems with pair wise equal eigenvalues and another is distinct. Further, Islam et al. [14] suggested an asymptotic method of Krylov-Bogoliubov-Mitropolskii for fifth order critically damped nonlinear systems. Furthermore, Rahaman and Kawser [15] expounded analytical approximate solutions of fifth order more critically damped nonlinear systems.
This study seeks to find solutions of fifth order critically damped nonlinear systems where two of the eigenvalues are equal and smaller than the other three distinct eigenvalues. This paper shows that the obtained perturbation results show good coincidence with the numerical results for different sets of initial conditions and eigenvalues.
2. The Method
Consider a fifth order weakly nonlinear ordinary differential system
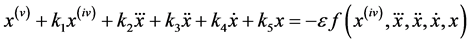 (1)
(1)
where 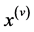 and
and 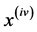 denote the fifth and fourth derivatives respectively and over dots represent the first, second and third derivatives of x with respect to t;
denote the fifth and fourth derivatives respectively and over dots represent the first, second and third derivatives of x with respect to t;  are constants,
are constants, 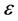 is a sufficiently small and positive
is a sufficiently small and positive
parameter and 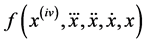 is the given nonlinear function. Let us choose that the characteristic equation of
is the given nonlinear function. Let us choose that the characteristic equation of
the linear equation of (1) has five eigenvalues, where two of the eigenvalues are equal and other three are distinct. Suppose the eigenvalues are 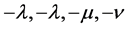 and
and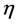 .
.
When , the solution of the corresponding linear equation of (1) is
, the solution of the corresponding linear equation of (1) is
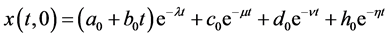 (2)
(2)
where  and
and 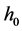 are integral constants.
are integral constants.
When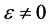 , following Alom [16] , an asymptotic solution of (1) is found in the form
, following Alom [16] , an asymptotic solution of (1) is found in the form
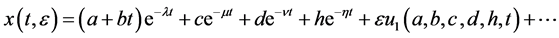 (3)
(3)
where  and h are functions of t and they satisfy the first order differential equations
and h are functions of t and they satisfy the first order differential equations

In order to determine the unknown functions 




where
and
In this investigation, we have expanded the function 

Here the limits of 


Following the KBM method, Sattar [7] , Alam [17] , Alam and Sattar ( [18] [19] ) imposed the condition that 



Now, equating the coefficients of 



Solution of Equation (10) is

where
Substituting the value of 

Different authors imposed different conditions according to the behavior of the systems, such as Alam ( [20] , [21] ) imposed the condition 







3. Example
As an example of the above method, we consider the weakly nonlinear differential system

Comparing (14) and (1), we obtain

Now, comparing Equations (6) and (15), we obtain

For Equation (14), the Equations (9) to (11) respectively become



The solution of the Equation (18) is

where 
Putting the value of 

Since the relation 



Solving Equation (22), we obtain

where 

where 


where 



where 

And the solution of the Equation (18) is

where 
Substituting the values of 


Here the equations of (28) have no exact solutions, but since 




We, therefore, obtain the first approximate solution of the Equation (14) as

where 

4. Results and Discussion
Generally, the perturbation solution is compared to the numerical solution in order to test the accuracy of the approximate solution obtained by a certain perturbation method. First, we have considered the eigenvalues 











Again, we have computed 












Finally, we have computed 












Figure 1. Comparison between perturbation and numerical results.
Figure 2. Comparison between perturbation and numerical results.
Figure 3. Comparison between perturbation and numerical results.
5. Conclusion
In this paper, we have obtained an analytical approximate solution based upon the KBM method of fifth order critically damped nonlinear systems. Moreover, we have shown in this paper that the results obtained by the proposed method correspond satisfactorily to the numerical results obtained by the fourth order Runge-Kutta method.
Acknowledgements
The authors appreciate the precious comments of Mr. Md. Mizanur Rahman, Associate Professor, Department of Mathematics, Islamic University, Bangladesh, on the earlier draft of this article. Special thanks are due to Mr. Md. Imamunur Rahman who has assisted the authors in editing this paper.
Cite this paper
Md. FirojAlam,M. AbulKawser,Md. MahafujurRahaman, (2015) Asymptotic Solutions for the Fifth Order Critically Damped Nonlinear Systems in the Case for Small Equal Eigenvalues. American Journal of Computational Mathematics,05,414-425. doi: 10.4236/ajcm.2015.54036
References
- 1. Krylov, N.N. and Bogoliubov, N.N. (1947) Introduction to Nonlinear Mechanics. Princeton University Press, New Jersey.
- 2. Bogoliubov, N.N. and Mitropolskii, Y. (1961) Asymptotic Methods in the Theory of Nonlinear Oscillations. Gordan and Breach, New York.
- 3. Popov, I.P. (1956) A Generalization of the Bogoliubov Asymptotic Method in the Theory of Nonlinear Oscillations (in Russian). Doklady Akademii USSR, 3, 308-310.
- 4. Mendelson, K.S. (1970) Perturbation Theory for Damped Nonlinear Oscillations. Journal of Mathematical Physics, 2, 3413-3415.
http://dx.doi.org/10.1063/1.1665141 - 5. Murty, I.S.N., Deekshatulu, B.L. and Krishna, G. (1969) On an Asymptotic Method of Krylov-Bogoliubov for Over-Damped Nonlinear Systems. Journal of the Franklin Institute, 288, 49-65.
http://dx.doi.org/10.1016/0016-0032(69)00203-1 - 6. Murty, I.S.N. (1971) A Unified Krylov-Bogoliubov Method for Solving Second Order Nonlinear Systems. International Journal of Non-Linear Mechanics, 6, 45-53.
http://dx.doi.org/10.1016/0020-7462(71)90033-3 - 7. Sattar, M.A. (1986) An Asymptotic Method for Second Order Critically Damped Nonlinear Equations. Journal of the Franklin Institute, 321, 109-113.
http://dx.doi.org/10.1016/0016-0032(86)90065-7 - 8. Alam, M.S. (2001) Asymptotic Methods for Second Order Over-Damped and Critically Damped Nonlinear Systems. Soochow Journal of Mathematics, 27, 187-200.
- 9. Akbar, M.A., Paul, A.C. and Sattar, M.A. (2002) An Asymptotic Method of Krylov-Bogoliubov for Fourth Order Over-Damped Nonlinear Systems. GANIT: Journal of Bangladesh Mathematical Society, 22, 83-96.
- 10. Akbar, M.A., Alam, M.S. and Sattar, M.A. (2003) Asymptotic Method for Fourth Order Damped Nonlinear Systems. GANIT: Journal of Bangladesh Mathematical Society, 23, 41-49.
- 11. Akbar, M.A., Alam, M.S. and Sattar, M.A. (2005) A Simple Technique for Obtaining Certain Over-Damped Solutions of an n-TH Order Nonlinear Differential Equation. Soochow Journal of Mathematics, 31, 291-299.
- 12. Rahaman, M.M. and Rahman, M.M. (2015) Analytical Approximate Solutions of Fifth Order More Critically Damped Systems in the Case of Smaller Triply Repeated Roots. IOSR Journals of Mathematics, 11, 35-46.
- 13. Rahaman, M.M. and Kawser, M.A. (2015) Asymptotic Solution of Fifth Order Critically Damped Non-Linear Systems with Pair Wise Equal Eigenvalues and Another Is Distinct. Journal of Research in Applied Mathematics, 2, 1-15.
- 14. Islam, M.N., Rahaman, M.M. and Kawser, M.A. (2015) Asymptotic Method of Krylov-Bogoliubov-Mitropolskii for Fifth Order Critically Damped Nonlinear Systems. Applied and Computational Mathematics, 4, 387-395.
- 15. Rahaman, M.M. and Kawser, M.A. (2016) Analytical Approximate Solutions of Fifth Order More Critically Damped Nonlinear Systems. International Journal of Mathematics and Computation, 27, 17-29.
- 16. Alam, M.S. (2003) Asymptotic Method for Certain Third-Order Non-Oscillatory Nonlinear Systems. Journal of Bangladesh Academy of Sciences, 27, 141-148.
- 17. Alam, M.S. (2002) A Unified Krylov-Bogoliubov-Mitropolskii Method for Solving n-TH Order Nonlinear Systems. Journal of the Franklin Institute, 339, 239-248.
http://dx.doi.org/10.1016/S0016-0032(02)00020-0 - 18. Alam, M.S. and Sattar, M.A. (1996) An Asymptotic Method for Third Order Critically Damped Nonlinear Equations. Journal of Mathematical and Physical Sciences, 30, 291-298.
- 19. Alam, M.S. and Sattar, M.A. (1997) A Unified Krylov-Bogoliubov-Mitropolskii Method for Solving Third Order Nonlinear Systems. Indian Journal of Pure and Applied Mathematics, 28, 151-167.
- 20. Alam, M.S. (2002) Bogoliubov’s Method for Third Order Critically Damped Nonlinear Systems. Soochow Journal of Mathematics, 28, 65-80.
- 21. Alam, M.S. (2002) On Some Special Conditions of Third Order Over-Damped Nonlinear Systems. Indian Journal of Pure and Applied Mathematics, 33, 727-742.
- 22. Murty, I.S.N. and Deekshatulu, B.L. (1969) Method of Variation of Parameters for Over-Damped Nonlinear Systems. International Journal of Control, 9, 259-266.
http://dx.doi.org/10.1080/00207176908905749





































































