American Journal of Computational Mathematics
Vol.04 No.01(2014), Article ID:42296,23 pages
10.4236/ajcm.2014.41002
Inverse Bayesian Estimation of Gravitational Mass Density in Galaxies from Missing Kinematic Data
Dalia Chakrabarty1,2*, Prasenjit Saha3
1Department of Mathematics, University of Leicester, Leicester, UK
2Department of Statistics, University of Warwick, Warwick, UK
3Institute for Theoretical Physics, University of Zurich, Zurich, Switzerland
Email: *dc252@le.ac.uk
Copyright © 2014 Dalia Chakrabarty, Prasenjit Saha. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Dalia Chakrabarty, Prasenjit Saha. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.



ABSTRACT
Received November 30, 2013; revised December 30, 2013; accepted January 8, 2014
In this paper, we focus on a type of inverse problem in which the data are expressed as an unknown function of the sought and unknown model function (or its discretised representation as a model parameter vector). In par- ticular, we deal with situations in which training data are not available. Then we cannot model the unknown functional relationship between data and the unknown model function (or parameter vector) with a Gaussian Process of appropriate dimensionality. A Bayesian method based on state space modelling is advanced instead. Within this framework, the likelihood is expressed in terms of the probability density function (pdf) of the state space variable and the sought model parameter vector is embedded within the domain of this pdf. As the mea- surable vector lives only inside an identified sub-volume of the system state space, the pdf of the state space vari- able is projected onto the space of the measurables, and it is in terms of the projected state space density that the likelihood is written; the final form of the likelihood is achieved after convolution with the distribution of mea- surement errors. Application motivated vague priors are invoked and the posterior probability density of the model parameter vectors, given the data are computed. Inference is performed by taking posterior samples with adaptive MCMC. The method is illustrated on synthetic as well as real galactic data.
Keywords:
Bayesian Inverse Problems; State Space Modelling; Missing Data; Dark Matter in Galaxies; Adaptive MCMC
1. Introduction
The method of science calls for the understanding of selected aspects of behaviour of a considered system, given available measurements and other relevant information. The measurements may be of the variable
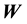
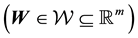 while the parameters that define the selected system behaviour may be
while the parameters that define the selected system behaviour may be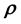 ,
,
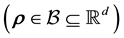 or the selected system behaviour can itself be an unknown and sought function
or the selected system behaviour can itself be an unknown and sought function
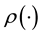 of the known input variable vector
of the known input variable vector
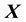
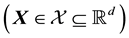 , so that
, so that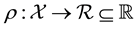 . In either case, we relate the measurements with the model of the system behaviour as in the equation
. In either case, we relate the measurements with the model of the system behaviour as in the equation
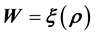 or
or
 where the function
where the function
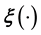 is unknown. Alternatively, in either case the scientist aims to solve an inverse problem in which the operator
is unknown. Alternatively, in either case the scientist aims to solve an inverse problem in which the operator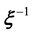 , when operated upon the data, yields the unknown(s).
, when operated upon the data, yields the unknown(s).
One problem that then immediately arises is the learning of the unknown function . Indeed
. Indeed
 is often unknown though such is not the norm―for example in applications in which the data is generated by a known projection of the model function onto the space
is often unknown though such is not the norm―for example in applications in which the data is generated by a known projection of the model function onto the space
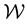 of the measurables,
of the measurables,
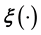 is identified as this known projection. Thus, image inversion is an example of an inverse problem in which the data are a known function of the unknown model function or model parameter vector [1-5, among others]. On the other hand, there can arise a plethora of other situations in science in which a functional relationship between the measurable
is identified as this known projection. Thus, image inversion is an example of an inverse problem in which the data are a known function of the unknown model function or model parameter vector [1-5, among others]. On the other hand, there can arise a plethora of other situations in science in which a functional relationship between the measurable
 and unknown
and unknown
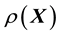 (or
(or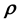 ) is appreciated but the exact form of this functional relationship is not known [6-12, to cite a few].
) is appreciated but the exact form of this functional relationship is not known [6-12, to cite a few].
This situation allows for a (personal) classification of inverse problems such that
• in inverse problems of Type I,
 is known where
is known where
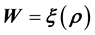 or
or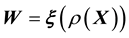 ,
,
• in inverse problems of Type II,
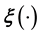 is unknown.
is unknown.
While inverse problems of Type I can be rendered difficult owing to these being ill-posed and/or ill- conditioned as well as in the quantification of the uncertainties in the estimation of the unknown(s), inverse problems of Type II appear to be entirely intractable in the current formulation of
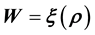 (or
(or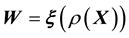 ), where the aim is the learning of the unknown
), where the aim is the learning of the unknown
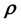 (or
(or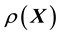 ), given the data. In fact, conventionally, this very general scientific problem would not even be treated as an inverse problem but rather as a modelling exercise specific to the relevant scientific discipline. From the point of view of inverse problems, these entails another layer of learning, namely, the learning of
), given the data. In fact, conventionally, this very general scientific problem would not even be treated as an inverse problem but rather as a modelling exercise specific to the relevant scientific discipline. From the point of view of inverse problems, these entails another layer of learning, namely, the learning of
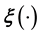 from the data―to be precise, from training data [13-15]. Here by training data we mean data that comprises values of
from the data―to be precise, from training data [13-15]. Here by training data we mean data that comprises values of
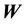 at chosen values of
at chosen values of
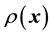 (or at chosen
(or at chosen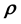 ). These chosen (and therefore known) values of
). These chosen (and therefore known) values of
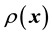 (or
(or ) are referred to as the design points, so that values of
) are referred to as the design points, so that values of
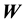 generated for the whole design set comprise the training data.Having trained the model for
generated for the whole design set comprise the training data.Having trained the model for
 using such training data, we then implement this learnt model on the available mea- surements―or test data―to learn that value of
using such training data, we then implement this learnt model on the available mea- surements―or test data―to learn that value of
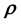 (or
(or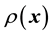 ) at which the measurements are realised.
) at which the measurements are realised.
It is in principle possible to generate a training data set from surveys (as in selected social science applications) or generate synthetic training data sets using simulation models of the system [16-18]. However, often the Physics of the situation is such that
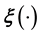 is rendered characteristic of the system at hand (as in complex physical and biological systems). Consequently, a simulation model of the considered system is only an approximation of the true underlying Physics and therefore risky in general; after all, the basic motivation behind the learning of the unknown
is rendered characteristic of the system at hand (as in complex physical and biological systems). Consequently, a simulation model of the considered system is only an approximation of the true underlying Physics and therefore risky in general; after all, the basic motivation behind the learning of the unknown
 (or
(or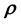 ) is to learn the underlying system Physics, and pivoting such learning on a simulation model that is of unquantifiable crudeness, may not be useful.
) is to learn the underlying system Physics, and pivoting such learning on a simulation model that is of unquantifiable crudeness, may not be useful.
Thus, in such cases, we need to develop an alternative way of learning
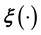 or if possible, learn the un- known
or if possible, learn the un- known
 (or
(or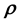 ) given the available measurements without needing to know
) given the available measurements without needing to know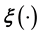 . It may appear that such is possible in the Bayesian approach in which we only need to write the posterior probability density of the unknown
. It may appear that such is possible in the Bayesian approach in which we only need to write the posterior probability density of the unknown
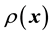 (or
(or ), given the data. An added advantage of using the Bayesian framework is that extra information is brought into the model via the priors, thus reducing the quantity of data required to achieve inference of a given quality. Importantly, in this approach one can readily achieve estimation of uncertainties in the relevant parameters, as distinguished from point estimates of the same. In this paper, we present the Bayesian learning of the unknown model parameters given the measurements but no training data, as no training data set is available. The presented methodology is inspired by state space modelling techniques and is elucidated using an application to astronomical data.
), given the data. An added advantage of using the Bayesian framework is that extra information is brought into the model via the priors, thus reducing the quantity of data required to achieve inference of a given quality. Importantly, in this approach one can readily achieve estimation of uncertainties in the relevant parameters, as distinguished from point estimates of the same. In this paper, we present the Bayesian learning of the unknown model parameters given the measurements but no training data, as no training data set is available. The presented methodology is inspired by state space modelling techniques and is elucidated using an application to astronomical data.
The advantages of the Bayesian framework notwithstanding, in systems in which training data is unavailable, fact remains that
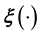 cannot be learnt. This implies that if learning of the unknown
cannot be learnt. This implies that if learning of the unknown
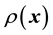 (or
(or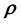 ) is attempted by modelling
) is attempted by modelling
 as a realisation from a stochastic process (such as a Gaussian Process (GP) or Ito Process or t-process, etc.), then the correlation structure that underlies this process is not known. However, in this learning approach, the posterior probability of the unknowns given the data invokes such a correlation structure. Only by using training data can we learn the covariance of the process that
as a realisation from a stochastic process (such as a Gaussian Process (GP) or Ito Process or t-process, etc.), then the correlation structure that underlies this process is not known. However, in this learning approach, the posterior probability of the unknowns given the data invokes such a correlation structure. Only by using training data can we learn the covariance of the process that
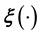 is sampled from, leading to our formulation of the posterior of the unknowns, given the measured data as well as the training data. To take the example of modelling
is sampled from, leading to our formulation of the posterior of the unknowns, given the measured data as well as the training data. To take the example of modelling
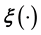 using a high-dimensional GP, it might be possible of course to impose the form of the covariance by hand; for example, when it is safe to assume that
using a high-dimensional GP, it might be possible of course to impose the form of the covariance by hand; for example, when it is safe to assume that
 is continuous, we could choose a stationary covariance function [19], such as the popular square exponential covariance or the Matern class of covariance functions [20], though parameters of such a covariance (correlation length, smoothness parameter) being unknown, ad hoc values of these will then need to be imposed. In the presence of training data, the smoothness parameters can be learnt from the data.
is continuous, we could choose a stationary covariance function [19], such as the popular square exponential covariance or the Matern class of covariance functions [20], though parameters of such a covariance (correlation length, smoothness parameter) being unknown, ad hoc values of these will then need to be imposed. In the presence of training data, the smoothness parameters can be learnt from the data.
For systems in which the continuous assumption is misplaced, choosing an appropriate covariance function and learning the relevant parameters from the measured data, in absence of training data, becomes even trickier. An example of this situation can arise in fact in an inverse problem of Type I―the unknown physical density of the system is projected onto the space of observables such that inversion of the available (noisy) image data will allow for the estimation of the unknown density, where the projection operator is known. Such a density function in real systems can often have disjoint support in its domain and can also be typically characterised by sharp density contrasts as in material density function of real-life material samples [21]. Then, if we were to model this discontinuous and multimodal density function as a realisation from a GP, the covariance function of such a process will need to be non-stationary. It is possible to render a density function sampled from such a GP to be differently differentiable at different points, using for example prescriptions advanced in the literature [22], but in lieu of training data it is not possible to parametrise covariance kernels to ensure the representative discontinuity and multimodality of the sampled (density) functions. Thus, the absence of training data leads to the inability to learn the correlation structure of the density function given the measured image data.
A way out this problem could be to make an attempt to construct a training data set by learning values of the unknown system behaviour function at those points in the domain of the density, at which measured data are available; effectively, we then have a set of data points, each generated at a learnt value of the function, i.e. this set comprises a training data. In this data set there are measurement uncertainties as well as uncertainty of estimation on each of the learnt values of the system function. Of course, learning the value of the function at identified points within the domain of the system function, is in itself a difficult task. Thus, in this paradigm, the domain
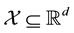 of the unknown system function
of the unknown system function
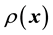 is discretised according to the set of values of
is discretised according to the set of values of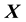 ,
,
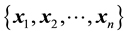 , at which the
, at which the
 measurements are available. In other words, the discretisation of
measurements are available. In other words, the discretisation of
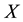 is dictated by the data distribution. Over each
is dictated by the data distribution. Over each
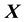 -bin, the function
-bin, the function
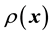 is held a constant such that for
is held a constant such that for
 in the i-th bin, the function takes the value
in the i-th bin, the function takes the value ,
,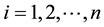 ; then we define
; then we define
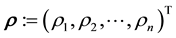 and try to learn this vector, given the data. Unless otherwise motivated, in general applications, the probability distribution of
and try to learn this vector, given the data. Unless otherwise motivated, in general applications, the probability distribution of
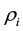 is not imposed by hand. In the Bayesian framework this exercise translates to the computing of the joint posterior probability density of
is not imposed by hand. In the Bayesian framework this exercise translates to the computing of the joint posterior probability density of
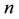 distribution-free parameters
distribution-free parameters
 given the data, where the correlation between
given the data, where the correlation between
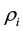 and
and
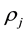 is not invoked,
is not invoked,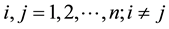 . Of course, framed this way, we can only estimate the value of the sought function
. Of course, framed this way, we can only estimate the value of the sought function
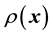 at identified values of
at identified values of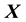 ―unless interpolation is used―but once the training data, thus constructed, is subsequently implemented in the modelling of
―unless interpolation is used―but once the training data, thus constructed, is subsequently implemented in the modelling of
 with a GP of appropriate dimensionality, statistical prediction at any value of
with a GP of appropriate dimensionality, statistical prediction at any value of
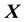 may be possible.
may be possible.
Above, we dealt schematically with the difficult case of lack of training data. However, even when a training data set is available, learning
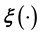 using such data can be hard. In principle,
using such data can be hard. In principle,
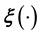 can be learnt using splines or wavelets. However, a fundamental shortcoming of this method is that splines and wavelets can fail to capture the correlation amongst the component functions of a high-dimensional
can be learnt using splines or wavelets. However, a fundamental shortcoming of this method is that splines and wavelets can fail to capture the correlation amongst the component functions of a high-dimensional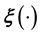 . Also, the numerical difficulty of the very task of learning
. Also, the numerical difficulty of the very task of learning
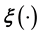 using this technique, and particularly of inverting the learnt
using this technique, and particularly of inverting the learnt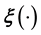 , only increases with dimensionality. Thus it is an improvement to model such a
, only increases with dimensionality. Thus it is an improvement to model such a
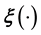 with a high-dimensional GP. A high-dimensional
with a high-dimensional GP. A high-dimensional
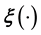 can arise in a real-life inverse problem if the observed data is high-dimensional, eg. the data is matrix-variate [23].
can arise in a real-life inverse problem if the observed data is high-dimensional, eg. the data is matrix-variate [23].
Measurement uncertainties or measurement noise is almost unavoidable in practical applications and therefore, any attempt at an inference on the unknown model parameter vector
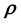 (or the unknown model function
(or the unknown model function ) should be capable of folding in such noise in the data. In addition to this, there could be other worries stemming from inadequacies of the available measurements―the data could be “too small” to allow for any meaningful inference on the unknown(s) or “too big” to allow for processing within practical time frames; here the qualification of the size of the data is determined by the intended application as well as the constraints on the available computational resources. However, a general statement that is relevant here is the fact that in the Bayesian paradigm, less data is usually required than in the frequentists’ approach, as motivated above. Lastly, data could also be missing; in particular, in this paper we discuss a case in which the measurable lives in a space
) should be capable of folding in such noise in the data. In addition to this, there could be other worries stemming from inadequacies of the available measurements―the data could be “too small” to allow for any meaningful inference on the unknown(s) or “too big” to allow for processing within practical time frames; here the qualification of the size of the data is determined by the intended application as well as the constraints on the available computational resources. However, a general statement that is relevant here is the fact that in the Bayesian paradigm, less data is usually required than in the frequentists’ approach, as motivated above. Lastly, data could also be missing; in particular, in this paper we discuss a case in which the measurable lives in a space
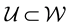 where
where
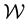 is the state space of the system at hand.
is the state space of the system at hand.
The paper is constructed as follows. In Section 2, we briefly discuss the outline of state space modelling. In the following Section 3, our new state space modelling based methodology is delineated; in particular, we explore alternatives to the suggested method in Subsection 3.1. The astrophysical background to the application using which our methodology is elucidated, is motivated in Section 4 while the details of the modelling are presented in Section 5. We present details of our inference in Section 6 and applications to synthetic and real data are considered in Section 7 and Section 8 respectively. We round up the paper with some discussions about the ramifications of our results in Section 9.
2. State Space Modelling
Understanding the evolution of the probability density function of the state space of a dynamical system, given the available data, is of broad interest to practitioners across disciplines. Estimation of the parameters that affect such evolution can be performed within the framework of state space models or SSMs [24-27]. Basically, an SSM comprises an observation structure and an evolution structure. Assuming the observations to be con- ditionally independent, the marginal distribution of any observation is dependent on a known or unknown stationary model parameter, at a given value of the state space parameter at the current time. Modelling of errors of such observations within the SSM framework is of interest in different disciplines [28,29].
The evolution of the state space parameter is on the other hand given by another set of equations, in which the uncertainty of the evolved value of the parameter is acknowledged. A state space representation of complex systems will in general have to be designed to capacitate high-dimensional inference in which both the evolutionary as well as observation equations are in general non-linear and parameters and uncertainties are non-Gaussian.
In this paper we present a new methodology that offers a state space representation in a situation when data is collected at only one time point and the unknown state space parameter in this treatment is replaced by the discretised version of the multivariate probability density function (pdf) of the state space variable. The focus is on the learning of the static unknown model parameter vector rather than on prediction of the state space parameter at a time point different to when the observations are made. In fact, the sought model parameter vector is treated as embedded within the definition of the pdf of the state space variable. In particular, the method that we present here pertains to a partially observed state space, i.e. the observations comprise measurements on only some―but not all―of the components of the state space vector. Thus in this paradigm, probability of the observations conditional on the state space parameters reduces to the probability that the observed state space data have been sampled from the pdf of the full state space variable vector, marginalised over the unobserved components. Here this pdf includes the sought static model parameter vector in its definition. In addition to addressing missing data, the presented methodology is developed to acknowledge the measurement errors that may be non-Gaussian.
The presented method is applied to real and synthetic astronomical data with the aim of drawing inference on the distribution of the gravitational mass of all matter in a real and simulated galaxy, respectively. This gravitational mass density is projected to be useful in estimating the distribution of dark matter in the galactic system.
3. Method in general
Here we aim to learn the unknown model parameter vector
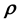 given the data, where data comprises
given the data, where data comprises
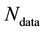 measurements of some (h) components of the d-dimensional state space parameter vector
measurements of some (h) components of the d-dimensional state space parameter vector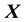 ; thus,
; thus,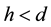 . Here
. Here . In fact, the data set is
. In fact, the data set is
 where the i-th observation is the vector
where the i-th observation is the vector . Let the state space be
. Let the state space be
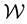 so that
so that . Let the observable vector be
. Let the observable vector be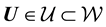 . Let
. Let , i.e. the probability density function of the state parameter vector
, i.e. the probability density function of the state parameter vector
 is
is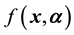 , where the distribution is parametrised by the parameter
, where the distribution is parametrised by the parameter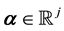 .
.
In light of this, we suggest that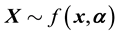 . Then had the observations lived in the state space
. Then had the observations lived in the state space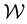 , we could have advanced the likelihood function in terms of
, we could have advanced the likelihood function in terms of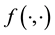 . However, here we deal with missing data that we know lives in the sub-space
. However, here we deal with missing data that we know lives in the sub-space
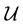 within
within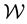 . Therefore, the data must be sampled from the density
. Therefore, the data must be sampled from the density
 that is obtained by marginalising the pdf
that is obtained by marginalising the pdf
 over
over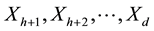 . In other words, the pdf
. In other words, the pdf
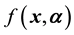 is projected onto the space of the observables, i.e. onto
is projected onto the space of the observables, i.e. onto ; the result is the projected or marginalised density
; the result is the projected or marginalised density
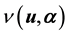 of the observables. Then under the assumption of the observed vectors being conditionally iid, the likelihood function is
of the observables. Then under the assumption of the observed vectors being conditionally iid, the likelihood function is

where

While the likelihood is thus defined, what this definition still does not include in it is the sought model parameter vector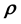 . In this treatment, we invoke a secondary equation that allows for the model parameter vector
. In this treatment, we invoke a secondary equation that allows for the model parameter vector
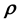 to be embedded into the definition of the likelihood. This can be accomplished by eliciting application specific details but in general, we suggest
to be embedded into the definition of the likelihood. This can be accomplished by eliciting application specific details but in general, we suggest


where
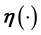 is a t-dimensional vector function of a vector.
is a t-dimensional vector function of a vector.
Given this rephrasing of the state space pdf, the projected density that the i-th measurement
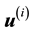 is sampled from, is re-written as
is sampled from, is re-written as

so that plugging this in the RHS of Equation (1), the likelihood is

However, it is appreciated that the pdf of the state space vector
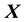 may not be known, i.e.
may not be known, i.e.
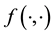 is unknown. This motivates us to attempt to learn the state space pdf from the data, simultaneously with
is unknown. This motivates us to attempt to learn the state space pdf from the data, simultaneously with . We consider the situation that training data is unavailable where training data would comprise a set of values of
. We consider the situation that training data is unavailable where training data would comprise a set of values of
 generated at chosen values of
generated at chosen values of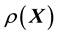 . However, since the very functional relationship (
. However, since the very functional relationship (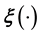 in the notation motivated above) between
in the notation motivated above) between
 and
and
 is not known, it is not possible to generate values of
is not known, it is not possible to generate values of
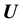 at a chosen value of
at a chosen value of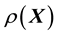 , unless of course, an approximation of unquantifiable crudeness for this functional relationship is invoked. Here we attempt to improve upon the prospect of imposing an ad hoc model of
, unless of course, an approximation of unquantifiable crudeness for this functional relationship is invoked. Here we attempt to improve upon the prospect of imposing an ad hoc model of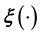 . Then in this paradigm, we discretise the function
. Then in this paradigm, we discretise the function .
.
This is done by placing the relevant ranges of the vectors
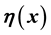 and
and
 on a grid of chosen cell size. Thus, for
on a grid of chosen cell size. Thus, for
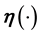 and
and
 being discretised into
being discretised into
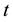 and j-dimensional vectors respectively, the discretised version of
and j-dimensional vectors respectively, the discretised version of
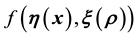 is then represented as the
is then represented as the
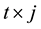 -dimensional vector
-dimensional vector
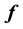 such that the p-th component of this vector is the value of
such that the p-th component of this vector is the value of
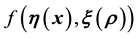 in the p-th “
in the p-th “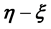 -grid cell”. Here, such a grid-cell is the p-th of the ones that the domain of
-grid cell”. Here, such a grid-cell is the p-th of the ones that the domain of
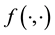 is discretised into,
is discretised into,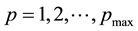 .
.
Given this discretisation of , the RHS of Equation (4) is reduced to a sum of integrals over the unobserved variable in each of the grid-cells. In other words,
, the RHS of Equation (4) is reduced to a sum of integrals over the unobserved variable in each of the grid-cells. In other words,

where
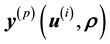 is the value that the vector of the unobserved variables takes up in the p-th
is the value that the vector of the unobserved variables takes up in the p-th
 -grid-cell. The integral on the RHS of Equation (6) represents the volume that the p-th
-grid-cell. The integral on the RHS of Equation (6) represents the volume that the p-th
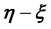 -grid-cell occupies in the space of the unobserved variable vector
-grid-cell occupies in the space of the unobserved variable vector . The value of
. The value of
 in the p-th
in the p-th
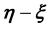 -grid-cell is dependent in general on
-grid-cell is dependent in general on
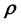 for a given data vector
for a given data vector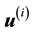 ; hence the notation
; hence the notation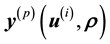 .
.
In other words, to compute the integral for each p (on the RHS of Equation (6)) we need to identify the bounds on the value of each component of
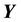 imposed by the edges of the p-th
imposed by the edges of the p-th
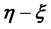 grid-cell. This effectively calls for identification of the mapping between the space of
grid-cell. This effectively calls for identification of the mapping between the space of
 and
and , and the space of the unobserved variables
, and the space of the unobserved variables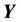 . Now the observation
. Now the observation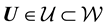 . Then
. Then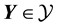 , where
, where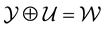 . Indeed, this mapping will be understood using the physics of the system at hand. We will address this in detail in the context of the application that is considered in the paper.
. Indeed, this mapping will be understood using the physics of the system at hand. We will address this in detail in the context of the application that is considered in the paper.
The likelihood function is then again rephrased as

using Equation (6).
However, the observed data is likely to be noisy too. To incorporate the errors of measurement, the likelihood is refined by convolving
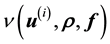 with the density of the error
with the density of the error
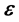 in the value of the observed vector
in the value of the observed vector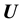 , where the error distribution is assumed known. Let the density of the error distribution be
, where the error distribution is assumed known. Let the density of the error distribution be
 where
where
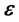 are the known parameters. Then the likelihood is finally advanced as
are the known parameters. Then the likelihood is finally advanced as

In a Bayesian framework, inference is pursued thereafter by selecting priors for the unknowns
 and
and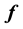 , and then using the selected priors in conjunction with the likelihood defined in Equation 8, in Bayes rule to give
, and then using the selected priors in conjunction with the likelihood defined in Equation 8, in Bayes rule to give
the posterior of the unknowns given the data, i.e. . In the context of the application at hand,
. In the context of the application at hand,
we will discuss all this and in particular, advance the data-driven choice of the details of the discretisation of the
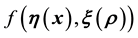 function. Posterior samples could be generated using a suitable version of Metropolis-Hastings and implemented to compute the 95% HPD credible regions on the learnt parameter values.
function. Posterior samples could be generated using a suitable version of Metropolis-Hastings and implemented to compute the 95% HPD credible regions on the learnt parameter values.
Alternative methods
We ask ourselves the question about alternative treatment of the data that could result in the estimation of the unknown model parameter vector . Let the sought model parameter be s-dimensional while the observable
. Let the sought model parameter be s-dimensional while the observable
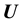 is an h-dimensional vector valued variable and there are
is an h-dimensional vector valued variable and there are
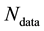 number of measurements of this variable available. Then the pursuit of
number of measurements of this variable available. Then the pursuit of
 can lead us to express the data as a function of the model parameter vector, i.e. write
can lead us to express the data as a function of the model parameter vector, i.e. write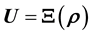 , where
, where
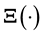 is an unknown, h-dimensional vector valued function of an s-dimensional vector. In order to learn
is an unknown, h-dimensional vector valued function of an s-dimensional vector. In order to learn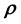 , we will need to first learn
, we will need to first learn
 from the data, as was motivated in the introductory section.
from the data, as was motivated in the introductory section.
As we saw in that section, the learning of this high-dimensional function from the data and its inversion are best tackled by modelling the unknown high-dimensional function with a Gaussian Process. [23] present a generic Bayesian method that performs the learning and inversion of a high-dimensional function given matrix-variate data within a supervised learning paradigm; the (chosen) stationary covariance function implemented in this work is learnt using training data and is subsequently used in the computation of the posterior probability of the unknown model parameter vector given the measured or test data, as well as the training data. In the absence of available training data, such an implementation is not possible, i.e. such a method is not viable in the unsupervised learning paradigm. In the application we discuss below, training data is not available and therefore, the modelling of the functional relation between data and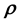 , using Gaussian Processes appears to not be possible. This shortcoming can however be addressed if simulations of the system at hand can be undertaken to yield data at chosen values of
, using Gaussian Processes appears to not be possible. This shortcoming can however be addressed if simulations of the system at hand can be undertaken to yield data at chosen values of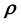 ; however, the very physical mechanism that connects
; however, the very physical mechanism that connects
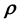 with the data may be unknown (as in the considered application) and therefore, such a simulation model is missing. Alternatively, if independently learnt
with the data may be unknown (as in the considered application) and therefore, such a simulation model is missing. Alternatively, if independently learnt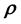 , learnt with an independent data set, is available, the same can be used as training data to learn
, learnt with an independent data set, is available, the same can be used as training data to learn
 given another data set. On such instances, the Gaussian Process approach is possible but in lieu of such training data becoming available, the learning of
given another data set. On such instances, the Gaussian Process approach is possible but in lieu of such training data becoming available, the learning of
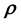 given the matrix-valued data can be performed in the method presented above. On the other hand, a distinct advantage of the method presented below is that it allows for the learning of the state space density in addition to the unknown model parameter vector.
given the matrix-valued data can be performed in the method presented above. On the other hand, a distinct advantage of the method presented below is that it allows for the learning of the state space density in addition to the unknown model parameter vector.
If the suggestion is to learn the unknown system function
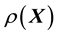 as itself a realisation of a GP, the question that then needs to be addressed is how to parametrise the covariance structure of GP in situations in which the data results from measurements of the variable
as itself a realisation of a GP, the question that then needs to be addressed is how to parametrise the covariance structure of GP in situations in which the data results from measurements of the variable
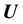 that shares an unknown functional relation with
that shares an unknown functional relation with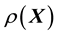 . In other words, in such situations, the unknown system function
. In other words, in such situations, the unknown system function
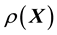 has to be linked with the available data via a functional relation, which however is unknown, as motivated above; we are then back to the discussion in the previous paragraph.
has to be linked with the available data via a functional relation, which however is unknown, as motivated above; we are then back to the discussion in the previous paragraph.
4. Case study
Unravelling the nature of Dark Matter and Dark Energy is one of the major challenges of today’s science. While such is pursued, the gathering of empirical evidence for/against Dark Matter (DM) in individual real-life observed astronomical systems is a related interesting exercise.
The fundamental problem in the quantification of dark matter in these systems is that direct observational evidence of DM remains elusive. In light of this, the quantification is pursued using information obtained from measurable physical manifestations of the gravitational field of all matter in an astronomical system, i.e. dark as well as self-luminous matter. Indeed, such measurements are difficult and physical properties that manifest the gravitational effect of the total gravitational field of the system would include the density of X-rays emitted by the hot gas in the system at a measured temperature [30], velocities of individual particles that live in the system and play in its gravitational field [31-35] and the deviation in the path of a ray of light brought about by the gravitational field of the system acting as a gravitational lens [36].
The extraction of the density of DM from the learnt total gravitational mass density of all matter in the system, is performed by subtracting from the latter, the gravitational mass density of the self-luminous matter. The density of such luminous matter is typically modelled astronomically using measurements of the light that is observed from the system. A reliable functional relationship between the total gravitational mass density and such photometric measurements is not motivated by any physical theories though the literature includes such a relationship as obtained from a pattern recognition study performed with a chosen class of galaxies [37].
In this work, we focus our attention to the learning of the total gravitational mass density in galaxies, the images of which resemble ellipses―as distinguished from disc-shaped galaxies for which the sought density is more easily learnt using measurement of rotational speed of resident particles. By a galactic “particle” we refer to resolved galactic objects such as stars. There could also be additional types of particles, such as planetary nebulae (PNe) which are an end state of certain kinds of stars; these bear signature marks in the emitted spectral data. Other examples of galactic particles could include old clusters of stars, referred to as globular clusters (GCs).
Data
As defined above, the space of all states that a dynamical system achieves is referred to as the system’s state space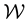 . Now, the state that a galaxy is in, is given by the location and velocity coordinates of all particles in the system. Here, the location coordinate is
. Now, the state that a galaxy is in, is given by the location and velocity coordinates of all particles in the system. Here, the location coordinate is
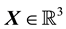 as is the velocity coordinate vector
as is the velocity coordinate vector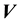 . Thus, in our treatment of the galaxy at hand,
. Thus, in our treatment of the galaxy at hand,
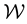 is the space of the particle location and velocity vector i.e. the space of the vector
is the space of the particle location and velocity vector i.e. the space of the vector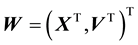 . We model the galactic particles to be playing in the average (gravitational) force field that is given rise to by all the particles in this system. Under the influence of this mean field, we assume the system to have relaxed to a stationary state so that there is no time dependence in the distribution of the vector
. We model the galactic particles to be playing in the average (gravitational) force field that is given rise to by all the particles in this system. Under the influence of this mean field, we assume the system to have relaxed to a stationary state so that there is no time dependence in the distribution of the vector
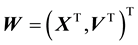 , where the 3-dimensional vector
, where the 3-dimensional vector
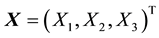 and
and . Then the pdf of the variable
. Then the pdf of the variable
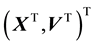 is
is , where
, where
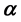 is a parameter vector.
is a parameter vector.
Our aim is to learn the density function of gravitational mass of all matter in the galaxy, given the data
 , where
, where . The physical interpretation of these observables is that
. The physical interpretation of these observables is that
 is the
is the
component of the velocity of a galactic particle that is aligned along the line-of-sight that joins the particle and the observer, i.e. we can measure how quickly the particle is coming towards the observer or receding away but cannot measure any of the other components of . Similarly, we know the components
. Similarly, we know the components
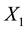 and
and
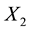 of the location
of the location
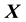 of a galactic particle in the galactic image but cannot observe how far orthogonal to the image plane the
of a galactic particle in the galactic image but cannot observe how far orthogonal to the image plane the
particle is, i.e.
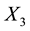 is unobservable. Thus
is unobservable. Thus
 but
but
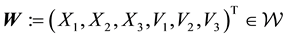 with
with . It merits mention that in the available data, values of
. It merits mention that in the available data, values of
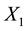 and
and
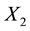 appear in the form of
appear in the form of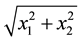 . Then the data
. Then the data .
.
Here
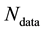 is typically of the order of 102. While for more distant galaxies,
is typically of the order of 102. While for more distant galaxies,
 is lower, recent advancements is astronomical instrumentation allows for measurement of
is lower, recent advancements is astronomical instrumentation allows for measurement of
 of around 750 planetary nebulae or PNe (as in the galaxy CenA, Woodley,
of around 750 planetary nebulae or PNe (as in the galaxy CenA, Woodley,
 Chakrabarty, under preparation). Such high a sample size is however more of an exception than the rule―in fact, in the real application discussed below, the number of
Chakrabarty, under preparation). Such high a sample size is however more of an exception than the rule―in fact, in the real application discussed below, the number of
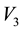 measurements of globular clusters (or GCs) available is only 29. In addition, the measurements of
measurements of globular clusters (or GCs) available is only 29. In addition, the measurements of
 are typically highly noisy, the data would typically sample the sub-space
are typically highly noisy, the data would typically sample the sub-space
 very sparsely and the data sets are typically one-time measurements. The proposed method will have to take this on board and incorporate the errors in the measurement of
very sparsely and the data sets are typically one-time measurements. The proposed method will have to take this on board and incorporate the errors in the measurement of . Given such data, we aim to learn the gravitational mass density of all matter― dark as well as self-luminous―at any location
. Given such data, we aim to learn the gravitational mass density of all matter― dark as well as self-luminous―at any location
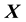 in the galaxy.
in the galaxy.
5. Modelling real data
In the Bayesian framework, we are essentially attempting to compute the posterior of the unknown gravitational mass density function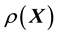 , given data
, given data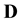 . Since gravitational mass density is non-negative,
. Since gravitational mass density is non-negative, . That we model the mass density to depend only on location
. That we model the mass density to depend only on location
 is a model assumption1.
is a model assumption1.
From Bayes rule, the posterior probability density of
 given data
given data
 is given as proportional to the product of the prior and the likelihood function, i.e. the probability density of
is given as proportional to the product of the prior and the likelihood function, i.e. the probability density of
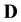 given the model for the unknown mass density. Now, the probability density of the data vector
given the model for the unknown mass density. Now, the probability density of the data vector
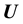 given the model parameters
given the model parameters
 is given by the probability density function
is given by the probability density function
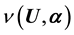 of the observable
of the observable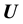 , so that, assuming the
, so that, assuming the
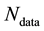 data vectors to be conditionally independent, the likelihood function is the product of the pdfs of
data vectors to be conditionally independent, the likelihood function is the product of the pdfs of
 obtained at the
obtained at the
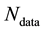 values of
values of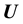 :
:

This is Equation (7) written in the context of this application. Given that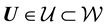 , the pdf of
, the pdf of
 is related to the pdf
is related to the pdf
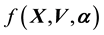 of the vector-valued variable
of the vector-valued variable
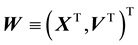 as
as

However, this formulation still does not include the gravitational mass density function
 in the definition of
in the definition of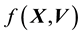 , we explore the Physics of the situation to find how to embed
, we explore the Physics of the situation to find how to embed
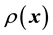 into the definition of the pdf of the state space variable
into the definition of the pdf of the state space variable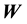 , and thereby into the likelihood. This is achieved by examining the time evolution of this pdf of the state space variable; we discuss this next.
, and thereby into the likelihood. This is achieved by examining the time evolution of this pdf of the state space variable; we discuss this next.
5.1. Evolution of f(X,W) and Embeddin ρ(X) in it
Here we invoke the secondary equation that tells of the evolution of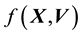 . In general, the pdf of the state space variable is a function of
. In general, the pdf of the state space variable is a function of ,
,
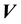 and time
and time . So the general state space pdf is expected to be written as
. So the general state space pdf is expected to be written as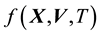 , with
, with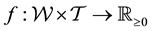 . It is interpreted as the following: at time
. It is interpreted as the following: at time
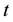
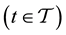 , the probability for
, the probability for
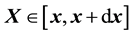 and
and
 for a galactic particle is
for a galactic particle is . However, we assume that the particles in a galaxy do not collide since the galactic particles inside it, (like stars), typically collide over time-scales that are
. However, we assume that the particles in a galaxy do not collide since the galactic particles inside it, (like stars), typically collide over time-scales that are
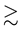 the age of galaxies [38]. Given this assumption of collisionlessness, the pdf of
the age of galaxies [38]. Given this assumption of collisionlessness, the pdf of
 remains invariant. Thus, the evolution of
remains invariant. Thus, the evolution of
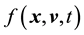 must is guided by the Collisionless Boltzmann Equation (CBE):
must is guided by the Collisionless Boltzmann Equation (CBE):
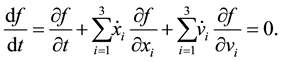 (11)
(11)
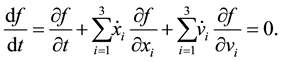
This equation suggests that when the state space distribution has attained stationarity, so that ,
,
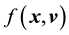 is a constant
is a constant
 at a given time. This is referred to as Jeans theorem [38]. In fact, the equation more correctly suggests that as long as the system has reached stationarity, at any given time,
at a given time. This is referred to as Jeans theorem [38]. In fact, the equation more correctly suggests that as long as the system has reached stationarity, at any given time,
 is a constant
is a constant
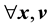 inside a well-connected region
inside a well-connected region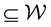 . Given this, the state space pdf can be written as a function of quantities that do not change with time2.
. Given this, the state space pdf can be written as a function of quantities that do not change with time2.
Theorem 5.1. Any function
 is a steady-state or stationary solution of the Collisionless Boltzmann
is a steady-state or stationary solution of the Collisionless Boltzmann
Equation i.e. a solution to the equation
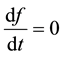 if and only if
if and only if
 is invariant with respect to time, for all
is invariant with respect to time, for all
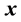 and
and
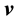 that lie inside a well-connected region
that lie inside a well-connected region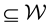 .
.
Proof. The proof is simple; for the proof we assume
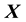 and
and
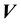 to take respective values of
to take respective values of
 and
and
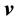 inside a well-connected sub-space of
inside a well-connected sub-space of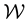 . Let a function of the vectors
. Let a function of the vectors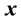 ,
,
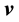 be
be
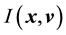 such that it remains
such that it remains
a constant w.r.t. time. Then
 Þ this function is a solution to the equation
Þ this function is a solution to the equation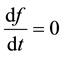 .
.
Let the equation
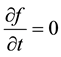 have a solution
have a solution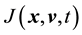 . This implies
. This implies , i.e.
, i.e.
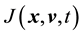 is a constant with respect to time. For this to be true,
is a constant with respect to time. For this to be true,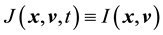 . Therefore the solution to
. Therefore the solution to
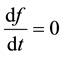 is a
is a
function of
 and
and
 that is a constant w.r.t. time.□
that is a constant w.r.t. time.□
In fact, any function of a time-invariant function of vectors
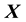 and
and
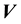 is also a solution to the CBE.
is also a solution to the CBE.
Now, in our work we assume the system to have attained stationarity so that the pdf of the state space variable has no time dependence. Then the above theorem suggests that we can write
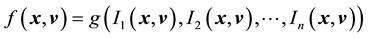 for any
for any , where
, where
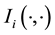 is any time-independent function of 2 vectors, for
is any time-independent function of 2 vectors, for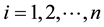 .
.
Now, upon eliciting from the literature in galactic dynamics [39,40] we realise the following.
・ The number
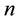 of constants of motion can be at most 5, i.e.
of constants of motion can be at most 5, i.e.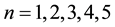 .
.
・ The pdf of the state space variable has to include particle energy , (which is one constant of motion), in its domain. Thus, we can write.
, (which is one constant of motion), in its domain. Thus, we can write.
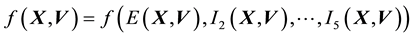 .
.
・ Energy
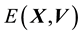 is given as the sum of potential energy
is given as the sum of potential energy
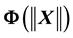 and kinetic energy
and kinetic energy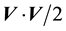 , i.e.
, i.e.



Here
 is the Euclidean norm. That the potential is maintained as dependent only of the location vector
is the Euclidean norm. That the potential is maintained as dependent only of the location vector
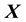 and not on
and not on
 stems from our assumption that there is no dissipation of energy in this system, i.e. we model the galaxy at hand to be a Hamiltonian system. Here, a basic equation of Physics relates the potential of the galaxy to the gravitational mass density of the system, namely Poisson Equation:
stems from our assumption that there is no dissipation of energy in this system, i.e. we model the galaxy at hand to be a Hamiltonian system. Here, a basic equation of Physics relates the potential of the galaxy to the gravitational mass density of the system, namely Poisson Equation:

where

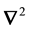 is the Laplace operator (in the considered geometry of the galaxy) and
is the Laplace operator (in the considered geometry of the galaxy) and
 is a known constant (the Universal gravitational constant).
is a known constant (the Universal gravitational constant).
On the basis of the above, we can write


At this point we recall the form of an isotropic function of 2 vectors [41-43].
Remark 5.2. A scalar function
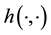 of two vectors
of two vectors
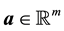 and
and
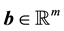 is defined as isotropic with respect to any orthogonal transformation
is defined as isotropic with respect to any orthogonal transformation
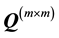 if
if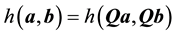 . Here
. Here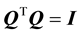 , the identity matrix and
, the identity matrix and . Under any such orthogonal transformation
. Under any such orthogonal transformation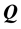 , only the magnitudes of the vectors
, only the magnitudes of the vectors
 and
and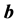 ,
,
and the angle between them remain invariant, where the angle between
 and
and
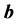 is
is . Therefore,
. Therefore,
it follows that
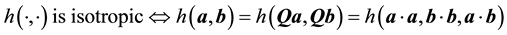 .
.
We also recall that in this application,
 by construction.
by construction.
This leads us to identify any pdf of the state space variable
 as isotropic if the pdf is expressed as a function of energy
as isotropic if the pdf is expressed as a function of energy
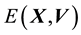 alone. This follows from Equation 18 since
alone. This follows from Equation 18 since
 Þ
Þ

which is compatible with the form of isotropic functions as per Remark 5.2. Thus, if the pdf of the state space variable is dependent on only 1 constant of motion―which by the literature in galactic dynamics has to be energy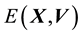 ―then
―then
 is an isotropic function of
is an isotropic function of
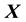 and
and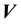 .
.
However, there is no prior reason to model a real galaxy as having an isotropic probability distribution of its state space. Instead, we attempt to
・ use as general a model for the state space distribution of the system as possible,
・ while ensuring that the degrees of freedom in the model are kept to a minimum to ease computational ease.
This leads us to include another time-invariant function
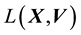 in the definition of the pdf of the state space variable in addition to
in the definition of the pdf of the state space variable in addition to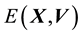 , such that the dependence on
, such that the dependence on
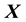 and
and
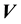 in
in
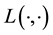 is not of the form that renders
is not of the form that renders
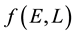 compatible with the definition of isotropic function, as per Remark 5.2, unlike
compatible with the definition of isotropic function, as per Remark 5.2, unlike .
.
This is so because

where
 represents the “cross-product” of the two 3-dimensional vectors
represents the “cross-product” of the two 3-dimensional vectors
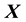 and
and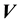 , i.e.
, i.e.

so that

Then, we set
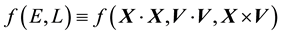 which is not compatible with the form of an isotropic function of the 2 vectors
which is not compatible with the form of an isotropic function of the 2 vectors
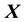 and
and . In other words, if the support of the pdf of
. In other words, if the support of the pdf of
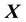 and
and
 includes
includes
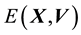 and
and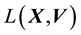 , then the state space distribution is no longer restricted to be isotropic.
, then the state space distribution is no longer restricted to be isotropic.
Such a general state space is indeed what we aimed to achieve with our model. At the same time, adhering to no more than 1 constant of motion in addition to energy
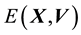 helps to keep the dimensionality of the domain of the pdf of the state space function to the minimum that it can be, given our demand that no stringent model-driven constraint be placed on the state space geometry. Thus, we use n = 2 in our model.
helps to keep the dimensionality of the domain of the pdf of the state space function to the minimum that it can be, given our demand that no stringent model-driven constraint be placed on the state space geometry. Thus, we use n = 2 in our model.
So now we are ready to express the unknown gravitational mass density function as embedded within the pdf of
 and
and
 as:
as:

using Equation (20). To cast this in the form of Equation (3), we realise that the unknown gravitational mass density function will need to be discretised; we would first discretise the range of values of
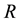 over which the gravitational mass density function
over which the gravitational mass density function
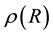 is sought. Let
is sought. Let
 such that
such that
 and let the width of each
and let the width of each
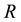 -bin be
-bin be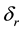 . Then
. Then
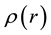 is discretised as the unknown model parameter vector
is discretised as the unknown model parameter vector

where

where .
.
Then following on from Equation (23) we write

This is in line with Equation (3) if we identify the function of the unknown model parameter vector
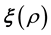 in the RHS of Equation (3) with the unknown gravitational mass density vector
in the RHS of Equation (3) with the unknown gravitational mass density vector . Then the pdf of the state space variables
. Then the pdf of the state space variables
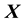 and
and
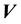 depends of
depends of
 and
and
 and
and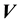 . Then the equivalent of Equation (4) is
. Then the equivalent of Equation (4) is

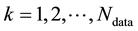 . Then plugging this in the RHS of Equation (1), the likelihood is
. Then plugging this in the RHS of Equation (1), the likelihood is

Then to compute the likelihood and thereafter the posterior probability of
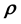 given data
given data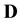 , we will need to compute the integral in Equation (27). According to the general methodology discussed above in Section 3, this is performed by discretising the domain of the pdf of the state space variable, i.e. of
, we will need to compute the integral in Equation (27). According to the general methodology discussed above in Section 3, this is performed by discretising the domain of the pdf of the state space variable, i.e. of . In order to achieve this discretisation we will need to invoke the functional relationship between
. In order to achieve this discretisation we will need to invoke the functional relationship between
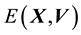 and
and . Next we discuss this.
. Next we discuss this.
5.2. Relationship between E(X,V) and L(X,V)
We recall the physical interpretation of
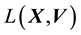 as the norm of the “angular momentum” vector, i.e.
as the norm of the “angular momentum” vector, i.e.

is the square of the speed
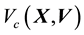 of circular motion of a particle with location
of circular motion of a particle with location
 and velocity
and velocity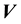 ; here, “circular motion” is motion orthogonal to the location vector
; here, “circular motion” is motion orthogonal to the location vector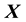 , distinguished from non-circular motion that is parallel to
, distinguished from non-circular motion that is parallel to
 and the speed of which is
and the speed of which is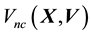 . Then as these two components of motion are mutually orthogonal, square of the particle's speed is
. Then as these two components of motion are mutually orthogonal, square of the particle's speed is

where
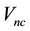 is the magnitude of the component of
is the magnitude of the component of
 that is parallel to
that is parallel to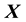 , i.e.
, i.e.

But we recall that energy
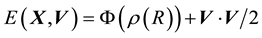 .
.
This implies that

where in the last equation, we invoked the definition of
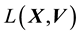 sing Equation (22).
sing Equation (22).
At this stage, to simplify things, we consciously choose to work in the coordinate system in which the vector
 is rotated to vector
is rotated to vector
 by a rotation through angle
by a rotation through angle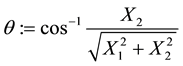 , i.e.
, i.e.

Then by definition,
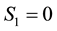 , i.e. the projection of the
, i.e. the projection of the
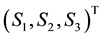 vector on the
vector on the
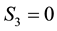 plane lies entirely along the
plane lies entirely along the
 -axis.
-axis.
This rotation does not affect the previous discussion since
・ the previous discussion invokes the location variable either via ,
,
・ or via
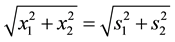 as within the data structure:
as within the data structure:
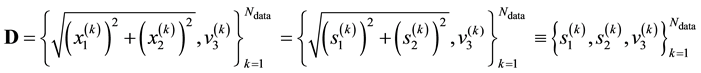 .
.
Having undertaken the rotation, we refer to
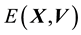 and
and
 as
as
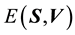 and
and
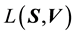 res- pectively.
res- pectively.
This rotation renders the cross-product in the definition of
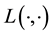 simpler; under this choice of the coordinate system, as
simpler; under this choice of the coordinate system, as


where

so that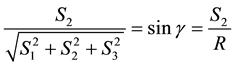 , so that in this rotated coordinate system, from Equation (31)
, so that in this rotated coordinate system, from Equation (31)

Also, the component of
 along the location vector
along the location vector
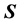 is
is .
.
From Equation (31) it is evident that for a given value
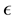 of
of , the highest value
, the highest value
 of
of
 is attained if
is attained if
 (all motion is circular motion). This is realised only when the radius
(all motion is circular motion). This is realised only when the radius
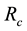 of the circular path of the particle takes a value
of the circular path of the particle takes a value
 such that
such that

The way to compute
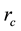 given
given
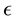 is defined in the literature [38] as the positive definite solution for
is defined in the literature [38] as the positive definite solution for
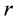 in the equation
in the equation

We are now ready to discretise the domain of the pdf of the state space variable, i.e. of
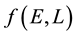 in line with the general methodology discussed above in Section 3 with the aim of computing the integral in Equation (27).
in line with the general methodology discussed above in Section 3 with the aim of computing the integral in Equation (27).
5.3. Discretisation of f(E,L)
We discretise the domain of
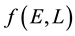 where this 2-dimensional domain is defined by the range of values
where this 2-dimensional domain is defined by the range of values
 and
and , by placing a uniform 2-dimensional rectangular grid over
, by placing a uniform 2-dimensional rectangular grid over
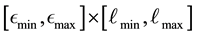 such that the range
such that the range
 is broken into E-bins each
is broken into E-bins each
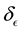 wide and the range
wide and the range
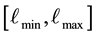 is broken into
is broken into
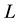 -bins each
-bins each
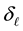 wide. Then each 2-dimensional
wide. Then each 2-dimensional
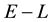 -grid cell has size
-grid cell has size . Then,
. Then,

where the number of E-bins is
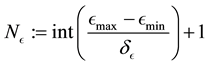 and the number of L-bins is
and the number of L-bins is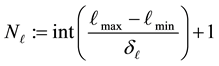 .
.
We then define the
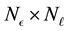 -dimensional matrix
-dimensional matrix

In our model this is the discretised version of the pdf
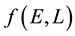 of the state space variable
of the state space variable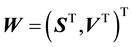 .
.
In this application, a particle with a positive value of energy is so energetic that it escapes from the galaxy. We are however concerned with particles that live inside the galaxy, i.e. are bound to the galaxy and therefore, the maximum energy that a galactic particle can attain is 0, i.e.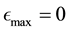 . Given the definition of energy
. Given the definition of energy
 we realise that the value of
we realise that the value of
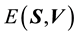 is minimum, i.e. as negative as it can be, if
is minimum, i.e. as negative as it can be, if , (i.e. velocity is zero) and
, (i.e. velocity is zero) and
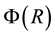 is minimum, which occurs at
is minimum, which occurs at . In other words, the minimum value of
. In other words, the minimum value of
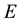 is
is
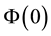 which is negative. In our work we normalise the value
which is negative. In our work we normalise the value
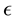 of
of
 by
by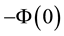 , so that
, so that . In other words, the aforementioned
. In other words, the aforementioned
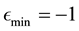 and
and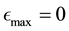 .
.
We normalise the value
 of
of
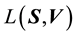 with the maximal value
with the maximal value
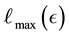 that
that
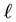 can attain for a given value
can attain for a given value
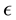 of
of
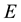 (Equation (36)). The maximum value that can be attained by
(Equation (36)). The maximum value that can be attained by
 is for
is for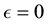 ; having computed
; having computed
 from Equation (37),
from Equation (37),
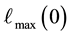 is computed. Then, as normalised by
is computed. Then, as normalised by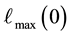 , the maximal value of
, the maximal value of
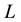 is 1. Also the lowest value of
is 1. Also the lowest value of
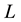 is 0, i.e.
is 0, i.e.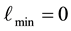 . In light of this, we rewrite Equation (38) as
. In light of this, we rewrite Equation (38) as

The E-binning and L-binning are kept uniform in the application we discuss below, i.e.
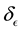 and
and
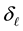 are constants.
are constants.
Data-driven binning
There are
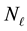 L-bins and
L-bins and
 E-bins. Above we saw that as the range covered by normalised values of
E-bins. Above we saw that as the range covered by normalised values of
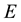 is
is , the relationship between
, the relationship between
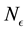 and E-bin width
and E-bin width
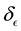 is
is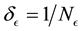 . We make inference on
. We make inference on
 within our inference scheme while the Physics of the situation drives us to a value of
within our inference scheme while the Physics of the situation drives us to a value of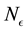 . It could have been possible to also learn
. It could have been possible to also learn
 from the data within our inference scheme but that would have been tantamount to wastage of information that is available from the domain of application.
from the data within our inference scheme but that would have been tantamount to wastage of information that is available from the domain of application.
We attempt to learn
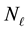 from the data within our inference scheme; for a given
from the data within our inference scheme; for a given ,
,
 is fixed by the data at hand. To understand this, we recall the aforementioned relation
is fixed by the data at hand. To understand this, we recall the aforementioned relation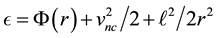 . Let in the available data set,
. Let in the available data set,
1) the minimum value of
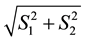 be
be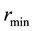 ,
,
2) the maximum value of
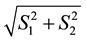 be
be
 so that the value of
so that the value of
 is no less than
is no less than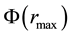 ,
,
3) the maximum value of
 be
be
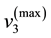 so that the unnormalised value of
so that the unnormalised value of
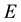 is no less than
is no less than

4) and the unnormalised
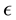 is no more than
is no more than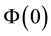 .
.
Thus, it is clear that the E-binning should cover the interval beginning at a normalised value of −1 and should at least extend to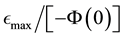 .
.
Then we set E-bin width
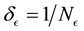 and learn number of L-bins,
and learn number of L-bins,
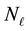 , from the data within our inference scheme. Then at any iteration, for the current value of
, from the data within our inference scheme. Then at any iteration, for the current value of
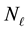 and the current
and the current
 (which leads to the current value of
(which leads to the current value of
 according to Equation (16)), placing
according to Equation (16)), placing
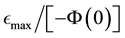 at the centre of the
at the centre of the
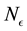 -th E-bin gives us
-th E-bin gives us

i.e.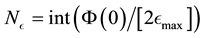 .
.
Experiments suggest that for typical galactic data sets,
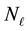 between 5 and 10 implies convergence in the learnt vectorised form of the gravitational mass density
between 5 and 10 implies convergence in the learnt vectorised form of the gravitational mass density . This leads us to choose a discrete uniform prior over the set
. This leads us to choose a discrete uniform prior over the set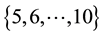 , for
, for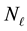 :
:
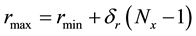
Again, the minimum and maximum values of
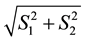 in the data fix
in the data fix
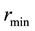 and
and
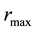 respectively, so that
respectively, so that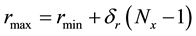 . The radial bin width
. The radial bin width
 is entirely dictated by the data distribution such that there is at least 1 data vector in each radial bin. Thus,
is entirely dictated by the data distribution such that there is at least 1 data vector in each radial bin. Thus,
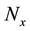 and
and
 are not parameters to be learnt within the inference scheme but are directly determined by the data.
are not parameters to be learnt within the inference scheme but are directly determined by the data.
5.4. Likelihood
Following Equation (7), we express the likelihood in this application in terms of the pdf of
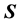 and
and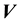 , marginalised over all those variables that we do not have any observed information on. Then for the data vector
, marginalised over all those variables that we do not have any observed information on. Then for the data vector , the marginal pdf is
, the marginal pdf is

where
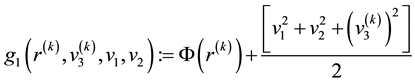
 ,
,
with
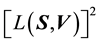 recalled from Equation 33, and we have used
recalled from Equation 33, and we have used

and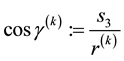 .
.
Then given that the range of values of
 and
and
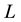 is discretised, we write
is discretised, we write

where
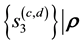 refer to the values taken by
refer to the values taken by
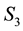 for a given
for a given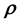 , inside the cd-th
, inside the cd-th
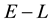 -grid-cell. Similarly,
-grid-cell. Similarly,
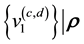 and
and
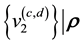 refer to the values of
refer to the values of
 and
and
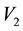 inside the cd-th
inside the cd-th
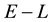 -grid-cell respectively, given
-grid-cell respectively, given .
.
Indexing the values of any of the unobserved variables in this grid-cell as conditional on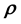 , is explained as follows.
, is explained as follows.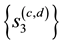 ,
,
 and
and
 are determined by the mapping between the space of
are determined by the mapping between the space of
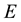 and
and
 and the space of the unobservables, namely
and the space of the unobservables, namely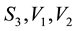 . This mapping involves the definition of
. This mapping involves the definition of
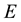 and
and
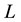 in terms of the state space coordinates
in terms of the state space coordinates , which in turn depends upon the function
, which in turn depends upon the function
 or its discretised version,
or its discretised version,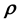 . Hence the values taken by any of the 3 unobservables in the cd-th
. Hence the values taken by any of the 3 unobservables in the cd-th
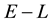 -grid-cell depend on
-grid-cell depend on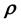 . Here
. Here
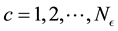 and
and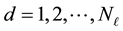 .
.
We realise that the integral on the RHS of Equation (45) represents the volume occupied by the
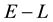 - grid-cell inside the space of the unobserved variables. The computation of this volume is now discussed.
- grid-cell inside the space of the unobserved variables. The computation of this volume is now discussed.
5.5. Volume of any E-L-grid-cell in terms of the unobservables
We begin by considering the volume of any
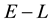 -grid-cell in the space of the 2 observables,
-grid-cell in the space of the 2 observables,
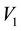 and
and , at a given value of
, at a given value of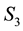 . Thereafter, we will consider the values of the 3rd unobservable,
. Thereafter, we will consider the values of the 3rd unobservable,
 , in this grid-cell.
, in this grid-cell.
The definition
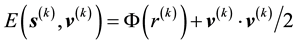 (Equation refeqn:ljhamela) implies that for the k-th data vector
(Equation refeqn:ljhamela) implies that for the k-th data vector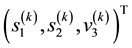 , all particles with
, all particles with
 and energy
and energy
 will obey the equation
will obey the equation

i.e. for , all particles lying in the c-th E-bin will lie in the space of
, all particles lying in the c-th E-bin will lie in the space of
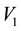 and
and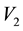 , within a circular annulus that is centred at (0,0) and has radii lying in the interval
, within a circular annulus that is centred at (0,0) and has radii lying in the interval
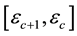 where
where

For , the definition
, the definition
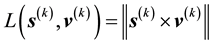 provides a representation for all particles in the d-th L-bin with given observed values of
provides a representation for all particles in the d-th L-bin with given observed values of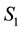 ,
,
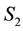 and
and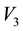 .
.
It then follows from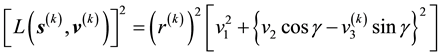 , (Equation (33)) that for the k-th
, (Equation (33)) that for the k-th
data vector, all particles with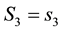 , and in the d-th L-bin
, and in the d-th L-bin
 will obey the equation
will obey the equation

where we have recalled
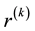 from Equation (44). This implies that for
from Equation (44). This implies that for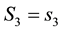 , all particles lying in the d-th L-bin, will lie in the space of
, all particles lying in the d-th L-bin, will lie in the space of
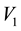 and
and , along an ellipse centred at
, along an ellipse centred at
 with semi-minor axis
with semi-minor axis
lying in the interval of
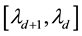 and semi-major axis lying in the interval
and semi-major axis lying in the interval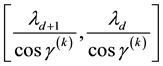 . Here,
. Here,

Collating the implications of Equation (46) and Equation (48), we get that at a given value of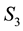 , particles with observed data
, particles with observed data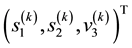 , (with energies) in the c-th E-bin and (momenta) in the d-th L-bin will lie in the space of
, (with energies) in the c-th E-bin and (momenta) in the d-th L-bin will lie in the space of
 and
and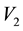 , within an area bound by the overlap of
, within an area bound by the overlap of
1) the circular annular region centred at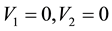 , extending in radii between
, extending in radii between
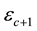 and
and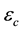 .
.
2) the elliptical annular region centred at , extending in semi-minor between
, extending in semi-minor between
 and
and
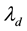 and semi-major axis in
and semi-major axis in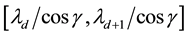 , where
, where
 .
.
The area of these overlapping annular regions represents the volume of the cd-th
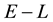 -grid-cell in the space of
-grid-cell in the space of
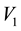 and
and , at the value
, at the value
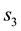 of
of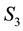 . Thus, the first step towards writing the volume of the cd-th
. Thus, the first step towards writing the volume of the cd-th
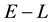 - grid-cell in terms of the unobservables, is to compute the area of these overlapping annular regions in the space of
- grid-cell in terms of the unobservables, is to compute the area of these overlapping annular regions in the space of
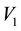 and
and . Such an area of overlap is a function of
. Such an area of overlap is a function of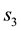 . At the next step, we integrate such an area over all allowed
. At the next step, we integrate such an area over all allowed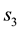 , to recover the volume of the cd-th
, to recover the volume of the cd-th
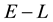 -grid-cell in the space of
-grid-cell in the space of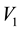 ,
,
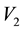 and
and , i.e. the integral on the RHS of Equation (45).
, i.e. the integral on the RHS of Equation (45).
There can be multiple ways these annular regions overlap; three examples of these distinct overlapping geometries are displayed in Figure 1. In each such geometry, it is possible to compute the area of this region of overlap since we know the equations of the curves that bound the area. However, the number of possible geometries of overlap is in excess of 20 and identifying the particular geometry to then compute the area of overlap in each such case, is tedious to code. In place of this, we allow for a numerical computation of the area of overlap; this method works irrespective of the particulars of the geometry of overlap. We identify the maximum and minimum values of
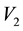 allowed at a given value of
allowed at a given value of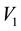 , having known the equations to the bounding curves, and compute the area of overlap in the plane of
, having known the equations to the bounding curves, and compute the area of overlap in the plane of
 and
and
 using numerical integration.
using numerical integration.
This area of overlap in the plane defined by
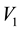 and
and
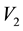 is a function of
is a function of
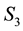 since the equations of the bounding curves are expressed in terms of
since the equations of the bounding curves are expressed in terms of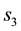 . The area of overlap is then integrated over all values that
. The area of overlap is then integrated over all values that
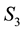 is permitted to take inside the cd-th
is permitted to take inside the cd-th
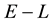 -grid-cell. For any
-grid-cell. For any
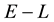 -grid-cell, the lowest value
-grid-cell, the lowest value
 can take is zero. For
can take is zero. For , and
, and , the maximum value of
, the maximum value of
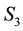 is realised (by recalling Equation (35)) as the solution to the equation
is realised (by recalling Equation (35)) as the solution to the equation

where
 is the projection of
is the projection of
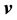 along the
along the
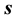 vector (discussed in Section 5.2). Thus,
vector (discussed in Section 5.2). Thus,
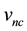 is given by the inner product of
is given by the inner product of
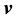 and the unit vector parallel to
and the unit vector parallel to :
:


Figure 1. Figure showing 3 of the many ways of overlap between the contours drawn in the space of V1 and V2, at neighbouring values of E (the circular contours in red) and at neighbouring values of L (the elliptical contours in black).
where

Using this in Equation (50) we get

This implies that given the observations represented by the k-th data vector

The highest positive root for




So now we have the value of the integral over












5.6. Normalisation of the marginal pdf of the state space vector
As we see from Equation (45), the marginal pdf of











where the possible values of







5.7. Incorporating measurement uncertainties
Following Equation (8) the likelihood is defined as the product over all data, of the convolution of the error distribution at the k-th datum and value of the marginalised pdf for this








For any other distribution of the uncertainties in the measurement of

5.8. Priors
In the existing astronomical literature, there is nothing to suggest the pdf of the state space variable in a real galaxy though there are theoretical models of the functional dependence between stellar energy (E) and angular momentum (L) and pdf of










As far as priors on the gravitational mass density are concerned, astronomical models are available [38]. All such models suggest that gravitational mass density is a monotonically decreasing function of


i.e.








5.9. Posterior
Given the data, we use Bayes rule to write down the joint posterior probability density of


where we used


constant and therefore can be subsumed into the constant of proportionality that defines the above relation.
We marginalise







(recalling Equation (57)). Integrating this term over a fixed interval of vales of









We discuss the implemented inference next.
6. Inference
We intend to make inference on each component of the vector













First we discuss performing inference on


It is on the parameters







where the choice of a folded normal [47] or truncated normal proposal density is preferred over a density that achieves zero probability mass at the variable value of 0. This is because there is a non-zero probability for the gravitational mass density to be zero in a given radial bin. Here







We choose the folded normal proposal density given its ease of computation:

It is evident that this is a symmetric proposal density. We discuss the acceptance criterion in this standard Metropolis-Hastings scheme, after discussing the proposal density of the components of the matrix


If





Along similar lines, we make inference directly on

Let in the n-th iteration, the current value of



proposed candidate is sampled from the folded normal density


is again the empirical variance of the chain between the





We propose



where the bounds of the interval

Given that we are making inference on the



RHS of Equation (59).
Then given that the proposal densities that components of





where the uniform random variable
7. Illustration on synthetic data
In this section we illustrate the methodology on synthetic data set simulated from a chosen models for the pdf of





where





values. From these 2 chosen pdfs,







Figure 2. Left: gravitational mass density parameters learnt using synthetic data sets














Figure 3. Left: Trace of the joint posterior probability density of all the unknowns, given the synthetic data sets





8. Illustration on real data
In this section we present the gravitational mass density parameters and the state space pdf parameters learnt for the real galaxy NGC3379 using 2 data sets













9. Discussions
In this work we focused on an inverse problem in which noisy and partially missing data on the measurable






























The distribution of the gravitational mass in the system is indicated by the function
the discretised form of this function defines the parameters




Figure 4. Left: The left panel represents the
























learnt gravitational mass density function might give an erroneous indication of how much gravitational mass there is in this galaxy and of corse how that mass is distributed. It may be remarked that in lieu of such prior knowledge about the topology of the system state space, it is best to consider the least constrained of models for the state space pdf, i.e. to consider this pdf to be dependent on both


It is also to be noted that the estimate for the gravitational mass density in the real galaxy NGC3379 appears to depend crucially on which data set is being implemented in the estimation exercise. It is possible that the underlying pdf of the variable



References
- V. Jugnon and L. Demanet, “Interferometric Inversion: A Robust Approach to Linear Inverse Problems,” In: J. M. Bernardo, J. O. Berger, A. P. Dawid and A. F. M. Smith, Eds., Proceedings of SEG Annual Meeting, Houston, September 2013, pp. 5180-5184.
- P. Qui, “A Nonparametric Procedure for Blind Image Deblurring,” Computational Statistics and Data Analysis, Vol. 52, No. 10, 2008, pp. 4828-4842. http://dx.doi.org/10.1016/j.csda.2008.03.027
- M. Bertero and P. Boccacci, “Introduction to Inverse Problems in Imaging,” Taylor and Francis. 1998. http://dx.doi.org/10.1887/0750304359
- P. Kutchment, “Generalised Transforms of the Radon Type and Their Applications,” In: G. Olafsson and E. T. Quinto, Eds., The Radon Transform, Inverse Problems, and Tomography, Vol. 63, American Mathematical Society, 2006, p. 67. http://dx.doi.org/10.1090/psapm/063/2208237
- T. E. Bishop, S. D. Babacan, B. Amizik, A. K. Katsaggelos, T. Chan and R. Molina, “Blind Image Deconvolution: Problem Formulation and Existing Approaches,” In: P. Campisi and K. Egiazarian, Eds., Blind Image Deconvolution: Theory and Ap- plications, CRC Press, Boca Raton, 2007, pp. 1-41
- R. L. Parker, “Geophysical Inverse Theory,” Princeton series in Geophysics, Princeton University Press, Princeton, 1994.
- A. Tarantola, “Inverse Problem Theory and Methods for Model Parameter Estimation,” SIAM, Philadelphia. 2005. http://dx.doi.org/10.1137/1.9780898717921
- A. M. Stuart, “Bayesian Approach to Inverse Problems,” provides an introduction to the forthcoming book Bayesian Inverse Problems in Differential Equations by M. Dashti, M. Hairer and A. M. Stuart, 2013. available at arXiv:math/1302.6989.
- A. M. Stuart, “Inverse Problems: A Bayesian Perspective,” Cambridge University Press, Acta Numerica, Vol. 19, 2010, pp. 451-559. http://dx.doi.org/10.1017/S0962492910000061
- D. Draper and B. Mendes, “Bayesian Environmetrics: Uncertainty and Sensitivity Analysis and Inverse Problems,” 2008. http://users.soe.ucsc.edu/~draper/draper-brisbane-2008.pdf
- A. F. Bennett and P. C. McIntosh, “Open Ocean Modeling as an Inverse Problem: Tidal Theory,” Journal of Physical Oceano- graphy, Vol. 12, No. 10, 1982, pp. 1004-1018. http://dx.doi.org/10.1175/1520-0485(1982)012<1004:OOMAAI>2.0.CO;2
- W. P. Gouveia and J. A. Scales, “Bayesian Seismic Waveform Inversion: Parameter Estimation and Uncertainty Analysis,” Journal of Geophysical Research, Vol. 130, No. B2, 1998, pp. 2759-2779. http://dx.doi.org/10.1029/97JB02933
- S. Strebelle, “Conditional Simulation of Complex Geological Structures Using Multiple-Point Statistics,” Mathematical Geol- ogy, Vol. 34, No. 1, 2002, pp. 1-21. http://dx.doi.org/10.1023/A:1014009426274
- J. Caers, “Geostatistical Reservoir Modelling Using Statistical Pattern Recognition,” Journal of Petroleum Science and Engi- neering, Vol. 29, No. 3-4, 2001, pp. 177-188. http://dx.doi.org/10.1016/S0920-4105(01)00088-2
- M. J. Way, J. D. Scargle, K. M. Ali and A. N. Srivastava, “Advances in Machine Learning and Data Mining for Astronomy,” Data Mining and Knowledge Discovery Series, Chapman and Hall/CRC, Boca Raton, 2012.
- Y. Liu, A. Harding, W. Abriel and S. Strebelle, “Multiple-Point Simulation Integrating Wells, Three-Dimensional Seismic Data, And Geology,” AAPG Bulletin, Vol. 88, No. 7, 2004, pp. 905-921. http://dx.doi.org/10.1306/02170403078
- M. Henrion, D. Mortlock, D. Hand and A. Gandy, “Classification and Anomaly Detection for Astronomical Survey Data,” In: J. M. Hilbe, Ed., Astrostatistical Challenges for the New Astronomy, Springer, Berlin, 2013, pp. 149-184.
- V. M. Krasnopolsky, M. Fox-Rabinovitz and D. V. Chalikov, “New Approach to Calculation of Atmospheric Model Physics: Accurate and Fast Neural Network Emulation of Longwave Radiation in a Climate Model,” Monthly Weather Review, Vol. 133, No. 5, 2004, pp. 1370-1383. http://dx.doi.org/10.1175/MWR2923.1
- C. E. Rasmussen and C. K. I. Williams, “Gaussian Processes for Machine Learning,” The MIT Press, New York, 2006.
- G. Tilmann, K. William and S. Martin, “Matern Cross-Covariance Functions for Multivariate Random Fields,” Journal of the American Statistical Association, Vol. 105, No. 491, 2010, pp. 1167-1177. http://dx.doi.org/10.1198/jasa.2010.tm09420
- D. Chakrabarty, F. Rigat, N. Gabrielyan, R. Beanland and S. paul, “Bayesian Density Estimation via Multiple Sequential In- versions of 2-D Images with Application in Electron Microscopy,” Technical Report, Submitted 2013.
- C. J. Paciorek, M. J. Schervish, “Spatial Modelling Using a New Class of Nonstationary Covariance Functions,” Environme- trics, Vol. 17, No. 5, 2006, pp. 483-506. http://dx.doi.org/10.1002/env.785
- D. Chakrabarty, M. Biswas, S. Bhattacharya, “Bayesian Learning of Milky Way Parameters Using New Matrix-Variate Gaus- sian Process-based Method,” Technical Report, Submitted 2013.
- M. West and P. Harrison, “Bayesian Forecasting and Dynamic Models,” Springer-Verlag, New York, 1997.
- A. Pole, M. West and P. Harrison, “Applied Bayesian Forecasting and Time Series Analysis,” Texts in Statistical Science, Taylor and Francis, New York, 1994.
- A. Harvey, S. J. Koopman and N. Shephard, “State Space and Unobserved Component Models: Theory and Applications,” Cambridge University Press, Cambridge, 2012.
- B. P. Carlin, N. G. Polson and D. S. Stoffer, “A Monte Carlo Approach to Nonnormal and Nonlinear State-Space Modeling,” Journal of the American Statistical Association, Vol. 87, No. 418, 1992, pp. 493-500. http://dx.doi.org/10.1080/01621459.1992.10475231
- A. J. Winship, S. J. Jorgensen, S. A. Shaffer, I. D. Jonsen, P. W. Robinson, D. P. Costa and B. A. Block, “State-Space Frame- work for Estimating Measurement Error from Double-Tagging Telemetry Experiments,” Methods in Ecology and Evolution, Vol. 3, No. 2, 2012, pp. 291-302. http://dx.doi.org/10.1111/j.2041-210X.2011.00161.x
- J. Knape, N. Jonzen, M. Skold and L. Sokolov, “Multivariate State Space Modelling of Bird Migration Count Data,” In: D. L. Thompson, E. G. Gooch and M. J. Conroy, Eds., Modeling Demographic Processes in Marked Populations, Springer, Berlin, 2009.
- S. Pellegrini and L. Ciotti, “Reconciling Optical and X-Ray Mass Estimates: The Case of the Elliptical Galaxy NGC3379,” Monthly Notices of the Royal Astronomical Society, Vol. 370, No. 4, 2006, pp. 1797-1803. http://dx.doi.org/10.1111/j.1365-2966.2006.10590.x
- L. Coccato, O. Gerhard, M. Arnaboldi, et al., “Kinematic Properties of Early-Type Galaxy Haloes Using Planetary Nebulae,” Monthly Notices of the Royal Astronomical Society, Vol. 394, No. 3, 2009, pp. 1249-1283. http://dx.doi.org/10.1111/j.1365-2966.2009.14417.x
- P. Côté, D. E. McLaughlin, J. G. Cohen and J. P. Blakeslee, “Dynamics of the Globular Cluster System Associated with M49 (NGC4472): Cluster Orbital Properties and the Distribution of Dark Matter,” Astrophysical Journal, Vol. 591, No. 2, 2003, pp. 850-877. http://dx.doi.org/10.1086/375488
- A. J. Romanowsky, N. G. Douglas, M. Arnaboldi, K. Kuijken, M. R. Merrifield, N. R. Napolitano, M. Capaccioli and K. C. Freeman, “A Dearth of Dark Matter in Ordinary Elliptical Galaxies,” Science, Vol. 301, No. 5640, 2003, pp. 1696-1698. http://dx.doi.org/10.1126/science.1087441
- D. Chakrabarty, “Inverse Look at the Center of M15,” Astronomical Journal, Vol. 131, No. 5, 2006, pp. 2561-2570. http://dx.doi.org/10.1086/501433
- D. Chakrabarty and S. Raychaudhury, “The Distribution of Dark Matter in the Halo of the Early-Type Galaxy NGC 4636,” Astronomical Journal, Vol. 135, No. 6, 2008, pp. 2350-2357. http://dx.doi.org/10.1088/0004-6256/135/6/2350
- L. V. E. Koopmans, “Gravitational Lensing & Stellar Dynamics,” European Astronomical Society Publications Series, Vol. 20, 2006, pp. 161-166. http://dx.doi.org/10.1051/eas:2006064
- D. Chakrabarty and B. Jackson, “Total Mass Distributions of Sersic Galaxies from Photometry and Central Velocity Disper- sion,” Astronomy and Astrophysics, Vol. 498, No. 2, 2009, pp. 615-626. http://dx.doi.org/10.1051/0004-6361/200809965
- J. R. Binney and S. Tremaine, “Galactic Dynamics,” Princeton University Press, Princeton, 1987.
- G. Contopoulos, “A Classification of the Integrals of Motion,” Astrophysical Journal, Vol. 138, 1963, pp. 1297-1305. http://dx.doi.org/10.1086/147724
- J. R. Binney, “Dynamics of Elliptical Galaxies and Other Spheroidal Components,” Annual Review of Astronomy and Astro- physics, Vol. 20, 1982, pp. 399-429. http://dx.doi.org/10.1146/annurev.aa.20.090182.002151
- I. S. Liu, “Continuum Mechanics,” Springer-Verlag, New York, 2002.
- C. Truesdell, W. Noll and S. S. Antman, “The Non-Linear Field Theories of Mechanics,” Volume 3, Springer-Verlag, New York, 2004. http://dx.doi.org/10.1007/978-3-662-10388-3
- C. C. Wang, “On Representations for Isotropic Functions,” Archive for Rational Mechanics and Analysis, Vol. 33, No. 4, 1969, pp. 249-267. http://dx.doi.org/10.1007/BF00281278
- J. F. Navarro, C. S. Frenk and S. D. M. White, “The Structure of Cold Dark Matter Halos,” Astrophysical Journal, Vol. 462, 1996, p. 563. http://dx.doi.org/10.1086/177173
- W. J. G. de Blok, A. Bosma and S. McGaugh, “Simulating Observations of Dark Matter Dominated Galaxies: Towards the Optimal Halo Profile,” Monthly Notices of the Royal Astronomical Soc, Vol. 340, No. 2, 2003, pp. 657-678. http://dx.doi.org/10.1046/j.1365-8711.2003.06330.x
- H. Haario, M. Laine, A. Mira and E. Saksman, “DRAM: Efficient Adaptive MCMC,” Statistics and Computing Vol. 16, No. 4, 2006, pp. 339-354. http://dx.doi.org/10.1007/s11222-006-9438-0
- F. C. Leone, R. B. Nottingham and L. S. Nelson, “The Folded Normal Distribution,” Technometrics, Vol. 3, No. 4, 1961, pp. 543. http://dx.doi.org/10.1080/00401706.1961.10489974
- N. G. Douglas, N. R. Napolitano, A. J. Romanowsky, L. Coccato, K. Kuijken, M. R. Merrifield, M. Arnaboldi, O. Gerhard, K. C. Freeman, H. Merrett, E. Noordermeer and M. Capaccioli, “The PN.S Elliptical Galaxy Survey: Data Reduction, Planetary Nebula Catalog, and Basic Dynamics for NGC 3379,” Astrophysical Journal, Vol. 664, No. 1, 2007, pp. 257-276. http://dx.doi.org/10.1086/518358
- G. Bergond, S. E. Zepf, A. J. Romanowsky, R. M. Sharples and K. L. Rhode, “Wide-Field Kinematics of Globular Clusters in the Leo I Group,” Astronomy & Astrophysics, Vol. 448, No. 1, 2006, pp. 155-164. http://dx.doi.org/10.1051/0004-6361:20053697
NOTES

*Corresponding author.

1We assume that (the system is Hamiltonian so that) the gravitational potential of the galaxy is independent of velocities and depend only on location; since gravitational potential is uniquely determined for a given system geometry, by the gravitational mass density (via Poisson Equation), the latter too is dependent only on X.

2To be precise, the state space pdf should be written as a function of integrals of motion, which remain constant along the trajectory from one point in W to another, during the motion.

