American Journal of Computational Mathematics
Vol.3 No.4(2013), Article ID:39765,21 pages DOI:10.4236/ajcm.2013.34037
On the Rate of Convergence of Some New Modified Iterative Schemes
Department of Mathematics, M.D.U, Rohtak, India
Email: *sanjay.sanju84@gmail.com
Copyright © 2013 Renu Chugh, Sanjay Kumar. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 2, 2013; revised October 2, 2013; accepted October 9, 2013
Keywords: Metric Space; New Modified Ishikawa; New Modified Agarwal et al.; New Modified SP; New Modified Noor
ABSTRACT
In this article, following Bizare and Amriteimoori [1] and B. Parsad and R. Sahni [2], we modify Ishikawa, Agarwal et al., Noor, SP iterative schemes and compare the rate of convergence of Ishikawa, Agarwal et al., Noor, SP and new modified Ishikawa, Agarwal et al., Noor, SP iterative schemes not only for particular fixed value of 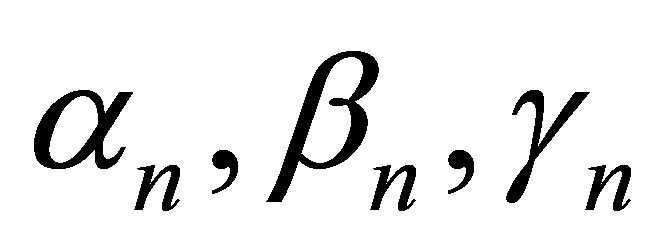 but also for varying the value of
but also for varying the value of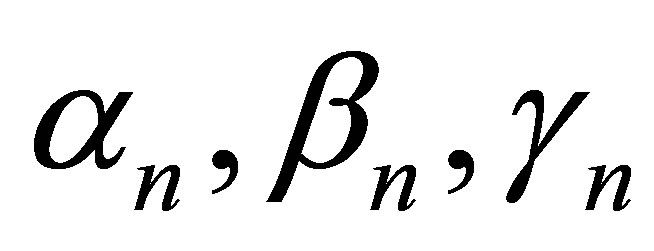 . With the help of two numerical examples, we compare the converging step.
. With the help of two numerical examples, we compare the converging step.
1. Introduction
Let X be a complete metric space and T be self map, then 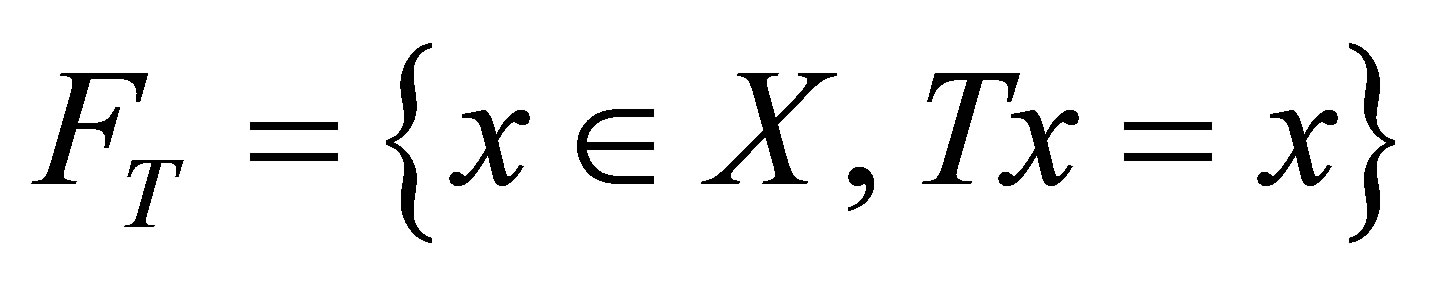 is called set of fixed points of T. Now in literature, there are several iteration processes to find the fixed point of any equation. In complete metric space, Picard iteration process is defined as
is called set of fixed points of T. Now in literature, there are several iteration processes to find the fixed point of any equation. In complete metric space, Picard iteration process is defined as
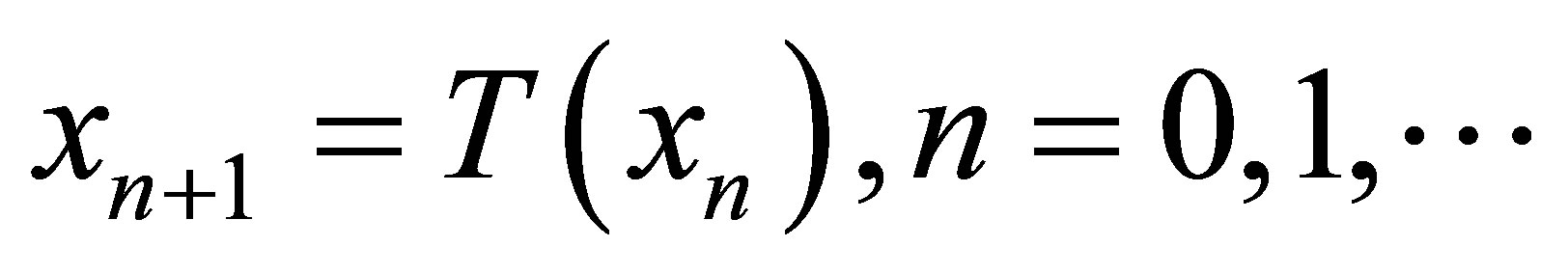
which is used to approximate fixed points of mappings satisfying the condition
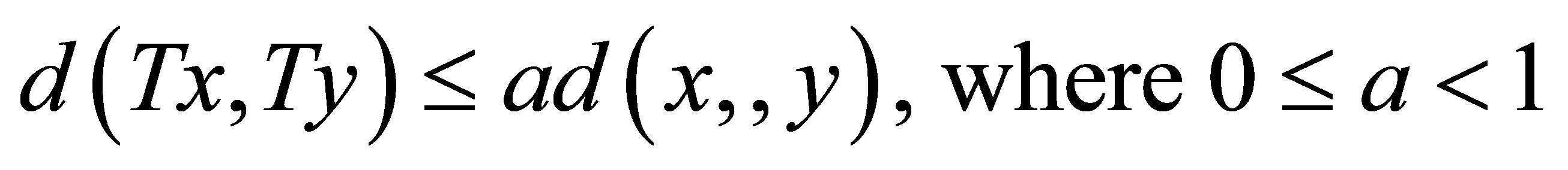
called Banach contraction condition.
In Ishikawa iteration process [3], 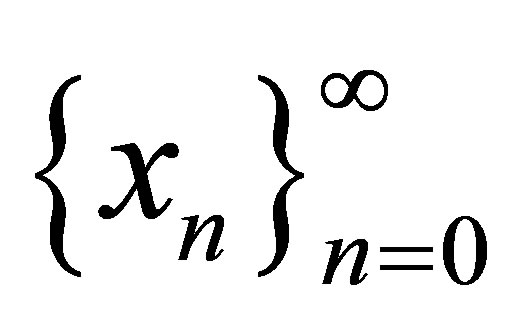 is defined as
is defined as
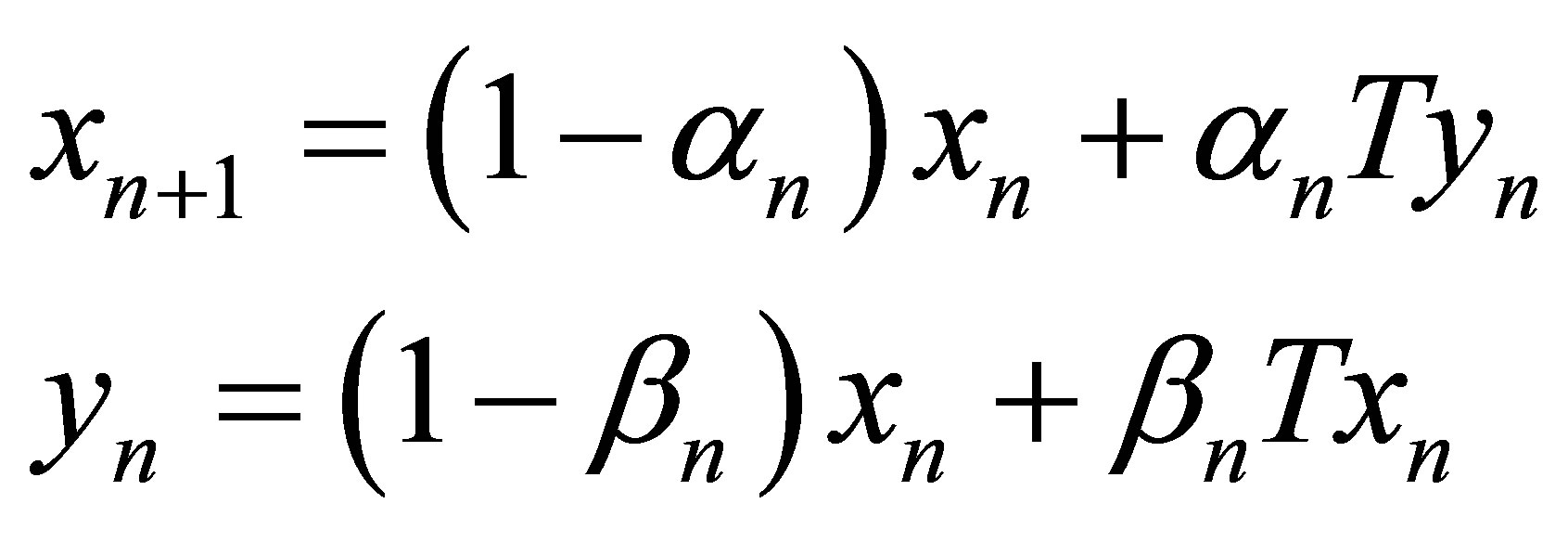
where 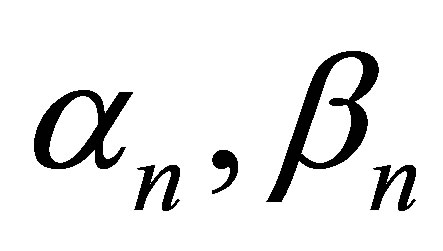 are real sequences in [0,1].
are real sequences in [0,1].
Now for Agarwal et al. iteration [4], 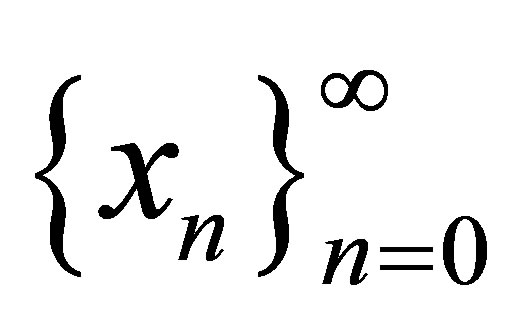 is defined as
is defined as
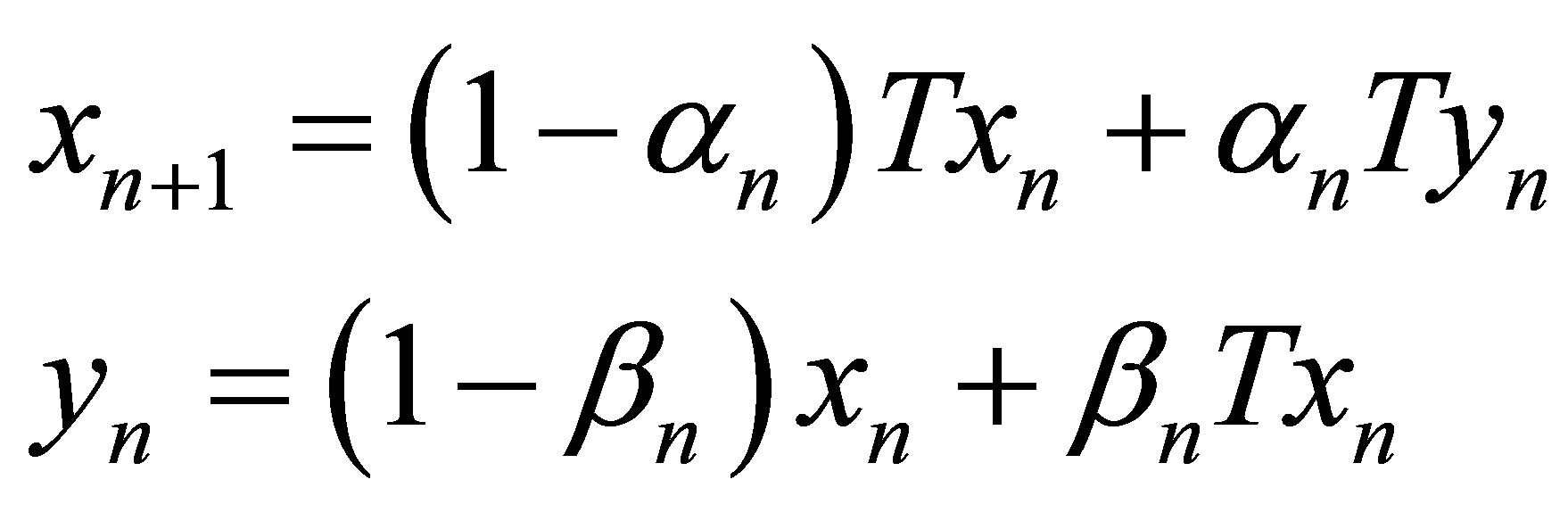
where 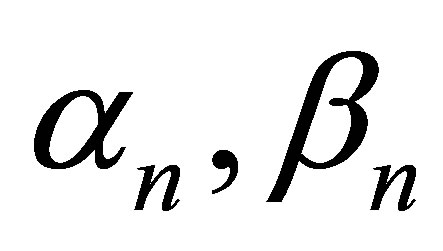 are real sequences in [0,1].
are real sequences in [0,1].
M. A. Noor defines [5] 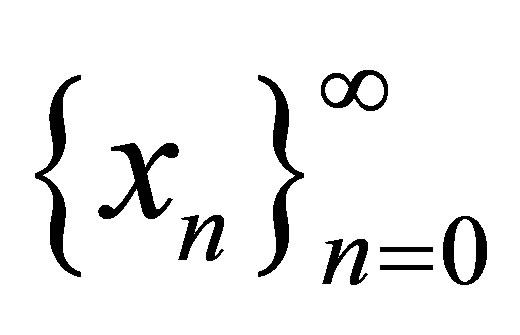 as
as
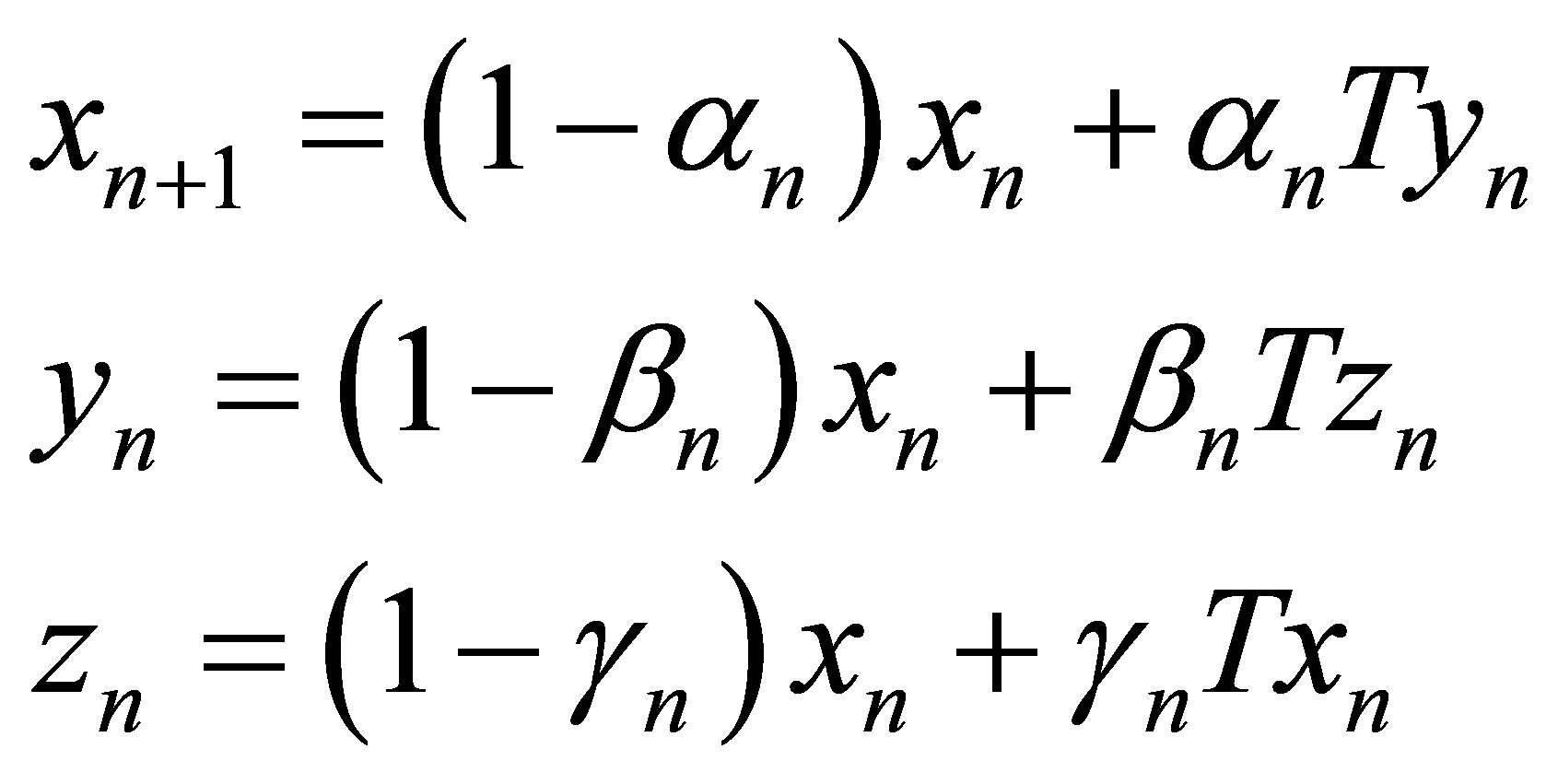
where  are real sequences in [0,1].
are real sequences in [0,1].
For SP iteration [6]  is defined as
is defined as
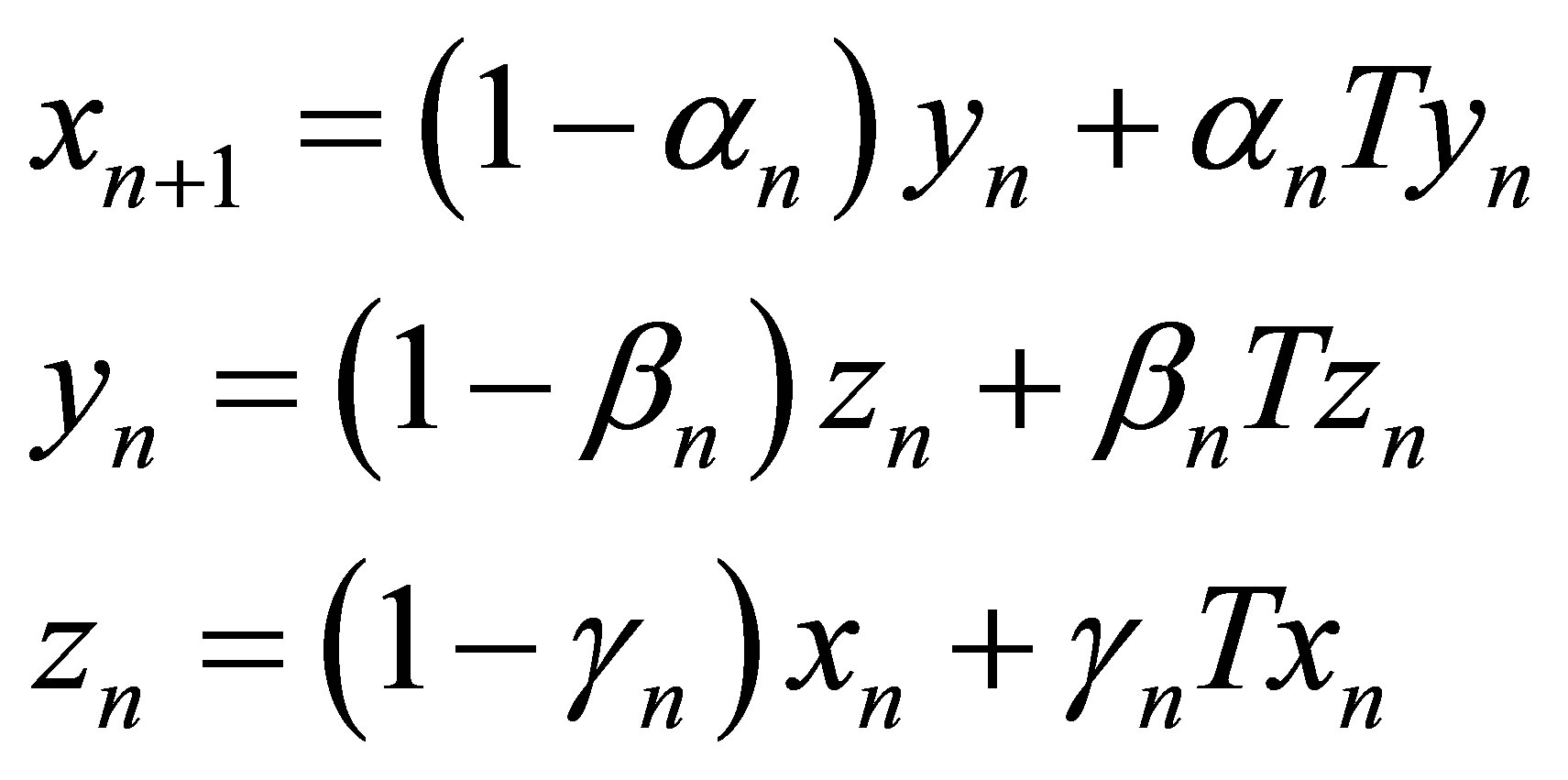
where 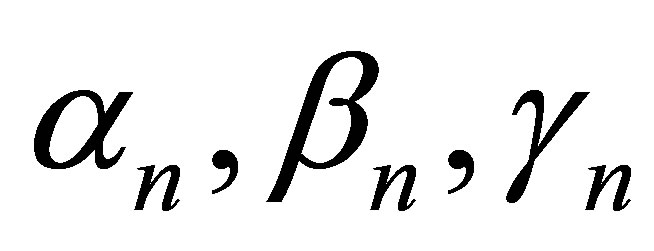 are real sequences in [0,1].
are real sequences in [0,1].
2. Preliminaries
In this paper following Bizare and Amriteimoori [1] and B. Parsad and R. Sahni [2] we prove the basic results in sequel. In [1] Bizare and Amriteimoori improved the picard iteration under following conditions:
1) Initial approximation is chosen in the interval [a, b], where function is defined.
2) Function has continuous derivative on (a, b).
3) 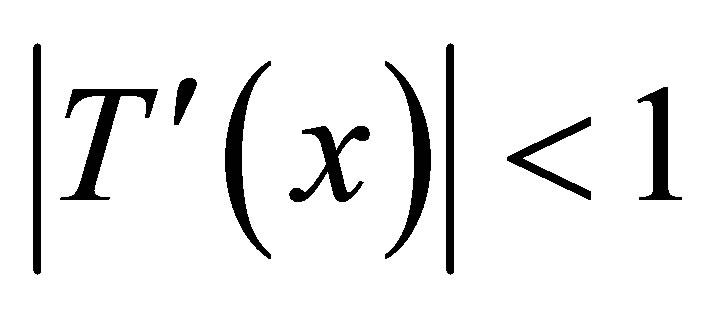 for all
for all 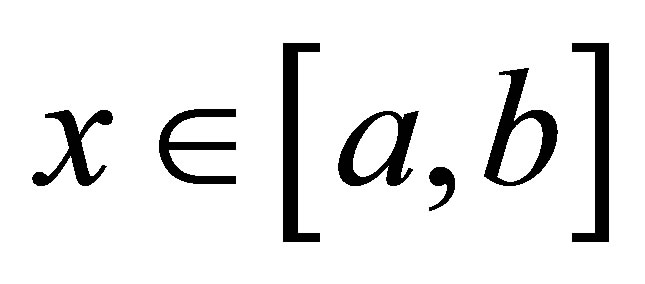
4) 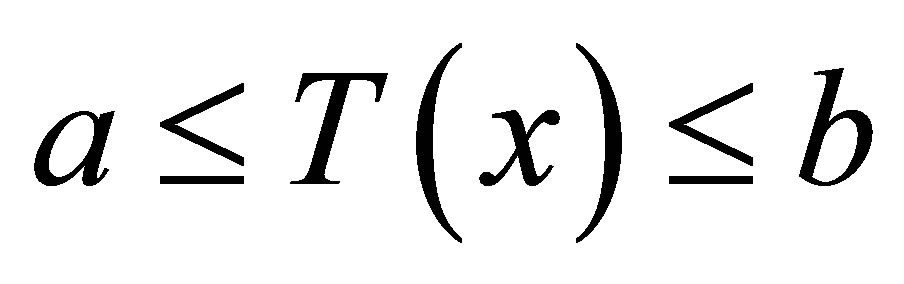 for all
for all 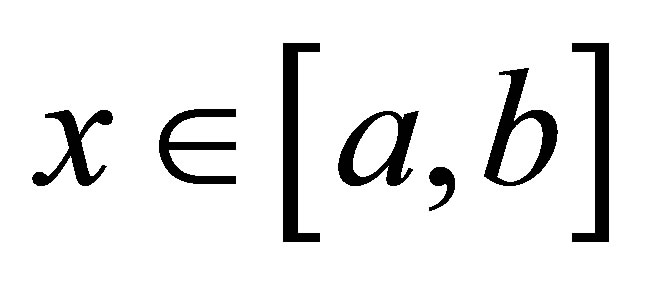
Definition 2.1 [1]. Let 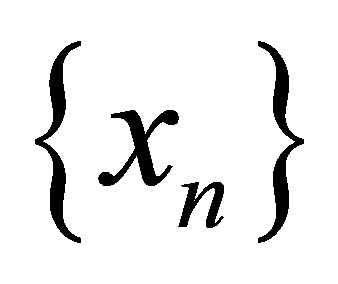 converges to α. If there exists an integer constant q and a real +ve constant C such that
converges to α. If there exists an integer constant q and a real +ve constant C such that
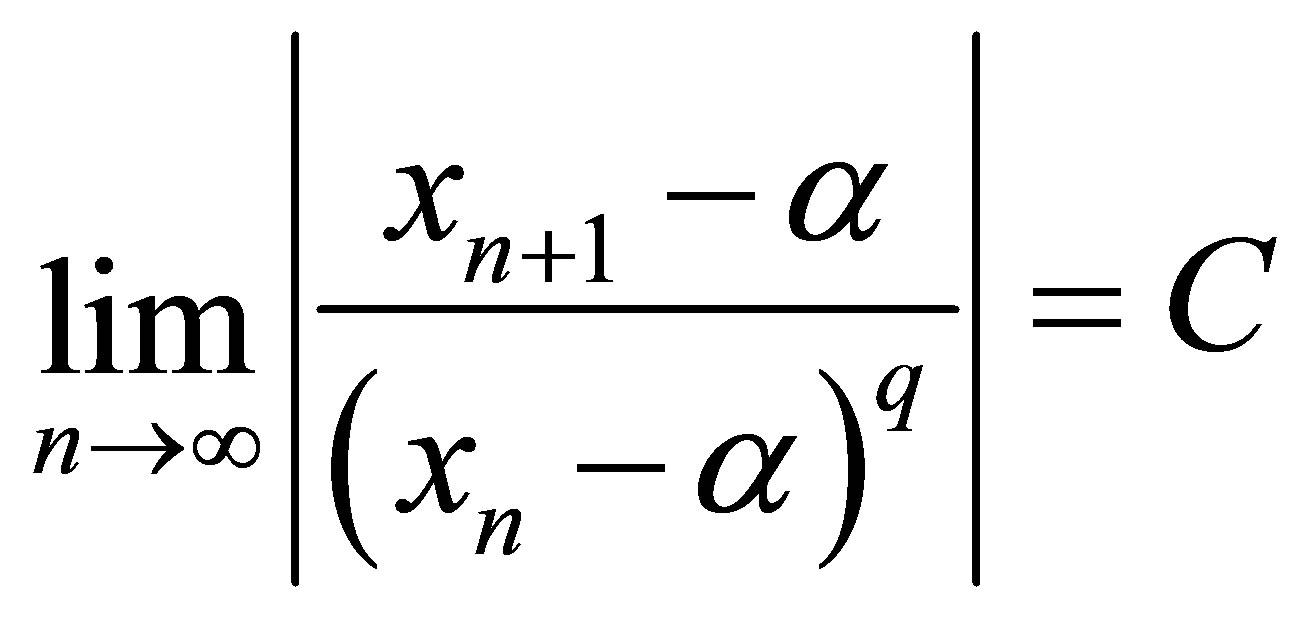
q is called order and C is called constant of convergence
Theorem 2.2([1,7]). Let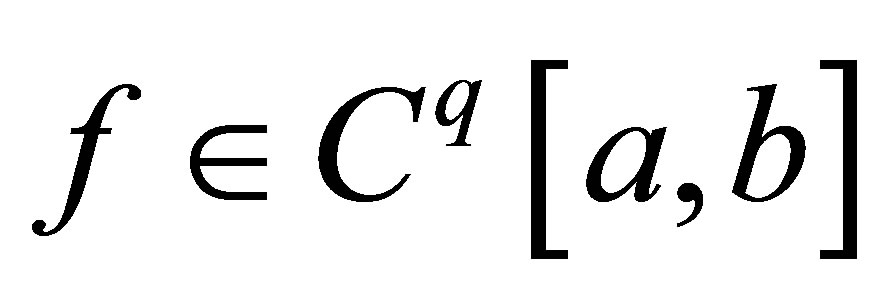 , if
, if 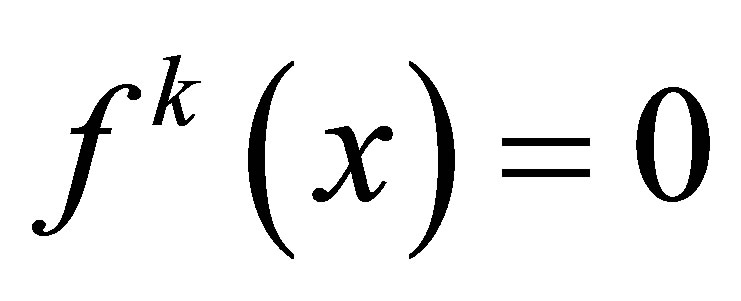 for
for 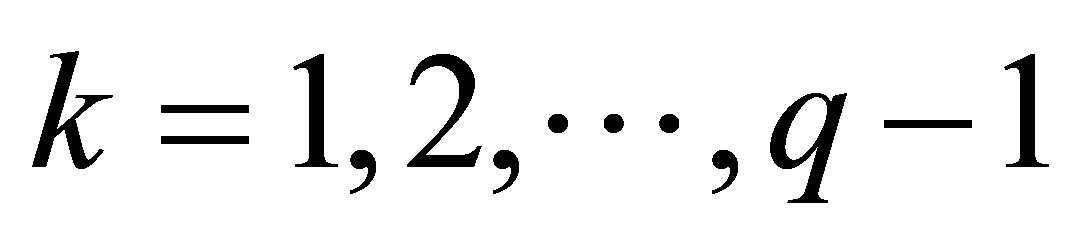 and
and 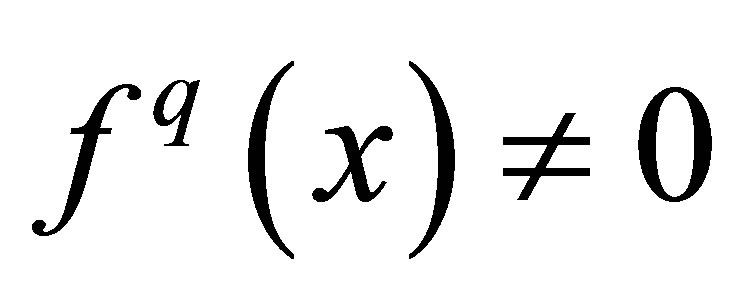 then sequence
then sequence 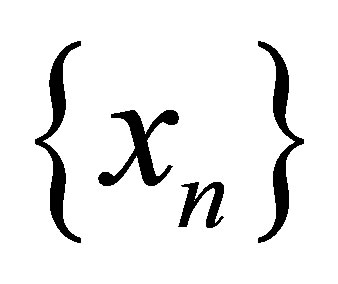 is of order q.
is of order q.
To improve the order of convergence of fixed iterative schemes, such that
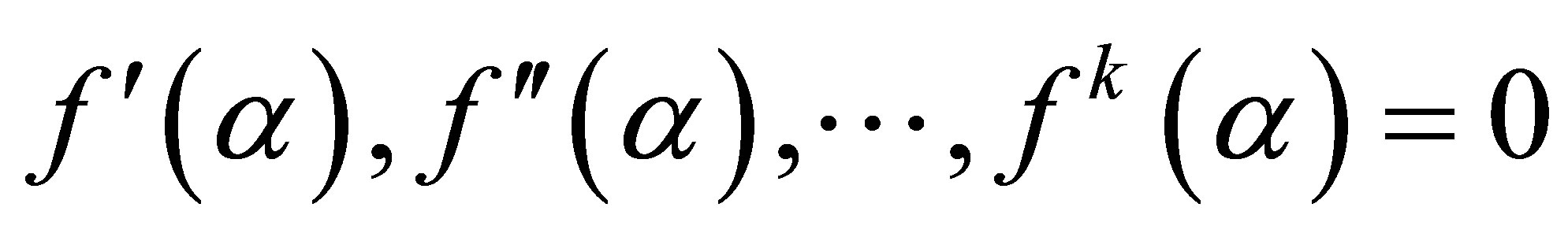 . We determines
. We determines 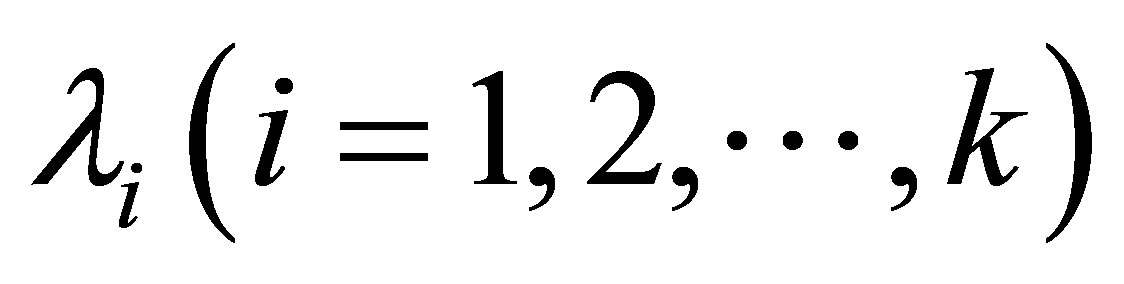 from the following equation
from the following equation
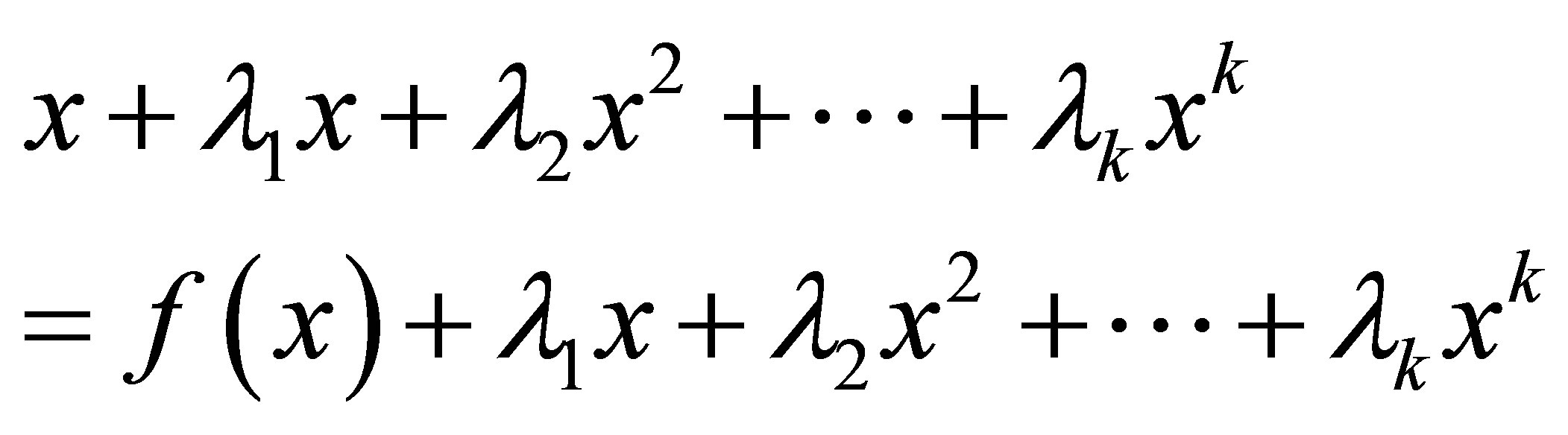
which becomes
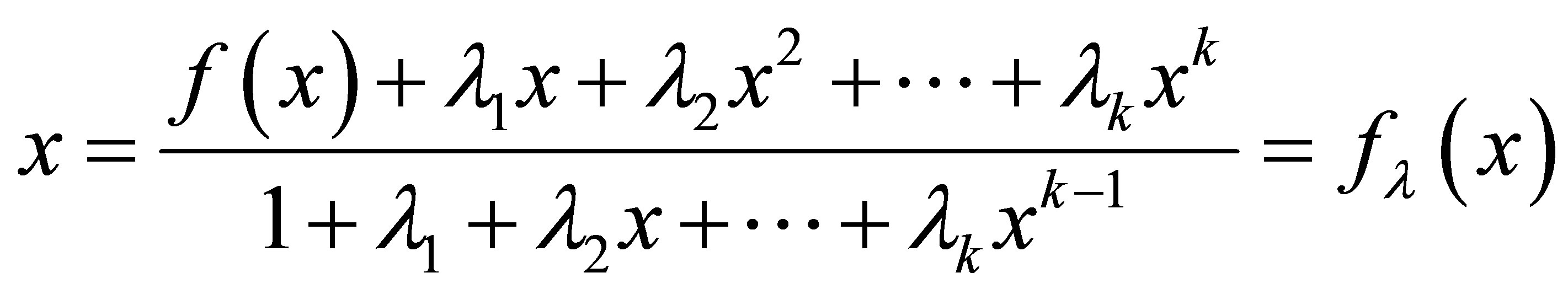 this is fixed point equation form .Now the assumption that
this is fixed point equation form .Now the assumption that 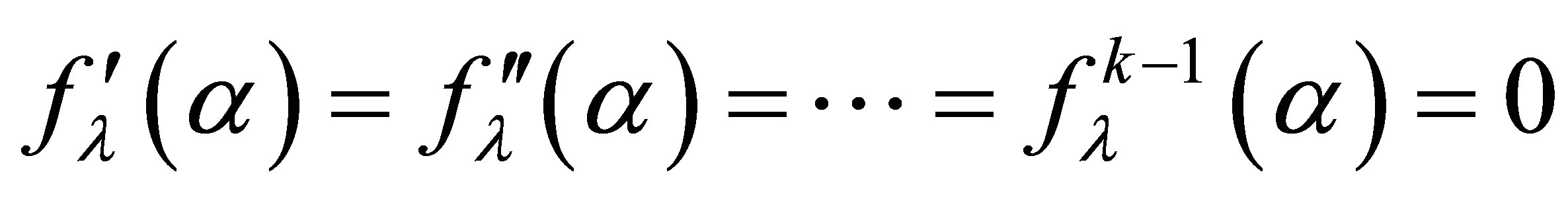 yields to a system of linear equations which after solving [1] converted into upper triangular matrix which have nonzero diagonal entries. It means determinant is nonzero. So we determine
yields to a system of linear equations which after solving [1] converted into upper triangular matrix which have nonzero diagonal entries. It means determinant is nonzero. So we determine 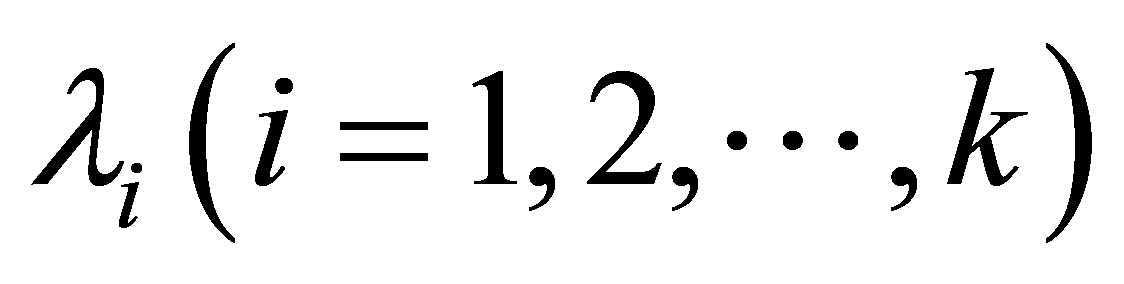 uniquely.
uniquely.
Now the new Picard iteration becomes
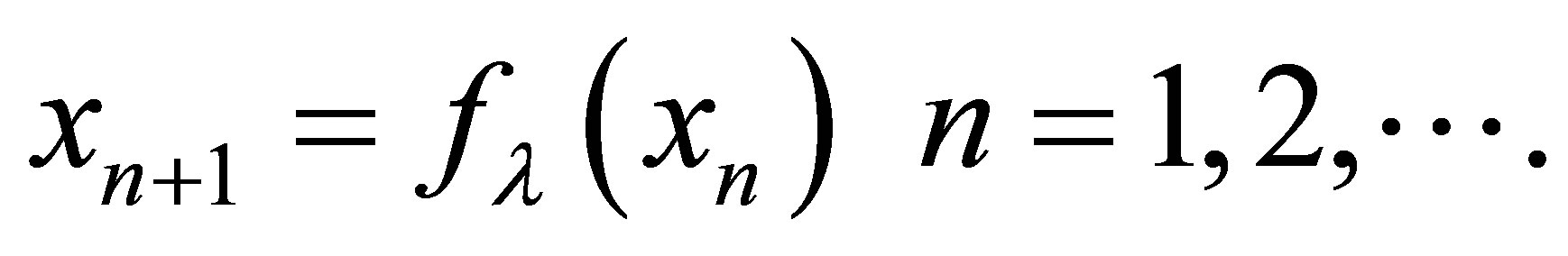 (1)
(1)
where
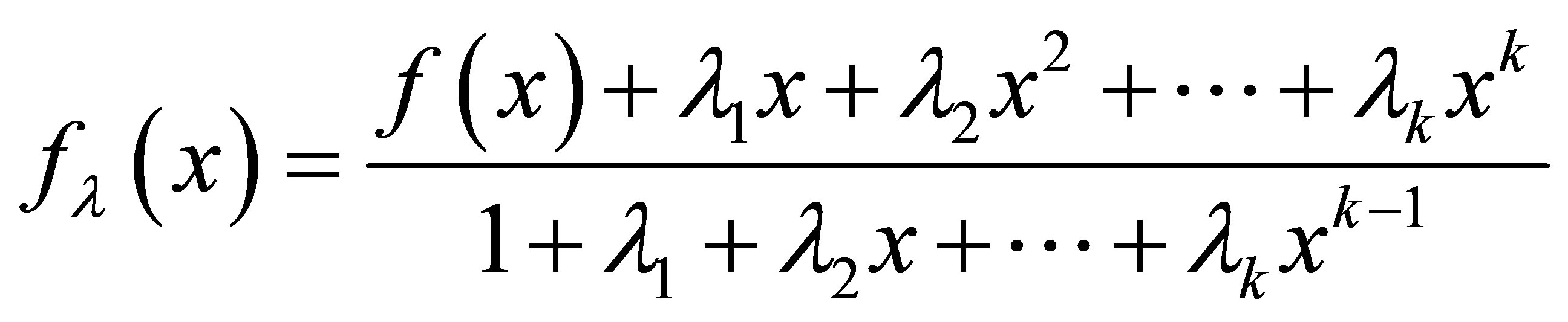 (2)
(2)
Following Bhagwati Parsad and Ritu Shani [2] the new modified Ishikawa, Agarwal et al., Noor, SP iterations are defined as:
New modified Ishikawa iteration scheme
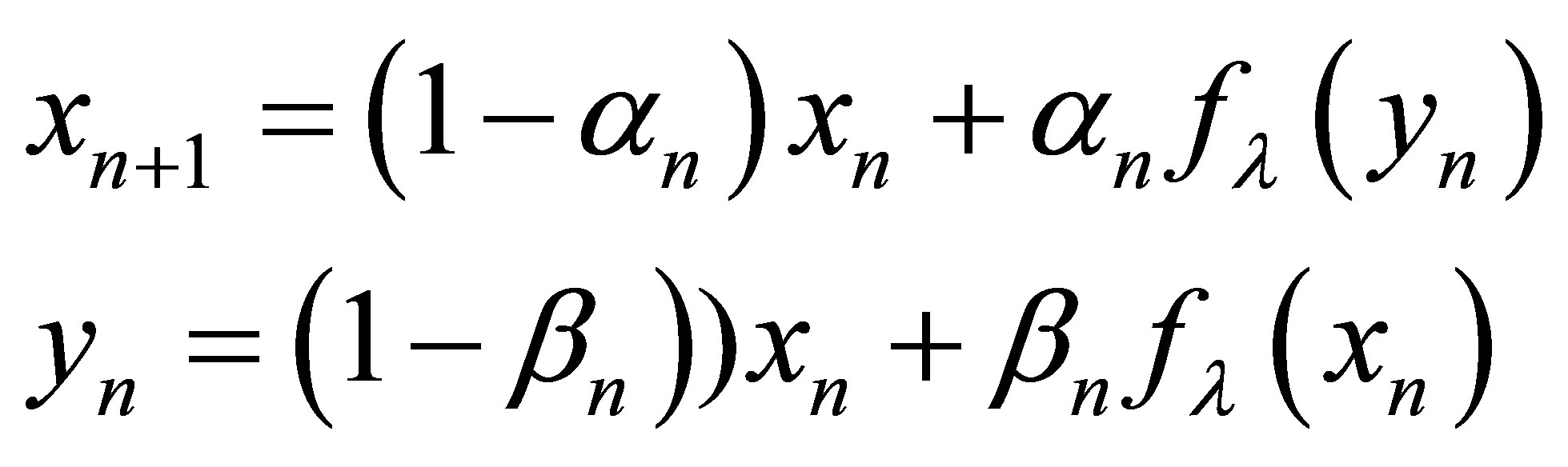 (3)
(3)
New modified Agarwal et al. iteration scheme
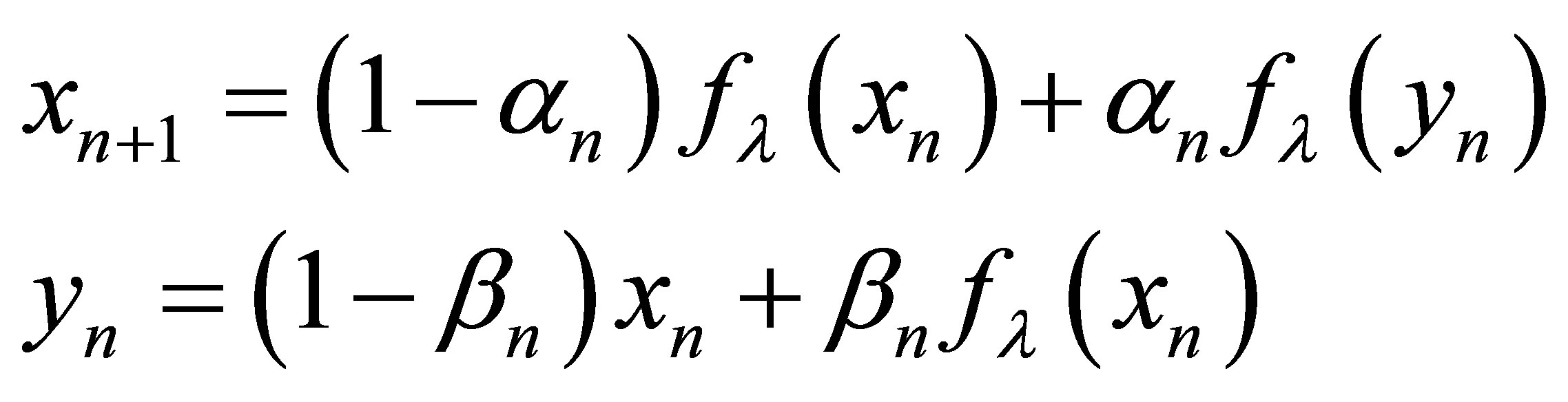 (4)
(4)
New modified Noor iteration scheme
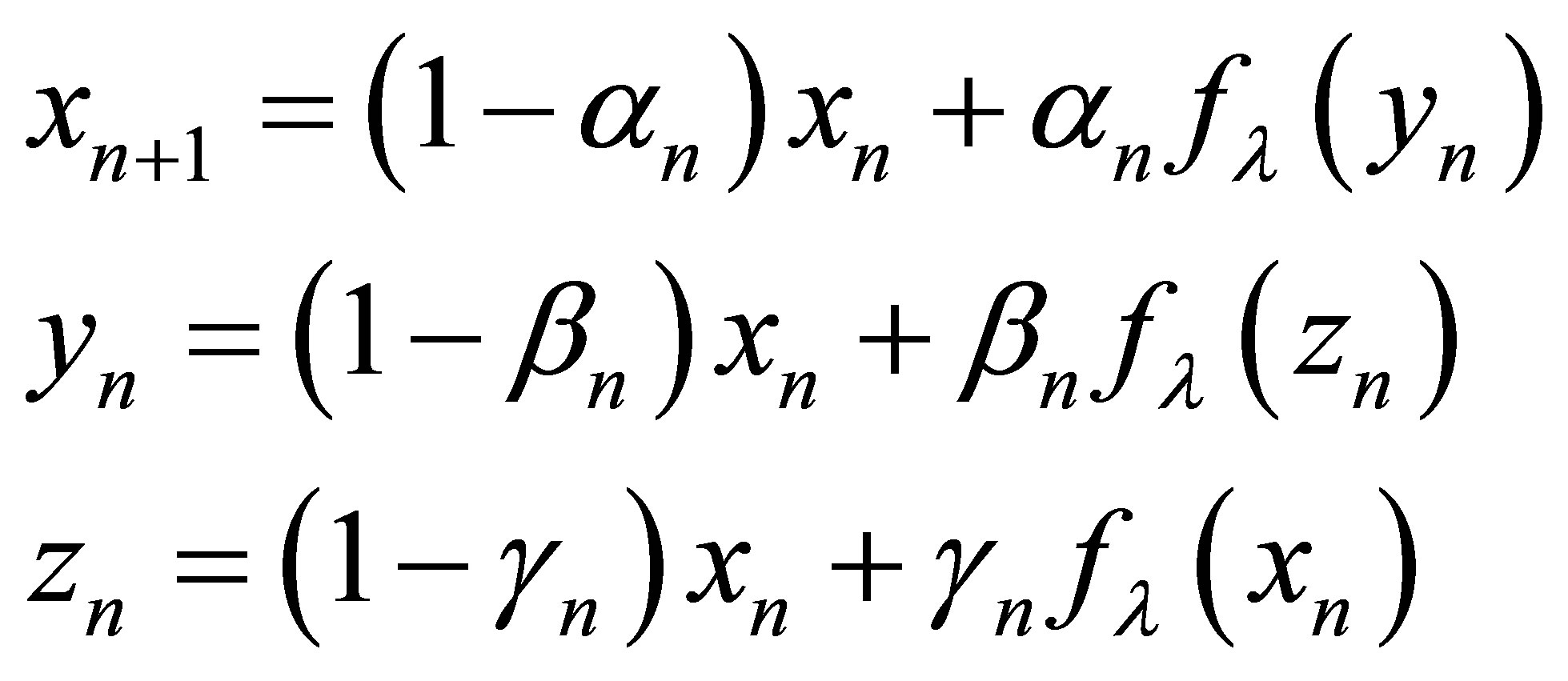 (5)
(5)
New modified SP iteration scheme
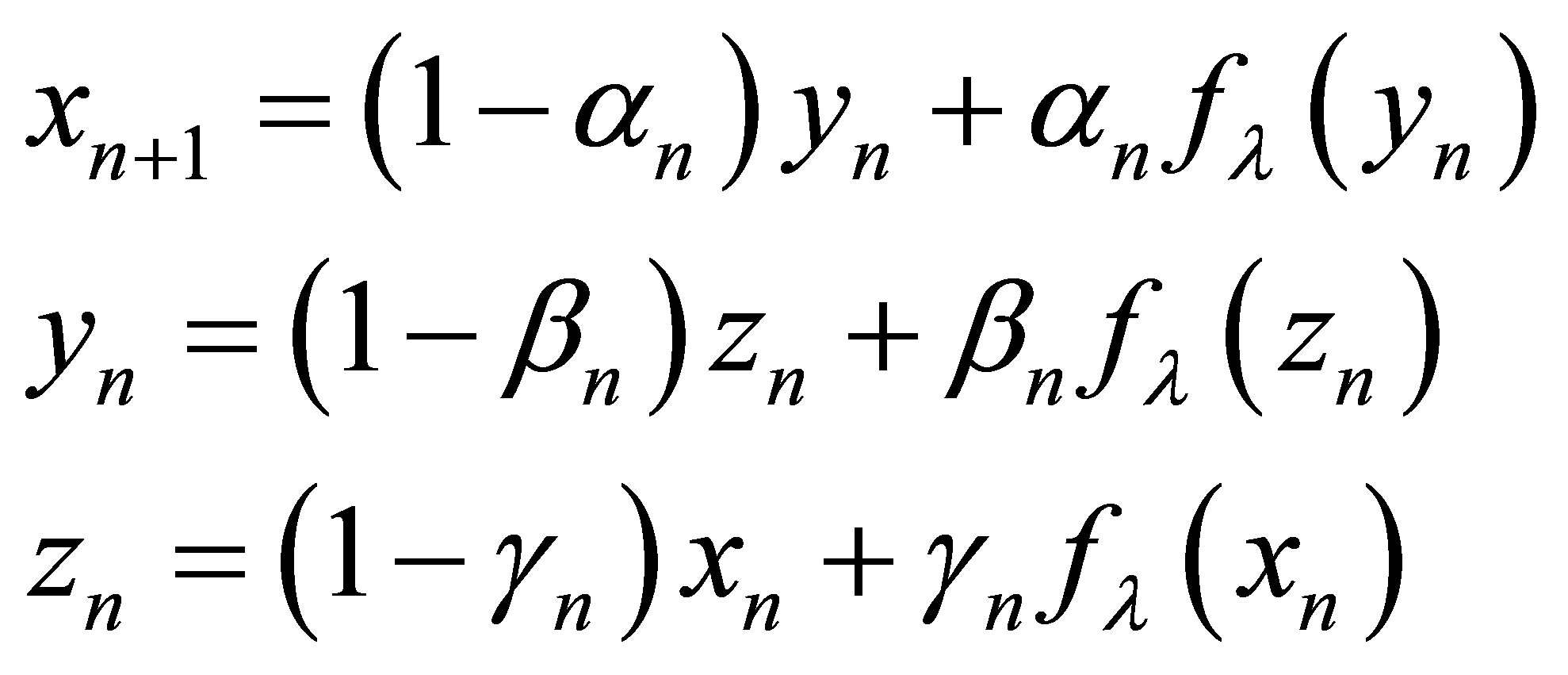 (6)
(6)
where 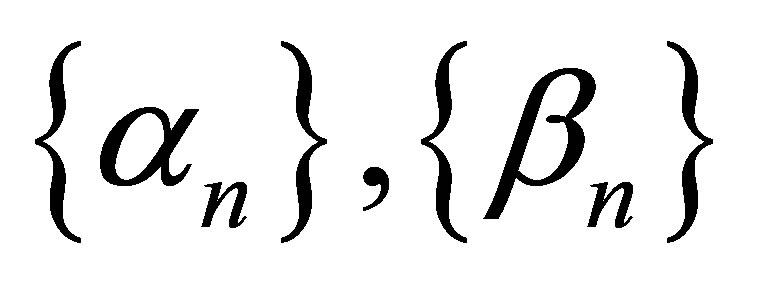 and
and 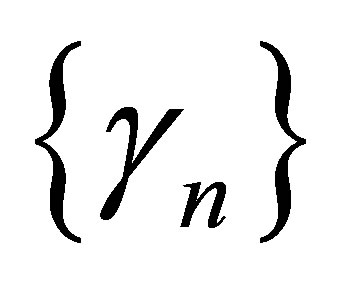 are real sequences in [0, 1].
are real sequences in [0, 1].
In this article, we compare the rate of convergence of new modified iterative schemes and simple iterative schemes with the help of the following examples
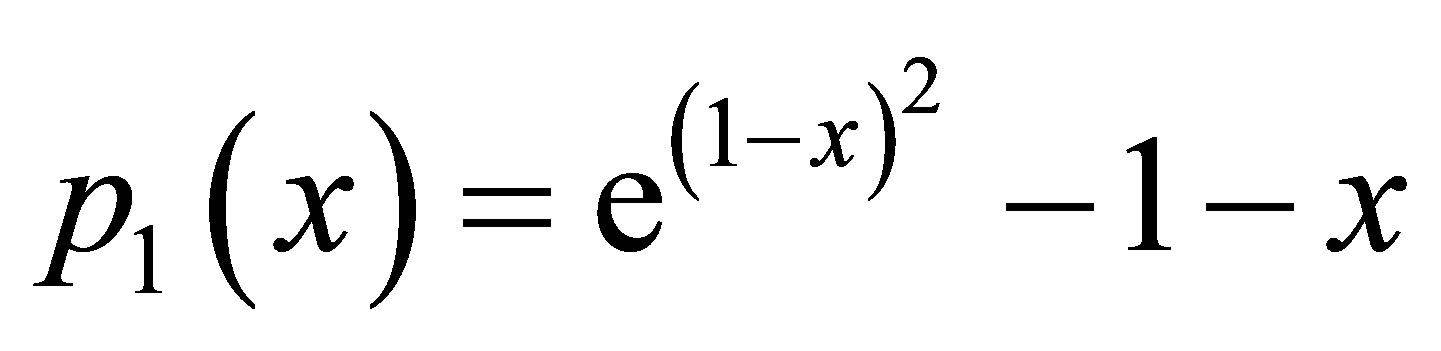 (7)
(7)
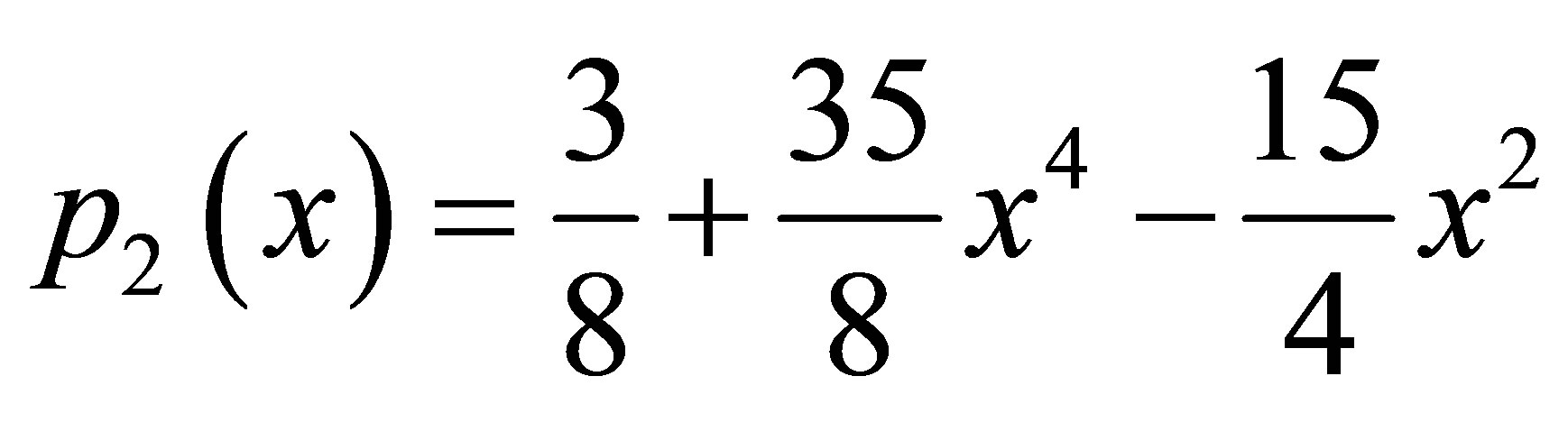 (8)
(8)
To find the fixed point we write 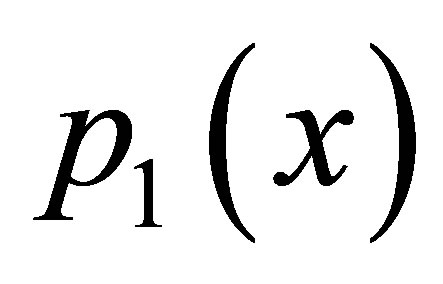 and
and 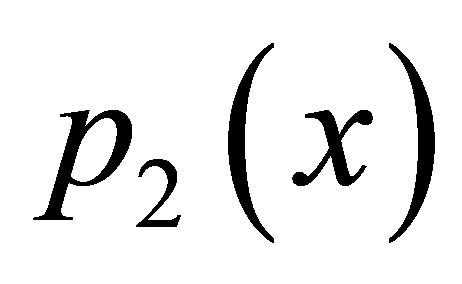 as
as
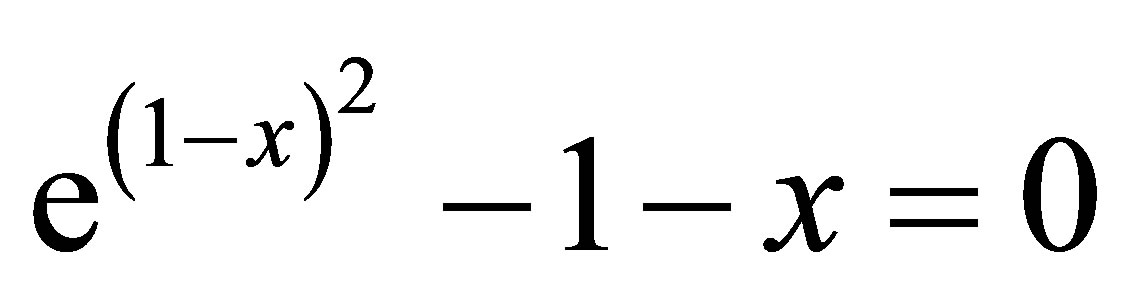 and
and 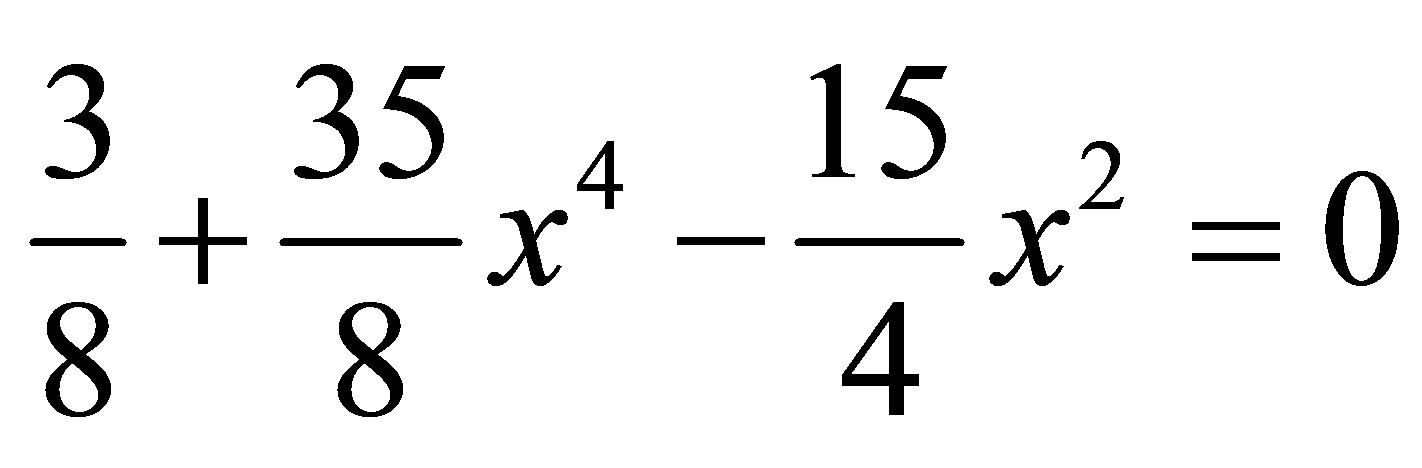
both equations has unique root in the interval (0,1) so we convert this in the fixed point form
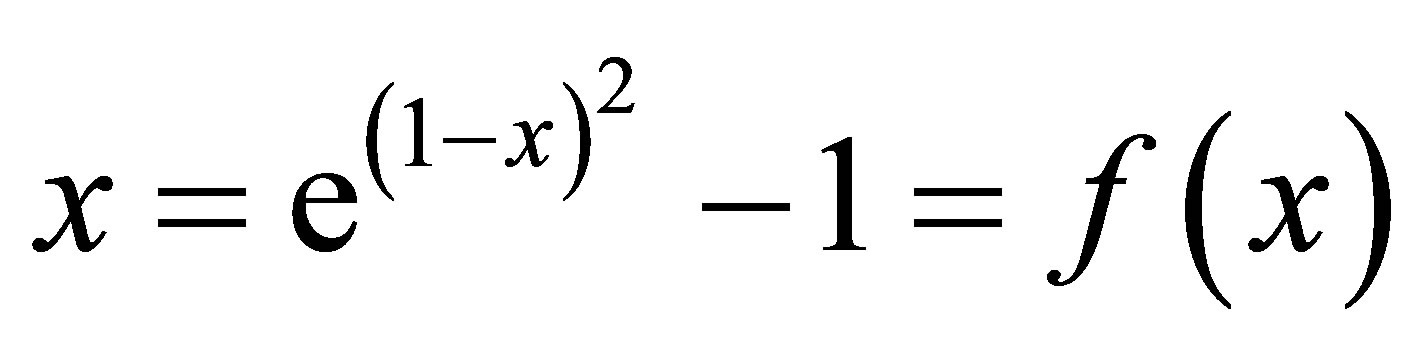 and
and 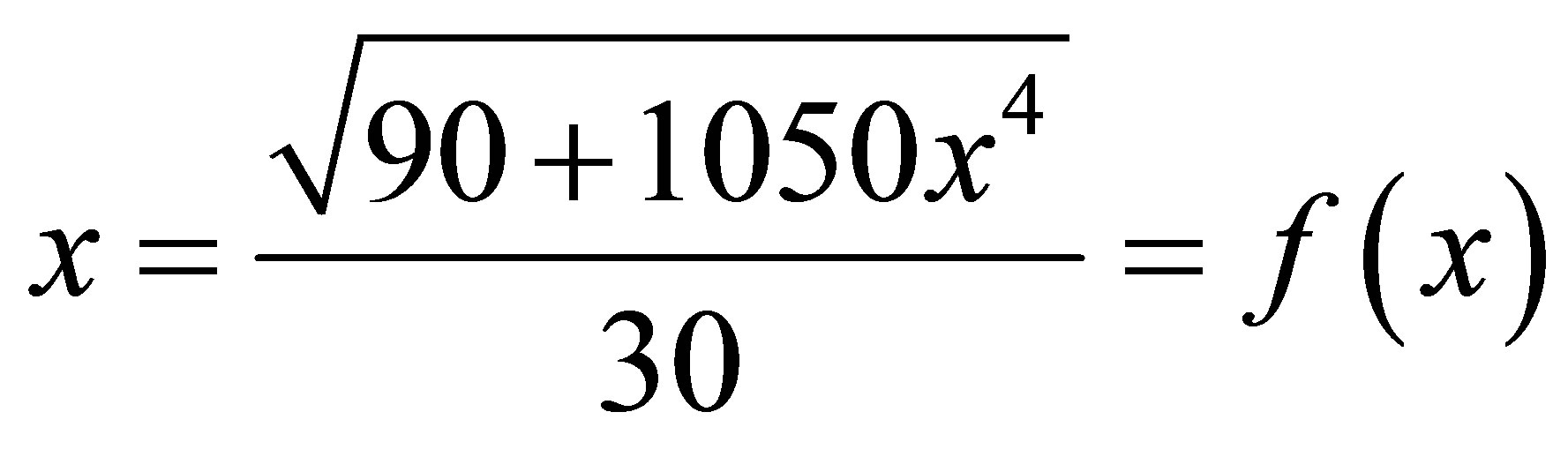
and take 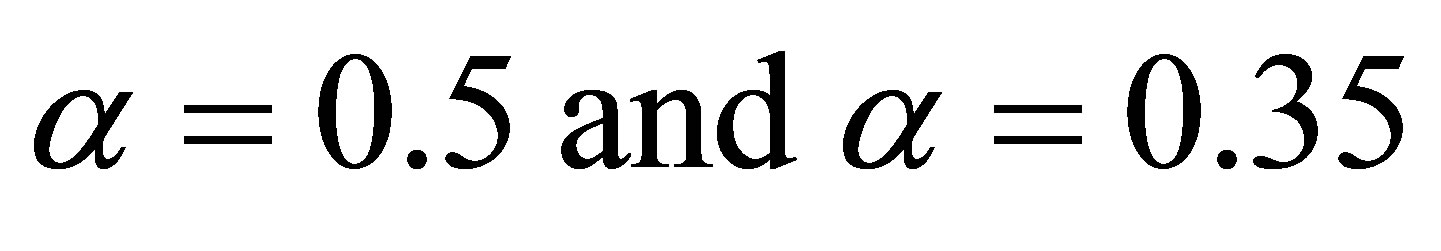 respectively. Now we solve it by
respectively. Now we solve it by
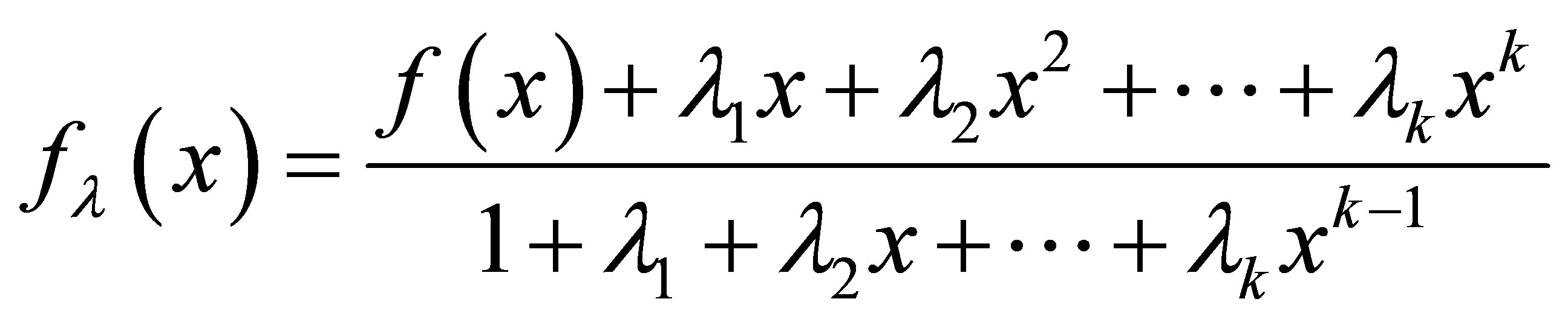
For respective value of α, 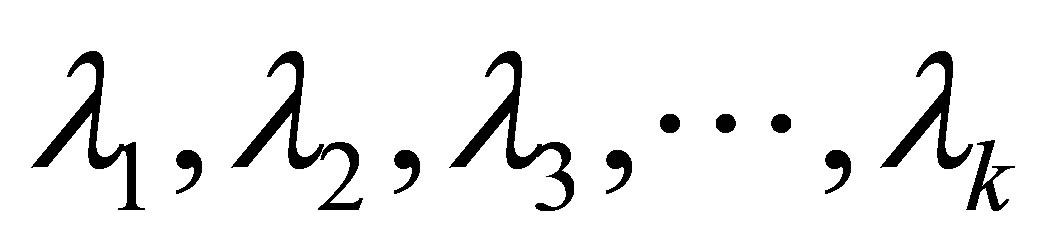 can be determined uniquely from system of linear equations as in
can be determined uniquely from system of linear equations as in
[5] for α = 0.5 and 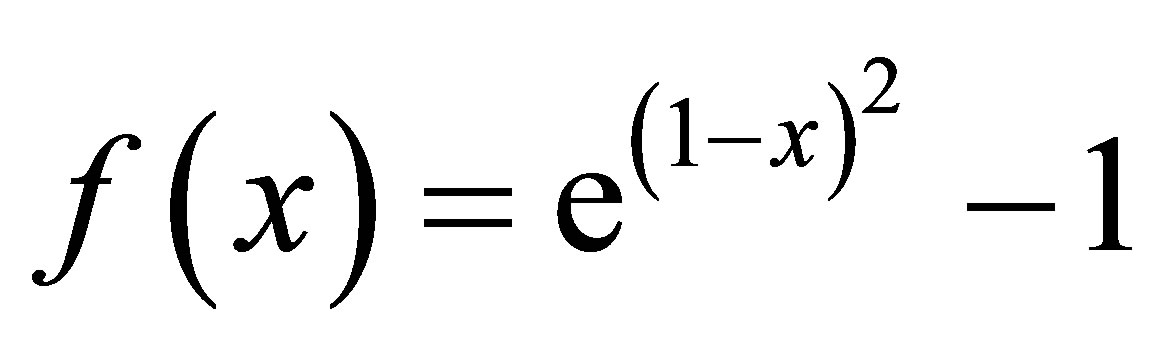 we have
we have
 (9)
(9)
After solving the system of linear equations we have
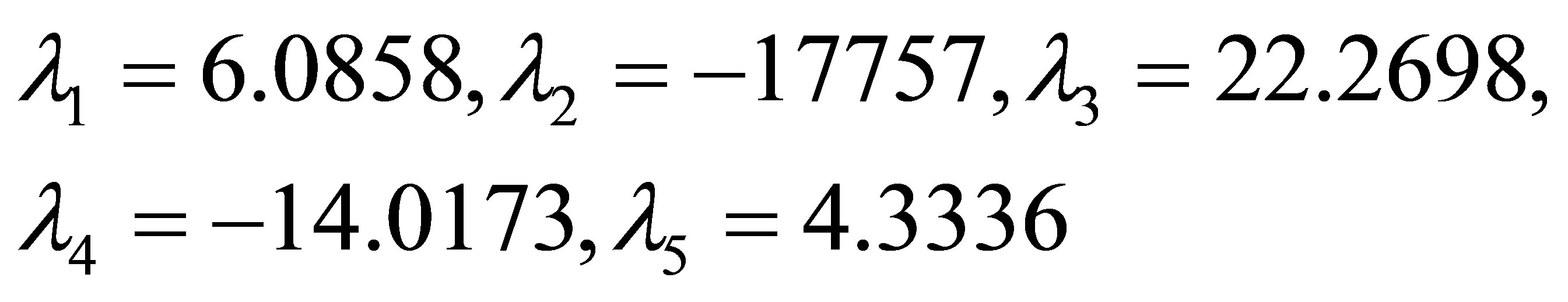
for second polynomial equation where α=0.35 and
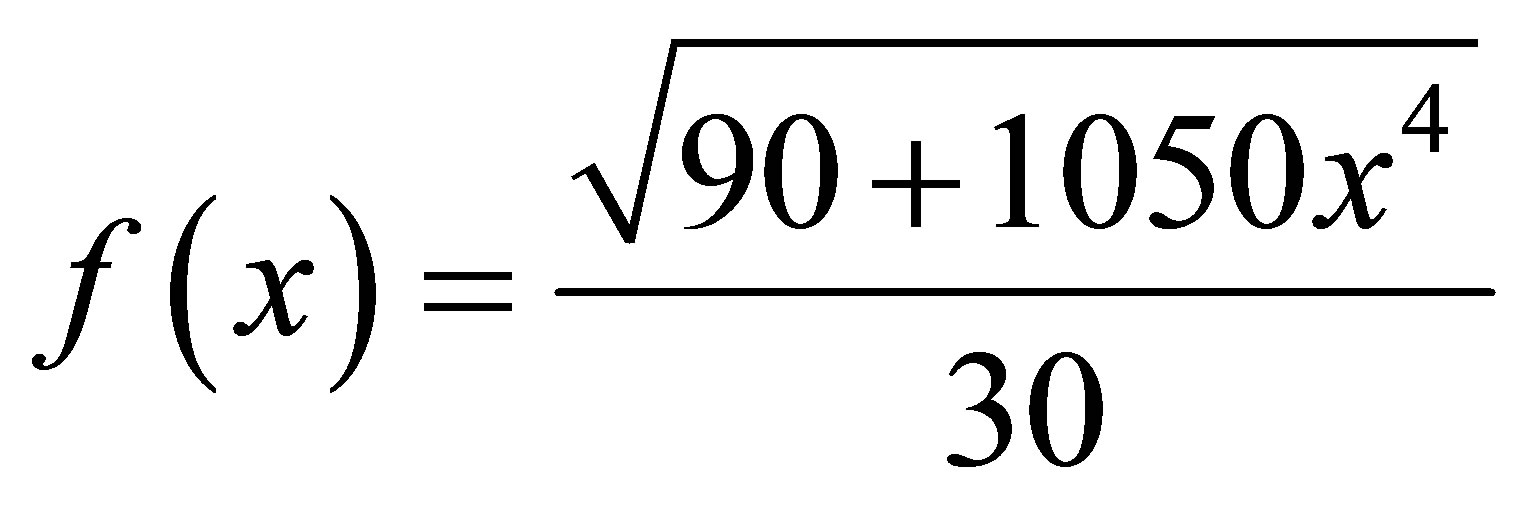
System of linear equations become
 (10)
(10)
Hence we get

3. Experiments
Now using the value of 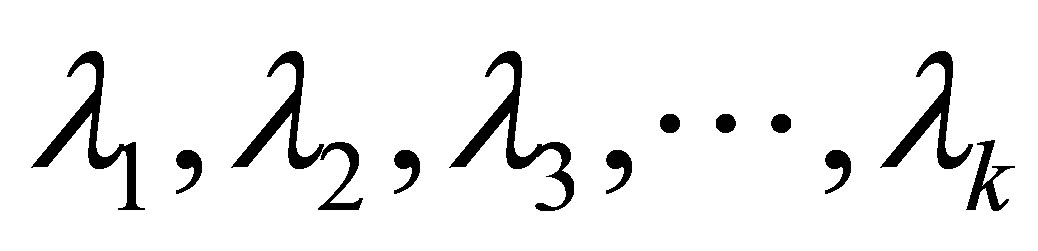 and iterative schemes we have following Tables 1-24, andFigures 1-16.
and iterative schemes we have following Tables 1-24, andFigures 1-16.
We take 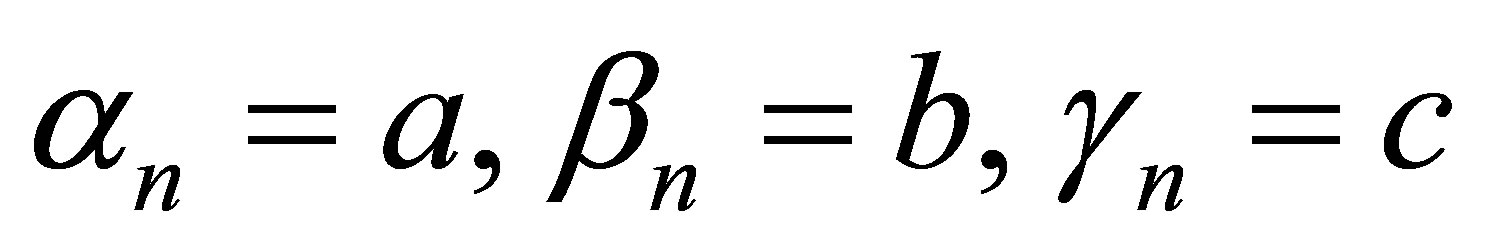
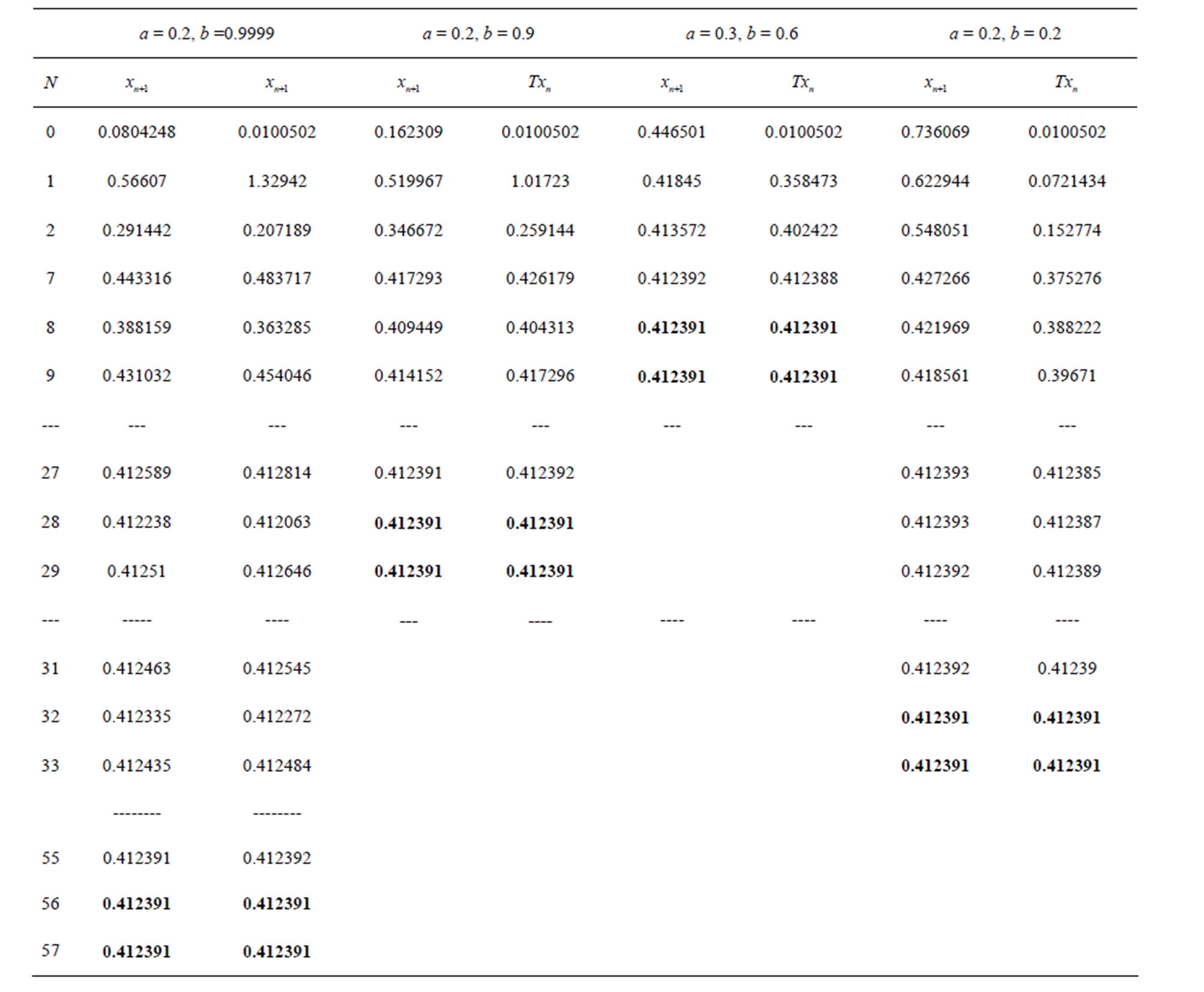
Table 1. Simple Ishikawa for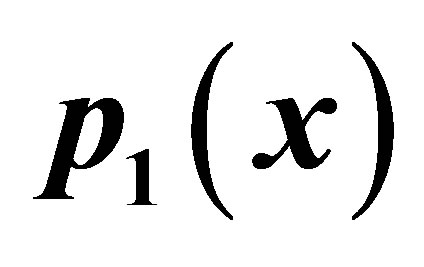 .
.
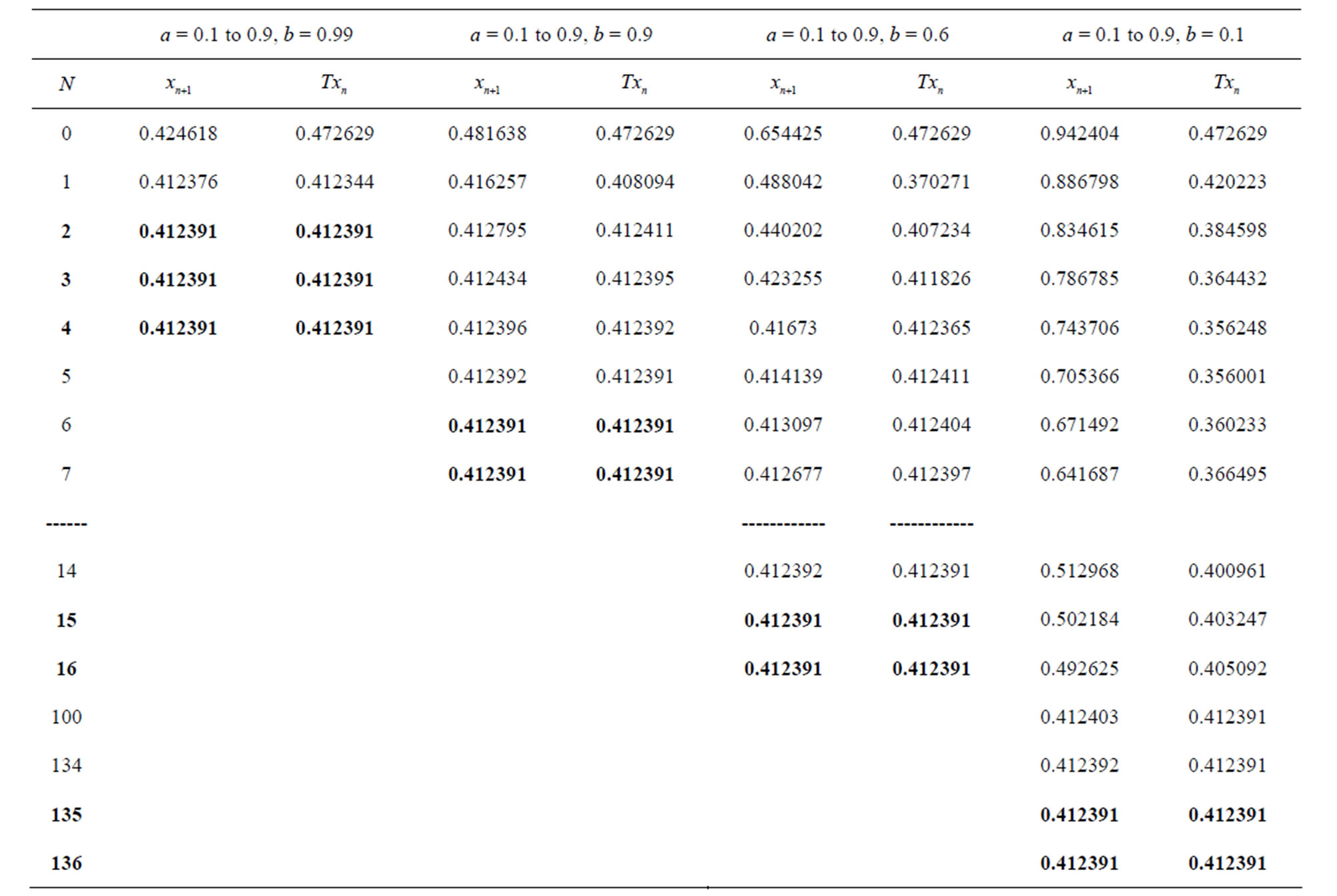
Table 2. Modified Ishikawa for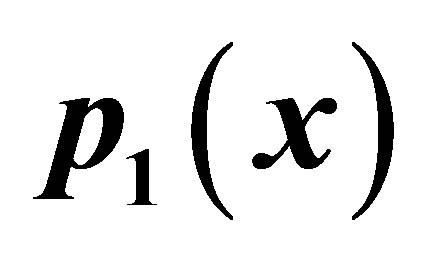 .
.
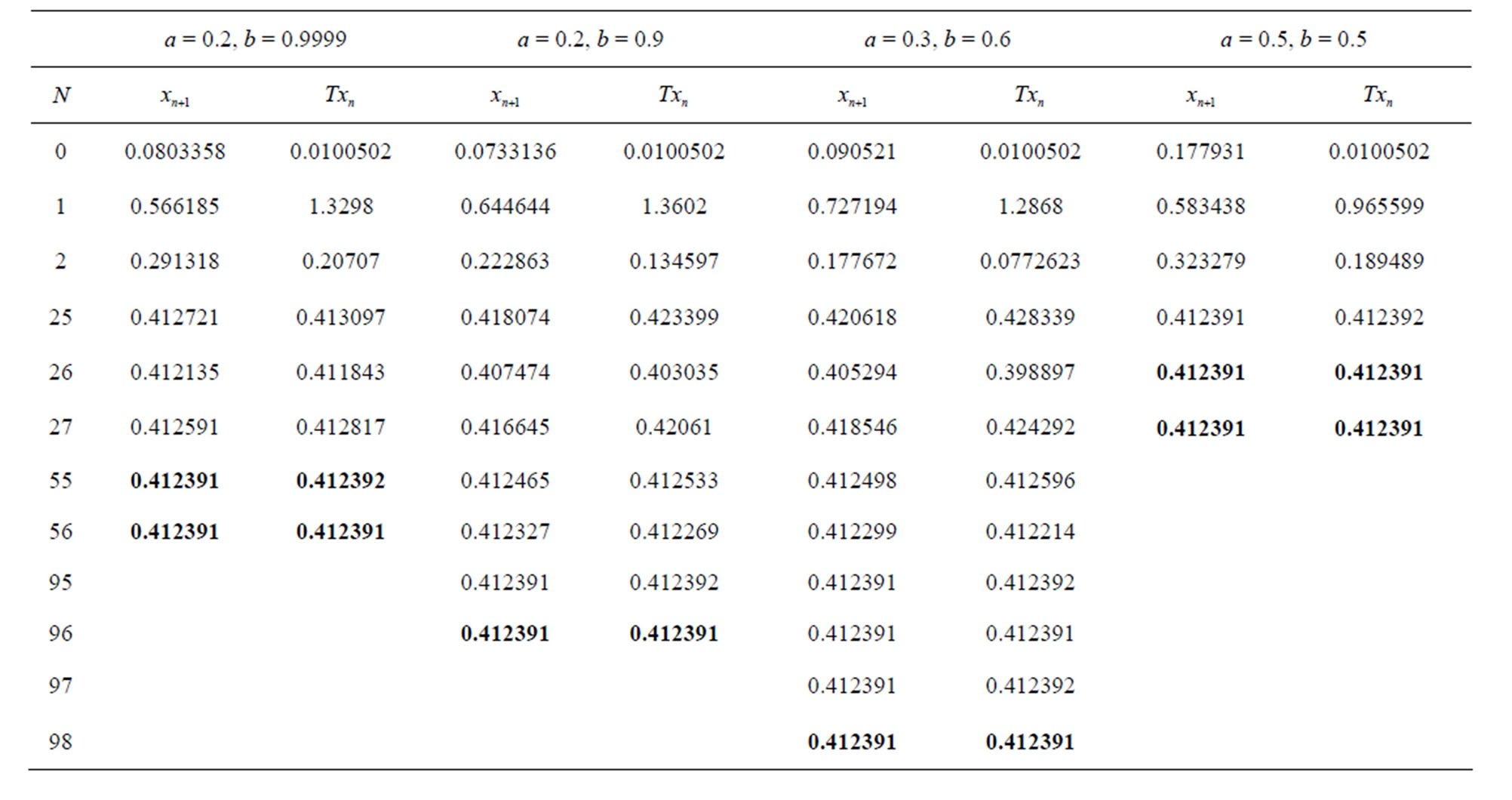
Table 3. Simple Agarwal et al. for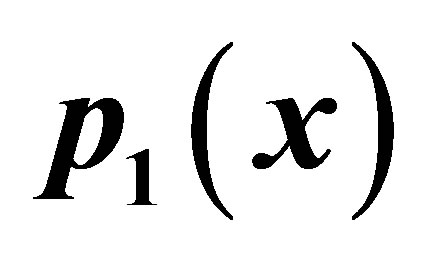 .
.
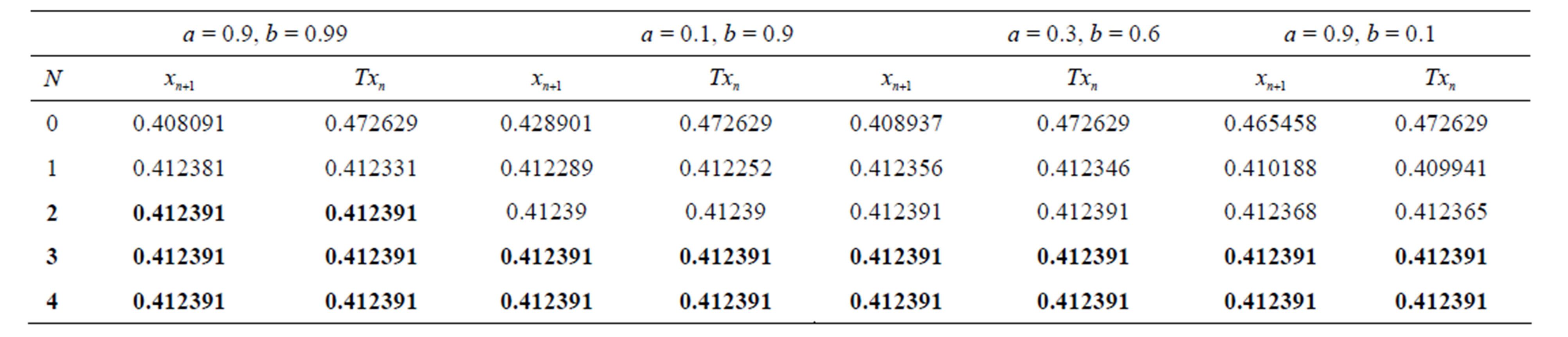
Table 4. Modified Agarwal et al. for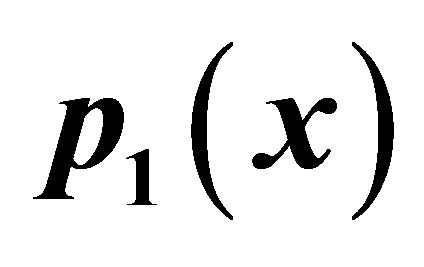 .
.
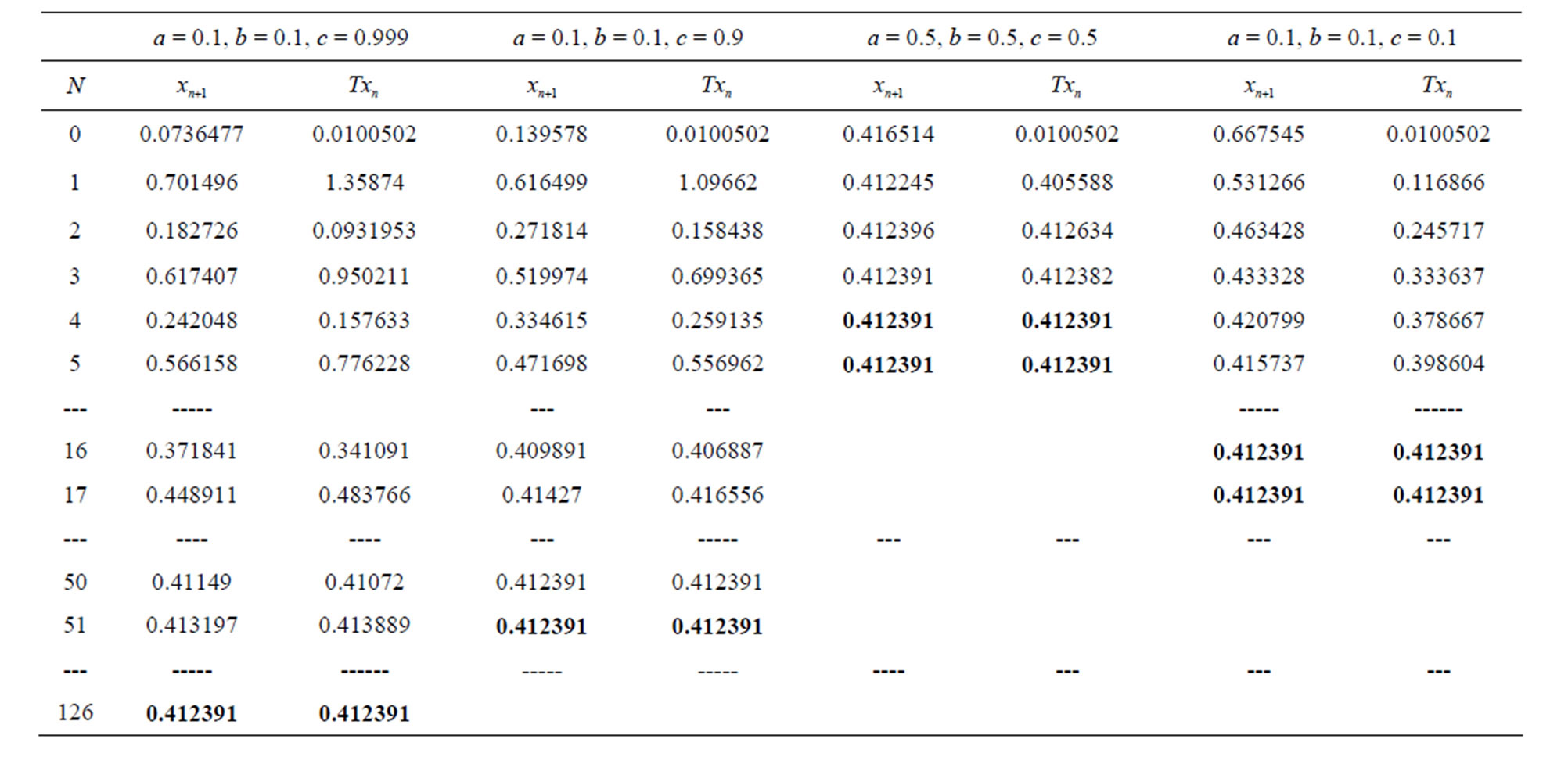
Table 5. Simple SP for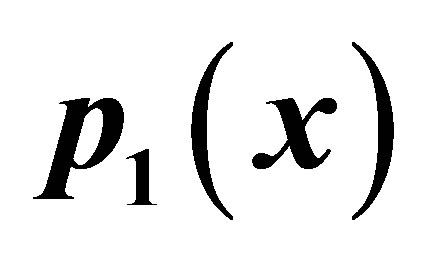 .
.
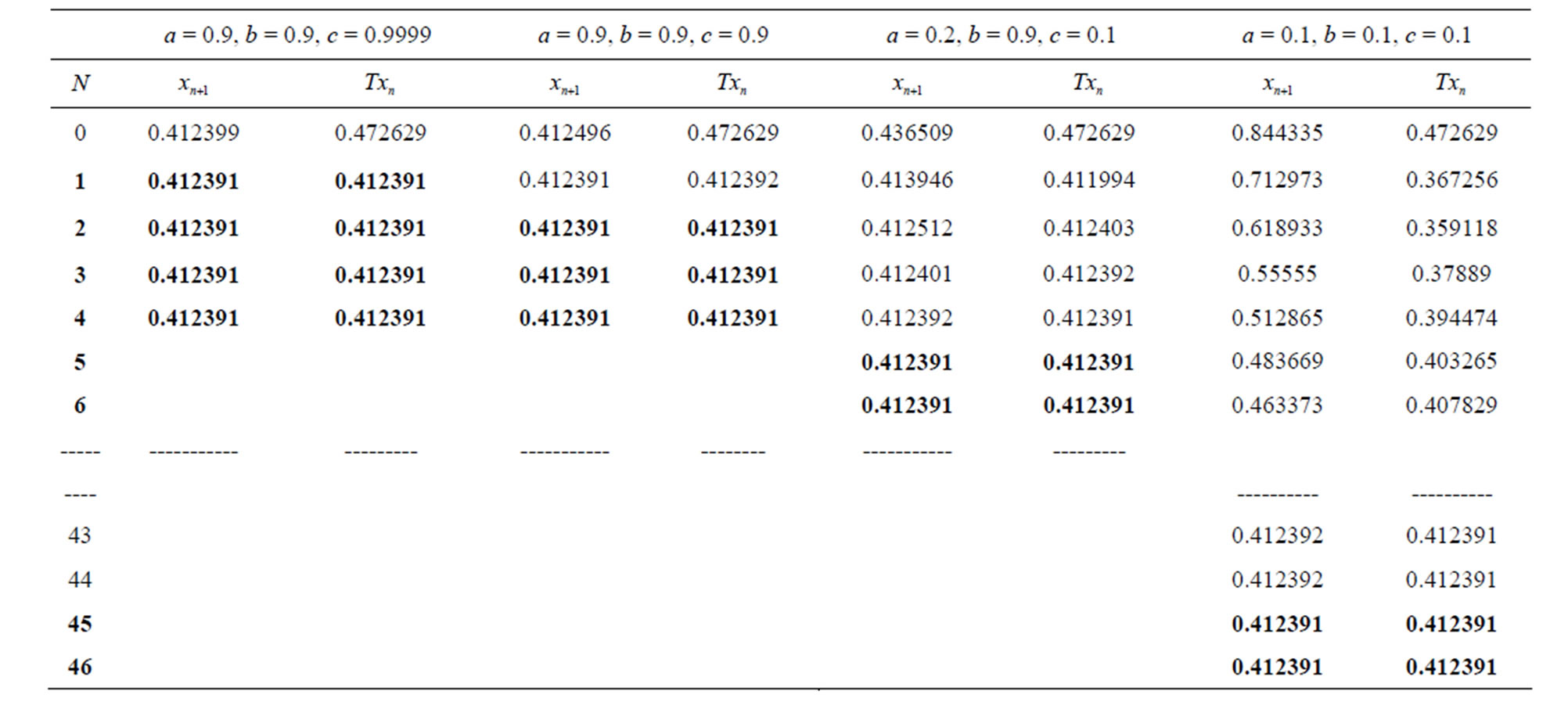
Table 6. Modified SP for .
.
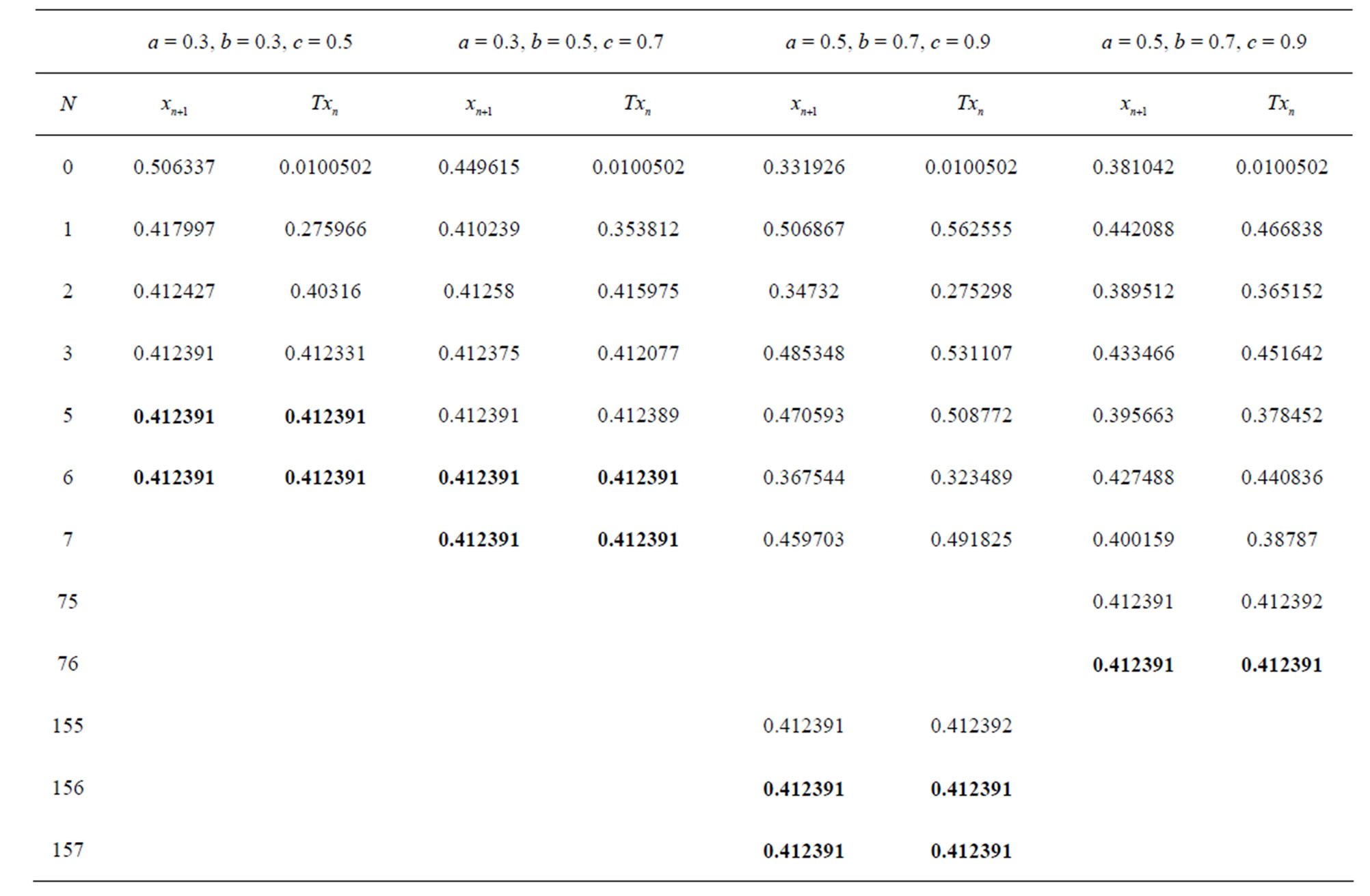
Table 7. Simple Noor for .
.
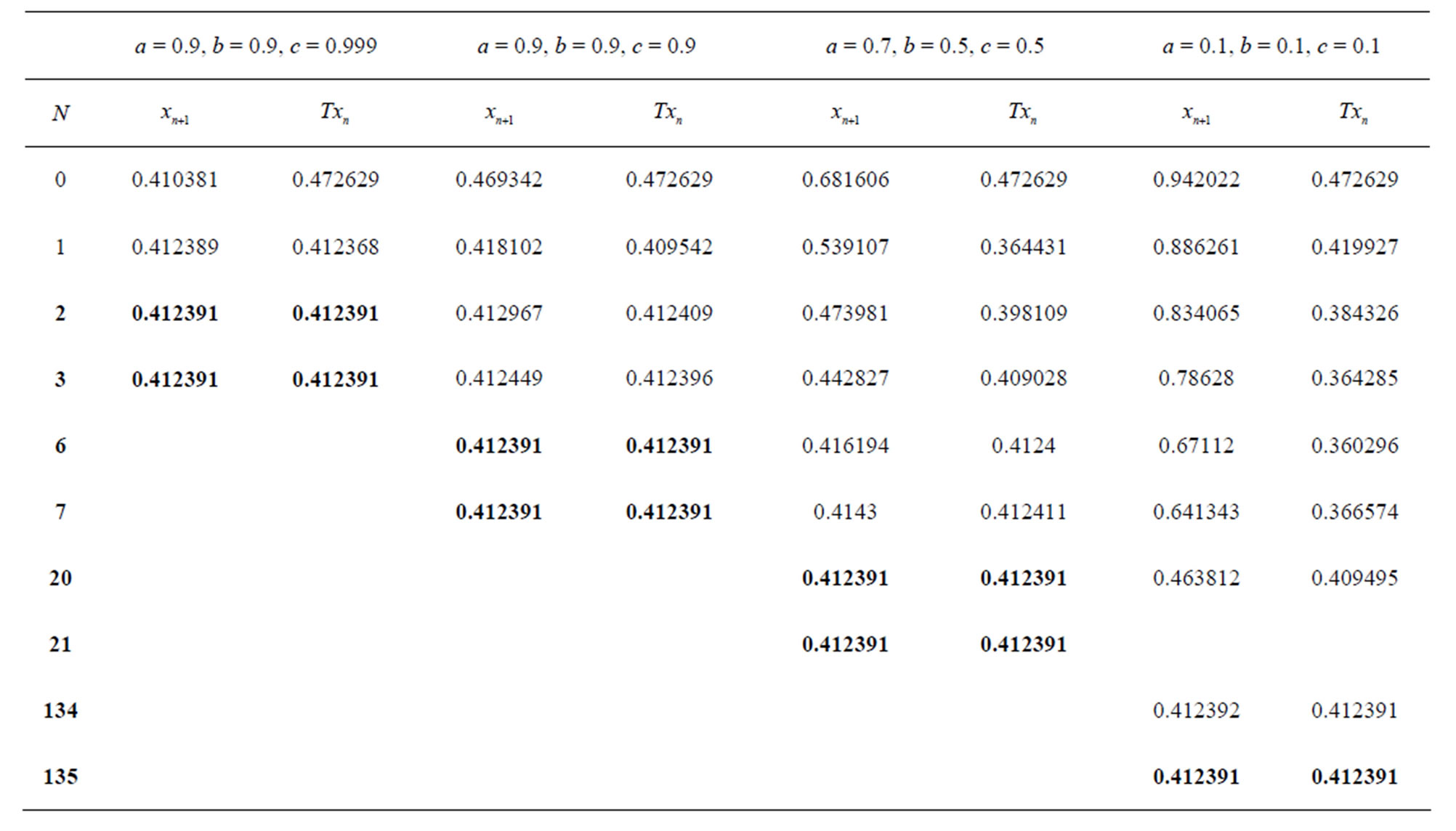
Table 8. Modified Noor for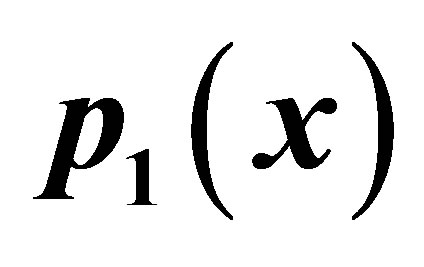 .
.
 (a)
(a)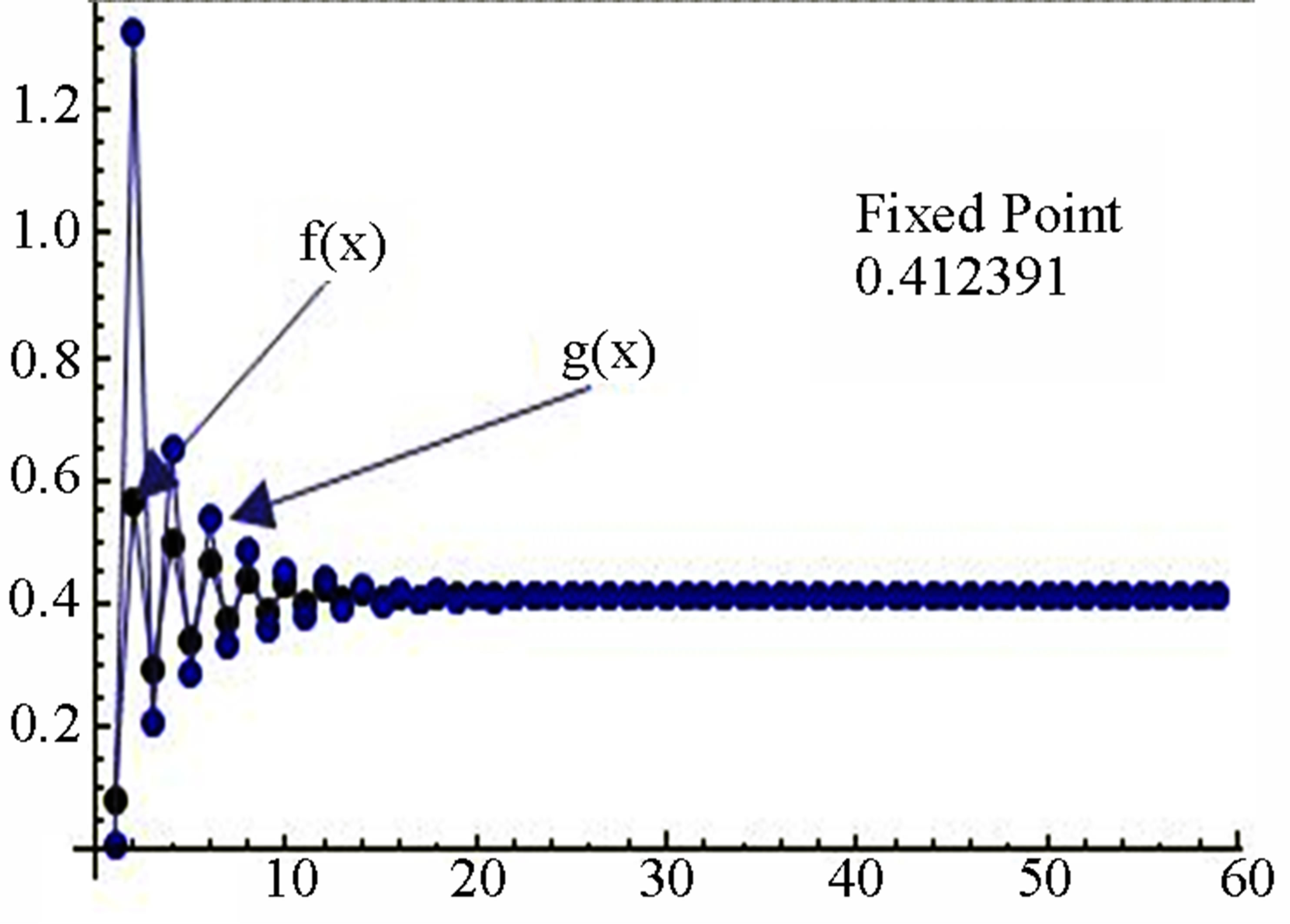 (b)
(b)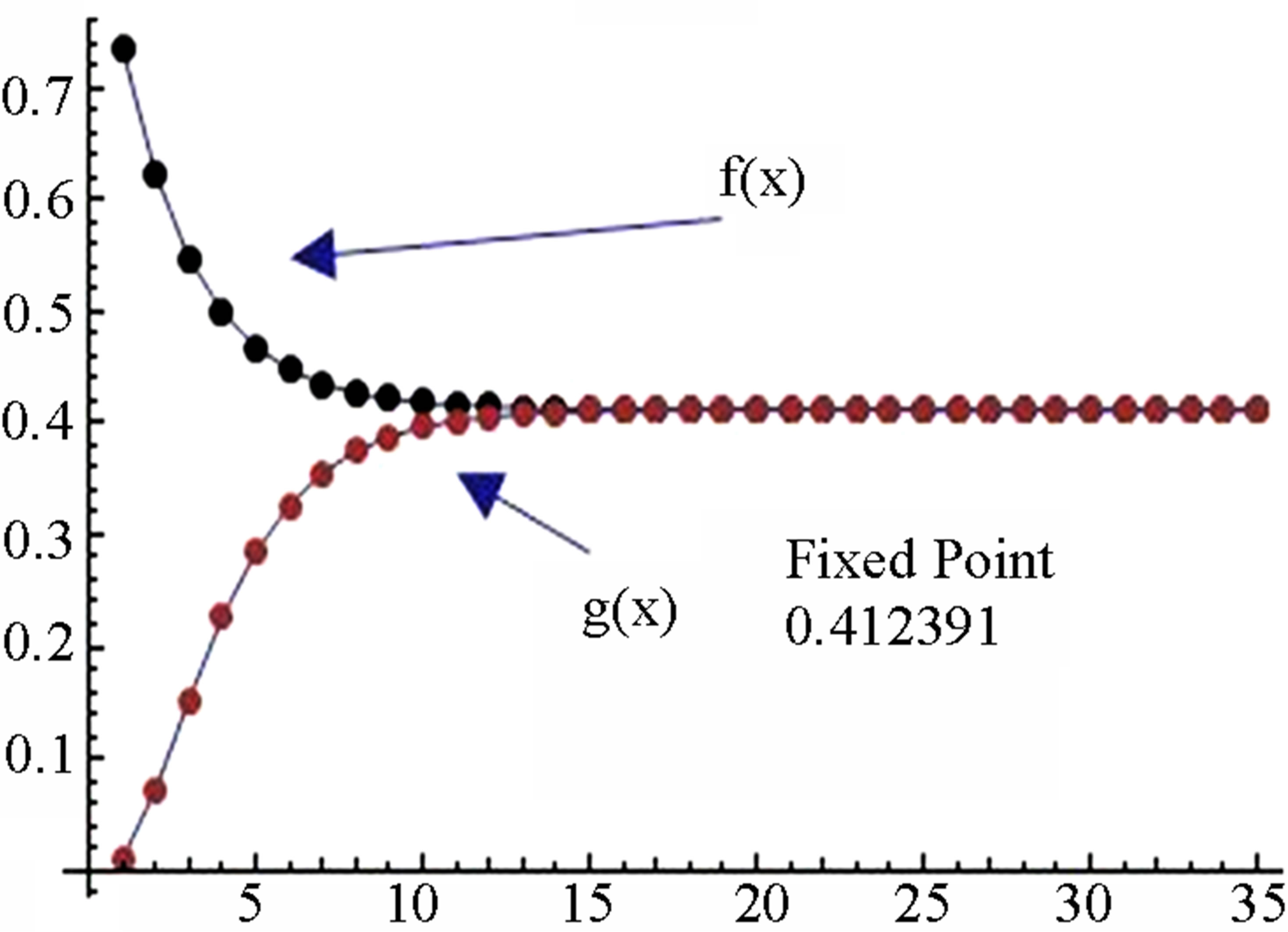 (c)
(c)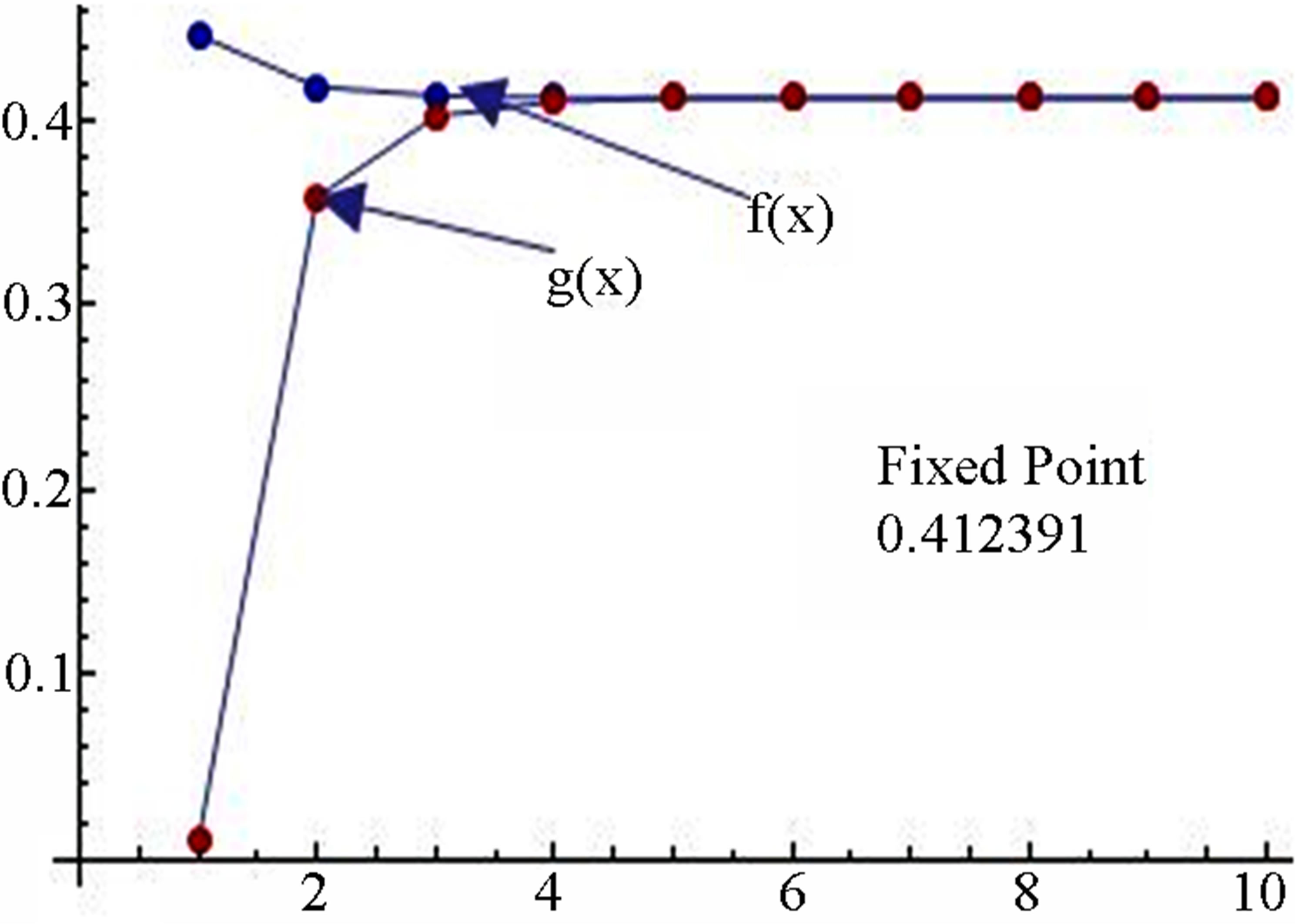 (d)
(d)
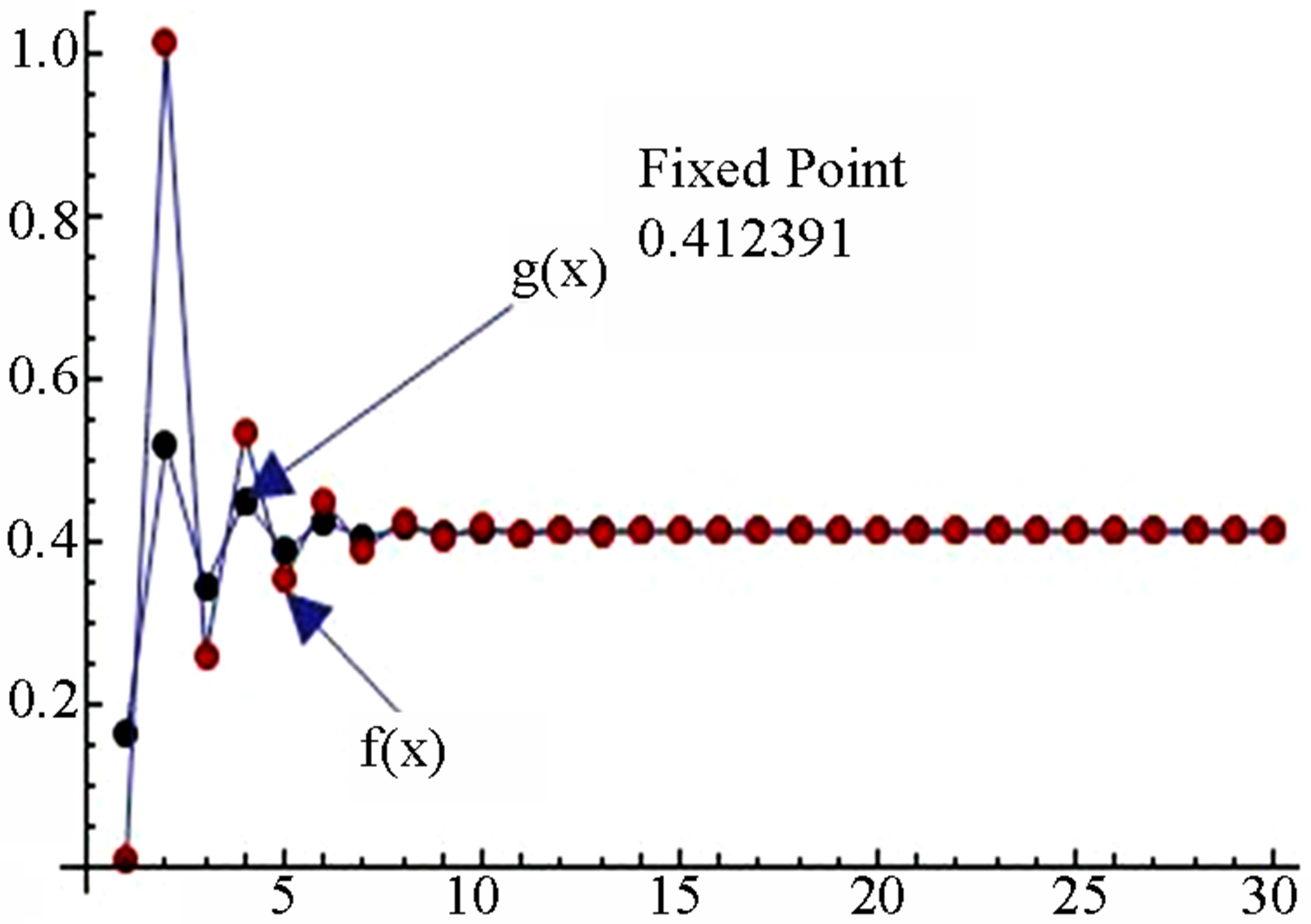
Figure 1. Graphical observations of simple Ishikawa iteration for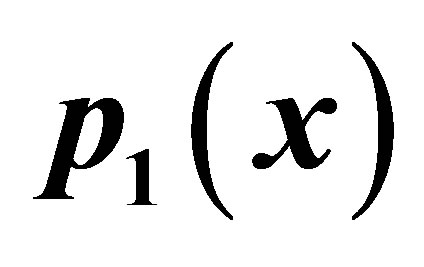 . Here (a)-(d) show the graph for Table 1. The merging point with value 0.412391 is fixed point.
. Here (a)-(d) show the graph for Table 1. The merging point with value 0.412391 is fixed point.
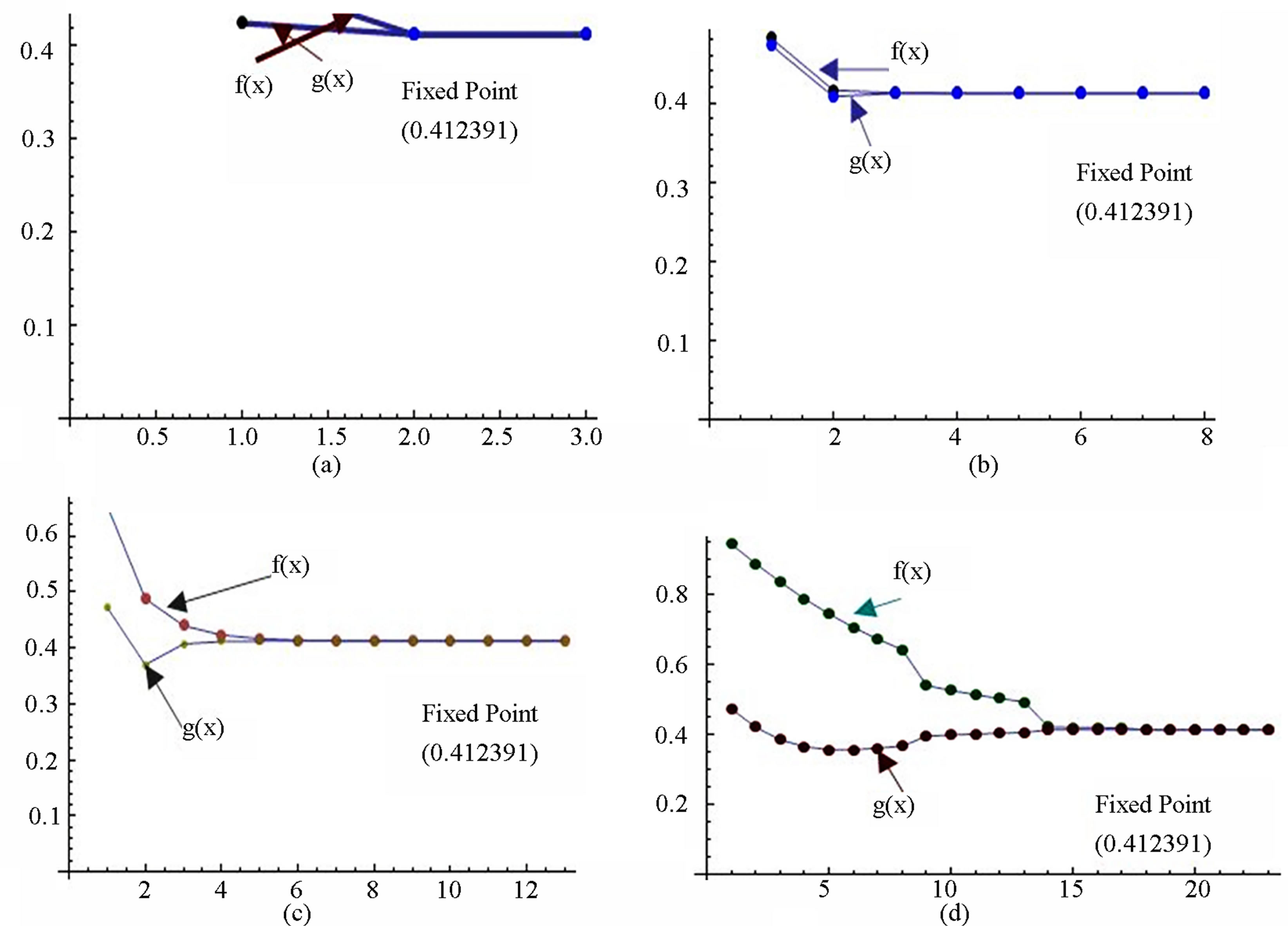
Figure 2. Graphical observations of new modified Ishikawa iteration for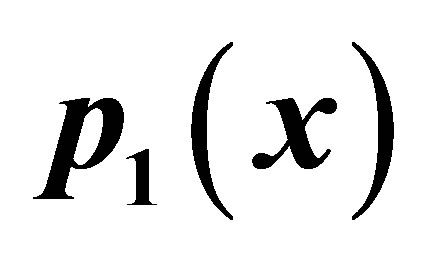 . Here (a)-(d) show the graph for Table 2. The merging point with value 0.412391 is fixed point.
. Here (a)-(d) show the graph for Table 2. The merging point with value 0.412391 is fixed point.
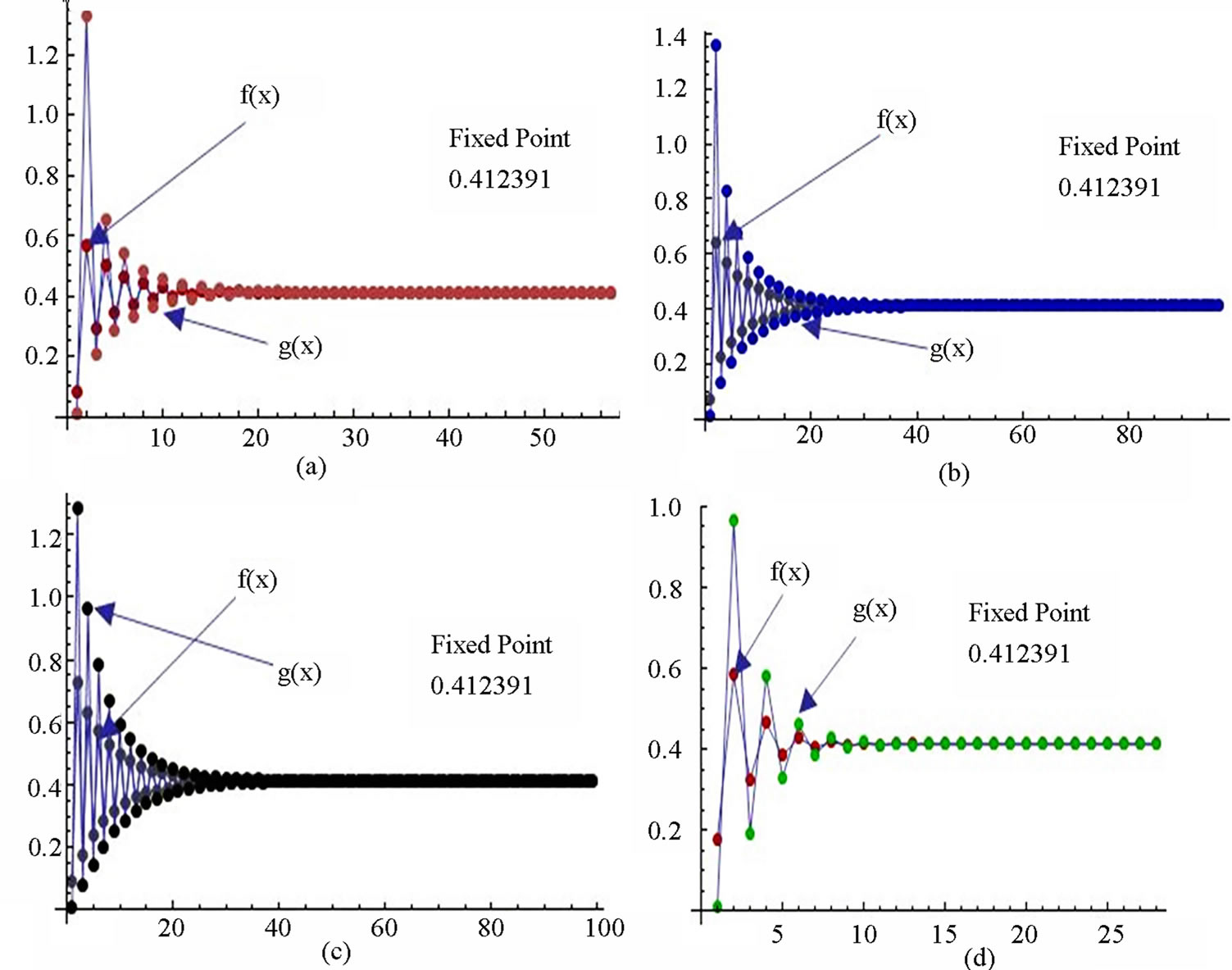
Figure 3. Graphical observations of simple Agarwal et al. iteration for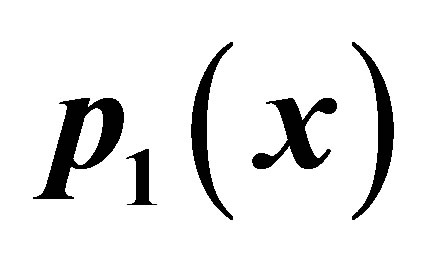 . Here (a)-(d) show the graph for Table 3. The merging point with value 0.412391 is fixed point.
. Here (a)-(d) show the graph for Table 3. The merging point with value 0.412391 is fixed point.
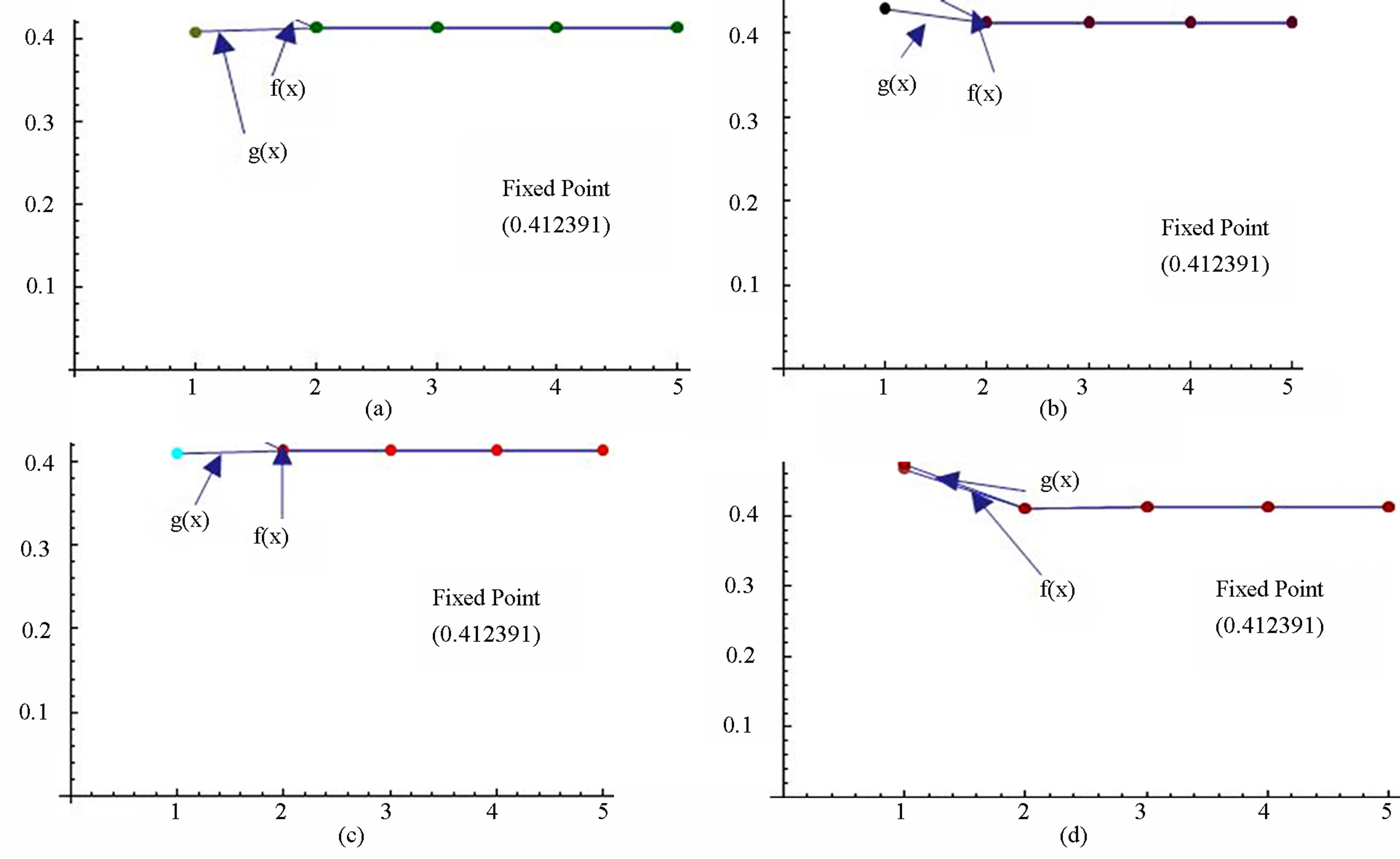
Figure 4. Graphical observations of new modified Agarwal et al. iteration for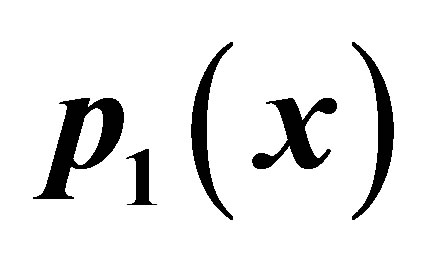 . Here (a)-(d) show the graph for Table 4. The merging point with value 0.412391 is fixed point.
. Here (a)-(d) show the graph for Table 4. The merging point with value 0.412391 is fixed point.
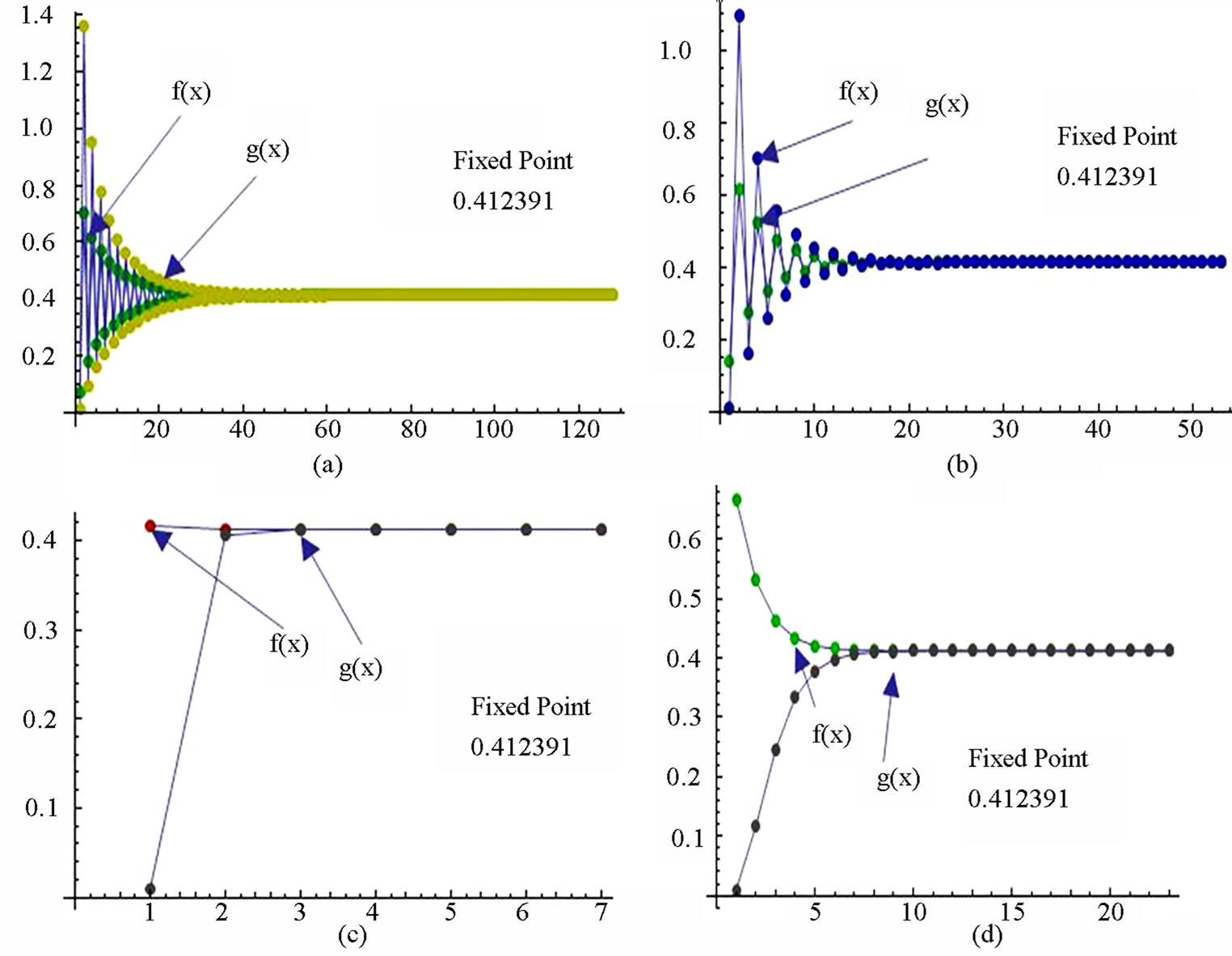
Figure 5. Graphical observations of simple SP iteration for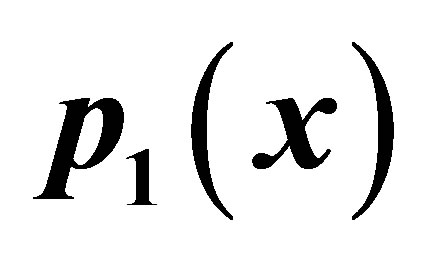 . Here Here (a)-(d) show the graph for Table 5. The merging point with value 0.412391 is fixed point.
. Here Here (a)-(d) show the graph for Table 5. The merging point with value 0.412391 is fixed point.
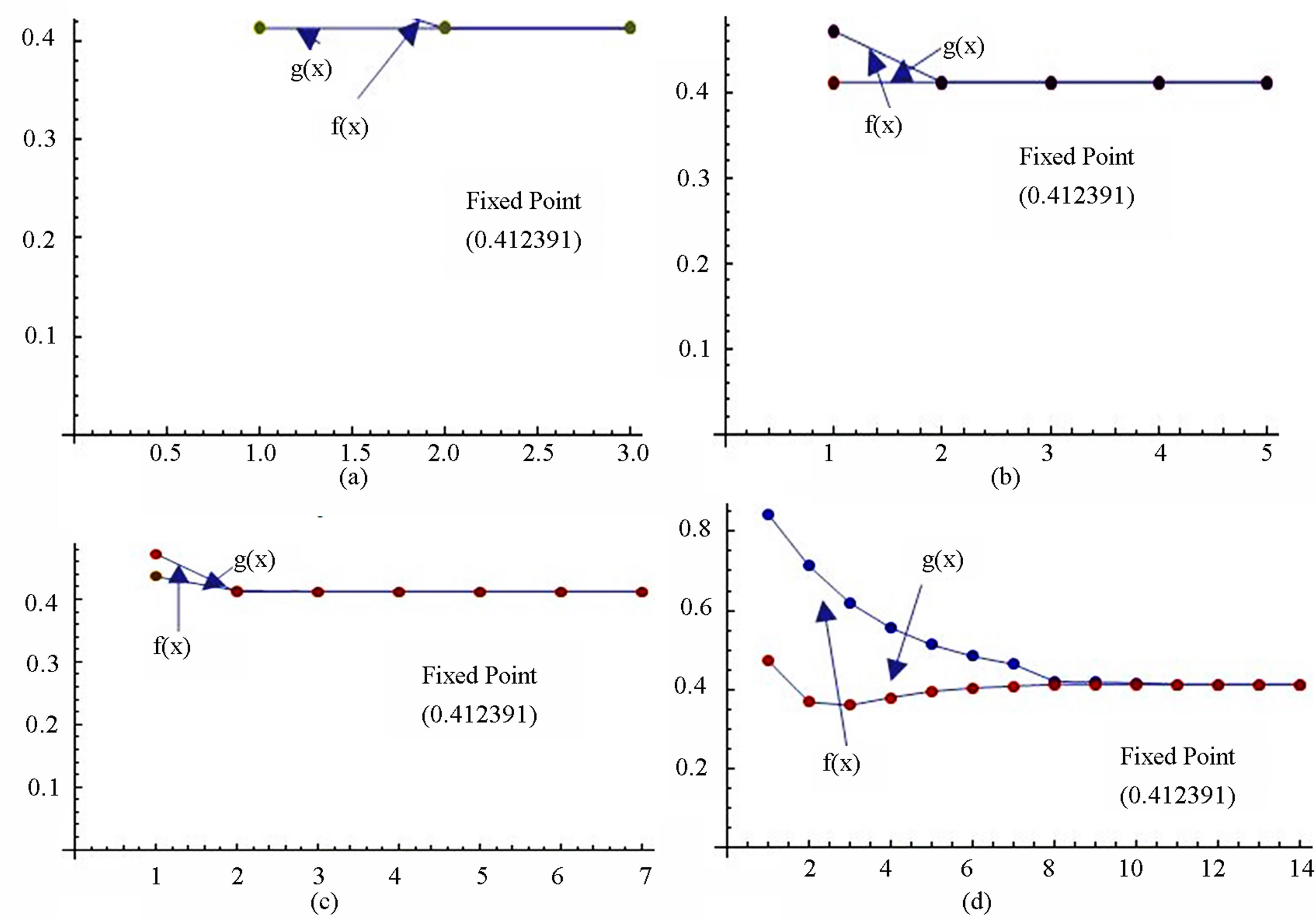
Figure 6. Graphical observations of new modified SP iteration for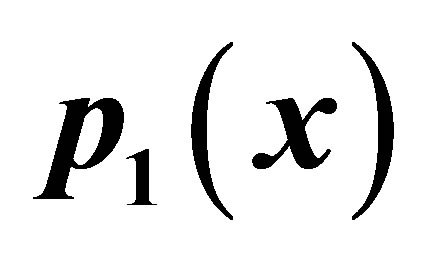 . Here (a)-(d) show the graph for Table 6. The merging point with value 0.412391 is fixed point.
. Here (a)-(d) show the graph for Table 6. The merging point with value 0.412391 is fixed point.
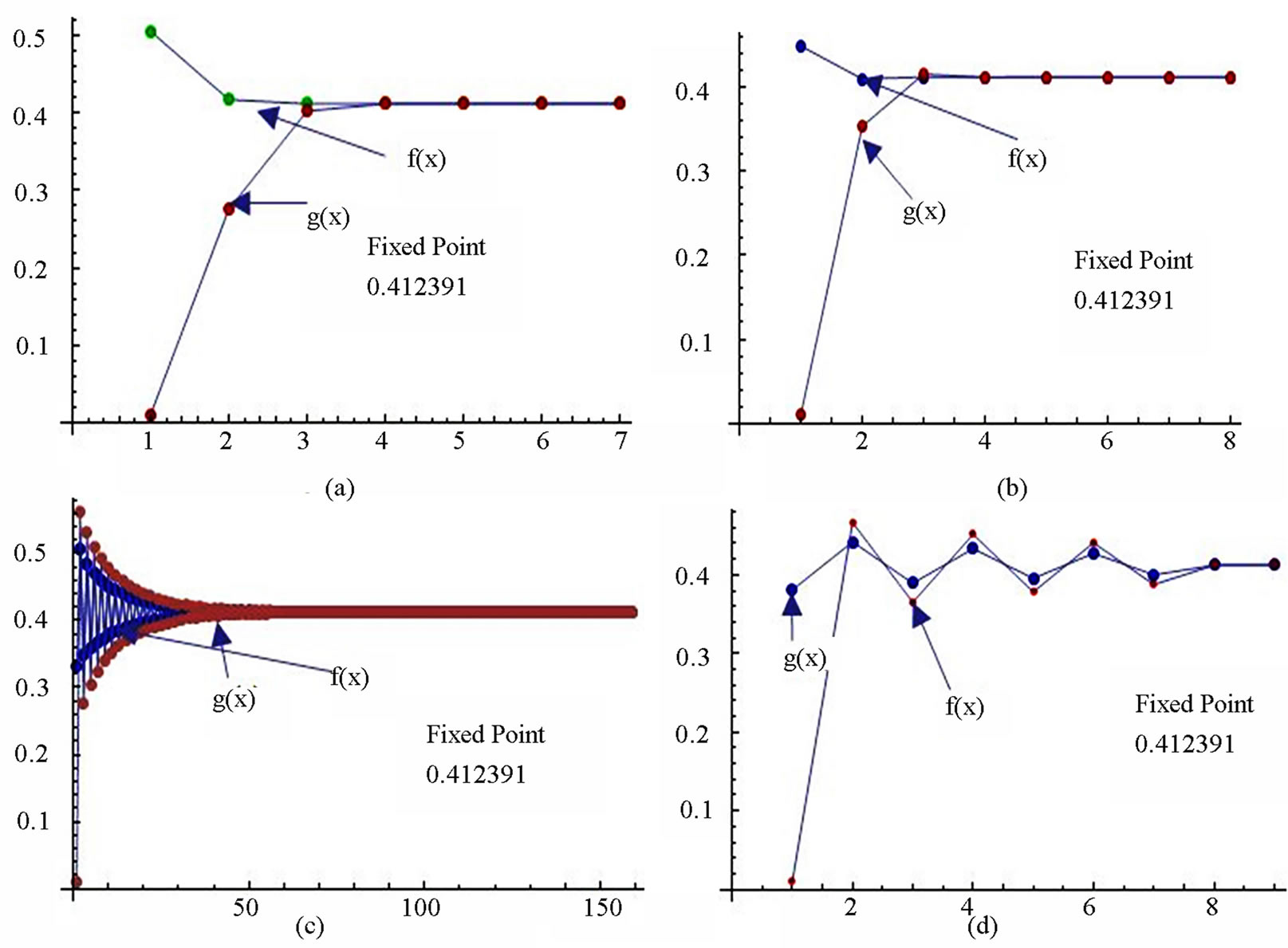
Figure 7. Graphical observations of simple Noor iteration for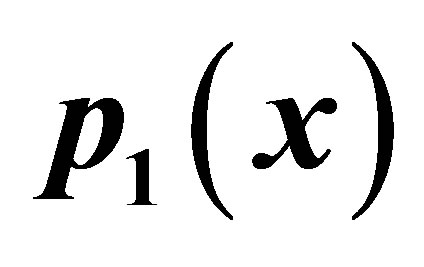 . Here (a)-(d) show the graph for Table 7. The merging point with value 0 .412391 is fixed point.
. Here (a)-(d) show the graph for Table 7. The merging point with value 0 .412391 is fixed point.
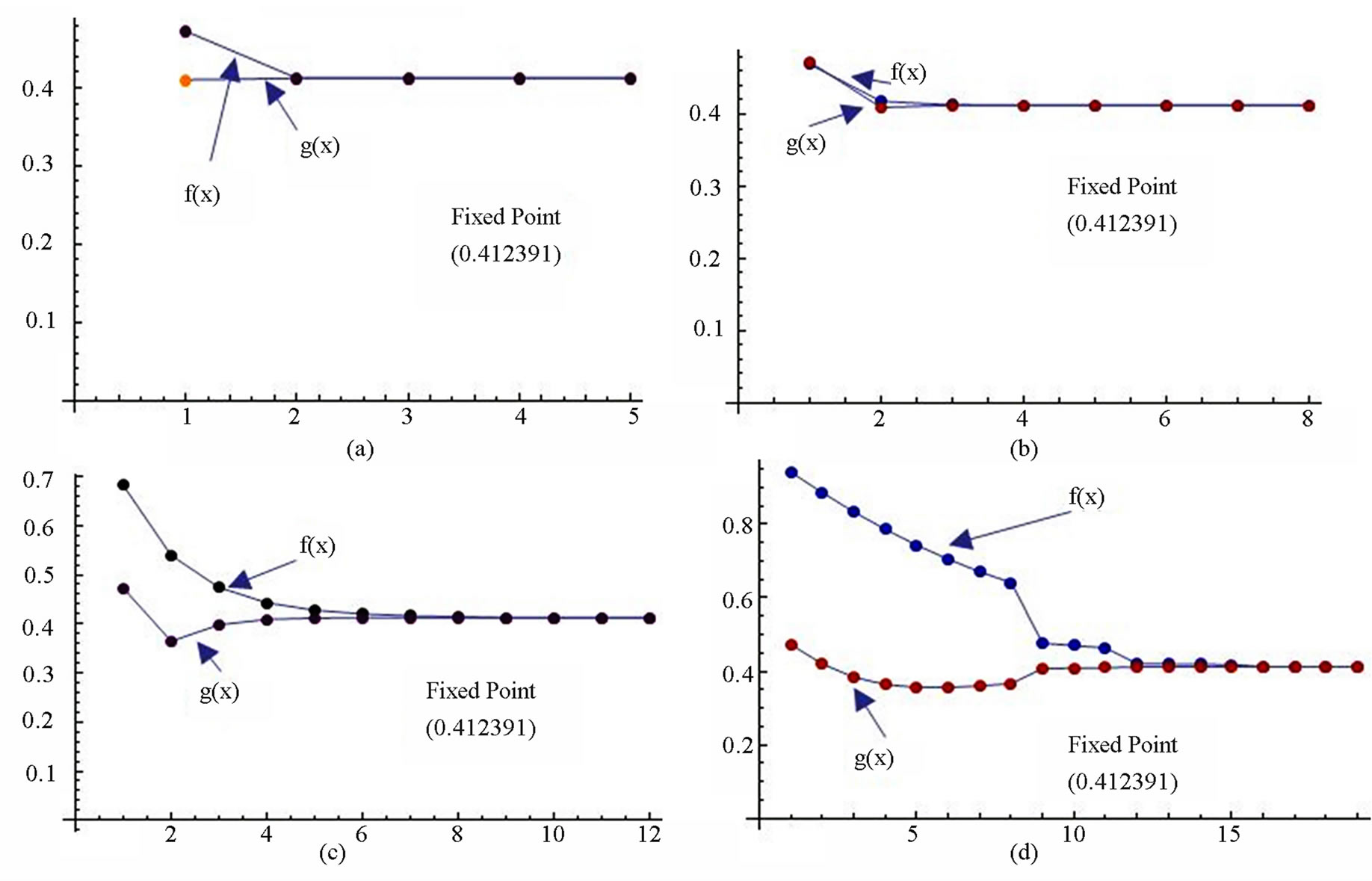
Figure 8. Graphical observations of new modified Noor iteration for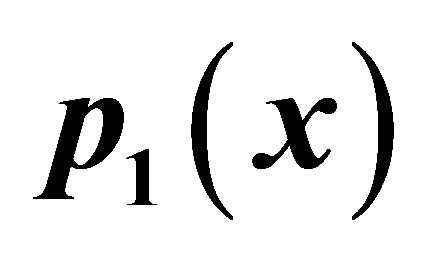 . Here (a)-(d) show the graph for Table 8. The merging point with value 0.412391 is fixed point.
. Here (a)-(d) show the graph for Table 8. The merging point with value 0.412391 is fixed point.
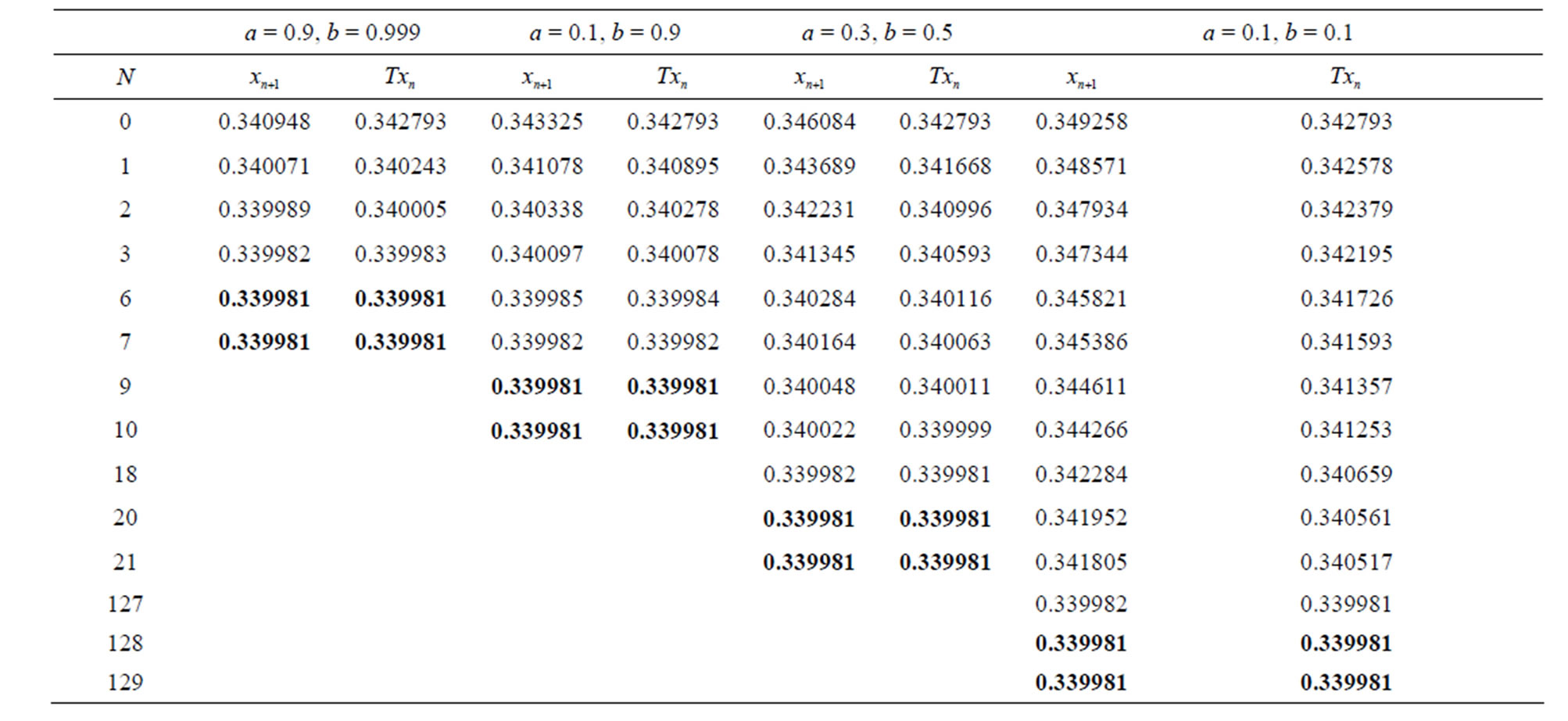
Table 9. Simple Ishikawa for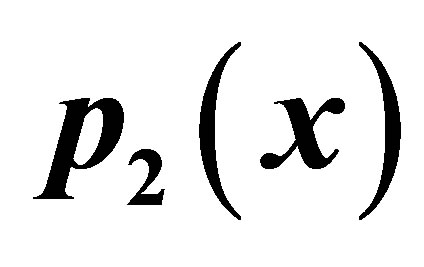 .
.
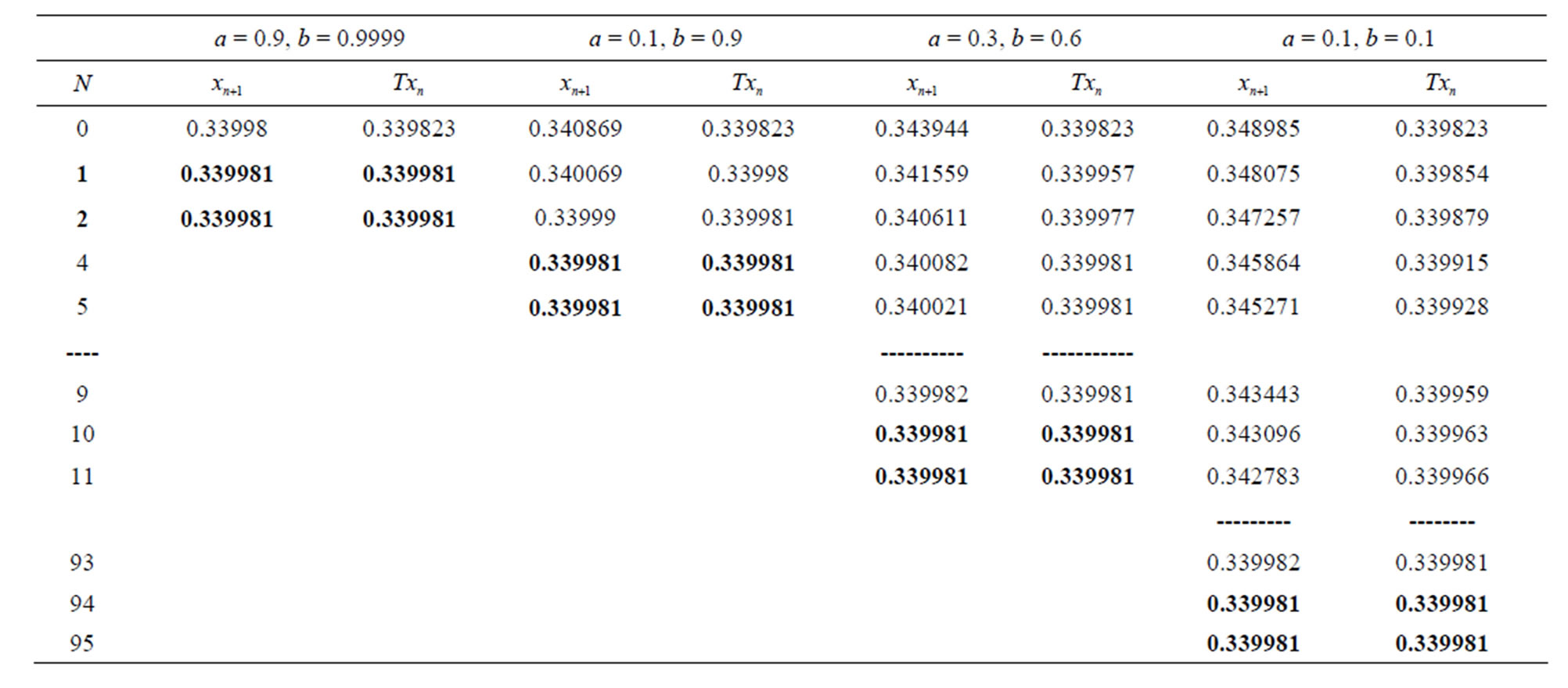
Table 10. Modified Ishikawa for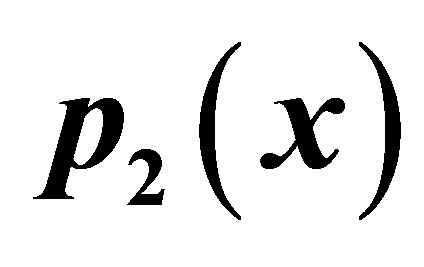 .
.
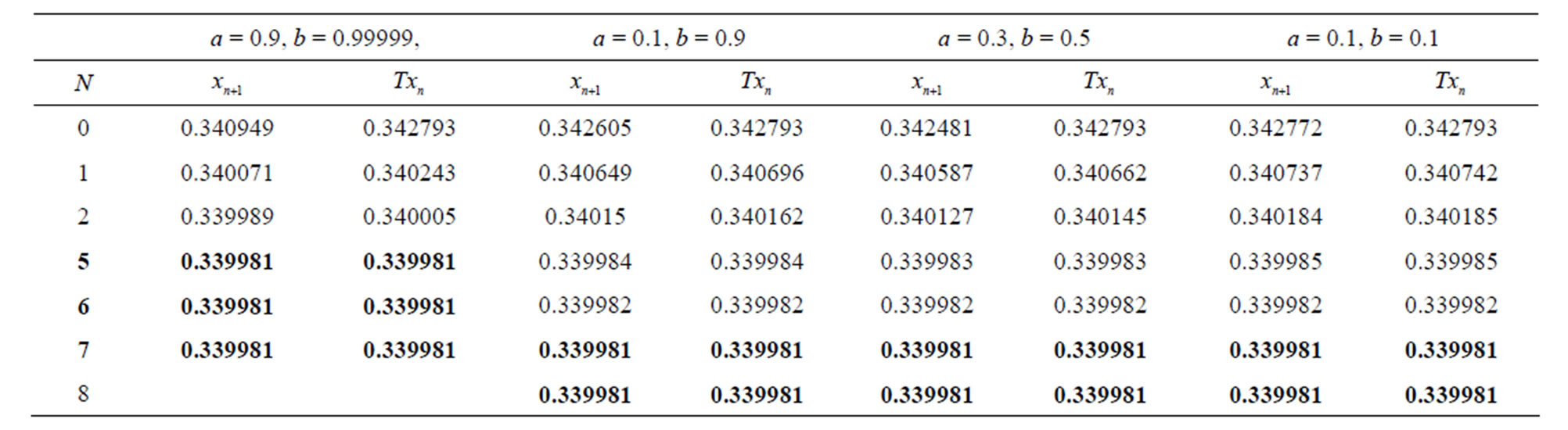
Table 11. Simple Agarwal et al. for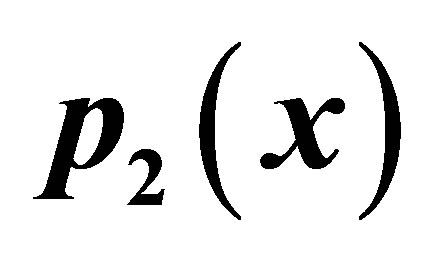 .
.
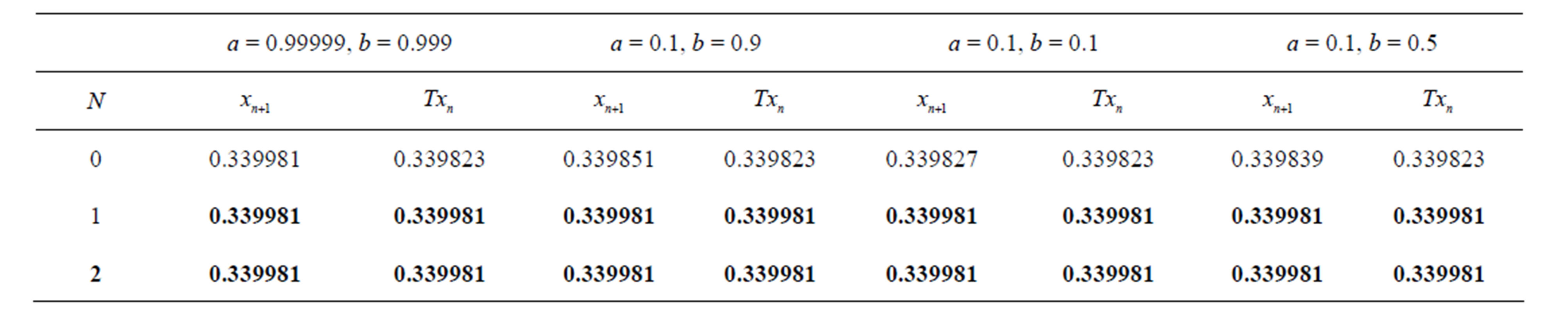
Table 12. Modified Aggarwal et al. for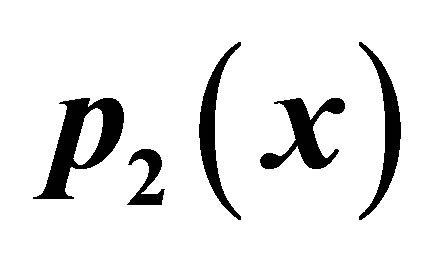 .
.
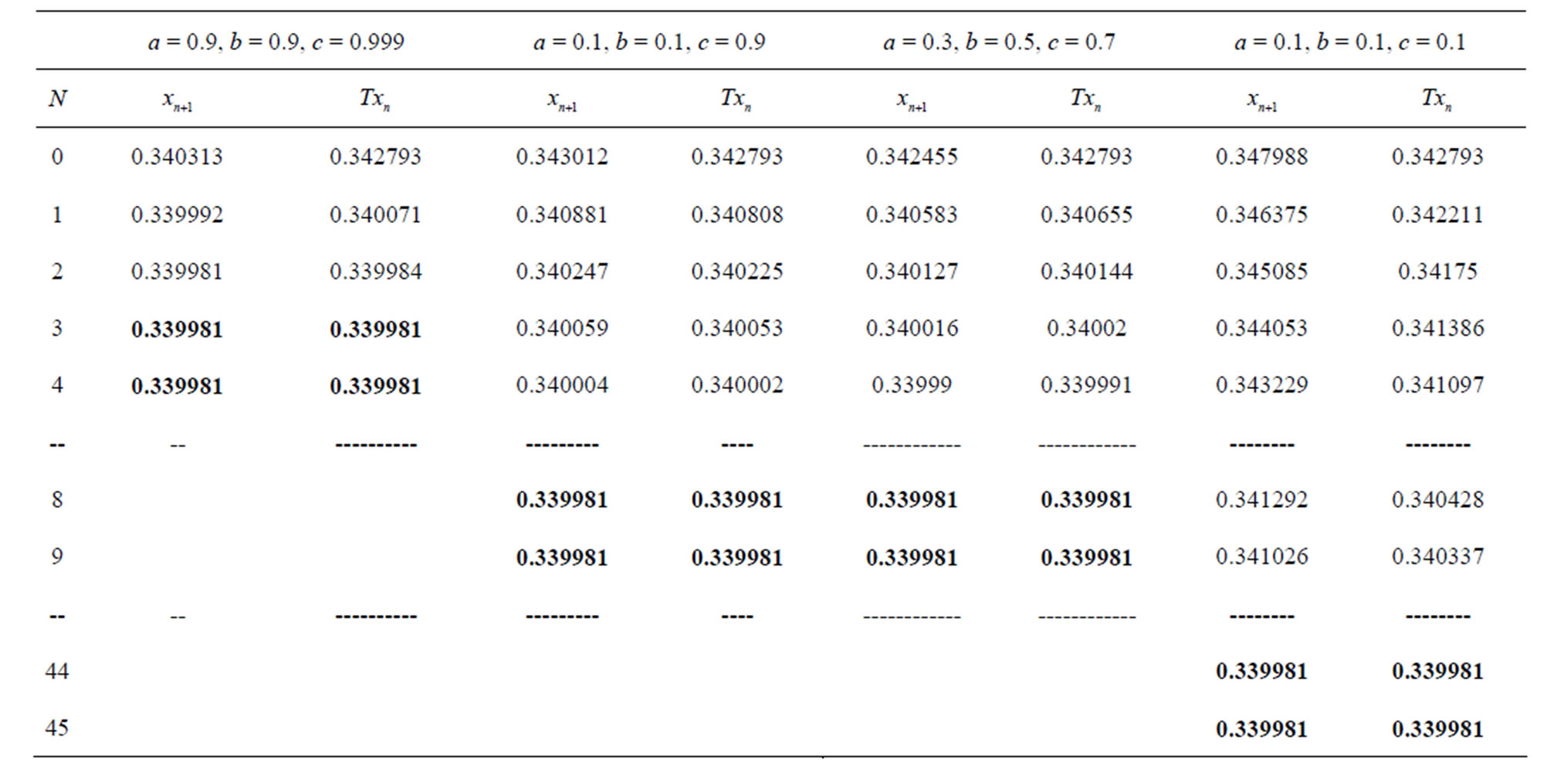
Table 13. Simple SP for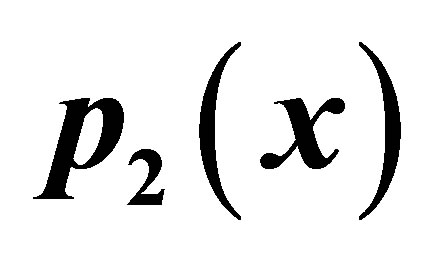 .
.
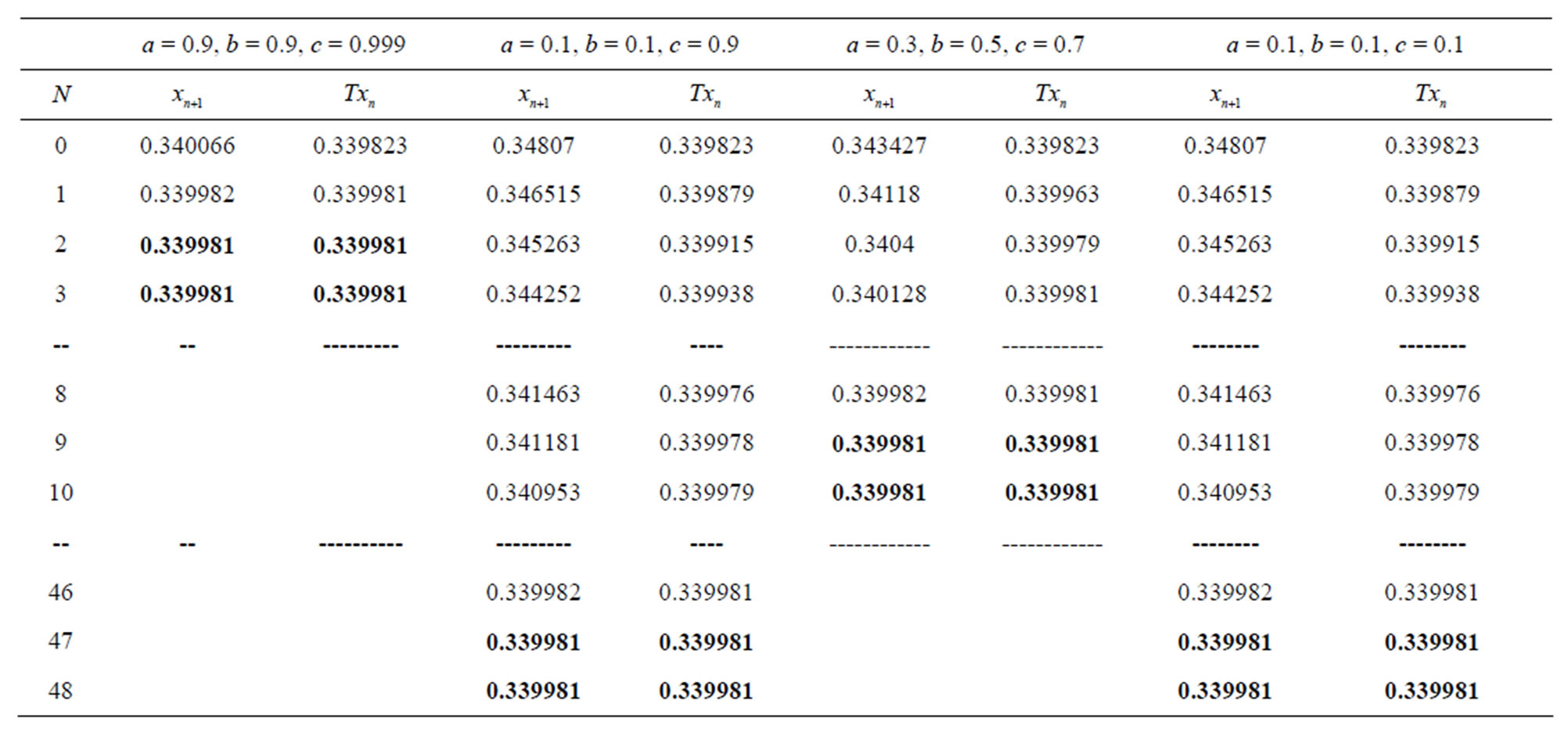
Table 14. Modified SP for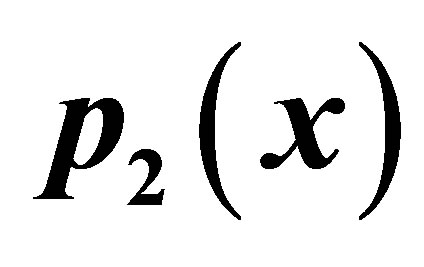 .
.
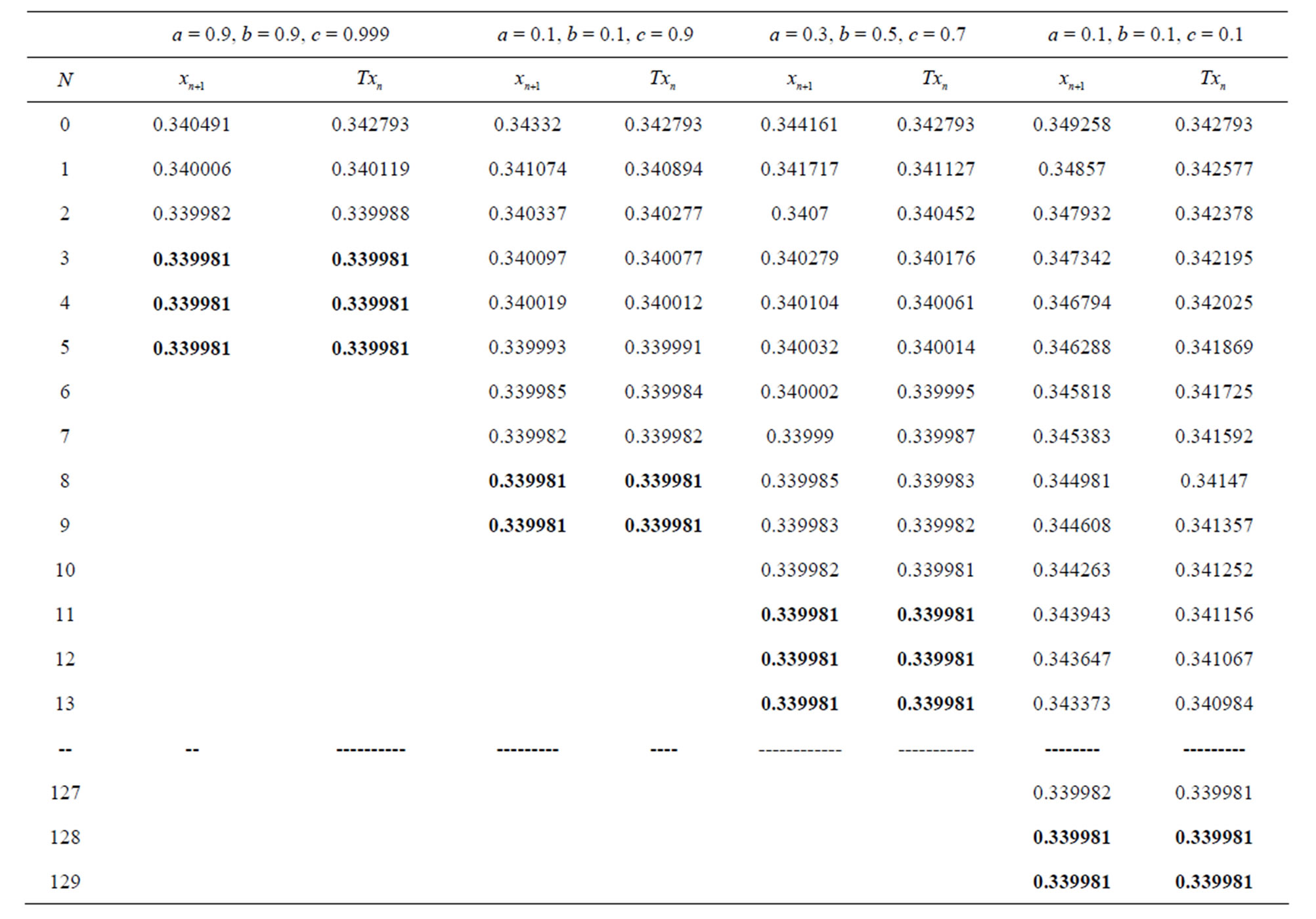
Table 15. Simple Noor for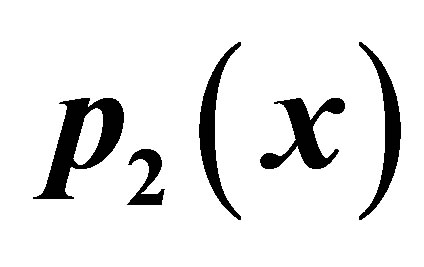 .
.
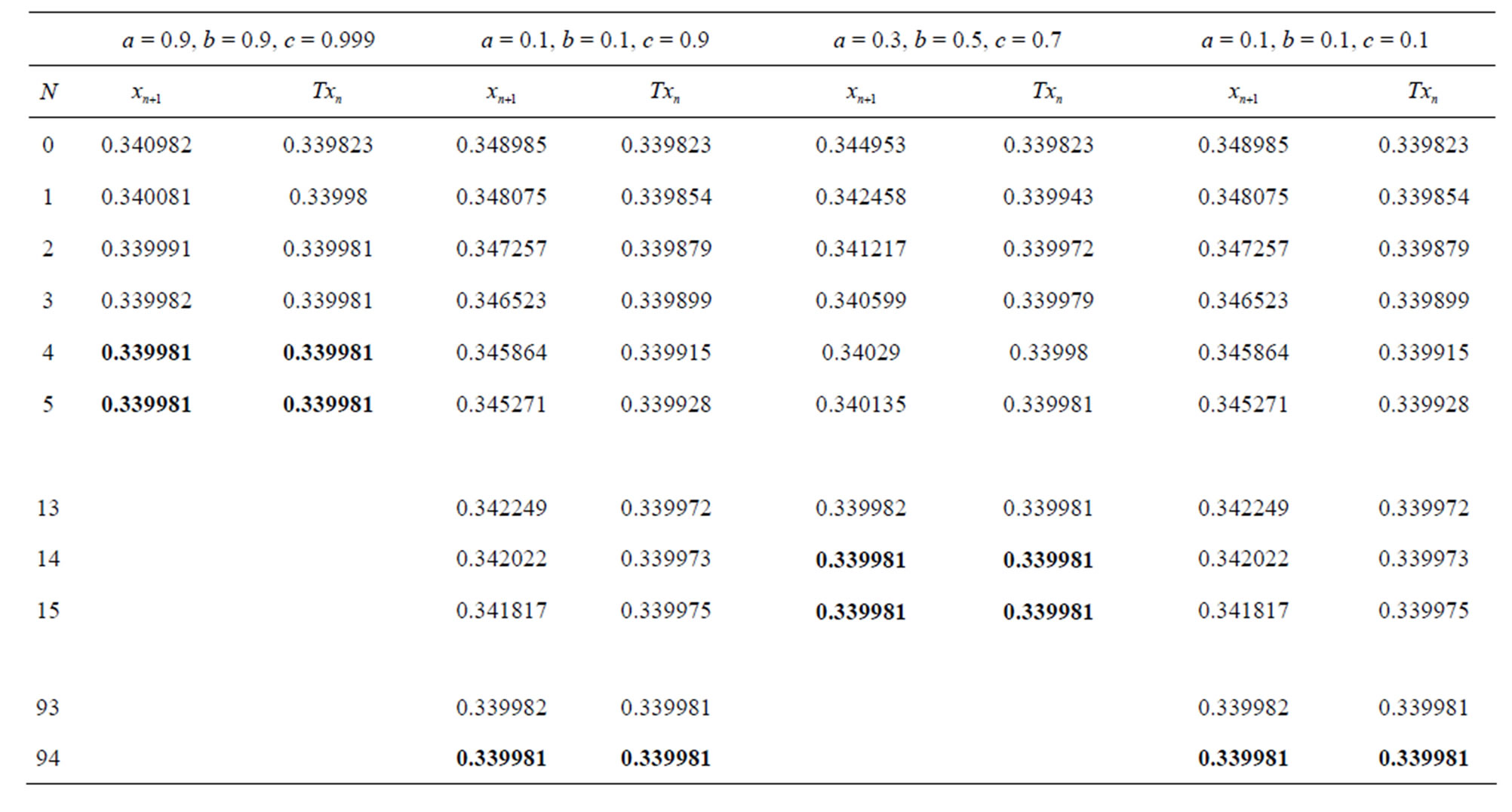
Table 16. Modified Noor for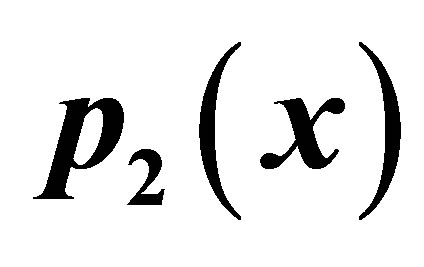 .
.
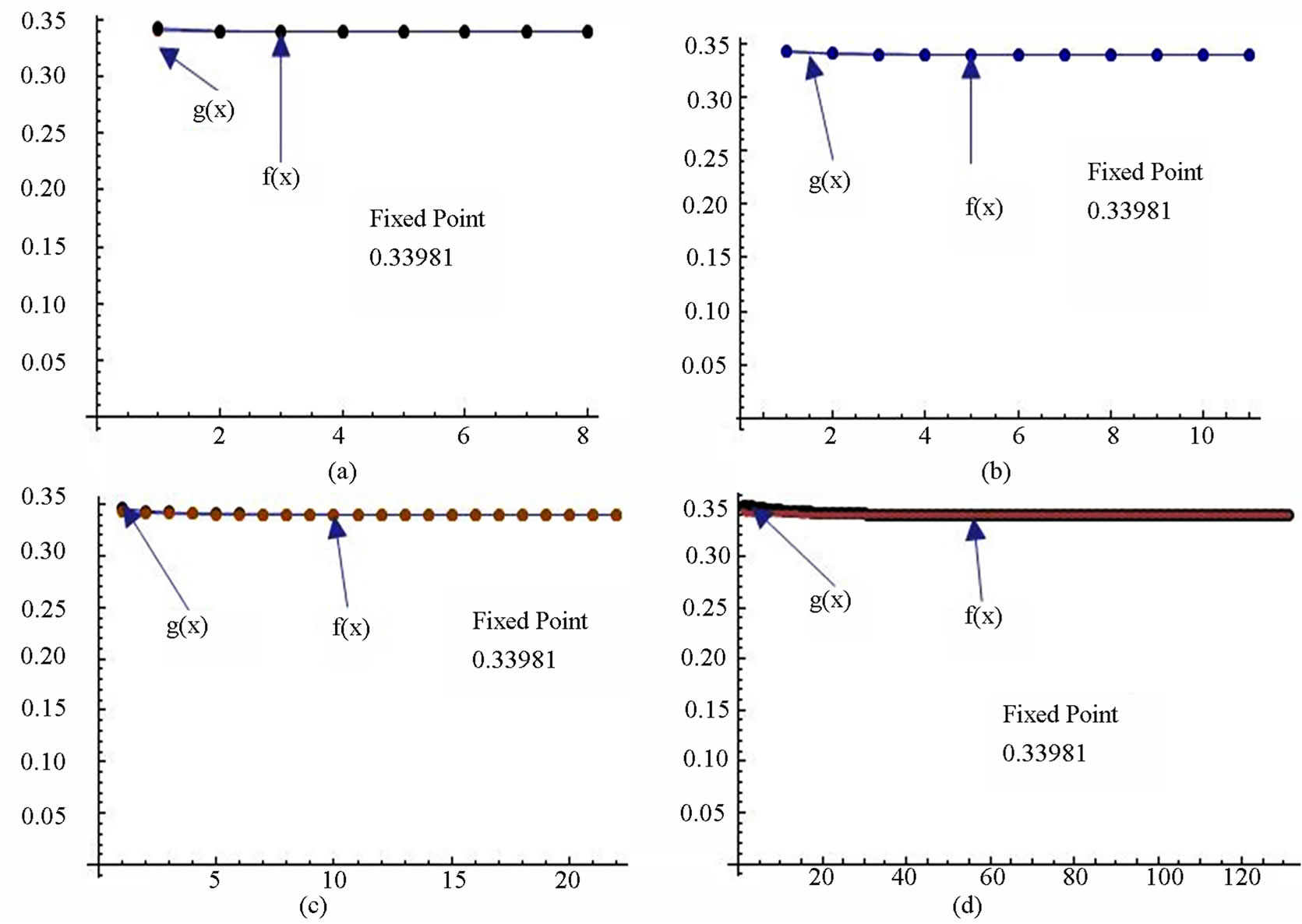
Figure 9. Graphical observations for simple Ishikawa iteration for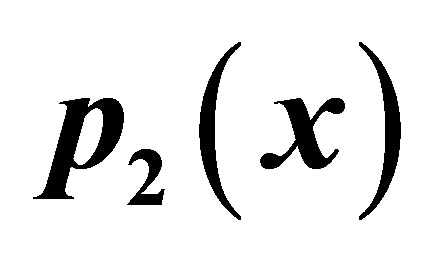 . Here (a)-(d) show the graph for Table 9. The merging point with value 0.33981 is fixed point.
. Here (a)-(d) show the graph for Table 9. The merging point with value 0.33981 is fixed point.
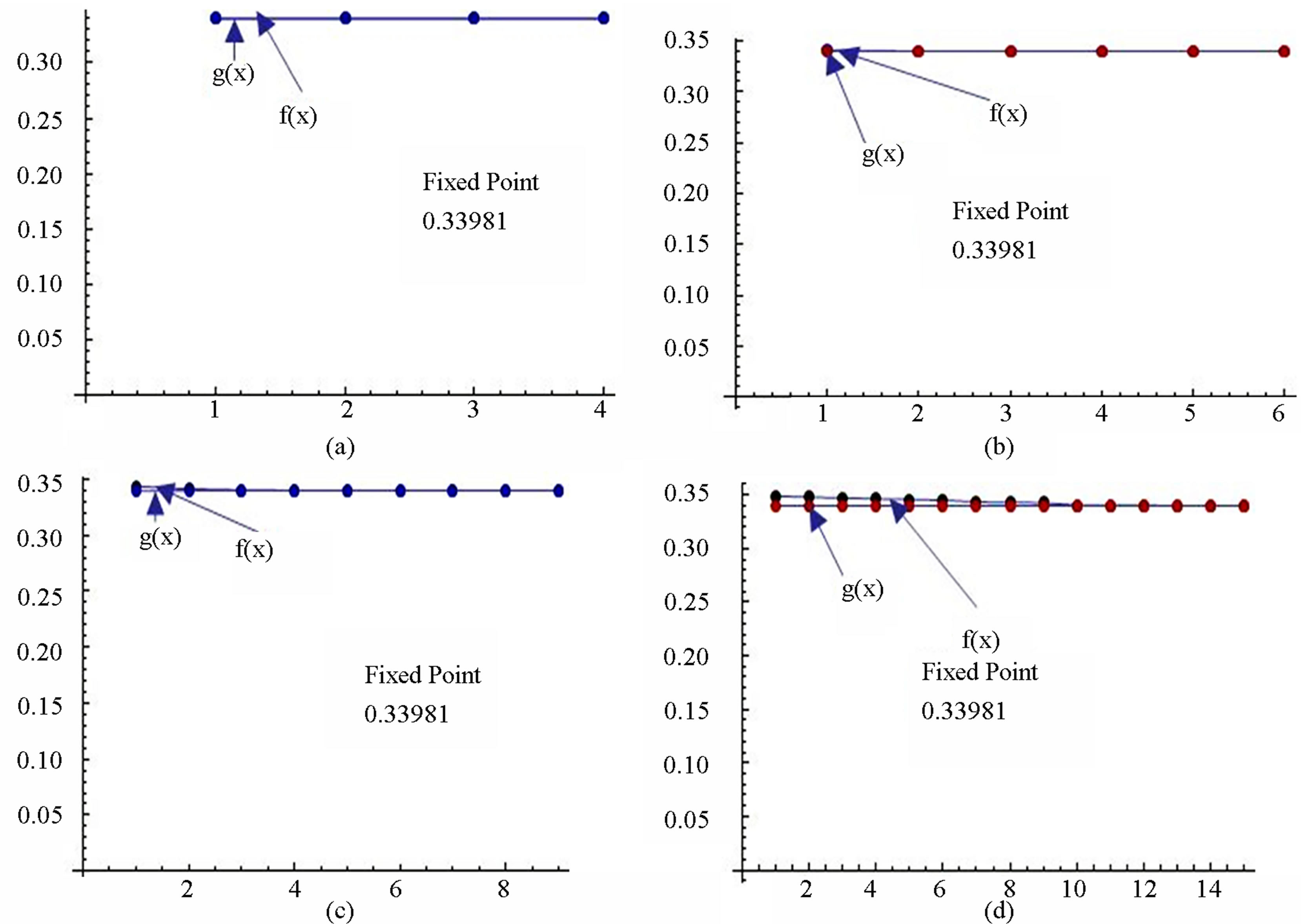
Figure 10. Graphical observations for new modified Ishikawa iteration for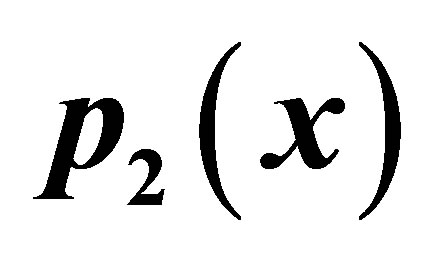 . Here (a)-(d) show the graph for Table 10. The merging point with value 0.33981 is fixed point.
. Here (a)-(d) show the graph for Table 10. The merging point with value 0.33981 is fixed point.
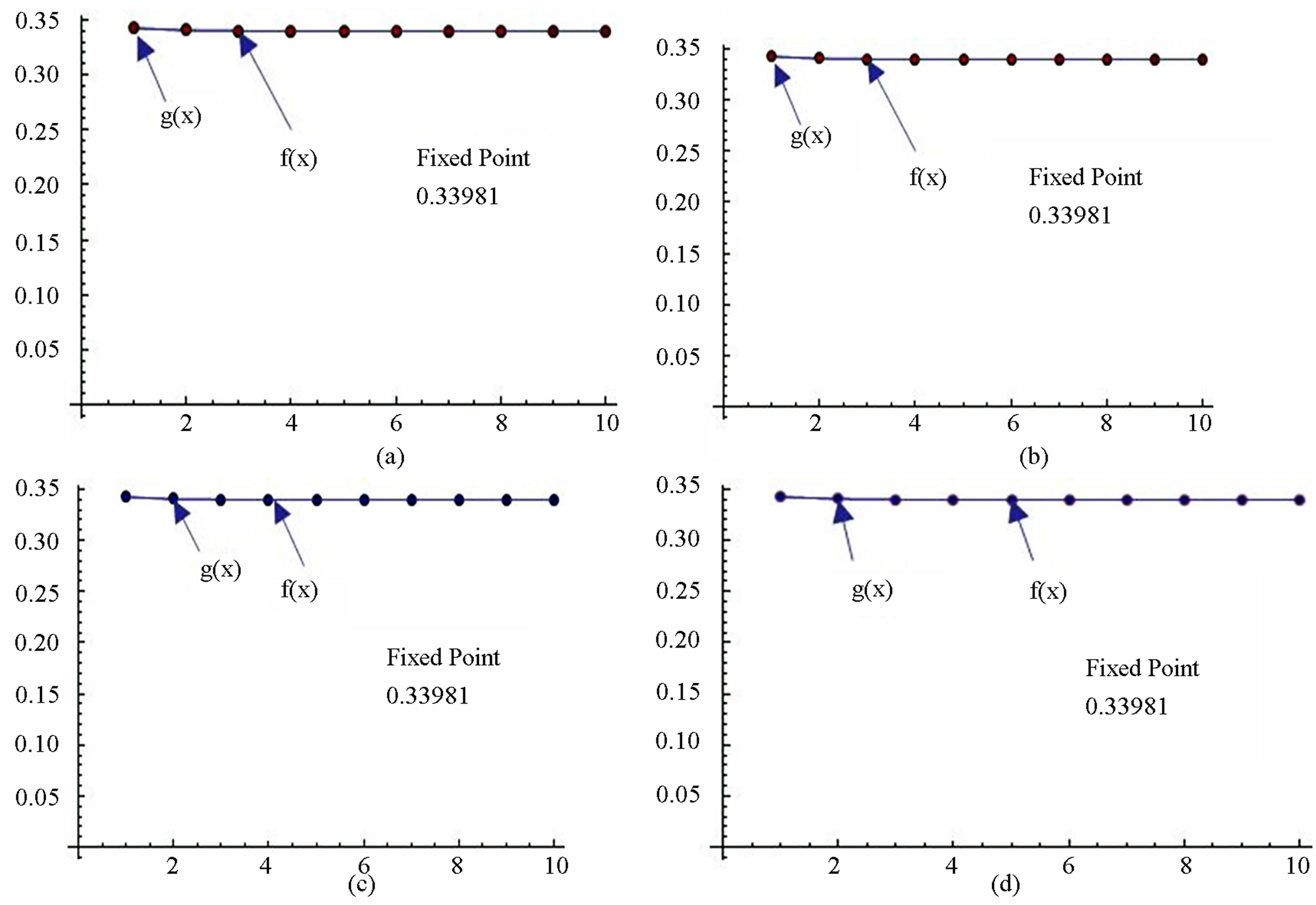
Figure 11. Graphical observations for simple Agarwal iteration for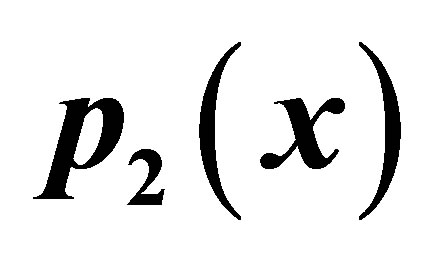 . Here (a)-(b) show the graph for Table 11. The merging point with value 0.33981 is fixed point.
. Here (a)-(b) show the graph for Table 11. The merging point with value 0.33981 is fixed point.
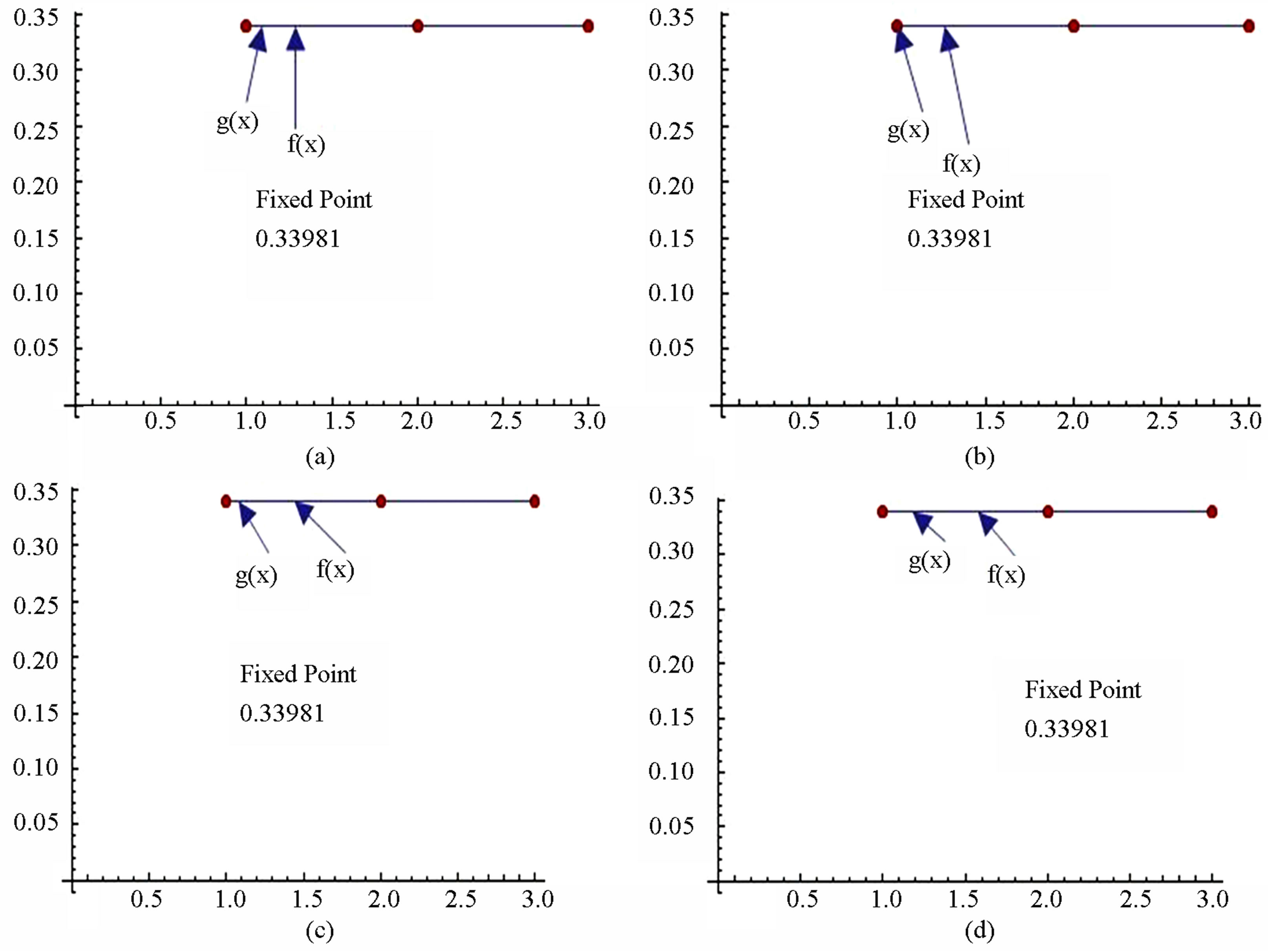
Figure 12. Graphical observations for simple Agarwal iteration for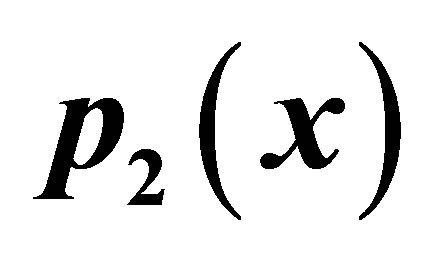 . Here (a)-(b) show the graph for Table 12. The merging point with value 0.33981 is fixed point.
. Here (a)-(b) show the graph for Table 12. The merging point with value 0.33981 is fixed point.
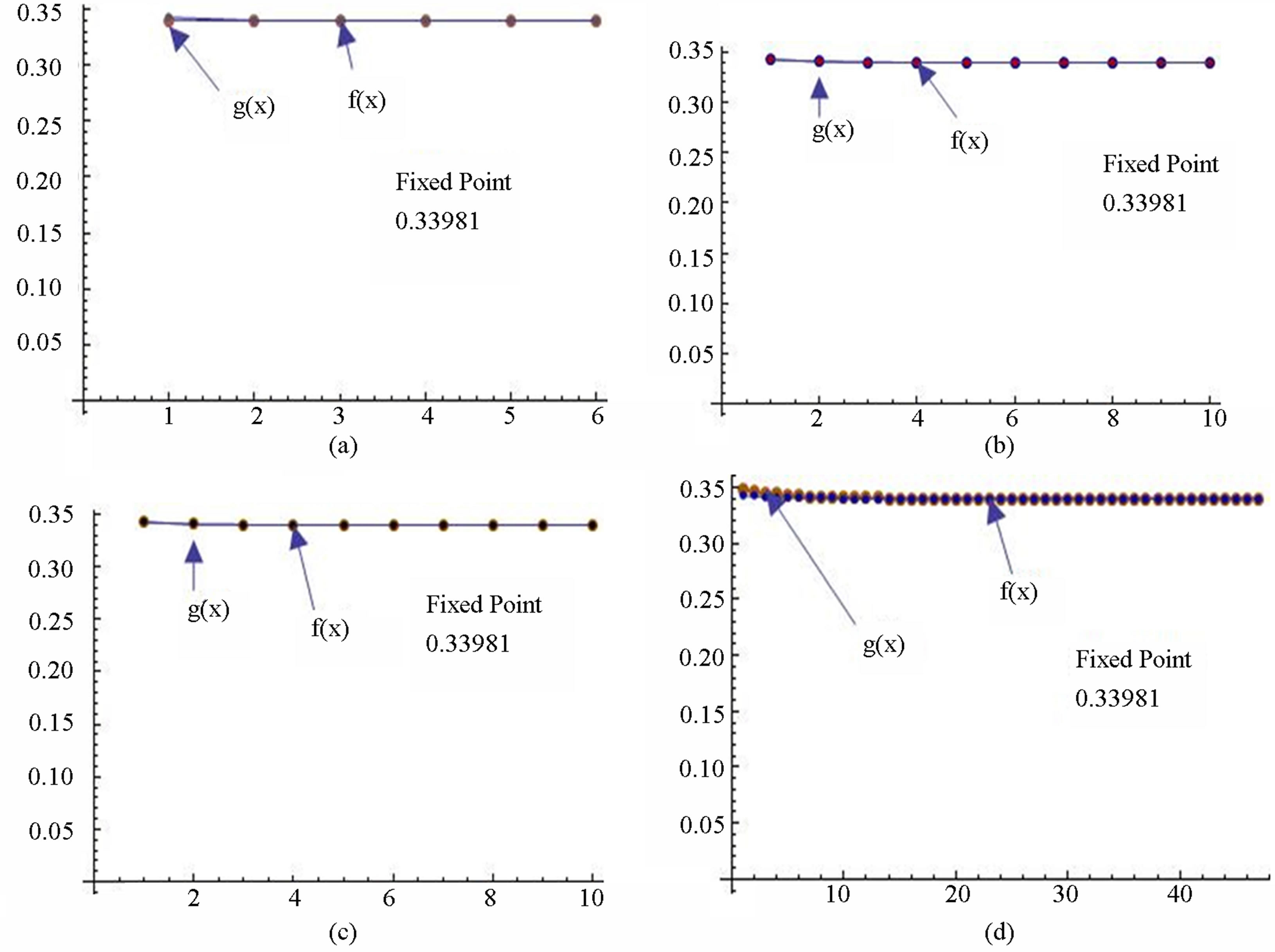
Figure 13. Graphical observations for simple SP iteration for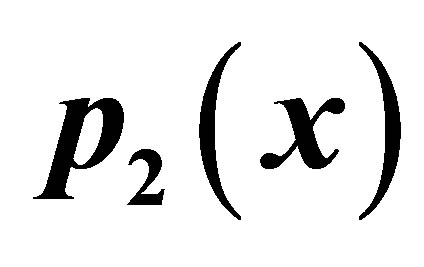 . Here (a)-(b) show the graph for Table 13. The merging point with value 0.33981 is fixed point.
. Here (a)-(b) show the graph for Table 13. The merging point with value 0.33981 is fixed point.
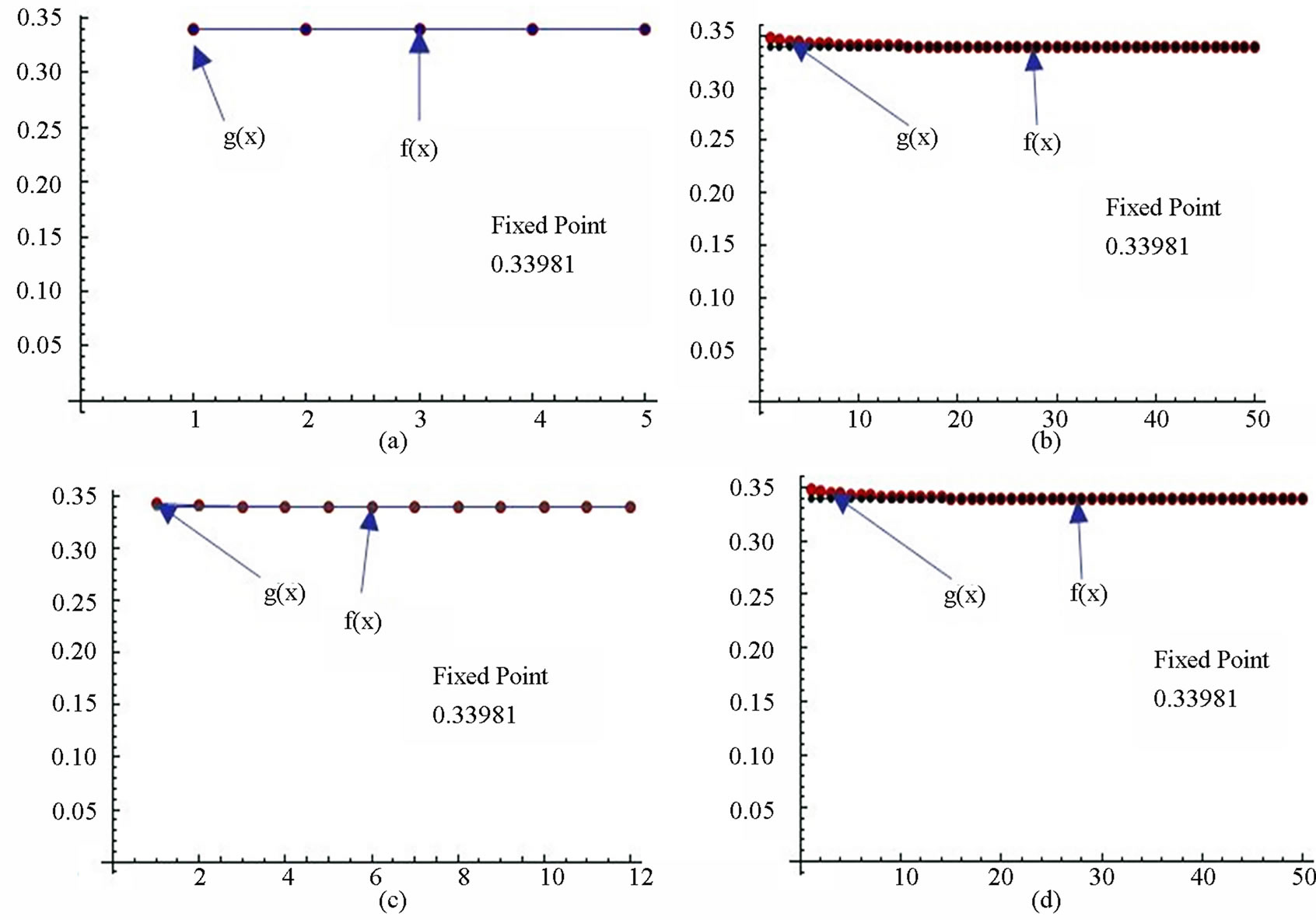
Figure 14. Graphical observations for new modified SP iteration for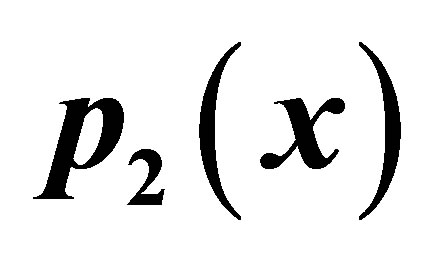 . Here (a)-(b) show the graph for Table 14. The merging point with value 0.33981 is fixed point.
. Here (a)-(b) show the graph for Table 14. The merging point with value 0.33981 is fixed point.
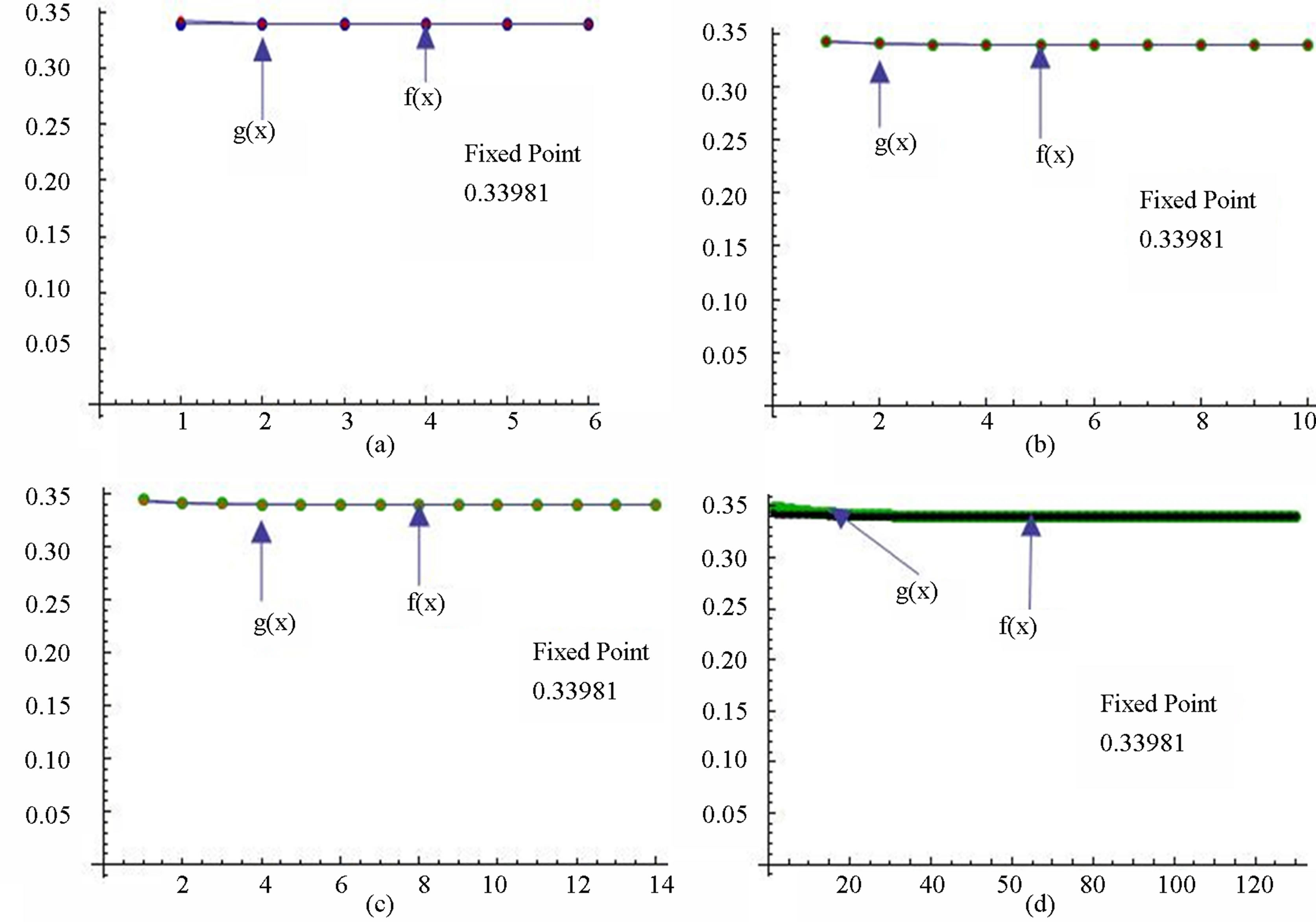
Figure 15. Graphical observations for simple Noor iteration for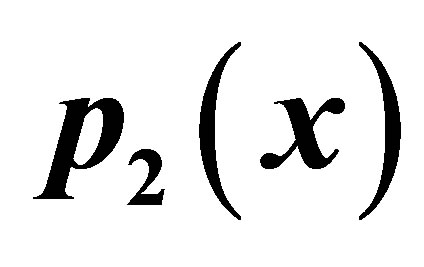 . Here (a)-(b) show the graph for Table 15. The merging point with value 0.33981 is fixed point.
. Here (a)-(b) show the graph for Table 15. The merging point with value 0.33981 is fixed point.
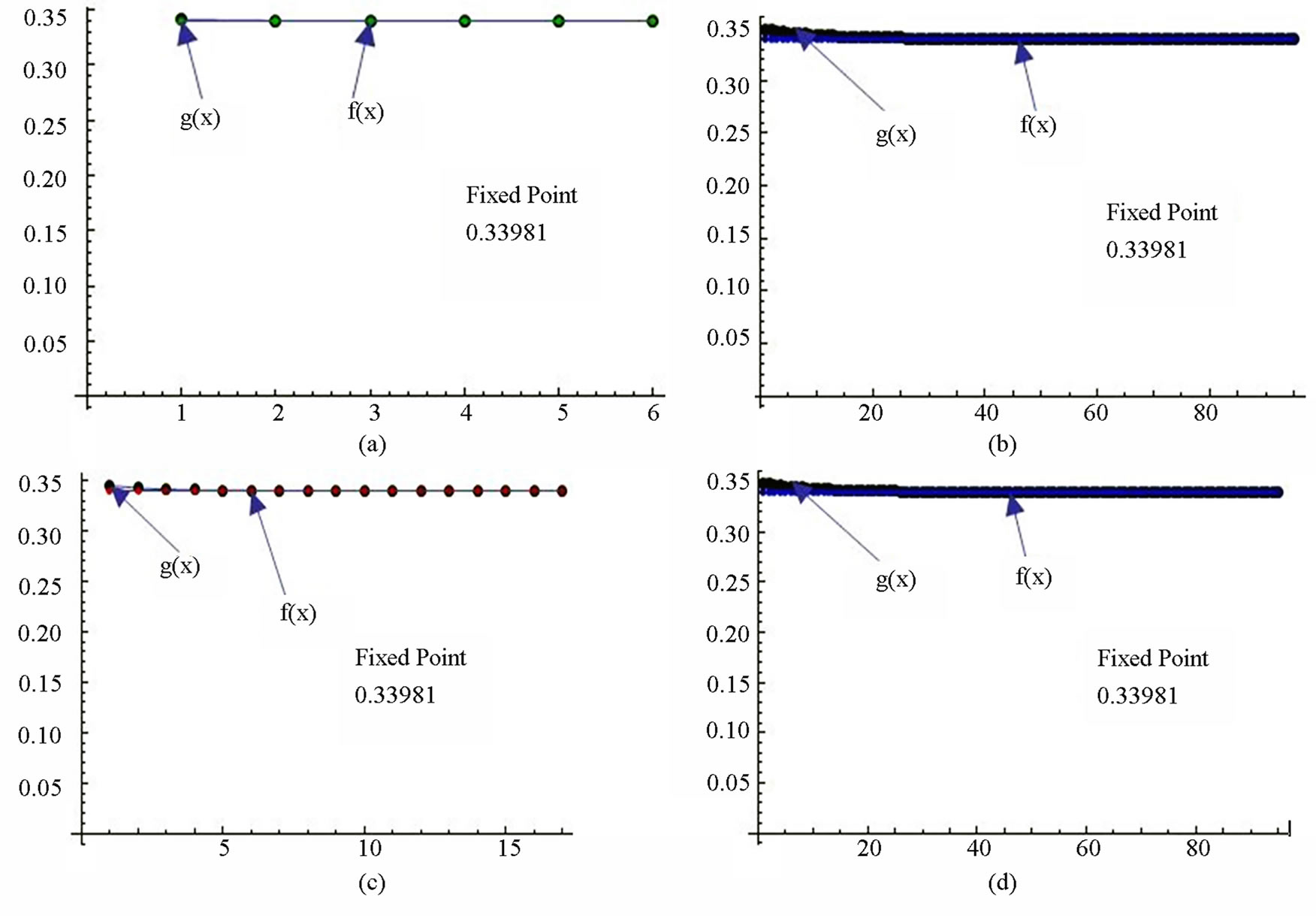
Figure 16. Graphical observations for new modified Noor iteration for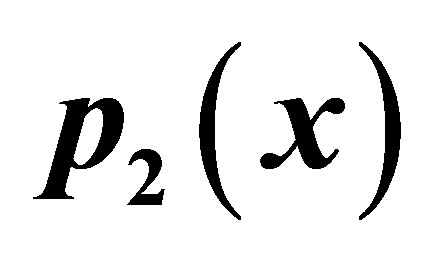 . Here(a)-(b) show the graph for Table 16. The merging point with value 0.33981 is fixed point.
. Here(a)-(b) show the graph for Table 16. The merging point with value 0.33981 is fixed point.
4. Observations
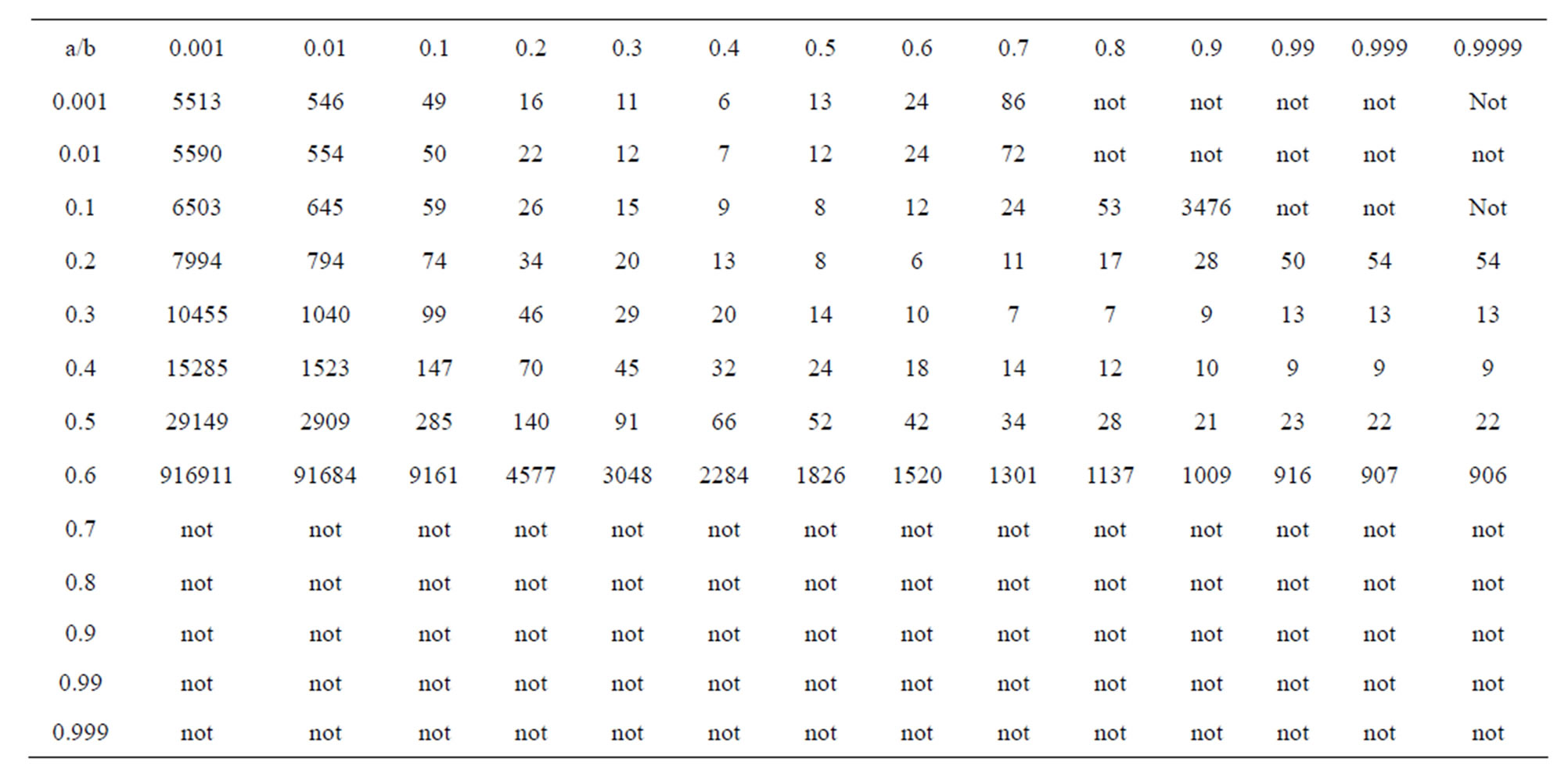
Table 17. Simple-Ishikawa for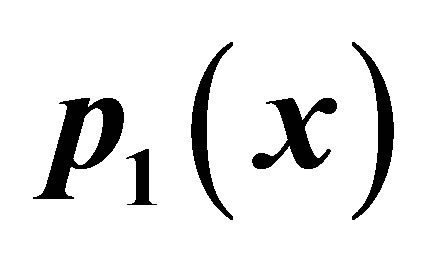 .
.
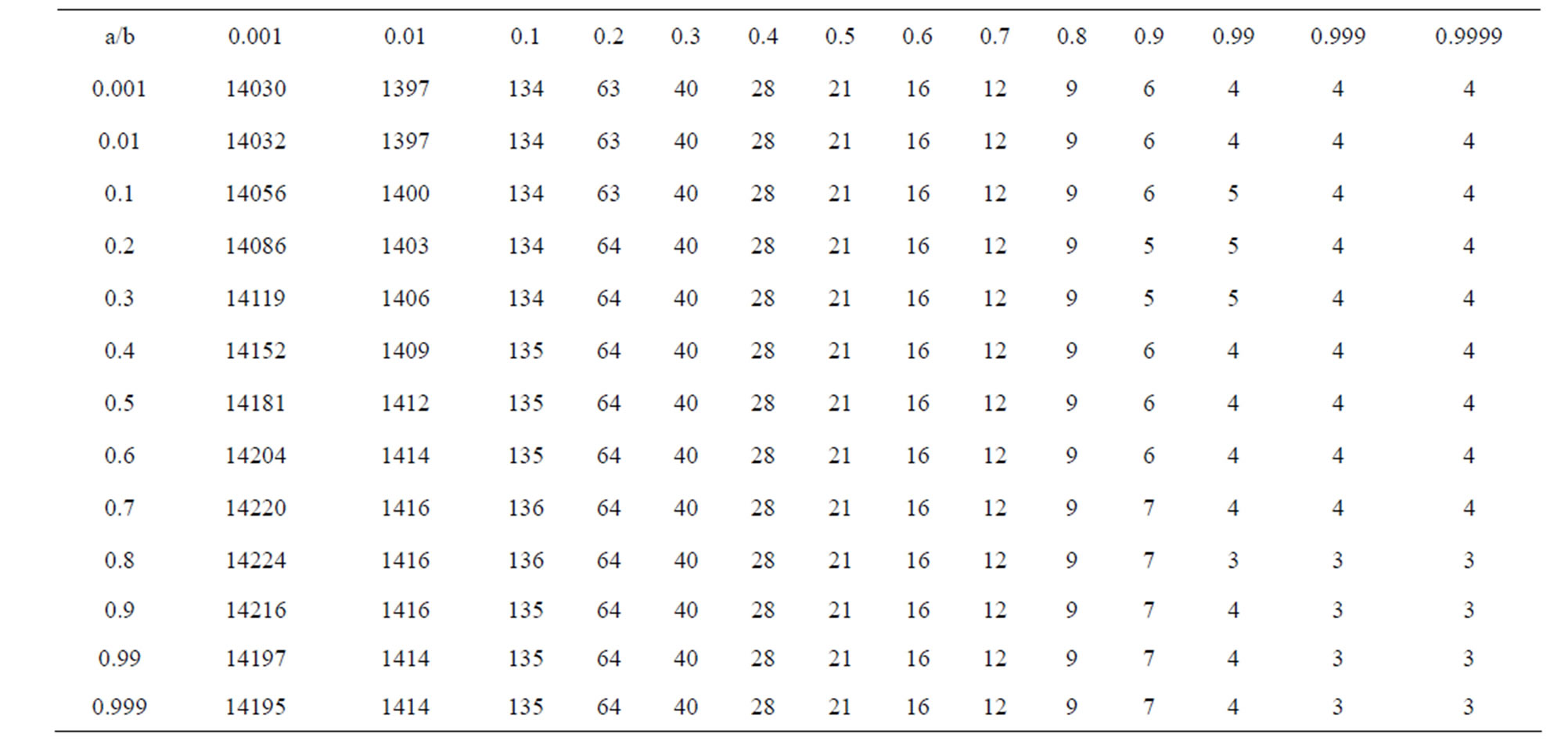
Table 18. Modified-Ishikawa for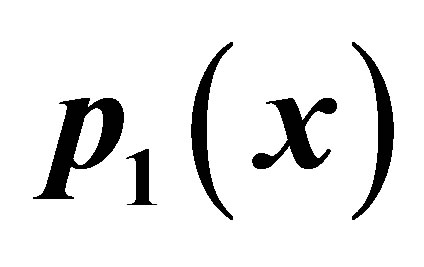 .
.

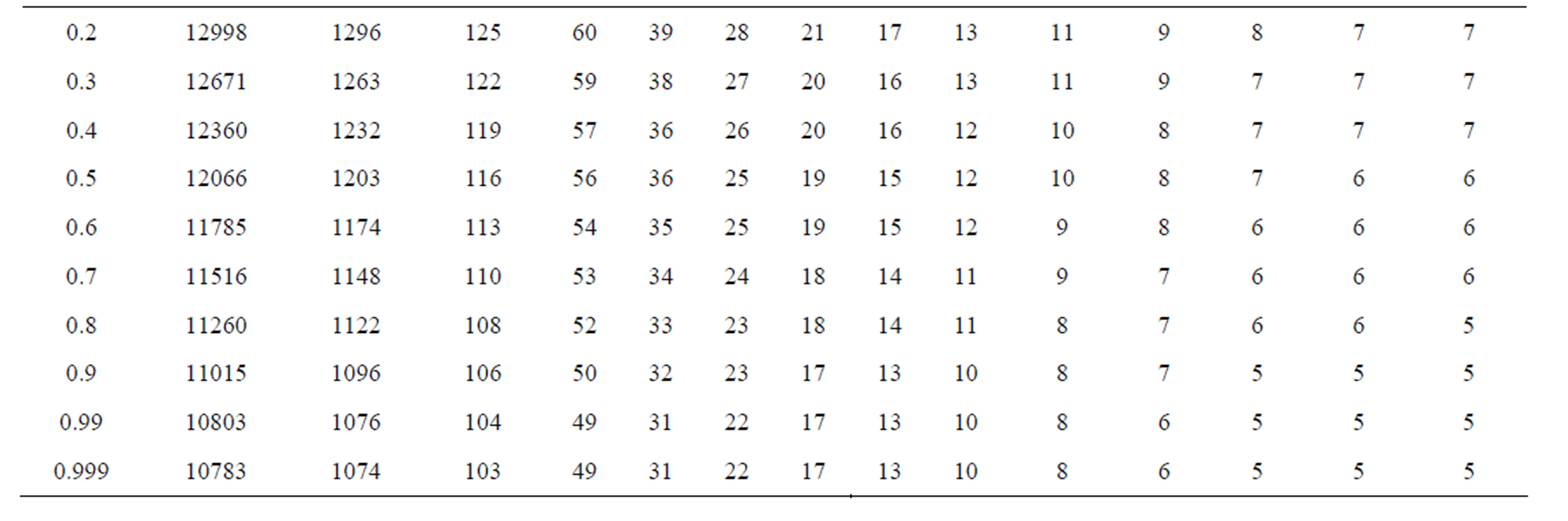
Table 19. Simple-Ishikawa for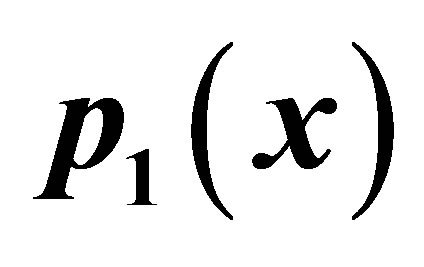 .
.
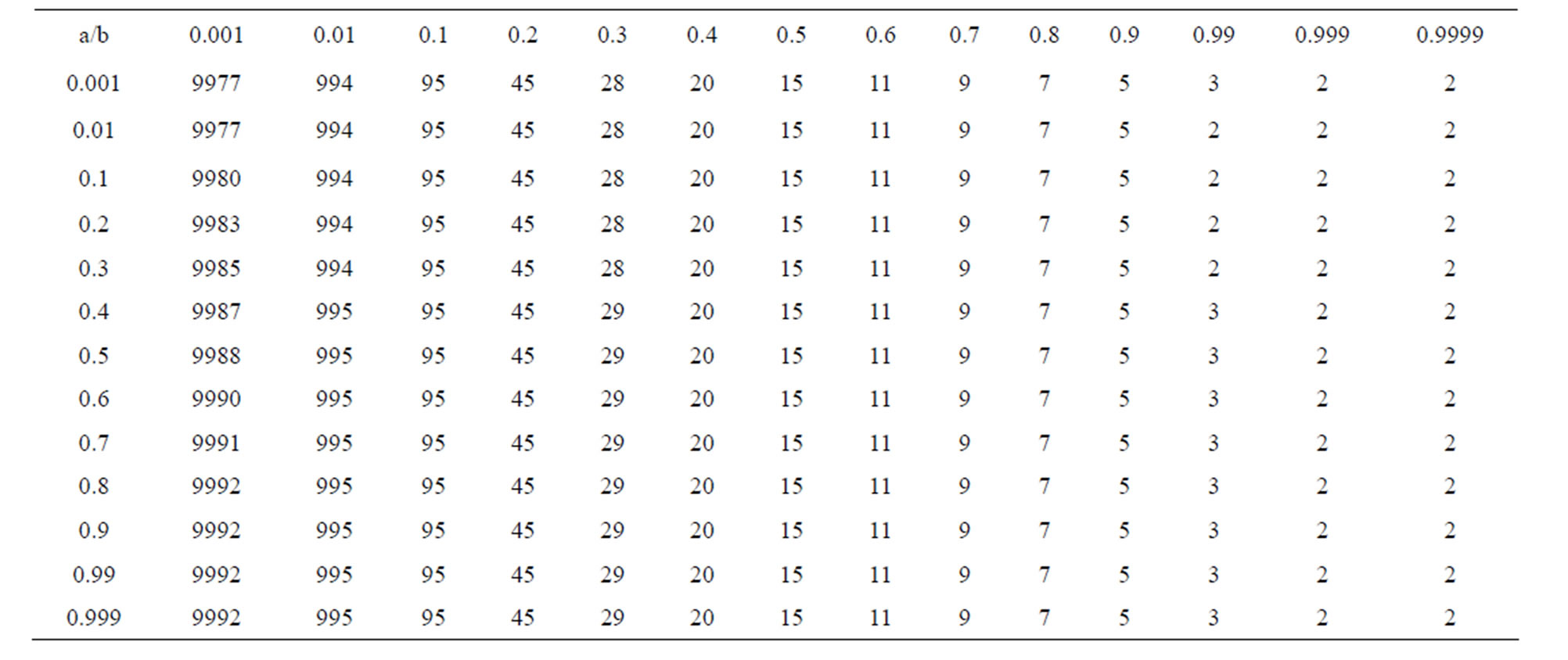
Table 20. Modified-Ishikawa for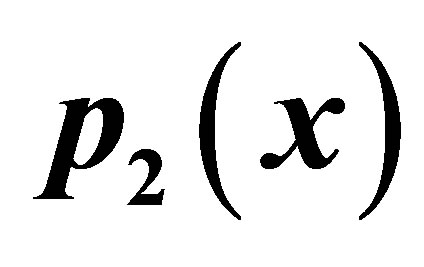 .
.
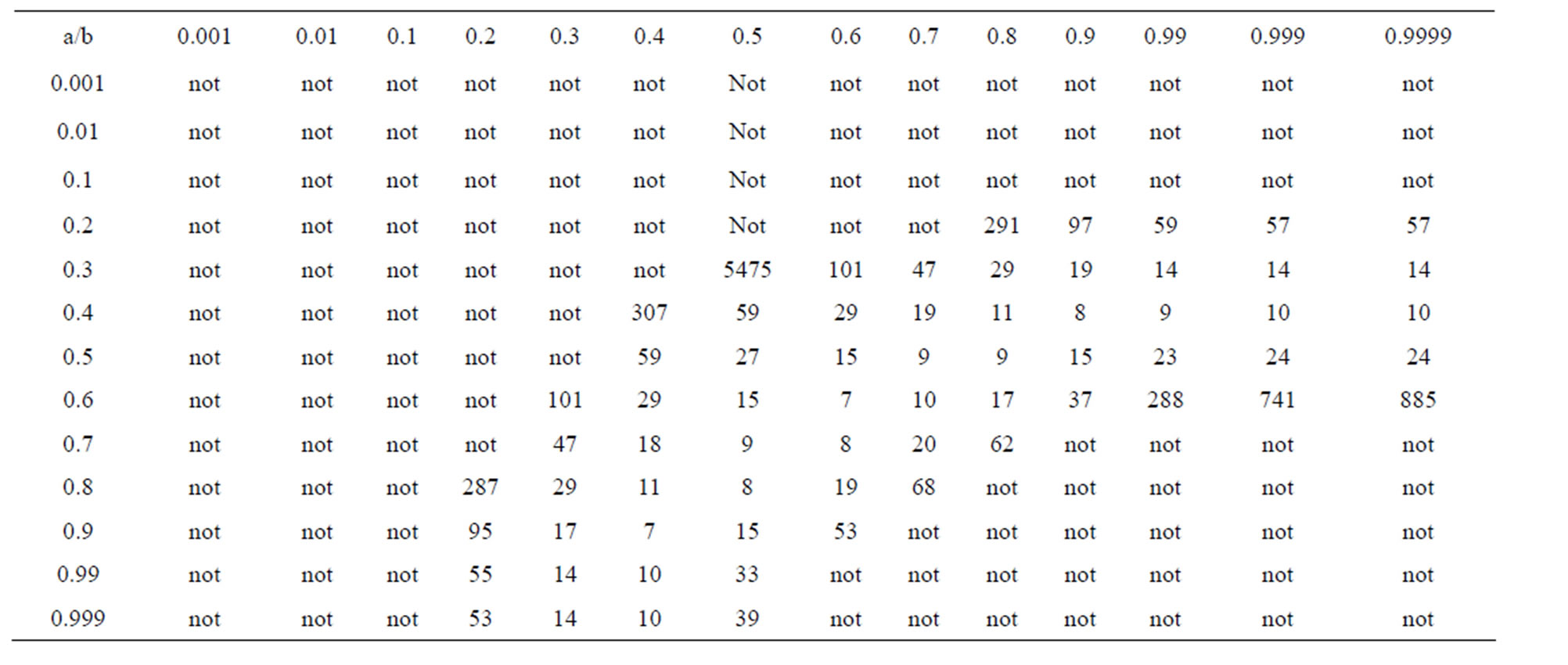
Table 21. Simple-Agarwal for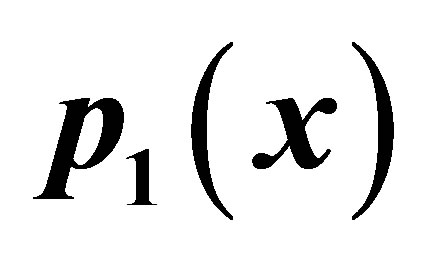 .
.
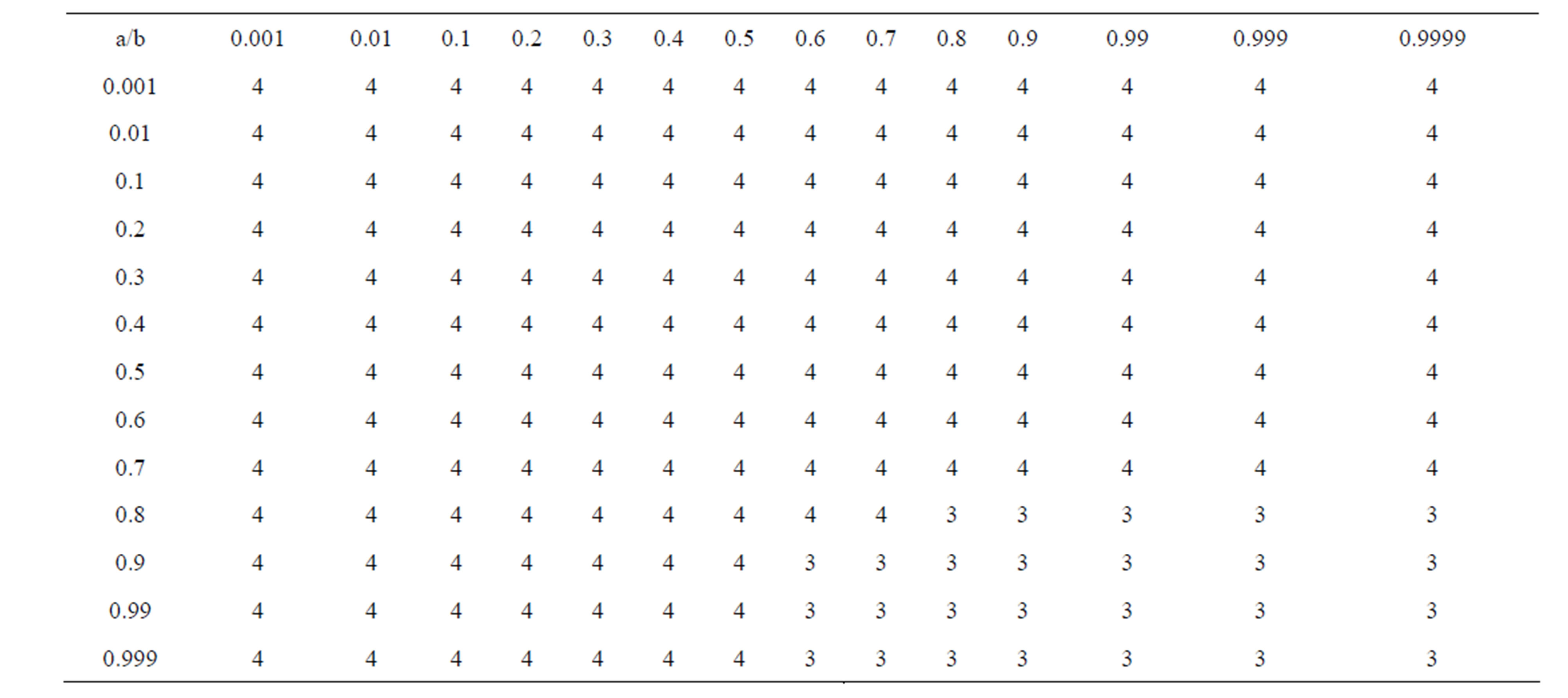
Table 22. Modified-Agarwal for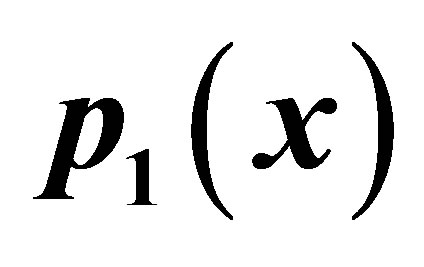 .
.
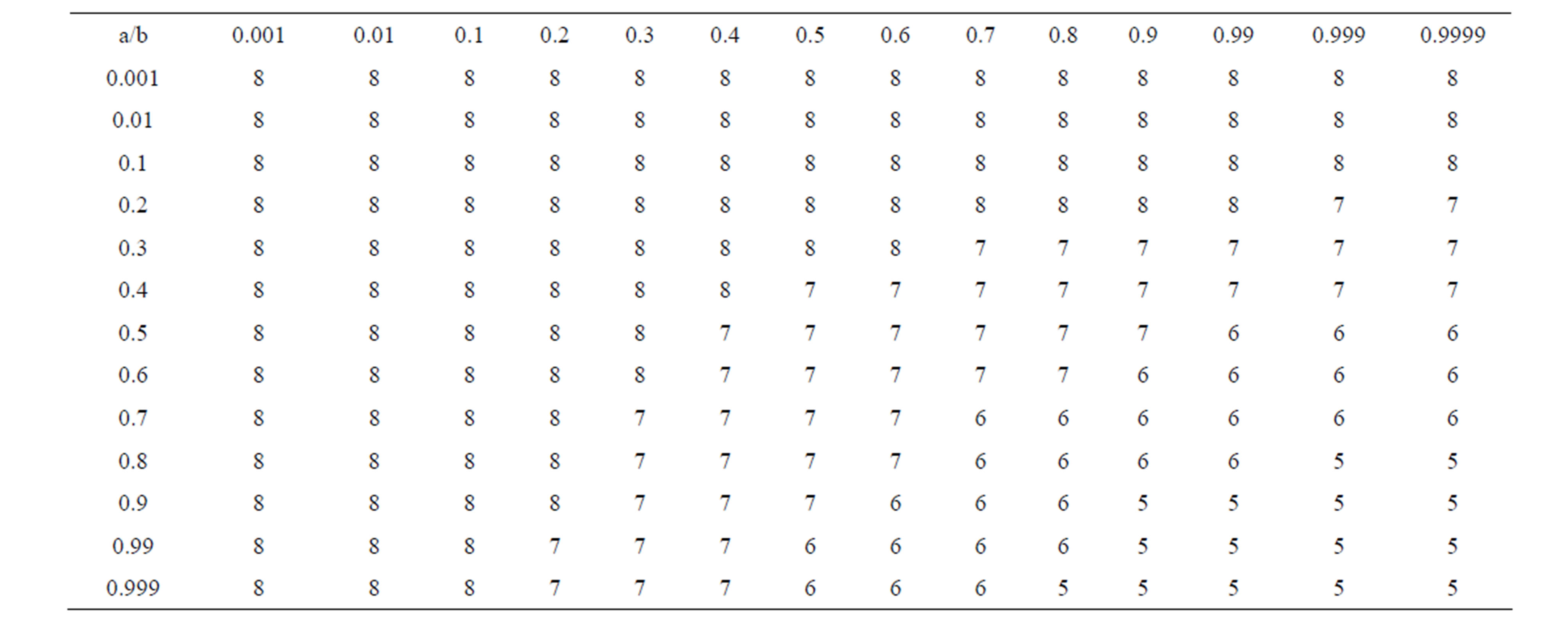
Table 23. Simple-Agarwal for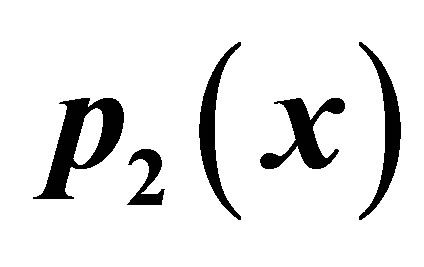 .
.
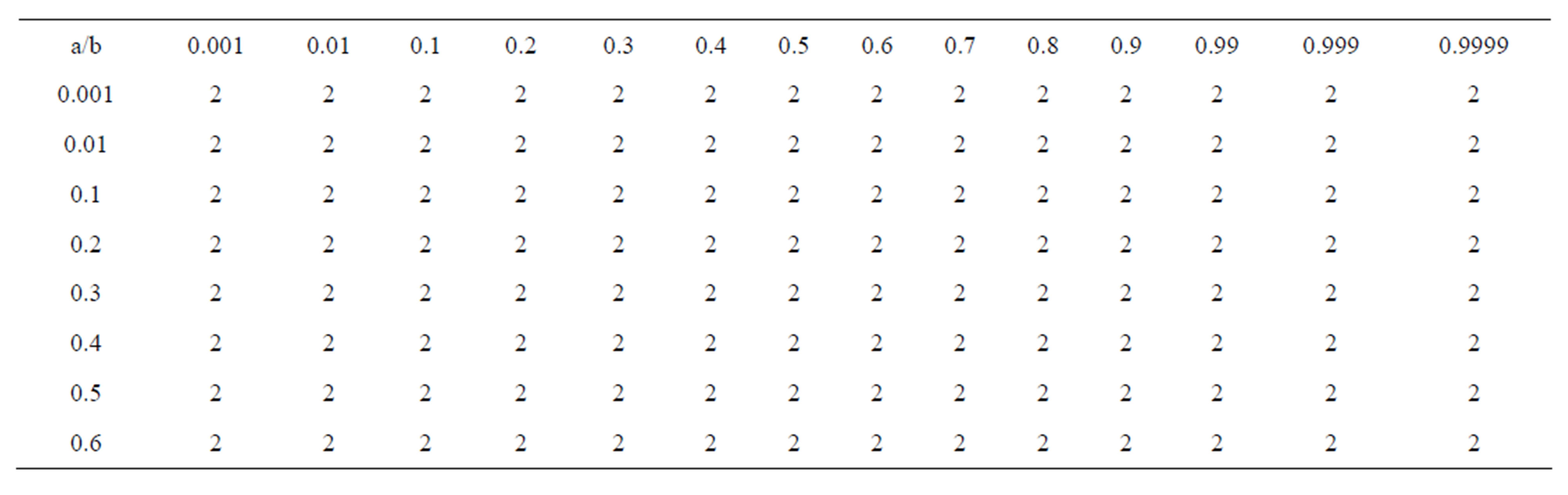

Table 24. Modified-Agarwal for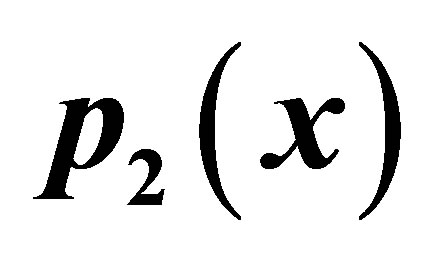 .
.
We have noted the converging step of different iterations in tabular form and compare the conversing step for different value of a, b, c. Now by comparative analysis we noted that
1) For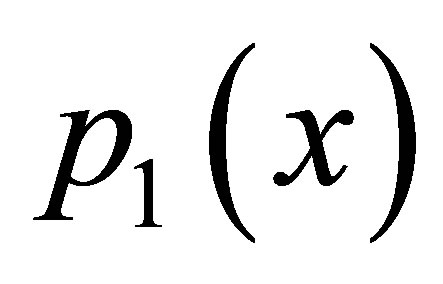 , simple Ishikawa do not converge for
, simple Ishikawa do not converge for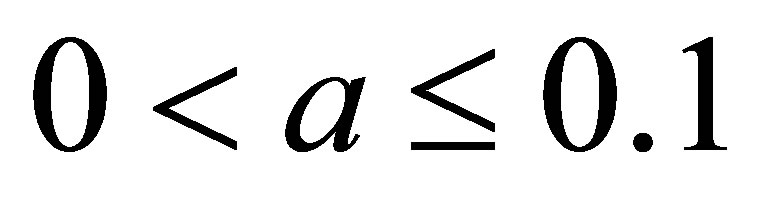 ,
, 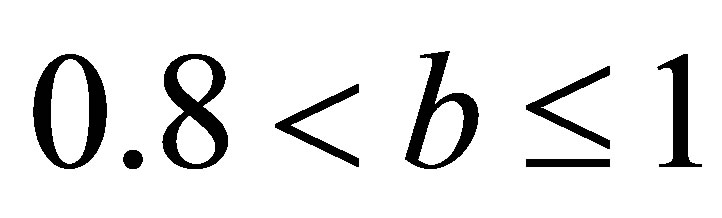 and
and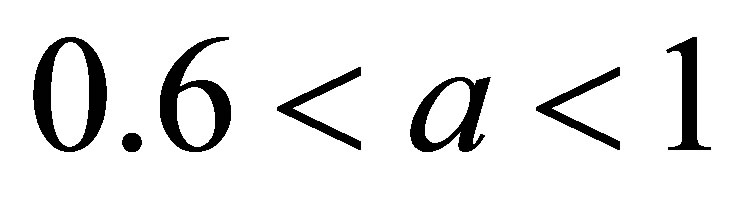 ,
, 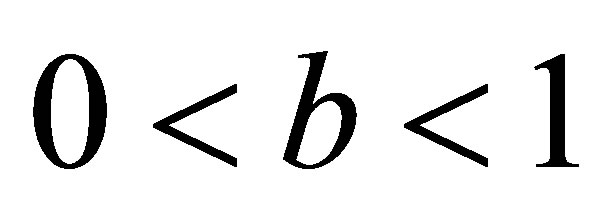 but new modified Ishikawa converges for all values of a and b converges faster than Ishikawa iteration for corresponding values of a, b. Also it converges at lesser step as a and b both approaches one but not so in case of simple Ishikawa as observe from Tables 17 and18. Similarly if we compare the both iterations for
but new modified Ishikawa converges for all values of a and b converges faster than Ishikawa iteration for corresponding values of a, b. Also it converges at lesser step as a and b both approaches one but not so in case of simple Ishikawa as observe from Tables 17 and18. Similarly if we compare the both iterations for 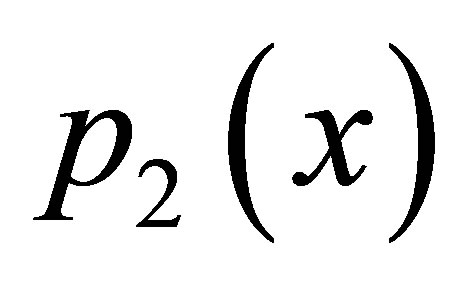 as observed from Tables 19 and 20 that as we increase values of a and b simultaneously than converging step decreases for both iterations but modified Ishikawa iteration converges at lesser step for
as observed from Tables 19 and 20 that as we increase values of a and b simultaneously than converging step decreases for both iterations but modified Ishikawa iteration converges at lesser step for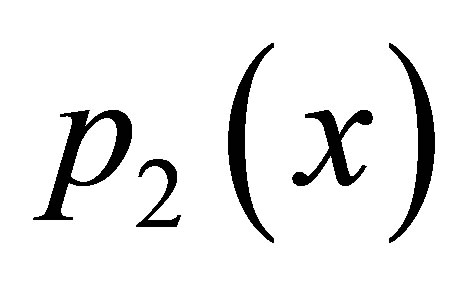 .
.
2) As observed from Tables 21 and 22 for 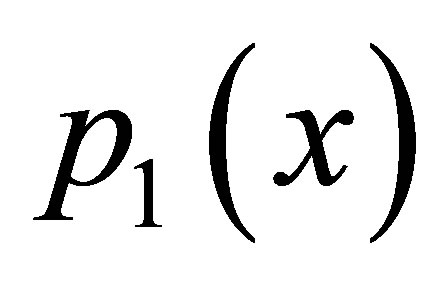 simple Agarwal et al. do not converge for all values of a and b it converges for
simple Agarwal et al. do not converge for all values of a and b it converges for
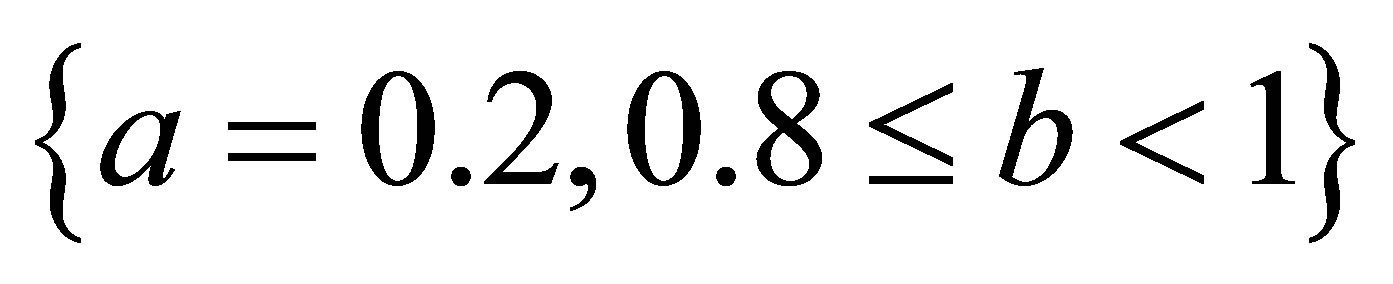 ,
, 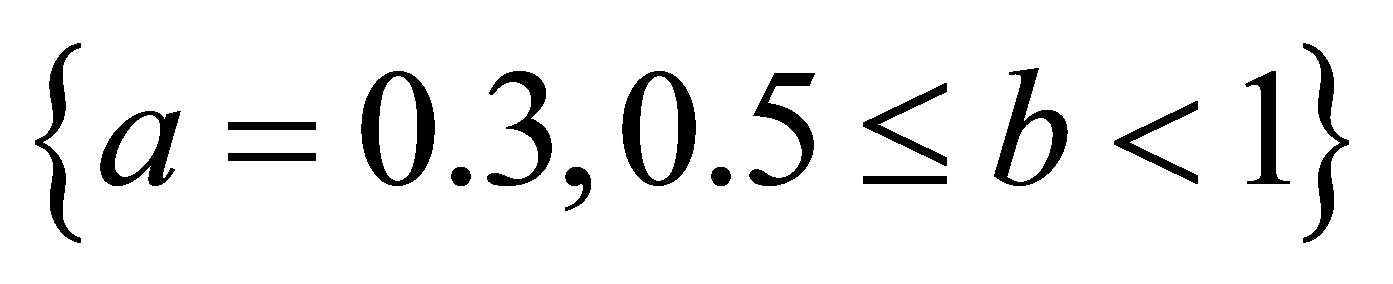 ,
, 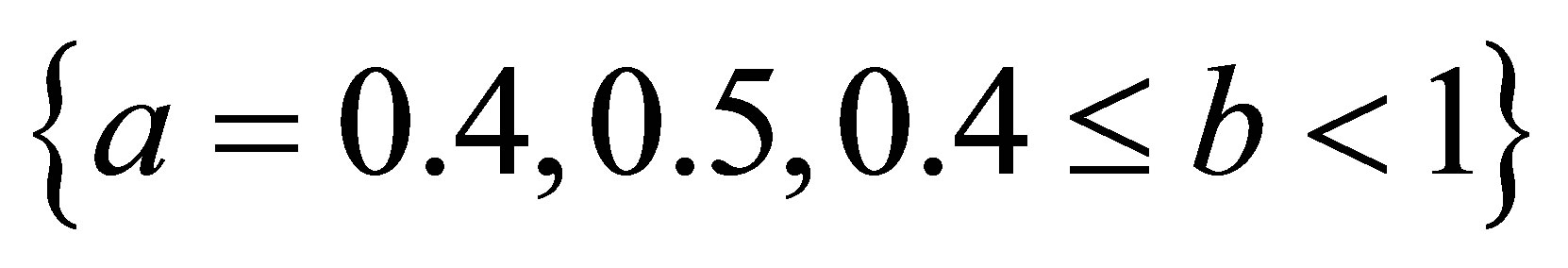 ,
, 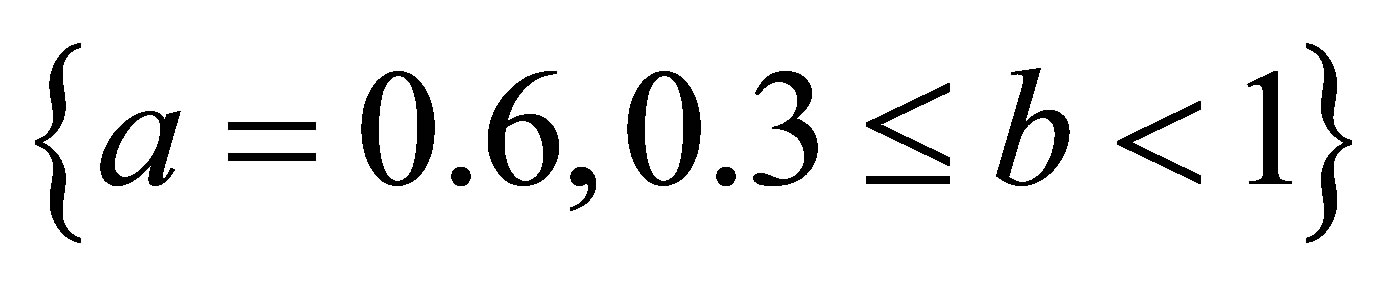 ,
, 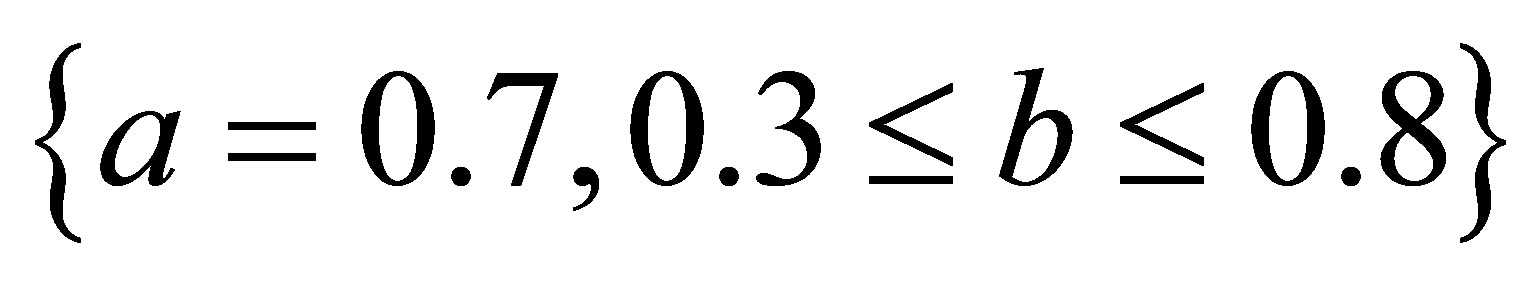 ,
, 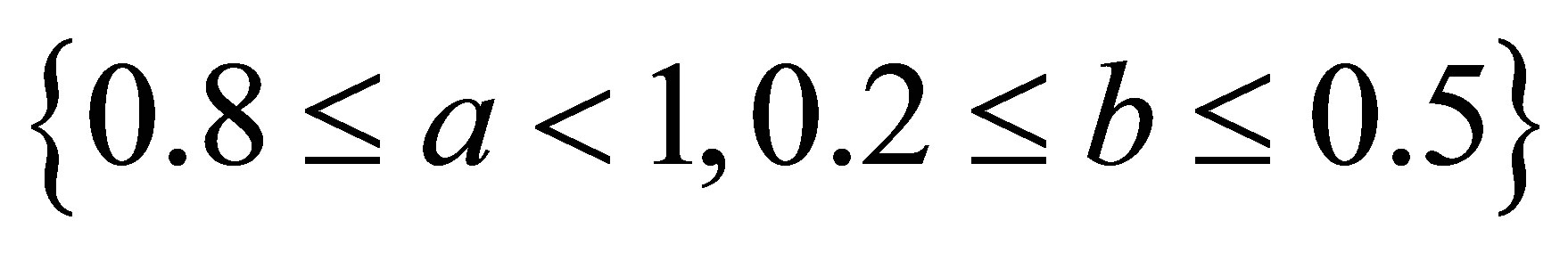
but modified new Agarwal et al. iteration converges at lesser step for all values of a, b. For  both iterations converge for all values of a and b but modified iteration converges faster than simple iteration 3) The simple SP iteration converges at lesser step for
both iterations converge for all values of a and b but modified iteration converges faster than simple iteration 3) The simple SP iteration converges at lesser step for 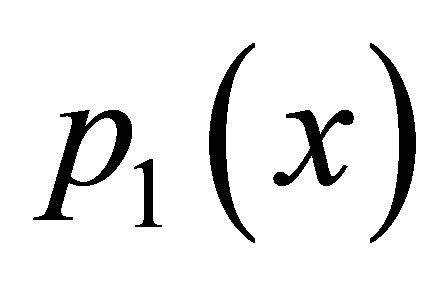 when a = 1/2, b = 1/2, c = 1/2 as we increases a and b the step of convergence increases. But do not converge if a and b approaches to one whereas modified new SP iteration converges for all values of a, b, c and at lesser step than simple SP. For
when a = 1/2, b = 1/2, c = 1/2 as we increases a and b the step of convergence increases. But do not converge if a and b approaches to one whereas modified new SP iteration converges for all values of a, b, c and at lesser step than simple SP. For 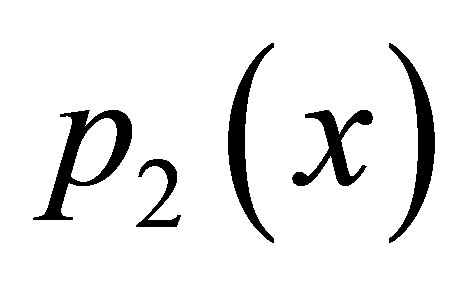 both iteration converges for all values of a, b and c but modified new SP converge faster than Simple SP iteration.
both iteration converges for all values of a, b and c but modified new SP converge faster than Simple SP iteration.
4) For simple Noor and modified new Noor iteration result is same as for SP and modified new SP iterations.
5. Conclusion
By the observation formed from the program and graph drawn in C++ and Mathematica for 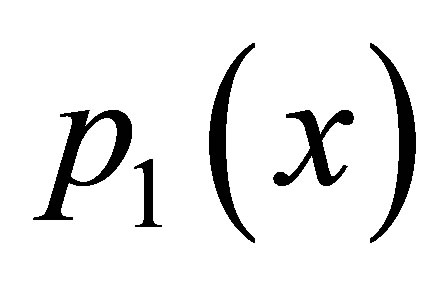 and
and 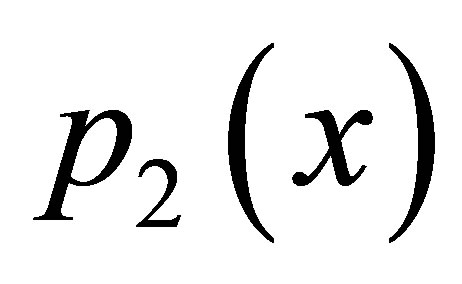 polynomial, we conclude that the modified Ishikawa, Agarwal et al., SP, Noor are faster than simple Ishikawa, Agarwal et al., SP, Noor; but if we compare modified Ishikawa, Agarwal et al., SP, Noor with decreasing order of rate of convergence of modified Agarwal et al., SP, Noor, Ishikawa, modified new Agarwal et al. have consistent rate of convergence. The graphs drawn are based on data formed from C++ program and plot the data in mathematica to show the fixed point.
polynomial, we conclude that the modified Ishikawa, Agarwal et al., SP, Noor are faster than simple Ishikawa, Agarwal et al., SP, Noor; but if we compare modified Ishikawa, Agarwal et al., SP, Noor with decreasing order of rate of convergence of modified Agarwal et al., SP, Noor, Ishikawa, modified new Agarwal et al. have consistent rate of convergence. The graphs drawn are based on data formed from C++ program and plot the data in mathematica to show the fixed point.
REFERENCES
- J. Biazar and A. Amirteimoori, “An Improvement to the Fixed Point Iterative Method,” Applied Mathematics and Computation, Vol. 182, No. 1, 2006, pp. 567-571. http://dx.doi.org/10.1016/j.amc.2006.04.019
- B. Prasad and R. Sahni, “Convergence of Some General Iterative Schemes,” International Journal of Mathematical Analysis, Vol. 5, No. 25, 2011, pp. 1237-1242.
- S. Ishikawa, “Fixed Points by a New Iteration Method,” Proceedings of the American Mathematical Society, Vol. 44, No. 1, 1974, pp. 147-150. http://dx.doi.org/10.1090/S0002-9939-1974-0336469-5
- R. P. Agarwal, D. O’Regan and D. R. Sahu, “Iterative Construction of Fixed Points of Nearly Asymptotically Non-Expansive Mappings,” Journal of Nonlinear and Convex Analysis, Vol. 8, No. 1, 2007, pp. 61-79.
- M. A. Noor, “New Approximation Schemes for General Variational Inequalities,” Journal of Mathematical Analysis and Applications, Vol. 251, No. 1, 2000, pp. 217-229. http://dx.doi.org/10.1006/jmaa.2000.7042
- W. Phuengrattana and S. Suantai, “On the Rate of Convergence of Mann, Ishikawa, Noor and SP Iterations for Continuous Functions on an Arbitrary Interval,” Journal of Computational and Applied Mathematics, Vol. 235, No. 9, 2011, pp. 3006-3014. http://dx.doi.org/10.1016/j.cam.2010.12.022
- E. Babolian and J. Biazar, “On the Order of Convergence of Adomian Method,” Applied Mathematics and Computation, Vol. 130, No. 2-3, 2002, pp. 383-387. http://dx.doi.org/10.1016/S0096-3003(01)00103-5
NOTES
*Corresponding author.

