American Journal of Computational Mathematics
Vol.3 No.1(2013), Article ID:28991,10 pages DOI:10.4236/ajcm.2013.31002
Computational Results on Quadratic Functional Model for the Tokens of Nuclear Safety
Department of Mathematics, University of Ilorin, Ilorin, Nigeria
Email: omolehin_joseph@yahoo.com, *jubril_aminu@yahoo.co.uk, krauf@unilorin.edu.ng
Received August 2, 2012; revised October 15, 2012; accepted November 25, 2012
Keywords: Control Operator; Nuclear Tokens; CGM Algorithm; Optimal
ABSTRACT
In this work, Nuclear Reactor safety was modeled inform of quadratic functional. The nuclear tokens are structured and used as elements of the control matrix operator in our quadratic functional. The numerical results obtained through Conjugate Gradient Method (CGM) algorithm identify the optimal level of safety required for Nuclear Reactor construction at any particular situation.
1. Introduction
Nuclear reactors accidents occur when the coolant ceases to work, the reactor will be overheated and produced excess heat in form of steam. Most of the internal component of the reactors are made from zirconium in zircalloy cladding used in fuel rods oxidizes in reaction with steam to produce zirconium oxide and hydrogen [1]. When mixed with air, hydrogen is flammable and its detonation will destroy the containment structure which house the reactor. As a result of this, radiation is released to the surrounding causing environmental hazard [2-5]. This work derived the equations for the rate of heat of different reactors from energy balance equations. These equations are structured in parametric form to obtain the basis of the mathematical model solvable by the Conjugate Gradient Method (CGM) algorithm. The obtained numerical results generate the minimal disaster associated with nuclear reactors.
2. Energy Balance
The following results were obtained through Energy Balance Equations. See [6]. For the purpose of our study, we shall arrange the equations in terms of the rate of heat.
2.1. The Energy Balance for Chemical Reactors
Let us consider arbitrary reactor volume element. From the conservation of energy for a reactor system we obtain the following:
 (1)
(1)
Equation (1) can be represented mathematically as:
 (2)
(2)
where  means energy per unit mass,
means energy per unit mass,  is the mass inflow,
is the mass inflow, 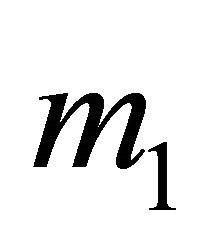 is the mass outflow and
is the mass outflow and  is the rate of heat.
is the rate of heat.
The total rate of work done on a reactor system is expressed as follows:
 (3)
(3)
where  = total rate of work done,
= total rate of work done,
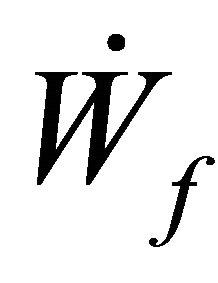 = rate of work done by flowstream
= rate of work done by flowstream
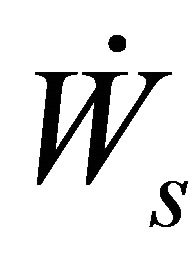 = rate of work done by shaft
= rate of work done by shaft
 = rate of work done by boundary The Rate of work done Flowstream can be represented by
= rate of work done by boundary The Rate of work done Flowstream can be represented by 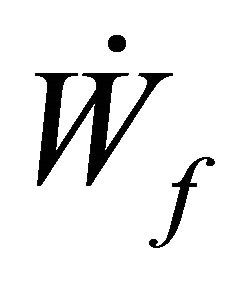 such that
such that
 (4)
(4)
where  = area of reactor (inflow),
= area of reactor (inflow),  = area of reactor (outflow),
= area of reactor (outflow), 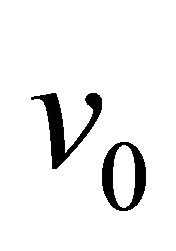 = inflow volume of reactor,
= inflow volume of reactor, ![]() = outflow volume of reactor,
= outflow volume of reactor, 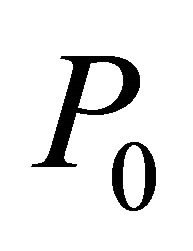 = inflow pressure,
= inflow pressure,  = outflow Pressure,
= outflow Pressure, 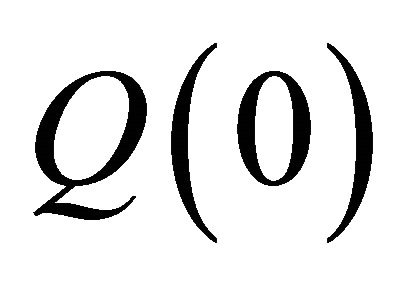 = flowrate (in),
= flowrate (in), 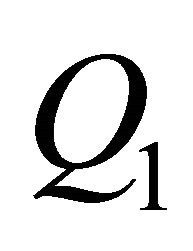 = flowrate (out), m = mass
= flowrate (out), m = mass 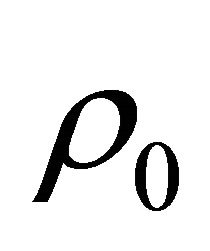 = inflow density,
= inflow density, 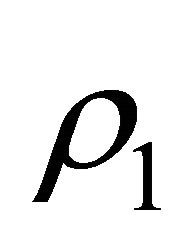 = outflow density and
= outflow density and 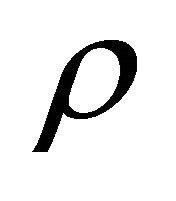 = general density, also
= general density, also
 (5)
(5)
Substituting (5) in (4) and using the result in (3), we obtain
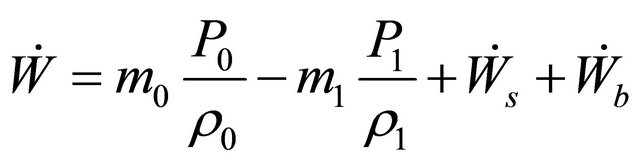 (6)
(6)
The energy terms of total energy composed in Internal U, Kinetic K and Potential energy  is expressed as:
is expressed as:
 (7)
(7)
Substituting (7) in (2), we obtain
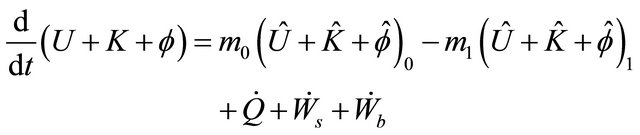 (8)
(8)
but in chemical reactors, only the internal energy is considered with the enthalphy 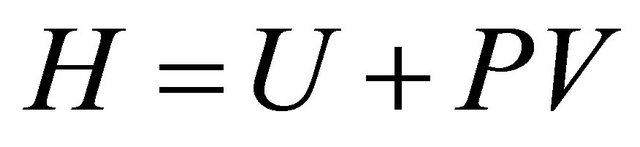 per unit mass, hence 8 becomes
per unit mass, hence 8 becomes
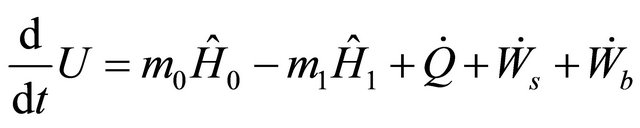 (9)
(9)
2.2. The Batch Reactor
The batch reactors have no flowstream (i.e. 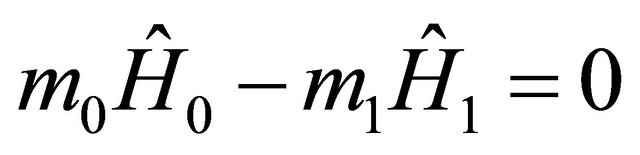 ). Therefore, Equation (9) in terms of rate of heat becomes
). Therefore, Equation (9) in terms of rate of heat becomes
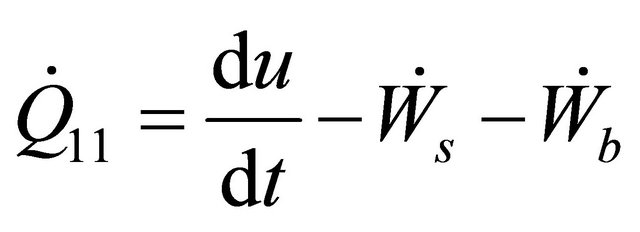 (10)
(10)
Neglecting the work done by stirrer because the mixture is not highly viscous, so the stirring operation do not draw significant power, (10) yield
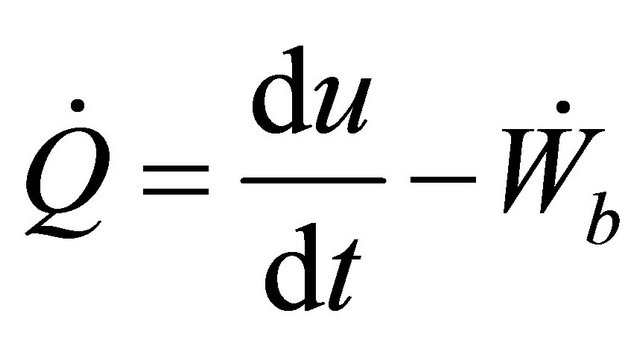 (11)
(11)
and we know that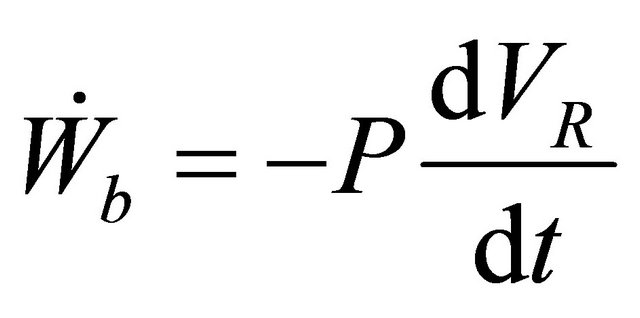 , hence (11) becomes
, hence (11) becomes
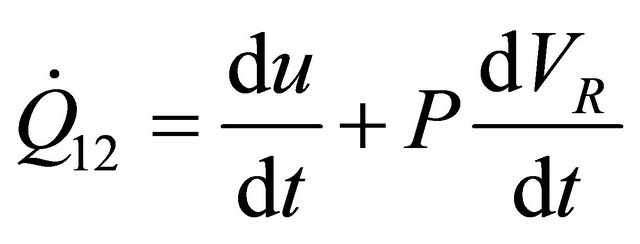 (12)
(12)
For Batch reactor in terms of enthalpy, we have
 (13)
(13)
Taking the differential of (13) for 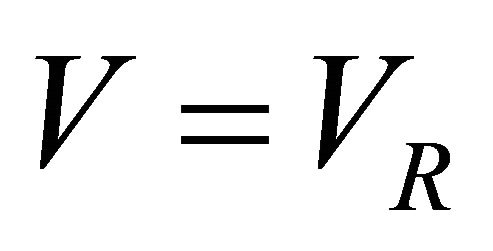 and substituting in (12), we obtain
and substituting in (12), we obtain
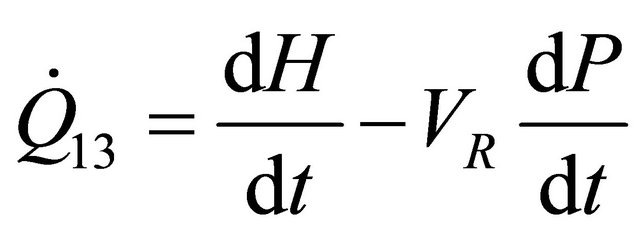 (14)
(14)
We now consider enthalpy as a function of temperature T, pressure P and number of moles nj, and express its differentials as
 (15)
(15)
The first partial derivative is the definitions of the heat capacity, 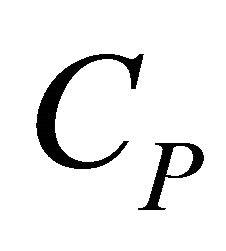 , that is
, that is
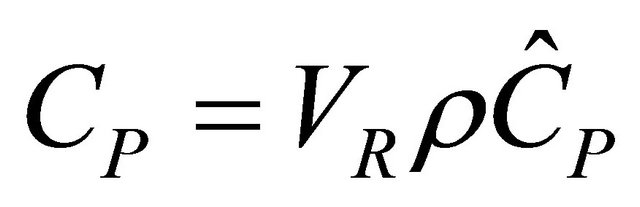 (16)
(16)
The second partial derivative can be expressed as
 (17)
(17)
where 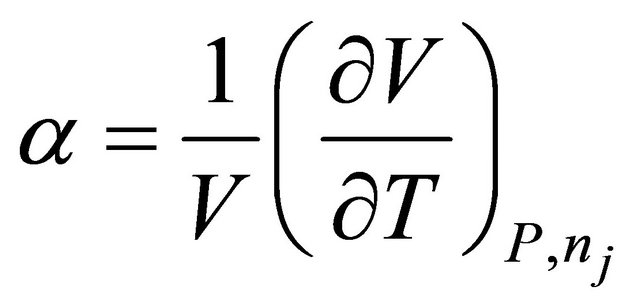 is the coefficient of expansion of mixture.
is the coefficient of expansion of mixture.
The final partial derivatives are the partial molar enthalpies, 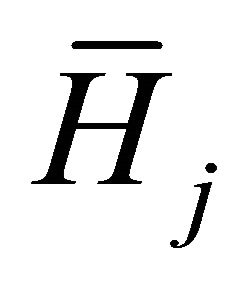
 (18)
(18)
Substituting (16), (17) and (18) in (15) and using the result in (14), we obtain
 (19)
(19)
But the material balance for batch reactor is
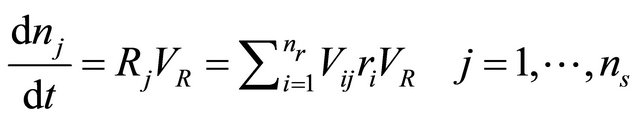 (20)
(20)
where  is the stoichiometric coefficient for species j and reaction i,
is the stoichiometric coefficient for species j and reaction i,  is the production rate for jth species and
is the production rate for jth species and 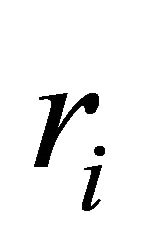 is the reaction rate for ith reaction.
is the reaction rate for ith reaction.
And the heat of reaction is
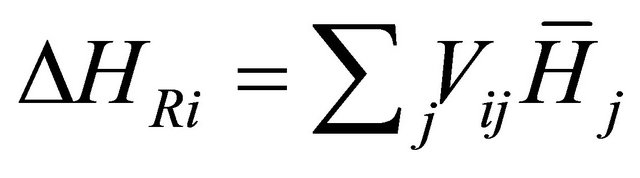 (21)
(21)
Substituting (20) and (21) in (19) we obtain
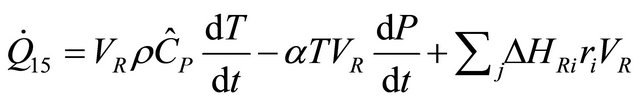 (22)
(22)
The constant-pressure batch reactor is the incompressible-fluid and for 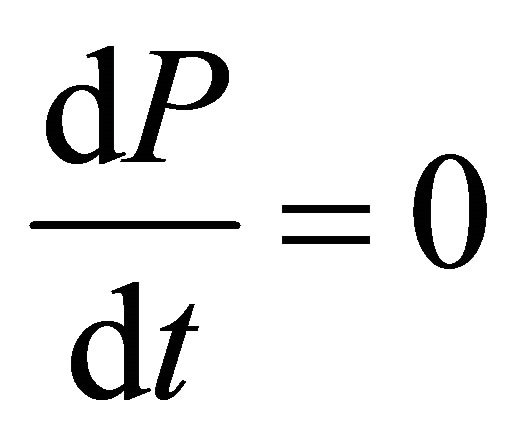 then Equation (22), becomes
then Equation (22), becomes
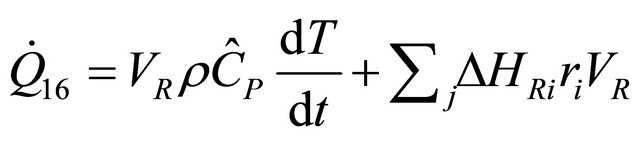 (23)
(23)
If the heat removal is manipulated to maintain constant reactor temperature, the time derivative in Equation (23) vanishes leaving
 (24)
(24)
When CA = concentration of species A, k = reaction rate constant,  and
and 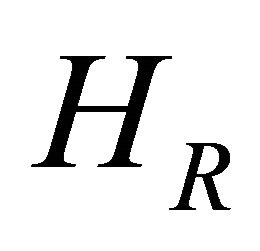 is the enthalpy change on reaction then Equation (24) becomes
is the enthalpy change on reaction then Equation (24) becomes
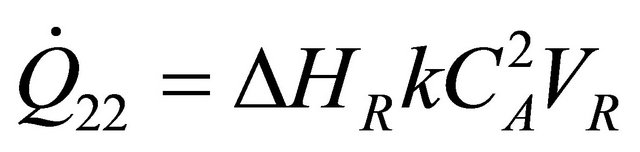 (25)
(25)
For the constant-volume batch reactor, we considered the pressure as function of temperature, volume and number of moles, and also expressed its differentials as:
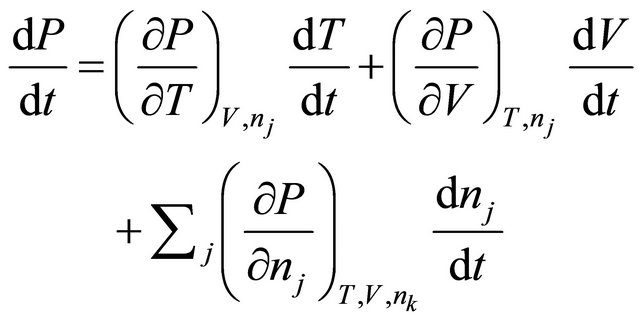 (26)
(26)
For reactor operation at constant volume, 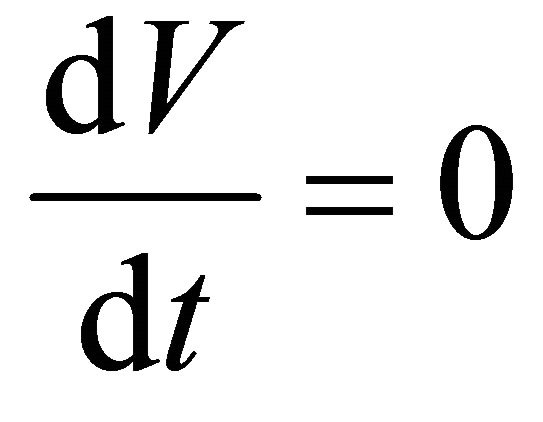 and forming time derivatives, just as we did in (15) to (17) and substituting into Equation (19) gives
and forming time derivatives, just as we did in (15) to (17) and substituting into Equation (19) gives
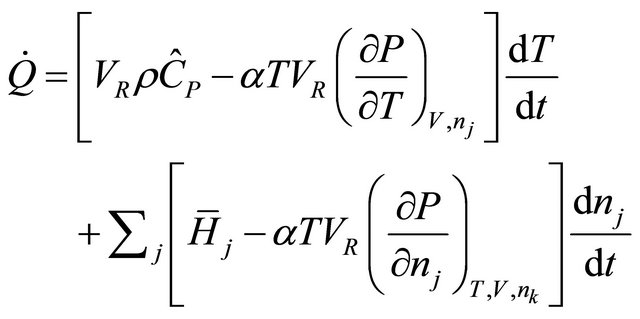 (27)
(27)
Note that the first term in brackets is the total constant-volume heat capacitythat is 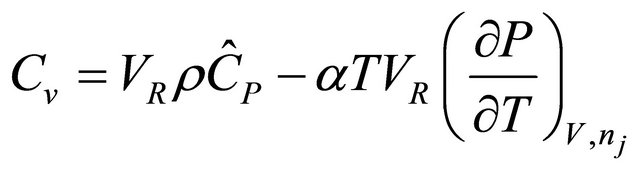 (28)
(28)
Substitution (28) and the material balance in (20), yields the rate of heat for the energy balance of the Constant-Volume batch Reactor. That is
 (29)
(29)
If we consider a constant volume-ideal gas, where  and
and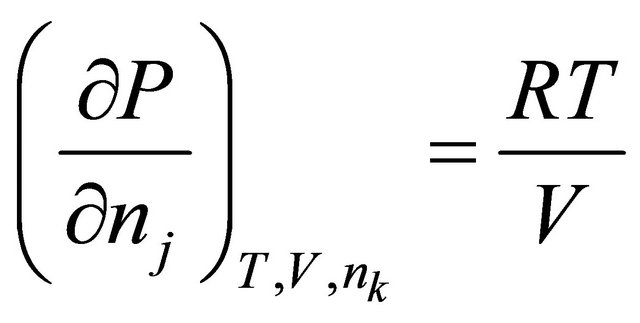 . Substituting these into (29) gives
. Substituting these into (29) gives
 (30)
(30)
where
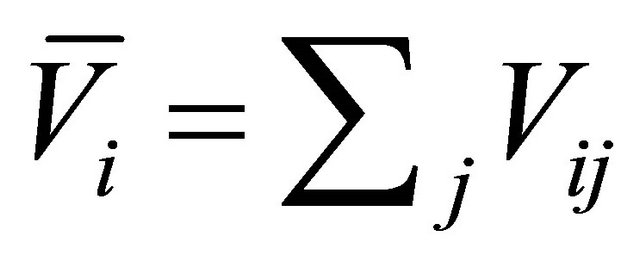 (31)
(31)
2.3. The Continuous Stirred Tank Reactor (CSTR)
In order to describe the dynamic operation of a CSTR, the energy balance equation must be developed. The CSTR has flowstream, hence using the Equations (8)
 (32)
(32)
As in (9) only the internal energy is considered. The out flow stream is flowing out of a well-mixed reactor, thus, the CSTR rate of heat equation using (32) is
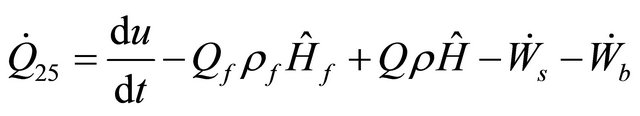 (33)
(33)
where  = volumetric flow rate,
= volumetric flow rate,  = flow density,
= flow density,  = flow enthalpy,
= flow enthalpy,  = flow concentration with component j and Q = flow rate.
= flow concentration with component j and Q = flow rate.
As before, if sharf work is neglected for the CSTR, Equation (33) becomes
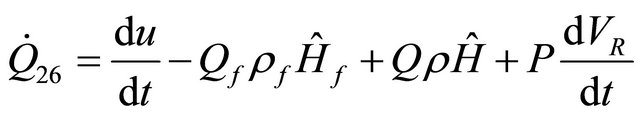 (34)
(34)
and if the enthalpy is considered, we obtain
 (35)
(35)
We consider the change in enthalpy of the continuous stirred tank reactor (CSTR) as a function of temperature, pressure and number of moles, and express its differentials as
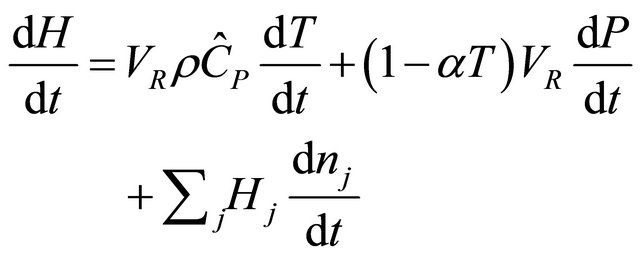 (36)
(36)
and substituting into Equation (35) gives
 (37)
(37)
The material balance for the CSTR is
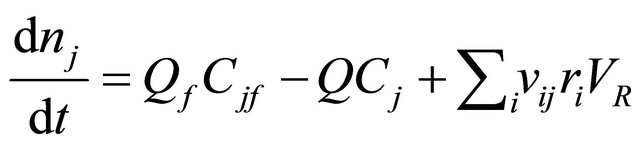 (38)
(38)
After substituting (38) in (37) and re-arrangement yields
 (39)
(39)
The equation of rate of heat for constant-pressure in CSTR that is Incompressible-fluid and its mean in Equation (39) is 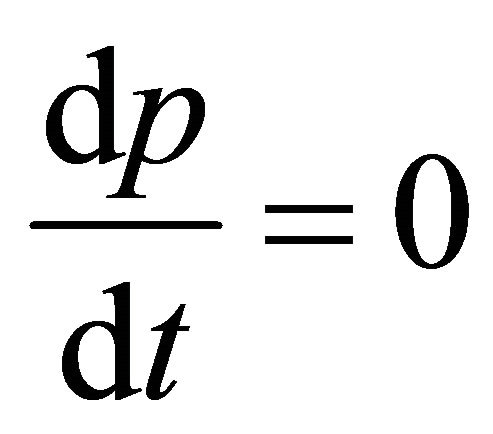 and hence we have
and hence we have
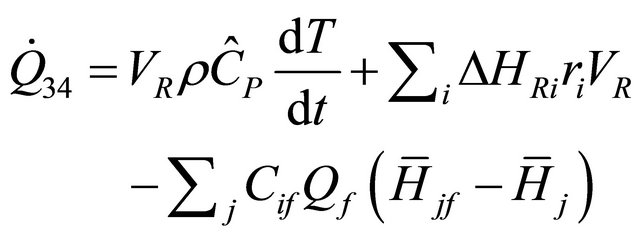 (40)
(40)
From Equation (40), we obtained the equation of rate of heat for constant-volume in CSTR as follows:
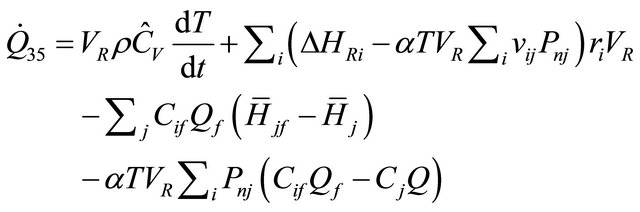 (41)
(41)
Also, from Equation (41), the equation of rate of heat for ideal gas is:
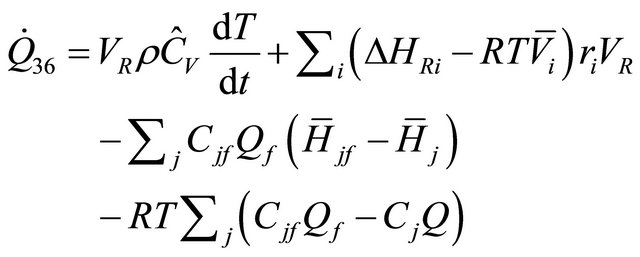 (42)
(42)
For steady state constant, we have
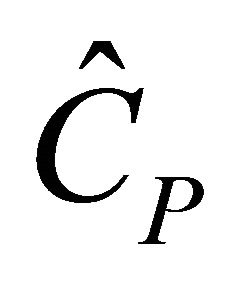 ,
, 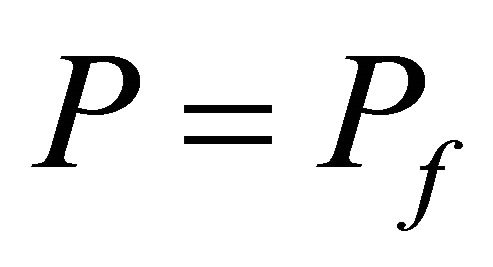 and
and 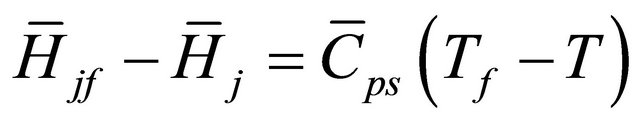 (43)
(43)
If we re-arrange Equation (39) in the form
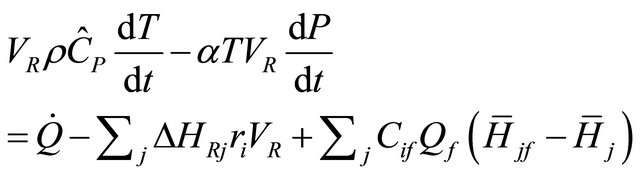 (44)
(44)
By setting the Right hand side of (44) equals zero and substituting (43) in the result gives
![]() (45)
(45)
The heat removal rate of CSTR required bringing CSTR reactor out-flow stream from final temperature Tf to temperature T and is given (from 45) by
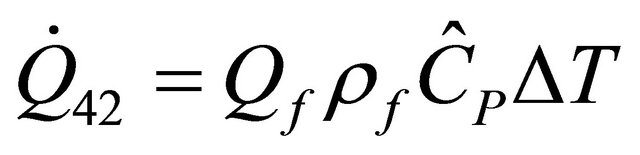 (46)
(46)
2.4. The Semi-Batch Reactor
The development of the semi-batch reactor energy balance follows directly from the CSTR energy balance derivation of the rate of heat by setting Q = 0. The main results in this paper are therefore summarized below:
Neglecting the Kinetic Energy in Equation (33) of the CSTR, when Q = 0, we obtain
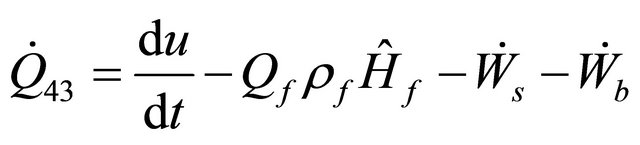 (47)
(47)
Also, by neglecting the Sharf work and consider the Enthalpy when Q = 0 in (34) and (35) yields
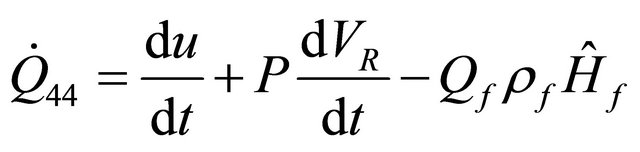 (48)
(48)
and if the enthalpy is used, we obtain
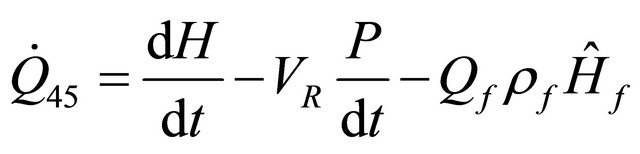 (49)
(49)
By setting Q = 0 in Equations (37) and (39) respectively, we have the enthalpy change of semi-batch reactor as
 (50)
(50)
and
 (51)
(51)
The constant pressure semi-batch reactor is the incompressible-fluid batch reactor and in Equation (51)
when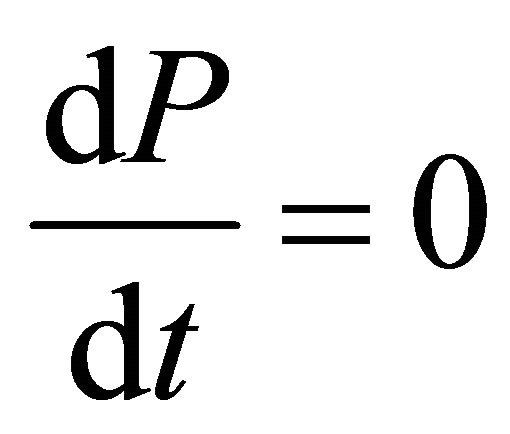 , we obtain
, we obtain
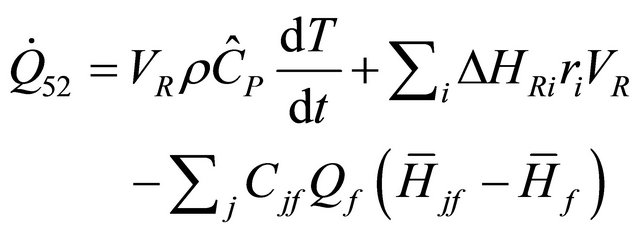 (52)
(52)
For steady state semi-batch reactor when  is constant, we have
is constant, we have
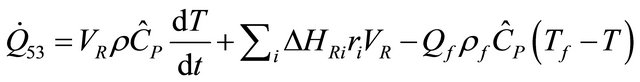 (53)
(53)
The equation is derived from the energy balance equation for Plug-flow reactor (PFR) single phase for rate of heat, and is given by:
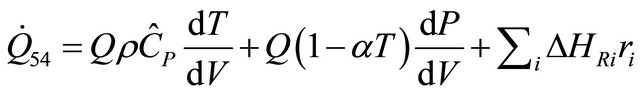 (54)
(54)
Neglecting pressure drop or ideal gas for PFR and from (54), for an Ideal gas 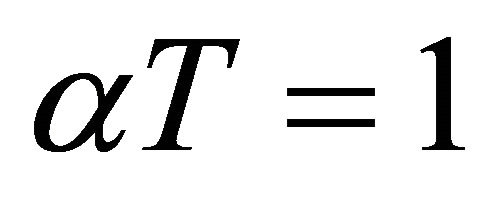 we have
we have
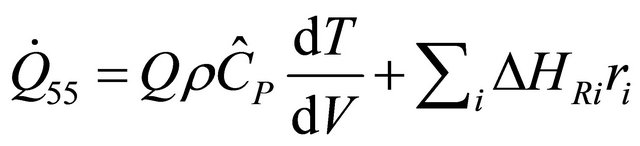 (55)
(55)
The rate of heat equation of PFR for Incompressible fluid is obtain by setting  in Equation (54)
in Equation (54)
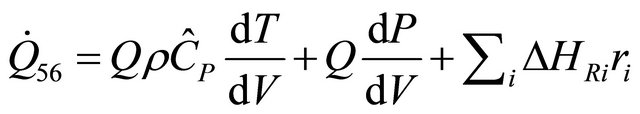 (56)
(56)
The remaining six existing equations related to the rate of heat of a reactor for temperature of heat transfer medium  are as stated below:
are as stated below:
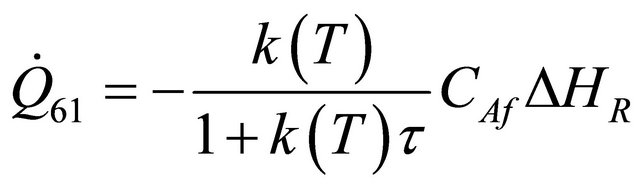 (57)
(57)
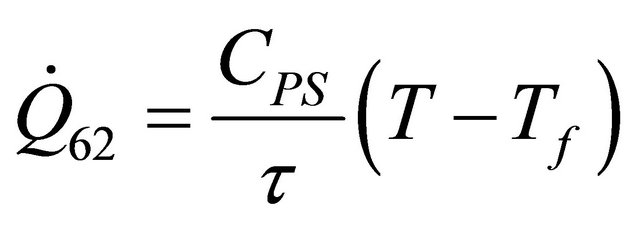 (58)
(58)
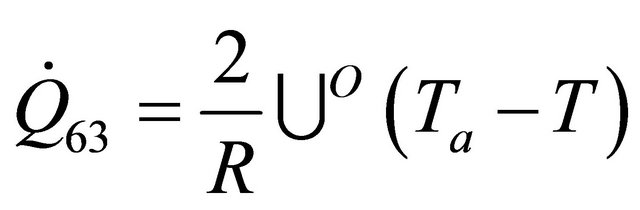 (59)
(59)
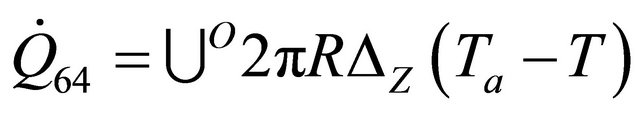 (60)
(60)
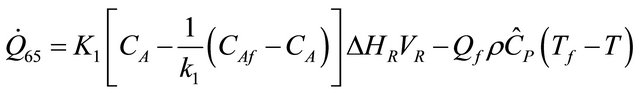 (61)
(61)
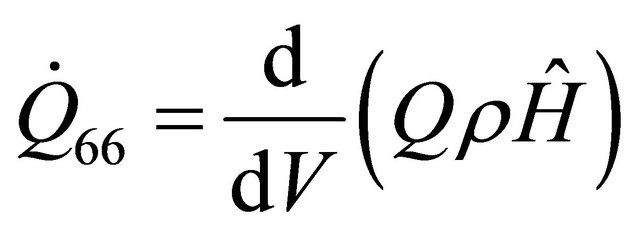 (62)
(62)
The equations derived above from the energy balance equation of chemical reactors [7] are thirty; namely: (10), (12), (14), (19), (22)-(25), (29), (30), (33)-(35), (37), (39)-(42) and (45)-(56). These equations with the six existing equations, namely (57)-(62), were structured into mathematical model in form of quadratic functional. The model with some given existing nuclear tokens were solved by the Conjugate Gradient Method algorithm, with MATLAB as a support soft-ware.
3. The Gradient Method (CGM) Algorithm
The CGM algorithm was originally developed by Hestenes and Stiefel [8] to minimize and solve problems in quadratic functional of the form:
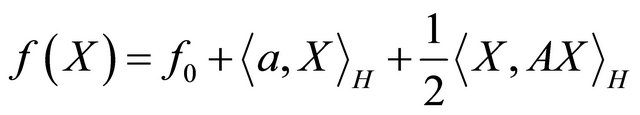 (3.0.1)
(3.0.1)
where f0, is a constant in H, x is a vector in H. A is a positive definite, symmetric and constant matrix operator.
It has a well worked out theory with an elegant convergence profile. No approximation is used in the proving its convergency.
3.1. Property of Conjugate Gradient Method (CGM) Algorithm
Some of the several properties of CGM are:
1) It has a quadratic convergence property that is for a quadratic functional on an n-dimensional Hilbert space, it converges in at most n steps.
2) It requires a relatively small increase in computer time per iteration and memory space.
3) It has a well worked out theory.
3.2. Algorithm
The first element of the descent sequence 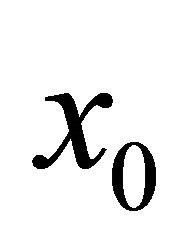 is simply guessed. The remaining members of the sequence are then found as follows:
is simply guessed. The remaining members of the sequence are then found as follows:
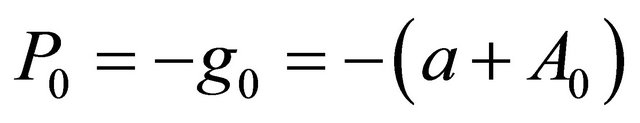 (3.2.1)
(3.2.1)
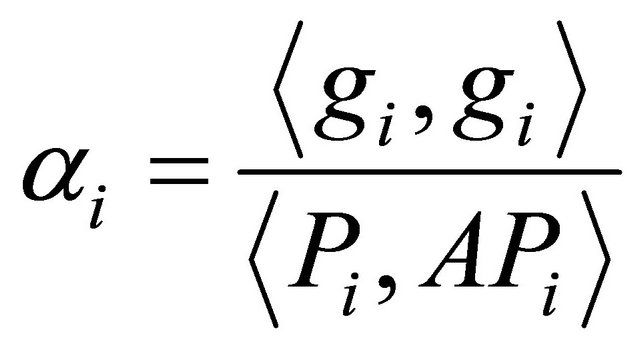
 (3.2.2)
(3.2.2)
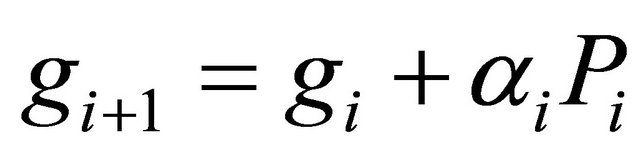 (3.2.3)
(3.2.3)

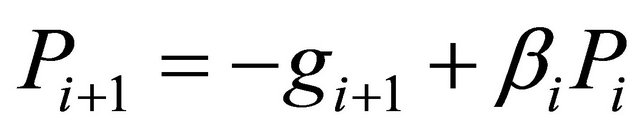 (3.2.4)
(3.2.4)
where gi is the gradient at the ith element of the descent sequence Xi.
It has been proved that the algorithm converges at most, in n iteration in a well posed problem and the convergence rate is given as:
 (3.2.5)
(3.2.5)
where m and M are smallest and spectrums of matrix A respectively. That is, for an n dimensional problem, the algorithm will converge in at most n iterations [9].
4. Computational Results
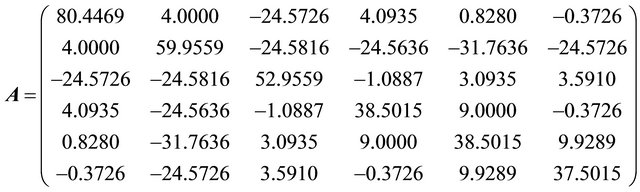
Our model is:
 (4.0.1)
(4.0.1)
where  i.e.,
i.e., 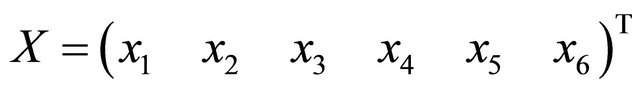 ,
,  ,
, 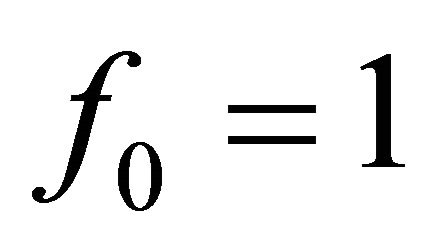 and
and
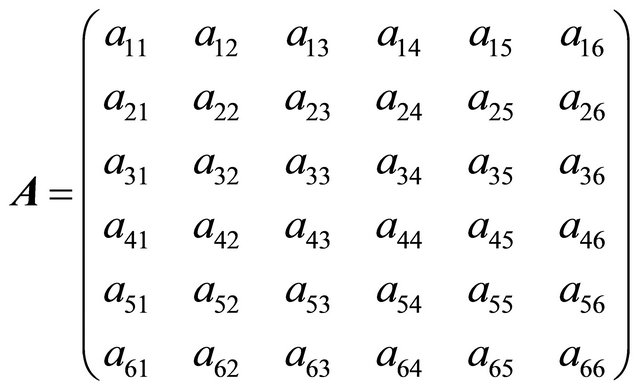
where  = values of the rate of heat,
= values of the rate of heat, ; and
; and .
.
Numerical values are now calculated for our parameters or tokens. In all cases our initial guess is 0 vector that is  and the results are as shown below:
and the results are as shown below:
Problem 1 (For arbitrary tokens)

Problem 2 (For arbitrary tokens)

Problem 3 (For nuclear tokens)
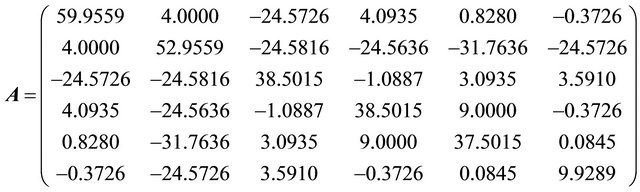
Problem 4 (For nuclear tokens)
4.1. Tables of Results
The following tables are Table 1 for Problem 1, Table 2 for problem 2, Table 3 for problem 3 and Table 4 for problem 4 respectively.
4.2. Discussion of Results
The initial nuclear tokens used in problems 1 and 2 to represent the vectors and control operators of the quadratic model were arbitrary. Our results clearly shown that arbitrary composition of nuclear tokens will not guarantee safety. This is evidence from Tables 1 and 2 (non convergence) which did not satisfied the properties of the CGM algorithm. See [10].
After restructuring, nuclear tokens were used as the vectors and control operators of the quadratic model to generate problems 3 and 4 and were solved using the CGM algorithm. We were able to get two results that converge (Tables 3 and 4). The convergency satisfied the properties of the CGM algorithm, which shows good results. See [11] and [12].
5. Conclusions
The nuclear reactors tokens are the main components that make up the reactors, example of the components are Internal energy, Reactor volume, Molar mass and so on, which produces the rate of heat of the reactor that causes
Table 1. Generated from problem 1.

Continued
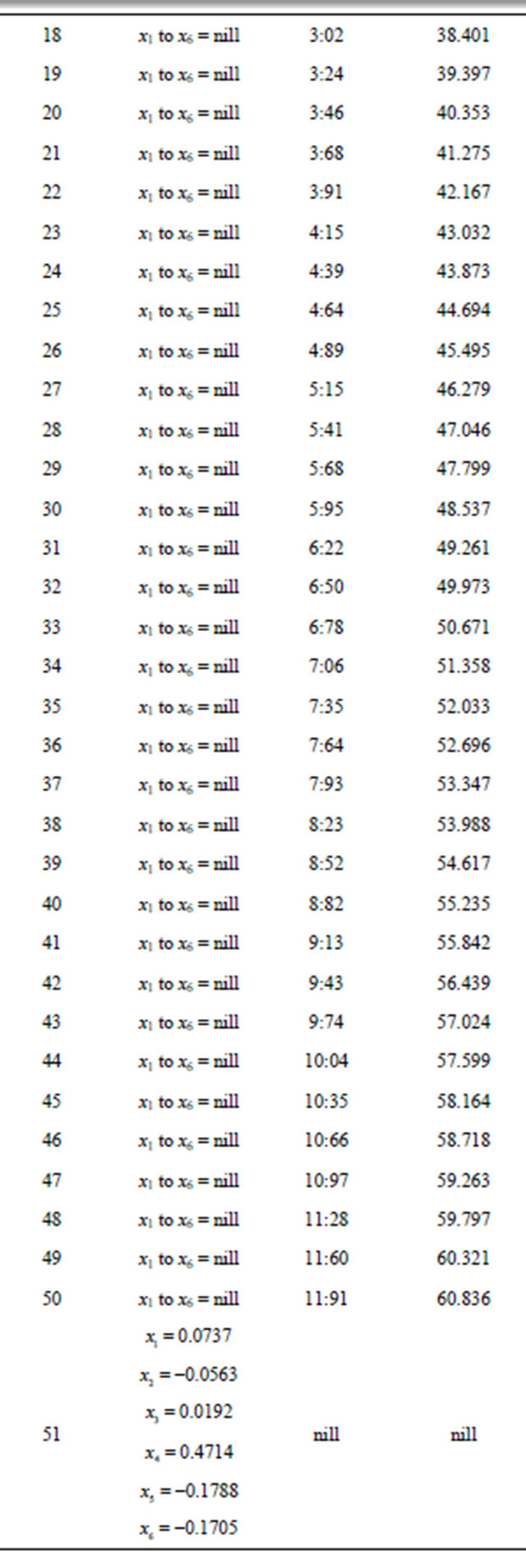
Table 2. Generated from problem 2.

Continued
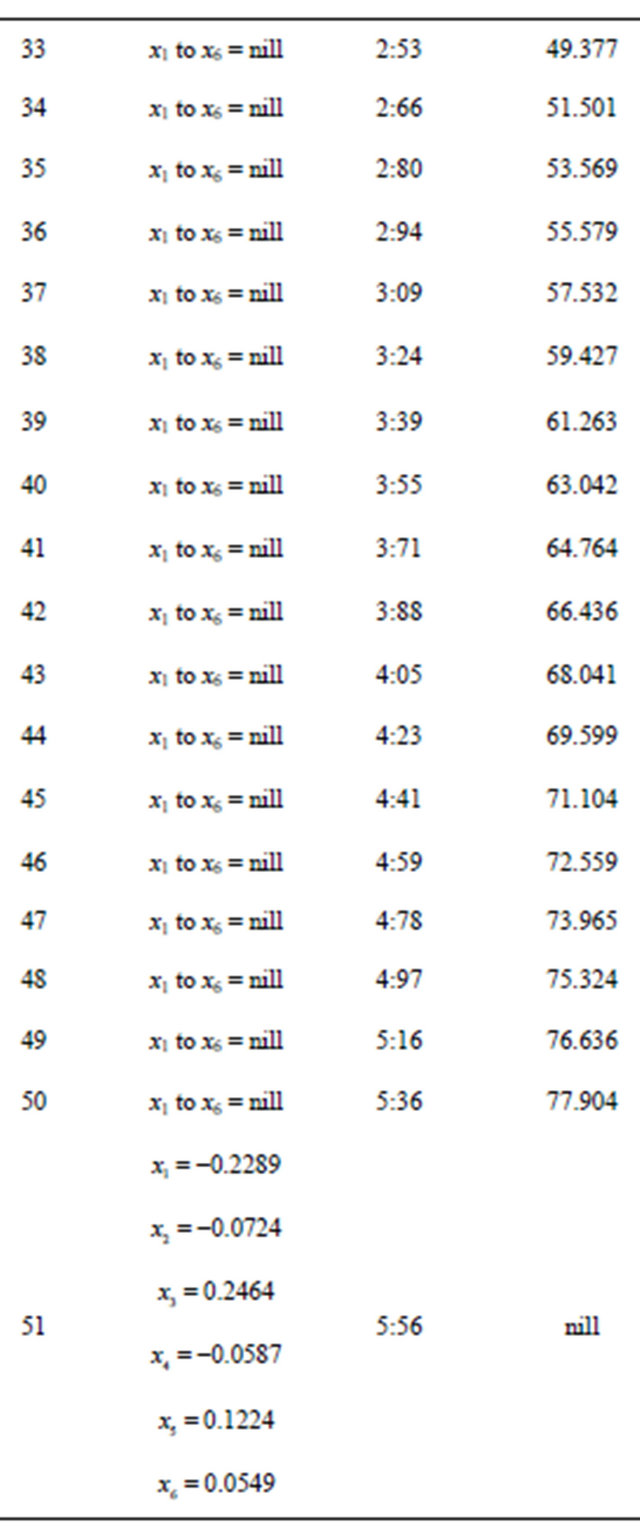
Table 3. Generated from problem 3.
Continued

Table 4. Generated from problem 4.

Continued

the accidents. See [13-20].
Our results clearly indicate that if the nuclear tokens are used for the structured model, which are used for the construction of nuclear reactors, then the nuclear safety will be maximized while the disaster will be minimized.
REFERENCES
- Nuclear Energy Agency, “Nuclear Fuel Behaviour in Loss-of-Coolant-Accident (LOCA) Conditions,” 2009, p. 141. http://wwwoecd-nea.org/nsd/reports/2009/nea6846-LOCA.pdf
- A. C. Kadak, et al., “A Response to the Environmental and Economic Challenge of Global Warming,” Handbook, Massachusetts Institute of Technology, 1998, pp. 1-6.
- Encyclopaedia Britannica, “Windmill Power,” Ultimate Refrence Suite: Chicago Encyclopaedia Britannica, Knoxville, 2010.
- Encyclopaedia Britannica, “Hydroelectric Power,” Ultimate Refrence Suite: Chicago Encyclopaedia Britannica, Knoxville, 2010.
- C. K. Otto, “Fossil Fuel Power,” University of Tennessee, Ultimate Refrence Suite: Chicago Encyclopaedia Britannica, Knoxville, 2011.
- “The Enargy Balance for Chemical Reactors,” 1st Edition, Nob Hill Publishing LLC, Madison, 2011, pp. 1-182. www.che.wisc.edu/home/jbraw/chemreacfun/chb/slides-enbal.pdf
- J. O. Omolehin, L. Aminu and K. Rauf, “Control Approach to Nuclear Safety,” Applied Mathematics—Open Special Issues “Optimization”, Scientific Research, 2012. http://www.scirp.org/journal/am
- J. O. Omolehin, K. Rauf and D. J. Evans, “Conjugate Gradient Method Approach to Queue Theory,” International Journal of Computer Mathematics, Vol. 82, No. 7, 2005, pp. 829-835. http://www.tandf.co.uk/journals
- J. O. Omolehin, “On the Control of Reaction Diffusion Equation,” Ph.D. Thesis, University of Ilorin, Ilorin, 1991.
- T. Gland, “Constrained Optimization Using Multiplier Methods with Application to Control Problems,” University of Lund, Lund, Report No. 7603, 1976.
- International Atomic Energy Agency, “Structure of Nuclear Power Plant Design Characteristics in the IAEA Power Reactor Information System,” IAEA, Vienna, 2007, pp. 9-17.
- S. Frank, “Nuclear Reactors,” Kennesaw State University, Kennesaw, 2009, pp. 1-13. www.chemcases.com/nuclear/nc-10.html
- Wikipedia, “Boiling Water Reactor Safety System,” The Free Encyclopedia, 2011, pp. 2-9. en.wikipedia.org/wiki/Boiling-water-reactor-safety-systems
- S. Ashok, “Solar Energy,” Department of Engineering, Pennsylvania State University, Ultimate Refrence Suite: Chicago Encyclopaedia Britannica, Knoxville, 2011.
- J. S. Walker, “The Three Mile Island: A Nuclear Crises in Historical Perspective,” University of California Press, Berkeley, 2004, pp. 216-265.
- “The Chernobyl Facts,” 2011. http://www.chernobyl-interntional.org/documents/chernobylfacts2.pdf
- Wikipedia, “Fukushima Daiichi Nuclear Reactor Disaster,” The Free Encyclopedia, 2011, pp. 5-27. en.wikipedia.org/wiki/Fukushima-Daiichi-nuclear-diaster
- Wikipedia, “Energy in Japan,” The Free Encyclopedia, 2009, p. 1. en.wikipedia.org/wiki/Electricity-sector-in-Japan
- International Atomic Energy Agency, “Mitigation of Hydrogen Hazard in Water Cooled Power Reactors,” IAEA, Vienna, 2001, pp. 3-10. http://www-pub.iaea.org/MTCD/publicatuion/PDF/te-1196-prn.pdf
- G. H. Brian, “Energy Equations for Reactors,” Department of Chemical Engineering and Material Science, University of California, Lecture Note, Davis, 2010, pp. 9-13.
NOTES
*Corresponding author.

