American Journal of Computational Mathematics
Vol.2 No.4(2012), Article ID:25492,11 pages DOI:10.4236/ajcm.2012.24035
Optimal Recovery of Holomorphic Functions from Inaccurate Information about Radial Integration
Department of Mathematics and Statistics, State University of New York at Albany, Albany, USA
Email: adegraw@albany.edu
Received April 30, 2012; revised August 20, 2012; accepted September 2, 2012
Keywords: Approximation; Optimal Recovery; Holomorphic
ABSTRACT
This paper addresses the optimal recovery of functions from Hilbert spaces of functions on the unit disc. The estimation, or recovery, is performed from inaccurate information given by integration along radial paths. For a holomorphic function expressed as a series, three distinct situations are considered: where the information error in 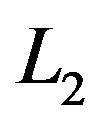 norm is bound by
norm is bound by 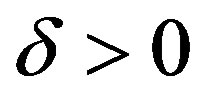 or for a finite number of terms the error in
or for a finite number of terms the error in 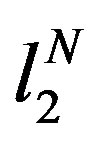 norm is bound by
norm is bound by 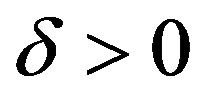 or lastly the error in the
or lastly the error in the 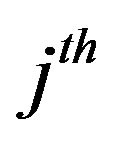 coefficient is bound by
coefficient is bound by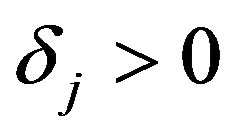 . The results are applied to the Hardy-Sobolev and Bergman-Sobolev spaces.
. The results are applied to the Hardy-Sobolev and Bergman-Sobolev spaces.
1. Introduction
Let W be a subset of a linear space X, let Z be a normed linear space, and T the linear operator 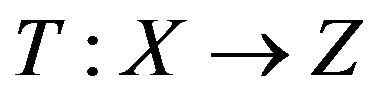 that we are trying to recover on
that we are trying to recover on  from given information. This information is provided by a linear operator
from given information. This information is provided by a linear operator 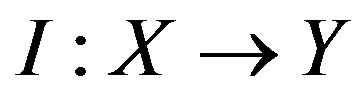 where Y is a normed linear space. For any
where Y is a normed linear space. For any 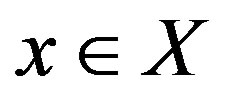 we know some
we know some 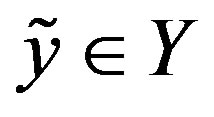 that is near
that is near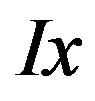 . That is, we know
. That is, we know 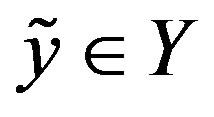 such that
such that
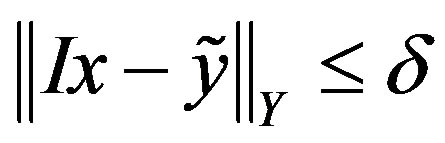 (1)
(1)
for some . The value
. The value  is our inaccurate information. Now we try to approximate the value of
is our inaccurate information. Now we try to approximate the value of 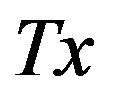 from
from  using an algorithm or method,
using an algorithm or method,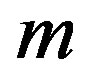 . Define a method to be any mapping
. Define a method to be any mapping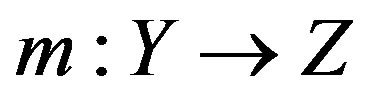 , and regard
, and regard 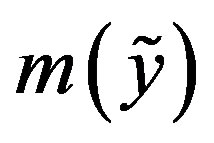 as the approximation to
as the approximation to 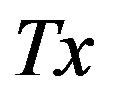 from the information
from the information . Our goal is to minimize the difference of
. Our goal is to minimize the difference of
 and
and 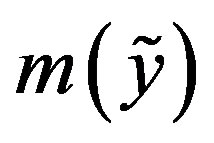 in
in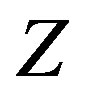 , i.e. minimize
, i.e. minimize 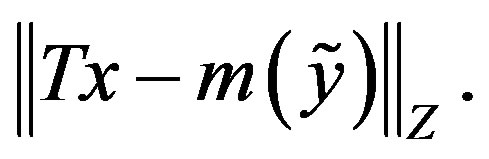
However, the size of  varies since
varies since 
can be chosen to be any  satisfying (1). Furthermore
satisfying (1). Furthermore 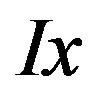 varies depending on the
varies depending on the  chosen. So the error of any single method is defined as the worst case error
chosen. So the error of any single method is defined as the worst case error
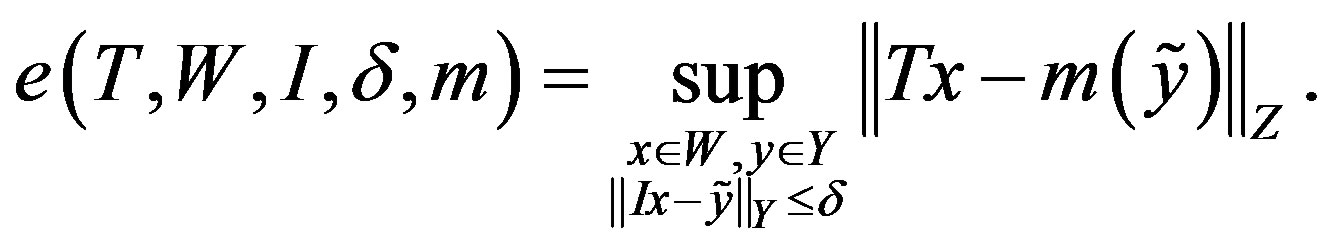
Now the optimal error is that of the method with the smallest error. Thus the error of optimal recovery is defined as
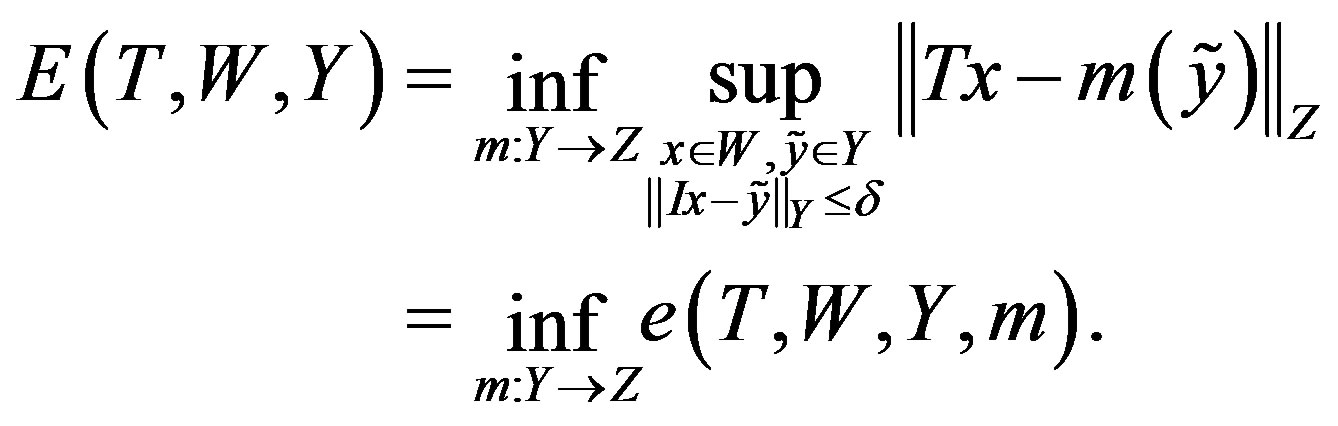 (2)
(2)
For the problems addressed in this paper, let 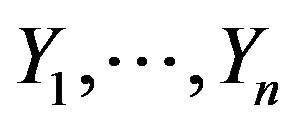 be linear spaces with semi-inner norms
be linear spaces with semi-inner norms 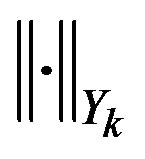 and
and 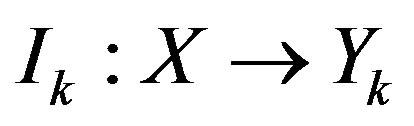 linear operators,
linear operators,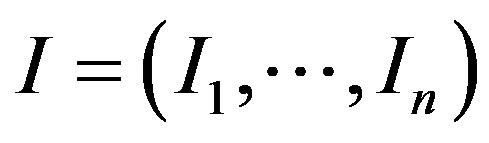 . We want to recover
. We want to recover 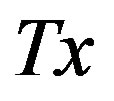 for
for

(where if 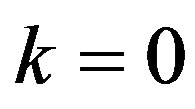 we let
we let ), if we know the values
), if we know the values
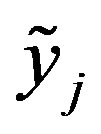 satisfying
satisfying 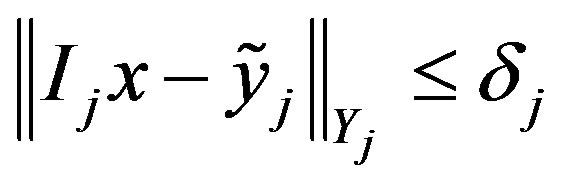 for
for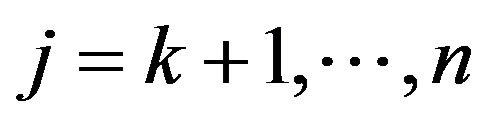 .
.
Define the extremal problem
 (3)
(3)
This problem is dual to (2).
2. Construction of Optimal Method and Error
The following results of G. G. Magaril-Il’yaev and K. Yu. Osipenko [1] are applied to several problems of optimal recovery.
Theorem 1: Assume that there exist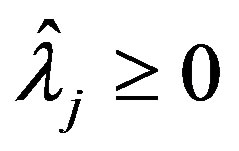 ,
,  such that the solution of the extremal problem
such that the solution of the extremal problem
 (4)
(4)
is the same as in (3). Assume also that for each
 there exists
there exists
 which is a solution to
which is a solution to
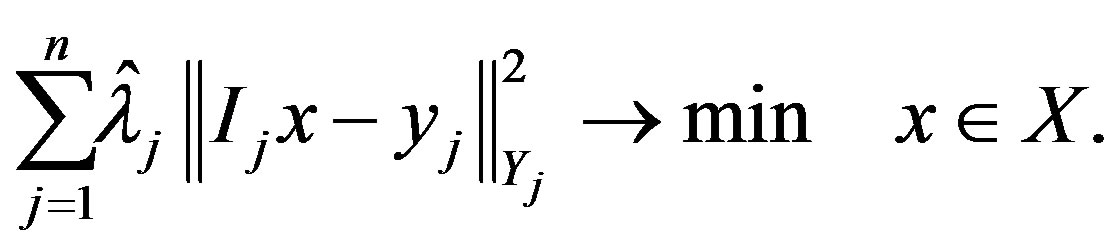 (5)
(5)
Then for all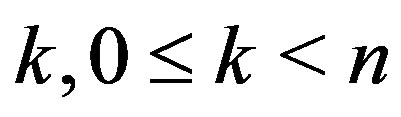 ,
,
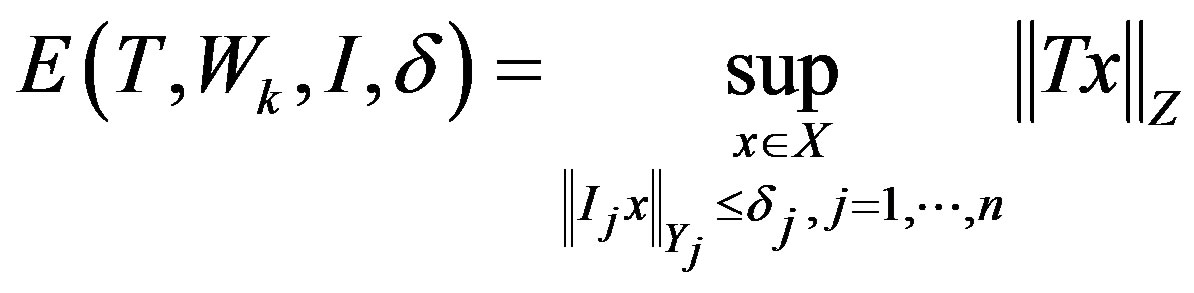
and the method
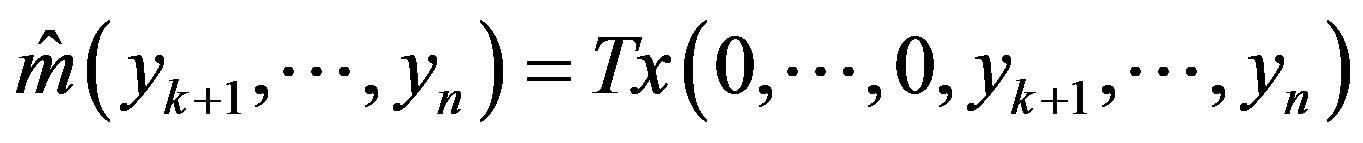 (6)
(6)
is optimal.
Theorem 1 gives a constructive approach to finding an optimal method 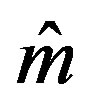 from the information. It follows from results obtained in [1-7] (see also [8] where this theorem was proven for one particular case.)
from the information. It follows from results obtained in [1-7] (see also [8] where this theorem was proven for one particular case.)
In order to apply Theorem 1 the values of extremal problems (4) and the dual problem (3) must agree. The following result, also due to G. G. Magaril-Il’yaev and K. Yu Osipenko [1], provides conditions under which the solution of problems (3) and (4) will agree.
Typically, when one encounters extremal problems, one approach is to construct the Lagrange function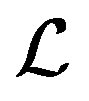 . For an extremal problem of the form of (4), the corresponding Lagrange function is
. For an extremal problem of the form of (4), the corresponding Lagrange function is

Furthermore, 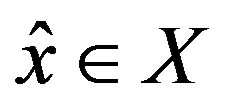 is called an extremal element if
is called an extremal element if
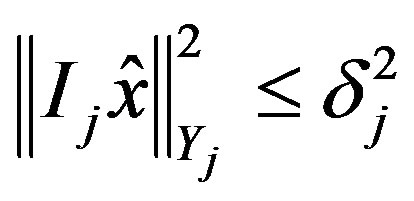 for
for 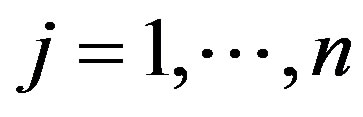 and thus admissible in (4)
and thus admissible in (4)
and

Theorem 2: Let 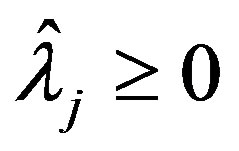 and
and 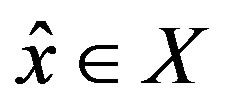 be such that
be such that
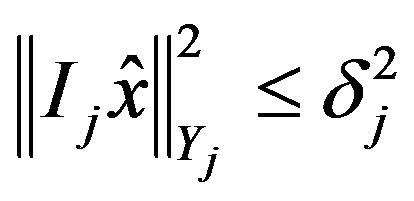 for
for 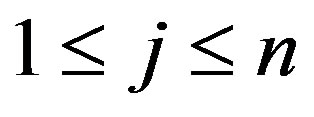 and 1)
and 1) 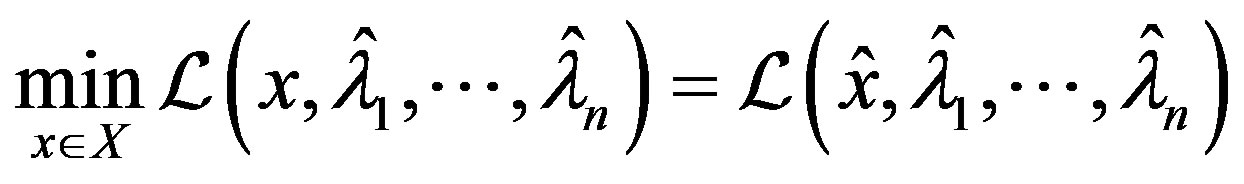
2) 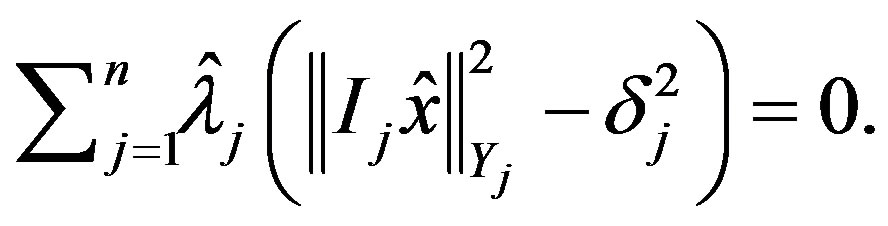
Then 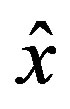 is an extremal element and
is an extremal element and
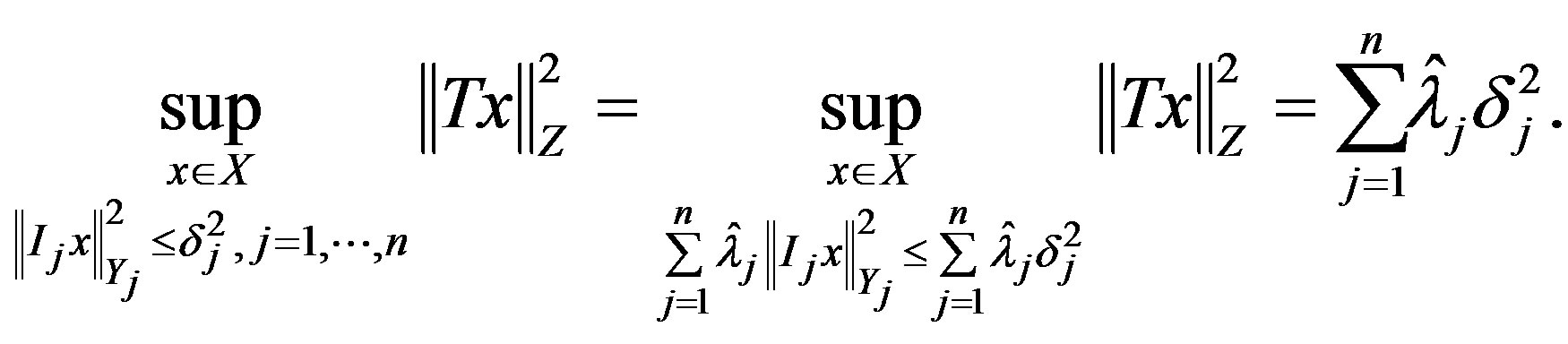
If we wish to combine Theorems 1 and 2 to determine an optimal error and method then we must show the posed problem is able to satisfy equating extremal problems (3) and (4). Through Theorem 2 we have such a means available.
3. Main Results
Consider the class of functions defined on the unit disc 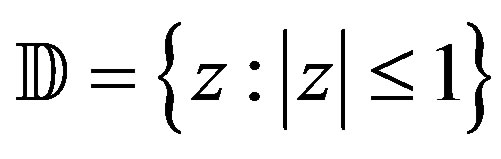 given by
given by
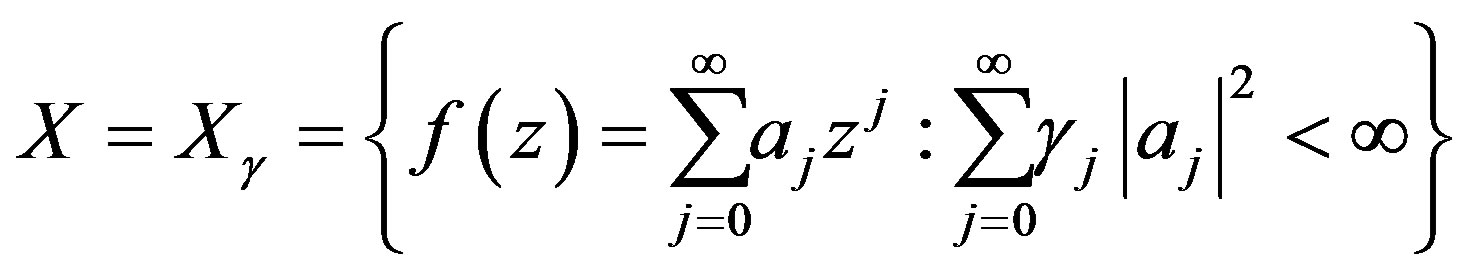 (7)
(7)
for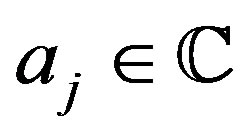 ,
, 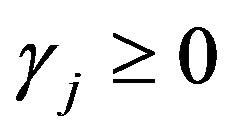 satisfying
satisfying
 (8)
(8)
and
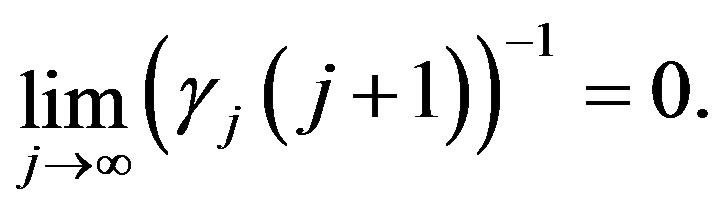 (9)
(9)
Therefore, any 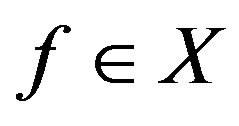 is holomorphic in the unit disc by (6). We define the semi-norm in
is holomorphic in the unit disc by (6). We define the semi-norm in 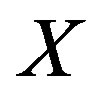 as
as
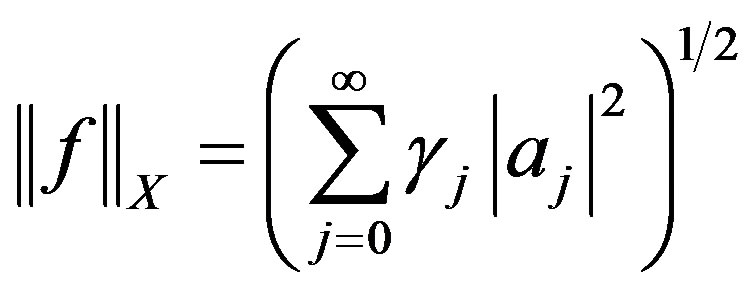
and
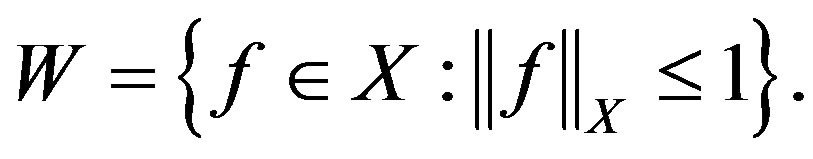 (10)
(10)
Let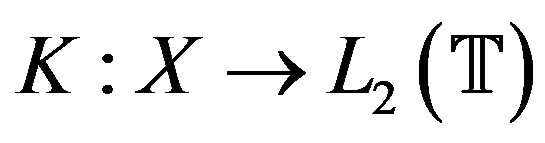 ,
,  , be a linear operator given by
, be a linear operator given by

That is, 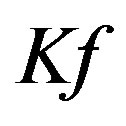 is the radial integral of
is the radial integral of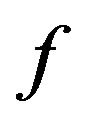 . To see that
. To see that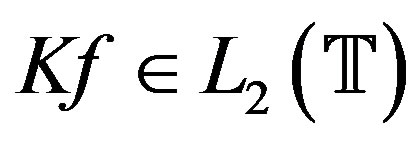 , by (7) we have for all but finitely many
, by (7) we have for all but finitely many ,
,
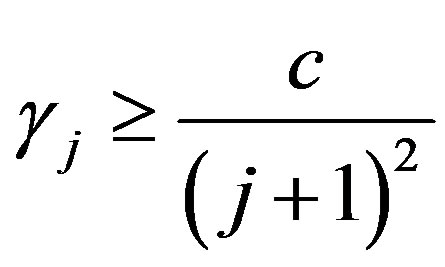 for some
for some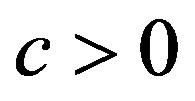 . Thus if
. Thus if 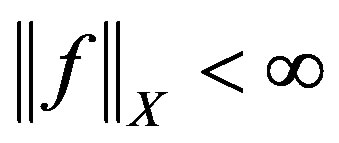 then
then
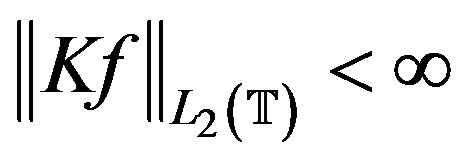 .
.
We assume to know 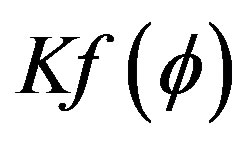 given with a level of accuracy. That is, for a given
given with a level of accuracy. That is, for a given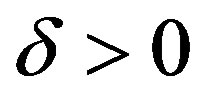 , we know a
, we know a 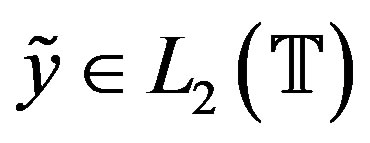 such that
such that
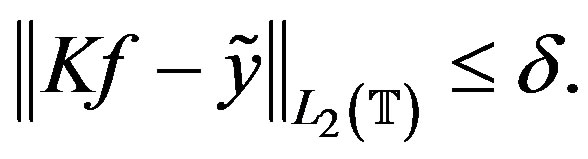 (11)
(11)
The problem of optimal recovery is to find an optimal recovery method of the function 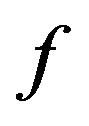 in the class
in the class 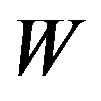 from the information
from the information  satisfying (9). The error of a given method is measured in the
satisfying (9). The error of a given method is measured in the  norm defined by
norm defined by
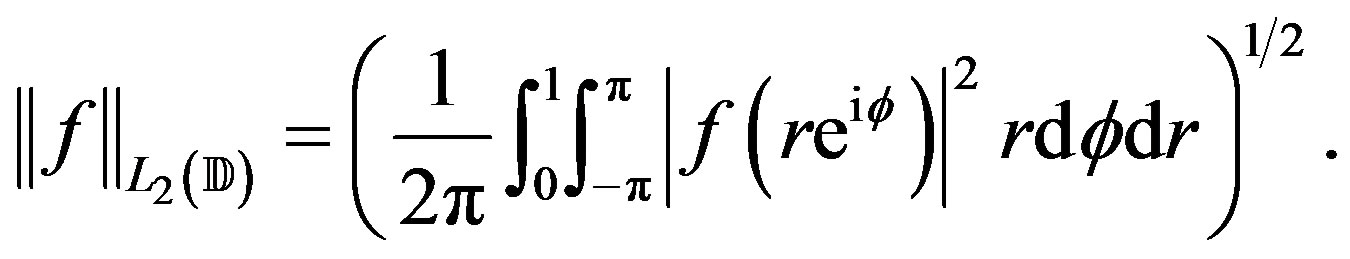
Any method  is admitted as a recovery method. Let
is admitted as a recovery method. Let 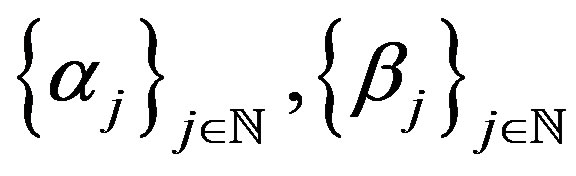 be sequences of non-negative real numbers such that
be sequences of non-negative real numbers such that
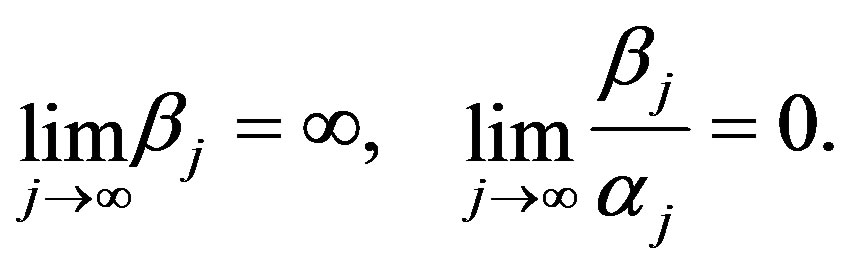
Define 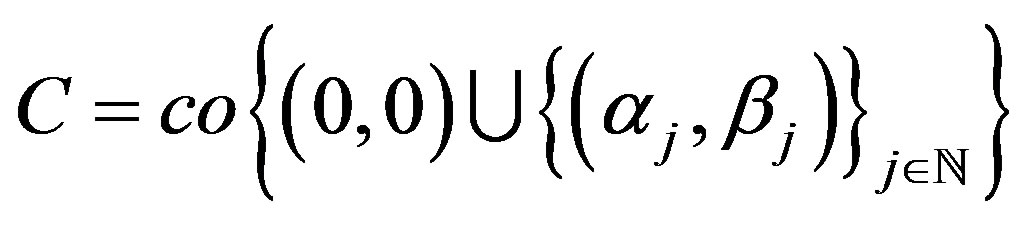 to be the convex hull. Define
to be the convex hull. Define 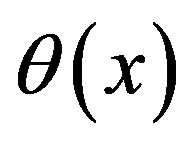 for
for  by
by
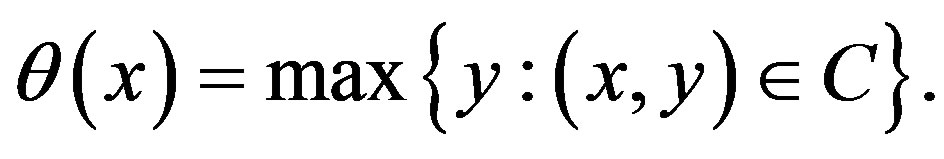
Lemma 1: The piecewise linear function  with points of break
with points of break 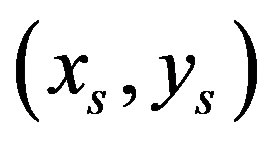
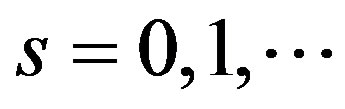 , with
, with 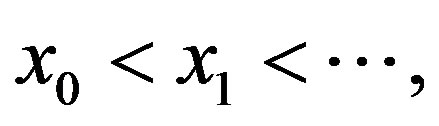 for
for 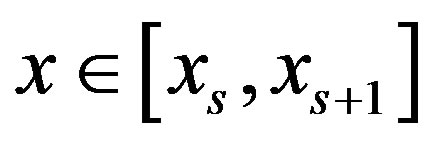 given by
given by 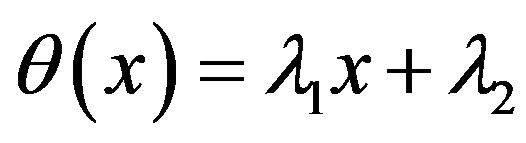 is such that
is such that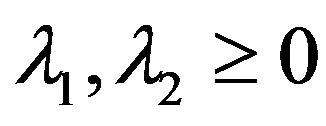 .
.
Proof. Assume that 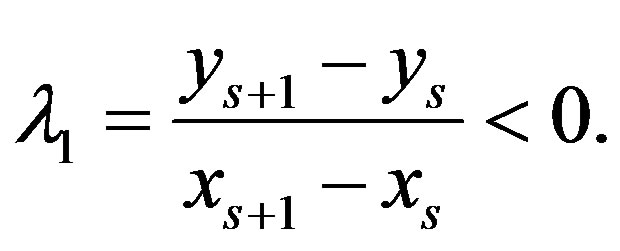 It means that
It means that
 . Since
. Since  and
and  as
as 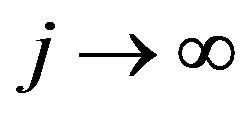 there is a
there is a 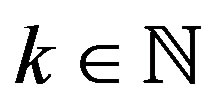 such that
such that 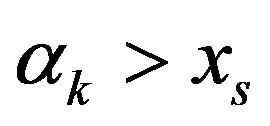 and
and . Then the interval between
. Then the interval between 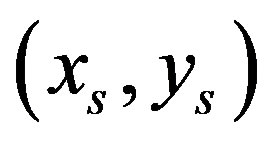 and
and 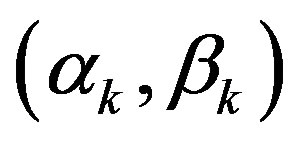 belongs to
belongs to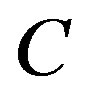 . Consequently,
. Consequently, 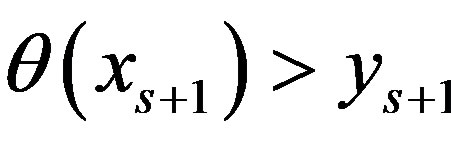 and
and 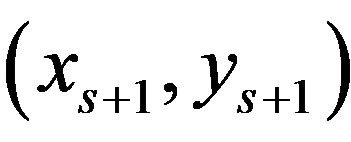 is not a point of break of
is not a point of break of .
.
Assume that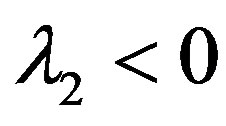 . Since
. Since 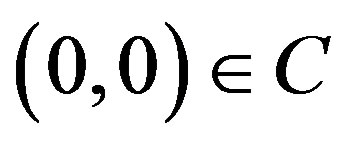 the interval between
the interval between 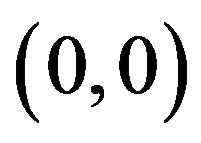 and
and  belongs to
belongs to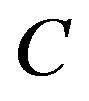 . Geometrically, the line
. Geometrically, the line 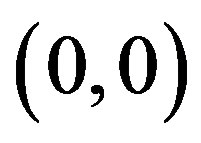 to
to  will lie above the line
will lie above the line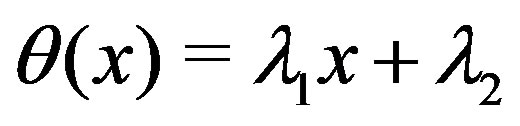 . It means that
. It means that 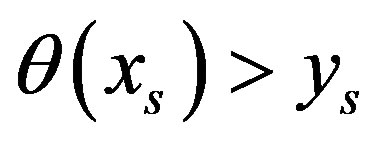 contradicting that
contradicting that 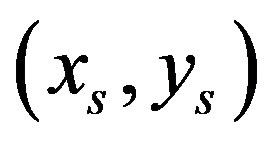 is a point of break of
is a point of break of .
.
Note that as 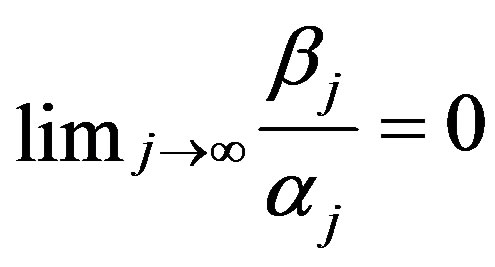 then for any fixed
then for any fixed  the slopes between points
the slopes between points 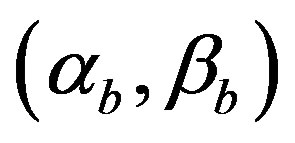 and
and 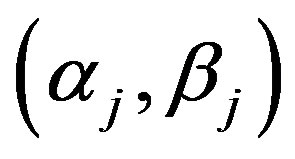 also tends to 0 as
also tends to 0 as
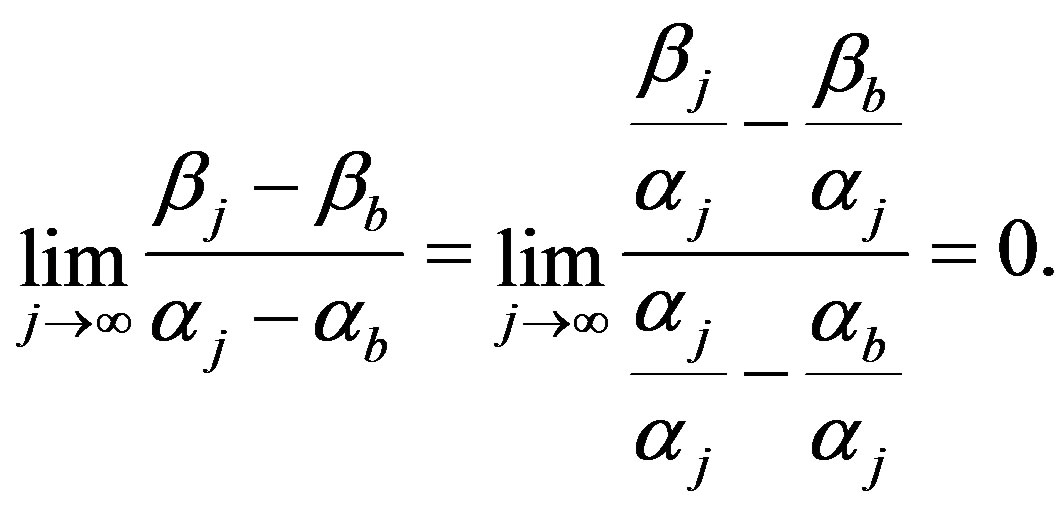
3.1. Inaccuracy in 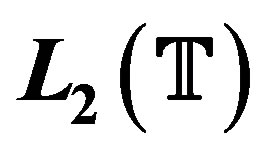 Norm
Norm
Consider the points in  given by
given by
 and define the convex hull of the origin and this collection of points as
and define the convex hull of the origin and this collection of points as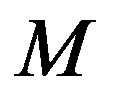 :
:
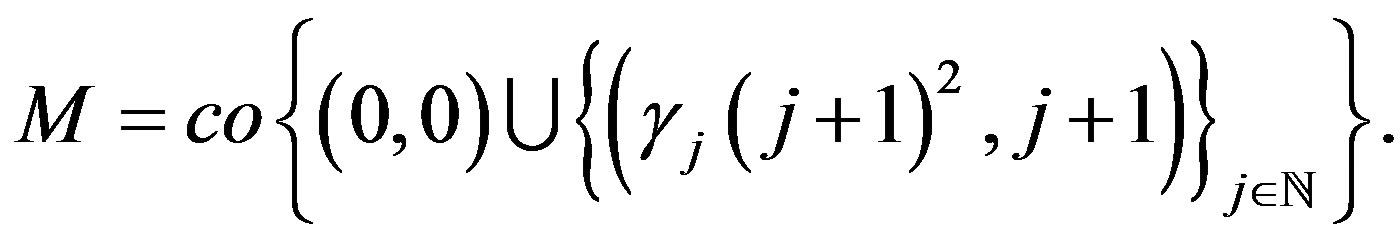 (12)
(12)
Let
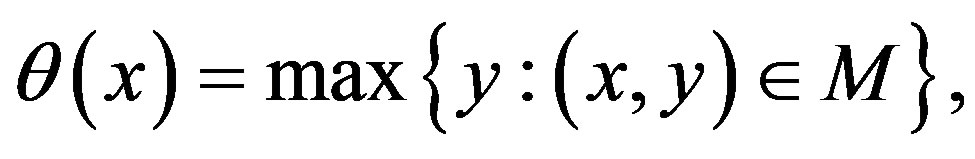 (13)
(13)
thus  is a piecewise linear function. Let
is a piecewise linear function. Let ,
,  be the points of break of
be the points of break of  with
with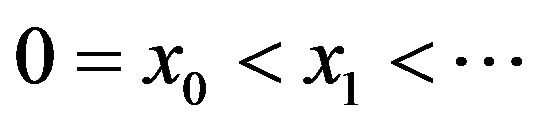 . By (7) the assumption for Lemma 1 is satisfied by
. By (7) the assumption for Lemma 1 is satisfied by 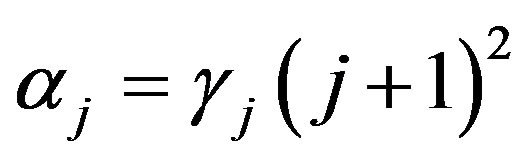 and
and .
.
Theorem 3: Suppose that 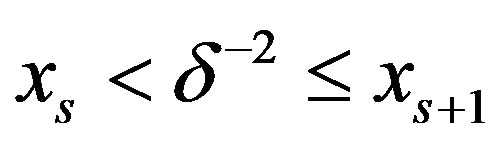 with
with 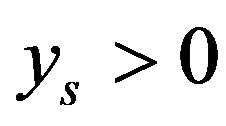 . Let
. Let
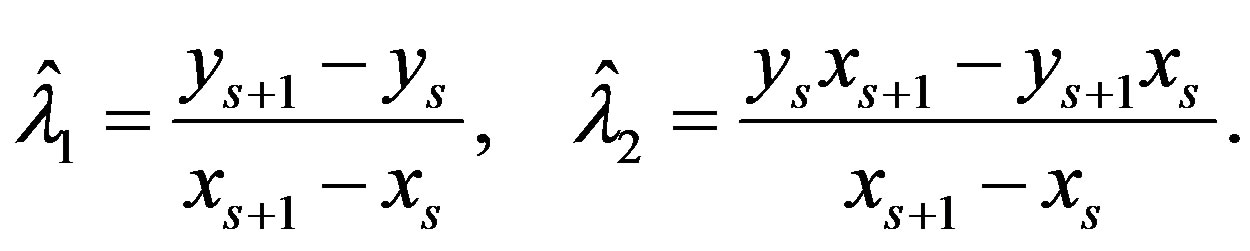 (14)
(14)
Then the error of optimal recovery is
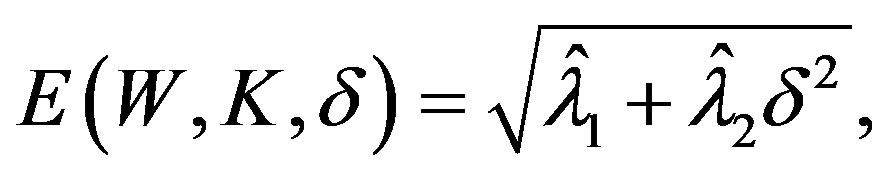 (15)
(15)
and
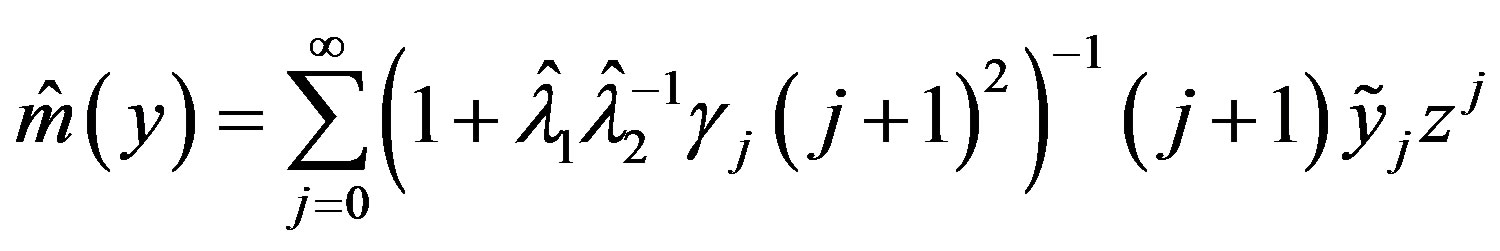 (16)
(16)
is an optimal method of recovery. If 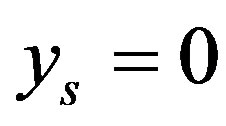 then
then
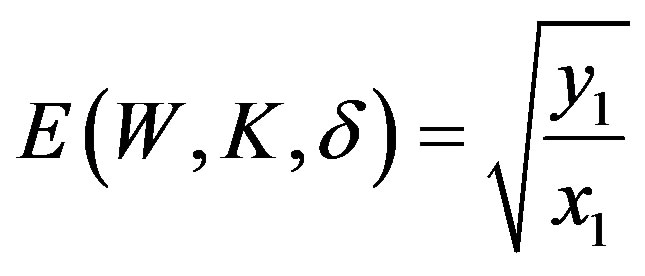 and
and  is an optimal method.
is an optimal method.
Proof. Consider the dual extremal problem
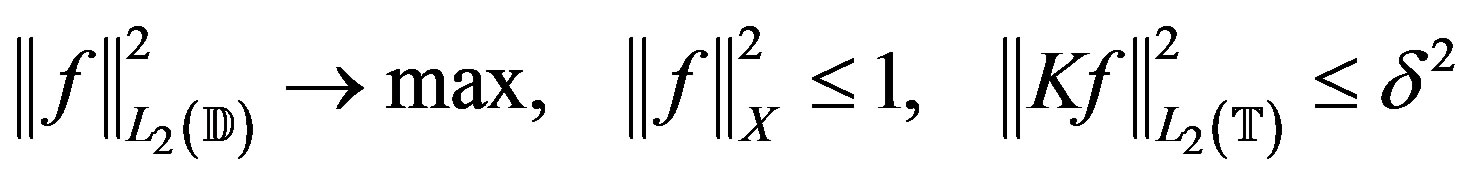 (17)
(17)
which can be written as
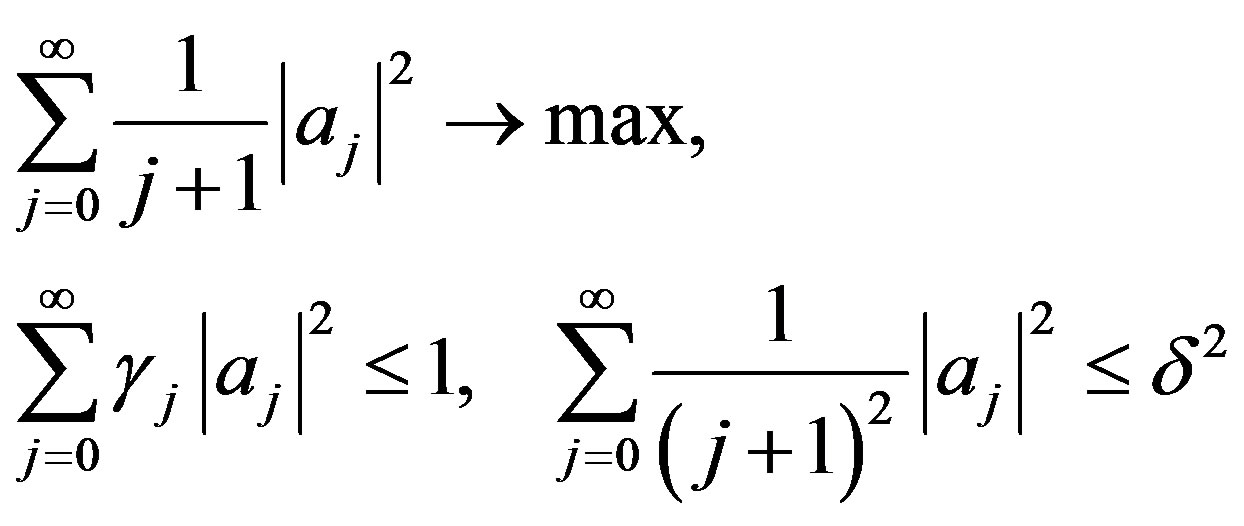
where . Define the corresponding Lagrange function as
. Define the corresponding Lagrange function as
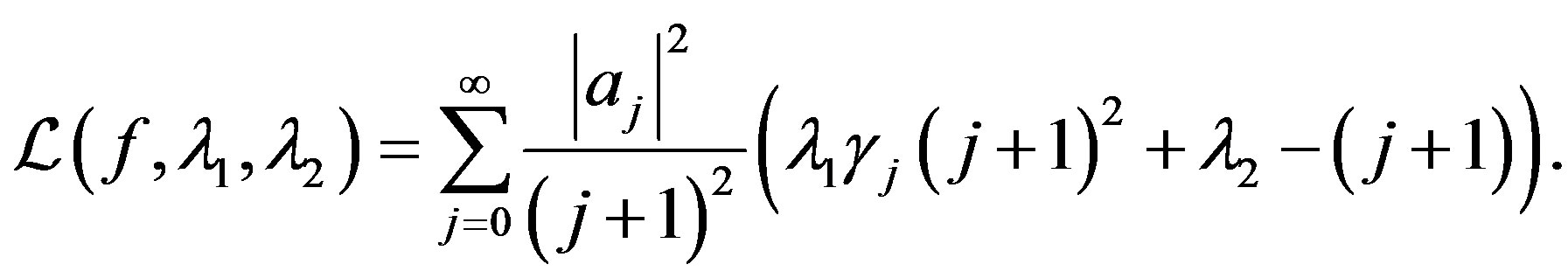
Let the line segment between successive points
 and
and 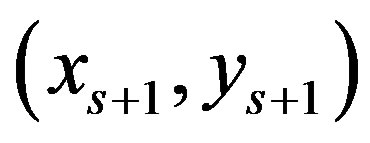 be given by
be given by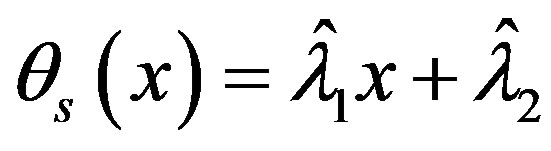 .
.
That is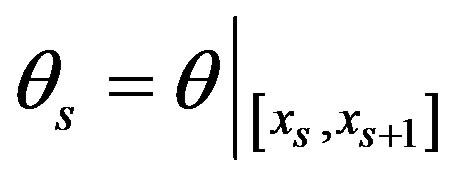 . Thus
. Thus 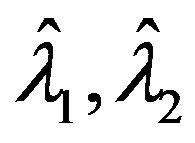 are given by (12). Take any
are given by (12). Take any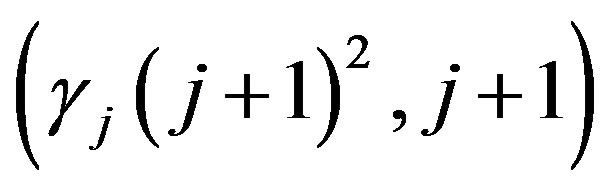 , then by definition of the function
, then by definition of the function  we have
we have
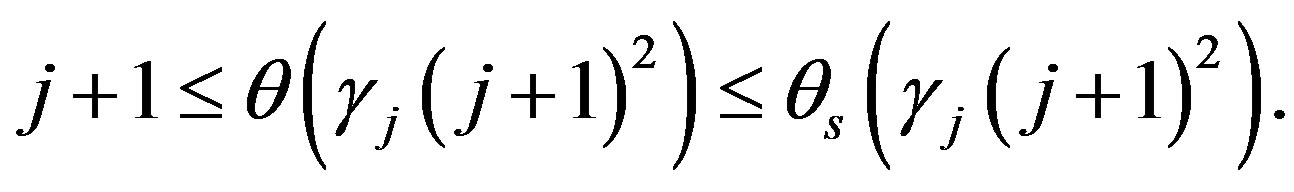
Thus for all 
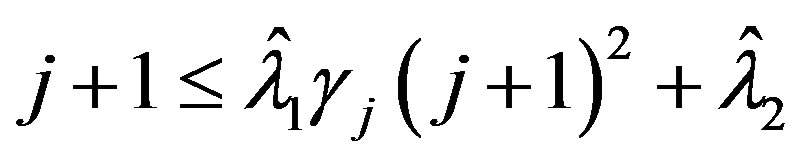
and hence 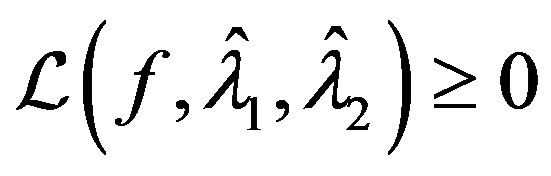 for any
for any .
.
We proceed to the construction of a function  admissable in (15) that also satisfies
admissable in (15) that also satisfies
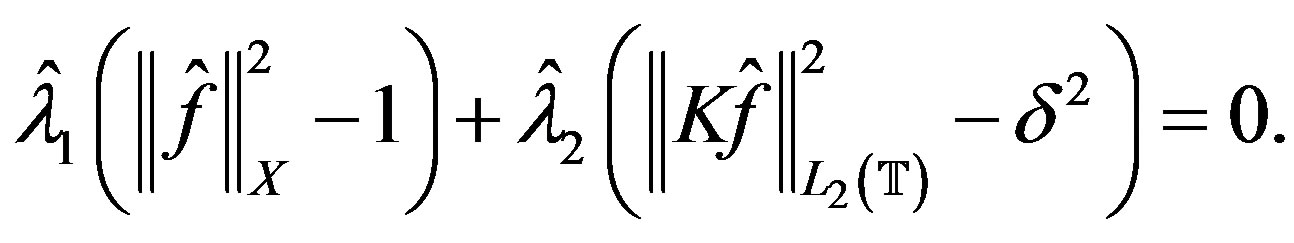 Assume
Assume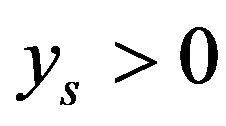 .
.
As 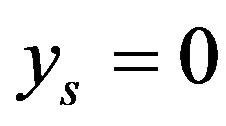 if and only if
if and only if 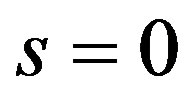 and
and 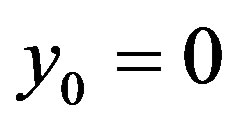 then
then  if and only if
if and only if  or
or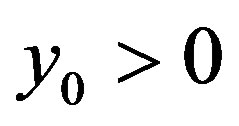 . Let
. Let  be the indices that satisfy
be the indices that satisfy
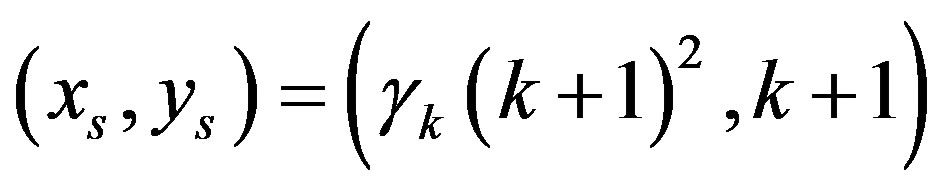
and
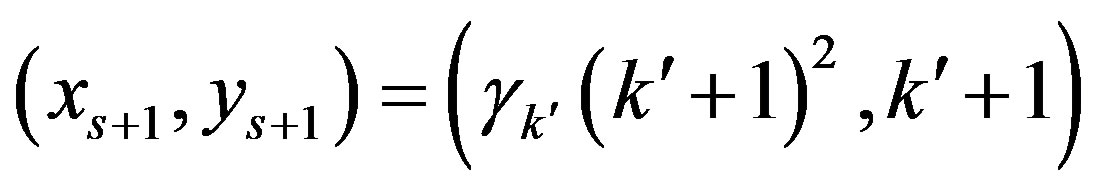 .
.
We let  for
for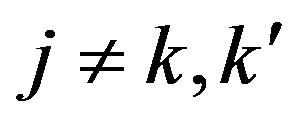 , and choose
, and choose 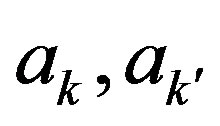 so that they satisfy the conditions
so that they satisfy the conditions
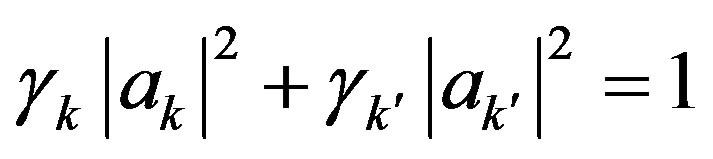
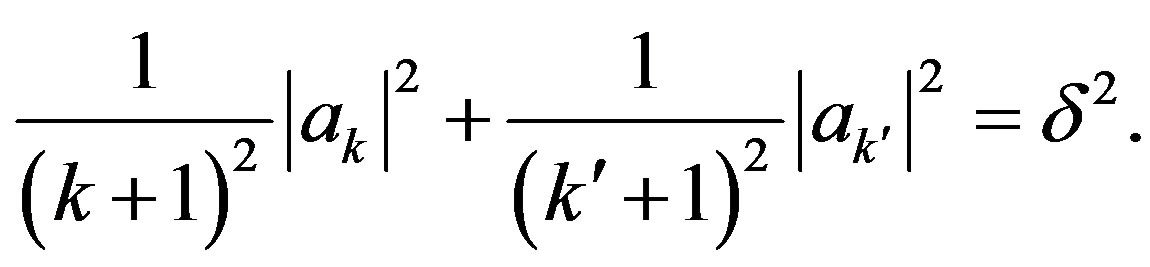 (18)
(18)
From these conditions let
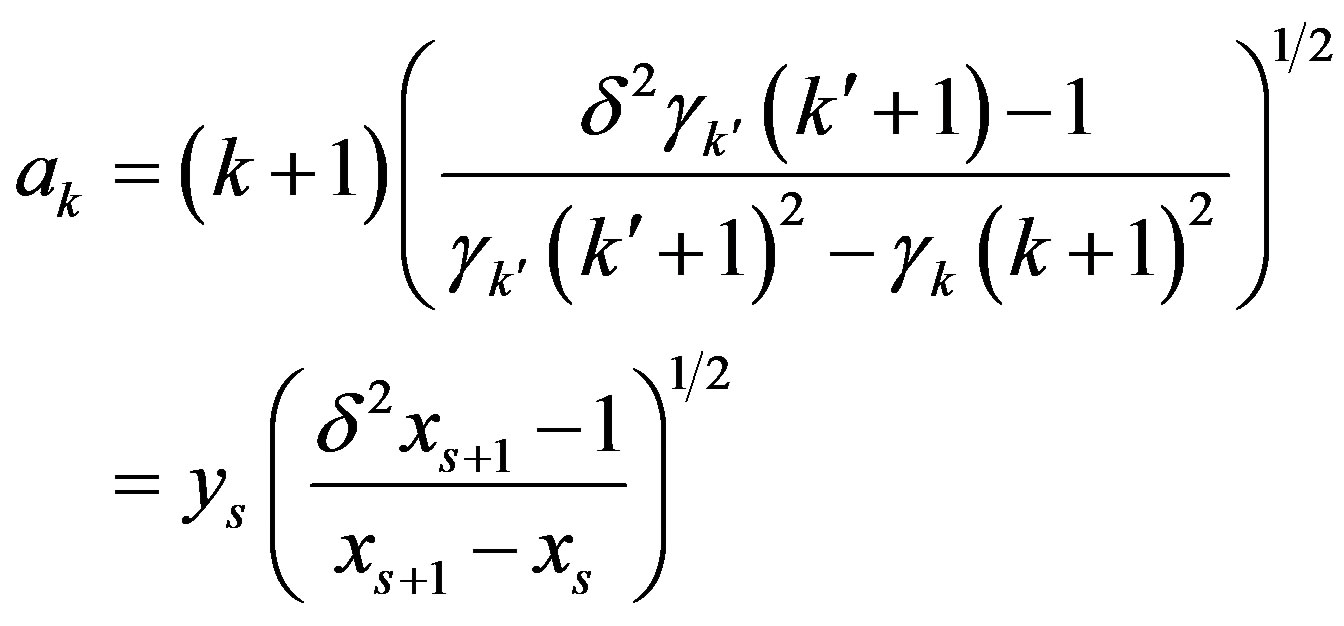
 (19)
(19)
and
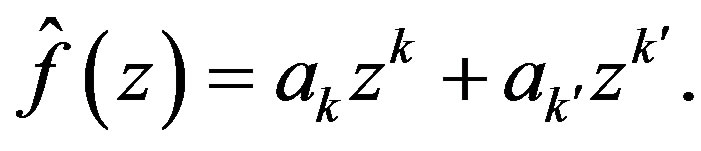 (20)
(20)
Now if 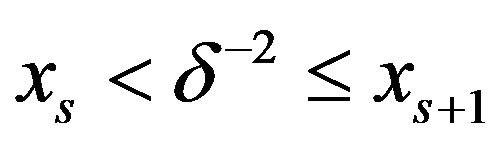 with
with 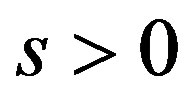 or
or 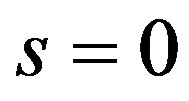 and
and
 the function
the function 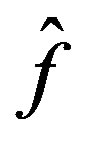 is admissible in (15) and
is admissible in (15) and
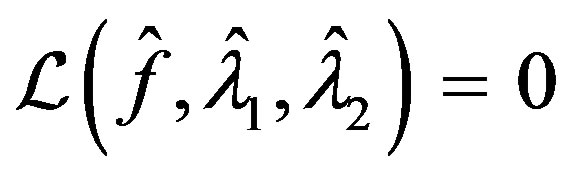 , that is
, that is 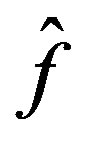 minimizes
minimizes 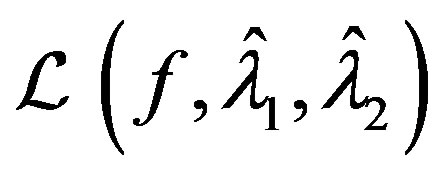
and condition 1) of Theorem 2 is satisfied. Furthermore, by construction,  satisfies condition 2) of Theorem 2.
satisfies condition 2) of Theorem 2.
If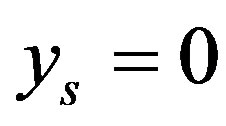 , that is
, that is 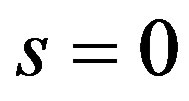 and
and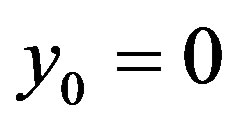 , define
, define 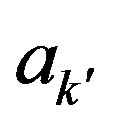 as in (17). Then as
as in (17). Then as 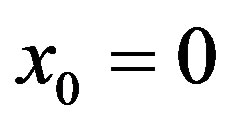
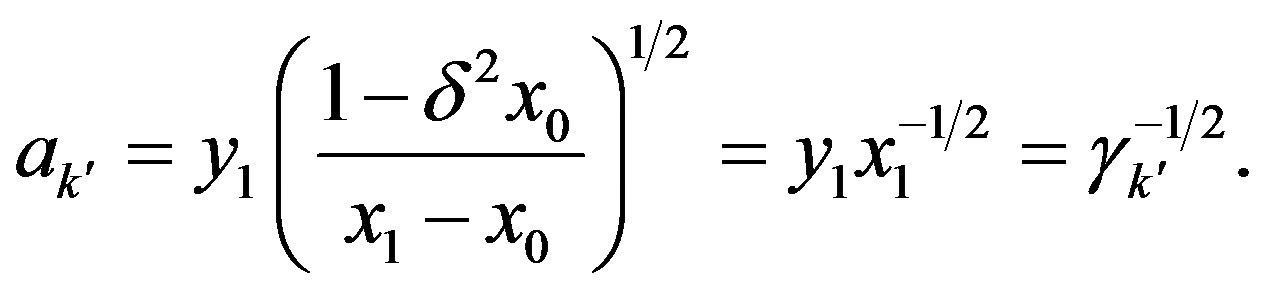
So let  and we have
and we have

Thus the function 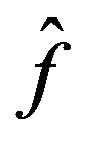 is admissable in (15) and satisfies 1) and 2) of Theorem 2. It should be noted that in this case
is admissable in (15) and satisfies 1) and 2) of Theorem 2. It should be noted that in this case 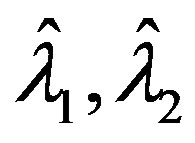 are simply
are simply  and
and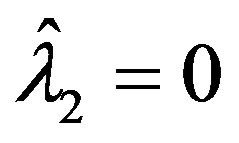 .
.
Now we proceed to the extremal problem
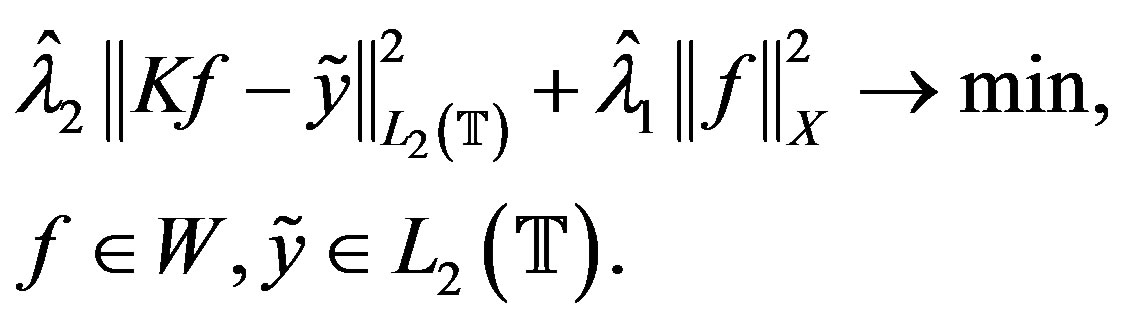 (21)
(21)
This problem may be rewritten as

which has solution
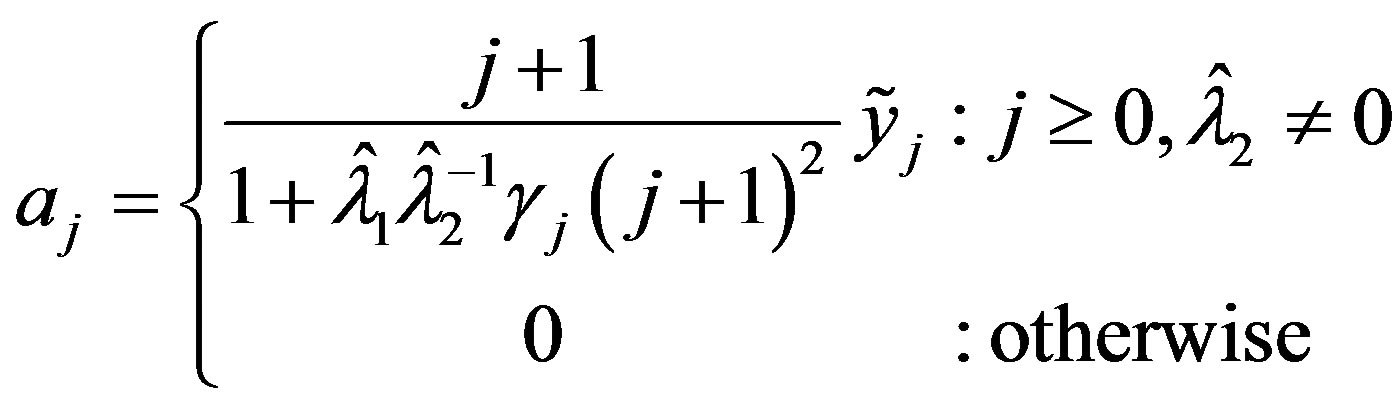
So for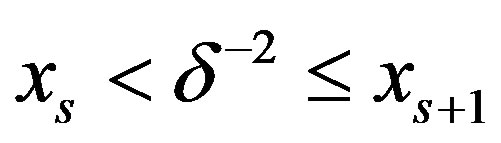 ,
, 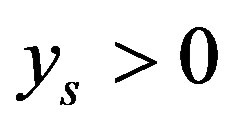 by Theorems 1 and 2, (14) is an optimal method and the error of optimal recovery is given by (13). If
by Theorems 1 and 2, (14) is an optimal method and the error of optimal recovery is given by (13). If 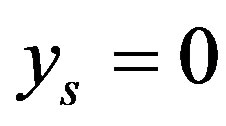 then
then
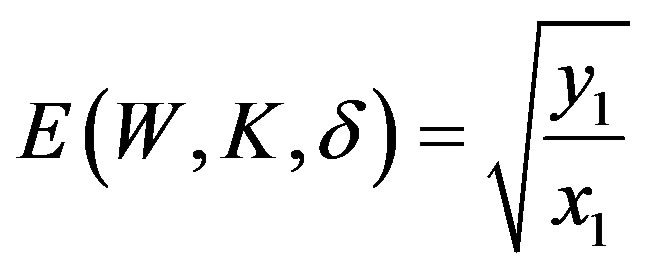 and
and 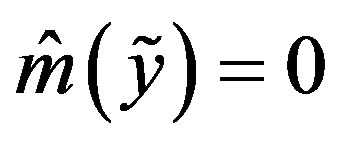 is an optimal method.
is an optimal method. 
It should be noted that for fixed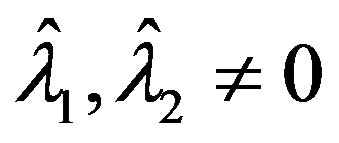 , that is for a fixed
, that is for a fixed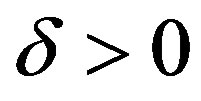 , the terms
, the terms
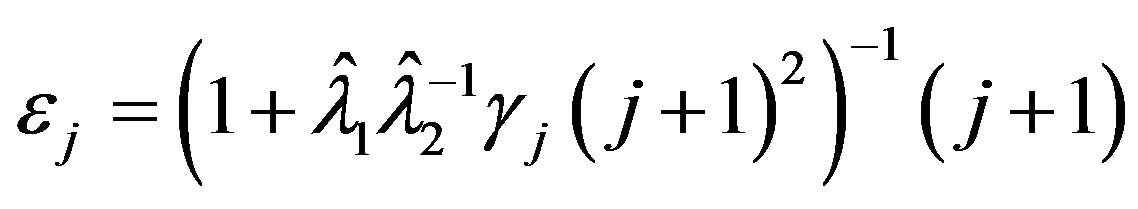
will have the property, 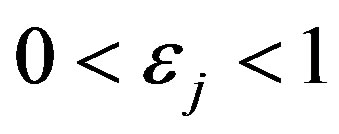 and
and 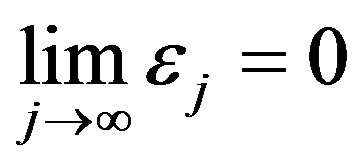 as
as . So
. So  smooths approximate values of the coefficients of
smooths approximate values of the coefficients of 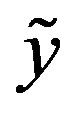 by the filter
by the filter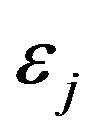 .
.
3.2. Inaccuracy in 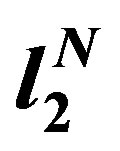 Norm
Norm
Our next problem of optimal recovery remains to recover 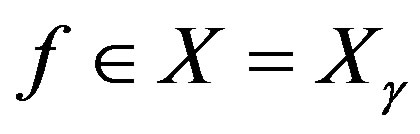 from inaccurate information pertaining to the radial integral of f. However, the inaccurate information we are given are the values
from inaccurate information pertaining to the radial integral of f. However, the inaccurate information we are given are the values
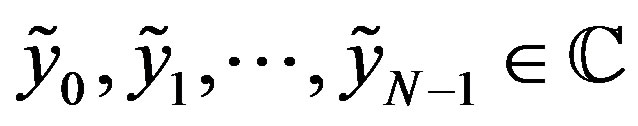 such that
such that

where  is the
is the 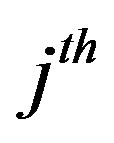 coefficient of the radial integral
coefficient of the radial integral ,
,

Denote
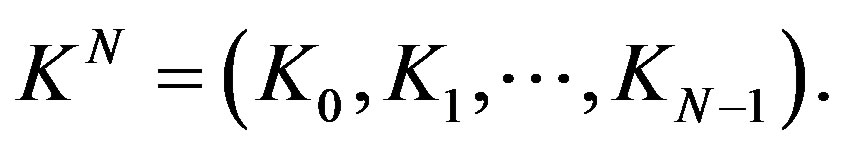
We again consider the space of functions 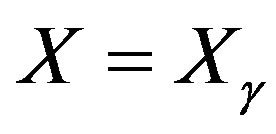 given by (5) and
given by (5) and 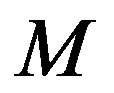 and
and  defined by (10) and (11) respectively but now add the condition
defined by (10) and (11) respectively but now add the condition
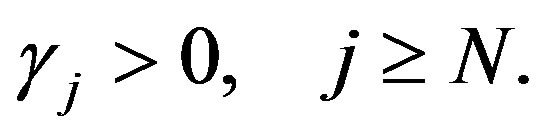 (22)
(22)
The problem of optimal recovery on the class 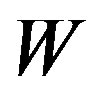 given by (8) is to determine the optimal error
given by (8) is to determine the optimal error
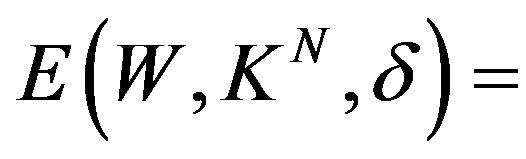 (23)
(23)
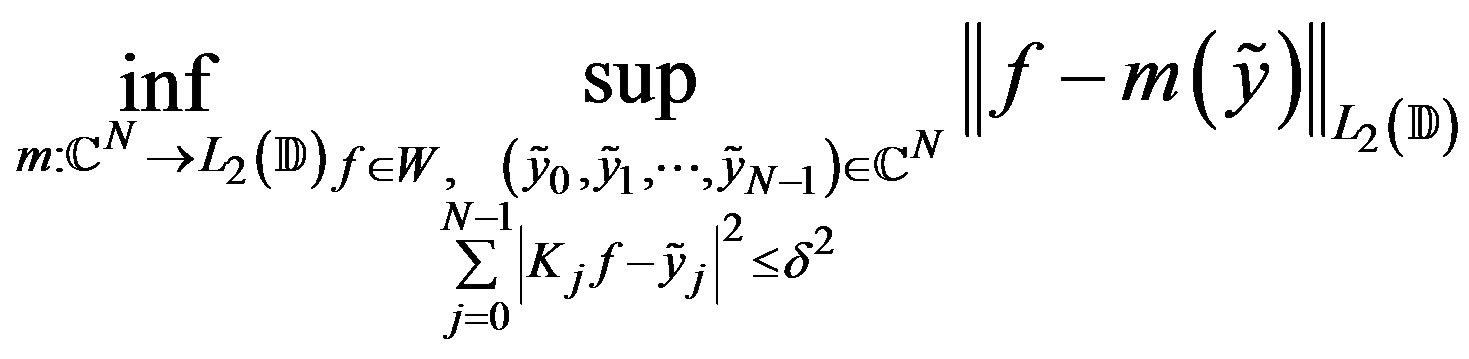 (24)
(24)
and an optimal method 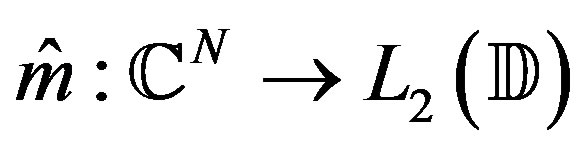 obtaining this error.
obtaining this error.
Define 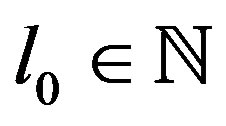 as the largest index such that
as the largest index such that
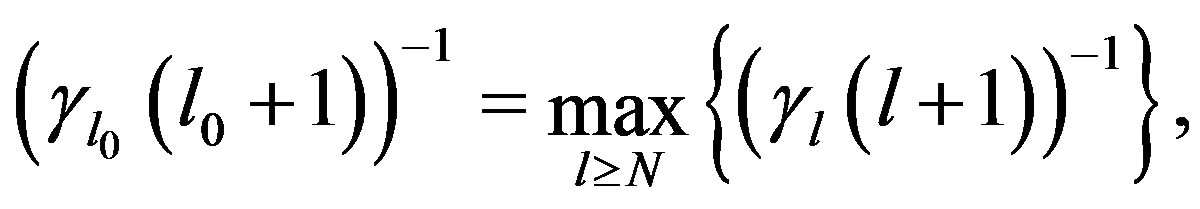 (25)
(25)
which by (7) exists, and
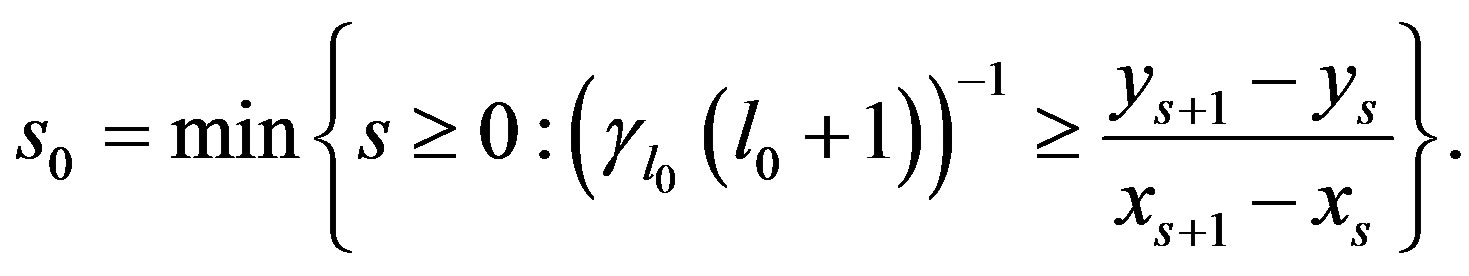 (26)
(26)
Theorem 4: Suppose 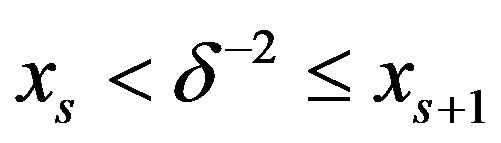 with
with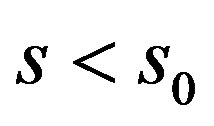 . If
. If
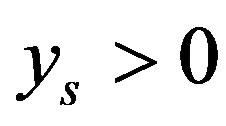 let
let 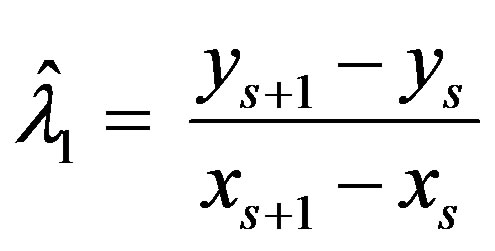 and
and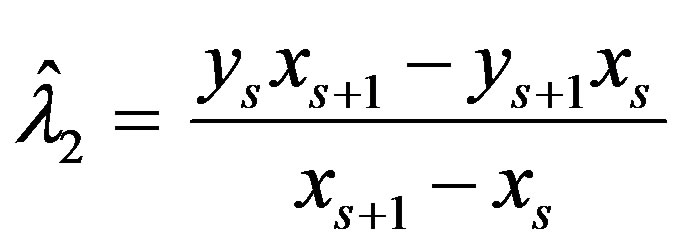 .
.
Then the optimal error is
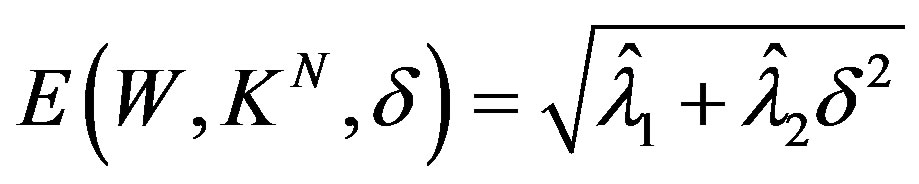 (27)
(27)
and
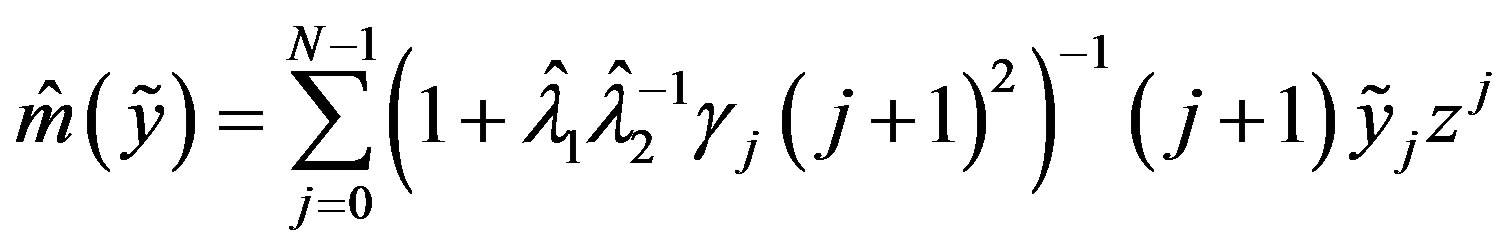 (28)
(28)
is an optimal method. If 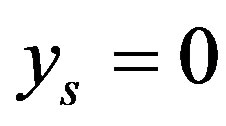 then
then
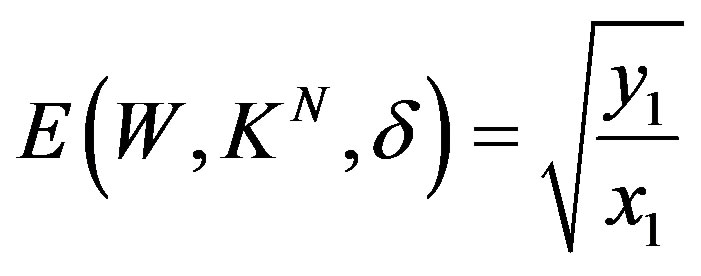 and
and 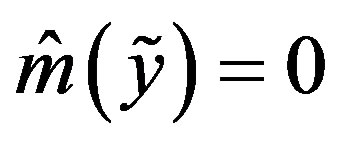 is an optimal method.
is an optimal method.
If  and
and 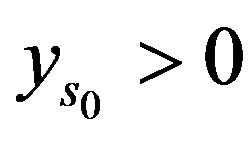 then with
then with
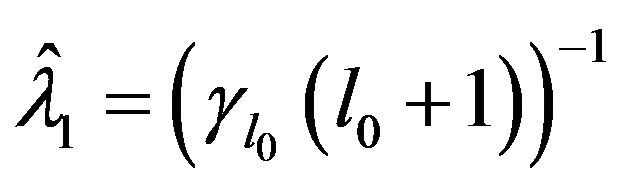 and
and 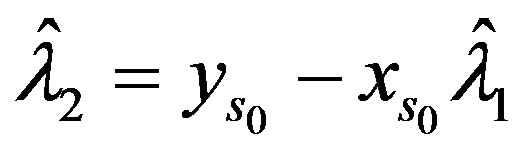 the error of optimal recovery is (22) and (23) is an optimal method. For
the error of optimal recovery is (22) and (23) is an optimal method. For
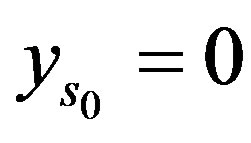 ,
, 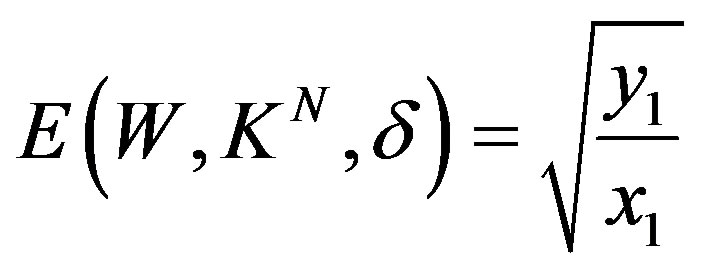 and
and  is an optimal method.
is an optimal method.
Proof. For the cases 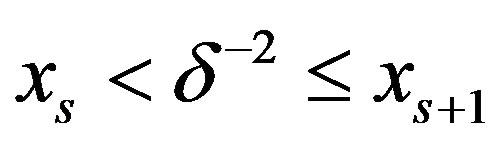 with
with  we simply apply the same structure of proof as in Theorem 3. For the case
we simply apply the same structure of proof as in Theorem 3. For the case 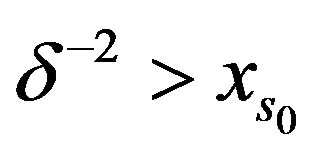 there remains some work.
there remains some work.
Our construction will depend on whether or not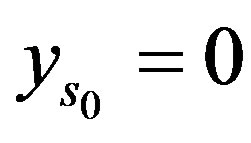 , that is whether or not
, that is whether or not 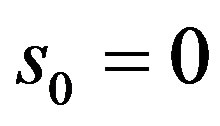 with
with
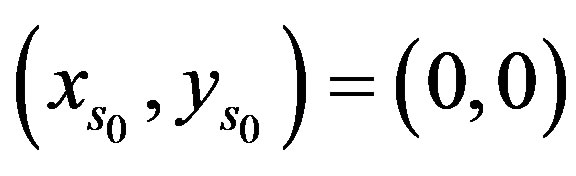 .
.
First we notice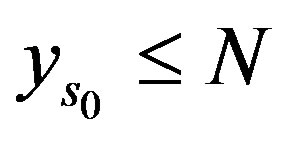 . Assume not. Then if
. Assume not. Then if  we also know
we also know 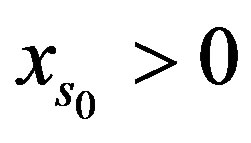 since for all
since for all 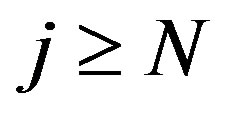 we assumed
we assumed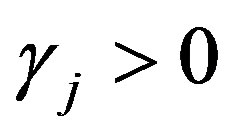 . Since
. Since 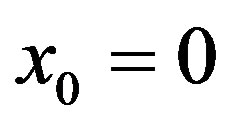 we know
we know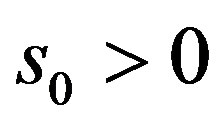 . Then by definition of
. Then by definition of 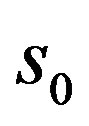 we know for
we know for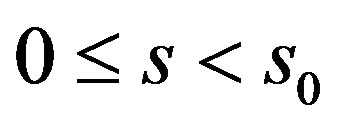 ,
,

and substituting 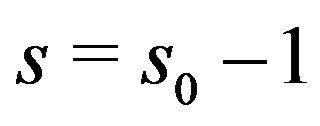 we have
we have
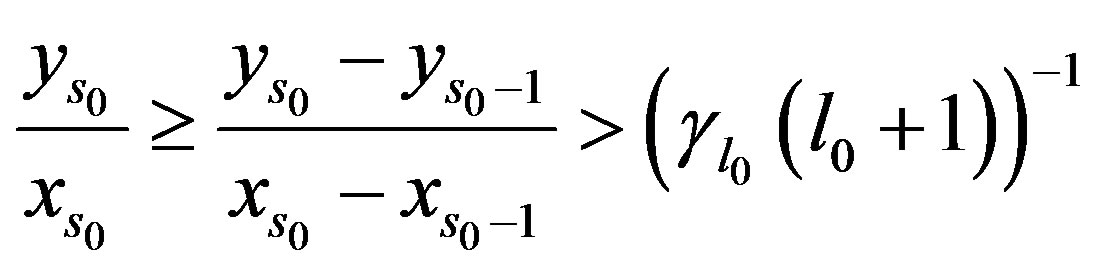
which contradicts the definition of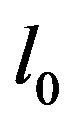 . Therefore
. Therefore
 and if
and if 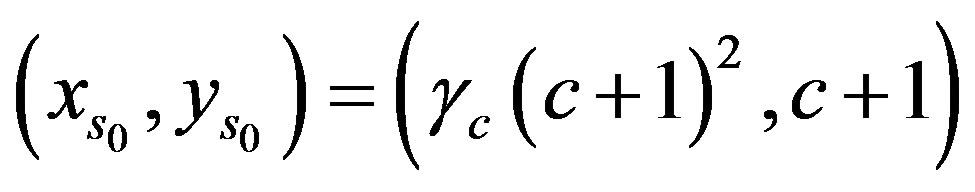 then
then
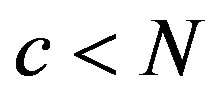 .
.
In either case, 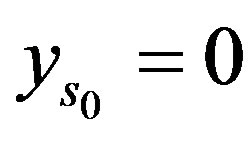 or
or , the dual problem is of the form
, the dual problem is of the form
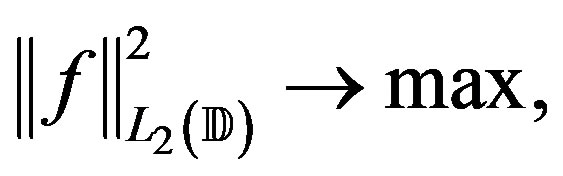 (29)
(29)
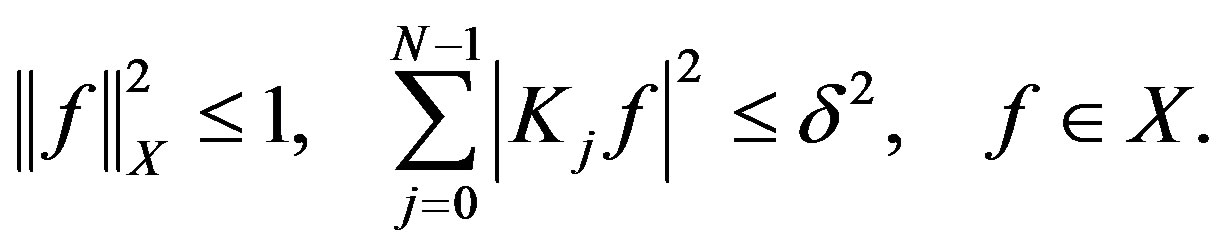
The corresponding Lagrange function is then
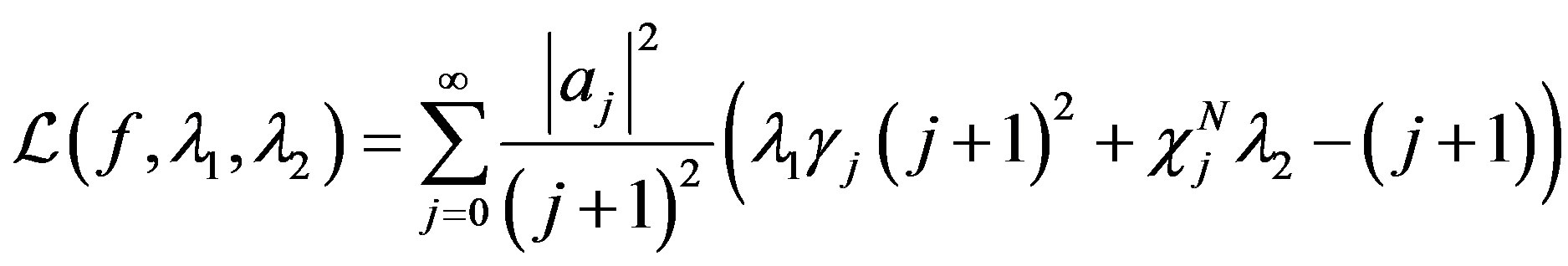
where 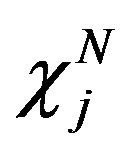 is the characteristic function of
is the characteristic function of
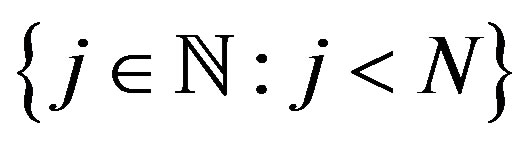 .
.
Case 1): 
If 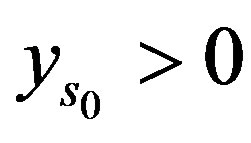 let
let  correspond to the index satisfying
correspond to the index satisfying
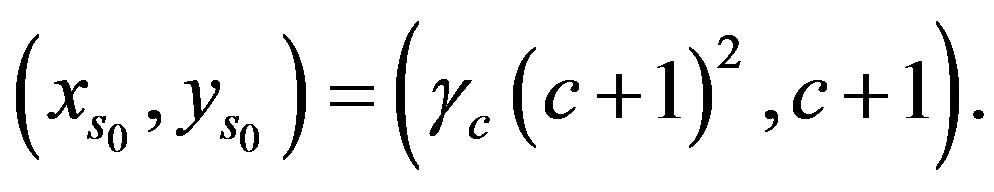
To determine 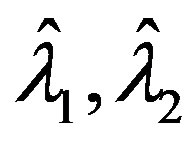 let
let  be the line through the point
be the line through the point 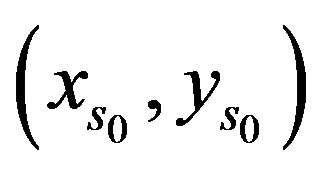 that is parallel to the line from the origin to
that is parallel to the line from the origin to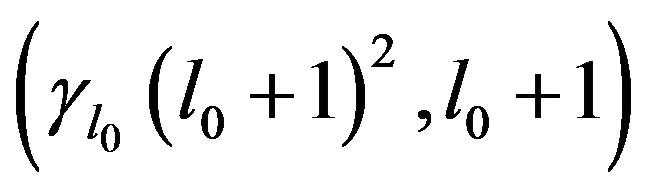 . That is, let
. That is, let
 (30)
(30)
So for any point of break we have 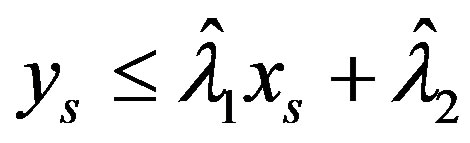 and for any index
and for any index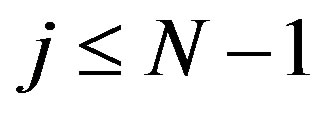 , we obtain
, we obtain
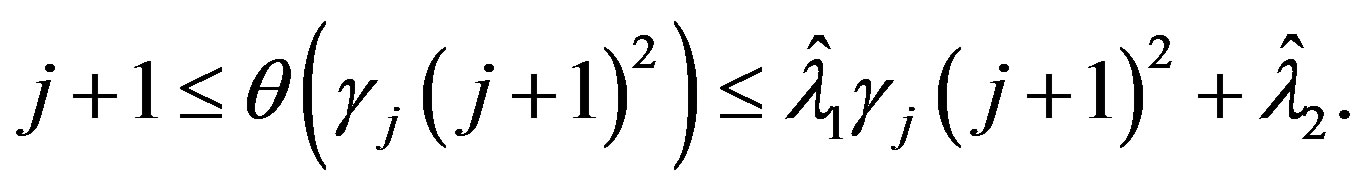
If 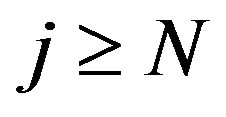 then
then
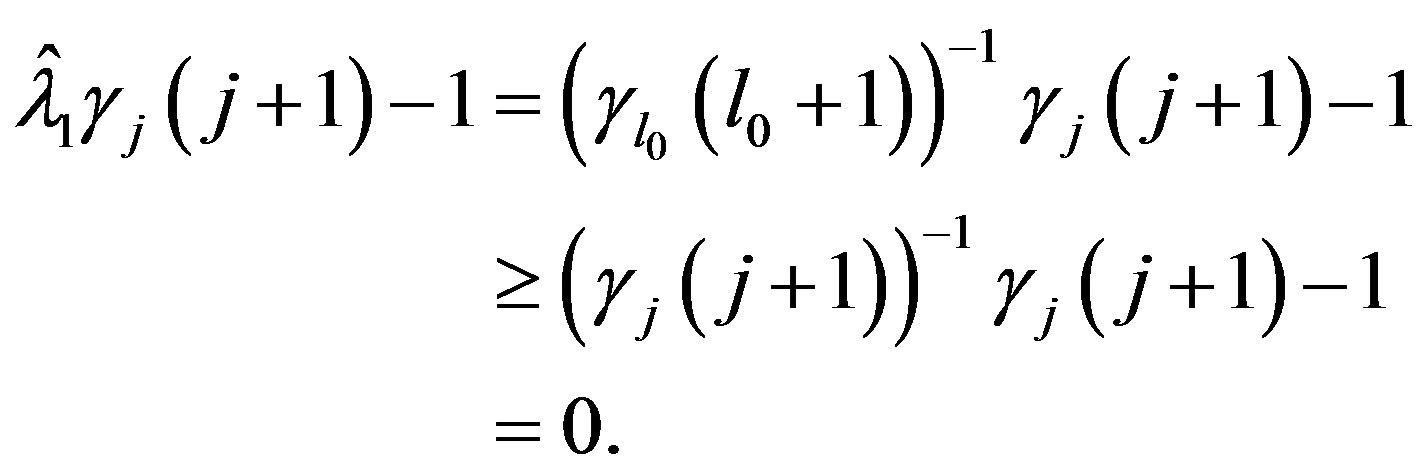
Thus for the chosen  and
and  and any
and any  we have
we have .
.
To construct 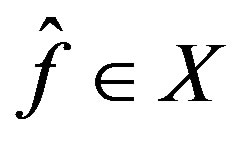 admissable in (24), let
admissable in (24), let 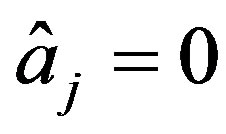 for
for 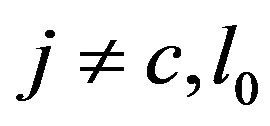 and define
and define 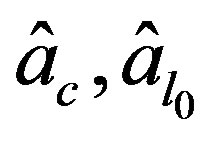 by the system
by the system
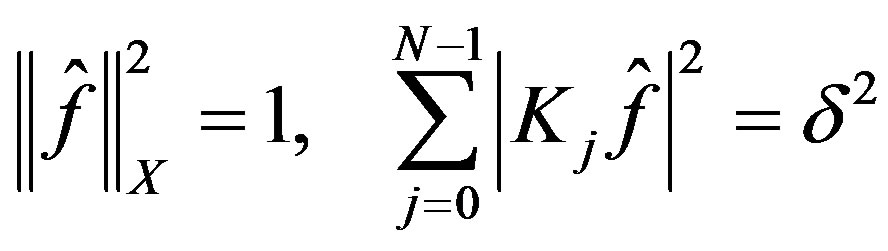
and since  this becomes
this becomes
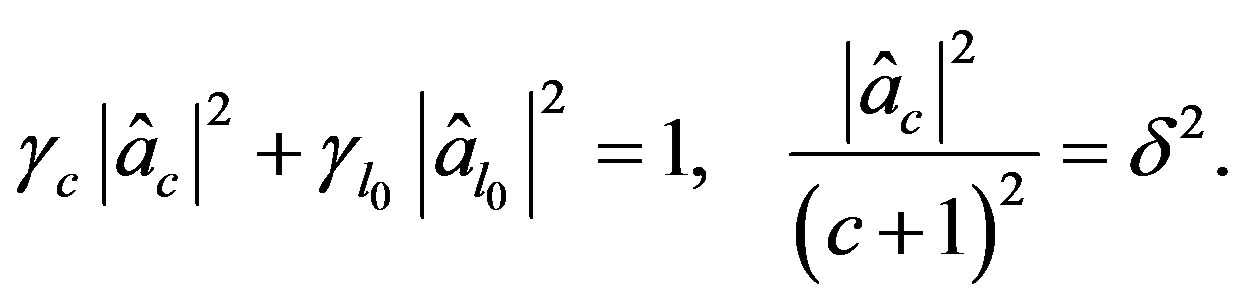
So let 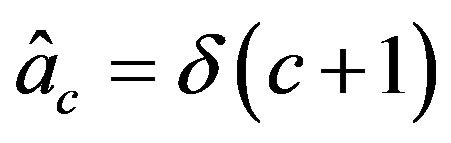 and
and .
.
Then for 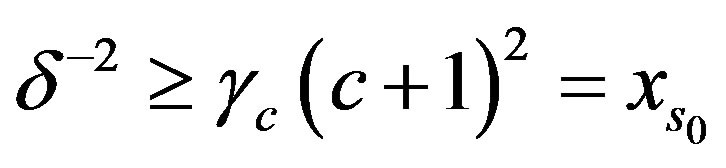 the function
the function
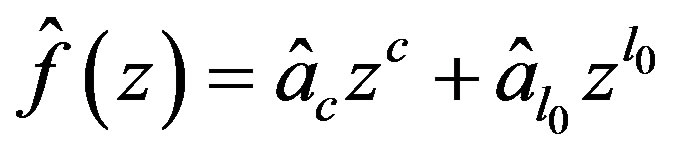 is admissable in (24) with
is admissable in (24) with
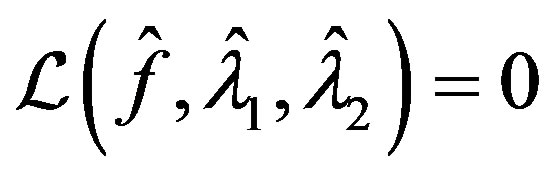
Therefore 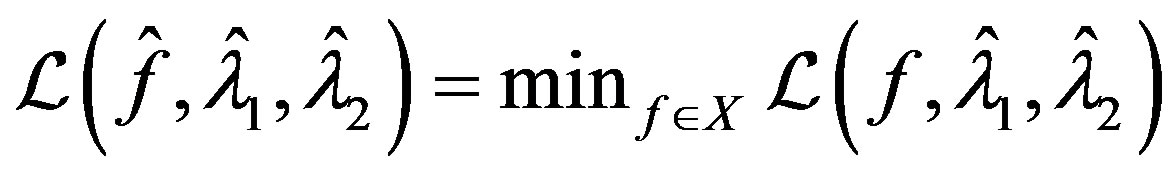 and by construction we have
and by construction we have 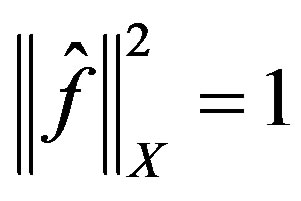 and
and 
so that

and conditions (a) and (b) of Theorem 2 are satisfied.
Case 2): 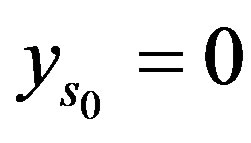
If  then
then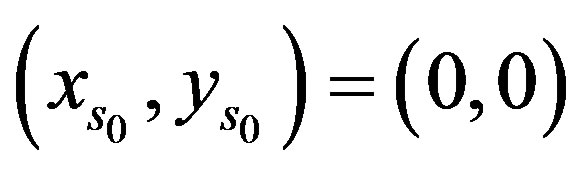 , and
, and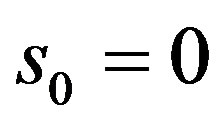 , as this is the only point in the set
, as this is the only point in the set
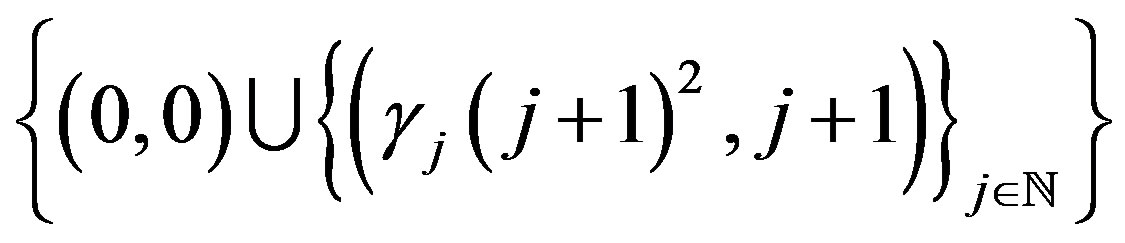 with a
with a 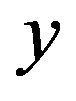 -coordinate of
-coordinate of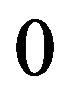 . Furthermore, as
. Furthermore, as 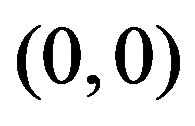 is a point of break of
is a point of break of  we know
we know 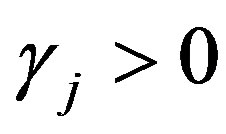 for all
for all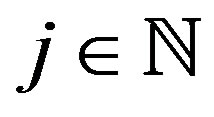 . Since
. Since 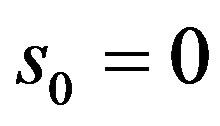 then by the definition of
then by the definition of 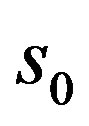 we know
we know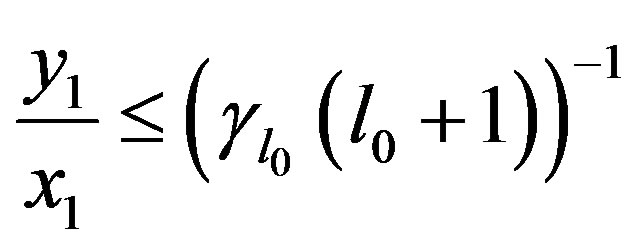 . As
. As
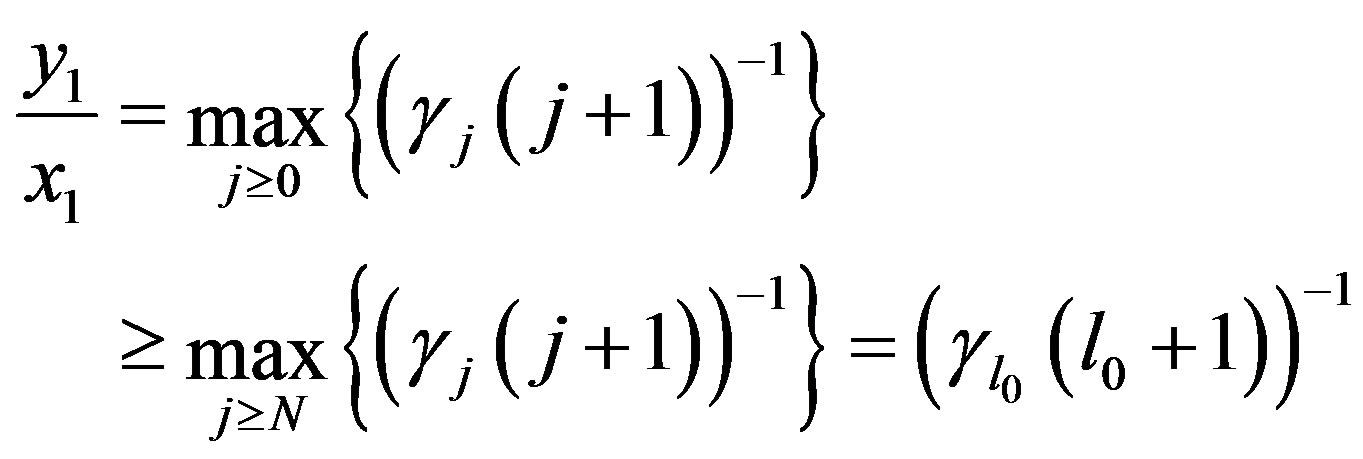 (31)
(31)
then we obtain equality,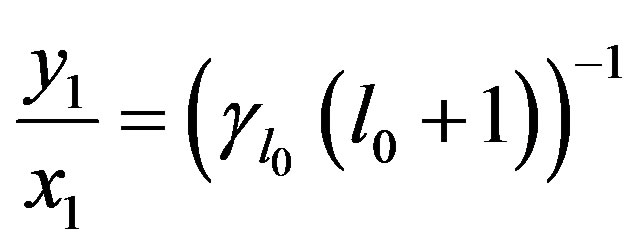 .
.
Define  by (25) so
by (25) so  and
and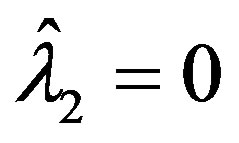 . If we let
. If we let 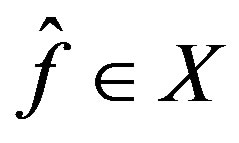 be
be 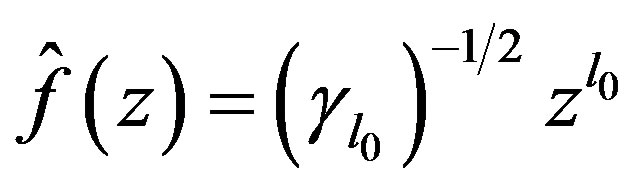 then
then

In addition  is admissable in extremal problem (24)
is admissable in extremal problem (24)
as 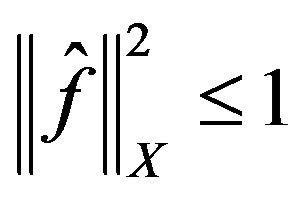 and
and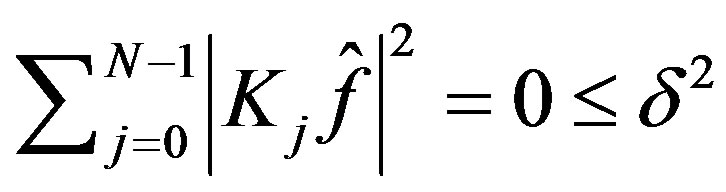 .
.
To justify 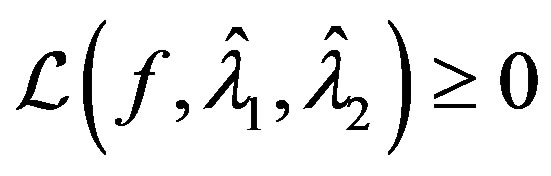 simply note that as
simply note that as
 satisfies (26) and
satisfies (26) and 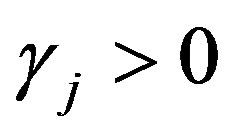 for all
for all 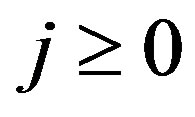 then
then
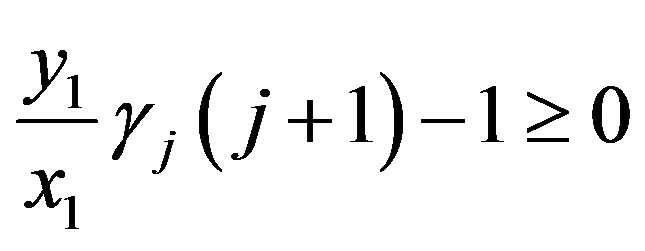 . So we have
. So we have
 . Since
. Since
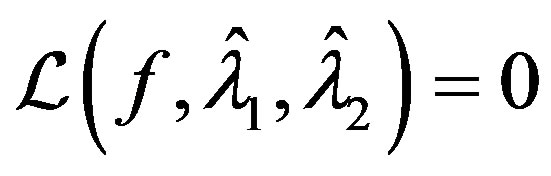 then
then 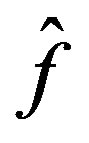 minimizes
minimizes .
.
For both cases, we now consider extremal problem
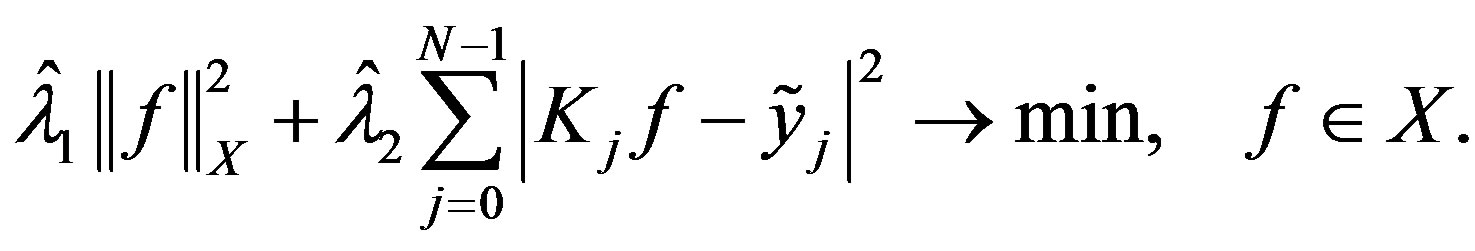 (32)
(32)
This problem can be written as
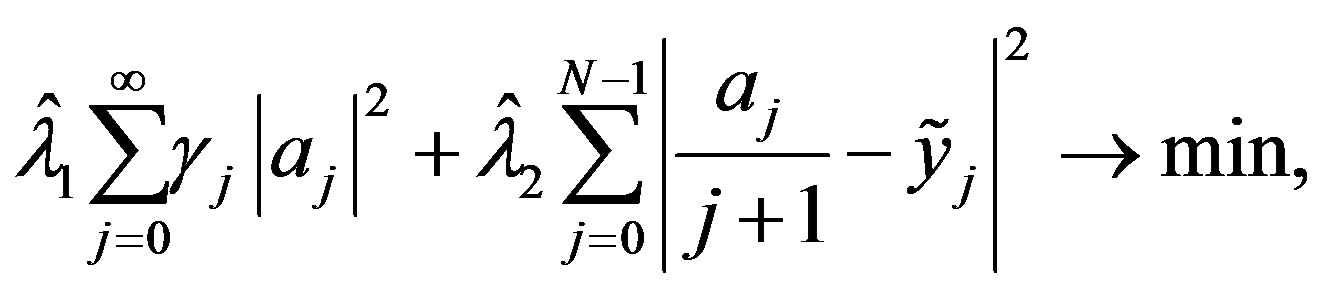
which will have solution
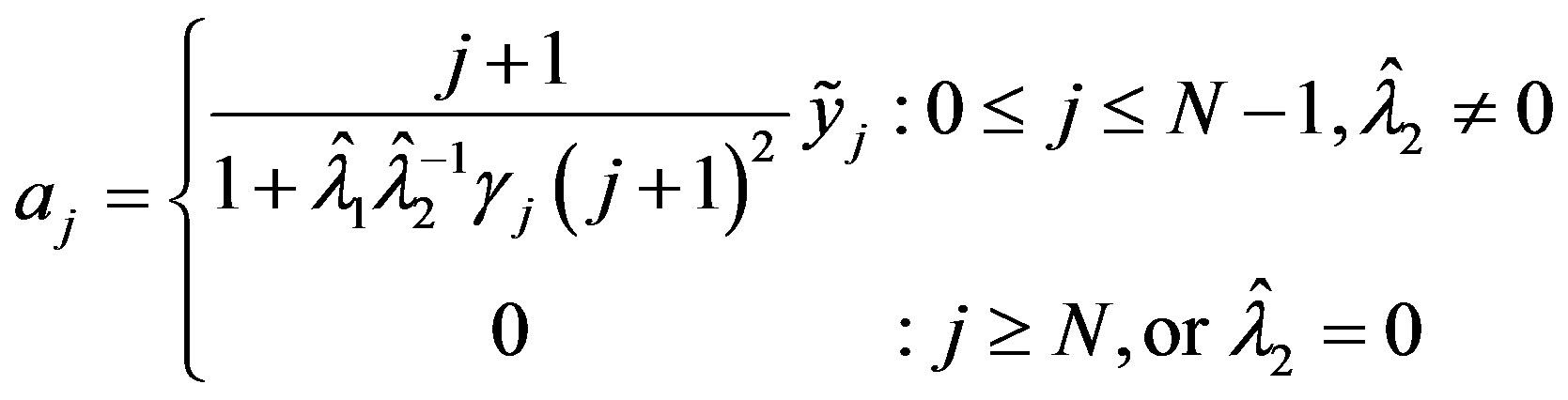
So by Theorems 1 and 2 we have obtained the optimal error and an optimal method for all scenarios. In each case i and ii,  and
and  are given by (25). In each case, the error of optimal recovery is
are given by (25). In each case, the error of optimal recovery is
 which for case 2) simplifies to
which for case 2) simplifies to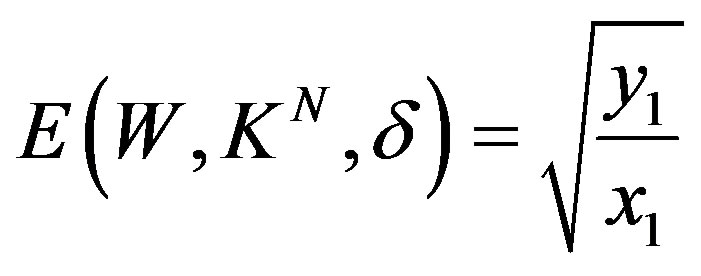 . Also for each case, a method of optimal recovery is given by
. Also for each case, a method of optimal recovery is given by 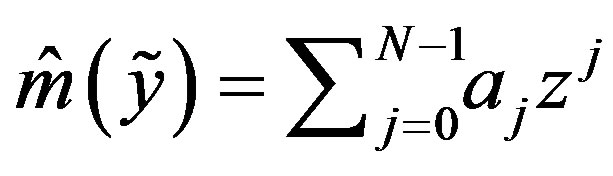 where in case 2) this simplifies to
where in case 2) this simplifies to 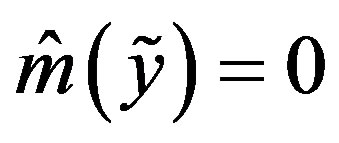 since in case 2),
since in case 2),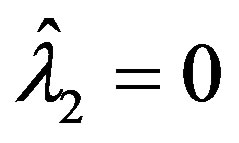 .
.
One may be able to reduce the amount information needed without affecting the error of optimal recovery. Therefore, by reducing the number of terms in the optimal method we reduce the compututaions needed. The following ideas are in [9]. We consider the subset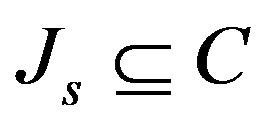 ,
, 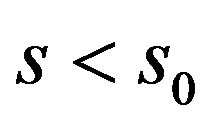 as the set of all points whose slope to the origin is greater than the slope of
as the set of all points whose slope to the origin is greater than the slope of 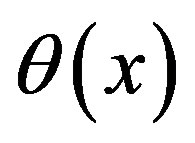 for
for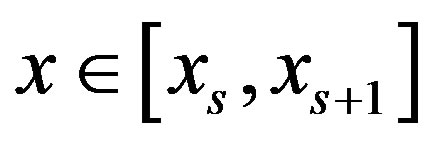 , that is the slope of the line segment between points
, that is the slope of the line segment between points 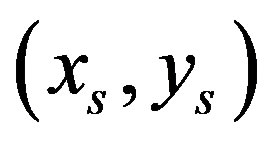 and
and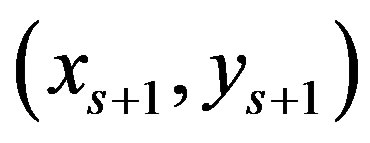 . Define the sets
. Define the sets
 (33)
(33)
for 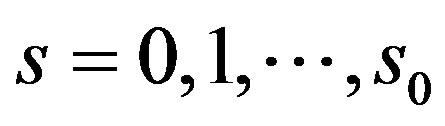 where if
where if 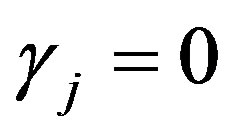 define
define
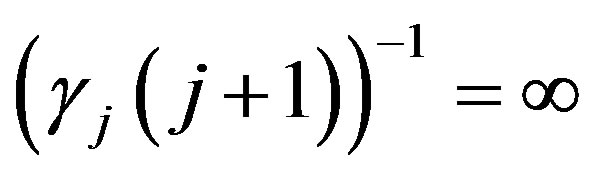 . Now consider the same problem as stated in Theorem 4 using only information
. Now consider the same problem as stated in Theorem 4 using only information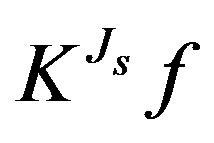 . For
. For
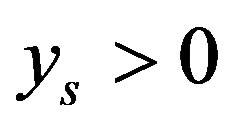 , we have
, we have  and so
and so
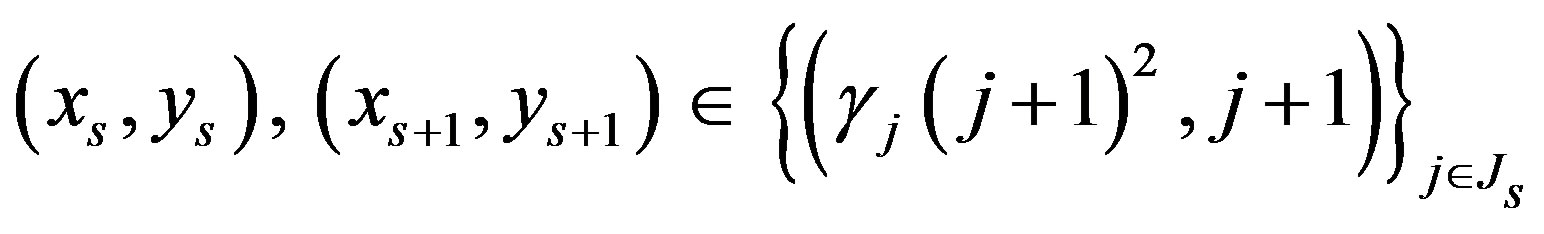 . In this situation,
. In this situation, 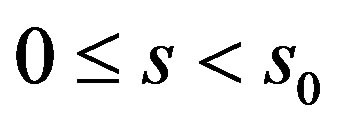 with
with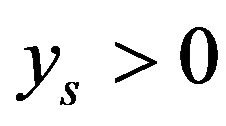 , it was shown that the error of optimal recovery only involves the two points
, it was shown that the error of optimal recovery only involves the two points
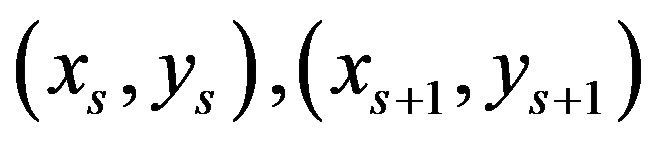 then the reduction in information from
then the reduction in information from 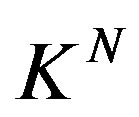 to
to  will not change the error. That is
will not change the error. That is
 and if
and if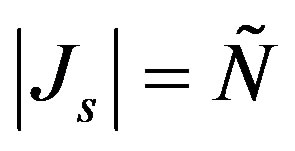 , an optimal method is
, an optimal method is
 (34)
(34)
where .
.
3.3. Varying Levels of Accuracy Termwise
In Theorems 3 and 4 the inaccuracy of the information given is a total inaccuracy. That is, the inaccuracy 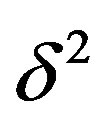 is an upper bound on the sum total of the inaccuracies in each term, be it a finite or infinite sum. For Theorems 3 and 4 however, there is no way to tell how the inaccuracy is distributed. In particular, with regards to Theorem 4, the situations in which the given information
is an upper bound on the sum total of the inaccuracies in each term, be it a finite or infinite sum. For Theorems 3 and 4 however, there is no way to tell how the inaccuracy is distributed. In particular, with regards to Theorem 4, the situations in which the given information 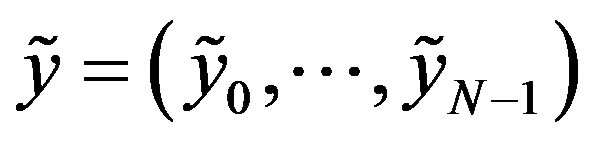 satisfies
satisfies
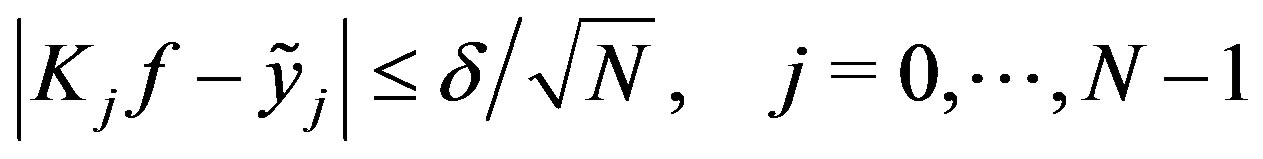
or for some particular 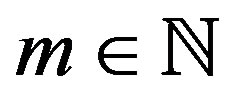 satisfying
satisfying 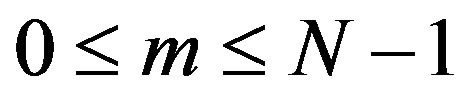
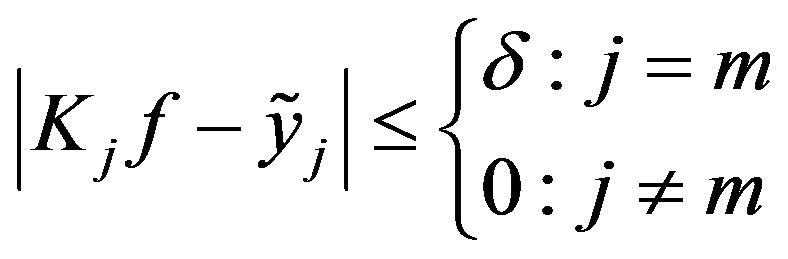
are treated the same. For the next problem of optimal recovery we address this ambiguity. The problem of optimal recovery is to determine an optimal method and the optimal error of recovering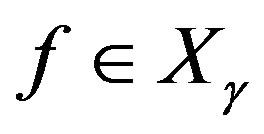 , from the information
, from the information 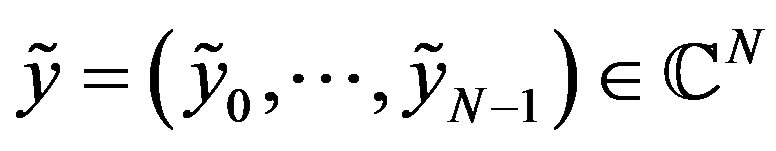 satisfying
satisfying
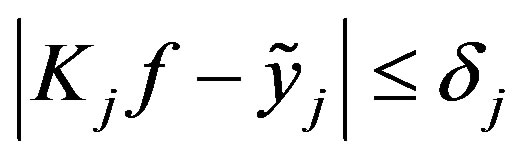
for some prescribed 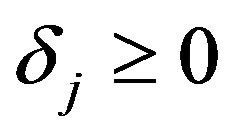 and
and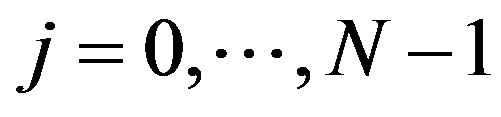 .
.
To define 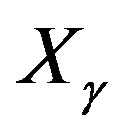 use conditions (6) and (20) as previously but impose an additional restriction. We add the condition
use conditions (6) and (20) as previously but impose an additional restriction. We add the condition
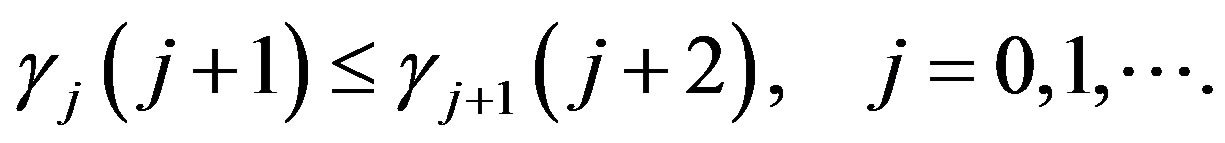
Define 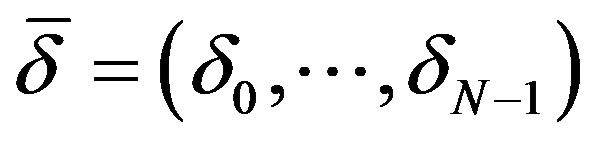 where
where 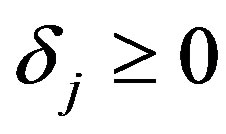 are the levels of accuracy. If
are the levels of accuracy. If 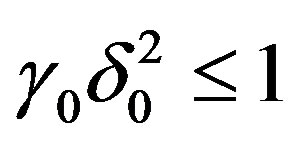 define
define
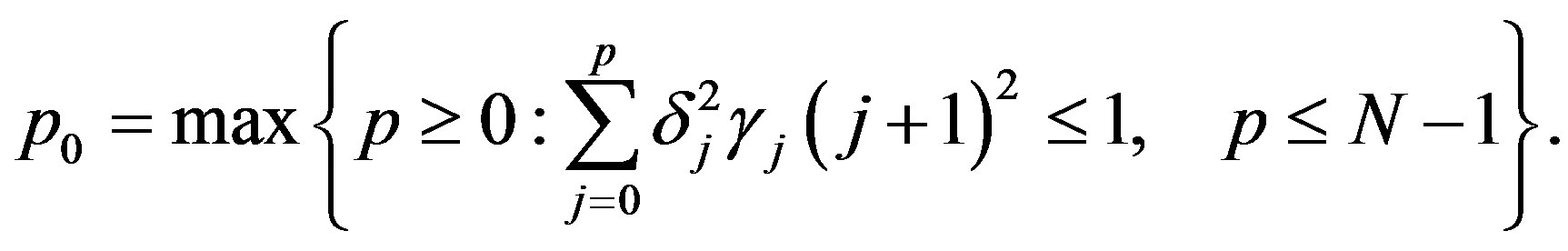 (35)
(35)
So 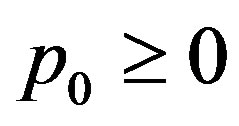 and furthermore
and furthermore . The case
. The case 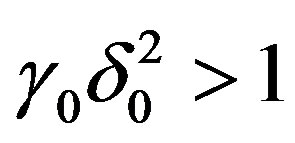 will be treated seperately.
will be treated seperately.
Theorem 5: If 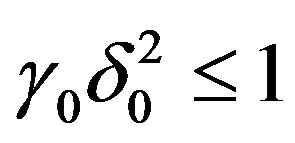 let
let
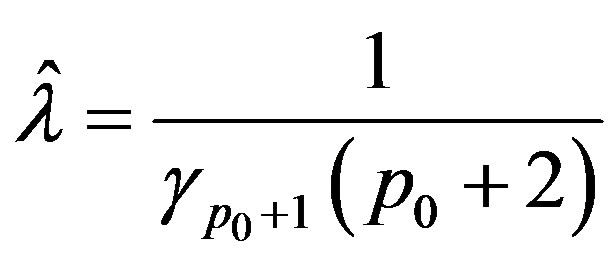 (36)
(36)
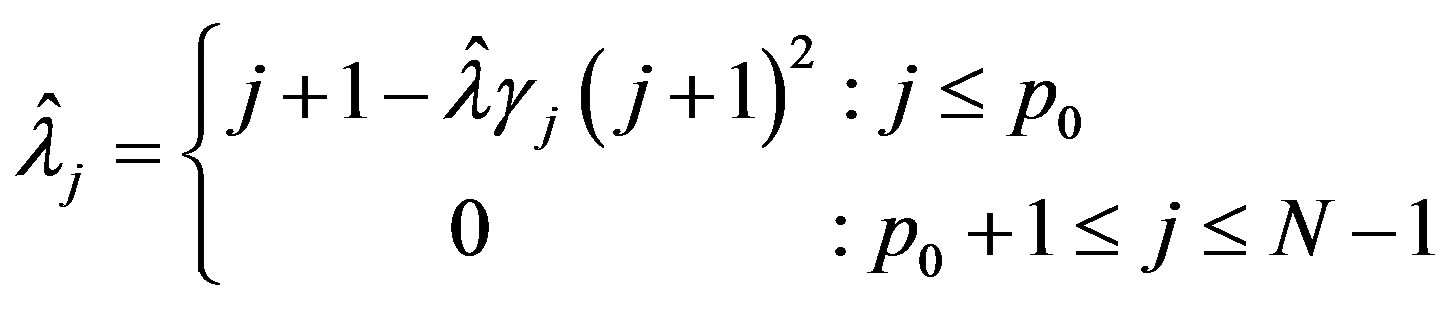
then the error of optimal recovery is given by
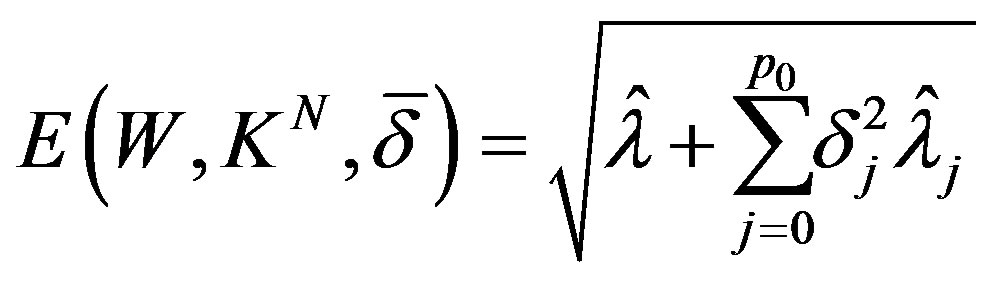 (37)
(37)
and
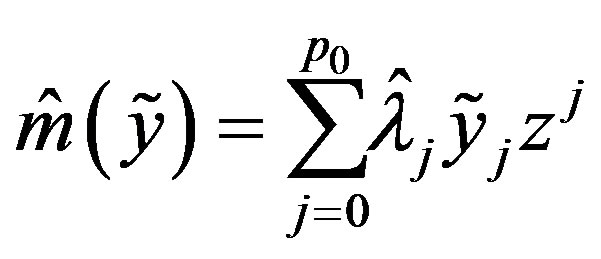 (38)
(38)
is an optimal method.
If 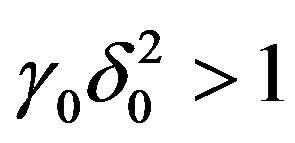 then
then 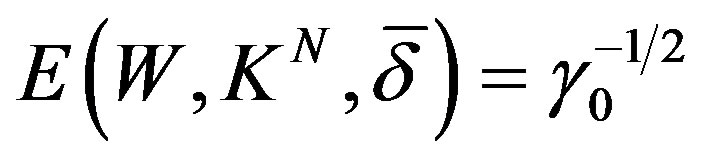 and
and 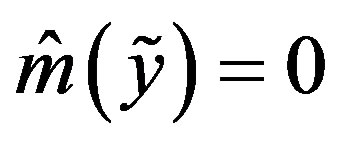 is an optimal method.
is an optimal method.
Proof. The dual problem in this situation is
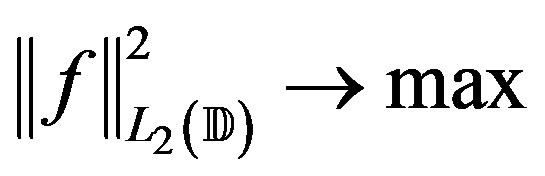 (39)
(39)
 (40)
(40)
with the corresponding Lagrange function
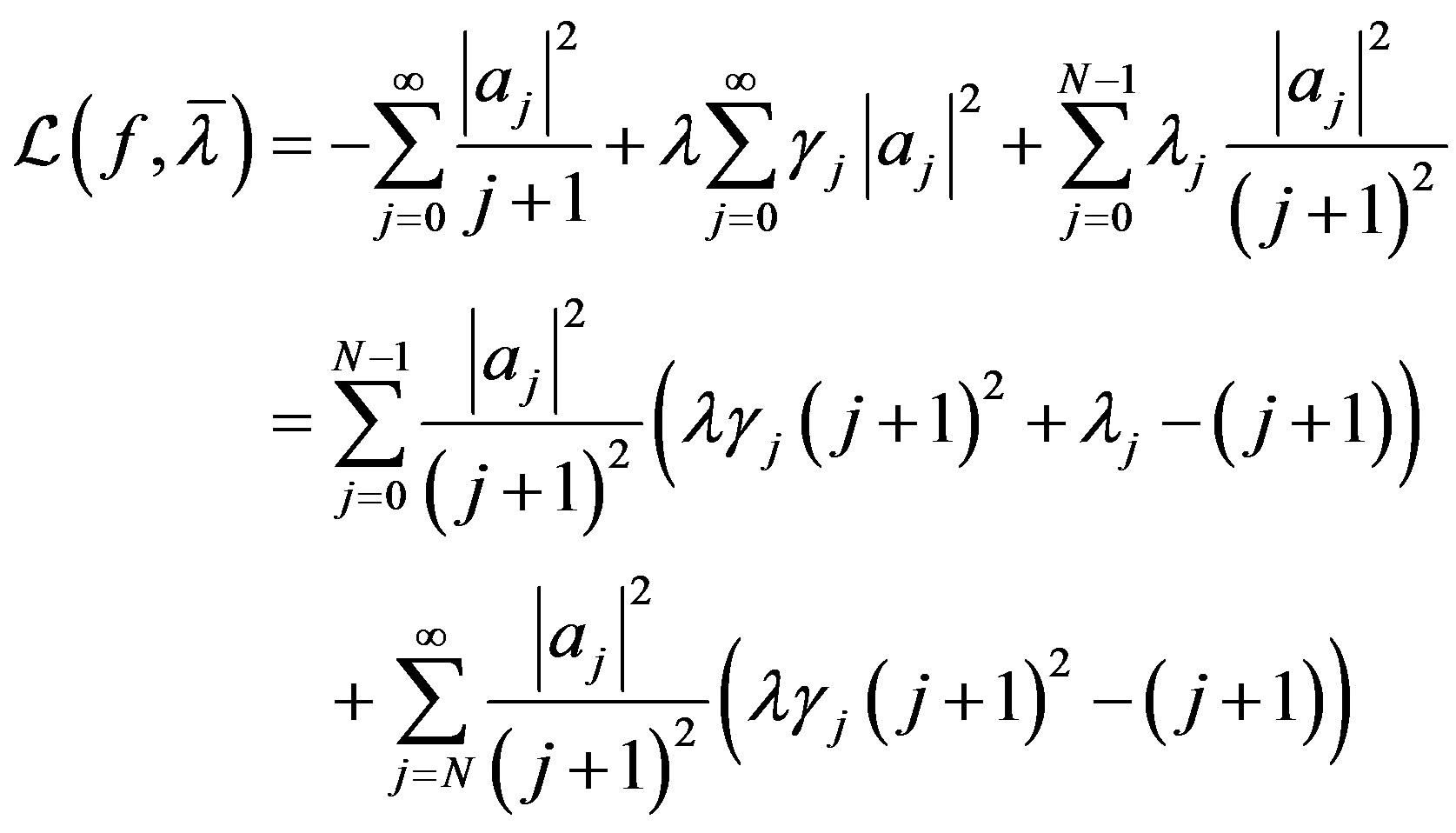
The method of proof will be to first determine
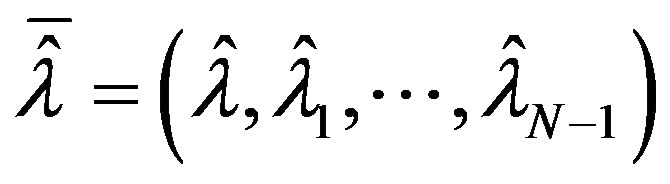 with
with 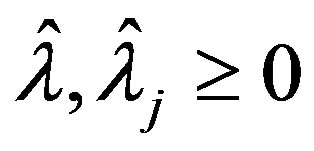 and
and  admissable in (31) and satisfying 1) and 2) of Theorem 2.
admissable in (31) and satisfying 1) and 2) of Theorem 2.
If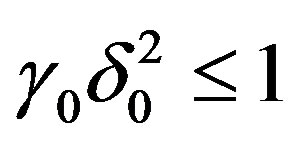 , define
, define  and
and  as follows:
as follows:
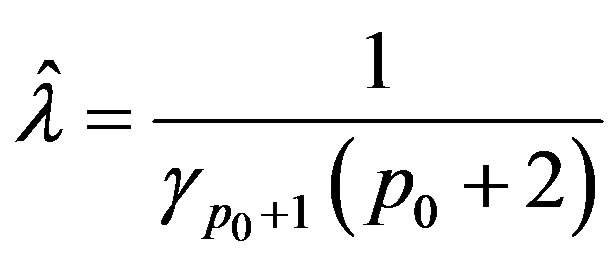
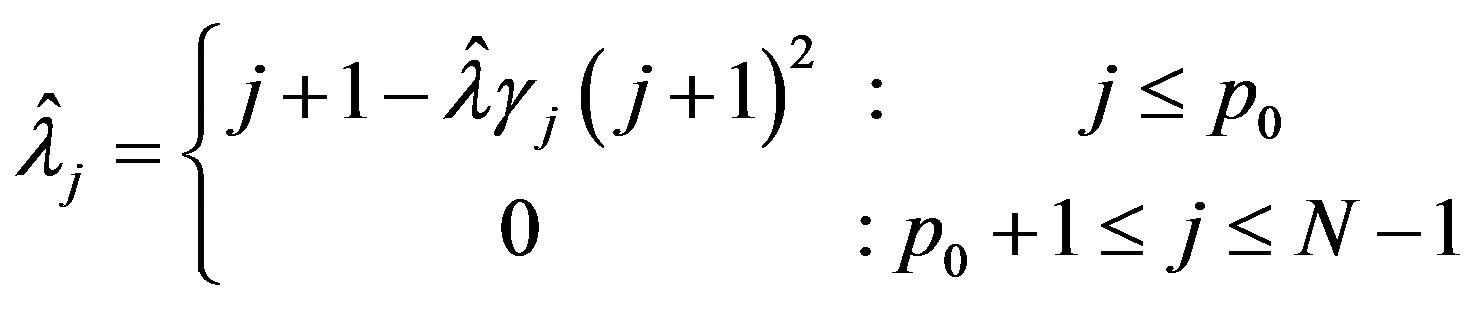
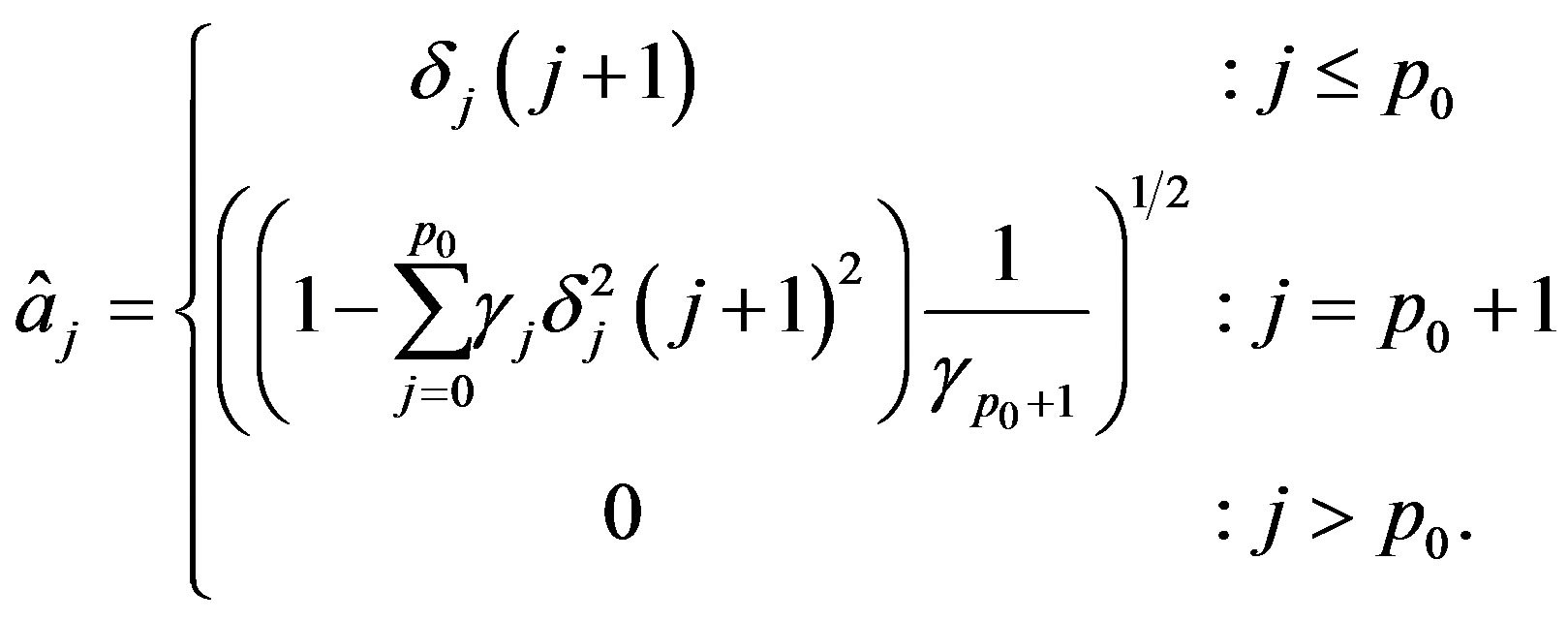
To verify 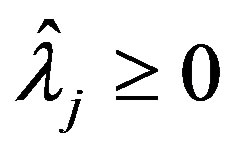 assume
assume  in which case
in which case
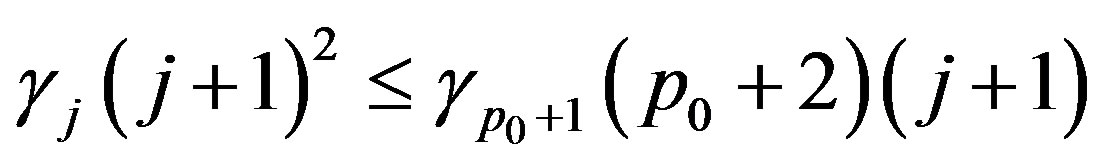 and hence
and hence
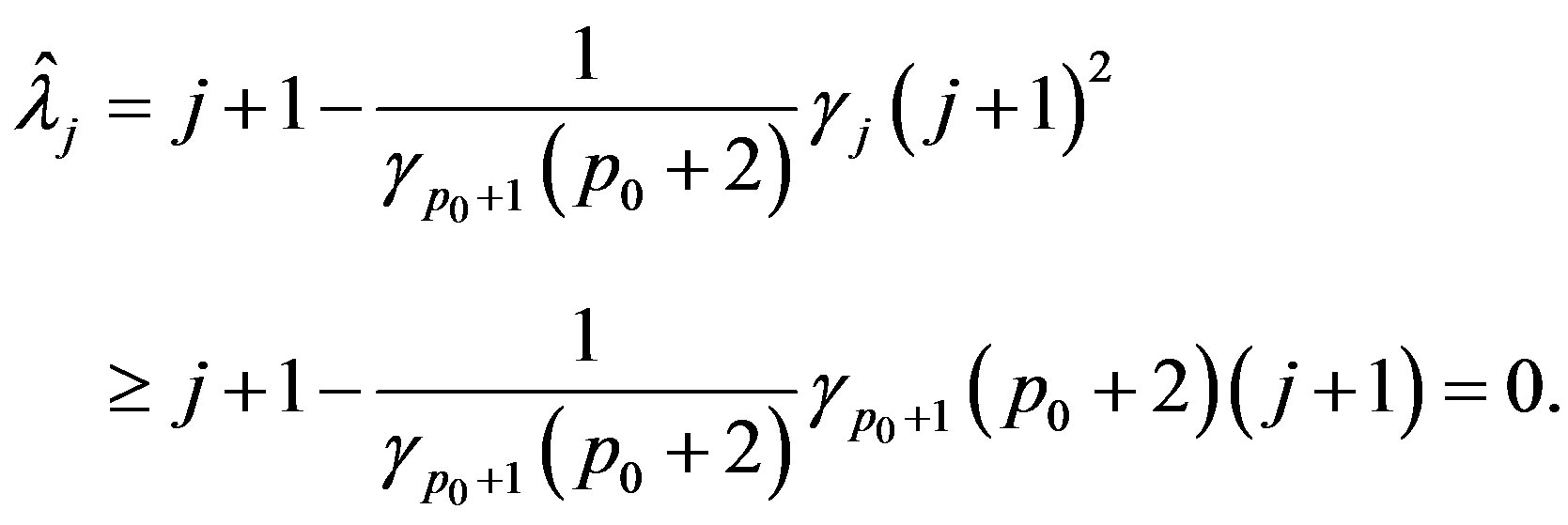
To show for the chosen 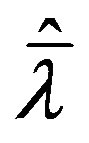 and any
and any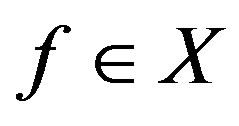 ,
,
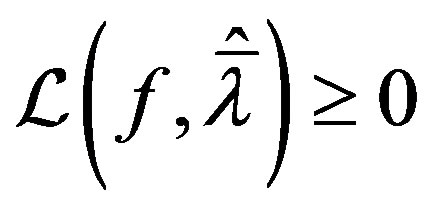 , we consider the cases
, we consider the cases 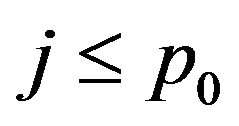 or
or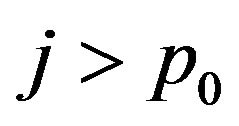 .
.
For 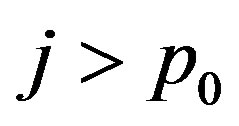 we know by assumption
we know by assumption
 and hence
and hence
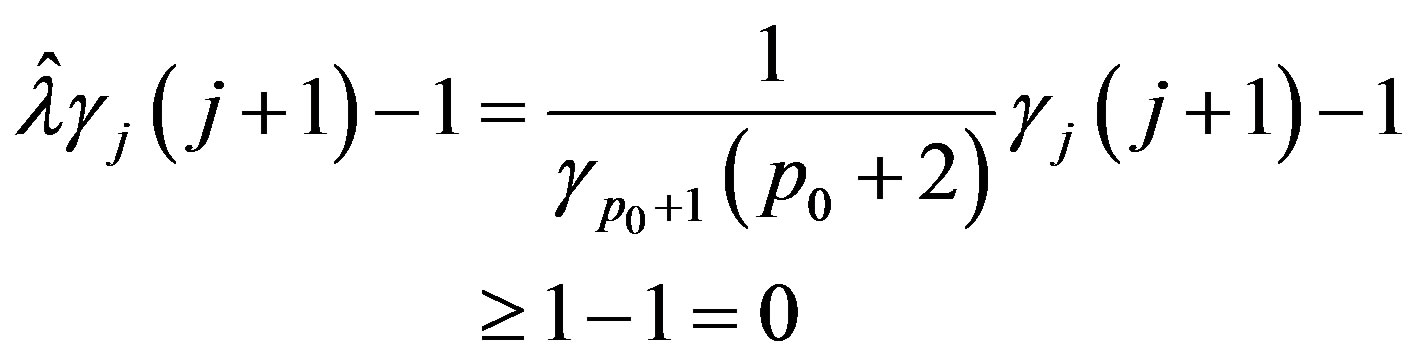
For 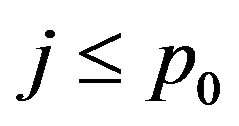
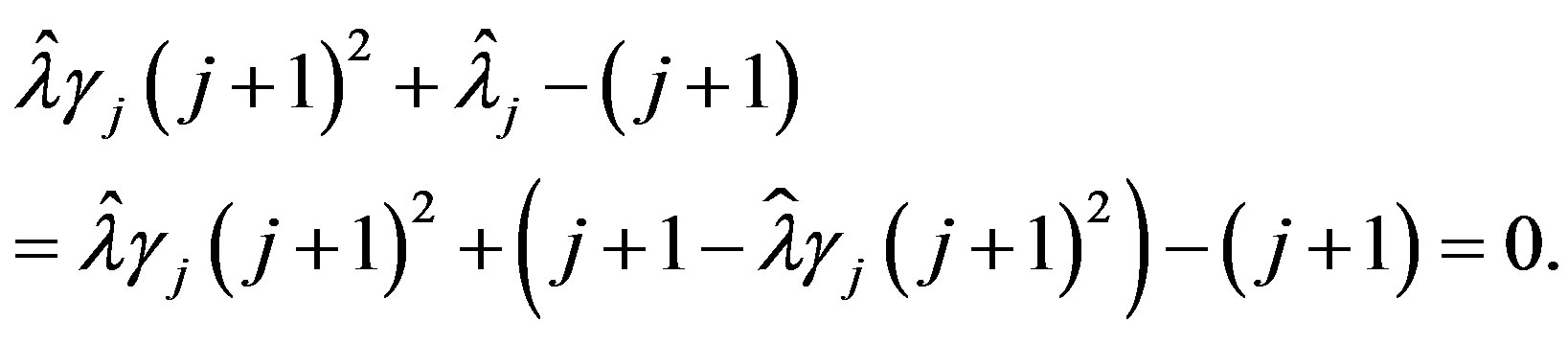
Thus for any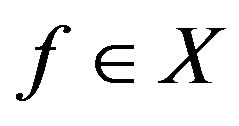 ,
, . For the constructed
. For the constructed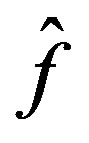 , it can be shown that
, it can be shown that 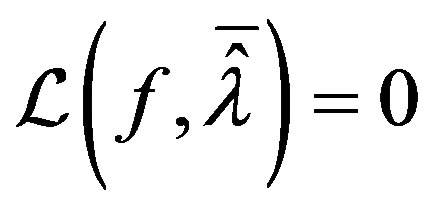 as desired. and thus
as desired. and thus 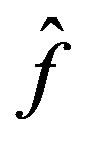 minimizes the Lagrange function.
minimizes the Lagrange function.
To show 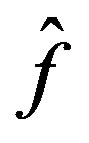 is admissable in (31) we can clearly see that for
is admissable in (31) we can clearly see that for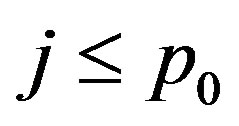 ,
,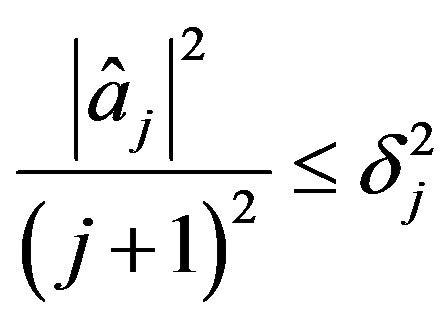 . It remains to show
. It remains to show 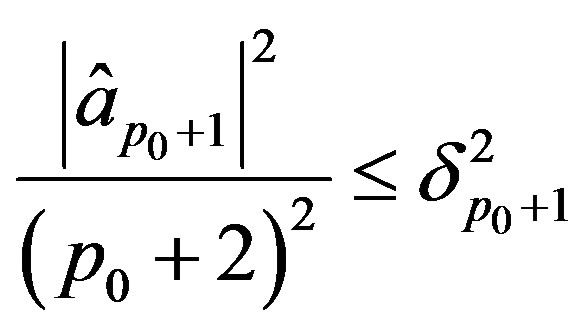 for
for . Assume not, then
. Assume not, then
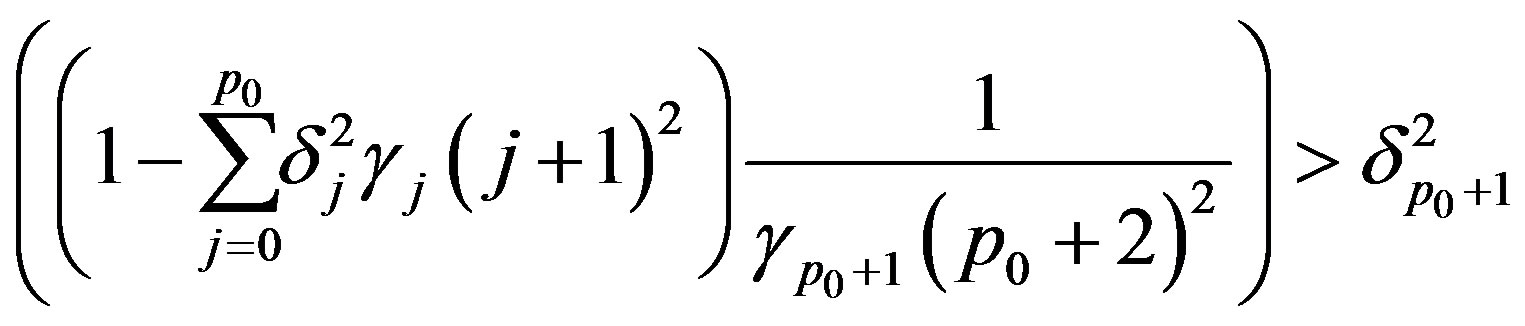
which occurs if and only if

which contradicts the definition of 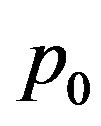 unless
unless 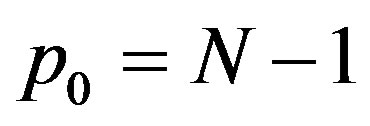 . If
. If 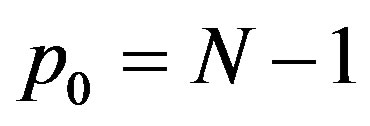 then
then 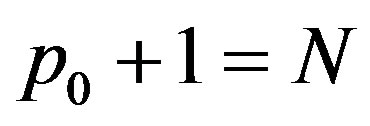 and hence we no longer need the condition
and hence we no longer need the condition 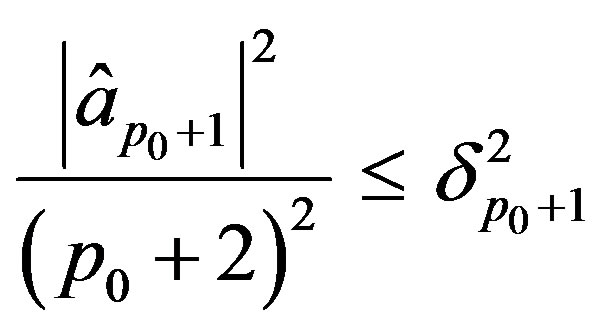 in order for
in order for 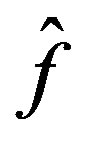 to satisfy (31).
to satisfy (31).
Furthermore

and so 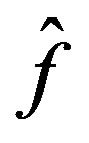 is admissable in (31).
is admissable in (31).
By the construction of 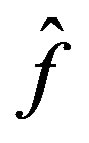 we also have the results
we also have the results
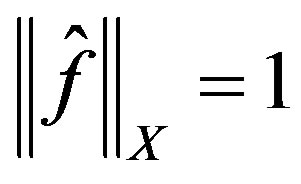 and
and 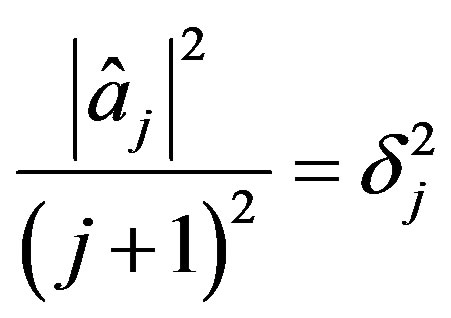 for
for 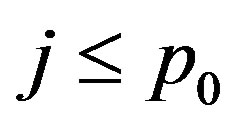 while
while 
for . Thus
. Thus  satisfies 2) of Theorem 2 as
satisfies 2) of Theorem 2 as
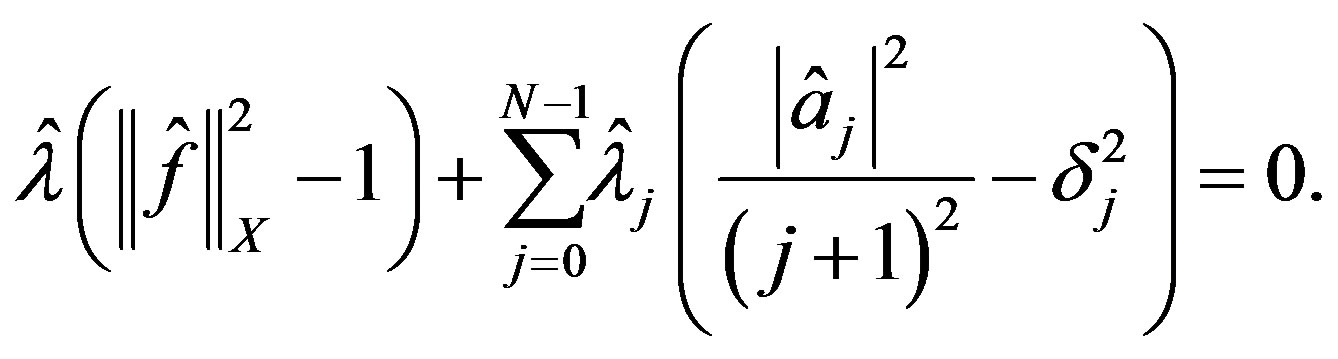
We now proceed to the extremal problem
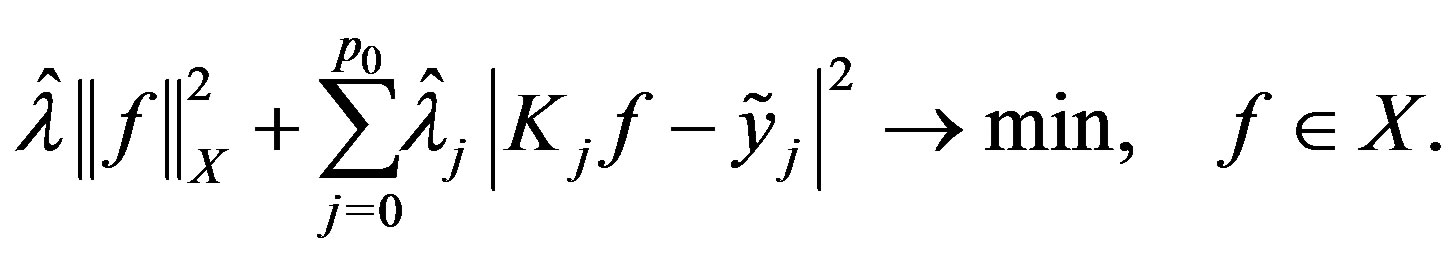
Notice the upper bound on the sum is 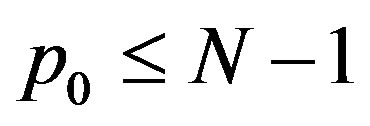 as
as 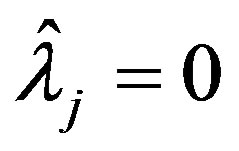 for any
for any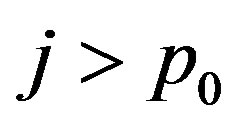 . This extremal problem will have solution
. This extremal problem will have solution

Therefore the error of optimal recovery is given by

and
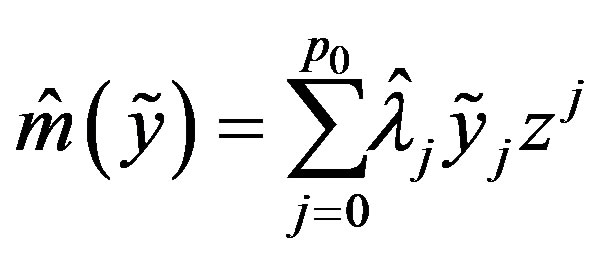
is an optimal method.
Now we proceed to the case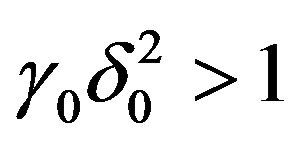 . Choose
. Choose 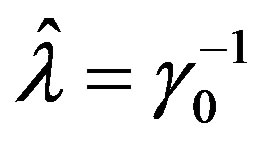 and
and  for
for . Then as
. Then as 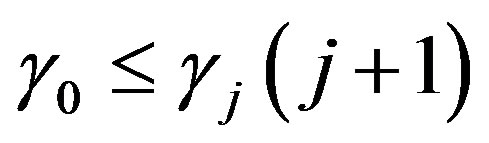 for all
for all 

Thus 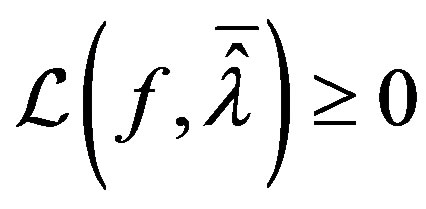 for all
for all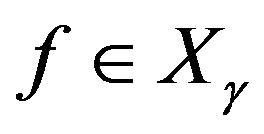 . Let
. Let 
and 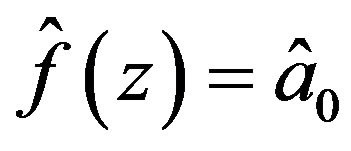 and notice
and notice 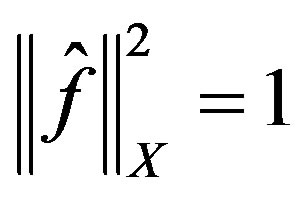 and clearly
and clearly
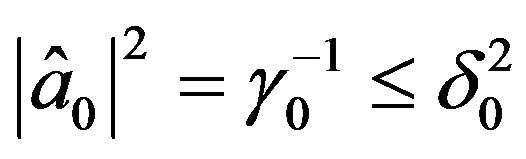 so
so  is admissable in (31). Furthermore
is admissable in (31). Furthermore
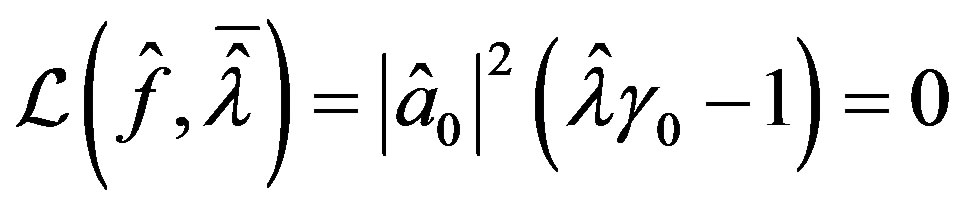
and so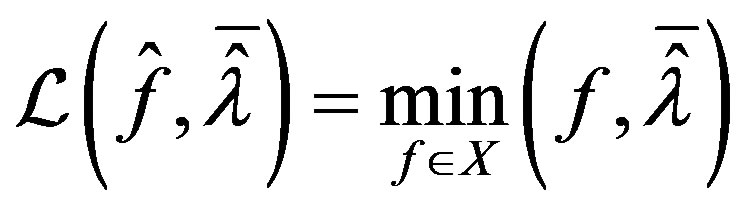 . Also,
. Also,
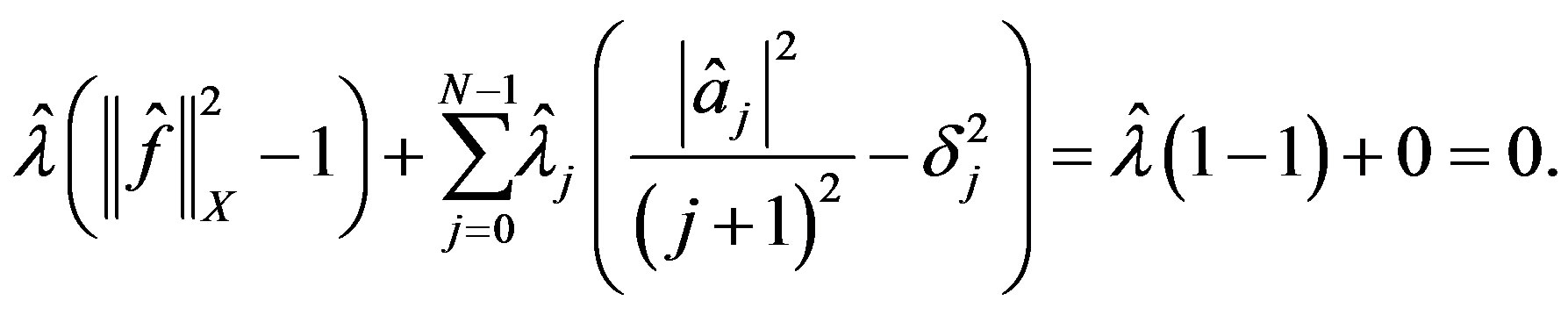
Therefore 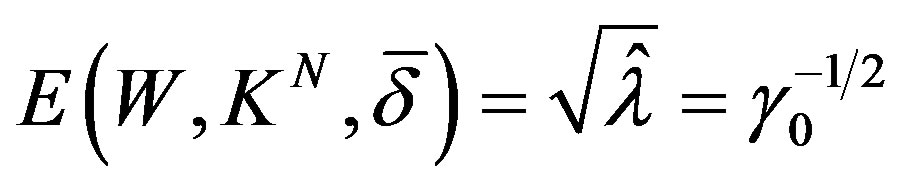 and
and 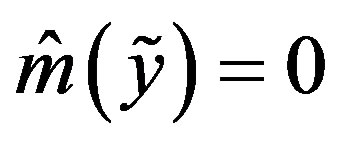
is an optimal method. 
The optimal method may not use all of the information provided as 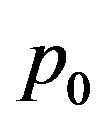 may be less than
may be less than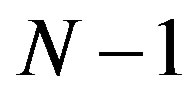 . Thus increasing
. Thus increasing 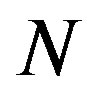 may not change
may not change 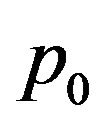 and hence not change the error or the method. If
and hence not change the error or the method. If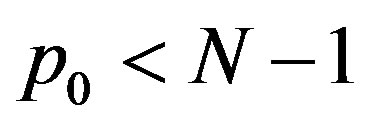 , then
, then
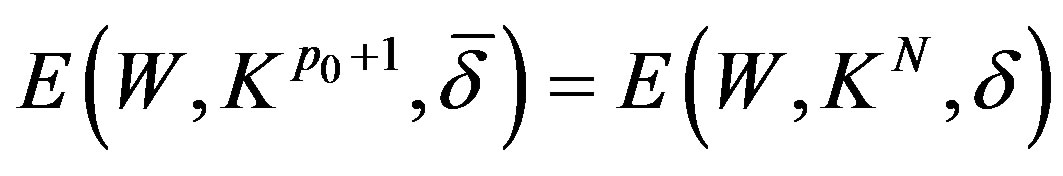
and we can reduce the amount of information needed for a given optimal error.
If 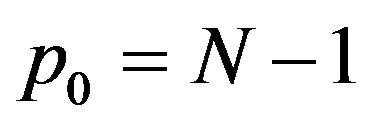 we may be able to reduce the error of optimal recovery if we have more information available. Fix
we may be able to reduce the error of optimal recovery if we have more information available. Fix . The greater number of terms we have of
. The greater number of terms we have of 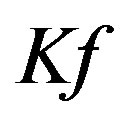 then the better we may be able to approximate
then the better we may be able to approximate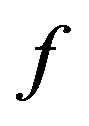 , that is the smaller the optimal error of recovery. Let
, that is the smaller the optimal error of recovery. Let
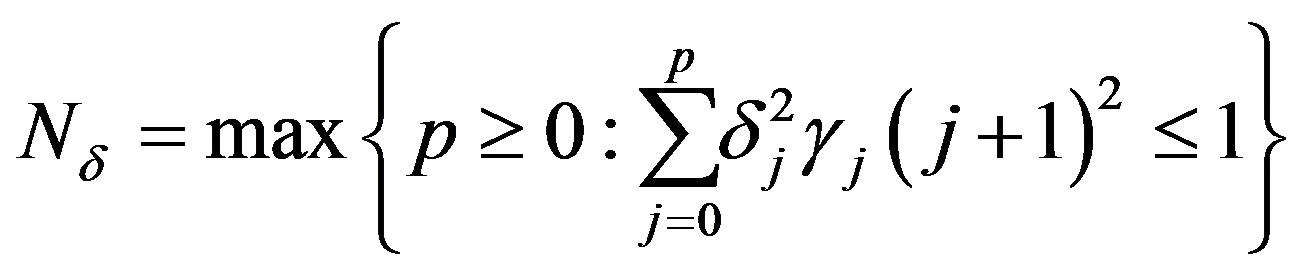 (41)
(41)
and for 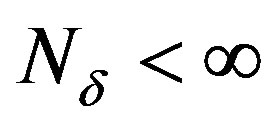
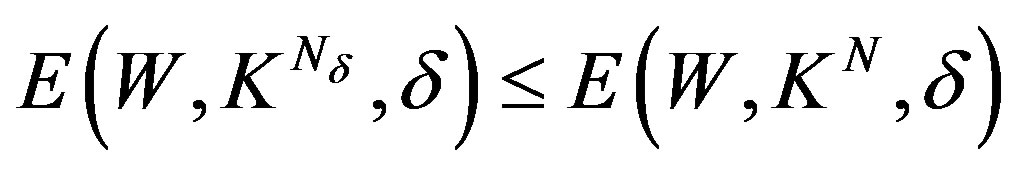
for any . If we know the first
. If we know the first  terms with some errors, then further increasing the terms will not yield a decrease in the error of optimal recovery.
terms with some errors, then further increasing the terms will not yield a decrease in the error of optimal recovery.
3.4. Applications: The Hardy-Sobolev and Bergman-Sobolev Classes
We now apply the general results to the Hardy-Sobolev and Bergman-Sobolev spaces of functions on the unit disc. Let  denote the set of functions holomorphic on the unit disc. Define the Hardy space of functions
denote the set of functions holomorphic on the unit disc. Define the Hardy space of functions
 as the set of all
as the set of all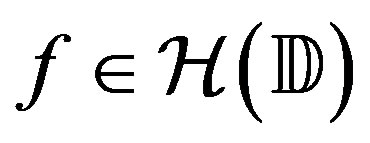 ,
, 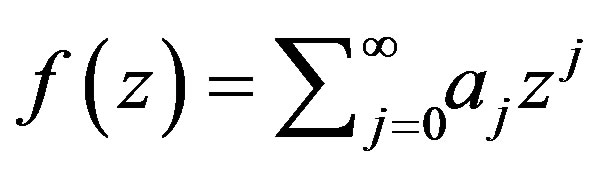 with
with 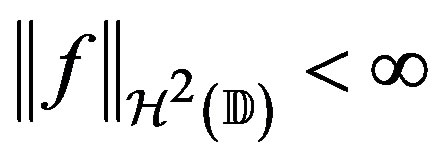 where
where
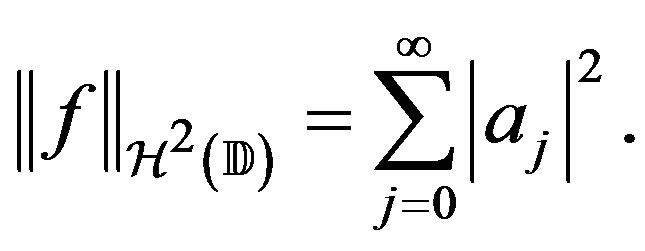
The Hardy-Sobolev space of functions,  , are those
, are those 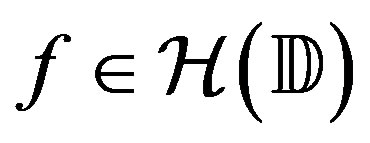 such that
such that 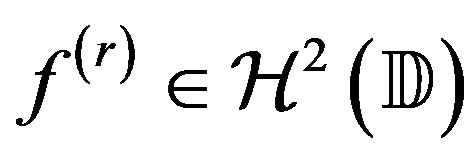 and
and
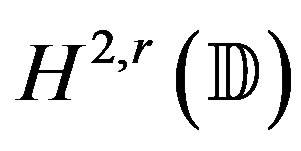 is the class consisting of those
is the class consisting of those 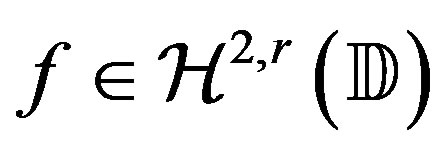
with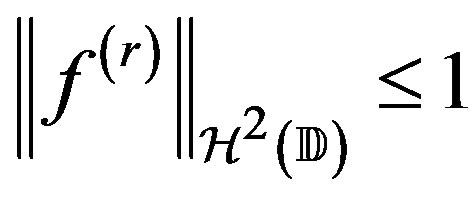 . The Bergman space of functions
. The Bergman space of functions
 is the space of all
is the space of all 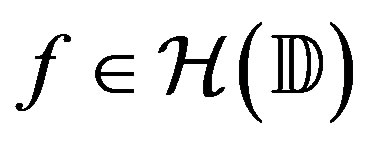 such that
such that
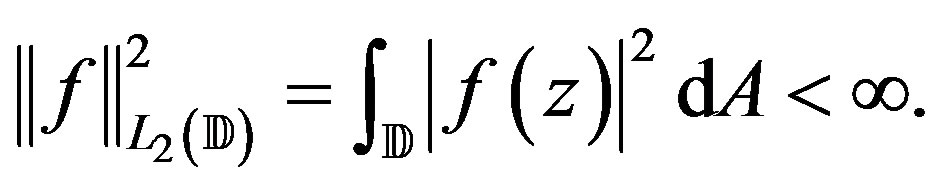
That is,  is the space of all holomorphic functions in
is the space of all holomorphic functions in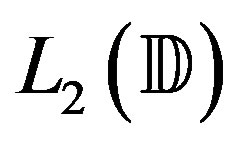 . The Bergman-Sobolev space of functions,
. The Bergman-Sobolev space of functions, 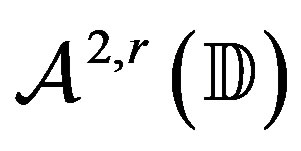 , consists of
, consists of 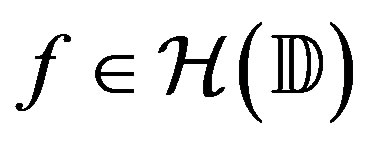 with
with
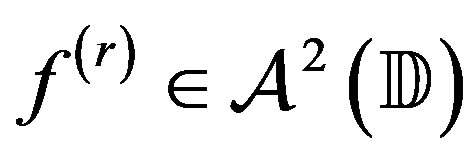 and
and  as the class of all
as the class of all
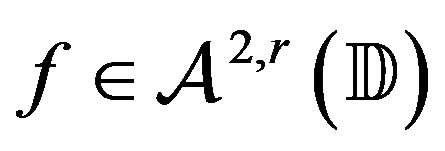 with
with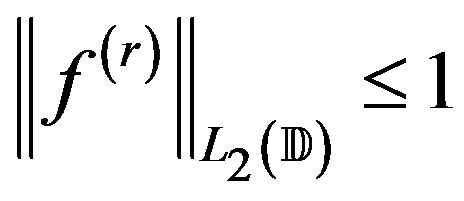 .
.
So each space can be considered as the space  with
with

For each space of functions we have the collection of points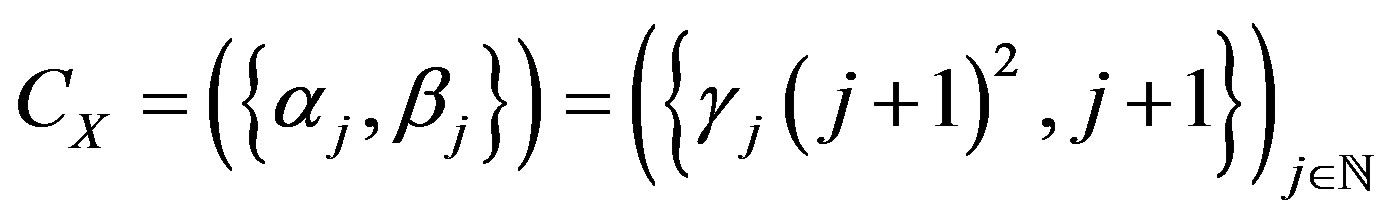 . If
. If
 then for
then for 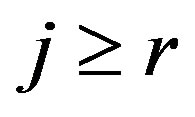
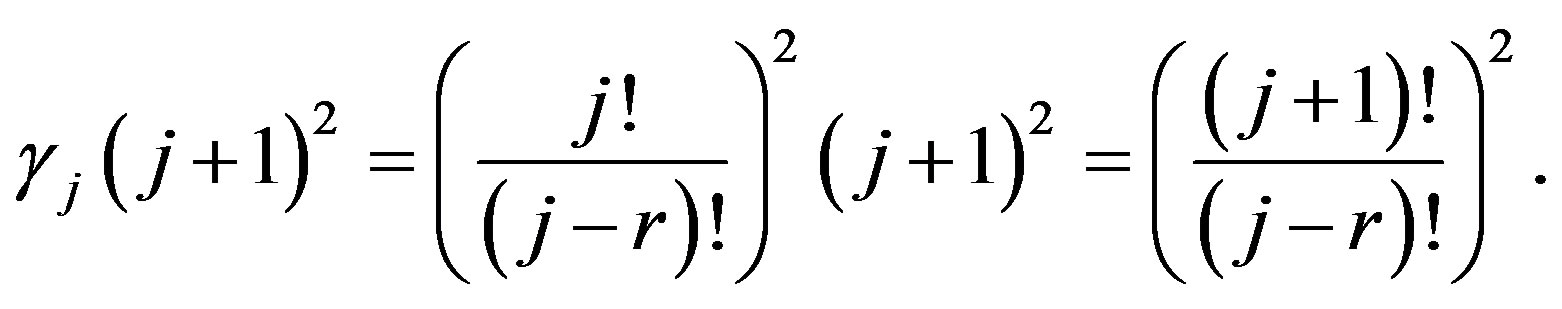
Therefore for 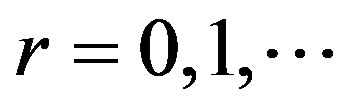
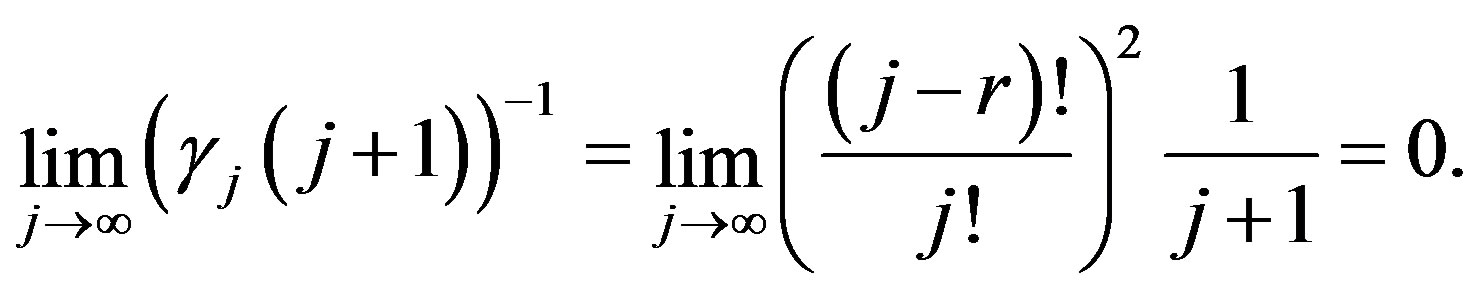
In this case we consider the collection of points

It is easy to see that if 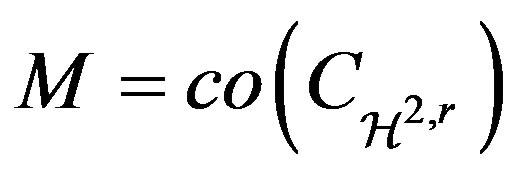 then the piecewise linear function
then the piecewise linear function  will have points of break
will have points of break
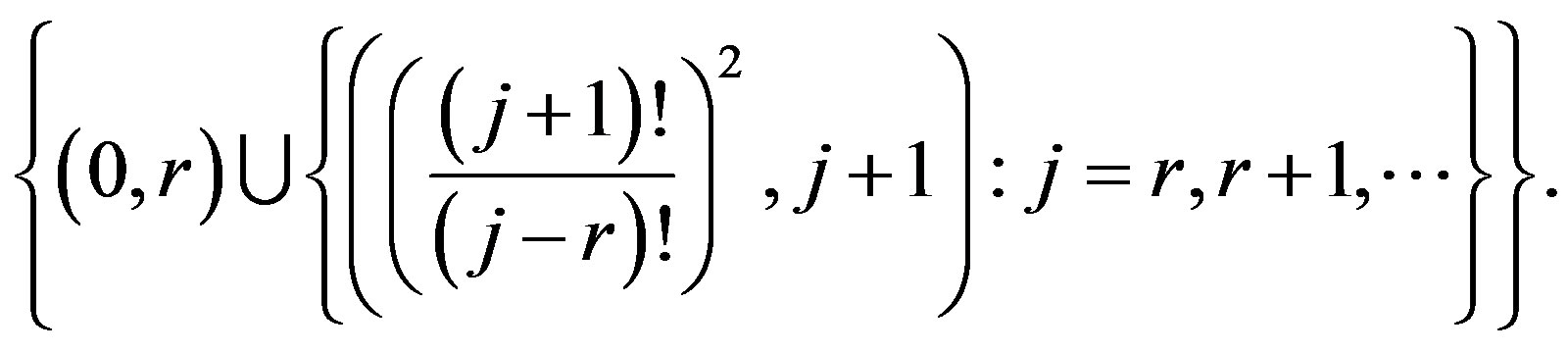 (42)
(42)
For the space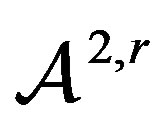 , the points to consider are
, the points to consider are
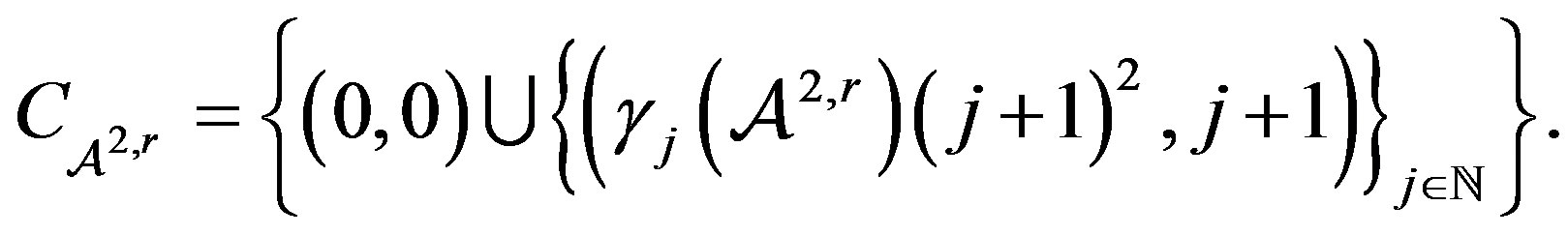
Again let 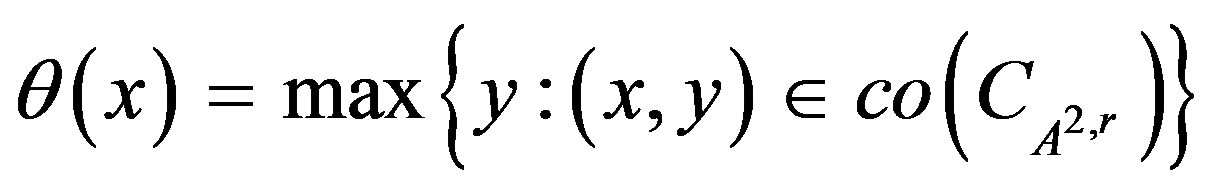 and thus the points of break of
and thus the points of break of  will be precisely
will be precisely
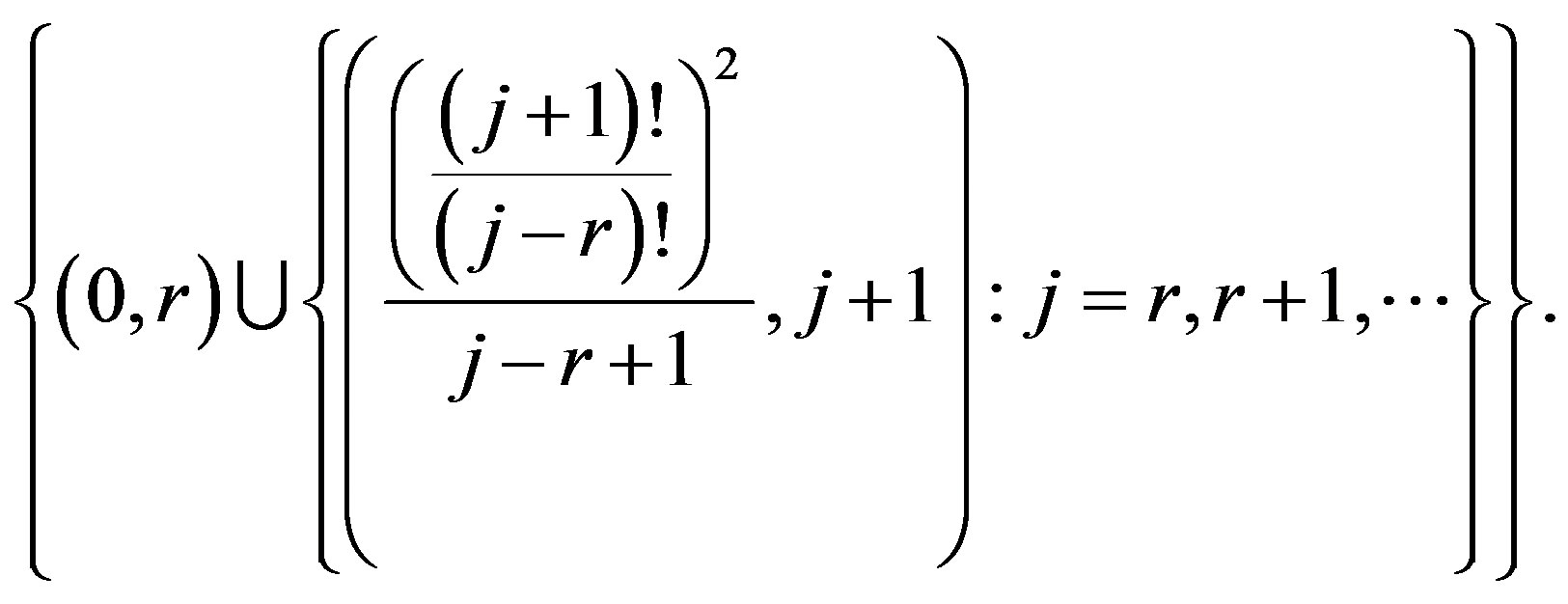
For the special case of , the function
, the function  has only a single point of break at the origin as
has only a single point of break at the origin as
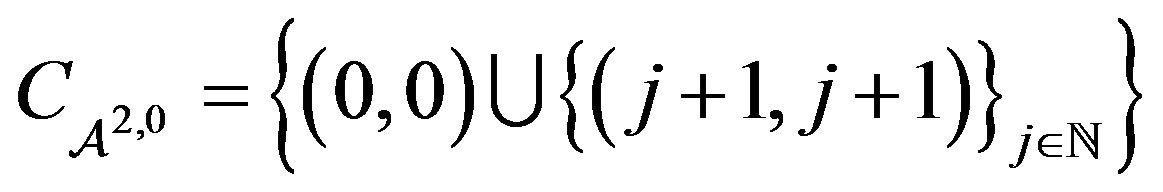
so that  for
for . Furthermore,
. Furthermore, 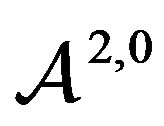 does not satisfy (7) as
does not satisfy (7) as
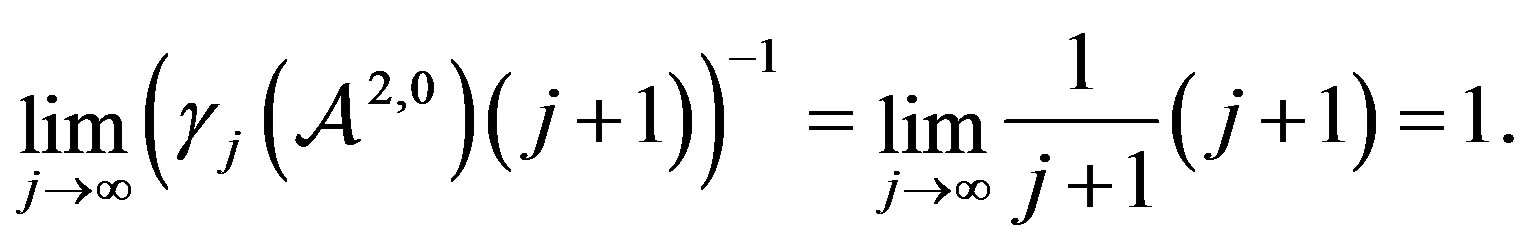
Thus, in the applications of the general results, this case will be treated separately.
For notational purposes, let ,
,  be the points of break of
be the points of break of  for the space
for the space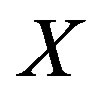 .
.
Corollary 1. Let  or
or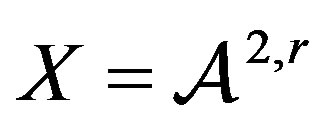 . If
. If 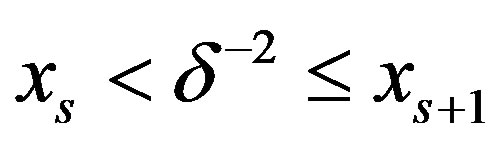 with
with 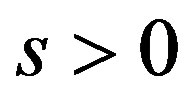 or
or 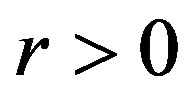 then the error of optimal recovery is given by (13) and (14) is an optimal method. If
then the error of optimal recovery is given by (13) and (14) is an optimal method. If 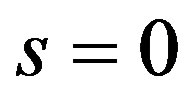 and
and 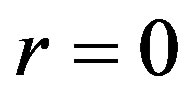 then
then 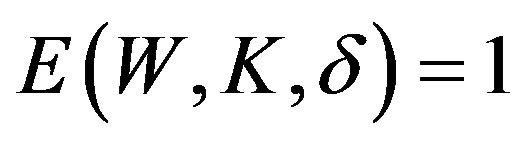 and
and 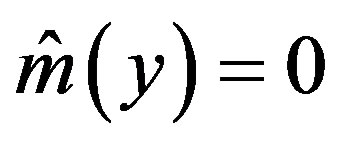 is optimal.
is optimal.
Proof. For the spaces 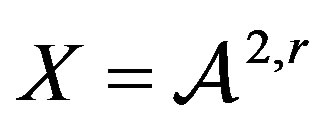 or
or ,
, 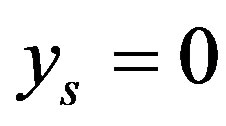 if and only if
if and only if 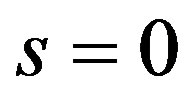 and
and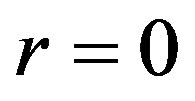 . Thus
. Thus 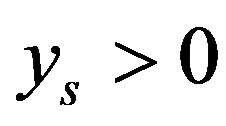 if and only if
if and only if 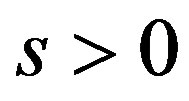 or
or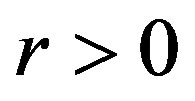 . Thus apply Theorem 3 to obtain the result for all spaces except
. Thus apply Theorem 3 to obtain the result for all spaces except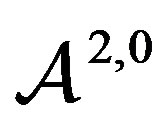 . The dual problem in the case
. The dual problem in the case 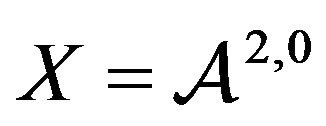 leads to a simple Lagrange function. The dual problem is specifically
leads to a simple Lagrange function. The dual problem is specifically
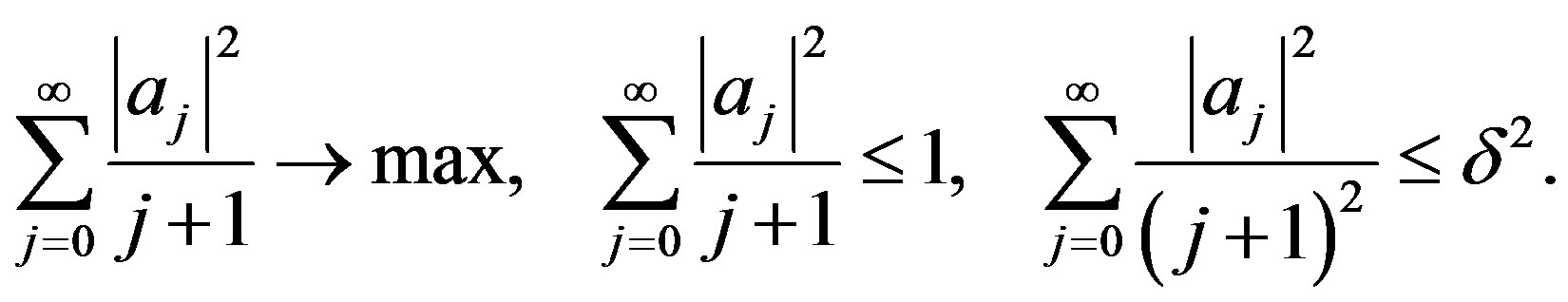
Therefore the Lagrange function is simply given by
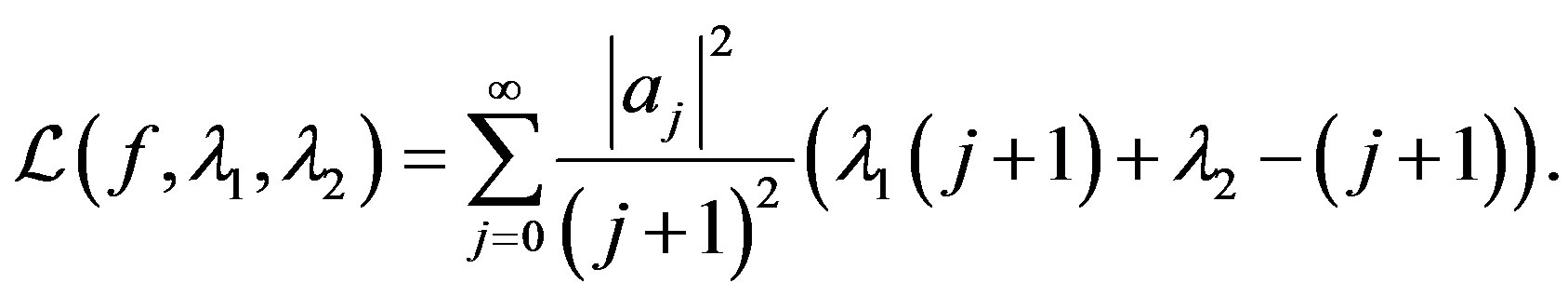
Now if we let  and
and  then
then
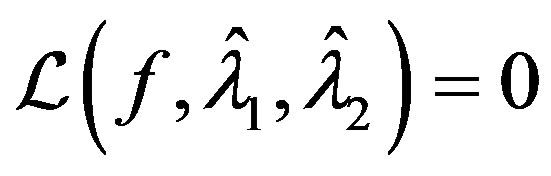 for any
for any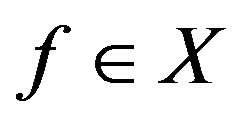 . So now proceed as in Theorem 3. As any
. So now proceed as in Theorem 3. As any 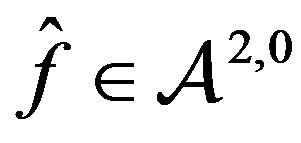 will minimize
will minimize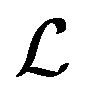 , choose
, choose 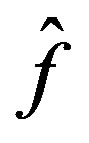 as in (18). The extremal problem (19) is solved similarly, and as
as in (18). The extremal problem (19) is solved similarly, and as 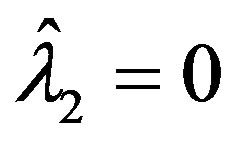 then
then 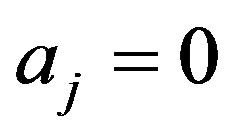 for
for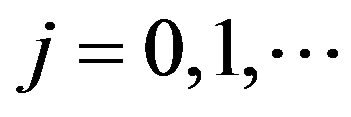 .
. 
It should be noted that the optimal method described is stable with respect to the inaccurate information data.
We now apply Theorem 4 to the Hardy-Sobolev spaces  and Bergman-Sobolev spaces
and Bergman-Sobolev spaces  in which
in which 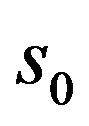 is explicitly defined to be the smallest nonnegative integer satisfying
is explicitly defined to be the smallest nonnegative integer satisfying
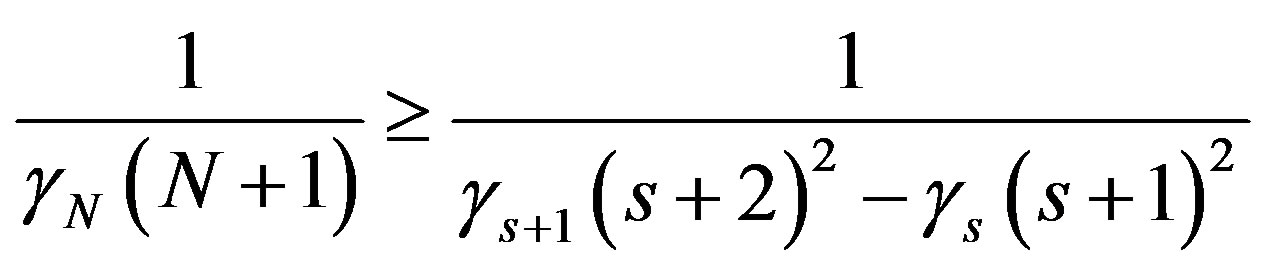
For the case ,
,  for all
for all . Thus
. Thus 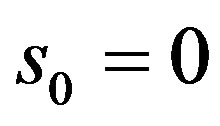 does not depend on
does not depend on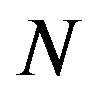 . So
. So
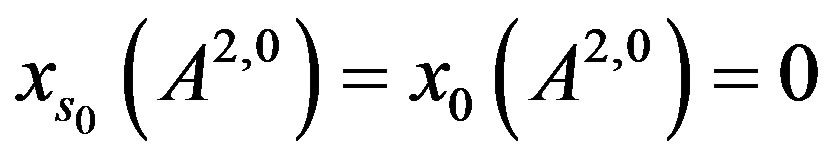 and hence for any
and hence for any  we are in the case
we are in the case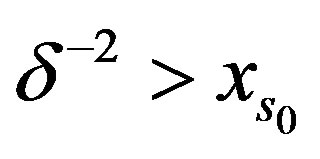 .
.
Corollary 2. Let 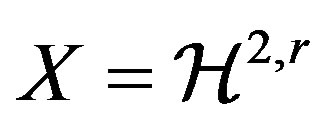 or
or . Suppose
. Suppose 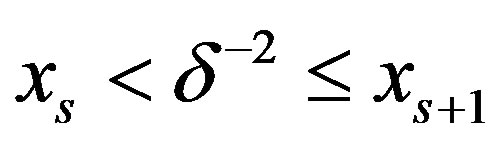 with
with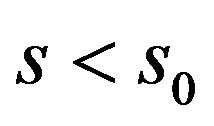 . If
. If 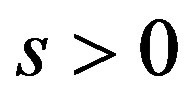 or
or  then let
then let
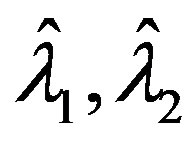 be given by (12) and the optimal error is given by
be given by (12) and the optimal error is given by
(13) and (23) is an optimal method. If  and
and 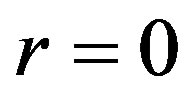 then
then 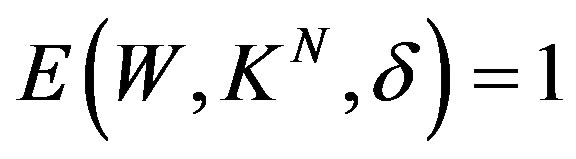 and
and  is an optimal method.
is an optimal method.
Otherwise suppose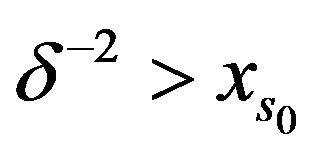 . If
. If 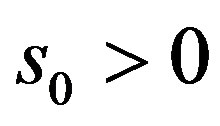 or
or 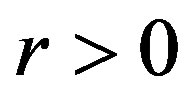 then the optimal error is given by (13) and (23) is an optimal method with
then the optimal error is given by (13) and (23) is an optimal method with 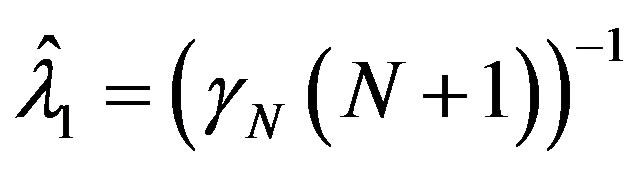 and
and
 . If
. If 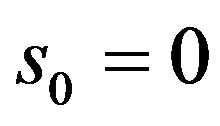 and
and 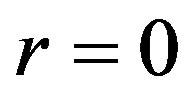 then
then
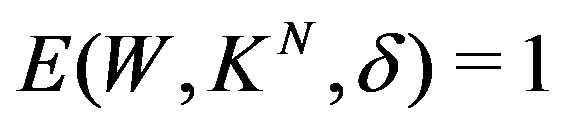 and
and 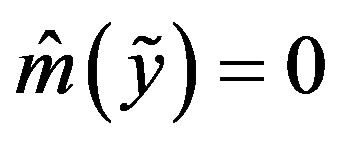 is an optimal method.
is an optimal method.
Proof. As previously stated, if 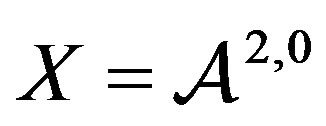 the only break point of
the only break point of  is
is 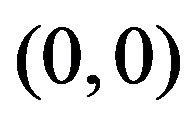 and furthermore as
and furthermore as 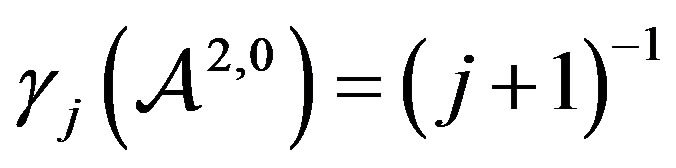 then
then  given by (21) does not exist so we treat this special case. In this case, the dual extremal problem is
given by (21) does not exist so we treat this special case. In this case, the dual extremal problem is
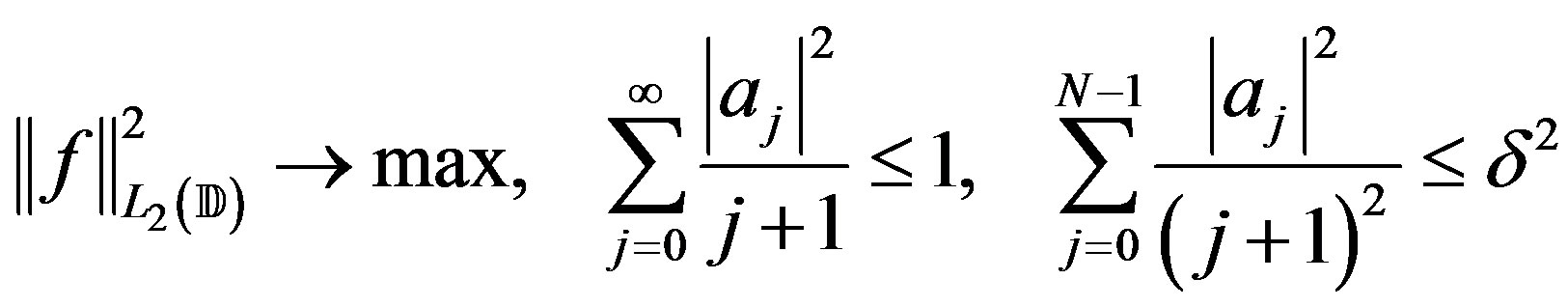
and the corresponding Lagrange function is simply
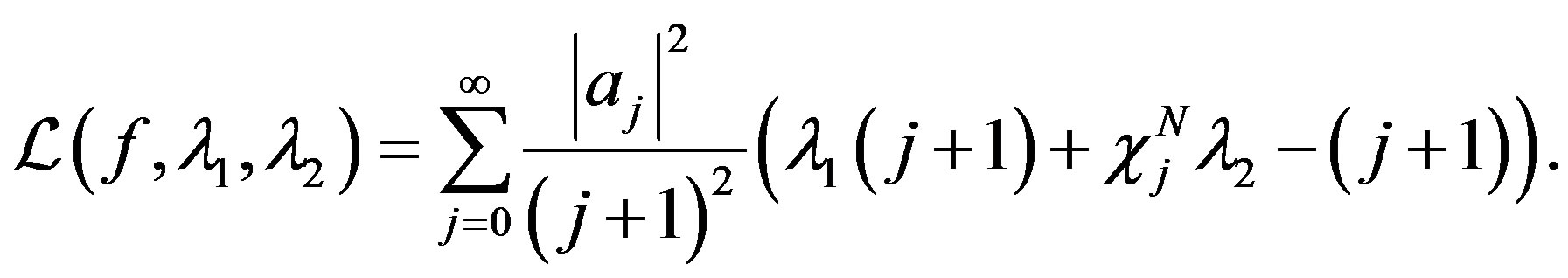
If  and
and  then
then 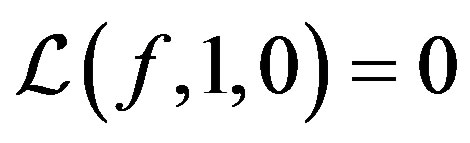 for any
for any
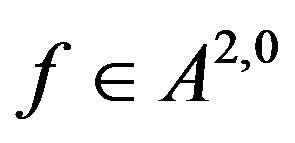 . Now proceed as in the proof of Theorem 4 to obtain the result.
. Now proceed as in the proof of Theorem 4 to obtain the result. 
We now apply Theorem 5 to the spaces 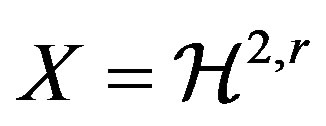 or
or 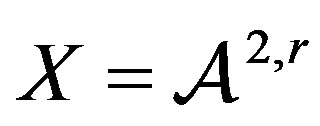 for
for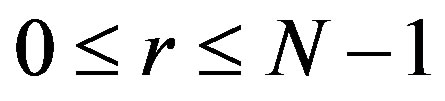 . In this situation
. In this situation 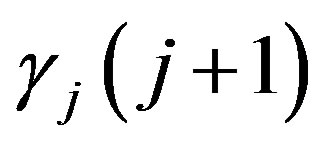 will be a non-decreasing sequence for all
will be a non-decreasing sequence for all . Also, for any
. Also, for any 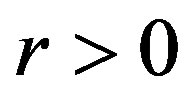 we have
we have 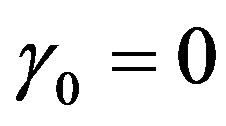 and we are always in the case
and we are always in the case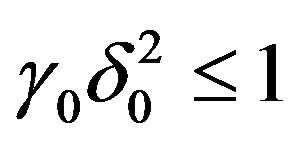 . For
. For  then for both the Hardy and Bergman spaces
then for both the Hardy and Bergman spaces 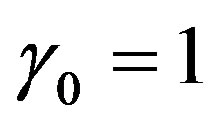 and so the condition
and so the condition  will be satisfied if we know
will be satisfied if we know 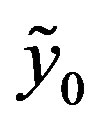 satisfying
satisfying
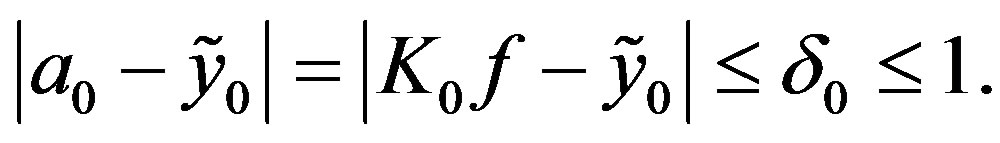
Corollary 3. Let 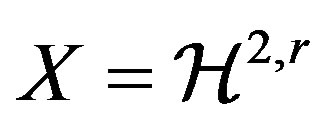 or
or 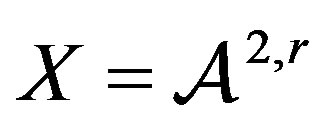 with
with 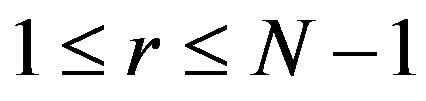 or
or 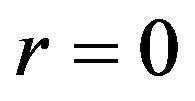 and
and 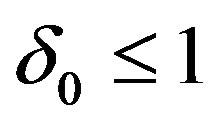 and
and 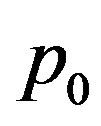 given by (27). Let
given by (27). Let ,
, 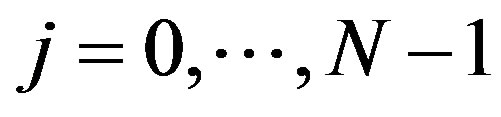 be given by (28). Then the error of optimal recovery is given by (29) and (38) is an optimal method. If
be given by (28). Then the error of optimal recovery is given by (29) and (38) is an optimal method. If 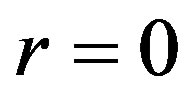 and
and 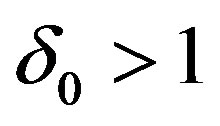 then
then 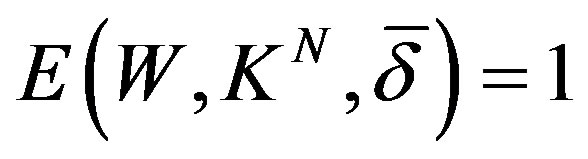 and
and 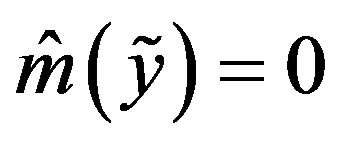 is an optimal method.
is an optimal method.
Proof. For Theorem 5 we simply used conditions (6) and (20), both of which are satisfied by 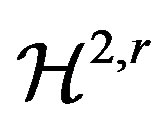 and
and  for all
for all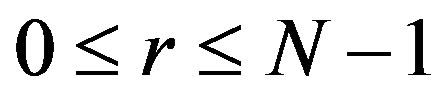 .
.
As a direct consequence of Theorem 5, we consider the situation in which we have a uniform bound on the inaccuracy of each of the first 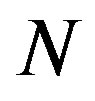 terms of
terms of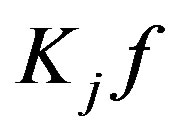 . That is we take
. That is we take 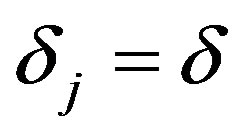 for every
for every . If
. If 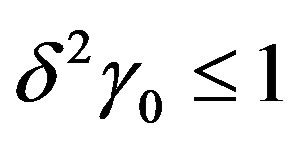 we define
we define 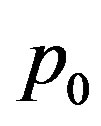 similarly as
similarly as
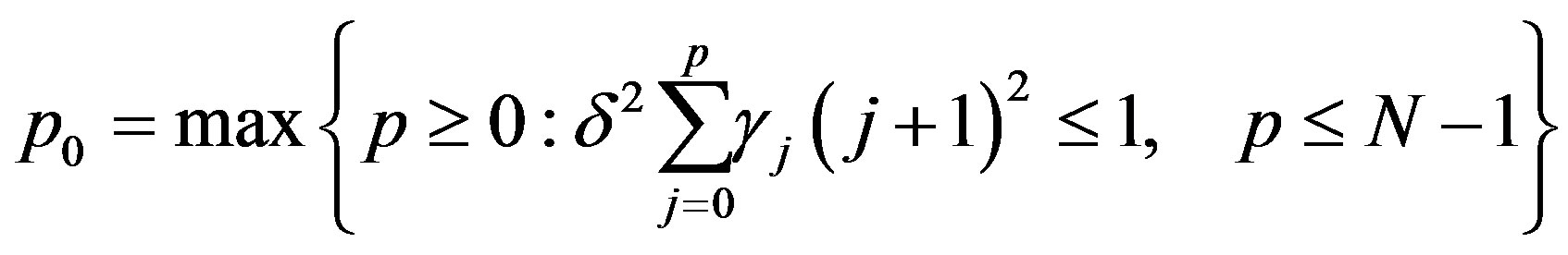
and the apriori information is given by the values 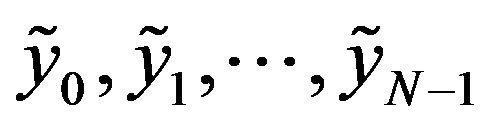 such that
such that
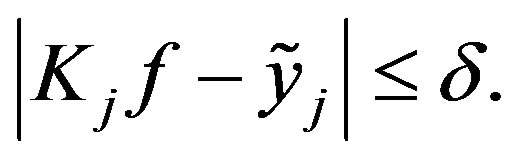
Again we will only need the values 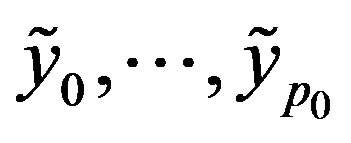 for an optimal method.
for an optimal method.
As previously noted, since the optimal method and error of optimal recovery only use up to the 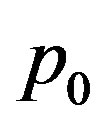 term then any information beyond may be disregarded if
term then any information beyond may be disregarded if  as additional information will not decrease the error of optimal recovery.
as additional information will not decrease the error of optimal recovery.
REFERENCES
- K. Y. Osipenko, “Optimal Recovery of Linear Operators from Inaccurate Information,” MATI-RSTU, Department of Mathematics, Washington DC, 2007, pp. 1-87.
- G. G. Magaril-Il’yaev and K. Y. Osipenko, “Optimal Recovery of Functions and Their Derivatives from Fourier Coefficients Prescribed with an Error,” Sbornik: Mathematics, Vol. 193, No. 3, 2002, pp. 387-407.
- G. G. Magaril-Il’yaev and K. Y. Osipenko, “Optimal Recovery of Functions and Their Derivatives form Inaccurate Information about the Spectrum and Inequalities from Derivatives,” Functional Analysis and Its Applications, Vol. 37, No. 3, 2003, pp. 203-214. doi:10.1023/A:1026084617039
- A. G. Marchuk and K. Y. Osipenko, “Best Approximations of Functions Specified with an Error at a Finite Number of Points,” Mathematical Notes of the Academy of Sciences of the USSR, Vol. 17, No. 3, 1975, pp. 207- 212. doi:10.1007/BF01149008
- A. A. Melkman and C. A. Micchelli, “Optimal Estimation of Linear Operators in Hilbert Spaces from Inaccurate Data,” SIAM Journal on Numerical Analysis, Vol. 16, No. 1, 1979, pp. 87-105. doi:10.1137/0716007
- K. Y. Osipenko, “Best Approximation of Analytic Functions from Information about Their Values at a Finite Number of Points,” Mathematical Notes of the Academy of Sciences of the USSR, Vol. 19, No. 1, 1976, pp. 17-23. doi:10.1007/BF01147612
- K. Y. Osipenko, “The Hardy-Littlewood-Polya Inequality for Analytic Functions from Hardy-Sobolev Spaces,” Sbornic: Mathematics, Vol. 197, No. 3, 2006, pp. 315- 334.
- K. Y. Osipenko and M. I. Stessin, “Hadamard and Schwarz Type Theorems and Optimal Recovery in Spaces of Analytic Functions,” Constructive Approximation, Vol. 31, No. 1, 2009, pp. 37-67.
- K. Y. Osipenko and N. D. Vysk, “Optimal Recovery of the Wave Equation Solution by Inaccurate Input Data,” Matematicheskie Zametki, Vol. 81, No. 6, 2007, pp. 723- 733.

