Journal of Encapsulation and Adsorption Sciences
Vol.06 No.03(2016), Article ID:70273,21 pages
10.4236/jeas.2016.63007
Sol-Gel γ-Al2O3 Nanoparticles Assessment of the Removal of Eosin Yellow Using: Adsorption, Kinetic and Thermodynamic Parameters
Mohamed S. Thabet1*, Ahmed M. Ismaiel2
1Department of Chemistry, Faculty of Science, Al-Azhar University, Cairo, Egypt
2Department of Chemistry, Faculty of Science, Jazan University, Jazan, Saudi Arabia

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: May 30, 2016; Accepted: August 26, 2016; Published: August 31, 2016
ABSTRACT
The adsorption behavior of eosin yellow (EY) from aqueous solution onto γ-Al2O3 nanoparticles in batch technique was studied. γ-Al2O3 NPs was prepared and characterized by SEM, TEM, XRD and FTIR analysis. The effect of pH, dosage of adsorbent, contact time, temperature, and the initial concentration of dye was investigated. The maximum amount of dye removal found about 99.36% at pH 4, the adsorption dose 1 g/L, with the initial dye concentration of 100 mg/L, and the temperature of 25˚C, with contact time 120 min. The adsorption behavior of the eosin yellow dye is applicable to Langmuir isotherm model, with the maximum sorption capacity of 47.78 mg/g of γ-Al2O3. The kinetic data also described by the pseudo-second-order model with a correlation coefficient (0.9999), and the mechanism of the process showed a multi-linear steps and the intra-particle diffusion was not only rate controlling step. The adsorption process was endothermic with positive enthalpy of 121.8 kJ/mol, and showed spontaneous process with a mean free energy −5.19 kJ/mol, and increase randomness, 369.77 J/mol. k, at the adsorbent solution interface. The adsorption process was chemisorption in nature The activation energy estimated from Arrhenius and modified Arrhenius is 40.9 kJ/mol, 106.37 kJ/mol respectively. The sticking probability of EY onto Al2O3 NPs very high estimated from the value of S* < 1, (4.82E−19).
Keywords:
Eosin Y, Adsorption, Nanoparticles, Aluminum Oxide, Thermodynamic Parameters, Kinetics

1. Introduction
The dyes appear in the environment in the form of wastewater colored of many manu- facturing industries, such as paper, textile, leather, cosmetic, and printing [1] , [2] . The highest number of these dyes is toxic, carcinogenic effect, and this poses a serious hazard to aquatic living organisms [3] - [5] . The aromatic complex structure of dyes makes them more stable and difficult to remove from water. Several types of methods are utilized for the removal of dyes pollutants from industrial wastewater, such as, photochemical oxidation, chemical coagulation, electrochemical degradation ozone treatment ultra-filtration, biosorption [4] , [5] . Adsorption, nanofiltration, ozonation, electro flotation have different advantages of removing dyes [2] , [4] . These processes have different advantages of removing dyes.
The most efficiency in recent years to removal of dyes pollutants is adsorption technique [3] , [6] , due to the procedure simplicity, ease of technique, operation, and its non-sensitivity to toxic materials. There are two different mechanisms of adsorption technique (physical and chemical) influenced by several factors, such as temperature, pH, adsorbate/adsorbent interaction, contact time, particle size, moreover, to reduce the procedure cost, used lower-cost material in the adsorption processes.
The most active area of research in recent year is the nanotechnology materials, the scale of nonmaterial from 1 to 100 nm, increased in application of nanoparticles due to large surface area, high thermal stability, and wide applicability in many areas, such as, chemistry energy, electronics, catalysis, and photochemistry [7] , [8] . The sol-gel method is used for preparation nanoparticles alumina, and several oxides [9] , [10] . Two reasons for difficult prepared nano scale γ-alumina (γ-Al2O3) powder, First, γ-Al2O3 is more stable after calcination at high temperature caused growth the powder, and make it difficult to get nano scale particles, second, during the dehydration process in the wet chemistry method the particles tend to aggregate. To solve this problem, it is needed to prepare the nano size of γ-Al2O3 by sol-gel technique. The advantage of this method is produced the ultrafine powder and size distribution of particles in a relatively short time at a very low temperature. The Eosin yellow dye is widely used in the detection of bacterial species as grame staining type due to the red color and strong absorption by red blood cells. The EY is highly toxic and affects on eye and skin irritation, damage to kidneys, liver and lung by ingestion and inhalation, thus very important to remove dye from wastewater to avoid the different damage.
In this study the efficiency of aluminum oxide NPs prepared by the sol-gel method for removal of eosin yellow was investigated by several parameters such as pH, time removal, dose adsorbent effects, Langmuir, Freundlich, Tempkin, Elovich and Dubinin-Radushkevich modelling isotherm, kinetic equations pseudo-first-order, pseudo- second-order, Elovich, and Bangham’s models and Thermodynamic parameters was investigated by Arrhenius, modified Arrhenius and Van’t Hoff equations. The experiment was carried out in batch mode at different temperatures.
2. Experimental
2.1. Materials and Methods
2.1.1. Properties of Adsorbent
Generic names of adsorbent are Eosin yellow, also known as Acid red 87, C.I. 45,380, Bromofluorescein; Sodium eosine, with Molecular Formula C20H6Br4Na2O5, and molecular weight equal 691.58 g/mol Figure 1.
The concentration of dye in solution was measured by a Shimadzu spectrophotometer (UV-1800, ENG 240 V, soft Japan) at maximum wavelength 516 nm.
2.1.2. γ-Al2O3 NPs Prepared by the Sol-Gel Method
Aluminum oxide NPs was synthesized through a sol-gel method at lower temperature with a simple equipment setup. The Aluminum oxide and Urea were dissolved in a certain amount of distilled water then Formaldehyde was added to the mixture stirred for 30 min at 200 RPM to complete dissolve at room temperature, then add ethylene glycol and NH4OH drop-wise to the mixture the pH about 8 - 9. Allow the mixture under vigorous stirring (500 RPM) for 2 h at 70˚C to obtain a gel form, dried the sample overnight and calcination at 500˚C for 3 hrs. The pH was adjusted by 0.1 NHCl and NaOH.
2.1.3. Characterization of Al2O3 NPs
The X-ray diffractogram of the sample was measured by using Shimadzu X-ray diffractometer (XRD-6000)-Japan with a scanning speed of 2θ = 2.5˚ min−1. FTIR spectroscopy was taken to confirm surface of γ-Al2O3 nanoparticles and examine the structure of adsorbed EY. The FT-IR spectra were recorded by (FT-IR-6300 model), the absorption spectra at resolution 4 cm−1 over the range (400 - 4000 cm−1). The scanning electron microscope (SEM) micrographs were measured using a model of JEOL-JSM-5500 LV (Japan). Transmission Electron Microscope (TEM) Measured technique using by a JEM-100 CX electron microscope at an accelerating voltage of 200 KV. The sample was put on the carbon foil with a micro grid and observed with minimum electron irradiation to prevent damage to sample structure.
Figure 1. Ball and stick structure of EY.
2.2. Equilibrium Studies
Using the batch process in order to evaluate the effect of parameters affects on the amount of dye adsorbed at equilibrium, qe (mg/g), such as the effect of initial concentration of dye, contact time, pH and temperature. To determine the residual concentration of the dye sample solution was withdrawn at certain time by using UV-V is spectrophotometer at λmax of 516 nm. Adsorption equilibrium calculated by equation:
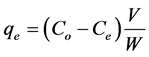 (1)
(1)
The percentage of adsorption was calculated by the following equation.
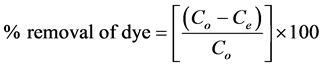 (2)
(2)
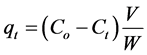 (3)
(3)
where Co, Ce, and Ct (mg/L) are the concentration of adsorbate at initial, equilibrium and at interval time respectively.
2.3. Adsorption Isotherms
Adsorption isotherms, used for presentation of the amount of solute adsorbed per unit of adsorbent, as a function of equilibrium concentration in bulk solution at constant temperature five isotherm models have been tested, namely, Langmuir [11] , Freundlich [12] , D-R, Elovich [13] and Tempkin [14] . The applicability of these isotherm equations to describe the adsorption process was adjudged by the correlation coefficient, R2 values.
2.4. Adsorption Kinetic
Kinetics is important for adsorption studies because it can predict the rate of pollutant removal from aqueous solutions and understanding the mechanism of sorption reactions for the data. In order to investigate the mechanism of dye sorption onto Al2O3 nanoparticles, pseudo-first-order [15] , pseudo-second-order [16] , Elovich [17] and Bangham’s models was adopted. The experiment was carried out in batch mode by taking 100 ml of different temperatures (25˚C, 35˚C, 45˚C, 55˚C, and 65˚C). Concentration of dye solution (75, 100, 150 and 200 mg/l) at pH 4.0 and with 1 g/L of Al2O3 NPs. Withdrawn of dye samples from the flask at regular time intervals, centrifuged and the concentration of dye in the supernatant solution was analyzed. A majority of adsorption from aqueous solutions was completed within 120 min.
2.5. Adsorption Thermodynamic
In order to investigate the type of adsorption process onto Al2O3 nanoparticles, Arrhenius and Van’t Hoff equations was adopted, and the probability sticking S* is a function of the adsorbate/adsorbent system under investigation. The value of activation energy confirmed that the chemisorption or physicsorption process, and the experimental was carried out in batch mode like procedure in above section.
3. Result and Discussion
3.1. Analysis of γ-Alumina NPs
FTIR is one of the powerful technique to explore the solid-liquid interface. The spectra of γ-Al2O3 before and after adsorption of EY can be shown in Figure 2. The FTIR spectra recorded from 500 to 4000 cm−1. The bands appeared in the range between 500 and 1000 cm−1, corresponding to the vibrational frequencies of co-ordinate O-Al-O characterized to nano amorphous γ-Al2O3 [18] , a stretching vibration of the Al-O-Al lie in the same range due to chemisorbed and adsorbed species at the surface. The broadening absorption bands appeared at ~545 and ~788 cm−1 contributed to octahedral and tetrahedral environments. The peak between 1070 and 612 cm−1 correspond to the Al-O vibration [19] , the absorption peaks, at 1456, 1570 cm−1, Furthermore, bands at 1338, 1250, 1066 cm−1 due to changes in the surface structure of Al particles when adsorbent attached to it. A small band is observed at 2900 cm−1 for the water molecule, the bands appearing at 1352, and 1407 cm−1 are typical for gamma-alumina. The Al-O vibration is observed at 1371 and 1363 cm−1. Bonded hydroxyl groups, isolated OH groups, and stretching vibrations of adsorbed water molecules appeared bands at 3471, and 3423 cm−1. After adsorbing eosin Y, obvious changes are observed at the frequency level of 1550 - 1650 cm−1 and 3415 cm−1 from spectrum, which indicates that the carboxylic group of the EY participate in the adsorption process. The additional peaks appeared in the region of 1100 - 1700 cm−1 represent the presence of physisorbed water [20] . The Morphological studies were carried out using SEM Figure 3(a) & Figure 3(b) and TEM Figure 3(c) & Figure 3(d) photographs, it can show that the SEM micrographs of the particles of γ-Al2O3 irregular shapes with a less agglomeration, high dispersion was
Figure 2. FTIR spectra of original γ-Al2O3 NPs after and before adsorption process.
Figure 3. SEM picture of the surface of γ-Al2O3 NPs sample Bar equal (a) 200 um; (b) 50 um, TEM image of the NPs sample surface of Bar equal (c) 100 um; (d) 500 um.
observed and the particles mostly in nano size. The produced nano-sized confirmed by TEM. Figure 3(c) & Figure 3(d) indicates that the particle shape is non-spherical and a size between 24 to 42 nm. A very small particle dispersed between large particles can be observed.
The X-ray diffraction pattern of sample calcined at 500˚C is shown in Figure 4, completely amorphous of gamma crystallite phase can be observed this indicates that the alumina prepared by sol-gel method is amorphous in structure, the characteristic alumina phase appeared broad peaks around 2θ equal 43˚, 37˚ and 64˚ [21] , [22] .
c
The pH of the dye solution (100 mL of 100 mg/L initial concentration) was adjusted to the range of 2 - 6, using either sodium hydroxide or hydrochloride acid. The adsorption of eosin Y for γ-Al2O3 NPs depends on pH. Figure 5 shows that, the maximum removals of 99.36% were achieved at pH 4.0, the adsorption capacity of γ-Al2O3 NPs increases drastically when pH increased from 2 to 4 and then fluctuated after pH 5, change in the nature and structure of both substances which subsequently control the type and strength of attractive or repulsive forces. In the acidic solution, the adsorption of anionic dye eosin Y process by γ-Al2O3 NPs is an electrostatic interaction, where the two species of aluminum hydroxide two species of positive charge 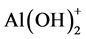 and
and  at low
at low
Figure 4. XRD diffraction pattern of sample calcined at 500˚C.
Figure 5. Effect of pH and various initial concentrations of EY on removal efficiency, Conditions: 100 ml of dye, pH = 4.0, adsorbent dosage 100 mg.
pH are highly present in this medium and reaches the positive charge which interacts with the anionic groups of the dye [23] . While at high pH greater than 4, little amount of hydroxide species appeared and more OH− ions present and compete with the anionic bromide groups of EY for the adsorption sites of γ-Al2O3 NPs, thus the available adsorption sites for anionic EY decrease [24] . The initial concentration effects on the removal efficiency as shown in (Figure 5). With an increase in initial dye concentrations, the more dye is left un-adsorbed in the solution due to the saturation of the binding sites; this indicates that energetically less favorable sites become involved, the equilibrium time depends on the molecular weight and the structural complexity of dye molecules.
3.3. Adsorption Models
3.3.1. Langmuir Isotherm Model
The Langmuir isotherm, which given by a non-linear form and the linear form Equation (4) and Equation (5).
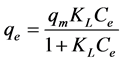 (4)
(4)
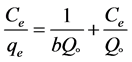 (5)
(5)
Equilibrium parameter RL can be calculated from below equation by Webber and Chakkravorti [25] and McKay’s research group [26] which is specified as a lining
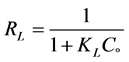 (6)
(6)
where, Co donated to the adsorbate initial concentration (mg/L), Langmuir constant KL A plot of Ce/qe against Ce gives a straight line with slope of 1/Qo and intercepts 1/QoKL and with highest correlation coefficient R2 = 0.9999 as shown in Figure 6(a). The data listed in Table 1. Which revealed that the qmax value is (47.78 mg∙g−1) and KL equal (0.1293 L∙mg−1). The lower RL values for all different concentrations (75 - 200 mg/l) of EY between (0.093 - 0.037) reflects that adsorption is more favorable and deduce that a monolayer formation is taking place during the adsorption of EY over the surface of Al2O3 NPs.
3.3.2. Dubinin-Radushkevich Adsorption Model
The Dubinin-Radushkevich isotherm used to evaluate the porosity properties of the adsorbent and the energy of adsorption process. Figure 6(b), show a good fit of the isotherm with the experimental data and give a straight line with the correlation coefficient 0.9925 by a plot of lnqe versus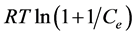 . The linear form of the D-R isotherm equation given by the following equation
. The linear form of the D-R isotherm equation given by the following equation
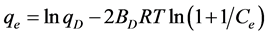 (7)
(7)
where R, is the gas constant (8.314 J/mol∙K), T absolute temperature (K) and Ce repre- sent to adsorbate equilibrium concentration (mg/L).
 (8)
(8)
The value of ED-R, Table 1, gives information about the type of adsorption mechanism as chemical ion exchange or physical adsorption. The value of ED equal 13.7 kJ/mol suggested that ion exchange is the major mechanism responsible for the adsorption process or chemical adsorption of dye molecule.
3.3.3. Freundlich Model
The Freundlich isotherm applicable for adsorption process, the value n, KF and R2 constants shown in Table 1, Figure 6(c). The R2 value is lower than the Langmuir value.
3.3.4. Tempkin Adsorption Model
To determine the heat of adsorption of adsorbate molecules with the extent of coverage over the surface of NPs applied Tempkin isotherm model at room temperature repre- sented by the Equation (7). From Figure 6(d) the Tempkin constant A (L/g), and heat
Figure 6. Adsorption isotherm models for EY on the surface of γ-Al2O3 NPs.
of adsorption B (J/mol) Equation (8) can be evaluated from the slope and intercept of linear line when plotting qe versus lnCe.

where,

R the gas constant (8.314 J/mol∙K), and T is the temperature, the positive value of constant B is 25.45 J/mol indicates an endothermic process. The fit to experimental data (R2 = 0.9868) and A = 565.13. The values of the Tempkin constants (A and B) and the correlation coefficient are listed in Table 1. The R2 value is higher than the Elovich value, but lower than the Freundlich Langmuir value.
3.3.5. Elovich Adsorption
The adsorption sites increased with time and form multilayer, Elovich model describes the adsorption process by the equation:

where KE is the Elovich equilibrium constant (Lmg−1) and qm is the Elovich maximum adsorption capacity (mgm−1) can be calculated from the slopes and the intercepts of the linear plot between ln(qe/Ce) versus qe give a straight line with the correlation coefficient 0.9834 and KE 1700 (L/mg). By comparison of the experimental points with the present isotherms, results show that isotherms gave good agreement with the experimental data Figure 6(e). The values of the regression coefficient (R2) for Langmuir isotherm close to unity (0.9999). The correlation coefficient of different adsorption models is lower than other applicable models and the order is Langmuir 0.9999 > D-R model 0.9925 > Freundlich 0.9871 > Tempkin 0.9868 > Elovich 0.9834.
3.4. Kinetic Studies
3.4.1. Pseudo-First Order Model
The pseudo-first-order kinetic model (the Lagergren kinetic equation) is given by:
Table 1. Adsorption parameter at different concentration of eosin dye onto γ-Al2O3 NPs.

where qe the amounts of dye adsorbed (mg/g) at equilibrium and qt at time t (min) and k1 (min−1) is the pseudo first-order rate constant. Calculated the values of k1 from the plots of 
3.4.2. Pseudo-Second Order Model
The rate equation for pseudo-second-order model is given by: [27]

where, k2 (gmol−1∙min−1) is the equilibrium rate constant of pseudo-second-order model, qt and qe are the amount of dye adsorbed at equilibrium and at time t. The value of k2 and qe can be obtained from the slope and intercept of plots of t/qt versus t. The plot of t/qt versus t is linear, showing that chemisorption is the main rate controlling step of the adsorption process. The calculated values of maximum adsorption capacities qe and the values of R2 obtained for the pseudo second order model are in accordance with the experimental values and suggested the applicability of the pseudo-second order kinetic model to describe the adsorption process of eosin Y uptake on the Al2O3 NPs adsorbents. This refers to that the overall rate of the adsorption process was controlled by the exchange of electrons between the sorbent and the sorbate or chemisorption which involved valence forces through sharing, and its agreement with the rate controlling step when the mechanism is chemisorption. Thus the adsorption obeys a pseudo second order model at different temperatures or concentration (Table 2, Figure 7).
3.4.3. Elovich Model [28]
This equation used when the adsorbing surface is heterogeneous. The Elovich equation used to describe the second order kinetic but the equation does not prove any definite mechanism for adsorbate-adsorbent, and the linear form is given as

The constant α (mg/g∙min) is the initial adsorption rate and β (g/mg) related to the extent of surface coverage and activation energy for chemisorption which can be evaluated from the slope and intercept of and the data fitted (Table 2, Figure 7). The plot is linear with good fitting with R2 > 0.95 at lower concentrations this indicate that the diffusion rate-limiting is the rate limiting step. The initial rate (α) not regular with increasing the initial dye concentration from 75 to 200 mg/l.
Table 2. Kinetic parameters of EY adsorption onto γ-Al2O3-NP-Conditions: 0.1 g adsorbent over 75 - 200 mg∙L−1 at optimum conditions of other variables.
3.4.4. Bangham’s Kinetic [29]
The Bangham’s equation used to check the adsorption process follow only to rate controlling step or not by using an equation.
Figure 7. Adsorption kinetic models of EY on γ-Al2O3 NPs at different concentration.

where Cs is the weight of adsorbent per liter of solution (g/L), and α (<1) and kb are con-
stants estimated from the slope and intercept when plot
against logt, (Table 2, Figure 7). Reveals that the line not prove linear curve at different concentrations, thus concluded that the adsorbate diffusion into the pores of NPs oxide is not the only rate-controlling step [30] . Both pore and film diffusion may be important to describe the removal of EY from aqueous solutions. On the other hand, the values of correlation coefficient for the Bangham’s model are higher than those resulting from Elovich model. This result confirmed that the pore diffusion is the rate-control- ling step.
3.5. Adsorption Mechanism Studies
The adsorption mechanism was investigated using the intra-particle diffusion model, Bangham’s and Boyd kinetics model at different initial concentration and Temperatures.
3.5.1. Intraparticle Diffusion Model
Both of the Pseudo-first and second order does not provide the mechanism of mass transport on the surface of adsorbent. A comprehensive model was also tested to assign the rate controlling step during adsorption of dyes on the surface of adsorbent [31] . The initial rate of intraparticle diffusion is given by Weber and Morries

where kid is the intraparticle rate constant (g∙mol−1∙min−1/2) and C is the intercept. The intraparticle diffusion model implies that the plot of qt versus t1/2 should be linear straight line when the adsorption mechanism follows the sole intraparticle diffusion process. From the Figure 8 can be show that the pass line through the origin point in law concentration and deviation at higher might be due to the difference in the mass transfer rate. From the data can be observed that the value of the intercept C increase from 1.2 to 22 to increase in EY concentration from 75 to 200 mg/l, respectively, mean that increasing in the thickness of the boundary layer which hence of internal mass transfer and decrease the chance of the external mass transfer. The values of R2 (Table 2) are greater than 0.97 for the lower concentration, indicating the applicability of this model. This confirmed that the rate-limiting step is the intraparticle diffusion process, and demonstrated that the role of intraparticle diffusion in the adsorption, this behavior concluded from the plot linearity.
Figure 8. Intraparticle diffusion model for adsorption of EY on γ-Al2O3 NPs at different temperature.
Three models can be interpreted the mechanism of resulting data and can be compared with each other with the correlation coefficient value The effects of temperature on the adsorption mechanism were shown in (Table 2, Figure 8) The line does not pass through the origin and show a multi-linear step, which prove that adsorption processes occur in two or more steps and the intra-particle diffusion was not only rate controlling step. Firstly, External surface adsorption is less apparent due to completely fast at the first 20 min due to the boundary layer diffusion of solute molecules or the instantaneous adsorption of dye on the external surface of adsorbent, Furthermore, it might due to the strong electrostatic attraction between the dye and adsorbent, intraparticle diffusion (second step) is a rate limiting step and The high affinity of adsorbate adsorbed on the adsorbent surface was shown in (third step) due to slow down the adsorption process. In three models can be seen that, the three different stages having non-zero intercepts suggests that intraparticle diffusion is not the only rate limiting step in the adsorption process.
3.5.2. The Elovich and Bangham’s Kinetic Models
Figure 8, Table 3 show that the data obtained from the Elovich and Bangham’s kinetic models was revealed that the adsorption kinetics is limited by the pore diffusion. The value of α and Kb decreases with increasing the temperature and good correlation coefficients in Bangham model than an Elovich kinetic model. The values of K constant of all stages showed an increase as temperature increases. This may be due to increase in boundary layer thickness would decrease the external mass transfer, thus increasing the chance of internal mass transfer. The third phase that does not pass through the original, so confirmed it as shown in previous figure.
3.6. Thermodynamic Studies [32]
3.6.1. Van’t Hoff Equation
Different parameters for adsorption was studied at different temperature. The Gibbs free energy ∆G°, enthalpy ΔH° and entropy ΔS° were calculated from van’t Hoff equation
Table 3. Different stages parameters of intraparticle diffusion model for adsorption of EY on γ-Al2O3 NPs at different temperature.
shown below



where K is the equilibrium constant, and equal qe/Ce the data listed in Table 4, Figure 9, the negative values of ∆G° indicated that the adsorption of the dye on nanoparticles is a spontaneous process. However, the values of ∆G° slowly increased with increasing the temperature, indicates that the adsorption presses became favorable at higher temperatures. The values of ΔH° and ΔS° were determined from the slope and intercept from the plot of 1/T versus logqe/Ce given in Equation (19), respectively.
The positive values of the enthalpy change (ΔH°) indicate that the adsorption process is endothermic. The value of ∆H° (121.8 kJ/mol) is greater than 40 kJ/mol indicates that the adsorption is chemisorption in nature and involves strong attraction between dye and surface of adsorbent. The positive value of ΔS° increasing randomness at the solid/solution interface and some structural changes in the adsorbate and adsorbents
Table 4. Thermodynamic parameters for EY adsorption onto γ-Al2O3 NPs.
Figure 9. The Van’t Hoff equation of adsorption process.
during the adsorption process of EY on the NPs [33] .
3.6.2. Arrhenius Equation
The rate of reaction increase with an increase the temperature, the type of adsorption process can be obtained from Arrhenius equation when used to calculate the activation energy the linear form represented as

where A is the pre-exponential factor and Ea is the activation energy, and R is the gas constant. The Ea can be evaluated from the slope of the curve between lnk vs. 1/T (Table 4, Figure 10(a)). From Arrhenius equation the value of activation energy is 40.97 kJ/mol confirmed that the chemisorption process as a result obtained from Van’t Hoff equation.
3.6.3. Modified Arrhenius Equation (Probability Sticking)
From Table 4 and Figure 10(b) can be calculate the energy of activation (Ea) and the propability sticking (S*), from the surface coverage (θ) as follows according to modified Arrhenius type equation [34] .

The S* is a function of the adsorbate/adsorbent system under investigation, its value lies in the range 0 < S* < 1 and is dependent on the temperature of the system. The value of θ can be calculated from the following equation


Figure 10. (a) Arrhenius and (b) modified Arrhenius for the adsorption process.

The Ea was calculated from the slope of the plot of 
4. Conclusions
This study presents the information about the effects of different parameters on the adsorption of EY as a model of anionic dye from water using γ-Al2O3 nanoparticles prepared by the sol-gel method, the main conclusions are:
・ Acidic pH is highly affect on the adsorption processes and the maximum removal about 99.36% was achieved at pH 4. These behaviors due to positive charge are highly present on the surface of γ-Al2O3.
・ The adsorption parameters are investigated using four adsorption models, Langmuir, Freundlich, Tempkin and Dubinin-Radushkevich, and the Langmuir isotherm have a high correlation coefficient.
・ The kinetics adsorption of EY on γ-Al2O3 NPs is fitted to pseudo-second-order model at different temperatures and the rate controlling step is chemisorption in nature and a strong attraction occurs between the dye and the surface of Al2O3 NPs.
・ The intra-particle diffusion model not only rate controlling step, the Elovich and Bangham’s kinetic models revealed that the adsorption kinetics is limited by the pore diffusion. This result confirmed that the pore diffusion is the rate-controlling step.
・ The negative value of free energy ∆G° and increasing with increasing the temperature indicates that the adsorption process is spontaneous, and more favorable at high temperature. This data is confirmed by the positive value of ΔH° (endothermic) and the positive value of ∆S°.
・ The chemisorption process is confirmed by Arrhenius, Vant’s Hoff, and modified Arrhenius activation models where the obtained values are 40.9 kJ/mol. 106.39 kJ/mol and the value of S* is <1, (4.82E−19) thus the sticking probability of EY onto Al2O3 NPs is very high.
Cite this paper
Thabet, M.S. and Ismaiel, A.M. (2016) Sol-Gel γ-Al2O3 Nanoparticles Assessment of the Removal of Eo- sin Yellow Using: Adsorption, Kinetic and Thermodynamic Parameters. Journal of En- capsulation and Adsorption Sciences, 6, 70- 90. http://dx.doi.org/10.4236/jeas.2016.63007
References
- 1. Macedo, M.I.F., Osawa, C.C. and Bertran, C.A. (2004) Sol-Gel Synthesis of Transparent Alumina Gel and Pure Gamma Alumina by Urea Hydrolysis of Aluminum Nitrate. Journal of Sol-Gel Science and Technology, 30, 135-140.
http://dx.doi.org/10.1023/B:JSST.0000039497.46154.8f - 2. Lefevre, G., Duc, M., Lepeut, P., Caplain, R. and Fedoroff, M. (2002) Hydration of Gamma- Alumina in Water and Its Effects on Surface Reactivity. Langmuir, 18, 7530-7537.
http://dx.doi.org/10.1021/la025651i - 3. Trueba, M. and Trasatti, S.P. (2005) Gamma-Alumina as a Support for Catalysts: A Review of Fundamental Aspects. European Journal of Inorganic Chemistry, 2005, 3393-3403.
http://dx.doi.org/10.1002/ejic.200500348 - 4. Wawrzkiewicz, M., Wigniewska, M., Gun’ko, V.M. and Zarko, V.I. (2015) Adsorptive Removal of Acid, Reactive and Direct Dyes from Aqueous Solutions and Wastewater Using Mixed Silica-Alumina Oxide. Powder Technology, 278, 306-315.
http://dx.doi.org/10.1016/j.powtec.2015.03.035 - 5. Weber, T.W. and Chakravo, R.K. (1974) Pore and Solid Diffusion Models for Fixed-Bed Adsorbers. AIChE Journal, 20, 228-238.
http://dx.doi.org/10.1002/aic.690200204 - 6. Mckay, G., Blair, H.S. and Gardner, J.R. (1982) Adsorption of Dyes on Chitin. 1. Equilibrium Studies. Journal of Applied Polymer Science, 27, 3043-3057.
http://dx.doi.org/10.1002/app.1982.070270827 - 7. Ho, Y.S. (2014) Using of “Pseudo-Second-Order Model” in Adsorption. Environmental Science and Pollution Research, 21, 7234-7235.
http://dx.doi.org/10.1007/s11356-013-2213-9 - 8. Peers, A.M. (1965) Elovich Adsorption Kinetics and Heterogeneous Surface. Journal of Catalysis, 4, 499-503.
http://dx.doi.org/10.1016/0021-9517(65)90054-0 - 9. Bhatnagar, A. and Jain, A.K. (2005) A Comparative Adsorption Study with Different Industrial Wastes as Adsorbents for the Removal of Cationic Dyes from Water. Journal of Colloid and Interface Science, 281, 49-55.
http://dx.doi.org/10.1016/j.jcis.2004.08.076 - 10. Mall, I.D., Srivastava, V.C., Agarwal, N.K. and Mishra, I.M. (2005) Adsorptive Removal of Malachite Green Dye from Aqueous Solution by Bagasse Fly Ash and Activated Carbon-Kinetic Study and Equilibrium Isotherm Analyses. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 264, 17-28.
http://dx.doi.org/10.1016/j.colsurfa.2005.03.027 - 11. Sonetaka, N., Fan, H.J., Kobayashi, S., Su, Y.C. and Furuya, E. (2009) Characterization of Adsorption Uptake Curves for Both Intraparticle Diffusion and Liquid Film Mass Transfer Controlling Systems. Journal of Hazardous Materials, 165, 232-239.
http://dx.doi.org/10.1016/j.jhazmat.2008.09.111 - 12. Du, W.L., Xu, Z.R., Han, X.Y., Xu, Y.L. and Miao, Z.G. (2008) Preparation, Characterization and Adsorption Properties of Chitosan Nanoparticles for Eosin Y as a Model Anionic Dye. Journal of Hazardous Materials, 153, 152-156.
http://dx.doi.org/10.1016/j.jhazmat.2007.08.040 - 13. Chatterjee, S., Chatterjee, S., Chatterjee, B.P., Das, A.R. and Guha, A.K. (2005) Adsorption of a Model Anionic Dye, Eosin Y, from Aqueous Solution by Chitosan Hydrobeads. Journal of Colloid and Interface Science, 288, 30-35.
http://dx.doi.org/10.1016/j.jcis.2005.02.055 - 14. Knies, J.L. and Kingsolver, J.G. (2010) Erroneous Arrhenius: Modified Arrhenius Model Best Explains the Temperature Dependence of Ectotherm Fitness. The American Naturalist, 176, 227-233.
http://dx.doi.org/10.1086/653662 - 15. Zeng, Z., Yu, J. and Guo, Z.X. (2005) Preparation of Functionalized Core-Shell Alumina/Polystyrene Composite Nanoparticles, 1—Encapsulation of Alumina via Emulsion Polymerization. Macromolecular Chemistry and Physics, 206, 1558-1567.
http://dx.doi.org/10.1002/macp.200500060 - 16. Chandradass, J., Jun, B. and Bae, D.S. (2008) Effect of Different Fuels on the Alumina-Zirconia Nanopowder Synthesized by Sol-Gel Autocombustion Method. Journal of Non- Crystalline Solids, 354, 3085-3087.
http://dx.doi.org/10.1016/j.jnoncrysol.2008.02.018 - 17. Li, J., Pan, Y.B., Xiang, C.S., Ge, Q.M. and Guo, J.K. (2006) Low Temperature Synthesis of Ultrafine Alpha-Al2O3 Powder by a Simple Aqueous Sol-Gel Process. Ceramics International, 32, 587-591.
http://dx.doi.org/10.1016/j.ceramint.2005.04.015 - 18. Chien, S.H. and Clayton, W.R. (1980) Application of Elovich Equation to the Kinetics of Phosphate Release and Sorption in Soils. Soil Science Society of America Journal, 44, 265-268.
http://dx.doi.org/10.2136/sssaj1980.03615995004400020013x - 19. Ho, Y.S. (2006) Review of Second-Order Models for Adsorption Systems. Journal of Hazardous Materials, 136, 681-689.
http://dx.doi.org/10.1016/j.jhazmat.2005.12.043 - 20. Ho, Y.S. (2004) Citation Review of Lagergren Kinetic Rate Equation on Adsorption Reactions. Scientometrics, 59, 171-177.
http://dx.doi.org/10.1023/B:SCIE.0000013305.99473.cf - 21. Temkin, M. and Pyzhev, V. (1940) Kinetics of Ammonia Synthesis on Promoted Iron Catalysts. Acta Physicochimica U.R.S.S., 12, 327-356.
- 22. Aharoni, C. and Suzin, Y. (1982) Application of the Elovich Equation to the Kinetics of Occlusion. 2. Analysis of Experimental-Data from the Literature. Journal of the Chemical Society, Faraday Transactions 1: Physical Chemistry in Condensed Phases, 78, 2321-2327.
http://dx.doi.org/10.1039/f19827802321 - 23. Freundlich, H. (1906) Concerning Adsorption in Solutions. Zeitschrift fur physikalische chemie-stochiometrie und verwandtschaftslehre, 57, 385-470.
- 24. Langmuir, I. (1918) The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum. Journal of the American Chemical Society, 40, 1361-1403.
http://dx.doi.org/10.1021/ja02242a004 - 25. Wang, J.A., Bokhimi, X., Morales, A., Novaro, O., Lopez, T. and Gomez, R. (1999) Aluminum Local Environment and Defects in the Crystalline Structure of Sol-Gel Alumina Catalyst. The Journal of Physical Chemistry B, 103, 299-303.
http://dx.doi.org/10.1021/jp983130r - 26. Tan, H.B. and Guo, C.S. (2011) Preparation of Long Alumina Fibers by Sol-Gel Method Using Malic Acid. Transactions of Nonferrous Metals Society of China, 21, 1563-1567.
http://dx.doi.org/10.1016/S1003-6326(11)60897-2 - 27. Li, Y.M. and Somorjai, G.A. (2010) Nanoscale Advances in Catalysis and Energy Applications. Nano Letters, 10, 2289-2295.
http://dx.doi.org/10.1021/nl101807g - 28. Sonia, S., Annsi, I.J., Kumar, P.S., Mangalaraj, D., Viswanathan, C. and Ponpandian, N. (2015) Hydrothermal Synthesis of Novel Zn Doped CuO Nanoflowers as an Efficient Photodegradation Material for Textile Dyes. Materials Letters, 144, 127-130.
http://dx.doi.org/10.1016/j.matlet.2015.01.026 - 29. Rafatullah, M., Sulaiman, O., Hashim, R. and Ahmad, A. (2010) Adsorption of Methylene Blue on Low-Cost Adsorbents: A Review. Journal of Hazardous Materials, 177, 70-80.
http://dx.doi.org/10.1016/j.jhazmat.2009.12.047 - 30. Zangeneh, H., Zinatizadeh, A.A.L., Habibi, M., Akia, M. and Isa, M.H. (2015) Photocatalytic Oxidation of Organic Dyes and Pollutants in Wastewater Using Different Modified Titanium Dioxides: A Comparative Review. Journal of Industrial and Engineering Chemistry, 26, 1-36. http://dx.doi.org/10.1016/j.jiec.2014.10.043
- 31. Verma, A.K., Dash, R.R. and Bhunia, P. (2012) A Review on Chemical Coagulation/Flocculation Technologies for Removal of Colour from Textile Wastewaters. Journal of Environmental Management, 93, 154-168.
http://dx.doi.org/10.1016/j.jenvman.2011.09.012 - 32. Hayat, H., Mahmood, Q., Pervez, A., Bhatti, Z.A. and Baig, S.A. (2015) Comparative Decolorization of Dyes in Textile Wastewater Using Biological and Chemical Treatment. Separation and Purification Technology, 154, 149-153.
http://dx.doi.org/10.1016/j.seppur.2015.09.025 - 33. Sharma, P., Kaur, H., Sharma, M. and Sahore, V. (2011) A Review on Applicability of Naturally Available Adsorbents for the Removal of Hazardous Dyes from Aqueous Waste. Environmental Monitoring and Assessment, 183, 151-195.
http://dx.doi.org/10.1007/s10661-011-1914-0 - 34. Kanagaraj, J., Senthilvelan, T. and Panda, R.C. (2015) Degradation of Azo Dyes by Laccase: Biological Method to Reduce Pollution Load in Dye Wastewater. Clean Technologies and Environmental Policy, 17, 1443-1456.
http://dx.doi.org/10.1007/s10098-014-0869-6






















