Journal of Encapsulation and Adsorption Sciences
Vol.1 No.3(2011), Article ID:7686,8 pages DOI:10.4236/jeas.2011.13007
On Single Compartment Pharmacokinetic Model Systems that Obey Michaelis-Menten Kinetics and Systems that Obey Krebs Cycle Kinetics
Department of Chemical Engineering, Roy G. Perry College of Engineering, Prairie View A & M University, Prairie View, TX, USA
E-mail: jyoti_kalpika@yahoo.com
Received June 10, 2011; revised July 12, 2011; accepted July 22, 2011
Keywords: Single Compartment Models, Michaelis and Menten Kinetics, Reactions in Circle, Subcritical Damped Oscillations, Pharmacokinetics
Abstract
The integration of Michaelis-Menten kinetics results in a trancedental equation. The results are not in a form that is readily usable. A more usable form of the model solutions is developed. This was accomplished by using Taylor series expansion of dimensionless concentration u in terms of its derivatives. The infinite series expression for dimensionless concentration is given. It can be seen that for times t <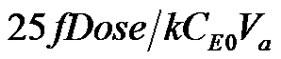 , the Taylor series expression evaluated near the origin up to the third derivative is a reasonable representation of the integrated solution. More terms in the Taylor series expression can be added to suit the application. It can vary with the apparent volume, dosage, enzyme concentration, Michaelis constant and the desired accuracy level needed. The single compartment model solution was obtained by the method of Laplace transform. It can be seen from Figure 2 that the dimensionless drug concentration in the compartment goes through a maxima. The curve is convex throughout the absorption and elimination processes. The drug gets completely depleted after a said time. The curve is asymmetrical with a right skew. The systems under absorption with elimination that obey the kinetics that can be represented by a set of reactions in circle were considered. A system of simple reactions in circle was taken into account. The concentration profile of the reactants were obtained by the method of Laplace transforms. The conditions when subcritical damped oscillations can be expected are derived. A model was developed for cases when absorption kinetics exhibit subcritical damped oscillations. The solution was developed by the method of Laplace transforms. The solution for dimensionless concentration of the drug in single compartment for different values of rate constants and dimensionless frequency are shown in Figures 6-9. The drug profile reaches a maximum and drops to zero concentration after a said time. The fluctuations in concentration depends on the dimensionless frequency resulting from the subcritical damped oscillations during absorption. At low frequencies the fluctuations are absent. As the frequency is increased the fluctuations in concentration are pronounced. The frequency of fluctuations were found to increase with increase in frequency of oscillations during absorption.
, the Taylor series expression evaluated near the origin up to the third derivative is a reasonable representation of the integrated solution. More terms in the Taylor series expression can be added to suit the application. It can vary with the apparent volume, dosage, enzyme concentration, Michaelis constant and the desired accuracy level needed. The single compartment model solution was obtained by the method of Laplace transform. It can be seen from Figure 2 that the dimensionless drug concentration in the compartment goes through a maxima. The curve is convex throughout the absorption and elimination processes. The drug gets completely depleted after a said time. The curve is asymmetrical with a right skew. The systems under absorption with elimination that obey the kinetics that can be represented by a set of reactions in circle were considered. A system of simple reactions in circle was taken into account. The concentration profile of the reactants were obtained by the method of Laplace transforms. The conditions when subcritical damped oscillations can be expected are derived. A model was developed for cases when absorption kinetics exhibit subcritical damped oscillations. The solution was developed by the method of Laplace transforms. The solution for dimensionless concentration of the drug in single compartment for different values of rate constants and dimensionless frequency are shown in Figures 6-9. The drug profile reaches a maximum and drops to zero concentration after a said time. The fluctuations in concentration depends on the dimensionless frequency resulting from the subcritical damped oscillations during absorption. At low frequencies the fluctuations are absent. As the frequency is increased the fluctuations in concentration are pronounced. The frequency of fluctuations were found to increase with increase in frequency of oscillations during absorption.
1. Introduction
The experimental, theoretical and computational analysis of rate of change with time of concentration and volume distribution of compounds administered externally such as drugs, metabolite, nutrients, harmones, toxins, in various regions of the human physiology is called pharmacokinetics [1,2]. Application of pharmacokinetics allows for the processes of liberation, absorption, distribution, metabolism and excretion to be characterized mathematically.
The absorption of drug can be affected by different methods. Drugs administered through the gastrointestinal tract, GI is referred to as enteral route of entry. Parenteral routes refer to all other types of drug entry. Drug administration: 1) beneath the tongue is by sublingual entry; 2) via the mouth is by buccal cavity; 3) through stomach by gastric entry; 4) through veins by IV therapy; 5) with/in the muscular by intramuscular therapy; 6) beneath the epidermal and dermal skin layers via subcutaneous therapy; 7) within the dermis by intradermal therapy; 8) by topical treatment applied to the skin by percutaneous therapy; 9) through mouth, nose, pharynz, trachea, bronchi, bronchioles, alveolar sacs, alveoli by inhalation; 10) is introduced into artery by intrarterial route; 11) to cerebrospinal fluid by intrathecal route; 12) within the vagina by vaginal route and; 13) through eye, intraocular route. Systemic circulation is reached by the drugs absorbed from the buccal cavity and the lower rectum.
Pharmacokinetics is modeled using compartment models. Compartmental methods [1] involve development of mathematical models to describe the change in concentration of drug with time. These models are similar to those developed in chemical reaction engineering and thermodynamics and biochemical kinetics. Compartmental models offer the advantage of prediction of drug concentration at any instant of time. There is a spectrum of pharmacokinetic models and computer software ranging from a simple one-compartmental pharmacokinetic mode with bolus administration with elimination to complex models that rely on the use of physiological information to ease development and validation.
Although there are number of discussions in the literature about pharmacokinetic models most of them deal with monotonic exponential decay of concentration. Very little attention is paid to oscillatory systems such as found in Krebs and systems that obey Michaelis-Menten kinetics. When the number of compartments in the model becomes large or when the kinetics becomes complex such as Michaelis-Menten or Krebs cycle no closed form analytical solution is possible [3]. Only for simple single and two compartment models closed formed analytical solutions are available. Lundquist and Wolthers [4] presented integrated solutions for 1 compartment model with Michaelis-Menten kinetics. This is a trancedental equation and not in a readily usable form. Beal [5] and Godfrey et. al. [6] examined the integrated form of solution for the same problem. They use implicit functions that can be calculated using table or numerical methods. These are not completely analytical solutions as some interim functions are invoked that cannot be calculated directly. Tand and Xiao [7] looked into this problem recently and suggested the Lambert W function that can be implemented using software libraries such as Matlab and Maple to fit the Michaelis-Menten parameters.
This study deals with application of single compartment model pharmacokinetic analysis to systems: 1) that obey Michaelis-Menten kinetics and; 2) Krebs cycle kinetics. Closed form analytical solutions are presented by using infinite series representation and method of Laplace transforms. A more useful closed form analytical solution is sought for Michealis-Menten kinetics. In the case of Krebs cycle the implications of oscillatory systems are discussed.
2. Michaelis-Menten Absorption With Elimination
A mass balance on the concentration of drug within the human anatomy for the case where the kinetics of absorption is in obeyance of Michaelis-Menten Kinetics with elimination can be written for Figure 1. as;
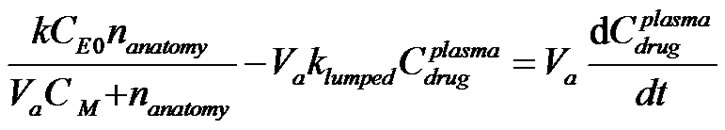 (1)
(1)
Let nanatomy be the amount of drug that is available for absorption. The absorption of the drug process can be described by Michaelis-Menten kinetics;
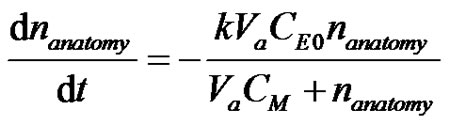 (2)
(2)
where k is the infusion Michaelis-Menten rate constant, CE0 is the total enzyme concentration and CM is the rate constant. It can be seen that (Levenspiel, 8) the Michaelis-Menten kinetics becomes independent of concentration at high drug concentration and becomes zeroth order and at the low concentration limit reverts to a simple first order rate expression. Integration of Equation (2) can be seen to be (9);
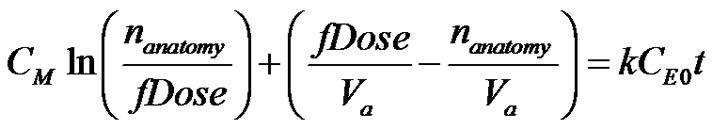 (3)
(3)
It can be seen that Equation (3) is in a form that is not readily usable in terms of a one-to-one mapping between the independent variable t and dependent variable nanatomy. A trancedental equation has to be solved for. In order to combine Equation (3) with Equation (1) and then solve for the concentration of drug in the plasma, a more us able form of Equation (3) is needed. This can be done
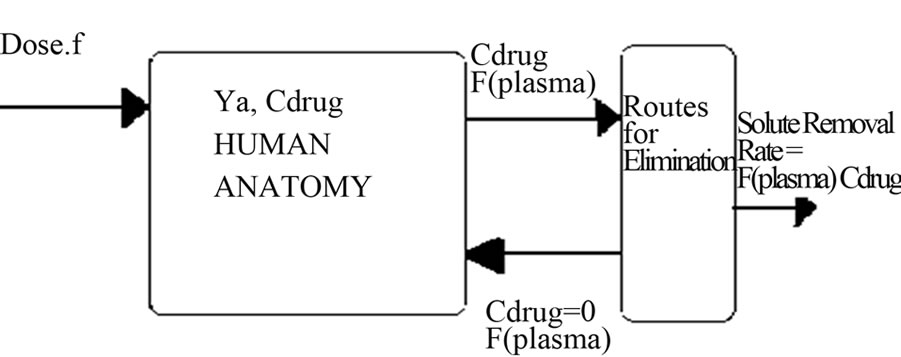
Figure 1. Single Compartment Model for Human Anatomy.
by realizing that any arbitrary function can be represented using the Taylor series. Taylor series representation of any arbitrary function is a infinite series containing derivatives of the arbitrary function about a particular point. Prior to obtaining the Taylor series Equation (3) is made dimensionless as follows;
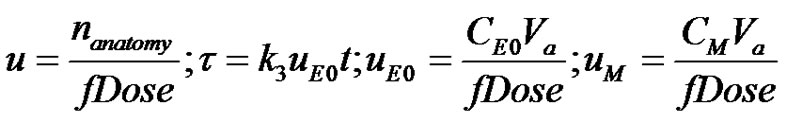 (4)
(4)
Equation (3) becomes;
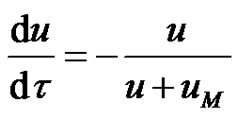 (5)
(5)
Taylor series in terms of derivatives of u evaluated at the point t = 0 can be written as follows;
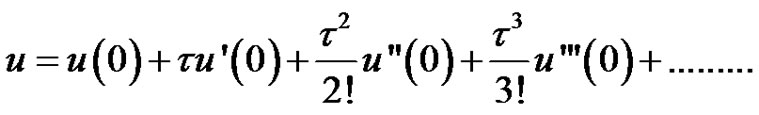 (6)
(6)
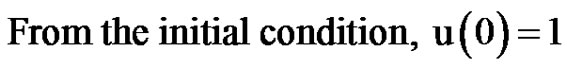 (7)
(7)
From Equation (5),
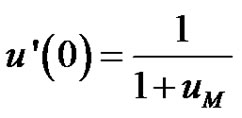 (8)
(8)
The initial value of the second derivative of the dimensionless concentration, u" can be seen to be;
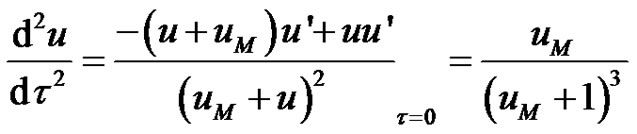 (9)
(9)
The initial value of the third derivative of the dimensionless concentration, u"' can be seen to be;
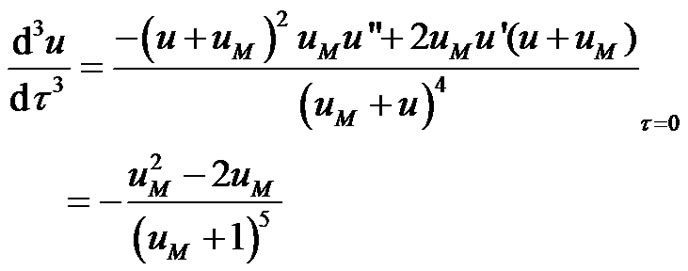 (10)
(10)
Plugging Equations (8-10) in Equation (6);
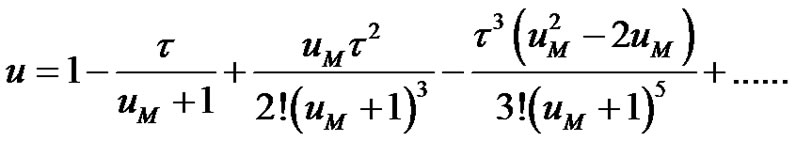 (11)
(11)
Equation (11) and Equation (3) are sketched for a particular value of uM =16, in Figure 2. It can be seen that for times t <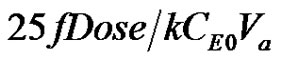 , the Taylor series expression evaluated near the origin up to the third derivative is a reasonable representation of the integrated solution given in Equation (3). More terms in the Taylor series expression can be added to suit the application and the apparent volume, dosage, enzyme concentration, Michaelis constant and the desired accuracy level needed as shown above.
, the Taylor series expression evaluated near the origin up to the third derivative is a reasonable representation of the integrated solution given in Equation (3). More terms in the Taylor series expression can be added to suit the application and the apparent volume, dosage, enzyme concentration, Michaelis constant and the desired accuracy level needed as shown above.
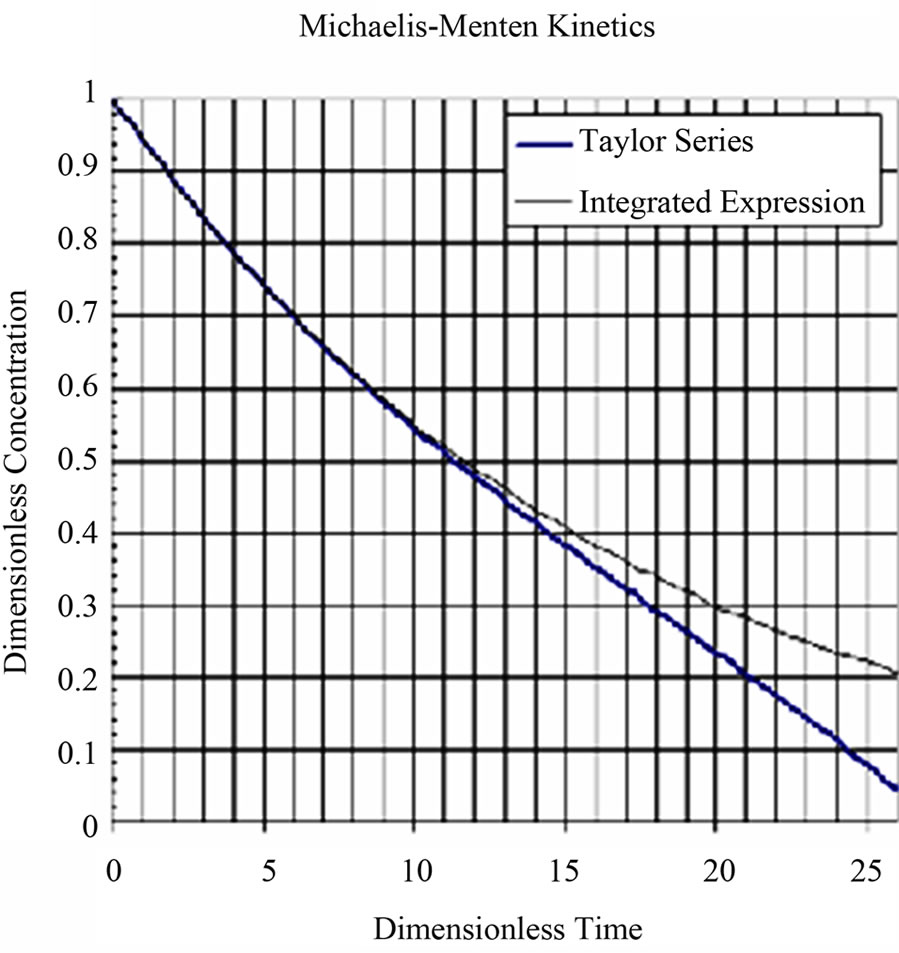
Figure 2. Michaelis-Menten Kinetics from the Integrated and Taylor Series Expressions.
Equation (11) and Equation (1) can be combined and the concentration of drug as a function of time can be solved for from the resulting equation by the method of Laplace transforms as follows. The combined equation is also made dimensionless;
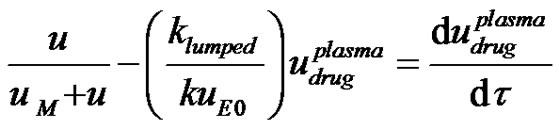 (12)
(12)
Combining Equation (11), Equation (5) and Equation (1);
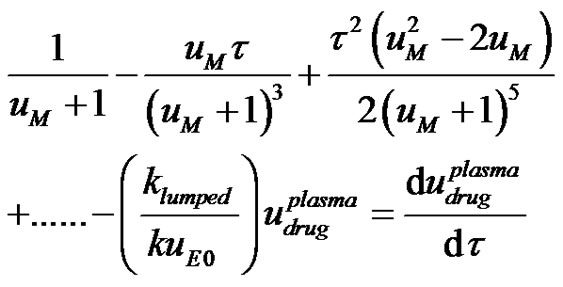 (13)
(13)
Obtaining the Laplace transform of the governing equation, Equation (13) for dimensionless drug concentration in the compartment (plasma);
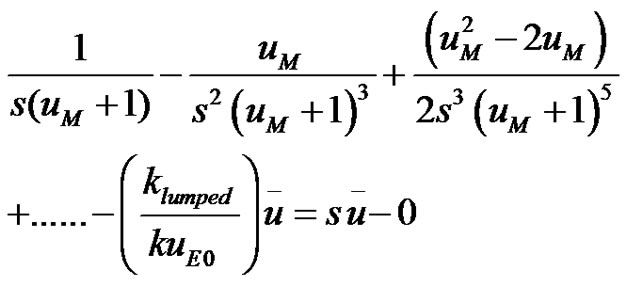 (14)
(14)
The transformed expression for dimensionless drug concentration in the compartment can be seen to be;
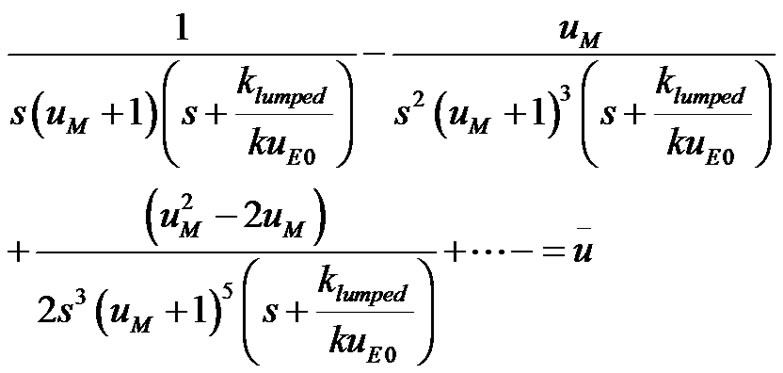 (15)
(15)
It can be seen that the inversion for each term in the infinite series is readily available from the tables [10]. Thus a non-linear differential equation was transformed using Taylor series and some manipulations into a equation with closed form analytical solution. The term by term inversion of Equation (15) can be looked from the Tables as;
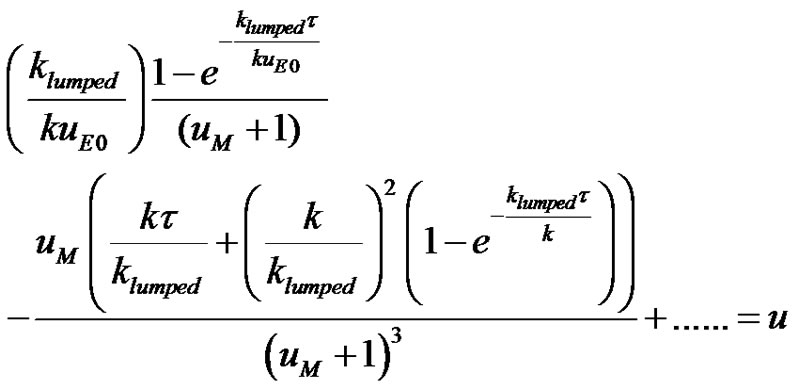 (16)
(16)
The dimensionless drug concentration in the compartment or plasma is shown in Figure 3. It can be seen from Figure 3. that the dimensionless drug concentration in the compartment goes through a maxima. The curve is convex throughout the absorption and elimination processes. The drug gets completely depleted after a said time. The curve is asymmetrical with a right skew. The constants used to construct Figure 3. using Microsoft MS soft MS Excel Spreadsheet were;
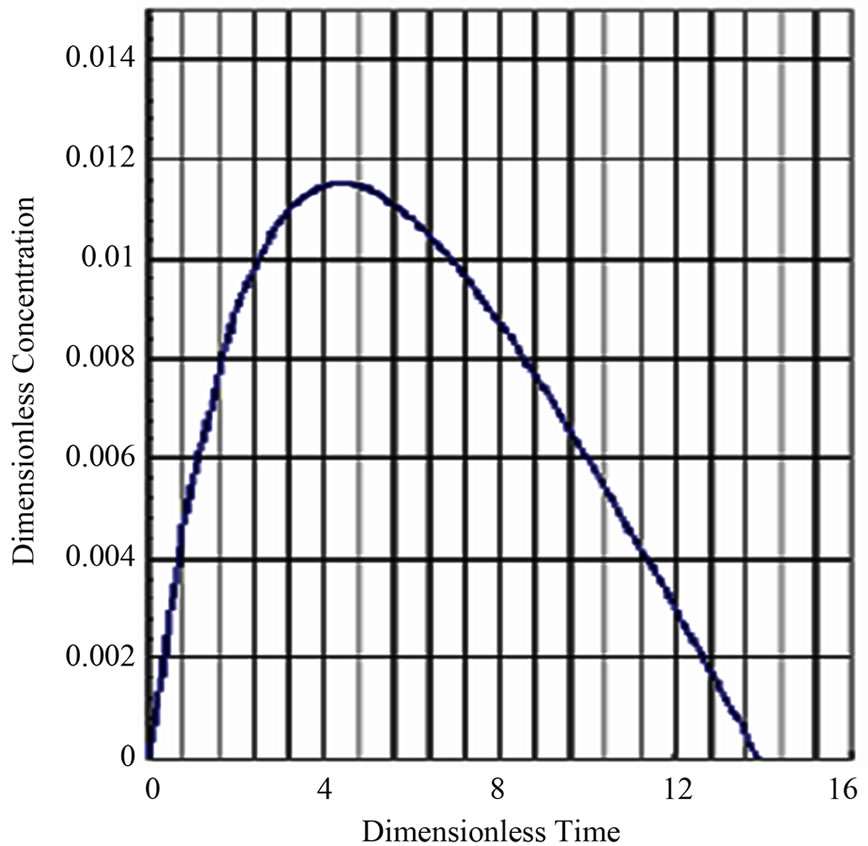
Figure 3. Michaelis-Menten Absorption and Elimination.
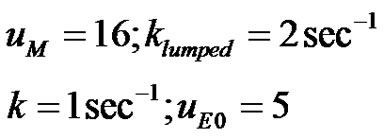
3. Analysis of Simple Reactions in Circle
The mathematical model predictions for drug concentration as discussed above depends on the nature of kinetics of absorption. It can be simple zeroth order, first order, second order, fractional order any order n. It can also be reversible in nature. It can obey Michaelis-Menten kinetics.
Sometimes in the absorption process the Krebs cycle [11] may be encountered. Reactions such as these can be represented by a scheme of reactions in circle (Sharma, 12). The essential steps in the Krebs cycle are formation of: i) A. Oxalic Acid; ii) B. Citric Acid; iii) C. Isocitric Acid; iv) D. a-Ketoglutaric Acid; v) E. Succyl Coenzyme A; vi) F. Succinic Acid; vii) G. Fumaric Acid; viii) H. Maleic Acid. There are other sets of reactions in metabolic pathways that can be represented by a scheme of reactions in circle. Systems of reactions in series and reactions in parallel have been introduced [8].
Consider a system of reactions in circle: i) System of 3 Reactants in Circle; ii) System of 4 Reactants in Circle; iii) System of 8 Reactants in Circle such as in Krebs Cycle and; iv) General Case. A scheme of reactants in circle is shown in Figure 4.
3.1. Reactions in Circle
The simple first order irreversible rate expressions for (i) 3 Reactants in Circle can be written as;
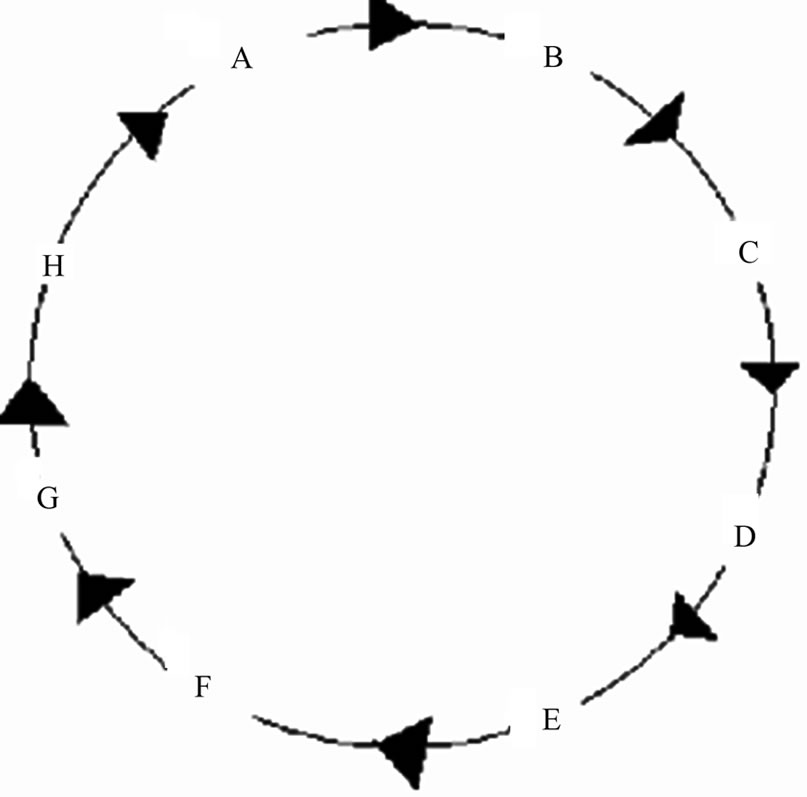
Figure 4. Simple Reactions in Circle Representation of Krebs Cycle.
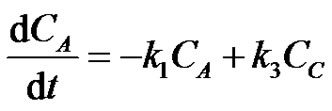 (17)
(17)
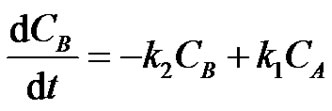 (18)
(18)
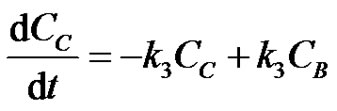 (19)
(19)
where, CA, CB and CC are the concentrations of the reactants A, B and C at any instant in time, t. Let the initial concentrations of reactants A, B and C be given by CA0, CB0 =0 and CC0=0. The Laplace transforms of Equations (17-19) are obtained as;
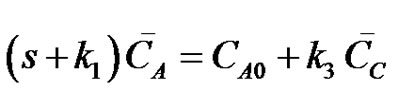 (20)
(20)
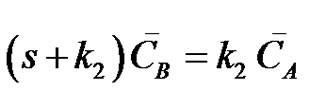 (21)
(21)
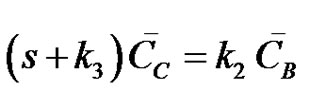 (22)
(22)
Eliminating CB and CC between Equations (20)-(22) the transformed expression for the instantaneous concentration of reactant A can be written as;
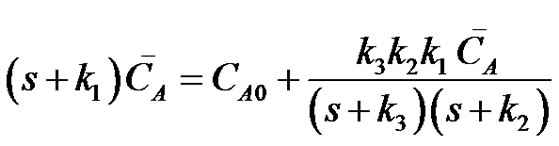 (23)
(23)
or,
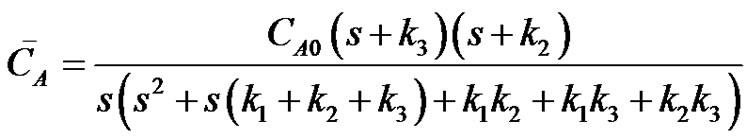 (24)
(24)
The inversion of Equation (24) can be obtained by use of the residue theorem. The 3 simple poles can be recognized in Equation (24) Further it can be realized that when the poles are complex, subcritical damped oscillations can be expected in the concentration of the reactant. This is when the quadratic,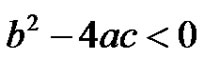 . This can happen when;
. This can happen when;
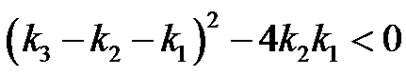 (25)
(25)
or,
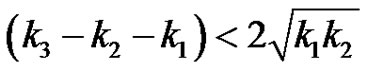 (26)
(26)
or,
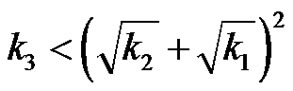 (27)
(27)
This expression is symmetrical with respect to reactants A, B and C. When the relation holds , i.e., when one reaction rate constant is less than the square of the sum of the square root of the rate constants of the other two reactions, the subcritical damped oscillations can be expected in the reactant concentration.
3.2. Reactions in Circle
The equivalent Laplace transformed expression for concentration of reactant A for a system of 4 reactions in circle assuming that all the reactions in the cycle obey simple, first order kinetics can be derived as;
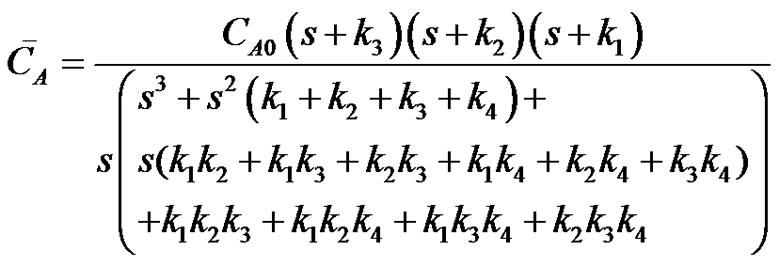 (28)
(28)
The conditions where the concentration can be expected to exhibit subcritical damped oscillations when the roots of the following equation becomes complex;
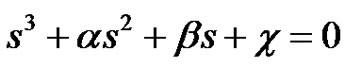 (29)
(29)
where,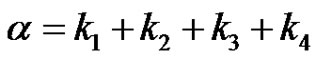 (30)
(30)
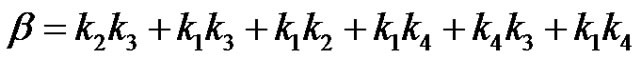 (31)
(31)
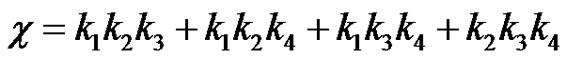 (32)
(32)
It can be seen that a is the sum of all the 4 reaction rate constants, b is the sum of product of all possible pairs of the reaction rate constants and c is the sum of product of all possible triple products of rate constants in the system of reactions in circle. Equation (29) can be converted to the depressed cubic equation by use of the substitution,
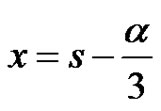 (33)
(33)
This method was developed in the Renaissance period (Ans Magna, (13)). The depressed cubic without the quadratic term will then be;
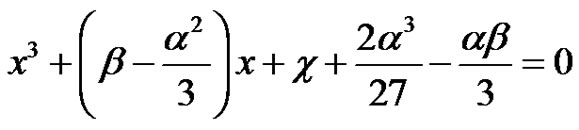 (34)
(34)
Let,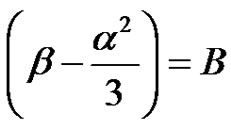 ;
;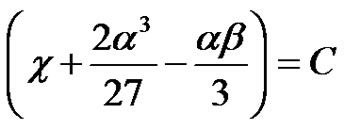 (35)
(35)
Then, Equation (29) becomes;
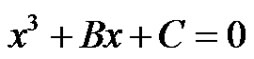 (36)
(36)
The complex roots to Equation (34) shall occur when D > 0, where,
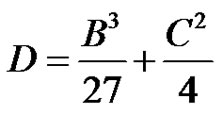 (37)
(37)
Thus the conditions when subcritical damped oscillations can be expected for a system of 4 reactions in circle is derived.
3.3. General Case of n Reactions in Circle
For the general case, of which the Krebs cycle with 8 reactions in circle is a particular case can be obtained by extension of the expressions derived for 3 reactions in circle and 4 reactions in circle. Aliter to this would be the method of Eigen values and Eigen vectors. The cases when l is imaginary is when the concentration of the species will exhibit subcritical damped oscillations are given by the characteristic equation (Varma and Morbidelli, (14));
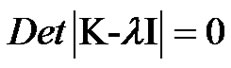 (38)
(38)
The size of the K matrix depends on the number of reactions in circle. For n reactions in circle K would be a n x n matrix. For the case of Krebs cycle it would be a 8 x 8 matrix (Figure 5).
Upon expansion an 8th order polynomial equation in l arises. Eight roots of the polynomial exist. Even if all the values in the characteristic matrix are real some roots may be complex. When complex roots occur they appear in pairs. The roots of the polynomial are called eigenvalues of the characteristic matrix. The polynomial equation is called the Eigen value equation.
4. Subcritical Damped Oscillations
As was discussed in the previous section, the concentration of the drug during absorption on account of kinetics such as the reactions in circle can undergo subcritical damped oscillations. In such cases, how can the absorption with elimination process be modeled ?

Figure 5. Characteristic Matrix for System of 8 Reactions in Circle
Let the solution for the dosage drug when absorbed by kinetics that result in a subcritical damped oscillations be given by;
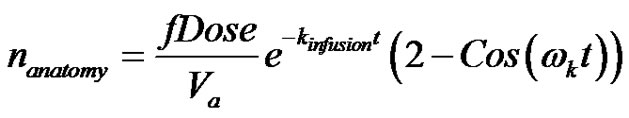 (39)
(39)
A mass balance on the concentration of drug within the human anatomy for the case of kinetics of absorption resulting in subcritical damped oscillation can be written for Figure 4 as;
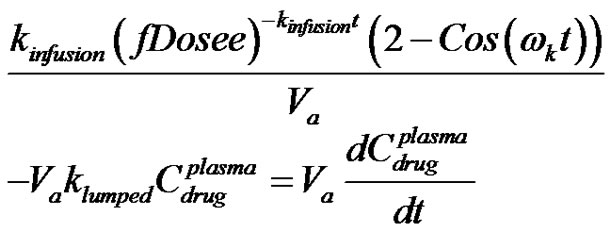 (40)
(40)
Equation (40) is the governing equation for concentration of drug in the single compartment. Equation (40) is made dimensionless by the following substitutions;
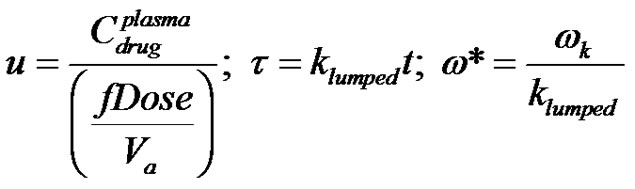 (41)
(41)
Plugging Equation (41) in Equation (40) becomes;
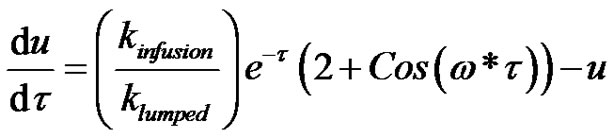 (42)
(42)
The concentration of drug as a function of time can be solved for by the method of Laplace transforms as follows. Obtaining the Laplace transforms of Equation (42);
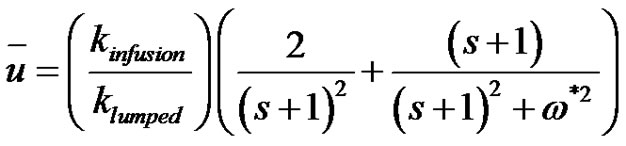 (43)
(43)
Obtaining the inverse of the transformed expression in Equation (43) by using the convolution property;
 (44)
(44)
The solution for dimensionless concentration of the drug in the single compartment for different values of rate constants and dimensionless frequency are shown in Figures 6-9. The drug profile reaches a maximum and drops to zero concentration after a said time. The fluctuations in concentration depends on the dimensionless frequency resulting from the subcritical damped oscillations during absorption. At low frequencies the fluctuations are absent. As the frequency is increased the fluctuations in concentration are pronounced. The frequency of fluctuations were found to increase with increase in frequency of oscillations during absorption.
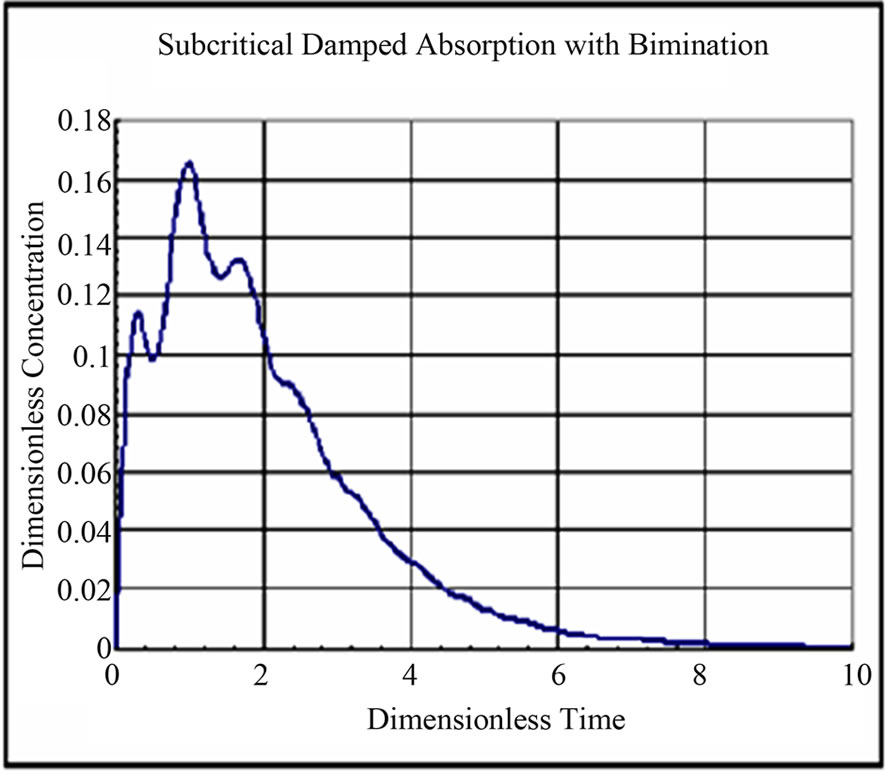
Figure 6. Dimensionless Concentration of Drug in Compartment w* = w/klumped = 8.
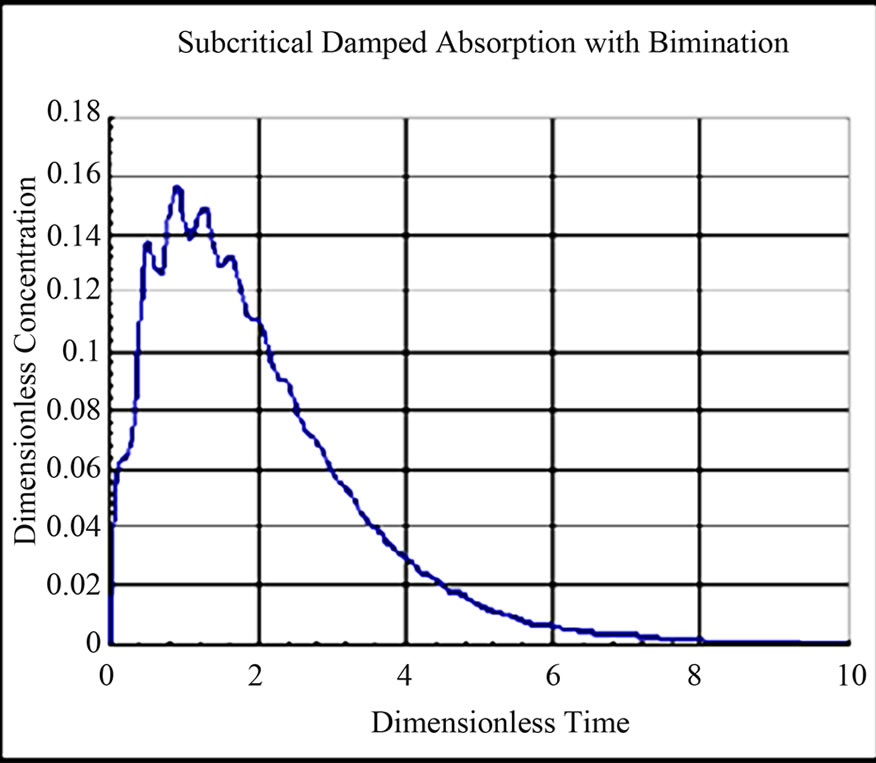
Figure 7. Dimensionless Concentration of Drug in Compartment w* = w/klumped = 16; kinfusion/klumped = 0.4
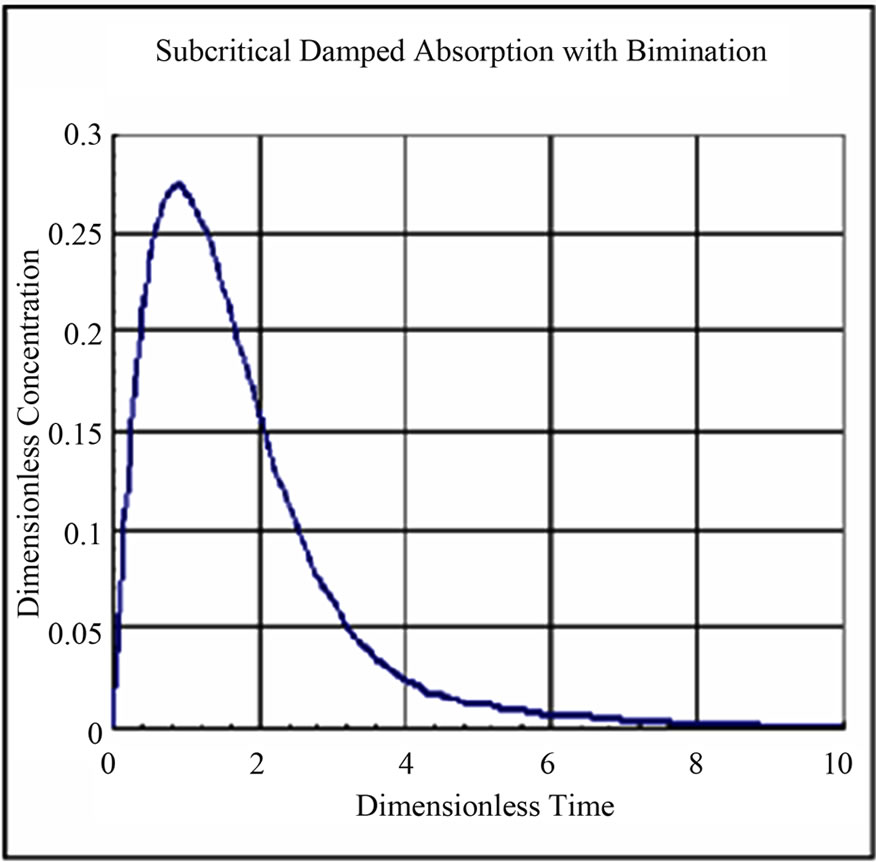
Figure 8. Dimensionless Concentration of Drug in Compartment, w* = 1, kinfusion/klumped = 0.4
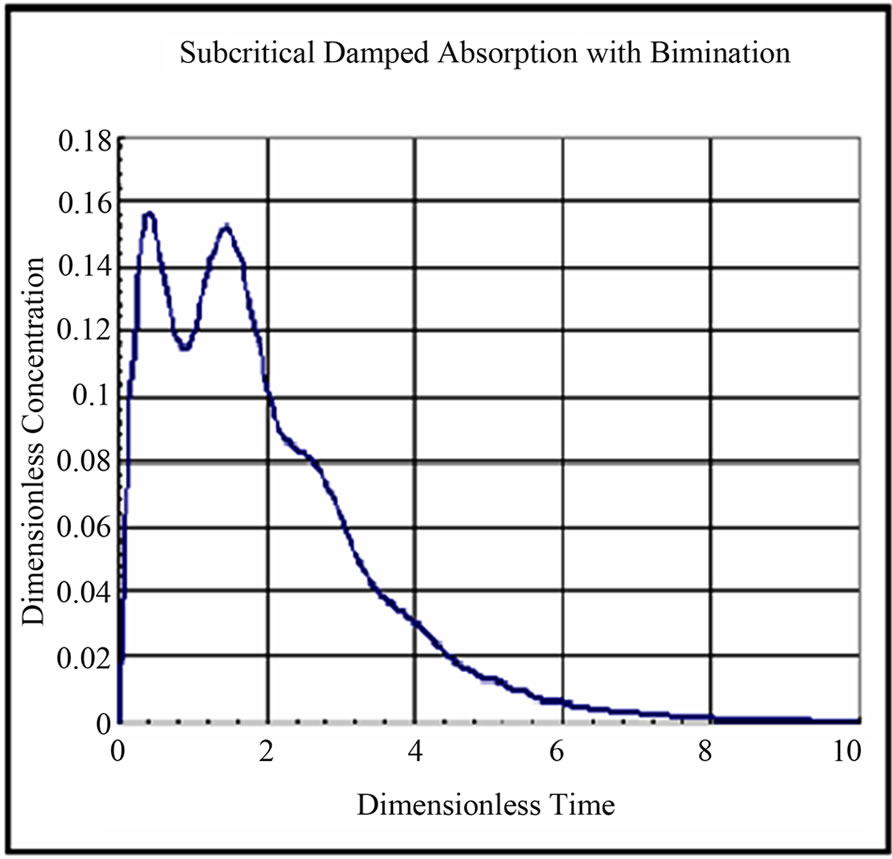
Figure 9. Dimensionless Concentration of Drug in Compartment w* = w/klumped = 5; kinfusion/klumped = 0.4
5. Conclusions
A closed form explicit, more useful solution for systems that obey Michaelis-Menten kinetics was developed. Taylor infinite series method was used along with dimensionless variables. The pharmacokinetic model with absorbtion and elimination in the Laplace domain can be inverted term by term by look-up from existing tables. The number of terms needed for a given application can be chosen for a given desired level of accuracy. A right skew and maxima was seen in the dimensionless concentration with time plot.
Subcritical damped oscillations can arise when the system obey the Krebs cycle kinetics. Such systems can be treated using the single compartment pharmacokinetic analysis. The drug concentration drops to zero concentration after a said time. This is au contrairie to decaying exponentially with the x axis as asymptote. A saw tooth pattern was seen in the concentration time plot for certain values of the frequency of oscillations and ratio of the rate constants of infusion and excretion. A bimodal concentration curve can be seen lower frequencies of fluctuations. At very low frequencies the concentration time curve was found devoid of concentration. At high frequencies the concentration time curve gets embedded with high frequency fluctuations.
6. Acknowledgements
This paper is a natural outgrowth from my instruction of Biofluid Dynamics at SASTRA University, Thanjavur, India 2003-2007 and CHEG 4033 Process Dynamics and Control at the department of Chemical Engineering at Prairie View A & M University, Prairie View, TX 77446 from Fall semester, 2009-2010.
7. References
[1] K. R. Sharma, “Transport Phenomena in Biomedical Engineering: Artificial Organ Design and Development and Tissue Engineering,” McGraw Hill, New York, 2010[2] R. L. Fournier, “Basic Transport Phenomena in Biomedical Engineering,” Taylor & Francis, Philadelphia, 1999.
[3] S. M. Skinner, R. E. Clark, N. Baker, R. A. Shipley and Am. J. Physiolo, “Complete Solution of the Three Compartment Model in Steady State After Single Injection of Radioactive Tracer,” Institute of Physics in Association with the American, Vol. 196, 1959, pp. 238-244.
[4] F. Lundquist and H. Wolthers, “The Kinetics of Alcohol Elimination in Man,” Acta Pharmacol Toxicol, Vol. 14, 1958, pp. 265-289. doi:10.1111/j.1600-0773.1958.tb01164.x
[5] S. L. Beal, “Computation of the Explicit Solution to the Michaelis-Menten Equation,” Journal of Pharmacokinetics and Biopharmaceutics, Vol. 11, 1983, pp. 641-657. doi:10.1007/BF01059062
[6] K. R. Godfrey and W. R. Fitch, “On the Identification of Michaelis-Menten Elimination Parameters from a Single Dose-Response Curve,” Journal of Pharmacokinetics and Biopharmaceutics, Vol. 12, 1984, pp. 193-221. doi:10.1007/BF01059062
[7] S. Tang and Y. Xiao, “One-Compartment Model with Michaelis-Menten Elimination Kinetics and Therapeutic Window: An Analytical Approach,” Journal of Pharmacokinetics and Pharmacodynamics, Vol. 34, 2007, pp. 807-827. doi:10.1007/BF01059062
[8] O. Levenspiel, “Chemical Reaction Engineering,” John Wiley & Sons, New York, 1999.
[9] L. Michaelis and M. L. Menten, “Die Kinetik der Intertinwerkung,” Biochemische Zeitschrift, Vol. 49, 1913, pp. 333-369.
[10] H. S. Mickley, T. K. Sherwood and C. E. Reed, “Applied Mathematics in Chemical Engineering,” McGraw Hill Book Company, New York, 1957.
[11] Sir H. A. Krebs, “Citric Acid Cycle,” Nobel Prize Lecture, 1953. http://nobel.se
[12] K. R. Sharma, “Subcritical Damped Oscillatory Kinetics of Simple Reactions in Circle,” chemcon conferences, Bubanewar, India, December, 2003.
[13] Ans. Magna, “Solution to the Cubic Equation,” Renaissance Mathematics, pp. 1501-1576.
[14] A. Varma and M. Morbidelli, “Mathematical Methods in Chemical Engineering,” Oxford University Press, Oxford, UK, 1997.

