Received 16 September 2015; accepted 6 November 2015; published 9 November 2015

ABSTRACT

It is shown that when backorders, setup times and dynamic demand are included in capacitated lot sizing problem, the resulting classical formulation and one of the transportation formulations of the problem (referred to as CLSP_BS) are equivalent. And it is shown that both the formulations are “weak” formulations (as opposed to “strong” formulation). The other transportation version is a strong formulation of CLSP_BS. Extensive computational studies are presented for medium and large sized problems. In case of medium-sized problems, strong formulation produces better LP bounds, and takes lesser number of branch-and-bound (B&B) nodes and less CPU time to solve the problem optimally. However for large-sized problems strong formulation takes more time to solve the problem optimally, defeating the benefit of strength of bounds. This essentially is because of excessive increase in the number of constraints for the large sized problems. Hybrid formulations are proposed where only few most promising strong constraints are added to the weak formulation. Hybrid formulation emerges as the best performer against the strong and weak formulations. This concept of hybrid formulation can efficiently solve a variety of complex real life large-sized problems.

Keywords:

Capacitated Lot Sizing, Linear Relaxation, Strong Formulation, Hybrid Formulation, Branch-and-Bound

1. Introduction and Literature Survey

Researchers have extensively studied the lot sizing problem in last five decades, but finding an effective and practicable solution to this problem in real time remains to be a challenge faced by the production planners in a manufacturing setup. This was evident from our recent visit to a leading Indian automobile manufacturer, located in the southern part of the country. Nearly all versions of capacitated lot sizing problem are NP-Hard; and hence better heuristics are required for solution.

Even the basic model of single item capacitated lot sizing problem (CLSP) is well known to be NP Hard [1] . With the addition of setup times, the problem becomes so hard that even finding a feasible solution is NP complete [2] . Chen & Thizy [3] showed that even without considering setup times, just the inclusion of setup cost makes the lot sizing problem strongly NP Hard. Hence it becomes actually intricate to solve a CLSP with considerations of realistic situations like capacity, backorders, setup times, setup costs, setup carryovers, etc.

The focus of this work is on the capacitated version of the lot sizing problems; the readers are hence referred to [4] that extensively reviews various research done on CLSP. Karimi et al. [4] concluded that although lot sizing had been one of the favorite research areas in last few decades but still the realistic and practical variants of the CLSP, specially which considers backorders, setup times and setup carry-overs, had not received much attention. Also Quadt & Kuhn [5] gave an extensive review of the literature on the different extensions of the capacitated lot sizing problem. It is again evident from the review work of Quadt & Kuhn [5] that models with inclusion of backorders have received least attention in the past. Hence despite a common outlook that lot sizing is an over-researched problem, it still remains to be one of the preferred research areas; this again becomes apparent from the most recent works of [6] -[8] , to name only a few.

Apart from the classical (denoted by PC) formulation of CLSP given by [9] , CLSP is also modelled as the transportation problem (denoted by PT) type of formulation or plant location type of formulation [10] and the shortest path (denoted by PS) type of formulation [11] . Alfieri et al. [10] took up the relative analysis of the PC, PT and PS models; however their analysis did not consider setup times and backorders. Later Denizel et al. [12] added setup times to their model and verified the proposed relationship between strength of different types of formulations.

Multi-item multi-period capacitated lot sizing problem with dynamic demands, backorders and setup times (CLSP_BS) is considered in this work. Apart from the formulation PC, two PT formulations (PT^a and PT^b) of CLSP_BS are considered in this work; and the relative strength of these three formulations is investigated. This is important because it has an impact on the choice of model formulation and the corresponding solution procedure. Also as it is observed by Alfieri et al. [10] that although PT provides better lower bounds, it takes more computational time as compared to PC. Hence choosing an appropriate formulation to solve the lot sizing problem is critical. Chen & Thizy [3] and Barany et al. [13] did mathematical comparison of the Lagrangian and linear relaxations for the classical version of the multi-item CLSP. They however did not consider the variables of backorders and setup times in their model.

Limiting the size of the problem by selective inclusion of variables and constraints in different forms has been attempted and discussed by some researchers in the recent past. Tightening of the MIP using extended formulations drastically amplifies the size of the problem. Hence Van Vyve and Wolsey [14] developed approximate extended formulations, where in order to get a good quality lower bound, partial reformulations were applied. Through a control parameter the trade-off between strength and size of formulation is manipulated. They basically used a coefficient modification based heuristic algorithm within the branch-and-cut enumeration framework. Pochet and Wolsey [15] gave that adding a limited number of (l, S) inequalities to the regular formulation and to the backlogging extensions gave improved upper bounds or same bounds as the transportation formulation in the presence of Wagner-Whitin costs. Akartunali and Miller [16] dealt with the multi level single resource big bucket problem with extension to backlogging and used the cutting planes to tighten their formulation. Their flexible and easy heuristics generate multiple solutions and competitive lower bounds. A complete mathematical survey of the compact extended formulations applied into the combinatorial optimization problems is done very recently by Conforti et al. [17] . They provide some mathematical tools for studying the extended formulations. The minimum size up to which an extended formulation could be compacted was also devised.

An interesting concept of hybrid formulations is introduced in this work, where a small percentage of the most promising strong constraints are added to the weak PT formulation to note that the hybrid formulations swiftly produce better bounds than the weak formulation and gives optimal solution in least time as compared to weak or the strong formulations. Hence for the large sized problem instances, hybrid formulations actually are the best performers.

Here we provide the breakup of this paper. In Section 2, we provide the classical and two types of transportation formulations. The relationship between cost structures of the two formulations is also shown which makes the classical and transportation formulations equivalent. In Section 3, linear programming (LP) relaxations of the three types of formulations are proposed. Section 4 provides empirical investigations on medium sized problems to note the behavior of strong and weak formulations. In Section 5 we attempt the large sized problems and note a reverse behavior of strong and weak formulations. Hybrid formulations are then proposed, which is shown to be the best performer as against strong and weak formulations. We conclude in Section 6 by highlighting the important contributions of this work.

2. Formulations

Here we discuss the classical and two transportation formulations of CLSP_BS. Conversion of classical formulation to the transportation formulation is done using a relationship between the cost parameters and the variables. Note the difference in the names of variables and parameters used in this paper compared to that existing in the literature. An attempt has been made to simplify the notations; viz. starting all variable names with X and Y, parameters cost by C, time by T, etc.

2.1. Classical Formulation of CLSP_BS: “PC”

The standard formulation of CLSP available in the literature is extended to include the proposed variables and situations. Note suffix “PC” added to the parameters―inventory and backorder costs, indicating their association only with the classical formulation of the problem.

Index:

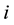: Item type,

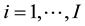
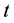: Planning period,

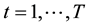
Variables:

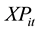: Number of items “i” to be produced during the period “t”

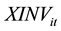: Number of items “i” carried as inventory at the end of period “t”

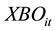: Number of items “i” that will be backordered from period “t”

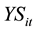: Binary variable for setup of the resource for item “i” during the period “t”

= 0 (if there is no setup required), 1 otherwise

Parameters:

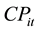: Unit cost of producing item “i” in period “t”

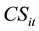: Unit cost of setup, for item “i” in period “t”

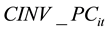: Unit cost of holding inventory of item “i” in period “t”.

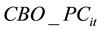: Unit cost of backordering item “i”, that was demanded during the period “t”

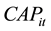: Capacity available to produce item “i” during the period “t”

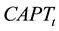: Capacity available in time units, in a period “t”

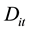: Demand of item “i” during the period “t”

: Time required to process the item “i”

: Time required to setup the production for item “i”

: Minimize

(1)

Subject to:

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(1) the objective of the problem, is to minimize the cost of production, setup, inventory and backlogging, summed over all items and time periods. (2) is the inventory balance constraint for each item and period. (3) is the time capacity limiting constraint, which ensures that the total time utilized in doing production and setups can atmost be equal to the maximum time available in any period. (4) is the production capacity constraint, ensuring the production quantity to be always less than or equal to the maximum production capacity available for all items and periods. (5) restricts non negativity over the production quantity and the quantity of items carried as inventory and backorders. (6) and (7) forces the initial and final inventory and backorders to be zero. (8) forces the setup variable to be binary for all items and for all the periods.

2.2. Transportation Formulation of CLSP_BS: “PT”

CLSP_BS can be reshaped using variable redefinition technique, in the form of a transportation problem. Note the suffix “PT” with the cost parameters in this formulation. Two versions of CLSP_BS (PT^a and PT^b) are presented in the following sub-sections.

Index:

: Item type,

, : Planning period;;

Variables:

: Number of items “i” produced in period “t” to satisfy demand of period “r”

: Binary variable for setup of the resource for item “i” during the period “t”

= 0 (if there is no setup required), 1 otherwise

Parameters:

: Unit cost of holding inventory of item “i” from period “t” to period “r”; (r ≥ t).

: Unit cost of backordering item “i”, which is produced in period “t”, but was required at period “r”; (r ≤ t).

: Demand of item “i” during the period “r”

2.2.1. Transportation Formulation 1 [PT^a]

PT^a: Minimize

(1a´)

Subject to:

(2´)

(3´)

(4´)

(5´)

and (8).

(1´) defines the objective seeking to minimize the cost of production, setup, inventory and backorders summed over all items and time periods. (2´) is the demand constraint ensuring production during the planning horizon to satisfythe demand of period “r”. (3´) limits the sum of production and the setup times to at most be equal to the maximum time available during the planning horizon. (4´) ensures that the maximum production is equal to the capacity available for all the items and periods. (5´) imposes a non-negativity on the variable.

2.2.2. Transportation Formulation 2 [PT^b]

A new constraint is defined here, considering the fact that the production of any item “i” in any period “t” to satisfy its demand of period “r” can at most be equal to the demand. This can be written mathematically as:

(6´)

This constraint also ensures a setup (and hence a probable production) in “t” to satisfy the demand of “r”. In formulation PT^b, we simply add (6´) to the formulation PT^a as follows:

PT^b: Minimize

(1b´)

Subject to: (2´)-(6´) and (8).

It is observed that constraint (6´) is mostly used in the literature where capacitated lot sizing problem is modeled as a transportation problem. But in presence of (2´) and (4´), which takes care of the demand and setup respectively, actually (6´) is not required. Soas brought in the later part of this paper (Section 4, Table 3), same objective value is obtained by solving PT^a and PT^b. (6´) being a strong constraint, its inclusion in the problem should be beneficial in terms of bounds. That is, relaxation of PT^b is expected to produce better bounds than that of PT^a. This behavior will be analyzed in the next sections.

2.3. Equivalence of Costs

Note that the costs defined in this work are general to also accommodate different setup cost for the same item in different periods; or different production cost for the same item in different periods, etc. Though such costs may not actually occur, but any such possibility is accounted for in the model. To generate inventory and the backorder costs for the transportation formulation, following relations are used:

for; and for (9)

for; and for (10)

3. Relaxations

3.1. Relaxations of Classical Formulation PC

In PC, when we relax the binary constraint to vary continuously between zero and one, we have its linear programming (LP) relaxation PC_r. Mathematically:

(11)

PC_r: Minimize (1); subject to: (2)-(6), (7) and (11).

3.2. Relaxations of Transportation Formulation

Again in the transportation formulation of the CLSP_BS when we relax the binary constraint to vary continuously between zero and one, it is referred to as a linear programming (LP) relaxation. Mathematically this is denoted by (11).

The LP relaxation may be referred to as: Minimize (1); subject to: (2´)-(5´) and (11). Also, the LP relaxation is referred to as: Minimize (1); subject to: (2´)-(6´) and (11).

4. Computational Experiences and Analysis

4.1. Experimental Setup

Here we perform empirical investigations on the randomized data sets, for the three formulations―PC, PT^a and PT^b. The experimental set up and the procedure, along with results and analysis is detailed in this section. A variety of small and large problem sizes―10 × 10 [(number of items) × (number of time periods)], 20 × 10, 10 × 20, 20 × 20 is considered. Number of binary variables for these problems is of the order O (I × T), I and T being the number of items and number of time periods in the planning horizon respectively. For each of these sizes, we solved 50 problem sets, each set containing a binary formulation and an LP relaxation of the classical and two types of transportation formulations. Experiments are performed using CPLEX 10.0 solver of GAMS 22.3 on a standalone 2.79 GHz core 2 Duo CPU with 1.96 GB RAM.

4.2. Creating Test Instances

The cost parameters used in the two formulations (PC and PT) are generated randomly, taking general guidance on generating random problems from the standard literatures viz. [18] -[20] and [5] the details of which is provided in this sub-section. We choose uniform distribution to generate parameters as this is traditionally used in the literature indicated above. Table 1 states the range of values of different parameters that are taken to form the random problems.

Inventory and backorder costs for the transportation formulation are calculated using Equations (9) and (10) respectively. As evident from the table that backorder costs is assumed to be higher than inventory carrying costs, as backorder cost also account for the loss of goodwill for the customer who could not be instantly served. It also implies that our model is comparatively more open to carry inventory, compared to incur backorders, as prompt satisfaction of the demand is primarily important in today’s competitive environment. The relation between demand and production capacity can also be stated in terms of tightness factor, which can be defined as the ratio of average periodic demand and production capacity. For an uncapacitated problem the value of tightness factor will be 0; while for the case when required capacity (demand) is exactly equal to the available capacity, the tightness factor is 1. For the data considered here, the tightness factor is about 0.8, which is rigid enough to produce some infeasible problems; such infeasible problems are eliminated from the problem sets.

4.3. Order of Problem

In four sizes of problems considered the number of binary variables is of the order (IT), the order of continuous variables in classical formulation PC is (3IT) and that of continuous variables in the transportation formulations is (IT²). Similarly, while the number of constraints in classical and PT^a transportation formulation is (2IT + T), the number of constraints in the PT^b swells to (IT² + 2IT + T). Hence as the problem size grows, number of variables and constraints increase accordingly.

4.4. Analysis of Results

Table 2 shows the average time taken by the different formulations and their LP relaxations. One may note that as the problem size increases computational time increases for all formulations and their relaxations. This table is provided here just to give a general idea to the reader about the computational time taken to solve a particular formulation or its relaxation. In order to actually compare the formulations and their relaxations on different

aspects, we perform a t-test the result of which is shown in the next tables.

In Table 3, for all the problem sizes we compare (using t test) different characteristics of PC with PT^a, and also those of PT^a with PT^b formulation. Parameters on which formulations are compared are the optimal values obtained by each of these formulations, the CPU time taken to obtain these optimal values, number of nodes traversed in the branch-and-bound (B&B) tree to reach this optimal value, the objective values of LP relaxation of the formulations, and CPU time taken to calculate the LP relaxation. Note that in Table 3, against the row comparing PT^a-PC, “Optimal” or “LP bounds” is the “t” calculated for difference between objective values of (PT^a/PC) and 1; and “CPU time” is the “t” calculated for difference between (CPU time for PT^a/CPU time for PC) and 1. Similarly for the parameter “B&B nodes”.

Note from Table 3 that for all the problem sizes considered, the optimal values obtained from the three formulations PC, PT^a and PT^b are all the same. Hence these formulations are actually the three ways to formulate the same problem. For all problem sizes, PT^a take more computational time, compared to PC.

Before moving on to compare the CPU times taken to calculate optimal values for PT^a and PT^b, note the significance of their LP bounds. Note that the objective value obtained by the LP relaxation of PC and PT^a are exactly the same, but there is a significant difference between LP bounds of PT^a and PT^b. For all problem sizes, PT^b invariably produces better (larger) LP bounds as compared to the PT^a. This is the reason of earmarking PT^b as the strong formulation and PT^a as the weak formulation of CLSP_BS.

As PT^b is a strong formulation rendering better LP bounds, it is able to calculate the optimal values in significantly less number of B&B nodes, invariably for all problem sizes. The significance level for the better LP bounds and lesser B&B nodes, both increases as the problem size increases, implying that the strength of a formulation is realized more for the larger problem sizes, hence useful for the practical lot sizing problems. t values indicate that LP relaxation of PC is solved faster than that of PT^a. This is the reason why computation of optimal solution takes significantly large time for PT^a and lesser time for PC, because quality of LP bounds is the same in both cases. However LP relaxation of PT^b takes more time to solve as compared to PT^a, but still PT^b is solvable optimally in significantly better CPU times than PT^a, because of the better quality bounds of PT^b than PT^a.

5. Hybrid Formulations

5.1. Large Sized Problems

We observed in the previous section that strong formulation PT^b produce better bounds than the weak formulation PT^a and hence CLSP_BS is optimally solvable in lesser number of B&B nodes and lesser CPU time by the formulation PT^b, compared to PT^a. In previous section, medium sized problems where the largest one of size 20 × 20 (with 400 binary variables) were solved. In order to perform a test on yet large sized problems, 50 sets for each of the four sizes―50 × 10, 50 × 20, 100 × 10 and 100 × 20 are solved. These problem instances are again solved using CPLEX 10.0 solver of GAMS 22.3 on a standalone 2.79 GHz Core 2 Duo CPU with 1.96 GB RAM.

5.2. Initial Analysis and Motivation for Hybrid Formulation

In Table 4 we note the average time taken by the different formulations and their LP relaxations. Note that the problem size 50 × 10 was solvable in a few seconds. However for the other 3 sizes, the number of variables increases 2 and 4 times respectively and hence CLSP_BS being an NP-hard problem the solver got out of memory after running for a few hours, while attempting to reach optimality. A small duality gap of 0.1% as the stopping criteria is introduced for the three large sizes―100 × 10, 50 × 20, and 100 × 20. These sizes were then solvable in a few seconds after the introduction of duality gap. One may note that as the problem size increases computational time increases for all formulations and their relaxations. This table is provided here just to give a general idea to the reader about the computational time taken to solve a particular formulation or its relaxation. In order to actually compare the formulations and their relaxations on different aspects, we perform a t-test the result of which is shown in the next tables.

In Table 5, for all problem sizes we compare different characteristics of PC with PT^a and also PT^a with PT^b. PT^H is the hybrid formulation, which will be discussed in Section 5.4. For problem size 50 × 10, the quality of LP bounds of PT^b are so good that despite its LP relaxation taking longer time to get solved, PT^b is optimally solved in lesser number of nodes and lesser CPU time as compared to the formulation PT^a.

However the same does not remain true for the larger sizes 50 × 20, 100 × 10 and 100 × 20. Now the CPU time taken to solve LP relaxation of PT^b takes much more time as compared to that of PT^a (apperent from the increased t-values). The quality of bounds remain to be good for PT^b as against PT^a. Due to this, while PT^b is optimally solvable in lesser number of nodes, it takes larger CPU time as compared to the problem PT^a. So the advantage of using a strong formulation, which was apparent for the medium sized problems, seems to have lost.

5.3. Most Promising Strong Constraints (MPS_Constr)

We develop a new set of strong demand constraints to tackle the problem of huge computational times taken by the LP relaxations of the strong constraints. New sets of modified demand constraint were built using the following procedure. To make a hybrid formulation, we add some percentage of most promising strong constraints to the weak formulation. But to decide the appropriate percentage of the total strong constraints, we varied it from 20% to 10% to 5% etc. In each such step, the bounds obtained by LP relaxation were observed to deteriorate; but there was a significant improvement in computational time for solving the LP relaxations of the hybrid formulation. After some iterations of trial and error, 5% of the strongest constraints were selected to be added to the weak formulation of CLSP_BS for making hybrid formulations. At this level, the bounds were only a little inferior, but LP relaxations took substantially less computational time, which significantly improves the overall computational times for solving the problem.

Building MPS_Constr

Sort the strong constraints in increasing order of demand. Set cut off number N = INT (0.05*K), where K is number of demand points (=ixr). Let the demand associated with this number N be. Prepare a set of most promising demands (MPD) =. Now, MPS_constr =.

5.4. Hybrid Formulation and Relaxation

Hybrid formulation of CLSP_BS, referred here as PT^H is described as follows:

PT^H: Minimize (1a´); Subject to (2´)-(5´), (8) and MPS_constr.

The constraint (8) can be replaced with (11) in the above formulation to get the LP relaxation as follows:

: Minimize (1a´); Subject to (2´)-(5´), (11) and MPS_constr.

5.5. Empirical Investigation for Hybrid Formulations

Here we provide results to verify the efficacy of hybrid formulation against strong and weak formulations. On the same experimental setup and problem-sets that were attempted in Section 5.2, for the sizes―50 × 20, 100 × 10 and 100 × 20, we solve hybrid formulation and its LP relaxation. Comparison of bounds, nodes and computational time given by hybrid formulation is compared with that of the strong and weak formulations using t-test.

Table 5 provides the comparison of hybrid formulation with PT^a and PT^b for the three larger sizes 50 × 20, 100 × 10 and 100 × 20. While strong formulation PT^b is optimally solvable in lesser number of B&B nodes than PT^a, it takes longer time to get solved because LP relaxation of PT^b takes longer CPU time than that of PT^a. is shown in Table 5. Note from the significant t values that hybrid formulation is the best performer in terms of computational time, when compared with strong and weak formulations.

As compared to PT^a, hybrid PT^H gives better LP bounds and optimally solves the problem in lesser B&B nodes and lesser CPU times. When compared to PT^b, PT^H generates inferior LP bounds but solves the problem optimally in lesser CPU time. The reason of this behavior is that although LP bounds of hybrid formulation are inferior (due to which PT^H has to traverses more number of B&B nodes), but its bounds at each node are obtained significantly quicker than the bounds of the strong formulation. This all is evident from the t values given below.

The primary reason because of which LP relaxation of strong formulation takes large computational time is heavy increase in the number of constraints, as its size grows beyond a level. While number of constraints in PT^a remains 2010, 2020 and 4020, it hugely swells to 12,010, 22,020 and 44,020 respectively in case of PT^b. More are the number of constraints, larger the time taken to solve the problem. Through the concept of hybrid formulations we try to limit the increase in number of constraints, while at the same time take the benefit of strongest constraints. Hence there is a modest increase in number of constraints for PT^H compared to PT^a, but sweeping decrease in number of constraints as against PT^b.

6. Conclusions

This work has attempted to cater to a variant of multi-item multi-period CLSP, which considers dynamic demand, backorders and setup times (CLSP_BS). Apart from considering a practically important variation of CLSP, the generality of the cost structure increases the applicability of this model into a variety of real life situations. A classical formulation and two transportation (strong and weak) formulations of this problem are compared.

The main emphasis of this work is the introduction of hybrid formulation of CLSP_BS, which is proved to be the best performer. It was observed that for large sized instances of CLSP_BS, strong formulation took lesser number of branch-and-bound nodes but more CPU time to optimally solve the problem, compared to the weak formulations. The reason of this behavior is an extreme increase in number of constraints for the strong formulation, due to which solving LP relaxation at each B&B node becomes time intensive. Hence despite obtaining better bounds and the problem getting solved in lesser number of B&B nodes, the problem actually takes longer time to get solved optimally. In hybrid formulation, we add few strongest constraints to the weak formulation, so that the quality of bounds of the strong formulation is retained while maintaining lesser number of constraints to obtain optimal solution faster. In this way, better characteristics of both strong and weak formulations are retained in the hybrid formulation. This concept of hybrid formulations can prove to be very efficient in solving the real life large sized problem instances in a variety of applications.

Cite this paper

MayankVerma,Renduchintala RaghavendraKumar Sharma, (2015) Hybrid Formulation of the Multi-Item Capacitated Dynamic Lot Sizing Problem. American Journal of Operations Research,05,503-513. doi: 10.4236/ajor.2015.56039

References

NOTES

^*Corresponding author. Current Affiliation: Atomic Energy Regulatory Board, Mumbai, India.