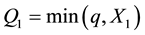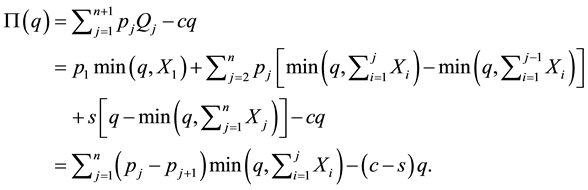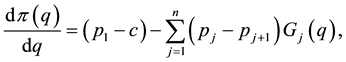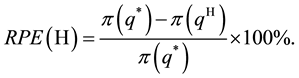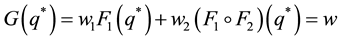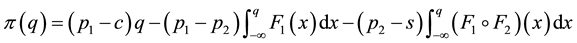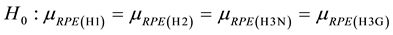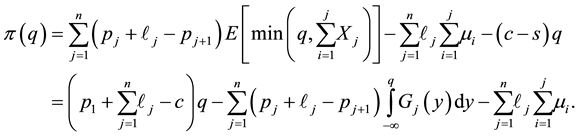American Journal of Operations Research
Vol.05 No.05(2015), Article ID:58900,9 pages
10.4236/ajor.2015.55027
A Newsvendor with Priority Classes and Shortage Cost
Bo Li1, Pillaiboothamgudi Sundararaghavan2, Udayan Nandkeolyar2*
1Ashland University, Ashland, OH, USA
2University of Toledo, Toledo, OH, USA
Email: bli@ashland.edu, p.sundararaghavan@utoledo.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 May 2015; accepted 16 August 2015; published 19 August 2015
ABSTRACT
We consider an extension of the standard newsvendor problem by allowing for multiple classes of customers. The product is first sold to customers with the highest priority, and the remaining units (if any) are sold at a discounted price to customers in decreasing order of priority until all classes of customers have been served, limited only by the available stock. Unsold items, if any, have a salvage value. The demands of different priority customers are independent random variables with known probability distributions. The problem is to find the purchase quantity that maximizes the expected profit. We show that this problem actually reduces to the standard newsvendor problem with the demand distribution being a mixture of the input demand distributions. Since this mixture of distributions is typically hard to handle analytically, we propose a simple general heuristic which can be implemented using different types of distributions. Some of these implementations produce near optimal solutions. We tested these implementations for the case of two demand classes of customers and found that they outperform previously published heuristics in almost all instances. We suggest applications for this model in the Chinese pharmaceutical industry, apparel industry, and perishable goods among others. We also propose an extension involving shortage cost.
Keywords:
Newsvendor Problem, Priority Demand Classes, Mixture Distribution, Heuristics

1. Introduction
Arrow et al. [1] and Morse and Kimball [2] were the first who formulated and solved the single-period, single- item stochastic inventory problem also known as the newsvendor or newsboy problem. Given one period as a planning horizon, relevant unit parameters such as purchasing cost c, selling price p, salvage value s, and the cumulative distribution function (CDF) F of random demand, the problem is to find the order quantity that maximizes the expected profit. This optimal quantity was found to be the smallest q for which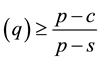 .
.
There have been many extensions to the newsvendor problem [3] . The extension studied in this paper assumes n classes of customers, and is in the spirit of the model introduced by Şen and Zhang [4] . In general, the product is sold for 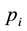 to the ith class of customers before the remaining units (if any) are sold at a discounted price
to the ith class of customers before the remaining units (if any) are sold at a discounted price 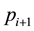 to the (i + 1)th class of customers. Thus, the newsvendor sells newspapers starting at the highest price location, and will move to the next highest price location after meeting the realized demand at the current location. For example, the price charged in the morning is higher than that in the afternoon. The model we examine is common, for example, in the apparel industry and retailing of perishable goods where discounts are used to sell excess inventory; see [5] [6] . We have also found an interesting potential application from our study of the Chinese pharmaceutical supply chain. In this supply chain, there are two classes of customers: hospitals and pharmacies. The demand of hospitals is expected to be met first, and the remaining units are sold to pharmacies at a lower price. Drugs may be considered similar to perishable products since distributors generally like to sell out each batch rather than carry forward inventory because of the proximity of expiry dates. Also items such as flu shots which are supplied only once a year are never carried forward.
to the (i + 1)th class of customers. Thus, the newsvendor sells newspapers starting at the highest price location, and will move to the next highest price location after meeting the realized demand at the current location. For example, the price charged in the morning is higher than that in the afternoon. The model we examine is common, for example, in the apparel industry and retailing of perishable goods where discounts are used to sell excess inventory; see [5] [6] . We have also found an interesting potential application from our study of the Chinese pharmaceutical supply chain. In this supply chain, there are two classes of customers: hospitals and pharmacies. The demand of hospitals is expected to be met first, and the remaining units are sold to pharmacies at a lower price. Drugs may be considered similar to perishable products since distributors generally like to sell out each batch rather than carry forward inventory because of the proximity of expiry dates. Also items such as flu shots which are supplied only once a year are never carried forward.
The main theoretical result of this paper is that the newsvendor problem with multiple demand classes characterized by decreasing prices actually reduces to the standard newsvendor problem with the demand distribution being a mixture of the input distributions, the selling price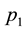 , the unit cost c, and the salvage value s. Since typically this mixture distribution does not have a closed analytical form, we propose a general heuristic that replaces it by a more tractable distribution with the same first two moments. We demonstrate that some implementations of this general heuristic produce near optimal solutions, and they significantly outperform the heuristics reported in the literature. We also present some extensions of the studied problem that involve shortage penalties and the case when only the means and the standard deviations of random demands are known [7] .
, the unit cost c, and the salvage value s. Since typically this mixture distribution does not have a closed analytical form, we propose a general heuristic that replaces it by a more tractable distribution with the same first two moments. We demonstrate that some implementations of this general heuristic produce near optimal solutions, and they significantly outperform the heuristics reported in the literature. We also present some extensions of the studied problem that involve shortage penalties and the case when only the means and the standard deviations of random demands are known [7] .
The paper is organized as follows. In Section 2, we provide some additional motivations related to the main problem addressed in this paper, and in Section 3 we formulate the problem and show its reduction to the standard newsvendor problem. In Section 4, we describe our proposed heuristics; their performance is empirically examined in Section 5. Section 6 indicates some extensions to the problem, while Section 7 presents some concluding remarks.
2. Motivation
First, we discuss the motivation generated by the practices we gleaned through our recent survey of the Chinese Pharmaceutical industry in Central China. Generally, the customers of a pharmaceutical distributor in China are classified into two types: Hospitals (including clinics) and retail pharmaceutical franchisees (Pharmacies). In China, hospitals and pharmacies are separate and both play important roles in the Pharmaceutical Supply Chain [8] [9] . Hospitals are the high-end customers to the Distributor, and the pharmacies represent the low-end segment. The State Drug & Food Administration holds an annual bidding conference for matching distributors in a region with medicines and the hospital network. At the end of the conference, every high volume medicine is assigned to a distributor exclusively for supplying all hospitals in the region at a fixed price for the entire year. Typical profit margin for the distributor selling to hospitals is around 15%. Each distributor is free to purchase any medicine from manufacturers or wholesalers, but they cannot supply to hospitals unless they have exclusive rights earned in the annual bidding process. The supply chain from manufacturer to distributor to hospitals is tightly regulated and has higher profit margin and monopolistic pattern for each medicine. However, the supply chain from manufacturer to wholesaler to distributors to pharmacies is loosely organized with both supply and price flexibility at the purchasing and selling end for each player. Typically, pharmacies offer lower profit margins, around 8%, because of significant competition from the supply and demand sides. These are governed by market forces. There are pharmaceuticals which are produced only once a year due to their seasonal nature of demand (such as flu shots) or due to constraints on expiry dates. From the perspective of the pharmaceutical distributor, this situation can be modeled as a problem of finding the order quantity given two types of customers with fixed prices (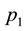 and
and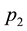 ) and
) and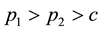 , where c is the unit cost.
, where c is the unit cost.
This model is also applicable for annual order placements by US manufactures to their Asian contract manufactures for apparels and fashion items, as well as for the general purchase of perishable items by the organizations which have multiple classes of customers with fixed known prices.
3. Main Theoretical Result
The general newsvendor problem with decreasing priority demand classes of customers can be formulated as follows. A product with a unit cost of c is sold to n classes of customers in a sequential order. It is sold first to the first class of costumers at a price of , next (if any units left) to the second class of customers at a price of
, next (if any units left) to the second class of customers at a price of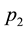 , and so on until the last class characterized by the price
, and so on until the last class characterized by the price 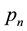 can be served. Any unsold units have a salvage values, and
can be served. Any unsold units have a salvage values, and 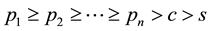 is assumed. For
is assumed. For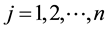 , let
, let 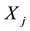 be the random demand of the jth class of customers and
be the random demand of the jth class of customers and 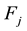 be its CDF. The random variables
be its CDF. The random variables 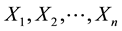 are independent and, without loss of generality, they are assumed to be continuous. If
are independent and, without loss of generality, they are assumed to be continuous. If 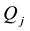 and
and 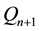
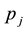
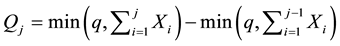
Therefore, letting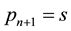
Since for any random variable Y whose CDF G has a finite mean,

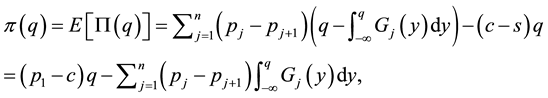
where 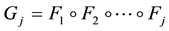
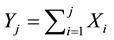
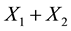
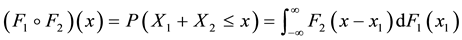
The first derivative of 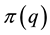
and the second derivative is obviously non-positive. Therefore, the expected profit 
the optimal purchase quantity q* is a solution to the equation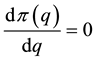
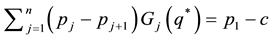
Letting now 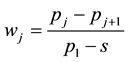
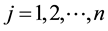
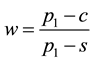
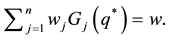
Since 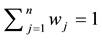
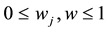
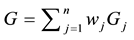
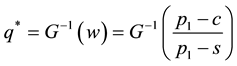
the newsvendor problem with n decreasing priority demand classes of customers actually reduces to the standard newsvendor problem with the demand CDF G, the unit selling price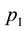
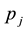
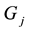

4. Heuristics
Şen and Zhang [4] proposed the following two heuristics, whose idea is to replace the original problem by some standard newsvendor problems:
H1. Define the standard newsvendor problem with the demand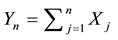
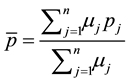
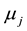

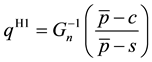
H2. Solve separately n standard newsvendor problems with the demands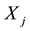
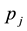
up the obtained purchase quantities. Thus,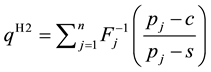
We have shown above that the problem under study can be reduced to a specific standard newsvendor prob-
lem, and the optimal purchase quantity is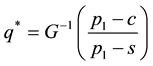
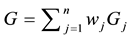
CDF G cannot be assumed to have a closed analytical form, and hence its inverse 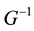
mined. Also, the equation 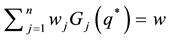
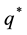
Therefore, the use of heuristics is fully justified. Although G is hard to handle, its moments (around zero) are
easily determined. Clearly, if 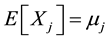
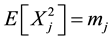
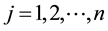
G are:
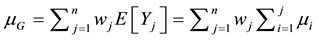
and

We propose a general heuristic named H3, which can be implemented by replacing the mixture CDF G by a more tractable CDF 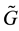

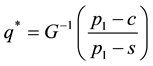
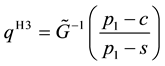

we developed four implementations of H3, named H3N, H3L, H3G and H3W, in which 
5. Computational Results
For a given heuristic H that yields the purchase quantity
For every conducted experiment, we computed the average and maximum relative percentage errors ARPE (H) and MRPE (H).
We have limited our experiments to the case n = 2, though they are easily extendable to any value of n. The demands 
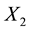
All numerical computations were performed using MS Excel. The optimal purchase quantity 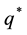
to which (3) is reduced for n = 2. Excel Solver was also used to determine 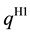
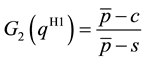
case of exponentially distributed demands. For normally distributed demands, we employed Excel function NORM.INV to find both 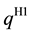
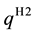
Whenever the expected profit,
(assume n = 2 in (1)) could not be analytically determined, we applied the Simpson method for approximating
the integrals 
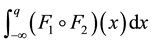
5.1. Instances of Şen and Zhang [4]
We reconsidered the 240 instances defined in Şen and Zhang [4] . In their work, the demands 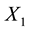
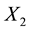
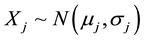
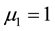
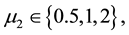
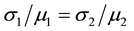
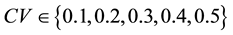

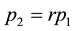
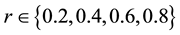
It should be added here that the presented errors are strongly biased upward by some rather unrealistic instances for which
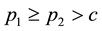
We found that in general the heuristics H3N and H3G with normal and gamma distributions for 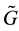
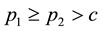
Table 1. The results on Şen and Zhang [4] instances.
5.2. Simulation Experiments
In all of our simulation experiments, it is assumed that there are only two classes of customers and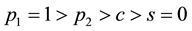
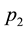
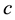
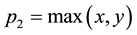
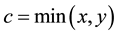

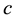
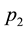
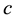
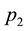
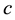
In order to have comparable results, we used the same 100 mean demands 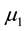
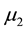
Let be the mean relative percentage error induced by heuristic H for a particular simulation experiment conducted on 100 problem instances. We are interested in testing the following null and alternative hypotheses:
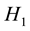
Since all of the heuristics are applied on the same instances, we have a dependent (matched) sampling. We tried to apply the ANOVA test for a randomized block design. Unfortunately, we were unable to verify the needed normality assumptions in any of the simulation experiments. Consequently, we turned to the non-para- metric Friedman test followed by the non-parametric HSD (honestly significance difference) Tukey’s test. For each simulation experiment, the null hypothesis stated above was rejected by Friedman’s test with a p-value of virtually zero in all of the 21 experiments. Therefore, below we present only the results of Tukey’s multiple comparison test conducted at a 5% significance level. For example, the notation 
First, we consider normally distributed demands 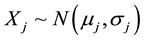

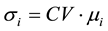
Next, we consider uniformly distributed demands X1 and X2with means μ1 and μ2,and the same range 2d.
Since the coefficient of variation for the uniform distribution on the interval 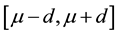
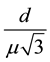
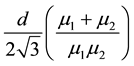

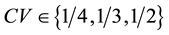
Table 2. The results on Dataset 1 for normally distributed demands.
Table 3. The results on Dataset 2 for normally distributed demands.
Table 4. The results on Dataset 3 for normally distributed demands.
are presented in Tables 5-7. It may be noted that H3N dominates all other heuristics for all datasets and CV values reported. H3G falls in the best performing heuristics group in all but three cases.
Finally, we consider exponentially distributed demands X1 and X2 with means 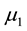
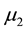
6. Extensions
In the standard newsvendor problem, no shortage cost is assumed if the purchased quantity is less than the demand. Although this cost might be difficult to define in practice, the authors of [7] and [10] assumed a known unit lost sales (shortage) cost of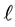
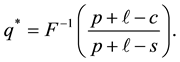
Table 5. The results on Dataset 1 for uniformly distributed demands.
Table 6. The results on Dataset 2 for uniformly distributed demands.
Table 7. The results on Dataset 3 for uniformly distributed demands.
Table 8. The results on Datasets 1, 2 and 3 for exponentially distributed demands.
Consequently, the optimal purchase quantity 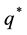

where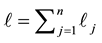
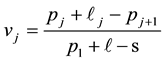
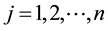
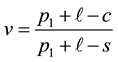
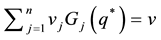
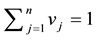
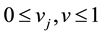
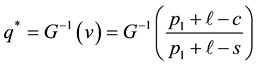
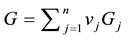
creasing priority demand classes and the shortage penalties reduces to the standard newsvendor problem with the demand CDF G, the selling price
We assumed so far that the demands 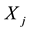
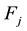
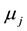
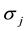
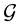
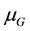
deviation 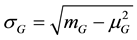

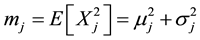
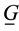


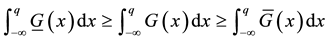
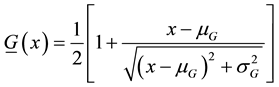
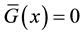
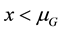
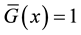
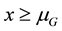
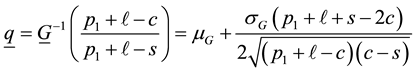
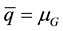
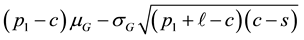
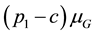
The quantities 
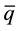


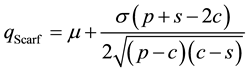
7. Conclusions
We reconsidered the Şen and Zhang [4] extension of the standard newsvendor problem with multiple classes of demand with decreasing selling prices. We showed that this extension actually reduces to the standard newsvendor problem with the demand distribution being a mixture of the input distributions, the selling price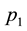
The two heuristics along with the two from previous work [4] were tested across different demand distributions and price/cost structures. This resulted in a total of 2100 problem instances that were solved using an exact algorithm and the four heuristics. In general, at least one of our heuristics produced a near optimal solution and was statistically proved to outperform the two heuristics proposed in Şen and Zhang [4] . Additional studies are needed to provide strict guidelines on the types of demand distributions for which a particular implementation of our heuristic (H3N or H3G) performs better. One can see a direct application of this model in determining order quantity for some Chinese pharmaceuticals which are ordered once a year or other applications such as annual orders for winter jackets and one time orders for perishables.
The reduction of the newsvendor problem with decreasing priority demand classes to the standard newsvendor problem revealed in this paper, remains valid when penalties are imposed for not meeting the demands. This reduction is also very useful in the case of incomplete probabilistic information about the demand distributions. In particular, we showed extensions of Scarf’s ordering rule when the means and standard deviations of random demands are the only parameters available. Additional studies are needed to consider different assumptions concerning the demands whose distributions cannot be fully specified. For example, the work of [10] seems to provide new opportunities in this matter.
Acknowledgements
We would like to thank Prof. Jerzy Kamburowski for his significant contributions to Sections 3 and 6.
Cite this paper
BoLi,PillaiboothamgudiSundararaghavan,UdayanNandkeolyar, (2015) A Newsvendor with Priority Classes and Shortage Cost. American Journal of Operations Research,05,337-346. doi: 10.4236/ajor.2015.55027
References
- 1. Arrow, K.J., Harris, T. and Marschak, J. (1951) Optimal Inventory Policy. Econometrica, 19, 250-272.
http://dx.doi.org/10.2307/1906813 - 2. Morse, M.P. and Kimball, G.E. (1951) Methods of Operations Research. M.I.T. Press, Cambridge, MA.
- 3. Qin, Y., Wang, R., Vakharia, A.J., Chen, Y. and Seref, M.M.H. (2011) The Newsvendor Problem: Review and Directions for Future Research. European Journal of Operational Research, 213, 361-374.
http://dx.doi.org/10.1016/j.ejor.2010.11.024 - 4. Sen, A. and Zhang, A.X. (1999) The Newsboy Problem with Multiple Demand Classes. IIE Transactions, 31, 431-444.
http://dx.doi.org/10.1080/07408179908969846 - 5. Khouja, M. (1995) The Newsboy Problem under Progressive Multiple Discounts. European Journal of Operational Research, 84, 458-466.
http://dx.doi.org/10.1016/0377-2217(94)00053-F - 6. Chung, K.-J., Ting, P.-S. and Hou, K.-L. (2009) A Simple Cost Minimization Procedure for the (Q,r) Inventory System with a Specified Fixed Cost per Stockout Occasion. Applied Mathematical Modelling, 33, 2538-2543.
http://dx.doi.org/10.1016/j.apm.2008.08.023 - 7. Alfares, H.K. and Elmorra, H.H. (2005) The Distribution-Free Newsboy Problem: Extensions to the Shortage Penalty Case. International Journal of Production Economics, 93-94, 465-477.
http://dx.doi.org/10.1016/j.ijpe.2004.06.043 - 8. Hu, J., Dai, Y. and Gu, K. (2010) Pharmaceutical Supply Chain in China: Challenges and Opportunities. CAPS Research: Institute for Supply Management and Carey School of Business at Arizona State University, 81.
- 9. Meng, Q., Cheng, G., Silver, L., Sun, X., Rehnberg, C. and Tomson, G. (2005) The Impact of China’s Retail Drug Price Control Policy on Hospital Expenditures: A Case Study in Two Shandong Hospitals. Health Policy and Planning, 20, 185-196.
http://dx.doi.org/10.1093/heapol/czi018 - 10. Perakis, G. and Roels, G. (2008) Regret in the Newsvendor Model with Partial Information. Operations Research, 56, 188-203.
http://dx.doi.org/10.1287/opre.1070.0486 - 11. Müller, A. and Stoyan, D. (2002) Comparison Methods for Stochastic Models and Risks. John Wiley & Sons, Hoboken.
- 12. Scarf, H. (1958) A Min-Max Solution of an Inventory Problem. In: Studies in the Mathematical Theory of Inventory and Production, Stanford University Press, Redwood City, CA, 201-209.
- 13. Gallego, G. and Moon, I. (1993) The Distribution Free Newsboy Problem: Review and Extensions. Journal of the Operational Research Society, 825-834.
http://dx.doi.org/10.1057/jors.1993.141
NOTES
*The author has passed away.