American Journal of Operations Research
Vol.05 No.03(2015), Article ID:55840,16 pages
10.4236/ajor.2015.53010
Developing Strong and Hybrid Formulation for the Single Stage Single Period Multi Commodity Warehouse Location Problem: Theoretical Framework and Empirical Investigation
R. R. K. Sharma, Parag Tyagi, Vimal Kumar, Ajay Jha
Department of Industrial & Management Engineering, IIT, Kanpur, India
Email: rrks@iitk.ac.in, tparag@iitk.ac.in, vimalkr@iitk.ac.in, ajjha@iitk.ac.in
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 March 2015; accepted 20 April 2015; published 21 April 2015
ABSTRACT
We note that the Single Stage Single Period Multi Commodity Warehouse Location Problem (SSSPMCWLP) has been first attempted by Geoffrion and Graves [1] , and that they use the weak formulation (in context of contribution of this paper). We give for the first time “strong” formulation of SSSPMCWLP. We notice advantages of strong formulation over weak formulation in terms of better bounds for yielding efficient Branch and Bound solutions. However, the computation time of “strong” formulation was discovered to be higher than that of the “weak” formulation, which was a major drawback in solving large size problems. To overcome this, we develop the hybrid strong formulation by adding only a few most promising demand and supply side strong constraints to the weak formulation of SSSPMCWLP. So, the formulations developed were put to test on various large size problems. Hybrid formulation is able to give better bound than the weak and takes much less CPU time than the strong formulation. So, a kind of trade off is achieved allowing efficiently solving large sized SSSPMCWLP in real times using hybrid formulation.
Keywords:
SSUWLP, SSSPMCWLP, Strong and Weak Constraints, Hybrid Formulation, RMIP

1. Introduction and Literature Survey
Warehousing is a key component of today’s business supply chain. It is not just a place to store finished goods but involves various value added functions like consolidation, packing and shipment of orders to customers. Organizations produce several commodities at various manufacturing sites, and generally it is not economical to get these commodities directly from plants to markets owing to distant market locations, associated demand disparities and uncertainties. Therefore, warehouses are installed at various locations between plants and markets to consolidate the localized customer demand. There can be more than one stage of the warehouse located between plants and the markets (Multistage Warehouse Location Problem). Among all considerations for securing a warehouse premise, the most important features are the space the warehouse can offer and its location. Generally, the sole objective in warehouse allocation problem is to minimize the total cost of transporting the goods from the manufacturing sites to the end customers via these warehouses.
We develop in this work the strong constraints for the multi-commodity case of Single Stage Single Period Capacitated Warehouse Location Problem (SSSPMCWLP). Here, “Capacitated” means that the capacity of a warehouse at a particular location is fixed and limited. This problem can be compared with a real life problem faced by Food Corporation of India (FCI) [2] . In India, FCI distributes a variety of food grains (wheat, rice, etc.) all over the country on a massive scale, purchasing them from various assigned locations called “MANDIS” directly from the farmers. FCI has a central office and five zones (North, South, East, North-East, and West). Each zone is further divided into regions, and each region is divided into several states and each state has several districts in it. From “MANDIS”, these grains are taken to central warehouses of each region and then transported to district warehouse as per the demand. From district warehouse, food grains are moved to depots, which distribute food grains directly to the public at a fair price. So, the MANDIS acts as plants or sources of food grain and district warehouses as demand points. Regional warehouses serve the intermediate transhipment points. The problem faced by FCI is to choose an optimum number of regional warehouse locations with sufficient capacity so as to minimize the sum of location and transportation costs of distributing food grains from MANDIS to these large Regional warehouses, and subsequently to smaller warehouses or district distribution centres. This results in SSSPMCWLP.
The importance of allocation of warehouses/facility between the production sites and the market can be depicted from the fact that this has been studied in its variant forms by long lists of researchers from last four decades and still remains the crucial decision of today’s supply chain design. Researchers have used several methods/approaches to reach the optimal solution. Warehouse allocation problem can be classified as:
1.1. Uncapacitated (SPLP) or Capacitated (CPLP)
Uncapacitated or Simple Plant Location Problems are those where it is assumed that facility has infinite storage space/handling capacity while the Capacitated Plant Location Problem implies that the capacity of the warehouse is limited and known in advance.
1.2. Single Commodity or Multi-Commodity
Single commodity means that there is only a single type of commodity and multi-commodity problems dealing with more than one type of commodities to be distributed.
1.3. Single Stage or Multi-Stage
Single stage refers to the real life problems where commodities are stored at one intermediate stage between plants and markets, while in the multi-stage problems, food grain distribution system commodities are stored at multiple stages (Figure 1 shows the schematic representation of single stage).
Our problem is multi-commodity single stage single period capacitated warehouse location problem (SSSPMCWLP), whose variants have been attempted by many researchers. An overview of the work done in the field of facility allocation can be found in review work of ReVelle and Eiselt [3] . Geoffrion and Graves [1] , Sharma [4] [5] , Drezner et al. [6] and Kouvelis et al. [7] have used weak formulation to address single stage capacitated ware house location problem (SSCWLP). Keskin and Uster [8] have attempted to solve SSCWLP problem with capacity limit at the manufacturing plant, and not on the warehouse. Geoffrion and Graves [1] and Sharma [4] have attempted the SSUWLP and have given completely different formulations considering two different real life problems. Geoffrion and Graves [1] gave a formulation for multi-commodity capacitated single- period version and successfully applied it to a real problem for a food firm using solution technique based on bender decomposition. Hindi and Basta [9] and Hindi et al. [10] solved the similar production-distribution pro-
Figure 1. Multi-commodity distribution from plants to markets via warehouses.
blem by a branch-and-bound algorithm. Sharma [4] formulated a fertilizer production-distribution system problem as a mixed zero-one integer linear programming problem (MILP).Sharma and Verma [11] gave strong and weak formulation for SSUWLP considering single commodity; they also gave hybrid formulation to get a better bound than the weak formulation along with lesser CPU time than the strong formulation. Montoya-Torres et al. [12] developed three-echelon un-capacitated facility location problem (TUFLP) where they minimized the total cost of warehouse location, production, and distribution of products and proposed a greedy randomized adaptive search procedure (GRASP) to solve the multi-item version of the TUFLP. Elson [13] proposed a different multi- commodity version of the plant-warehouse facility logistics problem, concentrating on a single echelon of transshipment/stocking points. Many researchers have worked on developing both heuristic solution methods and exact algorithms to solve capacitated plant location problem. Pirkul and Jayaraman [14] proposed a heuristic based on the Lagrangian relaxation of the model to solve the two-stage production-distribution system design problem (TSPDSDP) with multi-commodity. Keskin and Üster [8] proposed a scatter search algorithm with hybrid improvements including local search and path-relinking to solve a TSPDSDP in which a fixed number of intermediate facilities points are to be located between the plants and customer locations. Verma and Sharma [15] applied vertical decomposition and Lagrangian relaxation approach to solve SSCWLP. Sharma and Aggarwal [16] solved two-stage capacitated warehouse location problem (TSCWLP) by vertical decomposition method, which was attained by relaxing the associated flow balance constraints.
It may be noted that Sharma [17] , Sharma and Murali [18] , Sharma and Berry [3] and Sharma and Verma [12] have attempted single commodity problem and have used “Normalized” variables for developing their strong formulation. We attempt for the first time to give strong formulation for multi-commodity version of the location-distribution problem (SSSCPMCWLP) and have not used ‘Normalized’ variables due to obvious difficulty.
The remainder of this paper is organized as follows. Section 2 gives mathematical formulation of the SSSCPMCWLP based on the existing literature and our modifications. Section 3 provides theoretical framework for using strong formulation, followed by empirical justification of hybrid formulation trade off in relaxed bound values versus computation time. The results from empirical investigation are followed by conclusions in Section 4.
2. Mathematical Formulation of SSSCPMCWLP
2.1. Indices Used
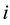 : Set of the supply points (plants);
: Set of the supply points (plants);
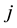 : Set of the potential warehouse points;
: Set of the potential warehouse points;
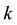 : Set of the markets;
: Set of the markets;
 : Set of the commodities.
: Set of the commodities.
2.2. Definition of Constants
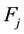 : Fixed cost of establishing and maintaining the warehouse at location “
: Fixed cost of establishing and maintaining the warehouse at location “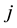 ”;
”;
 : Supply capacity of plant “
: Supply capacity of plant “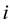 ” for commodity “
” for commodity “ ”;
”;
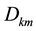 : Demand for commodity “
: Demand for commodity “ ” at market “
” at market “ ” ;
” ;
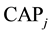 : Capacity of the warehouse at location “
: Capacity of the warehouse at location “ ” for all commodities (assumed that all the commodity are of same density and occupy same space**);
” for all commodities (assumed that all the commodity are of same density and occupy same space**);
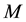 : A very large number, here taken as two times the maximumsupplyor maximum warehouse capacity;
: A very large number, here taken as two times the maximumsupplyor maximum warehouse capacity;








**: Even if the volume or density are different for commodities a conversion factor can be introduced to account for them in warehouse capacity constraint (say 

2.3. Definition of Decision Variables











2.4. Mathematical Model
Minimize

Subjected to:




Linking constraints

Positive and binary constraints on decision variables:



Relaxed binary constraints

Formulation I: Min (1); s.t. (2) - (5); (6); (9) - (11);
Formulation II: Min (1); s.t. (2) - (5); (7) - (8); (9) - (11).
3. Theoretical Framework and Empirical Verification
Theorem 1: LP relaxation of strong formulation (formulation II) gives superior bounds than the LP relaxation of weak formulation (formulation I) of SSSPMCWLP.
Proof: we see the feasible region of LP relaxation of formulation II is much smaller than feasible region of LP relaxation of formulation I, since
Though LP relaxation of weak formulation gives inferior bounds but are computed very fast (as it has linear number of linking constraints). LP relaxation of strong formulation gives superior bounds but it takes more time (as number of linking constraints are of order
The hybrid formulation is developed to take advantage of both (better bound of strong formulation and better computation time of weak formulation) by adding most promising constraints of the strong formulation to the weak formulation of the SSSPMCWLP. Those few ‘strong’ constraints added may be binding in strong formulation, and can carefully be obtained by sorting the demand and supply values and gradually iterating to get the desired result. We started with 20% of strong constraints then reduced to5%, by step size of 5% and later reduced with step size of 1%. In each step, we observed decrease in the bounds obtained by LP relaxation but also simultaneous significant improvement in computational time. After some iteration we arrived at desired/satis- factory level and decided that the top 2% of total “strong” demand and supply constraints were to be added to the “weak” formulation of SSSPMCWLP to get the required hybrid formulation. At this level, the bounds were only a little inferior from weak bounds, but took substantially less computational time compared to strong computational time; significantly improving the overall computational times for solving original SSSPMCWLP. This motivated us to develop the following procedure.
Procedure to build hybrid formulation constraints
Step 1: Sort demand points values in increasing order of demand 

Set cut off number
Let the demand associated with this number N and given m be:
Prepare a set of most promising demand points
Now,

Step 2: Sort supply points values in increasing order of demand 

Set cut off number
Let the Supply capacity associated with this number N and given m be:
Prepare a set of most promising supply points
Now,

Hybrid formulation (HF) and its relaxation (HFR)
HF: Minimize (1); subject to (2) - (6); (9) - (11); (13); (14);
HFR: Minimize (1); subject to (2) - (6); (9); (10); (12); (13); (14).
3.1. Empirical Investigation
GAMS programming is used to show the superiority of formulation (II) over formulation (I) and t-test has been conducted for the statistical significance of the results. To overcome the drawback of higher CPU time for strong formulation (Formulation II), a hybrid formulation is developed by adding the most promising supply and demand side strong linking constraint to the weak formulation. Here we have included 2% of the demand and strong side linking constraints to the weak formulation for which demand and supply are least.
Problem instances of the size 50 × 50 × 50 and 100 × 100 × 100 are solved in GAMS for the following four categories (Table 1) and as per assumptions given below:
1) In each problem instance demand for each commodity in each market is taken as uniformly distributed with lower bound of 100 units and upper bound of 150 units;
Table 1. Problem categories for SSSPMCWLP.
2) Total Supply Capacity of each commodity at any plant and Warehouse Capacity at any location is more than any market average demand and taken as per the above four categories in Table 1;
3) Warehouse Capacity and Supply Capacity of plants are also uniformly distributed;
4) Cost of carrying one unit from plant to warehouse is normally distributed with mean of 4000 and standard deviation of 300;
5) Cost of carrying one unit from warehouse to market is normally distributed with mean of 5000 and standard deviation of 400;
6) Fixed Cost of locating a warehouse is normally distributed with a mean of 10,000 and standard deviation of 1500.
Samples problems are solved by relaxing the 0 - 1 constraints for the location variable Yj (constraint (12) in place of constraint (11) in formulation I and formulation II).
GAMS code is written to generate the random values for supply capacity, warehouse capacity, demand, costs of transportation and fixed cost of warehouse location as per the above specified criteria. The same code solves both the formulation (I) and formulation (II) with the same input data. Same data is used to solve hybrid formulation, so that we can compare the objective function values and CPU time values for these three formulations. 30 Problems are solved for each of the four categories for each problem size (total number of problem instances solved = 240, 120 of each of the size 50 × 50 × 50 and 100 × 100 × 100) using a Intel (R) Core (TM) i7-4770S CPU @ 3.10GHz.
Objective function values and CPU time for each and every problem instance is recorded and statistical analysis (t-test) is done to check the superiority of formulation (II) over formulation (I) and superiority of hybrid formulation over other formulations with a confidence level of 99.5% (Tables 2-13).
3.1.1. Statistical Analysis
Hypothesis tests are conducted as follows:
I. To check improvement in objective function values of LP relaxed Strong Bound (formulation II) from LP relaxed Weak Formulation (formulation I)
µ1: Percentage increase in objective function value of LP relaxed formulation (II) over LP relaxed formulation (I).
Null hypothesis,
Alternate hypothesis,
From the statistical t-tables we have the critical value for t-stats at 


II. To check improvement in objective function values of LP relaxed Hybrid formulation vs. LP relaxed Weak Formulation (formulation I).
µ2: Percentage increase in objective function value of LP relaxed Hybrid formulation over LP relaxed Weak formulation (formulation I).
Null hypothesis,
Alternate hypothesis,
Result: Comparing the calculated t-values with critical t-values, the null hypothesis µ2 = 0 is rejected.
III. To check deterioration in CPU time values of LP relaxed Strong bound (formulation (II)) vs. LP relaxed Weak bound (formulation (I)).
t1: Percentage deterioration in CPU time for Strong formulation (II) over weak formulation (I).
Null hypothesis,
Alternate hypothesis,
Table 2. Problem size 50 × 50 × 50 of Category A.
Table 3. Problem size 50 × 50 × 50 of Category B.
Table 4. Problem size 50 × 50 × 50 of Category C.
Table 5. Problem size 50 × 50 × 50 of Category D.
Table 6. Problem size 100 × 100 × 100 of Category A.
Table 7. Problem size 100 × 100 × 100 of Category B.
Table 8. Problem size 100 × 100 × 100 of Category C.
Table 9. Problem size 100 × 100 × 100 of Category D.
Table 10. T-test results of objective function improvement of LP relaxed strong formulation over LP relaxed weak formulation.
Table 11. T-test results of objective function improvement of LP relaxed hybrid formulation over LP relaxed weak formulation.
Table 12. T-test results for CPU time deterioration of strong formulation (II) over weak formulation (I).
Table 13. T-test results for CPU time improvement of hybrid formulation over strong formulation.
Result: Comparing the calculated t-values with critical t-values, the null hypothesis t1 = 0 is rejected.
IV. To check improvements in CPU time values of Hybrid Formulation vs. Strong Formulation (Formulation I).
As we have added only 2% most promising demand and supply side strong linking constraint to the weak formulation to form hybrid formulation, therefore we expect the improvement in CPU time i.e. CPU time for Hybrid Formulation must be less than the CPU time for Strong Formulation. We conduct the following hypothesis test:
t2: Percentage improvement in CPU time i.e. decrement in the CPU time for hybrid formulation from Strong formulation.
Null hypothesis,
Alternate hypothesis,
Result: Comparing the calculated t-values with critical t-values, the null hypothesis t2 = 0 is rejected.
Looking at the t-tests done on the empirical results, we see all the null hypotheses have been rejected, implying differences in relaxed formulations results; strong constraints gave the superior bounds than the weak constraints. However, the CPU time for computation for LP relaxed strong formulations were significantly higher than the CPU time for LP relaxed weak formulations, which meant that the benefit of better bounds using stronger formulations is somewhat compromised by their higher computational time. Hybrid formulation values were intermediate between strong and weak formulations with significant improvement in bound values.
4. Conclusions
The SSSPMCWLP is often encountered in distribution networks which include cross-docks with known manufacturer and customer demand points. We develop strong and hybrid formulation for the SSSPMCWLP for the first time and show its merits over prevalent weak formulation in literature. The idea behind the hybrid formulation is to get advantages of both weak and strong formulation in terms of bound and computational time.
Computational study is done for a variety of problems of different sizes. We find that hybrid formulations of SSSPMCWLP is a good compromise, as it gives better bounds while not incurring greater computation burden.
References
- Geoffrion, A.M. and Graves, G.W. (1974) Multicommodity Distribution System Design by Benders Decomposition. Management Science, 20, 822-844. http://dx.doi.org/10.1287/mnsc.20.5.822
- FCI (Food Corporation of India) Official Website. http://fciweb.nic.in/
- ReVelle, C.S. and Eiselt, H.A. (2005) Location Analysis: A Synthesis and Survey. European Journal of Operational Research, 165, 1-19.
- Sharma, R.R.K. (1991) Modelling a Fertilizer Distribution System. European Journal of Operational Research, 51, 24- 34. http://dx.doi.org/10.1016/0377-2217(91)90142-I
- Sharma, R.R.K. and Berry, V. (2007) Developing New Formulations and Relaxations of Single Stage Capacitated Warehouse Location Problem (SSCWLP): Empirical Investigation for Assessing Relative Strengths and Computational Effort. European Journal of Operational Research, 177, 803-812. http://dx.doi.org/10.1016/j.ejor.2005.11.028
- Drezner, T., Drezner, Z. and Salhi, S. (2002) Solving the Multiple Competitive Facilities Location Problem. European Journal of Operational Research, 142, 138-151. http://dx.doi.org/10.1016/S0377-2217(01)00168-0
- Kouvelis, P., Rosenblatt, M.J. and Munson, C.L. (2004) A Mathematical Programming Model for Global Plant Location Problem: Analysis and Insights. IIE Transactions, 36, 127-144. http://dx.doi.org/10.1080/07408170490245388
- Keskin, B.B. and Üster, H. (2007) A Scatter Search-Based Heuristic to Locate Capacitated Transhipment Points. Computers & Operations Research, 34, 3112-3125. http://dx.doi.org/10.1016/j.cor.2005.11.020
- Hindi, K.S. and Basta, T. (1994) Computationally Efficient Solution of a Multiproduct, Two-Stage Distribution Location Problem. The Journal of the Operational Research Society, 45, 1316-1323.
- Hindi, K.S., Basta, T. and Pienkosz, K. (2006) Efficient Solution of a Multi-Commodity, Two-Stage Distribution Problem with Constraints on Assignment of Customers to Distribution Centres. International Transactions in Operations Research, 5, 519-527. http://dx.doi.org/10.1111/j.1475-3995.1998.tb00134.x
- Sharma, R.R.K. and Verma, P. (2012) Hybrid Formulations of Single Stage Uncapacitated Warehouse Location Problem: Few Theoretical and Empirical Results. International Journal of Operations and Quantitative Management (IJOQM), 18, 53-69.
- Montoya-Torres, J.R., Aponte, A. and Rosas, P. (2011) Applying GRASP to Solve the Multi-Item Three-Echelon Uncapacitated Facility Location Problem. Journal of the Operational Research Society, 62, 397-406. http://dx.doi.org/10.1057/jors.2010.134
- Elson, D.G. (1972) Site Location via Mixed-Integer Programming. The Journal of Operational Research Society, 23, 31-43. http://dx.doi.org/10.1057/jors.1972.4
- Pirkul, H. and Jayaraman, V. (1998) A Multi-Commodity, Multi-Plant, Capacitated Facility Location Problem: Formulation and Efficient Heuristic Solution. Computers & Operations Research, 25, 869-878. http://dx.doi.org/10.1016/S0305-0548(97)00096-8
- Verma, P. and Sharma, R.R.K. (2011) Vertical Decomposition Approach to Solve Single Stage Capacitated Warehouse Location Problem (SSCWLP). American Journal of Operations Research, 1, 100-117. http://dx.doi.org/10.4236/ajor.2011.13013
- Sharma, R.R.K. and Agarwal, P. (2014) Approaches to Solve MID_CPLP Problem: Theoretical Framework and Empirical Investigation. American Journal of Operations Research, 4, 142-154. http://dx.doi.org/10.4236/ajor.2014.43014
- Sharma, R.R.K. (1996) Food Grains Distribution in the Indian Context: An Operational Study. In: Tripathy, A. and Rosenhead, J., Eds., Operations Research for Development, Chapter 5, New Age International Publishers, New Delhi, 212-227.
- Sharma, R.R.K. and Muralidhar, A. (2009) A New Formulation and Relaxation of the Simple Plant Location Problem. Asia-Pacific Journal of Operational Research, 26, 1-11. http://dx.doi.org/10.1142/S0217595909002122








