American Journal of Operations Research
Vol.05 No.01(2015), Article ID:52930,24 pages
10.4236/ajor.2015.51002
JIT Mixed-Model Sequencing Rules: Is There a Best One?
Patrick R. McMullen
School of Business, Wake Forest University, Winston-Salem, North Carolina, USA
Email: mcmullpr@wfu.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 November 2014; revised 29 November 2014; accepted 10 December 2014
ABSTRACT
This research effort compares four sequencing rules intended to smooth production scheduling for mixed-model production systems in a Just-in-Time/Lean manufacturing environment (“JIT” hereafter). Each rule intends to schedule mixed-model production in such a way that manufacturing flexibility is optimized in terms of system utilization, units completed, average in-process inventory, average queue length, and average waiting time. A simulation experiment, where the various sequencing rules are tested against each other in terms of the above production measures, shows that three of the sequencing rules essentially offer the same performance, whereas one of them shows more variation.
Keywords:
JIT/Lean Manufacturing, Scheduling, Sequencing, Enumeration, Simulation

1. Introduction
In a JIT/Lean manufacturing environment, it is important to schedule production in such a way that units are manufactured in direct proportion to their demand. Otherwise, in-process inventories accumulate, throughput time increases, schedule compliance suffers, all resulting in sub-optimal performance [1] . Consider the simple example where four units of Item A are demanded, two units of Item B are demanded and one unit of Item C is demanded. One possible schedule is as follows: AAAABBC. While changeovers are minimized, units are not sequenced proportional to demand. The following schedule would be better in terms of “smoothing out” production in terms of demand: ABACABA [2] .
There are various strategies and algorithms used to find the “best” sequence in terms of smoothing out production. These sequencing algorithms vary in terms of details, but they all share the same intent of smoothing out sequencing as much as possible.
This paper explores four of the more common sequencing rules, uses them to sequence mixed-model production schedules, simulates production schedules under various conditions, and analyzes the performance of the various rules.
2. Sequencing Rules
Four sequencing rules are investigated for this research effort. Prior to presenting the individual rules, a few definitions are needed.
As an example for the sequence: ABACABA, we have 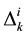 values of (2, 2, 2, 1) for
values of (2, 2, 2, 1) for 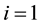 (Item A), (4, 3) for
(Item A), (4, 3) for 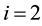 (Item B), and (7) for
(Item B), and (7) for 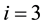 (Item C). When we calculate these
(Item C). When we calculate these 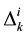 values, we assume that the sequence cycles over and over. For the
values, we assume that the sequence cycles over and over. For the 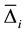 values, we simply use
values, we simply use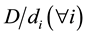 , yielding values of
, yielding values of 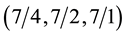 for this particular problem.
for this particular problem.
2.1. Minimize Maximum Response Gap (MRG)
The first objective function to be studied is the minimization of the maximum response time for a sequence [3] . Mathematically, this is as follows:
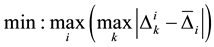 (1)
(1)
For our example problem, this objective function value would be as follows:
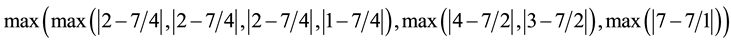 ,
,
which reduces to: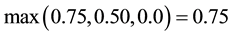 .
.
2.2. Minimize Average Gap Length (AGL)
The next objective to be studied is the minimization of the average distance between the actual gap and the average gap [4] [5] . Mathematically, this is as follows:
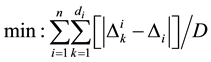 (2)
(2)
The example problem above, the objective function value would be as follows:
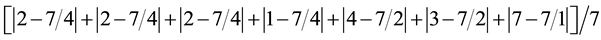 , resulting in a value of 0.3571.
, resulting in a value of 0.3571.
2.3. Minimize Gap Variation (VAR)
The next objective to be studied is the minimization of gap length variation [6] . Mathematically, this objective is as follows:
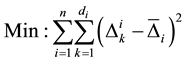 (3)
(3)
Using the example problem above, the objective function value would be: 
2.4. Minimize Usage Rate (USAGE)
The final objective function to be explored is the minimization of the usage rate―keeping as constant as possible in assigning units for sequencing [7] . Mathematically, this is as follows:

For the example problem, the objective function value is 1.7143, when using 
3. Experimentation
To determine which of the sequencing rules is most effective in terms of the JIT/Lean objectives mentioned previously, experimentation is conducted. Several problem sets are simulated according to their best sequence in terms of the objectives described above, simulation is performed, data is collected from the simulation, and analysis is made in an attempt to differentiate performance among the four presented objectives [8] .
3.1. Problem Sets
Eight problem sets are used for experimentation, starting with a small problem and having the problems grow large to the point where finding the optimal sequencing (via complete enumeration) in terms of the objective function values becomes computationally intractable. Table 1 shows the product mix details of the eight problem sets used, and the number of total permutations required for compute enumeration.
Complete enumeration is used for each problem set so that the optimal values for each objective function shown above are obtained. It is intended to show each objective function in its “best possible light”.
For each unique item, a processing time for the single-stage simulation has been assigned. In actuality, three different processing time templates have been assigned to each unique item: ascending processing times, descending processing times, and randomly assigned processing times on the uniformly-distributed interval (2, 10). Table 2 summarizes the processing times for each of the three variants, along with simulation settings.
3.2. Simulation Outputs
Several output measures are used to determine the performance of the sequencing rules. They are as follows:
・ Utilization?the average amount of time the system is busy.
・ Units completed?the average number of units completed by the system.
・ Average WIP level?the average number of units in the system at any given time.
Table 1. Details of problem sets.
Table 2. Simulation details.
・ Average Queue Length?average number of units waiting to be processed.
・ Average Waiting Time?average amount of time a unit spends waiting to be processed.
These performance measures are actual outputs from the simulation.
3.3. Design of Experiment
The general research question pursued is to determine whether or not the sequencing rules have an effect on the simulation performance measures. This question can be adequately addressed via Single-Factor ANOVA, with the sequencing rule as the experimental factor (of which there are four levels), and the simulation-based performance measure as the response variable.
Because there are eight different production models, three different processing time templates, and five different simulation-based performance measures, there are (8) (3) (5) = 120 different analyses to perform. Each of the (120) analyses utilize (25) simulation replications.
4. Experimental Results
Tables 3-10 show the results of the experiments for each unique analysis, specifically including the mean for each factor level, along with the F-statistics and associated p-value for each experiment. These tables show that the sequencing rule has an effect on the performance measure of interest (26) times of the (120) experiments conducted, using an 
Table 11 shows the similarity between all four of the sequencing objectives, based upon the sequences obtained via complete enumeration of all possible sequences for all (120) problems.
As one can see, there is a great deal of similarity between the MRG, AGL and VAR objective functions, while the USAGE objective function is absolutely unique from the other three. This is a reasonable explanation as to why USAGE is the biggest contributor to the significance of the sequencing rule.
Table 3. Model 1 results.
Table 4. Model 2 results.
Table 5. Model 3 results.
Table 6. Model 4 results.
Table 7. Model 5 results.
Table 8. Model 6 results.
Table 9. Model 7 results.
Table 10. Model 8 results.
Table 11. Similarity matrix.
5. Concluding Comments
An experiment was conducted to see if four popular sequencing rules have any effect on performance measures important to JIT/Lean manufacturing systems. Eight different problems were investigated, each with three processing time arrangements, and five different JIT/Lean manufacturing performance measures to study. For each of the four sequencing rules, complete enumeration of all feasible permutations was generated to find the “best” sequence in terms of the objective function associated with each sequencing rule. This was done to show each sequencing rule in its “best possible light”.
Experimentation shows statistical significance of the sequencing rule (26) times out of a possible (120) times. The USAGE sequencing rule is the reason for the significant difference in means (25) of these (26) times?(17) of these (25) times USAGE provides inferior results than the other three sequencing rules. USAGE is the most unique of the other sequencing rules and provides less consistent results as compared to the other three. This should not come as a surprise because the USAGE objective function only looks at a single instance of the sequence, whereas the other three sequencing rules explore the cyclic nature of the sequence?multiple instances of the repeated sequence. The upshot of this is that USAGE is a higher risk strategy than the others.
Every research effort provides opportunities for further exploration. This is no exception. Longer production sequences would be helpful if there is some way around the combinatorial limitations that exist at present. Additionally, multiple-stage simulated production runs might also yield some interesting results.
References
- Goldratt, E.M. and Cox, J. (1992) The Goal: A Process of Ongoing Improvement. North River Press, North Barrington.
- McMullen, P.R. (1998) JIT Sequencing for Mixed-Model Assembly Lines with Setups Using Tabu Search. Production Planning & Control, 9, 504-510. http://dx.doi.org/10.1080/095372898233984
- Kanet, J.J. (1981) Minimizing the Average Deviation of Job Completion Times About a Common Due Date. Naval Research Logistics Quarterly, 28, 643-651. http://dx.doi.org/10.1002/nav.3800280411
- Garcia-Villoria, A. and Pastor, R. (2013) Minimising Maximum Response Time. Computers & Operations Research, 40, 2314-2321. http://dx.doi.org/10.1016/j.cor.2013.03.014
- Salhi, S. and Garcia-Villoria, A. (2012) An Adaptive Search for the Response Time Variability Problem. Journal of the Operational Research Society, 63, 597-605. http://dx.doi.org/10.1057/jors.2011.46
- Hermann, J.W. (2007) Generating Cyclic Fair Sequences Using Aggregation and Stride. The Institute for Systems Research, ISR Technical Report 2007-12.
- Miltenburg, J. (1989) Level Schedules for Mixed-Model Assembly Lines in Just-in-Time Production Systems. Management Science, 35, 192-207. http://dx.doi.org/10.1287/mnsc.35.2.192
- Kelton, D.W., Sadowski, R.P. and Sturrock, D.T. (2004) Simulation with Arena. 3rd Edition, McGraw-Hill Higher Education, Boston.


