American Journal of Operations Research
Vol.4 No.1(2014), Article ID:41995,14 pages DOI:10.4236/ajor.2014.41002
Optimization of Energy Resource Management for Assembly Line Balancing Using Adaptive Current Search
Supaporn Suwannarongsri1, Tika Bunnag1, Waraporn Klinbun2
1Rattanakosin College for Sustainable Energy and Environment (RCSEE), Rajamangala University of Technology Rattanakosin, Nakhon Pathom, Thailand
2Faculty of Engineering and Technology, Panyapiwat Institute of Management, Nonthaburi, Thailand
Email: suwannarongsri@gmail.com, tbunnag@hotmail.com, warapornkli@pim.ac.th
Copyright © 2014 Supaporn Suwannarongsri et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Supaporn Suwannarongsri et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received December 4, 2013; revised January 4, 2014; accepted January 11, 2014
ABSTRACT
This paper aimed to present the optimization of energy resource management in a car factory by the adaptive current search (ACS)—one of the most efficient metaheuristic optimization search techniques. Assembly lines of a specific car factory considered as a case study are balanced by the ACS to optimize their energy resource management. The workload variance of the line is performed as the objective function to be minimized in order to increase the productivity. In this work, the ACS is used to address the number of tasks assigned for each workstation, while the sequence of tasks is assigned by factory. Three real-world assembly line balancing (ALB) problems from a specific car factory are tested. Results obtained by the ACS are compared with those obtained by the genetic algorithm (GA), tabu search (TS) and current search (CS). As results, the ACS outperforms other algorithms. By using the ACS, the productivity can be increased and the energy consumption of the lines can be decreased significantly.
Keywords: Adaptive Current Search; Assembly Line Balancing; Energy Resource Management; Metaheuristic Optimization
1. Introduction
Metaheuristic optimization is one of the most important issues in computer science and operation research. According to the energy resource optimization context, energy resource management is an alternative to increase the productivity or decrease the energy consumption. Especially in car assembly industries, total energy of such industries can be divided into two parts, i.e. main energy used for assembling products and supporting energy used for illumination, ventilation and so on. Minimized workload variance of the assembly line can increase productivity and also increase energy efficiency. Energy resource management can be considered as a class of non-polynomial time hard (NP-hard) combinatorial optimization problem [1,2]. So the problem usually possesses nonlinear and unsymmetrical terms as well as multiple local solutions. These cause the problem complex and difficult to solve by an exact method within a reasonable amount of time. In addition, inefficient algorithms are easily trapped due to its local solutions. To solve the problem, metaheuristic optimization methods are alternatives [3-5]. Over five decades, many metaheuristics such as genetic algorithm (GA), tabu search (TS), particle swarm optimization (PSO) and harmony search (HS) have been developed for combinatorial, continuous and multiobjective optimization problems [5,6]. Metaheuristics has been widely applied to various real-world engineering problems [7,8]. Some metaheuristics such as GA, TS, PSO and HS have been accepted and applied to some energy saving and management applications [9-12].
By literatures, several methods have been launched to solve the assembly line balancing (ALB) problems, for example, heuristic approaches [13,14], metaheuristics such as GA [15] and TS [16,17], and hybrid methods [18,19]. Although GA and TS could provide satisfactory results, they may be trapped by some local optima and spent amount of search time. One of the latest metahueristics is the current search (CS) [20]. The CS has been successfully applied to control engineering [21] and signal processing [22]. However, local entrapments in CS may occur. In order to improve its effectiveness, the CS needs to be modified. The modified version of the CS named adaptive current search (ACS) has been proposed [23]. The ACS shows the superior results to the conventional CS and other metaheuristic algorithms.
This paper proposes the application of the ACS to optimize energy resource management in a car factory. Three real-world assembly line balancing (ALB) problems from a specific car factory are conducted. The workload variance of such lines is minimized in order to increase the productivity and decrease the energy consumption. After an introduction in Section 1, the problem formulation of energy resource management of ALB problems is explained in Section 2. The ACS algorithms are briefly described in Section 3. Results of solving ALB problems by the ACS compared with GA, TS and CS are provided in Section 4, while discussions and conclusions are given in Section 5 and Section 6, respectively.
2. Problem Formulation
The problem formulation of energy resource management of ALB problems of a car factory in sense of energy resource management is presented in this Section. The ALB problem is considered as one of the classical industrial engineering problems [24]. An assembly line is a sequence of workstations connected together by a material handling system. It is used to assemble components or tasks into a final product. The fundamental of the line balancing problems is to assign the tasks to an ordered sequence of workstations in order to minimize the workload variance of the line, whereas satisfying two particular constraints. The first constraint is that the total processing time assigned to each workstation should be less than or equal to the cycle time. The second is that the task assignments should follow the sequential processing order of the tasks or the precedence constraints.
The ALB can be considered as the class of combinatorial optimization problems known as NP-hard [13,25]. Traditionally, the assembly line will be represented by the precedent diagram. Figure 1 shows the precedent diagram of a simple assembly line consisting of 29 tasks, where node weight stands for the task time in time units.
In this work, the single-model ALB problem is considered. Balancing of the lines can be measured by the workload variance [14,25]. Therefore, the goals of balancing lines are to minimize the workload variance. Analytical formulations for the ALB problems are stated in (1) - (4), where m is the number of workstations, W is the total processing time, c is the cycle time, Ti is the processing time of the ith workstation, Tid is the idle time, wv is the workload variance and E is the line efficiency.
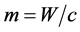 (1)
(1)
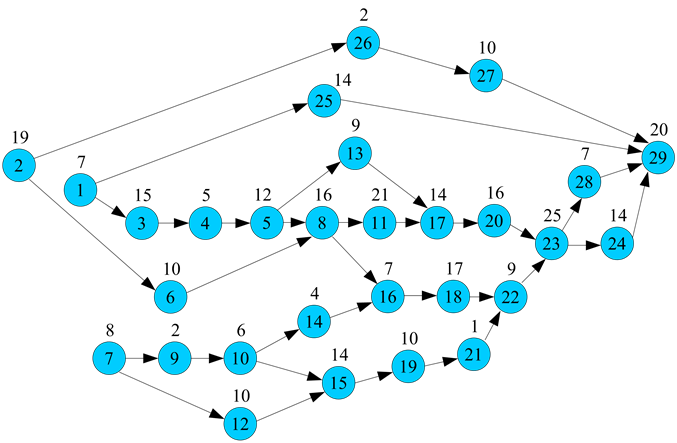
Figure 1. Precedent diagram of simple assembly line.
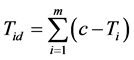 (2)
(2)
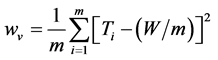 (3)
(3)
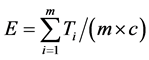 (4)
(4)
The ALB problem can be considered as the constrained optimization problem. The workload variance (wv) is performed as the objective function (J) stated in (5). J will be minimized according to the precedence constraints expressed in (6). Moreover, the constraint in (6) also indicates that the processing time Ti of the ith workstation must equal or less than the cycle time (c).
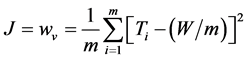 (5)
(5)
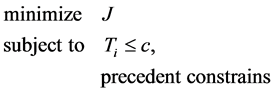 (6)
(6)
Once wv is reduced, E is then increased. Working time to complete the product can be also reduced. In sense of energy resource management, reduced workload variance can increase productivity and decrease total energy consumption. This approach can be represented by Figure 2. Assume that the total energy of the line consists of main energy used for assembling products and supporting energy used for illumination and ventilation systems. Total energy (Ztotal) is stated in (7), where Zmain is the main energy used for assembly and Zsupport is the supporting energy used for illumination and ventilation, respectively.
![]() (7)
(7)
Referring to Figure 2, a simple assembly line consists of 5 workstations. Time for finishing each product of unbalanced line in Figure 2(a) is equal to cycle time (c1), while that for finishing each product of balanced line in Figure 2(b) is equal to cycle time (c2). Once c2 < c1, this means that time for finishing each product of balanced line is less than unbalanced line does. Total energy per product (Ztotal/product) and supporting energy per product (Zsupport/product) can be calculated by (8) and (9), where Nitem is numbers of products produced within a certain period. It was found that, although the main energy used for assembling each product is a same value between unbalanced and balanced lines, total energy per product (Ztotal/product) and supporting energy per product (Zsupport/product) can be decreased when cycle time is reduced. By this approach, productivity can be increased and also total energy consumption can be decreased.
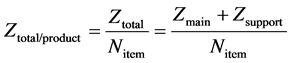 (8)
(8)
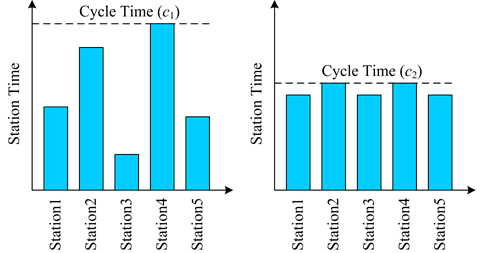 (a) (b)
(a) (b)
Figure 2. Assembly line consisting of 5 workstations: (a) unbalanced line, (b) balanced line.
 (9)
(9)
3. ACS Algorithm
In 2012, the current search (CS) was developed based on the principle of current divider in electric circuit theory [20-22]. The CS possesses both exploration and exploitation properties according to the metaheuristic optimization context. The advantages of the CS are that it can find any local solution in each search direction efficiently. It can perform unlimited search directions defined by users. However, the disadvantages of the CS are that its search process may be trapped or locked by any local solution. In addition, the search time consumed by the CS is depended on the numbers of search directions.
The adaptive current search (ACS), the modified version of the CS, is proposed in 2013 [23]. It provides the memory list (ML) and the adaptive radius (AR) mechanism inserting into the CS algorithms. The ML is used to escape from local entrapment caused by any local solution, while the AR is conducted to speed up the search process. The proposed ML consists of three levels: low, medium and high. The low-level ML is used to store the ranked initial solutions at the beginning of search process, the medium-level ML is conducted to store the solution found along each search direction, and the high-level ML is used to store all local solutions found at the end of each search direction. Performance evaluation of the ACS was performed against benchmark unconstrained and constrained optimization problems [23]. Compared with genetic algorithm (GA), tabu search (TS) and current search (CS), it was found that the ACS shows the superior results to the conventional CS and other algorithms. Some movements of the ACS search process over the search space can be depicted in Figure 3. The ACS algorithm is described as follows:
Step 1 Initialize the search space W, iteration counter k = j = 1, maximum allowance of solution cycling jmax, number of initial solutions N, number of neighborhood members n, search radius R, and low-level ML Y = Æ, medium-level ML G = Æ, and high-level ML X = Æ.
Step 2 Uniformly random initial solution Xi, i = 1,···,N within W.
Step 3 Evaluate the objective function f(Xi) for "X. Rank Xi that gives f(X1) <···< f(XN), then store ranked Xi into the low-level ML Y.
Step 4 Let x0 = xk as selected initial solution.
Step 5 Uniformly random neighborhood xi, i = 1,···,n around x0 within radius R.
Step 6 Evaluate the objective function f(xi) for "x. A solution giving the minimum objective function is set as x*.
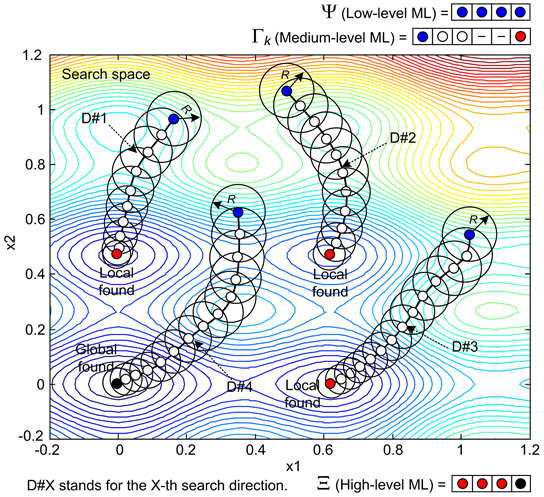
Figure 3. Some movements of ACS algorithm.
Step 7 If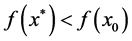 , keep x0 into medium-level ML Gk and set x0 = x*, set j = 1 and return to Step 5. Otherwise keep x* into medium-level ML Gk and update j = j + 1.
, keep x0 into medium-level ML Gk and set x0 = x*, set j = 1 and return to Step 5. Otherwise keep x* into medium-level ML Gk and update j = j + 1.
Step 8 If the search process moves close to the local solution, activate the AR mechanism by adjusting R = rR, 0 < r < 1.
Step 9 If j < jmax, return to Step 5. Otherwise keep x0 into high-level ML X and update k = k + 1.
Step 10 Terminate the search process when the termination criteria (TC) are met. The optimum solution found is x0. Otherwise return to Step 4.
4. Experimental Results
This Section presents the application of the ACS to optimize energy resource management of assembly line balancing (ALB) problems in a car factory. Sammitr Motors Manufacturing Public Co., Ltd. [26], a car factory located in Samut Sakhon, Thailand, is considered as a case study of this work. It produces car and truck body parts, moulds and fixtures for auto makers such as HINO, ISUZU, MITSUBISHI and NISSAN. Many kinds of car and truck body parts under “Sammitr” trademark are assembled from this factory. For a truck, it comprises of several parts, such as turning disk, dragging arm, frame, rear cap, side cap and so forth. In this factory, each part belongs itself assembly line. For this work, three ALB problems of that car factory, i.e. turning disk, dragging arm and frame assembly lines, are selected. Details of the selected ALB problems are described as follows.
• For the first ALB problem, turning disk assembly line consists of 63 tasks with total working time of 459.63 min. Details of turning disk assembly line are provided in Appendix, for example. Among those tasks, there are 24 tasks for welding (278.20 min.), 9 tasks for grinding and eroding (57.80 min.) and 11 tasks for moving (26.55 min.). Data from factory reveal that there are 5 workstations with the cycle time of 152.33 min. This means that time for finishing each product of this line is equal to 152.33 min.
• For the second ALB problem, dragging arm assembly line consists of 70 tasks with total working time of 307.41 min. Among them, there are 29 tasks for welding (184.67 min.), 7 tasks for grinding and eroding (36.28 min.) and 6 tasks for moving (18.00 min.). Data from factory show that there are 6 workstations with the cycle time of 123.02 min. Time for finishing each product of this line is equal to 123.02 min.
• For the third ALB problem, frame assembly line consists of 75 tasks with total working time of 1,334.27 min. Among them, there are 34 tasks for welding (853.95 min.), 4 tasks for grinding and eroding (55.71 min.) and 9 tasks for moving (165.28 min.). Data from factory indicate that there are 5 workstations with the cycle time of 651.94 min. This means that time for finishing each product of this line is equal to 651.94 min.
All three lines are run 440 min. per day, 25 days per month and 12 months per year. Power used for completing the product consists of one welding machine of 13 kW (a1 = 13,000 W × 1), one grinding and eroding motor of 1 Hp (a2 = 746 W × 1) and one crane motor of 2 Hp (a3 = 1,492 W × 1). Power used for illumination system comes from 18 halogen lamps of 400 W (b1 = 400 W × 18) and 84 fluorescent lamps with their ballasts of 36 W + 10 W (b2 = 46 W × 84). Power used for ventilation system comes from 12 motors of 3/4Hp (g = 559.50 W × 12). Therefore, the main energy used for assembly (Zmain) and the supporting energy used for illumination and ventilation (Zsupport) of these lines can be yearly calculated in kilowatt-hour (kWh) unit by (10) and (11), where T1 is time for welding, T2 is time for grinding and eroding, and T3 is time for moving. In this work, power for cutting, blowing, drilling and broaching are neglected.
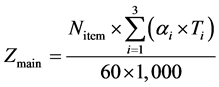 (10)
(10)
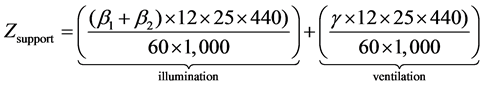 (11)
(11)
Data of all three ALB problems from factory are summarized in Table1 In this work, the ACS is conducted to solve the ALB problems. The ACS is used to address the number of tasks assigned for each workstation, while the sequence of tasks was assigned by factory. The workload variance (wv) performed as the objective function (J) stated in (5) will be minimized according to the precedence constraints expressed in (6).
In this paper, algorithms of GA and TS are omitted. Readers may refer to [27,28] for GA and [29,30] for TS, respectively. For all three ALB problems, the parameter settings for the GA follow MATLAB-GA Toolbox [28]
and for the TS follow [30]. The common search parameters of the CS and ACS are: n (number of neighborhood members) = 1,000, R (search radius) = 20% of search space and Imax (number of iterations) = 1,000. N (number of search directions) = 10 is required to terminate the search. For the ACS, R-adjustment (search radius adjustment of AR mechanism) is set as Imax = 500 ® R = 10% of search space and Imax = 750 ® R = 5% of search space.
The TS, CS and ACS algorithms were coded by MATLAB, while GA was conducted from MATLAB-GA Toolbox. All algorithms were run on Intel Core2 Duo 2.0 GHz 3 Gbytes DDR-RAM computer. Table 2 provides the boundaries of number of tasks for each workstation set for the corresponding search spaces. For all algorithms, 50 trials were run to obtain the best solution. Results obtained are summarized in Table 3, while convergent rates are plotted in Figure 4-Figure 6.
5. Discussions
As results of the first ALB problem in Table 3, turning disk assembly line arranged by factory and optimized by GA, TS, CS and ACS can be plotted in Figure 7-Figure 11 and Table 4-Table 8, respectively. The ACS provides superior results to other algorithms and certainly a factory. The workload variance (wv) obtained by the ACS is less than that obtained by GA, TS and CS. Once wv is reduced, the line efficiency (E) will be increased. It can be observed that E in Table 3 optimized by the ACS is the highest value.
By those results, percent of decreased total energy per produce (PDTE) and percent of decreased supporting energy per produce (PDSE) can be calculated by (12) and (13), where Ztotal/product,old is total energy per produce of factory, Ztotal/product,new is total energy per produce obtained by GA, TS, CS or ACS, Zsupport/product,old is supporting energy per produce of factory, and Zsupport/product,new is supporting energy per produce obtained by GA, TS, CS or ACS. Results are summarized in Table9
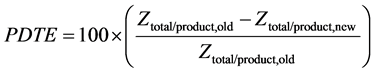 (12)
(12)
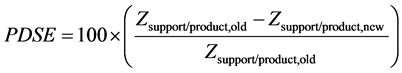 (13)
(13)
As results of the second and third ALB problems in Table 3, dragging arm and frame assembly lines arranged by factory and optimized by GA, TS, CS and ACS are omitted because they have a similar pattern to those of the first ALB problem shown in Figure 7-Figure 11 and Table 4-Table8 Referring to Table 3, the ACS provides superior results to other algorithms and a factory. The workload variance obtained by the ACS is less than that
Table 3. Results of ALB problems.
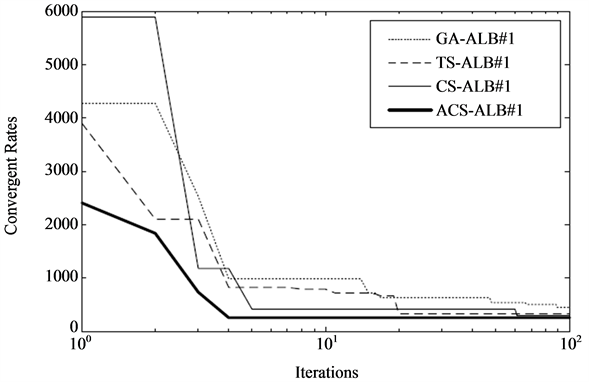
Figure 4. Convergent rate of the first ALB problem.
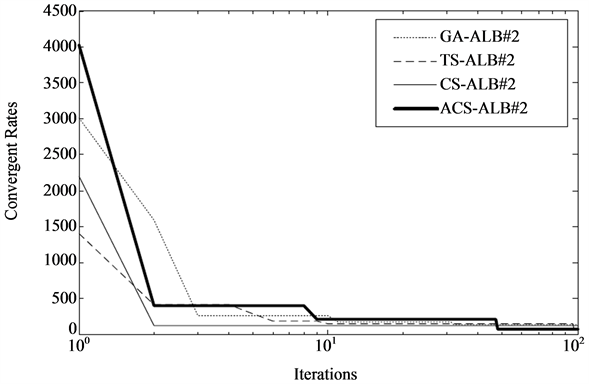
Figure 5. Convergent rate of the second ALB problem.
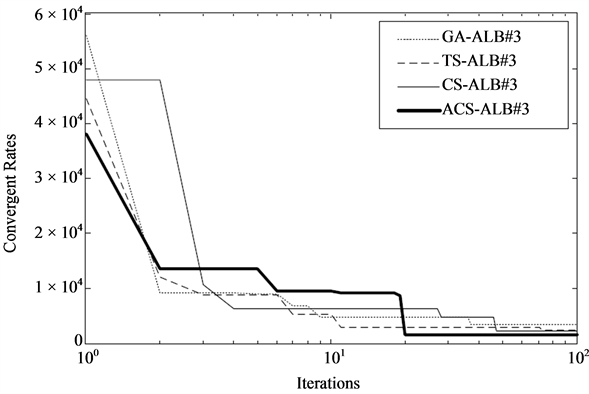
Figure 6. Convergent rate of the third ALB problem.
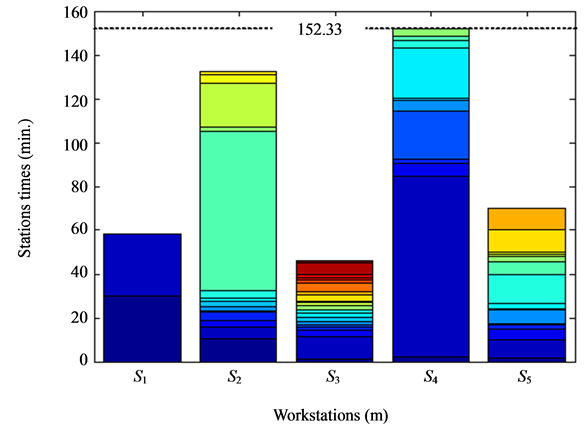
Figure 7. Turning disk assembly line by factory.
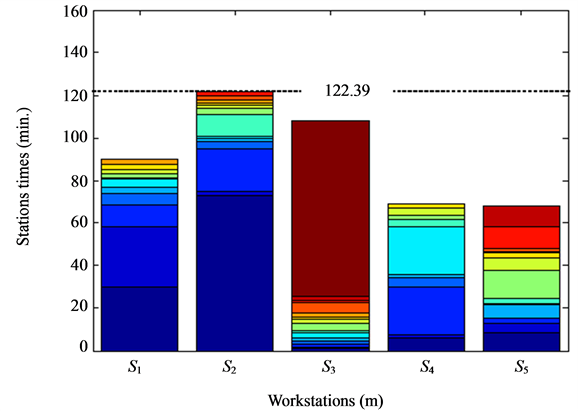
Figure 8. Turning disk assembly line by GA.

Figure 9. Turning disk assembly line by TS.
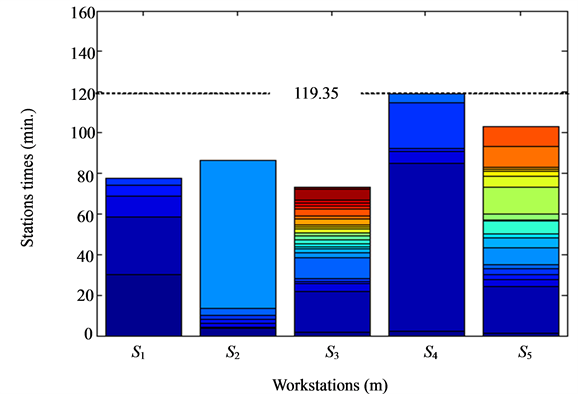
Figure 10. Turning disk assembly line by CS.
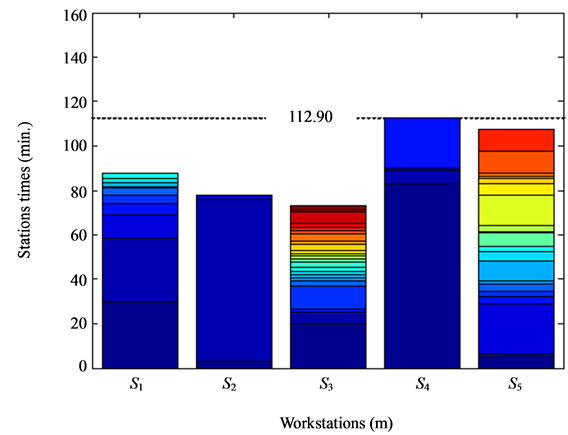
Figure 11. Turning disk assembly line by ACS.
Table 4. Tasks for turning disk assembly line by factory.
Table 8. Tasks for turning disk assembly line by ACS.
Table 9. Yearly results of energy resource management of ALB problems.
obtained by GA, TS and CS, while E obtained by the ACS is the highest. Productivity, total energy consumption, PDTE and PDSE can be yearly calculated and also summarized in Table9
Referring to Table 9, results of energy resource management of all three ALB problems are yearly summarized. It was found that productivity of all lines is significantly increased. The highest productivity of all lines is achieved due to the least workload variance obtained by the proposed ACS. For the first ALB problem once compared with factory, the productivity of 24.46%, 26.23%, 27.63% and 34.93% can be increased by GA, TS, CS and ACS, respectively. For the second ALB problem once compared with factory, the productivity of 70.03%, 86.42%, 91.23% and 95.42% can be increased by GA, TS, CS and ACS, respectively. For the third ALB problem once compared with factory, the productivity of 81.88%, 81.88%, 83.89% and 91.82% can be increased by GA, TS, CS and ACS, respectively. These cause total and main energies per year are increased proportionally, while supporting energy is unchanged. In contrast, once considering energy per product, it was found that total and supporting energies per product are decreased proportionally, while main energy is unchanged. As results in Table 9, for the first ALB problem once compared with factory, the total energy per product of 8.31%, 8.73%, 9.15% and 10.94% can be decreased by GA, TS, CS and ACS, respectively. For the second ALB problem once compared with factory, the total energy per product of 19.41%, 21.84%, 22.49% and 23.01% can be decreased by GA, TS, CS and ACS, respectively. For the third ALB problem once compared with factory, the total energy per product of 22.71%, 22.71%, 23.01% and 24.14% can be decreased by GA, TS, CS and ACS, respectively. In addition, for the first ALB problem once compared with factory, the supporting energy per product of 19.65%, 20.78%, 21.65% and 25.88% can be decreased by GA, TS, CS and ACS, respectively. For the second ALB problem once compared with factory, the supporting energy per product of 41.19%, 46.36%, 47.71% and 48.83% can be decreased by GA, TS, CS and ACS, respectively. For the third ALB problem once compared with factory, the supporting energy per product of 45.02%, 45.02%, 45.62% and 47.87% can be decreased by GA, TS, CS and ACS, respectively. It can be noticed that for all problems, the maximum PDTE and the maximum PDSE are achieved by the ACS.
6. Conclusion
Optimization of energy resource management for assembly line balancing (ALB) problems in a car factory by the adaptive current search (ACS) has been proposed in this paper. With proposed optimization approach, assembly lines are balanced in order to optimize their energy resources management. The ACS has been used to address the number of tasks assigned for each workstation. Three selected real-world ALB problems, i.e. turning disk, dragging arm and frame assembly lines, from a specific car factory are conducted. By comparison, the ACS outperforms genetic algorithm (GA), tabu search (TS) and current search (CS). Results obtained by the ACS are superior to those obtained by other algorithms. The workload variances of all lines obtained by the ACS are less than those obtained by GA, TS and CS, whereas the line efficiencies of all lines achieved by the ACS are the highest values among those algorithms. In sense of energy resource management optimization, it was found that the least workload variances obtained by the ACS caused the highest productivities of all lines. The maximum percent of decreased total energy per product and the maximum percent of decreased supporting energy per product are also successfully achieved due to the least workload variance obtained by the proposed ACS. It can be concluded that the ACS is one of the most efficient algorithms and can be an alternative to optimize the energy resource management problems.
Acknowledgements
The authors wish to thank Sammitr Motors Manufacturing Public Co., Ltd., Samut Sakhon, Thailand for supporting the practical data of assembly lines. Sincere thanks are due to the editor and anonymous reviewers for their constructive comments.
[1] REFERENCES
[2] W. C. Turner, “Energy Management Handbook,” Fairmont Press, USA, 2004.
[3] B. L. Capehart, W. C. Turner and W. J. Kennedy, “Guide to Energy Management,” Fairmont Press, USA, 1983.
[4] D. T. Pham and D. Karaboga, “Intelligent Optimization Techniques,” Springer, London, 2000. http://dx.doi.org/10.1007/978-1-4471-0721-7
[5] F. Glover and G. A. Kochenberger, “Handbook of Metaheuristics,” Kluwer Academic Publishers, New York, 2003.
[6] E. G. Talbi, “Metaheuristics form Design to Implementation,” John Wiley & Sons, New Jersey, 2009.
[7] X. S. Yang, “Nature-Inspired Metaheuristic Algorithms,” Luniver Press, United Kingdom, 2010.
[8] X. S. Yang, “Engineering Optimization: An Introduction with Metaheuristic Applications,” John Wiley & Sons, New Jersey, 2010. http://dx.doi.org/10.1002/9780470640425
[9] S. S. Rao, “Engineering Optimization: Theory and Practice,” John Wiley & Sons, New Jersey, 2009. http://dx.doi.org/10.1002/9780470549124
[10] K. Sopian, A. Zaharim, Y. Ali and Z. Nopiah, “Optimal Operational Strategy for Hybrid Renewable Energy System using Genetic Algorithms,” WSEAS Transactions on Mathematics, Vol. 7, No. 4,2008, pp. 130-140.
[11] Y. A. Katsigiannis and P. S. Georgilakis, “Optimal Sizing of Small Isolated Hybrid Power Systems Using Tabu Search,” Journal of Optoelectronics and Advanced Materials, Vol. 10, No. 5, 2008, pp. 1241-1245.
[12] V. Aristidis, P. Maria and L. Christos, “Particle Swarm Optimization (PSO) Algorithm for Wind Farm Optimal Design,” International Journal of Management Science and Engineering Management, Vol. 5, No. 1, 2010, pp. 53-58.
[13] T. Ratniyomchai, A. Oonsivilai, P. Pao-La-Or and T. Kulworawanichpong, “Economic Load Dispatch using Improved Harmony Search,” WSEAS Transactions on Systems and Control, Vol. 5, No. 4, 2010, pp. 248-257.
[14] M. D. Kilbridge and L. Wester, “A Heuristic Method of Assembly Line Balancing,” The Journal of Industrial Engineering, Vol. 12, No. 4, 1961, pp. 292-298.
[15] M. Amen, “Heuristic Methods for Cost-Oriented Assembly Line Balancing: A Comparison on Solution Quality and Computing Time,” International Journal of Production Economics, Vol. 69, No. 3, 2001, pp. 255-264. http://dx.doi.org/10.1016/S0925-5273(99)00096-1
[16] J. Rubinovitz and G. Lavitin, “Genetic Algorithm for Assembly Line Balancing,” International Journal of Production Economics, Vol. 41, No. 1-3, 1995, pp. 343-354. http://dx.doi.org/10.1016/0925-5273(95)00059-3
[17] W. C. Chiang, “The Application of the Tabu Search Metaheuristic to the Assembly Line Balancing Problem,” Journal of Operation Research, Vol. 77, 1998, pp. 209-227.
[18] S. D. Lapierre, A. Ruiz and P. Sariano, “Balancing Assembly Lines with Tabu Search,” European Journal of Operation Research, Vol. 168, No. 3, 2006, pp. 826-837. http://dx.doi.org/10.1016/j.ejor.2004.07.031
[19] J. G. Fernando and J. R. Almeida, “Hybrid Genetic Algorithm for Assembly Line Balancing,” Journal of Heuristics, Vol. 8, No. 6, 2002, pp.629-642. http://dx.doi.org/10.1023/A:1020377910258
[20] S. Suwannarongsri, S. Limnararat and D. Puangdownreong, “A New Hybrid Intelligent Method for Assembly Line Balancing,” Proceeding of the IEEE International Conference on Industrial Engineering and Engineering Management (IEEM 2007), Singapore, 2-4 December 2007, pp.1115-1119. http://dx.doi.org/10.1109/IEEM.2007.4419365
[21] A. Sukulin and D. Puangdownreong, “A Novel Metaheuristic Optimization Algorithm: Current Search,” Proceeding of the 11th WSEAS International Conference on Artificial Intelligence, Knowledge Engineering and Data Bases (AIKED'12), Cambridge, 22-24 February 2012, pp. 125-130.
[22] A. Sukulin and D. Puangdownreong, “Control Synthesis for Unstable Systems via Current Search,” Proceeding of the 11th WSEAS International Conference on Artificial Intelligence, Knowledge Engineering and Data Bases (AIKED '12), Cambridge, 22-24 February 2012, pp. 131-136.
[23] A. Sukulin and D. Puangdownreong, “Current Search and Applications in Analog Filter Design Problems,” Communication and Computer, Vol. 9, No. 9, 2012, pp. 1083-1096.
[24] S. Suwannarongsri, T. Bunnag and W. Klinbun, “Energy Resource Management of Assembly Line Balancing Problem Using Modified Current Search,” International Journal of Intelligent Systems and Applications (IJISA), Vol. 6, No. 2, 2013, in Press.
[25] A. L. Gutjahr and G. L. Nemhauser, “An Algorithm for the Balancing Problem,” Management Science, Vol. 11, No. 2, 1964, pp. 23-25. http://dx.doi.org/10.1287/mnsc.11.2.308
[26] A. L. Arcus, “COMSOAL: A Computer Method of Sequencing Operations for Assembly Line,” International Journal of Production Research, Vol. 4, 1966, pp. 25-32.
[27] Sammitr Motors Manufacturing Public Co., Ltd., 2013. http://www.sammitr.com/
[28] D. E. Goldberg, “Genetic Algorithms in Search Optimization and Machine Learning,” Addison Wesley Publishers, Boston, 1989.
[29] MathWorks, “Genetic Algorithm and Direct Search Toolbox: For Use with MATLAB,” User’s Guide, Version 1, MathWorks, Natick, 2005.
[30] F. Glover, “Tabu Search. Part I,” ORSA Journal on Computing, Vol. 1, No. 3, 1989, pp. 190-206.
[31] F. Glover, “Tabu Search. Part II,” ORSA Journal on Computing, Vol. 2, No. 1, 1990, pp. 4-32. http://dx.doi.org/10.1287/ijoc.2.1.4
Appendix


