American Journal of Operations Research
Vol.3 No.3(2013), Article ID:31666,5 pages DOI:10.4236/ajor.2013.33030
Geometric Study of the Weak Equilibrium in a Weighted Case for a Two-Dimensional Competition Game
1Departamento de Matemática Aplicada de la E.T.S.I. Caminos, Canales y Puertos. Universidad Politécnica de Madrid, Madrid, Spain
2Departamento de Matemática Aplicada, E.T.S. de Ingeniería, Universidad Pontificia Comillas de Madrid, Madrid, Spain
Email: marilo.lopez@upm.es, jrodrigo@upcomillas.es, jmanuel.sanchez@gmx.es
Copyright © 2013 López M. Dolores et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 18, 2013; revised February 22, 2013; accepted March 2, 2013
Keywords: Game Theory; Approximated Equilibrium; Location; Computational Geometry; Convex Hull
ABSTRACT
In this work, an improvement of the results presented by [1] Abellanas et al. (Weak Equilibrium in a Spatial Model. International Journal of Game Theory, 40(3), 449-459) is discussed. Concretely, this paper investigates an abstract game of competition between two players that want to earn the maximum number of points from a finite set of points in the plane. It is assumed that the distribution of these points is not uniform, so an appropriate weight to each position is assigned. A definition of equilibrium which is weaker than the classical one is included in order to avoid the uniqueness of the equilibrium position typical of the Nash equilibrium in these kinds of games. The existence of this approximated equilibrium in the game is analyzed by means of computational geometry techniques.
1. Introduction
Works exist that generalize the study of the Nash equilibrium in a competitive game with two players [1,2]. This generalization is usually performed by means of new definitions of equilibrium that are weaker than the classical one.
In this paper, the definition of weak equilibrium and the game stated in [1] is adapted to a more general game where an appropriate weight is assigned to each position the players aim for. The results included in said paper have been then generalized to be adapted to these new considerations.
The study carried out in this article after the consideration of weights implies a step forward with respect to the existing competition models, since it enables a better adaptation to real cases.
The description of the game is as follows: Two considered players want to earn the maximum number of points from a finite set of points in the plane. For this purpose they choose their positions in the plane to attract the largest possible weight of a given set of n weighted points in the plane .
.
The perpendicular bisector of the players’ locations partitions the plane into two regions. Each player is considered to capture those points which lie closer to their own position than to that of the other player [3-8]. The pay-off of each player is then the total weight of the captured points.
In formal terms, consider a strategic game 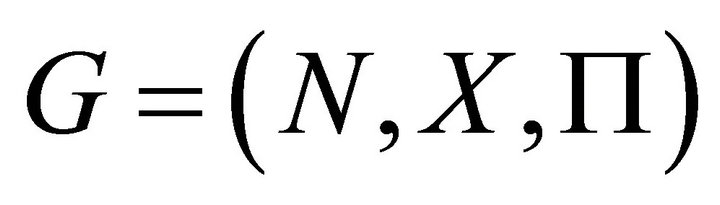 , where
, where is the set of two players,
is the set of two players,  is the strategy space, and
is the strategy space, and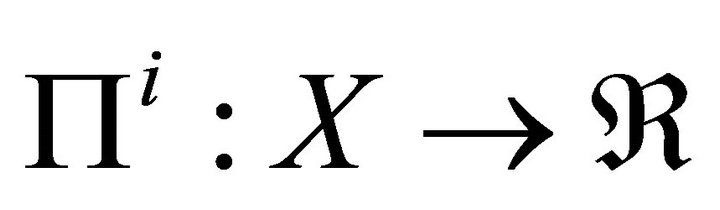 ,
, 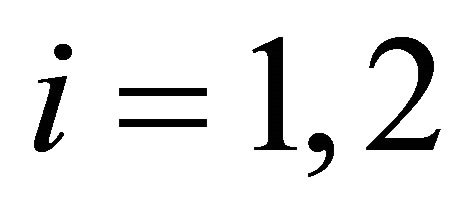 is the payoff function of each player.
is the payoff function of each player.
The description of the payoff function in the game presented above is given by:
 weight of the points pi such that
weight of the points pi such that
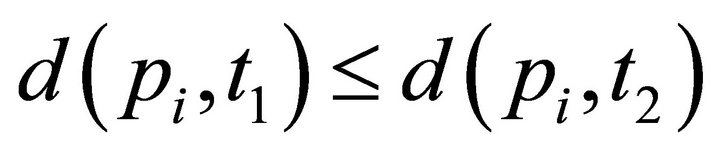
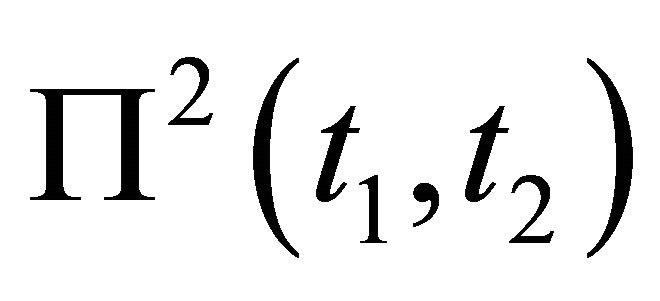 weight of the points pi such that
weight of the points pi such that
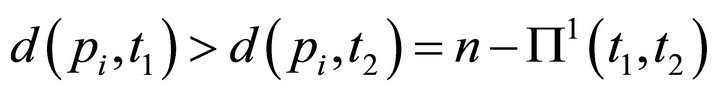
if , where
, where 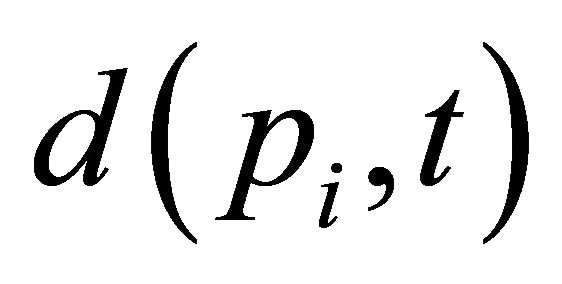 represents the Euclidean distance between the points pi, t. In the case where t1 = t2
represents the Euclidean distance between the points pi, t. In the case where t1 = t2
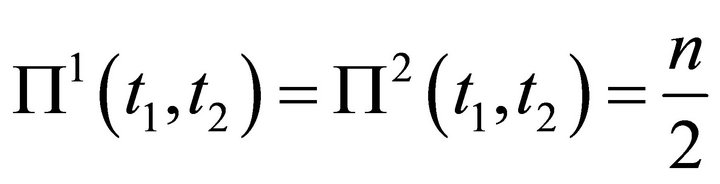 is defined.
is defined.
Therefore, if the weight of a point pi is defined as , with ki > 0 and
, with ki > 0 and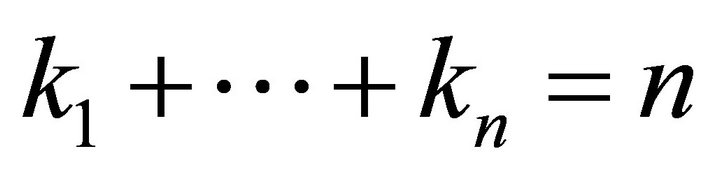 , then the payoff of the first player will be the sum of the weights of all positions located in the same half-plane as t1, including the points on the bisector. The payoff of the second player follows the same pattern, except for positions on the bisector.
, then the payoff of the first player will be the sum of the weights of all positions located in the same half-plane as t1, including the points on the bisector. The payoff of the second player follows the same pattern, except for positions on the bisector.
Along the paper, the following definitions apply:
1) The weight of a subset  of H is
of H is
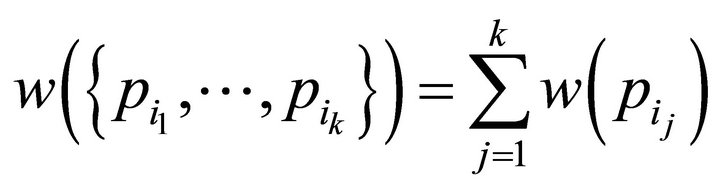 .
.
2) 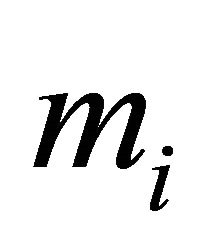 stands for the i-th weight bigger than
stands for the i-th weight bigger than 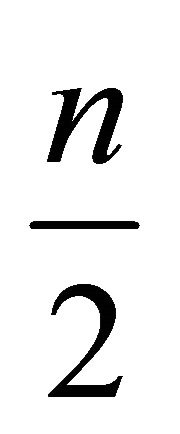 that can be attained by a subset of H. Therefore
that can be attained by a subset of H. Therefore 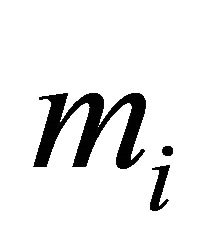 is recursively defined as follows:
is recursively defined as follows:
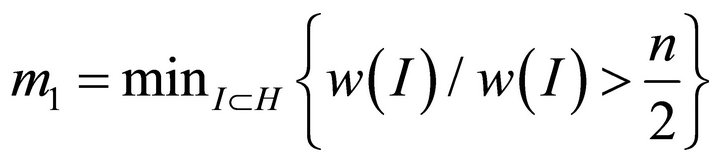 and
and
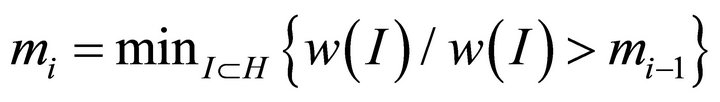 for
for .
.
3) 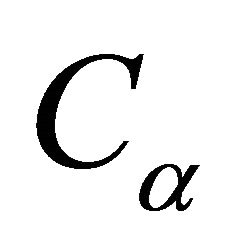 is the intersection of the convex hulls of the subsets of H with weight bigger than
is the intersection of the convex hulls of the subsets of H with weight bigger than . For a definition of the convex hull of a set, see [9].
. For a definition of the convex hull of a set, see [9].
The rest of this paper is structured as follows: In Section 2, necessary and sufficient conditions are presented for the weak equilibrium positions to exist in this weighted game. Section 3 studies the maximum number of weak equilibrium positions in which the two players are located in positions of H.
2. Weak Equilibrium
Lillo et al. 2007 [10] present necessary and sufficient conditions for the Nash equilibrium positions to exist in a game as the one considered in this paper. These conditions are stated in terms of geometric features such as convex hulls. The main conclusion is that the Nash equilibrium in the game, if it exists, is an unique point (t, t) for some . In other words, both players will choose the same position, except in cases where the points of H are aligned.
. In other words, both players will choose the same position, except in cases where the points of H are aligned.
To avoid this situation, a definition of equilibrium which is weaker than the classical one is proposed:
Definition 1: A strategy profile 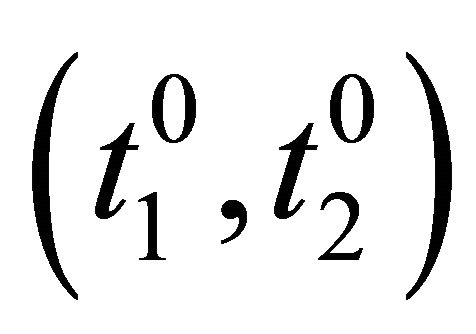 is a weak equilibrium if:
is a weak equilibrium if:
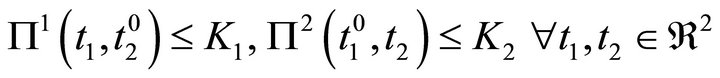 where
where
 and
and
 , that is to say
, that is to say
 is the least weight greater than
is the least weight greater than 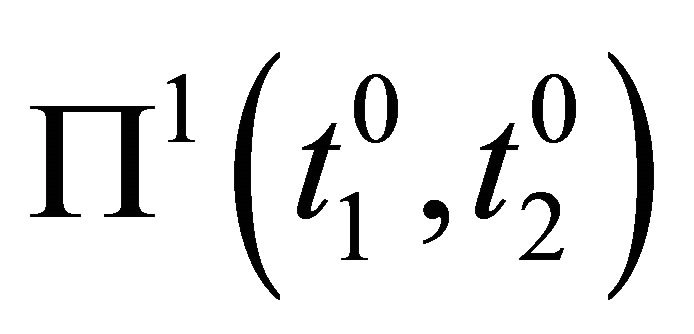 of a subset of H (analogously for
of a subset of H (analogously for ).
).
Remark: This definition is an adaptation to the discrete case of the 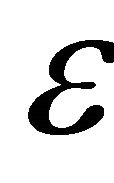 -equilibrium studied by Monderer and Shapley, 1996 [2].
-equilibrium studied by Monderer and Shapley, 1996 [2].
A geometric analysis is developed here that extends the concepts relative to the study of the Nash equilibrium in a weighted game and underlies the search for the equilibrium positions, if they exist, according to the new definition.
Proposition 1:
A weak equilibrium position  necessarily satisfies
necessarily satisfies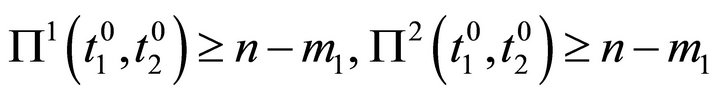 .
.
Proof:
If there exists a weak equilibrium position with, say,
 , then it is satisfied that
, then it is satisfied that
 , so
, so 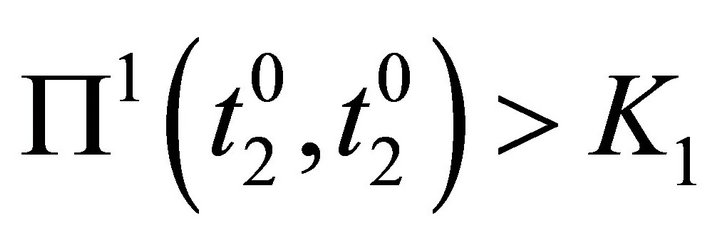 a contradiction because
a contradiction because  is a weak equilibrium position.
is a weak equilibrium position.
Remark: The proposition yields that the payoffs in a weak equilibrium position must be 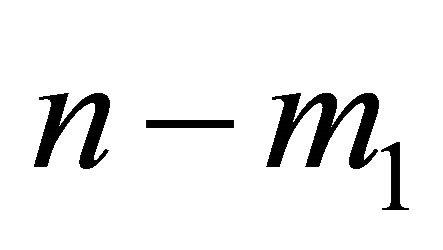 for a player and
for a player and  for the other or
for the other or 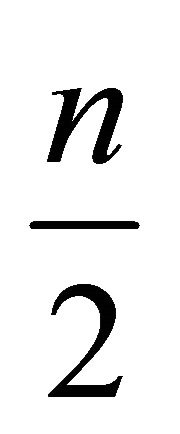 for both. It can be noted that
for both. It can be noted that 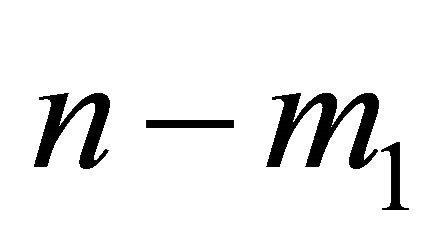 is the largest payoff smaller than
is the largest payoff smaller than 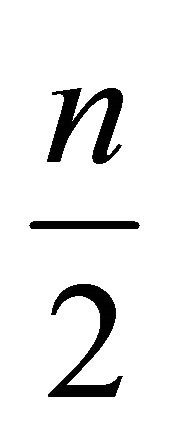 that a player can obtain.
that a player can obtain.
The following proposition gives a necessary and sufficient condition for the existence of weak equilibrium positions:
Proposition 2:
If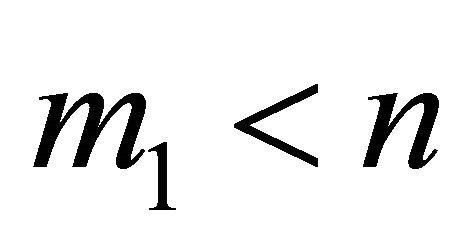 , then there exists weak equilibrium positions in the proposed game if and only if
, then there exists weak equilibrium positions in the proposed game if and only if .
.
Proof:
First it is seen that the condition is necessary: If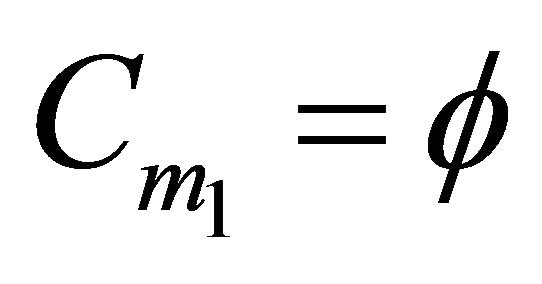 , then there exists a subset of H with weight greater than
, then there exists a subset of H with weight greater than 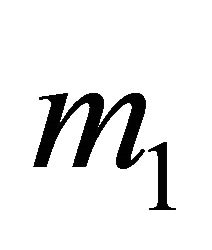 such that its convex hull does not contain the position
such that its convex hull does not contain the position  chosen by the second player (assumed without loss of generality that the payoff of the second player in said position is greater or equal than
chosen by the second player (assumed without loss of generality that the payoff of the second player in said position is greater or equal than
 ). So if the first player is located in the position
). So if the first player is located in the position 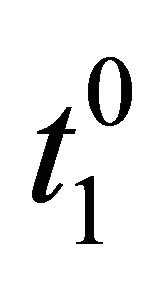 with a payoff lower than or equal to
with a payoff lower than or equal to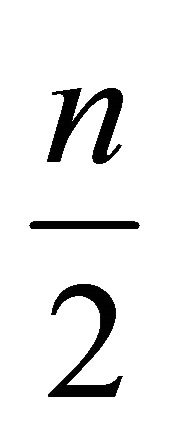 , then the first player can deviate to a position
, then the first player can deviate to a position 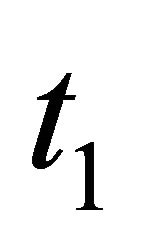 that separates
that separates 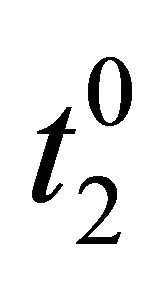 and the convex hull aforementioned, hence the first player will get a payoff greater than
and the convex hull aforementioned, hence the first player will get a payoff greater than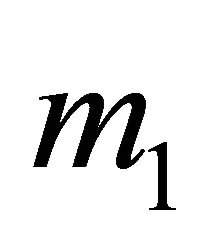 , therefore
, therefore
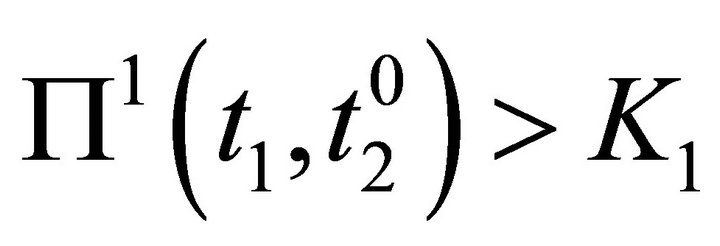 . Consequently, there is not a position
. Consequently, there is not a position
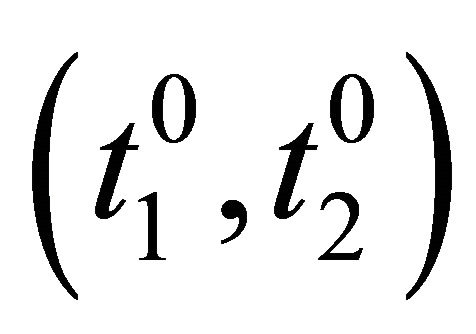 of weak equilibrium.
of weak equilibrium.
Now it is stated that the condition is sufficient: If 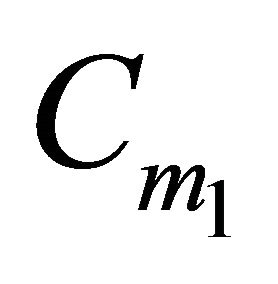 is not the empty set, then any player can locate in
is not the empty set, then any player can locate in 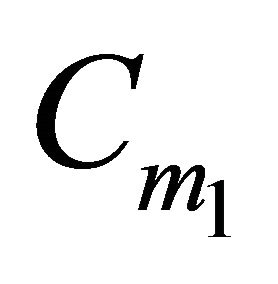 to ensure that the other player cannot get an earning bigger than
to ensure that the other player cannot get an earning bigger than 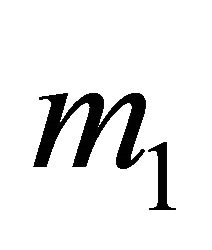 in any location, because the first player controls all the subsets of H with weight bigger than
in any location, because the first player controls all the subsets of H with weight bigger than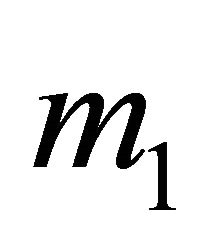 . Hence, every position
. Hence, every position 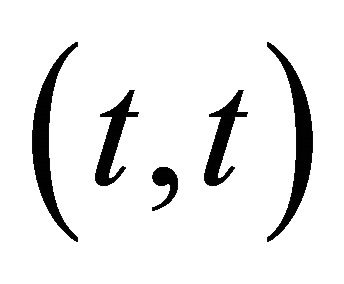 with
with  in
in 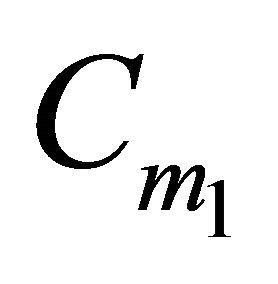 is a weak equilibrium position, because
is a weak equilibrium position, because 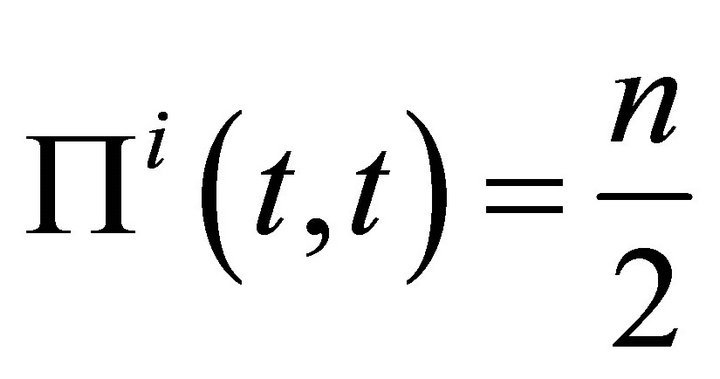 for
for 
and any player who deviates would obtain a payoff smaller or equal to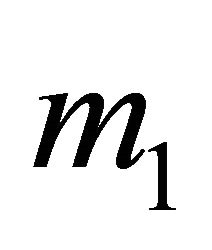 .
.
Now propositions 1 and 2 are applied to describe the weak equilibrium positions. The possible weak equilibrium positions in the proposed game are:
1) 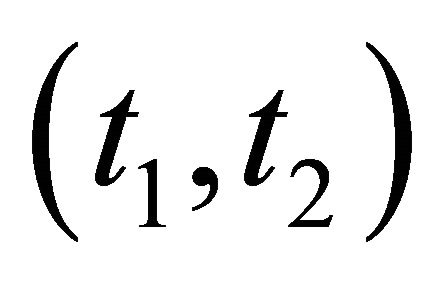 with
with ,
, 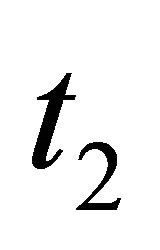 belonging to
belonging to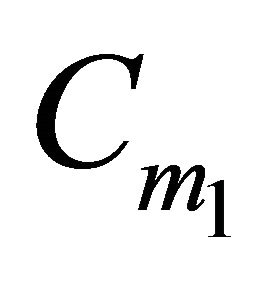 ,
,
 for
for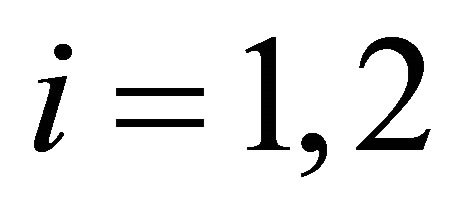 .
.
2) If there does not exist a combination of points of H with weight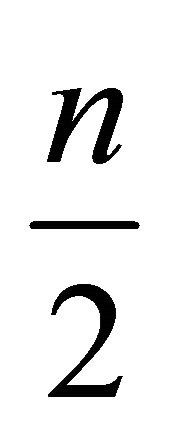 , the positions
, the positions 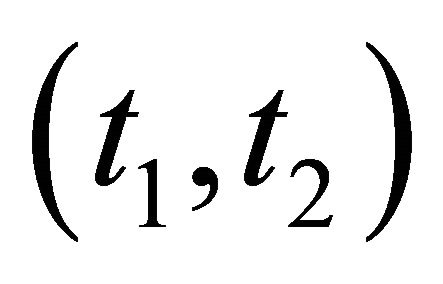 with one of the points, say
with one of the points, say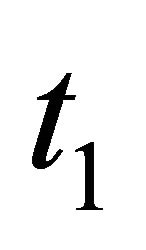 , belonging to
, belonging to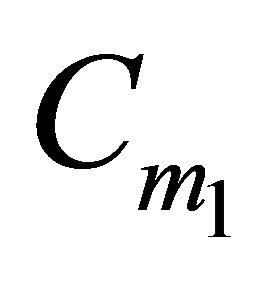 , the other one,
, the other one, 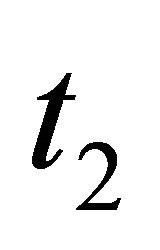 , belonging to
, belonging to ,
, 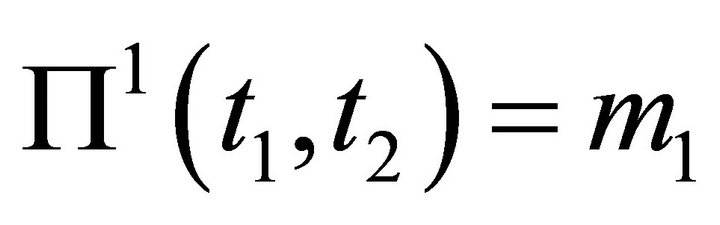 and
and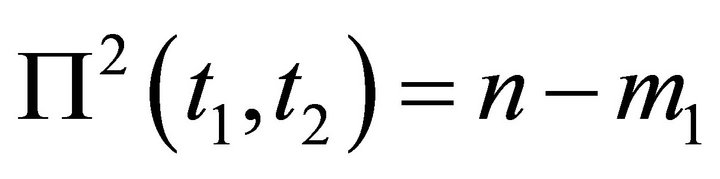 .
.
3) If there exists a combination of points of H with weight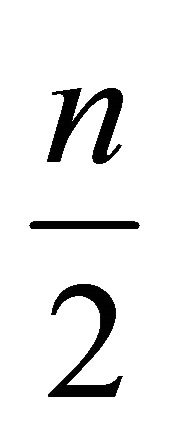 , the positions
, the positions 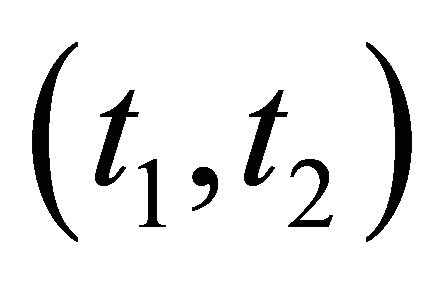 with one of the pointssay
with one of the pointssay , belonging to
, belonging to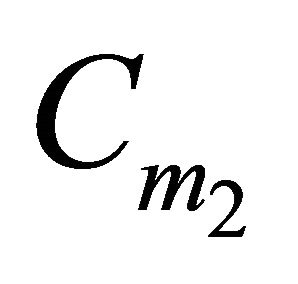 , the other point,
, the other point, 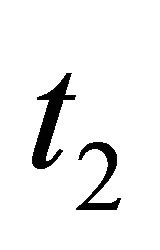 , belonging to
, belonging to ,
, 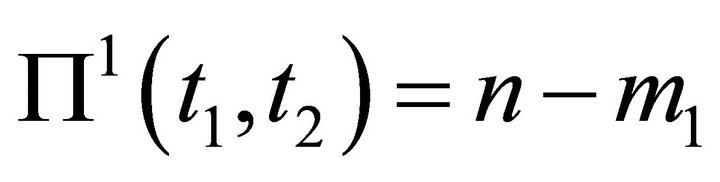 and
and .
.
3. Maximum Number of Weak Equilibrium Positions
Now the problem of finding the maximum number of points of H that can be included in  will be considered. This subset of H can be interesting for practical purposes, because it carries a large number of weak equilibrium positions in which at least one player locates in the position of one of the points in H. As an example, if the game has a political scope, where the players are parties and H is a finite set of types of voters, then this subset gives a large number of weak equilibrium positions with the parties fitting to one type of voters.
will be considered. This subset of H can be interesting for practical purposes, because it carries a large number of weak equilibrium positions in which at least one player locates in the position of one of the points in H. As an example, if the game has a political scope, where the players are parties and H is a finite set of types of voters, then this subset gives a large number of weak equilibrium positions with the parties fitting to one type of voters.
Concretely the following problem is considered:
Find the maximum number of points of H that can be included in 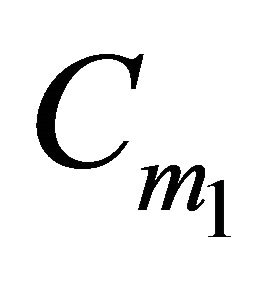 for all the possible configurations of
for all the possible configurations of 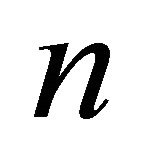 points in the plane (no three aligned) and all the possible assignations of weights for these
points in the plane (no three aligned) and all the possible assignations of weights for these 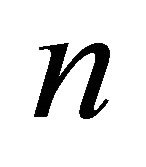 points with
points with . This last condition implies that
. This last condition implies that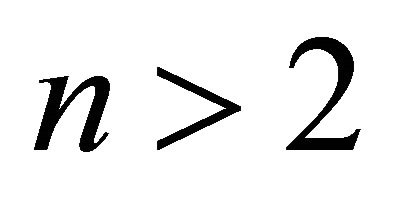 . The maximum number to be found is denoted by max.
. The maximum number to be found is denoted by max.
3.1. An Upper Bound
The following proposition gives an upper bound for max that is bounded in n. A preliminary lemma is needed:
Lemma 1:
There is some point of H in the boundary of the convex hull of H that does not belong to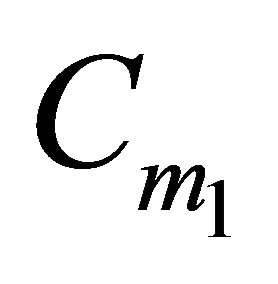 .
.
Proof:
If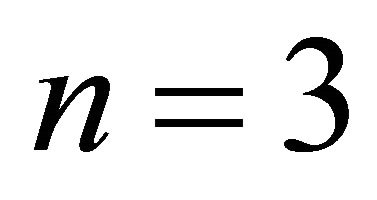 , then the points of H are in convex position (a point set is in convex position if every point of the set is a vertex of its convex hull), so the condition
, then the points of H are in convex position (a point set is in convex position if every point of the set is a vertex of its convex hull), so the condition 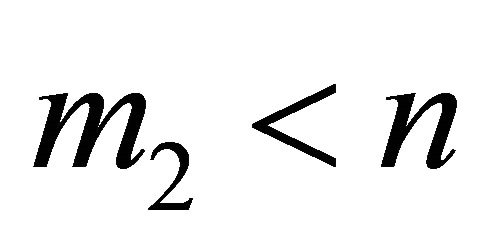 implies that there is a convex hull of a subset of H of weight
implies that there is a convex hull of a subset of H of weight 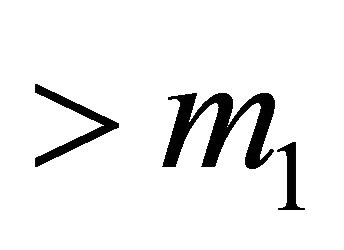 that does not contain every point of H. Hence there is a point of H in the boundary of the convex hull of H that does not belong to
that does not contain every point of H. Hence there is a point of H in the boundary of the convex hull of H that does not belong to .
.
If  and every point of H in the boundary of the convex hull of H belongs to
and every point of H in the boundary of the convex hull of H belongs to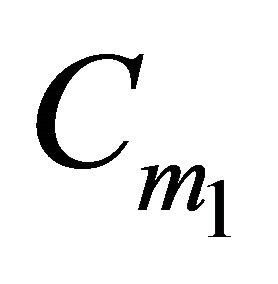 , then every subset of H with two elements must have weight
, then every subset of H with two elements must have weight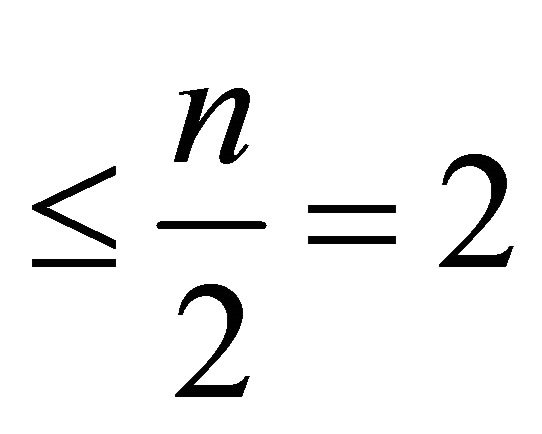 . Otherwisethere would be a subset of H of cardinal three with weight
. Otherwisethere would be a subset of H of cardinal three with weight , not containing every point of H in the boundary of the convex hull of H, a contradiction because
, not containing every point of H in the boundary of the convex hull of H, a contradiction because  contains every point of H in the boundary of the convex hull. With 4 being the weight of H, this implies that every subset of H with two elements must have weight = 2. But this is possible if and only if
contains every point of H in the boundary of the convex hull. With 4 being the weight of H, this implies that every subset of H with two elements must have weight = 2. But this is possible if and only if 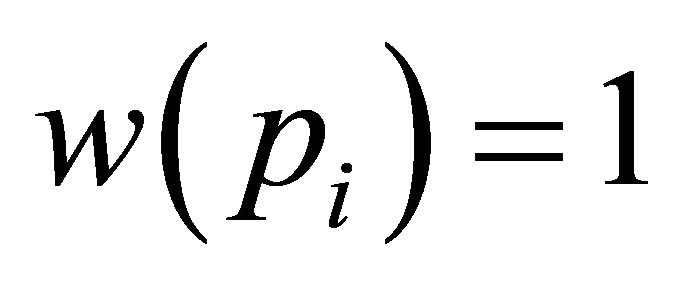 for every
for every  and then
and then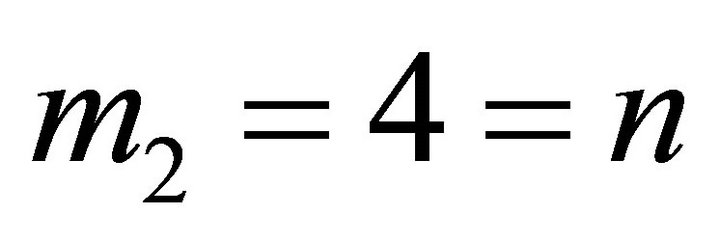 , a contradiction.
, a contradiction.
If 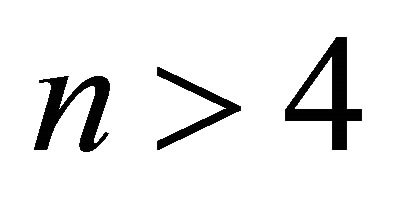 and every point of H in the boundary of the convex hull of H belongs to
and every point of H in the boundary of the convex hull of H belongs to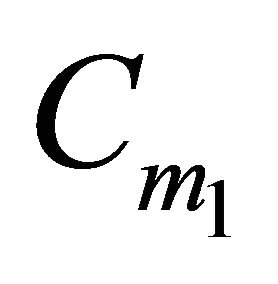 , then
, then  for every
for every 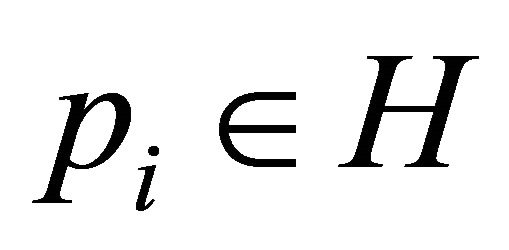 such that
such that 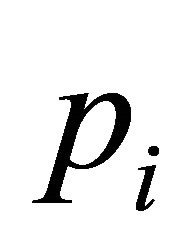 is in the boundary of the convex hull of H. Hence, if the four points of H with smallest
is in the boundary of the convex hull of H. Hence, if the four points of H with smallest 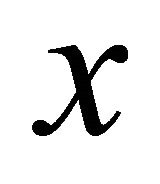 coordinate are considered, say
coordinate are considered, say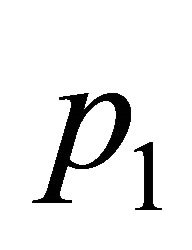 ,
,  ,
, 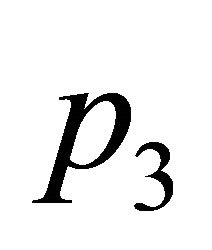 ,
,  , then
, then  is included in the convex hull of
is included in the convex hull of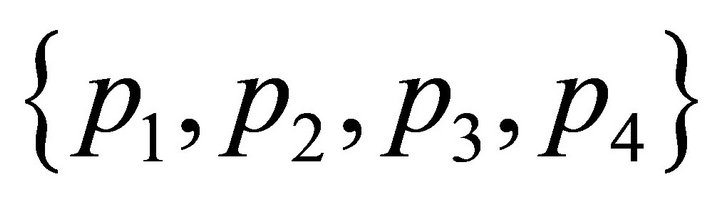 . So there is at least a point of H in the boundary of the convex hull of H that does not belong to
. So there is at least a point of H in the boundary of the convex hull of H that does not belong to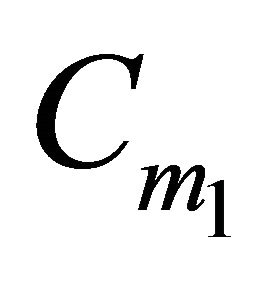 , which is the point of H with the greatest x coordinate, a contradiction.
, which is the point of H with the greatest x coordinate, a contradiction.
Proposition 3:
It is satisfied that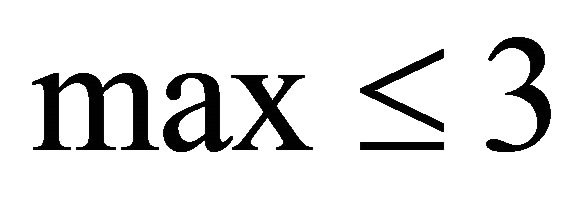 .
.
Proof:
Consider a point of H in the boundary of the convex hull of H and not belonging to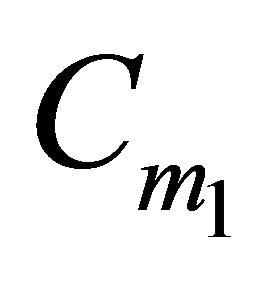 , say
, say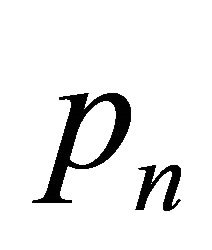 , which exists by lemma 1. Arrange the other points of H according to the angle with respect to
, which exists by lemma 1. Arrange the other points of H according to the angle with respect to , say
, say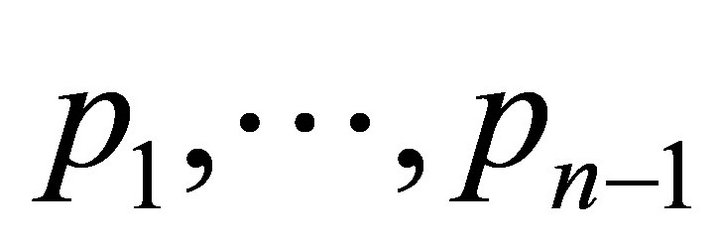 . The initial angle 0 is determined by a ray emanating from
. The initial angle 0 is determined by a ray emanating from  and containing a segment of the boundary of the convex hull of H. Hence, if
and containing a segment of the boundary of the convex hull of H. Hence, if  is the smallest index such that
is the smallest index such that
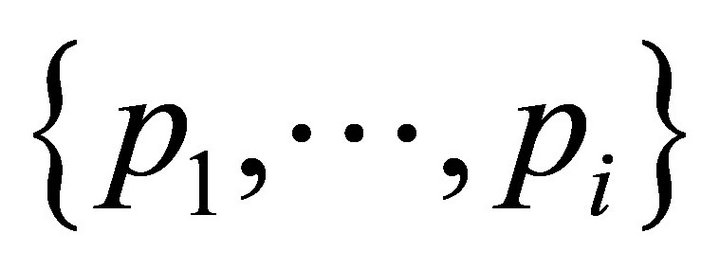 has weight greater than
has weight greater than , then
, then
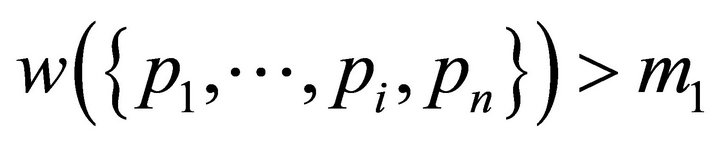 ,
, 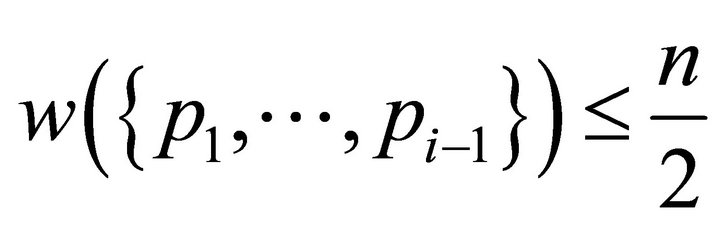 , so
, so
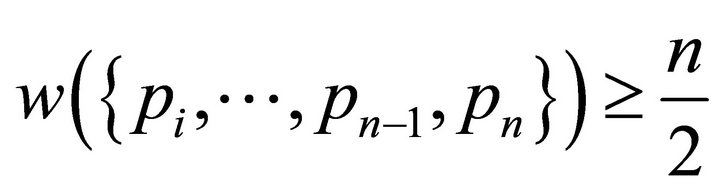 . This last inequality implies that
. This last inequality implies that
 , so
, so 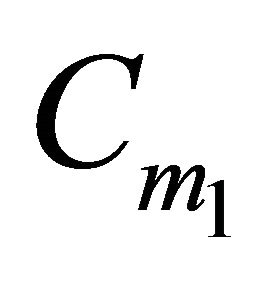 is included in the intersection of the convex hulls of
is included in the intersection of the convex hulls of ,
,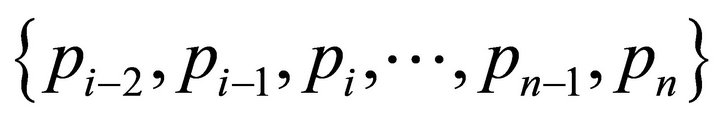 . This intersection is included in the region limited by the ray emanating from
. This intersection is included in the region limited by the ray emanating from 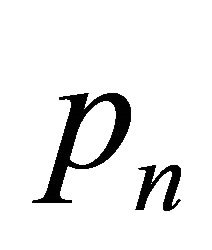 to
to 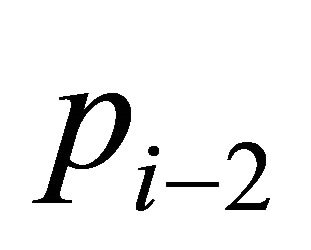 and the ray emanating from
and the ray emanating from 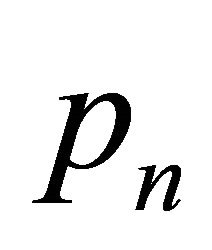 to
to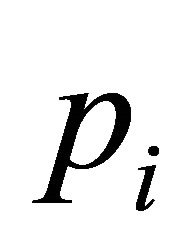 . This region contains four points of H:
. This region contains four points of H: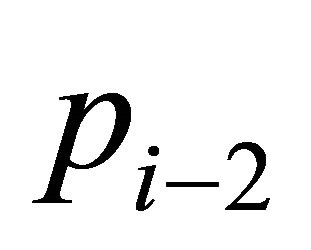 ,
, 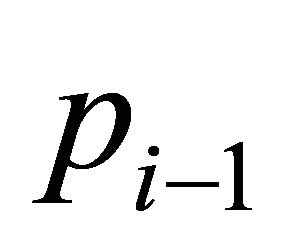 ,
, 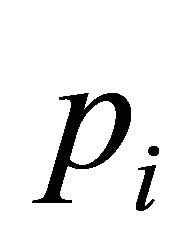 and
and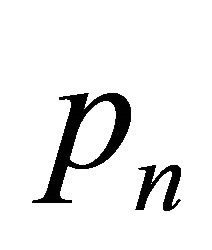 .
.
But 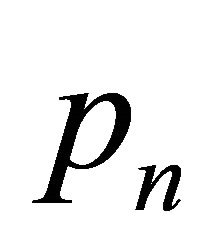 is not in
is not in 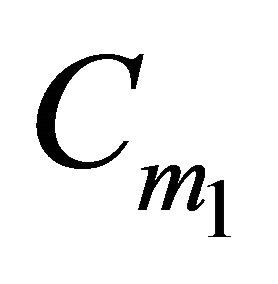 by the assumption, so at most three points of H can be located in
by the assumption, so at most three points of H can be located in 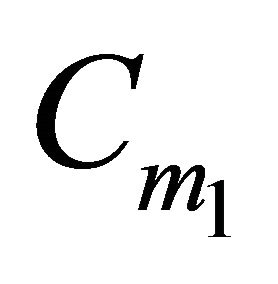 and then
and then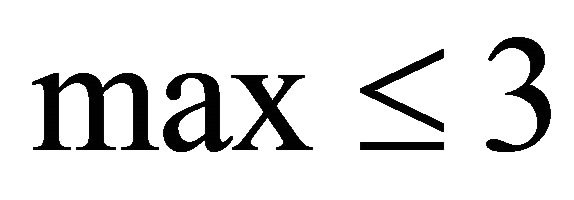 . Note that if
. Note that if , then
, then 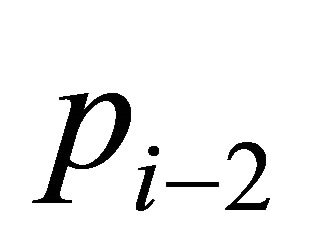 makes no sense. But in this case
makes no sense. But in this case 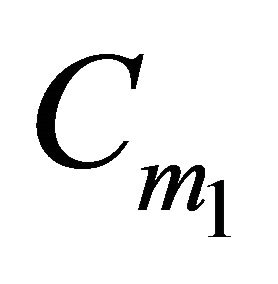 is included in the convex hull of
is included in the convex hull of , so at most two points of H are included in
, so at most two points of H are included in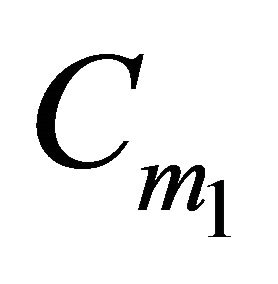 .
.
Remark: If 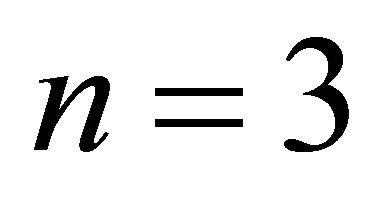 and
and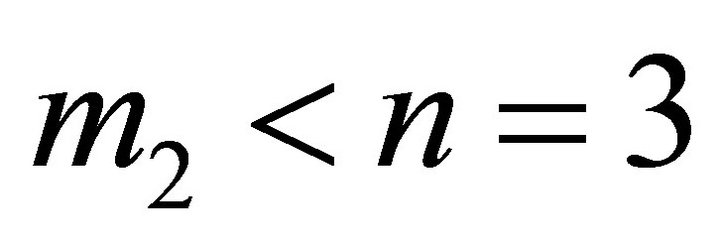 , then a point of H, say
, then a point of H, say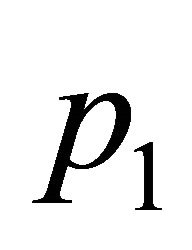 , must have weight
, must have weight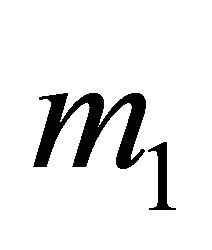 . Hence
. Hence 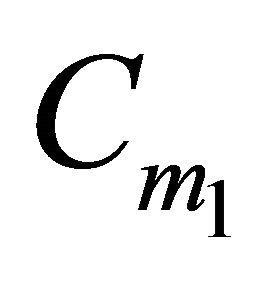 is contained in the intersection of the convex hulls of
is contained in the intersection of the convex hulls of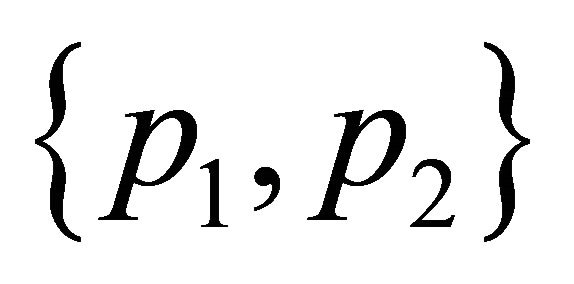 ,
,  , that is to say, in
, that is to say, in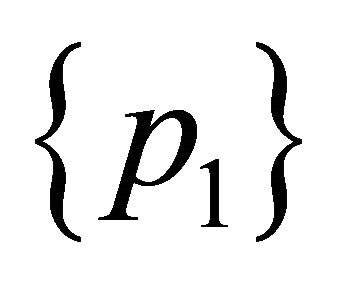 . As a matter of fact,
. As a matter of fact, 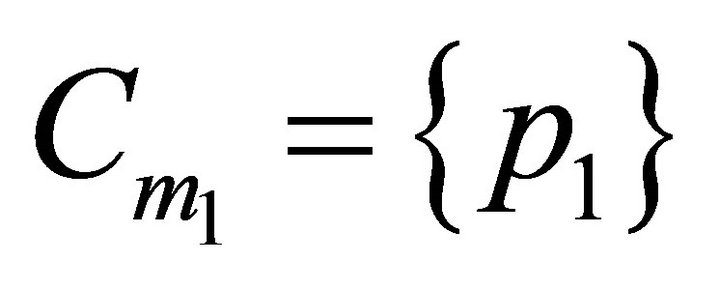 because every subset of H with weight greater than
because every subset of H with weight greater than 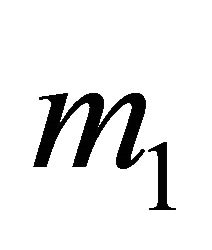 contains to
contains to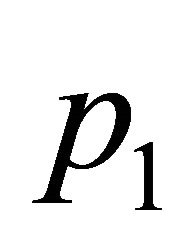 . So max = 1 for
. So max = 1 for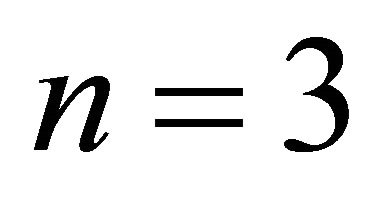 .
.
3.2. Examples Where the Upper Bound Is Attained
Now it can be seen that for even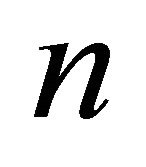 ,
, 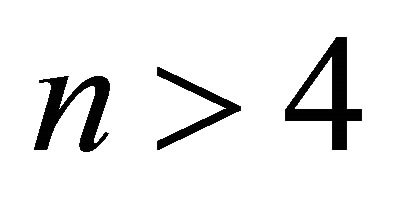 , the upper bound for max is attained in an example with equally weighted points, so
, the upper bound for max is attained in an example with equally weighted points, so 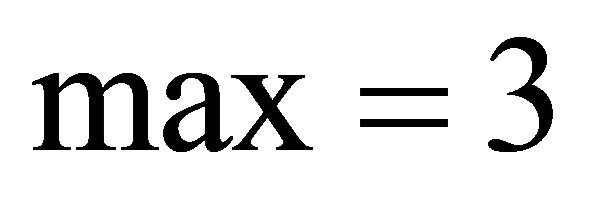 for even
for even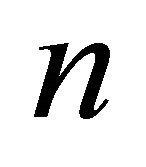 ,
,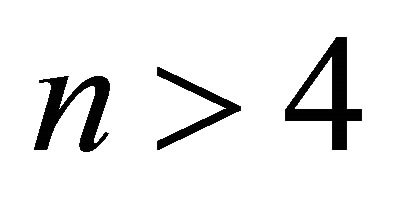 :
:
Example 1:
Let 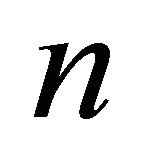 be an even number greater than 4 and consider
be an even number greater than 4 and consider 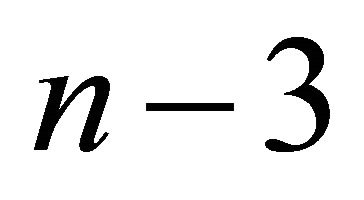 points
points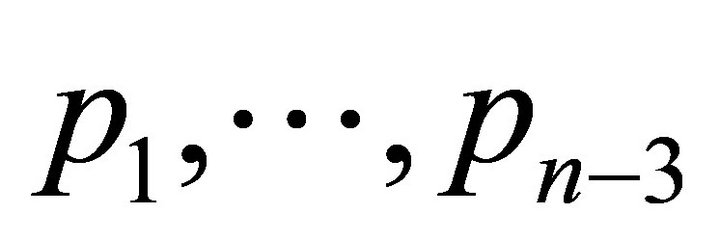 in convex position. If three new points
in convex position. If three new points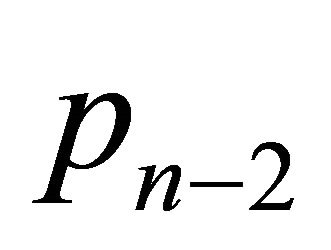 ,
,  ,
, 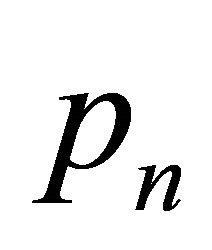 are located in the intersection
are located in the intersection 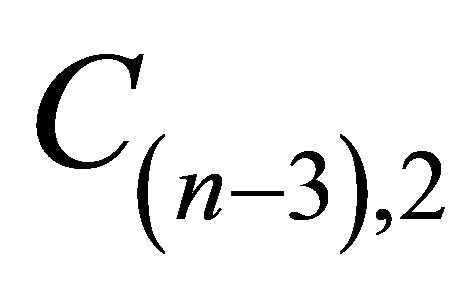 of the convex hulls of the subsets of
of the convex hulls of the subsets of
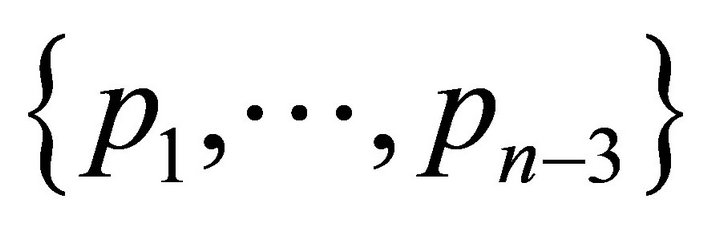 with
with 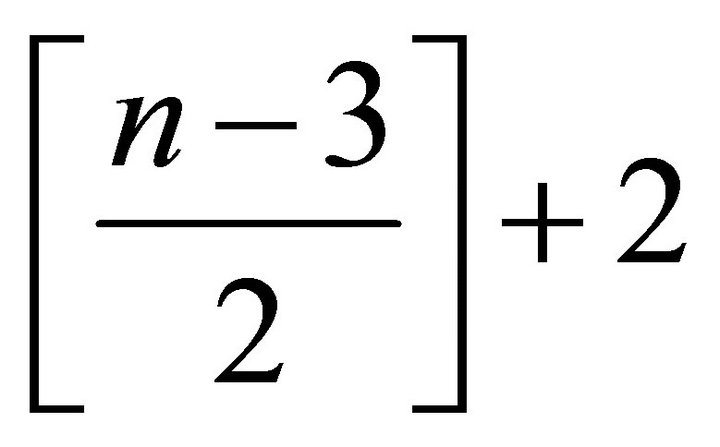 points, in such way that the
points, in such way that the 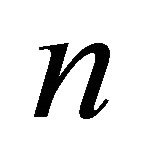 points are in general position (no three points in the same line) and weight 1 is assigned to each point, then a set
points are in general position (no three points in the same line) and weight 1 is assigned to each point, then a set 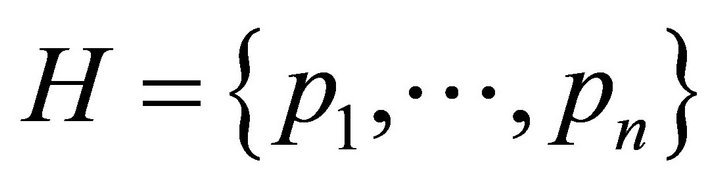 with three points in
with three points in 
 is obtained.
is obtained.
An example with 3 points in  can be seen for odd n,
can be seen for odd n, 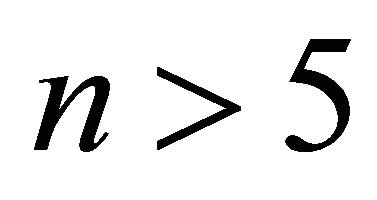 , so
, so 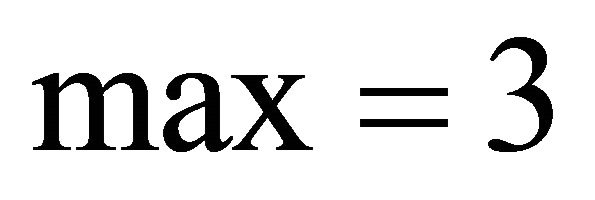 for odd
for odd ,
,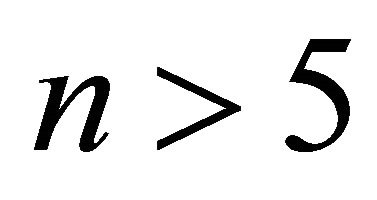 :
:
Example 2:
Consider 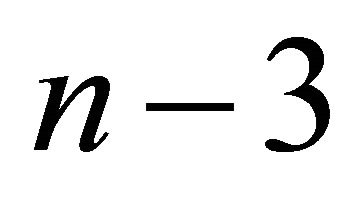 points
points  with weight
with weight
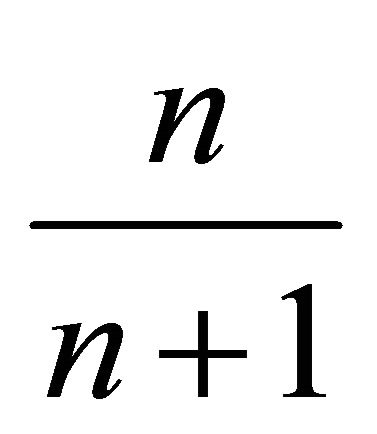 each in the vertices of a regular polygon, a point
each in the vertices of a regular polygon, a point 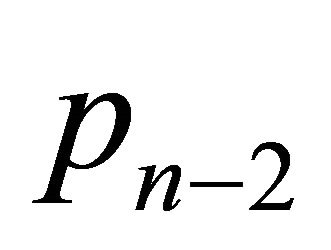 with weight
with weight  in
in 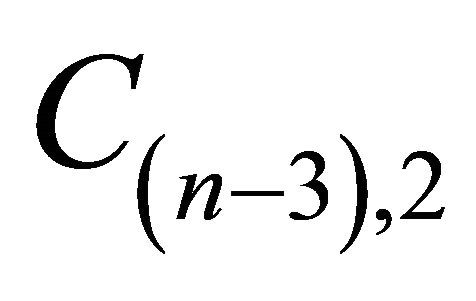 and two points
and two points ,
, 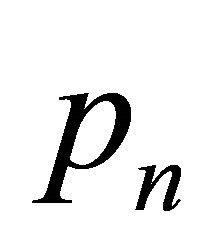 with weight
with weight 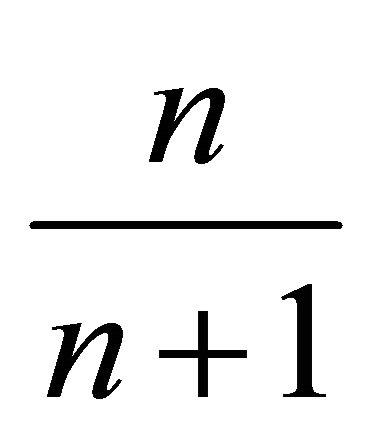 each and in
each and in . First it is noted that
. First it is noted that 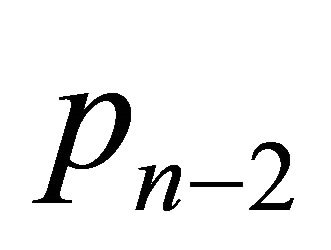 can be located in the intersection aforementioned and non-collinear with two points of
can be located in the intersection aforementioned and non-collinear with two points of 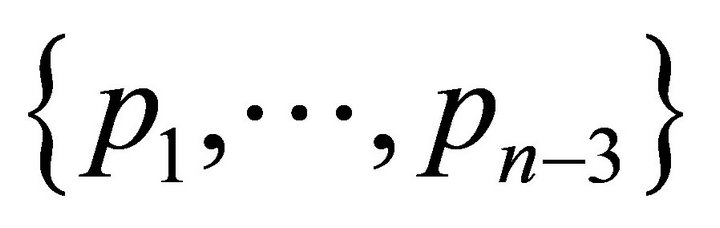 because that intersection does not have an empty interior set. In the same way it can be seen that the points
because that intersection does not have an empty interior set. In the same way it can be seen that the points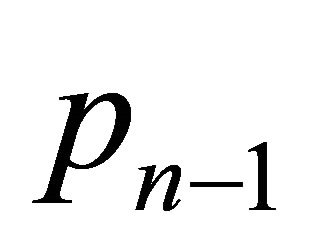 ,
,  can be located in
can be located in  such that the
such that the 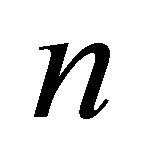 points are in general position because this last intersection also does not have an empty interior set.
points are in general position because this last intersection also does not have an empty interior set.
Now it can be seen that there does exist a subset of
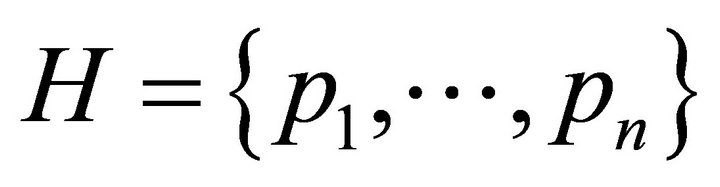 with weight
with weight . If it is considered
. If it is considered  points of weight
points of weight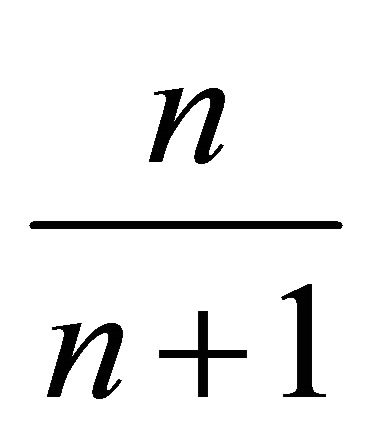 , then the weight of the subset is
, then the weight of the subset is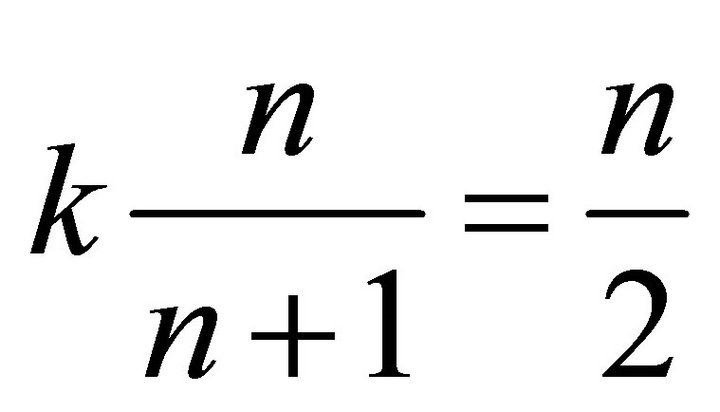 . Hence a subset of H with weight
. Hence a subset of H with weight 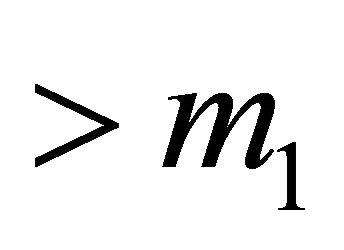 must contain
must contain 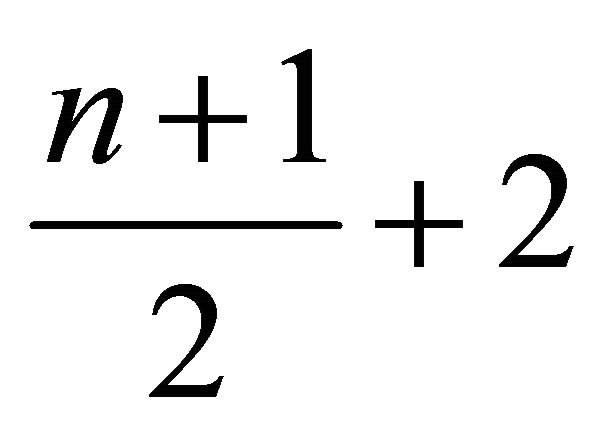 points of weight
points of weight 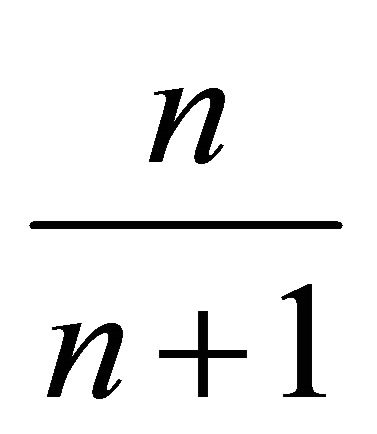 or
or 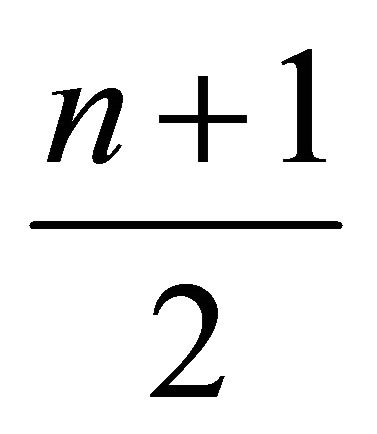 points of weight
points of weight  and
and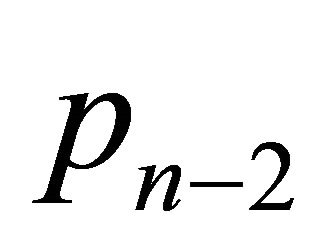 . In this last case, if said set of points does not contain both
. In this last case, if said set of points does not contain both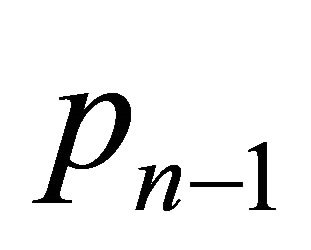 ,
,
 , then it must contain at least
, then it must contain at least 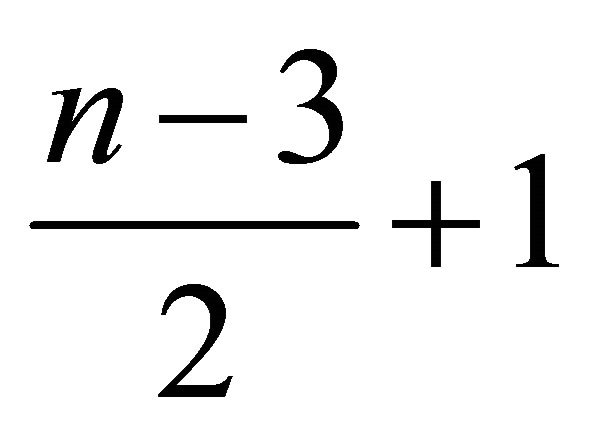 points from
points from
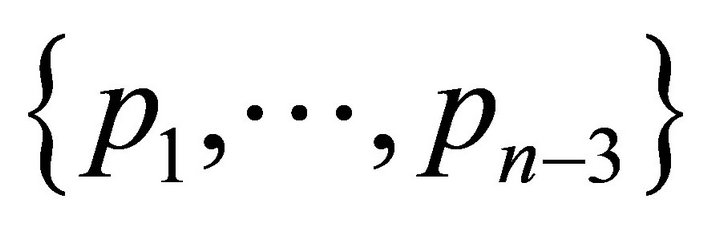 and
and , so its convex hull contains
, so its convex hull contains ,
,  by the construction of the set H. In the former case, the said set of points contains at least
by the construction of the set H. In the former case, the said set of points contains at least 
points from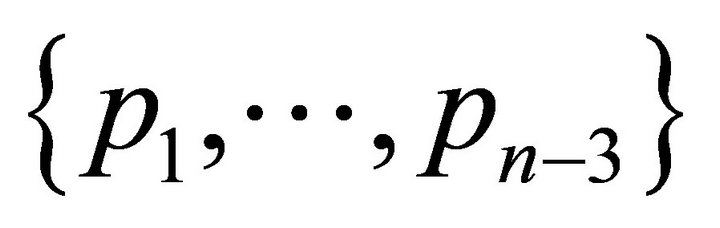 , so its convex hull contains
, so its convex hull contains ,
, 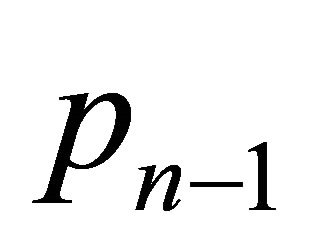 ,
, 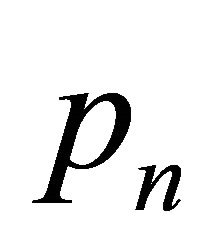 by the construction of the set H. Consequently,
by the construction of the set H. Consequently, 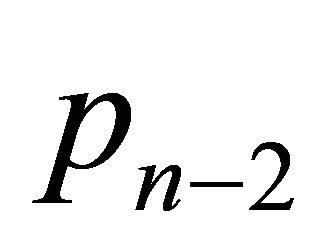 ,
, 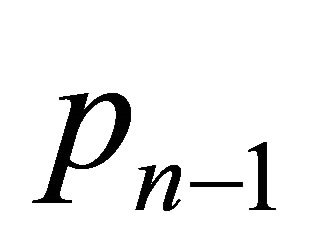 ,
, 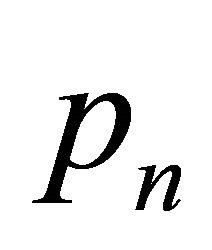 belong to
belong to 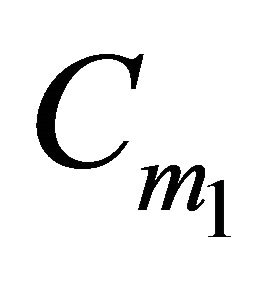 as desired.
as desired.
Now examples of sets H with three points in 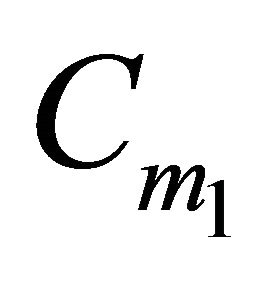 are shown for
are shown for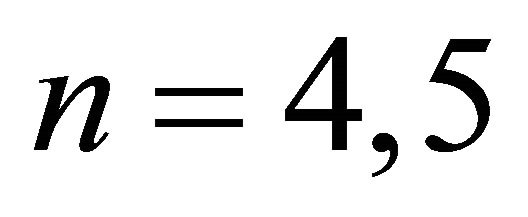 :
:
Example 3:
Consider three non-collinear points ,
, 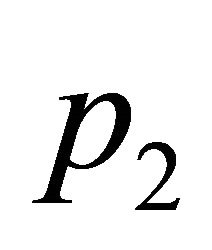 ,
, 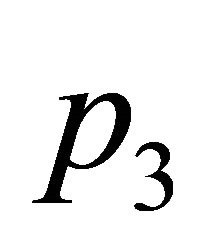 and a point
and a point  inside the triangle having vertices
inside the triangle having vertices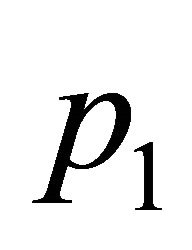 ,
, 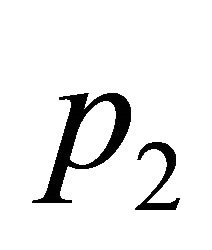 ,
,
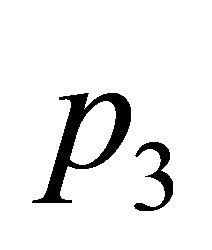 . Assign weight
. Assign weight 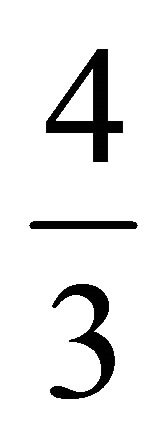 to
to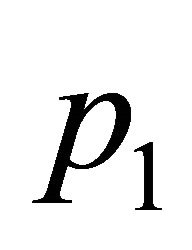 ,
,  ,
,  to
to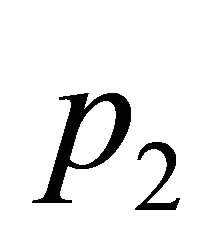 ,
, . See Figure 1. This allows for
. See Figure 1. This allows for , which is attained in the following subsets of
, which is attained in the following subsets of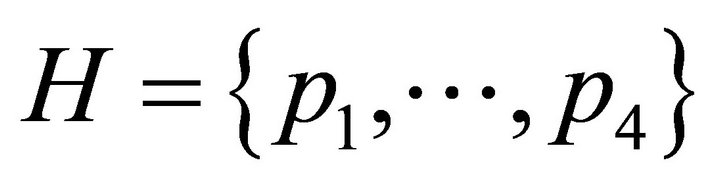 :
: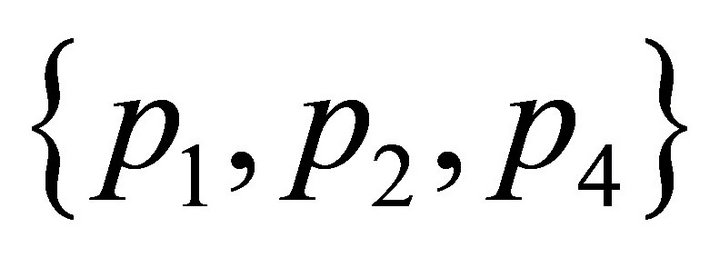 ,
, 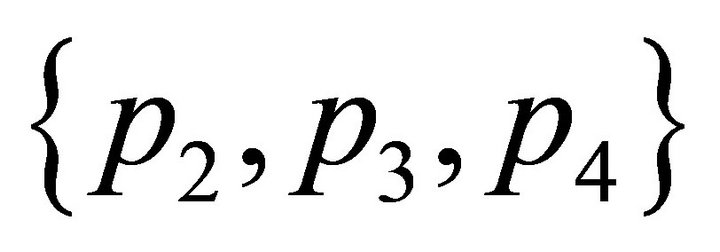 ,
,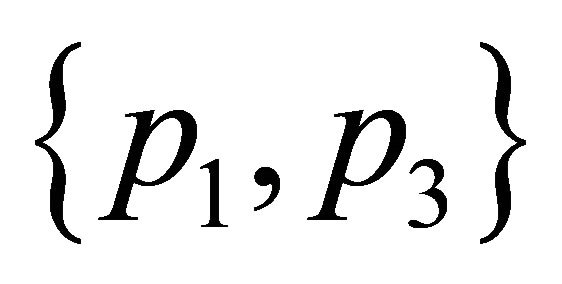 . Hence the subsets of
. Hence the subsets of  with weight
with weight 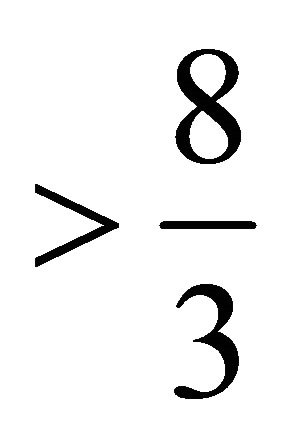 must contain
must contain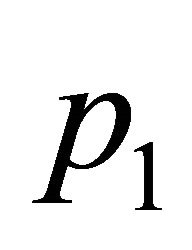 ,
, 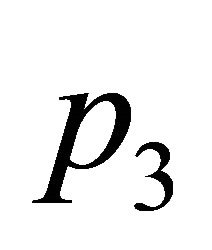 and one point of
and one point of
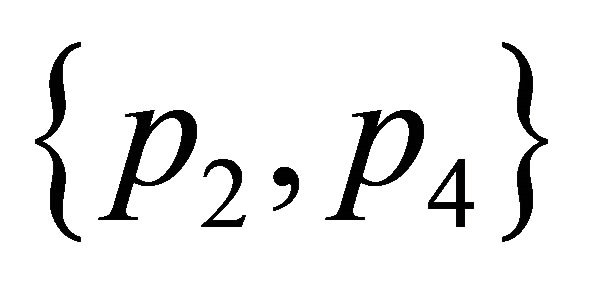 , and then their convex hulls contain the convex hull of
, and then their convex hulls contain the convex hull of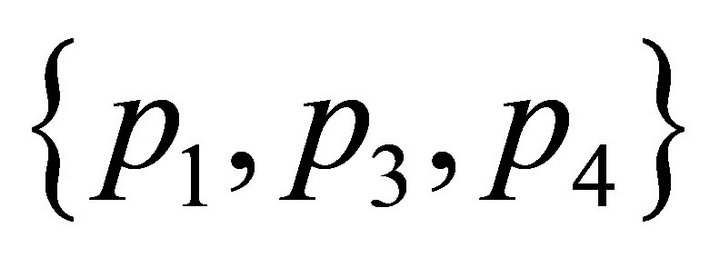 . This implies that
. This implies that 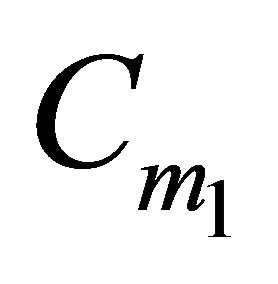 contains
contains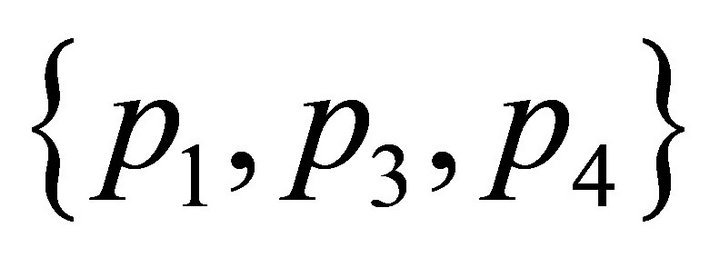 .
.
Example 4:
Consider three non-collinear points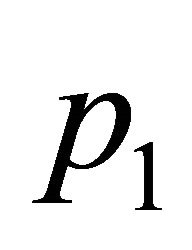 ,
, 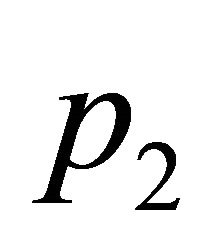 ,
, 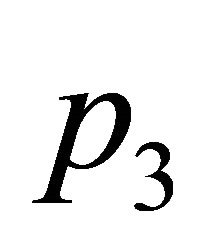 and two points
and two points ,
,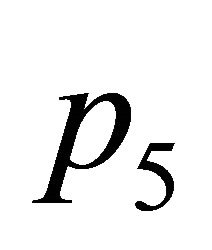 inside the triangle having vertices
inside the triangle having vertices
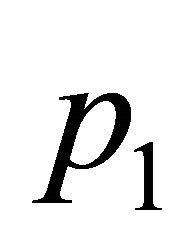 ,
,  ,
, . Assign weight
. Assign weight 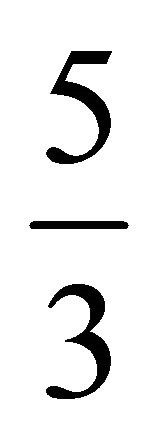 to
to ,
, 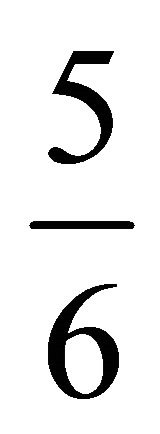 to
to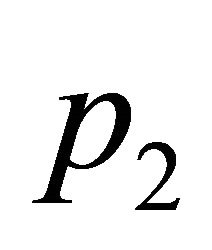 , …,
, …,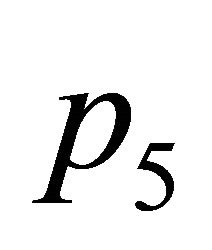 . See Figure 2. This allows for
. See Figure 2. This allows for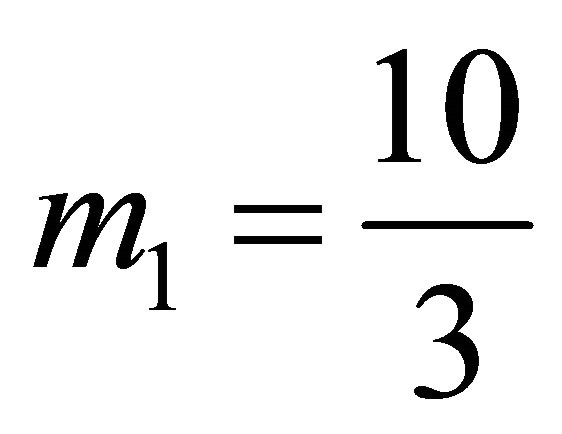 , which is
, which is
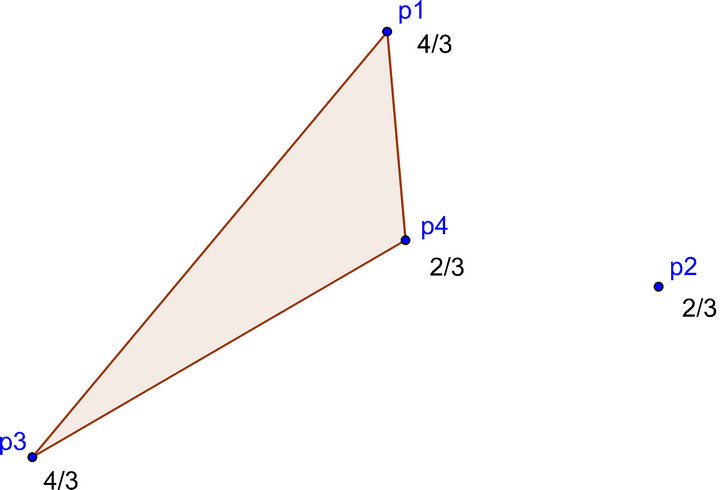
Figure 1. Example for n = 4.  is the shaded region.
is the shaded region.
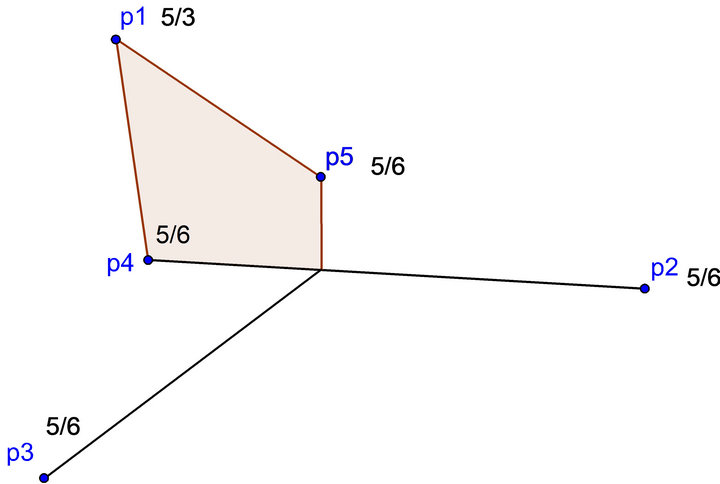
Figure 2. Example for n = 5. 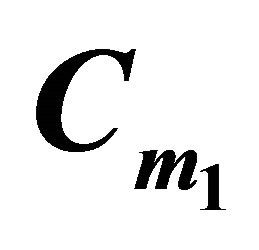 is the shaded region.
is the shaded region.
attained in the subsets of 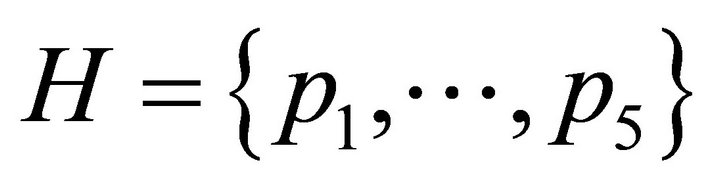 of cardinal three containing
of cardinal three containing  and in the set
and in the set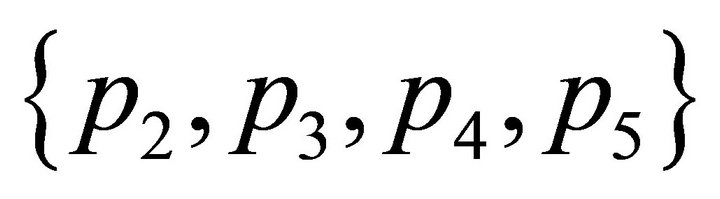 .
.
Hence the subsets of  with weight
with weight 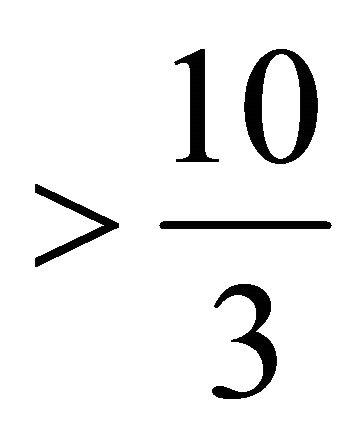 must contain to
must contain to  and at least three points of
and at least three points of , and then their convex hulls contain
, and then their convex hulls contain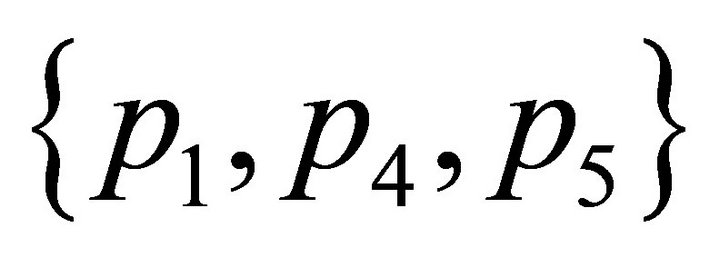 . This implies that
. This implies that 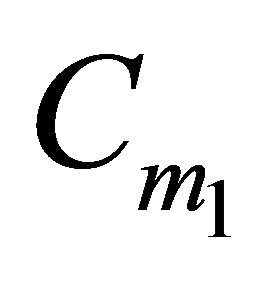 contains this set of three points of
contains this set of three points of .
.
Proposition 3, its remark and the previous examples yield the following corollary:
Corollary 1:
It is satisfied that 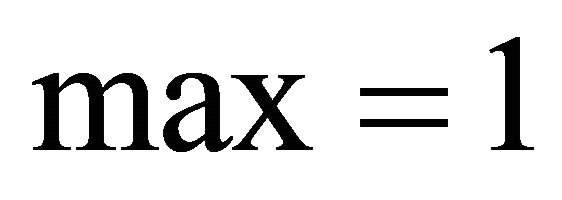 for
for .
.
4. Conclusions
A discrete two-dimensional competition model has been proposed and analysed using geometric strategies. To give the game a general scope, a weight to each point of the finite set which the players fight for has been assigned. In this model, Nash equilibrium positions in the majority of the situations do not exist, see [10]. To resolve this situation, a weakened definition of equilibrium has been presented, which ensures for each player that the other can not improve his payoff by more than one quantity if he changes his position. This new definition of equilibrium can be useful in cases which have no Nash equilibrium.
These considerations mean a step forward in the competition models existing in the literature and adapt better to real situations. For instance, if the game is applied to the optimum location of services to gain customers, assigning weights to the different customers implies the consideration that those who are potentially more related to the service can have a higher value in the competition.
The study of the existence and locations of weak equilibrium positions in this paper have been expanded in scope by applying techniques from computational geometry such as the intersection of convex hulls, which can be used because of the discrete nature of the game.
With respect to the study of the maximum number of weak equilibrium positions located in the set H of target points, it has been able to find that maximum for all the sets of n points and all the possible weightings of such points, thus obtaining a very general and original result. Furthermore, the presented examples show that the cases in which said maximum number is attained are the ones with equally or almost equally weighted points. Therefore, these are the most interesting cases for applied purposes.
REFERENCES
- M. Abellanas, M. López, J. Rodrigo and I. Lillo, “Weak Equilibrium in a Spatial Model,” International Journal of Game Theory, Vol. 40, No. 3, 2011, pp. 449-459. doi:10.1007/s00182-010-0241-y
- D. Monderer and L. S. Shapley, “Potential Games,” Games and Economic Behavior, Vol. 14, No. 1, 1996, pp. 124- 143. doi:10.1006/game.1996.0044
- M. Abellanas, I. Lillo, M. López and J. Rodrigo, “Electoral Strategies in a Dynamical Democratic System,” European Journal of Operational Research, Vol. 175, No. 2, 2006, pp. 870-878. doi:10.1016/j.ejor.2005.05.019
- M. Abellanas, M. López and J. Rodrigo, “Searching for Equilibrium Positions in a Game of Political Competition with Restrictions,” European Journal of Operational Research, Vol. 201, No. 3, 2010, pp. 892-896. doi:10.1016/j.ejor.2009.04.002
- R. Aurenhammer and R. Klein, “Voronoi Diagrams,” In: J.-R. Sack and J. Urrutia, Eds., Handbook of Computational Geometry, Elsevier Science Publishers B.V. NorthHolland, Amsterdam, 2000.
- A. Okabe, B. Boots, K. Sugihara and S. Chiu, “Spatial Tessellations Concepts and Applications of Voronoi Diagrams,” John Wiley & Sons, Chichester, 2000.
- D. Serra and C. Revelle, “Market Capture by Two Competitors: The Preemptive Location Problem,” Journal of regional Science, Vol. 34, No. 4, 1994, pp. 549-561. doi:10.1111/j.1467-9787.1994.tb00882.x
- M. Smid, “Closest Point Problems in Computational Geometry,” In: J.-R. Sack and J. Urrutia, Eds., Handbook on Computational Geometry, Elsevier Science, Amsterdam, 1997.
- M. de Berg, M. van Kreveld, M. Overmars and O. Schwarzkopf, “Computational Geometry-Algorithms and Applacations,”2nd Edition, Springer, New York, 1997.
- I. Lillo, M. López and J. Rodrigo, “A Geometric Study of the Nash Equilibrium in a Weighted Case,” Applied Mathematical Sciences, Vol. 55, No. 1, 2007, pp. 2715-2725.

