Received 1 April 2015; accepted 23 June 2015; published 26 June 2015

ABSTRACT

Based on Maxwell’s constraint counting theory, rigidity percolation in Ge_xSe_1-x glasses occurs when the mean coordination number reaches the value of 2.4. This corresponds to Ge_0.20Se_0.80 glass. At this composition, the number of constraints experienced by an atom equals the number of degrees of freedom in three dimensions. Hence, at this composition, the network changes from a floppy phase to a rigid phase, and rigidity starts to percolate. In this work, we use reverse Monte Carlo (RMC) modeling to model the structure of Ge_0.20Se_0.80 glass by simulating its experimental total atomic pair distribution function (PDF) obtained via high energy synchrotron radiation. A three-dimensional configuration of 2836 atoms was obtained, from which we extracted the partial atomic pair distribution functions associated with Ge-Ge, Ge-Se and Se-Se real space correlations that are hard to extract experimentally from total scattering methods. Bond angle distributions, coordination numbers, mean coordination numbers and the number of floppy modes were also extracted and discussed. More structural insights about network topology at this composition were illustrated. The results indicate that in Ge_0.20Se_0.80 glass, Ge atoms break up and cross-link the Se chain structure, and form structural units that are four-fold coordinated (the GeSe₄ tetrahedra). These tetrahedra form the basic building block and are connected via shared Se atoms or short Se chains. The extent of the intermediate ranged oscillations in real space (as extracted from the width of the first sharp diffraction peak) was found to be around 19.6 Å. The bonding schemes in this glass are consistent with the so-called “8-N” rule and can be interpreted in terms of a chemically ordered network model.

Keywords:

Chalcogenide Glasses, Rigidity Percolation, Reverse Monte Carlo Modeling, Atomic Pair Distribution Function (PDF), Ge_xSe_1-x Glasses

1. Introduction

Amorphous materials in general and amorphous chalcogenide glasses in particular play an essential rule in technological applications. Examples include infrared detectors, lenses and infrared optical fibers [1] [2] . Chalcogenide glasses, especially when doped with rare earth ions, have high refractive index, low phonon energy and high nonlinearity [3] . These physical properties make them superior in lasers, photonic integrated circuits and photon-induced refraction [4] . Amorphous chalcogenide semiconductors have also found emerging applications in electrical switches, based on their phase changes through an intense voltage or heat pulses [5] .

Deep understanding of the local structure of amorphous chalcogenides helps understand their remarkable physical and chemical properties and gives more insights about possible combinations to produce and design new useful materials.

In this paper, we focus on rigidity transition in binary chalcogenide glasses. Rigidity theory [6] - [8] predicts the mechanical properties of network glasses based on their chemical composition. In network glasses, interatomic distances and bond angles are fixed around their average values due to radial 2-body bond-stretching and angular 3-body bond-bending constraints, respectively. In this theory, J. C. Phillips [6] [7] introduced counting the average constraints experienced by each atom in the network. In three dimensions, a network is considered as floppy, when the average number of constraints per atom (n_c) is less than 3 (the number of degrees of freedom per atom in 3 dimensions), and is considered as stressed-rigid if n_c is greater than 3. The network is considered as isostatic when.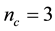

Simple enumeration of the average number of constraints experienced by an atom in a glassy network can predict its mechanical property, as well as the optimal isostatic composition, in which the network is rigid but stress-free. Rigidity theory has been applied to tetrahedral network glasses with changing composition and it was found that glass formation is optimal if the network is isostatic [9] .

The mean coordination number, 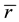(which should be distinguished from n_c), plays an important role in determining connectivity and rigidity of a network. In the case of a covalently bonded binary alloy with general formula A_xB_1-x, the value of 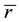is given by:

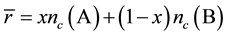(1)

In the mean-field approach, one considers a network of N atoms composed of 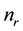atoms that are r-fold coordinated. The enumeration of mechanical constraints in this system gives r/2 bond-stretching constraints and 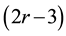bond-bending constraints [6] [7] .

The number of floppy modes, f, in a network of N atoms equals the difference between the total number of degrees of freedom (3N) and the total number of constraints present in the network, as given by [8] :

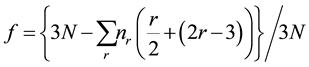(2)

where n_r is the number of r-fold coordinated atoms. This reduces to:

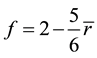(3)

This number of floppy modes, f, vanishes when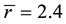. At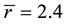, the glassy network is stable and has a mechanical threshold or critical composition at which the network changes from an elastically floppy type to a rigid type. Many experimental results confirm the mean-filed predictions and show responses to the rigidity percolation threshold [10] - [12] .

Among all chalcogenide glasses, the covalently bonded Ge_xSe_1-x system is of special interest. This system can be made as glasses over a wide composition range (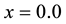to 0.42 atm.% germanium) [1] [2] [13] . This allows one to systematically tune its mechanical properties and network connectivity by altering the Ge:Se ratio. Rigidity percolation in Ge_xSe_1-x glasses occurs at Ge_0.20Se_0.80 where at this composition the value of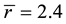. Despite the fact that many dramatic experimental findings were reported to occur at this composition [14] - [17] , very little information is known about the local structure of this important particular composition, as many experimental [18] - [23] and theoretical [23] - [28] studies focused on the stoicheometric composition GeSe₂ glass. Hence, a detailed determination of the local structure of Ge_0.20Se_0.80 glass is essential for understanding the onset of rigidity. Crucial questions whether Ge_0.20Se_0.80 glass forms a chemically ordered or a covalently random network and the possibility of broken chemical order remain subjects of concern.

The purpose of this paper is to build a structural model of the rigidity percolation threshold (Ge_0.20Se_0.80) glass from which we can extract different structural parameters that may resolve some controversial structural aspects. So, in this work, we study the short- and intermediate-range orders of Ge_0.20Se_0.80 glass using Reverse Monte Carlo (RMC) modeling by simulating its experimental total atomic pair distribution function (PDF). To the best of our knowledge, this is the first RMC modeling done on melt-quenched Ge_0.20Se_0.80 glass through directly simulating its high resolution real-space PDF data, obtained via high energy synchrotron radiation. In the following we give a brief theoretical account about PDF technique and RMC modeling.

2. Theory

2.1. The PDF Method

The atomic pair distribution function (PDF) technique is a total scattering technique that gives the local structural environment at the atomic scale. PDF technique allows for both the Bragg and diffuse scattering to be analyzed together on equal terms, revealing the short and intermediate range orders of the material [29] .

The atomic PDF, 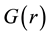, is defined as:

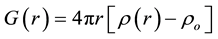(4)

where 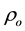is the average atomic number density, 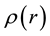is the atomic pair-density, and r is the radial distance.

The function is experimentally accessible and gives information about the number of atoms in a spherical shell of unit thickness at a distance r from a reference atom. It peaks at characteristic distances separating pairs of atoms, as shown schematically in Figure 1.

The PDF is related to the measured X-ray or neutron diffraction pattern through a Fourier transform:

(5)

where Q is the magnitude of the scattering vector, and is the total scattering structure function which contains the measured diffracted intensities of the material. The quantity is denoted by and is called the reduced structure function.

The structure function is related to the coherent part of the total scattering intensity of the material, and is given by [29] [30] :

(6)

where is the measured scattering intensity from a sample that has been properly corrected for background and other experimental effects and normalized by the flux and the amount of the sample in the beam. Here, and are the atomic concentration and X-ray atomic form factor, respectively, for the atomic species of type i.

As can be seen from Equations (4)-(6), is simply another representation of the diffraction data. However, exploring the diffraction data in real space has advantages especially in the case of materials with significant structural disorder [29] .

Modeling of the PDF data does not presume periodicity. Therefore, PDF technique is particularly useful for characterizing aperiodic distortions in crystals, analysis of nano structures and glasses.

Improper corrections in PDF data reduction result in distortions to but these distortions vary much more slowly than the signal and are manifested as sharp peaks at very low-r in the PDF in a region (typically < 1.0 Å) where no structural information exists [29] .

Coordination numbers and partial coordination numbers are extracted through integrating the corresponding peaks in the so-called radial distribution function (RDF), which is related to by:

(7)

2.2. The RMC Method

Reverse Monte Carlo (RMC) is an important structural modeling method based on experimental data. It began as a method for creating three-dimensional models of liquid structures. It has been developed considerably since then, and its applications have been applied to include crystalline, amorphous structures and magnetic materials [31] . A comprehensive review on the subject has been performed by Robert McGreevy [32] .

The general theme of this method is based on building a three dimensional structural configuration of atoms that have their calculated correlation functions consistent to some extent with the experimental ones. In RMC modeling, a set of points (atoms) are placed in a cubical box of edge-length L, with periodic boundary conditions. The types of the atoms in the box, their relative concentrations as well as their number densities are determined to be consistent with the material being modeled.

A set of experimental data, either in Q-space or in real space can be simulated. Starting from a completely random configuration of atoms, an atom is chosen randomly and moved a specific distance. Every time an atom is moved, the correlation functions are calculated from the new configuration and compared with the corresponding experimental correlation functions. If the move increases the agreement between the calculated and experimental data, the move is accepted, otherwise, it is accepted with some probability.

A set of physical structural constraints are inserted in the simulation process so as to improve the fit. These include the distance of closest approach, where no two atoms can come closer to each other by this distance. Coordination number constraints that are consistent with the chemistry of the material may also be inserted in the modeling process. These constraints aim towards improving the fit and making the resulting configuration more and more reasonable.

In RMC modeling, the RMC-calculated total PDF is given by:

(8)

where is the number of atoms between r and from the central atom, averaged over all atoms, and is the average atomic number density.

Similarly, for a model of two atom types i and j, the RMC-calculated partial PDF is given by:

(9)

Here, the is the number of atoms of type j, between r and, that are exist around the central atom of type i averaged over all atoms of type i.

The function to be minimized during each atom move is:

(10)

Here the sum is over m experimental points and is related to the experimental error in the PDF data. Any move that decreases is always accepted, if the move increases it is accepted with a probability given by. The process of moving atoms around continues until has reached an equilibrium value. The resulting RMC-generated configuration should be consistent with the experimental data within experimental errors.

Once the model is obtained, many structural parameters can be directly calculated, such as the partial coordination numbers, average coordination number, partial atomic pair distribution functions, partial structure functions, and the bond angle distributions.

It should be noted that the RMC-generated structural models are never unique. This should not be considered as a weakness of the method. RMC modeling is not supposed to give the structure of a given material, it just solves some questions about the structure of the material, and gives more insights about interpretation of the simulated experimental data. What we should look at it in RMC modeling is weather the generated model is useful or not. Does it give more insights into the structure or properties of the material that would not have been obtained without the model?

3. Experimental

3.1. The PDF Experiment

The Ge_0.20Se_0.80 glass was prepared using conventional melt quenching process. The details of the preparation and characterization process of the glass as well as the X-ray diffraction experiment performed on it are all mentioned in a previous publication [33] .

It should be noted that the use of high-energy X-ray synchrotron radiation (87.005 keV (Å)) at the MUCAT 6-ID-D beam line at the Advanced Photon Source (APS) allowed us to access a high value of wave vector Q of 26 Å^-1, where Q is the magnitude of the scattering vector, and is given by:. This allowed us to reduce several unwanted experimental effects such as absorption and multiple scattering, which in turn had a great impact on the real space resolution of the obtained PDF.

The measured reduced structure function, , and the corresponding atomic pair distribution function, , for the Ge_0.20Se_0.80 glass are plotted in Figure 2.

The curves in Figure 2 have not been smoothed and the low level of noise in, even at high-Q values, is apparent, which indicates that the experimental data are adequate and the raw data reduction was effective.

The high real space resolution of the current data set makes the analysis and the interpretations of the different peaks unambiguous.

3.2. The RMC Modeling

In the current RMC modeling process, we followed the following simulation protocol. A set of 2836 atoms were generated randomly inside a box of edge-length of 43.44 Å. This results in an average number density of 0.0346 atoms/ų, which is comparable with the experimental value of Ge_0.20Se_0.80 glass. From the 2836 atoms, 567 atoms were assigned to represent Ge and the remaining 2269 atoms were assigned to represent Se. These assignments mimics the concentrations of Ge and Se in Ge_0.20Se_0.80. RMCA program [34] was used in the modeling process. Initially, the program ran for 48 hours without any constraints to ensure the non existence of any memory effects. After that, the cut off distance (distance of closest approach) constraint as well as the coordination constraints were inserted in the simulation process. The coordination constraints we used are consistent with the Mott’s “8-N” rule [35] , where N is the number of valence electrons in the corresponding atom. Thus, two coordination constraints were assigned such that each Ge atom is 4-fold coordinated and each Se atom is 2-fold coordinated. In this protocol, the experimental total atomic pair distribution function (PDF) was directly simulated. The program ran for a week after which the value of began to saturate and reached a stable limit of around 1.0.

4. Results and Discussion

The quality of RMC simulation to the experimental total atomic pair distribution function () is shown in Figure 3, from which we see excellent agreement between the experimental and calculated data. This is obvious from the difference curve that is plotted offset below the two curves. The RMC-generated structural model is able to reproduce the positions, shapes and intensities of all the peaks in the experimental that extend till about 10 Å. It should be noted that the peaks in below 2.13 Å (the lower side of the first real peak) are unphysical, and they are due to terminating the Fourier transform at. These peaks are considered as termination ripples and they were ignored in the simulation process.

The obtained three-dimensional RMC configuration was tested for homogeneity, and structural defects, such as dangling bonds and it was found to be homogenous and reasonable. Figure 4 shows a snap shot representation of the RMC-generated structural model of Ge_0.20Se_0.80 as well as the Ge and Se sub-networks. The calculated PDF from the RMC-generated model was then Fourier transformed to obtain the calculated reduced structure function. Figure 5 shows a comparison between the experimental and calculated reduced structure functions. It is evident from Figure 5 that the calculated has a very good agreement with the experimental data regarding peak positions, especially for the first sharp diffraction peak, which is denoted by FSDP and indicated by an arrow in the inset of Figure 5. The FSDP has been a subject of debate in network glasses for its anomalies behavior [36] - [38] , and so its origin remains controversial, despite the qualitative

agreement that it is a signature of intermediate range order (IRO) in network glasses [39] . The small hump in the calculated at the location of the FSDP indicates that the generated model preserves correlations in the IRO that are responsible for the appearance of the FSDP. The excellent reproducibility of peak positions in the data, especially at high Q range, indicates that the short range order is very well reproduced, and the nearest neighbour bond lengths are accurate. However, the calculated data have their peaks lower in amplitudes than the corresponding experimental ones, which is due to the finite size of the generated model. So larger models (~100,000 atoms) can improve the simulation process.

The resulting RMC configuration was then used to calculate the full set of partial atomic pair distribution functions:, and. These partials were calculated using Equation 9, and are shown in Figure 6. From these partials, it is evident that the first PDF peak at 2.36 Å is mainly due to Ge-Se hetropolar bonds, and partially due to Se-Se homopolar bonds. The little hump in at 2.36 Å indicates the existence of very few Ge-Ge homopolar bonds. Structural correlations beyond the short range order can be clearly identified in the different partial PDFs and they extend till about 8 Å.

These partial PDFs, when summed up with proper averaging, gives the total atomic pair distribution function (G(r)). The advantage of the obtained RMC model, is that it enabled us to decompose G(r) into three sets of known origin. Structural correlations responsible for each peak in each partial PDF are now very well known and can be easily interpreted.

Many experimental findings [20] [27] indicated that GeSe₄ tetrahedra form the basic building blocks in Ge-Se networks. To test the validity of this assumption, we have extracted the relevant distances from the corresponding partial PDFs shown in Figure 6. Ge-Se nearest neighbour distance occurs at Å as extracted from the position of the first PDF peak in. Also, the Se-Se second neighbour distance occurs at Å as extracted from the position of the second peak in. The ratio is consistent with the ideal tetrahedral ratio of. This indicates that GeSe₄ tetrahedra form the basic building blocks in Ge_0.20Se_0.80 glass. Another proof of this fact is extracted from the bond angle distributions, discussed later in this paper.

Two competing structural models were proposed for these glasses. The first model is the chemically ordered network (CON) model [40] where all atoms are coordinated according to the “8-N” rule, and the number of hetropolar bonds is maximized. The second model is the random covalent network (RCN) [41] [42] at which there is no preference for either homopolar or hetropolar bonds, and the distribution of bond types is purely statistical. Both the CON and the RCN models give the same mean coordination number of (a condition that must be satisfied if, in accordance with the “8-N” rule, Ge is fourfold coordinated and Se is twofold coordinated in Ge_xSe_1-x glasses).

In order to extract the partial coordination numbers (this notation denotes the coordination of an atom of specie i by atoms of specie j), partial radial distribution functions were calculated through:

(11)

and the corresponding peaks in these partials were then integrated. Figure 7 shows the calculated partial coordination numbers as obtained by the current RMC modeling together with the expected values via the CON and the RCN models.

It is very clear, as can be seen from Figure 7 that the RMC-generated model is very close and consistent with the CON model, where the Ge atoms are four-fold coordinated to Se atoms to form GeSe₄ tetrahedra, with some amount of Se atoms are necessarily forced to form homopolar Se bonds. Having said that the structure of Ge_0.20Se_0.80 glass is consistent with the CON model does not fully characterize the short range order in this glass, as there are many different bonding configurations at which the GeSe₄ tetrahedra can link together, as we will see shortly.

Integration of the first peaks in partial RDFs yields that, , and. Based on these values, and, and this results in a mean coordination number of. Here is calculated through:

(12)

Hence, the number of floppy modes, as given by Equation (3), vanishes for the Ge_0.20Se_0.80 glass, which indicates that its network is rigid. The above results are also consistent with the “8-N” rule, where we found that Ge

is 4-fold coordinated and Se is 2-fold coordinated.

The structure of amorphous Se consists mainly of Se chains with some few rings [43] . Each Se atom is bound to two other Se, in accordance with the “8-N” rule, at a distance of 2.34(2) Å. When 20 atm.% Ge is added to Se to form amorphous Ge_0.20Se_0.80 glass, Ge atoms break-up and cross link the Se chain structure, and form structural units that are four-fold coordinated (i.e. the GeSe₄ tetrahedral units). Existence of Se-Se homopolar bonds, and as indicated by Figure 7, indicates the existence of short Se chains. This shows the different linkage schemes of the GeSe₄ tetrahedra, where linkage through a single Se atom (corner-sharing configuration), two Se atoms (edge-sharing configuration), and through short Se chains are all present in this glass.

In Figure 8 we show the calculated six possibilities of bond angle distributions from the RMC-generated structural model for Ge_0.20Se_0.80 glass. Here, we calculated the angular distributions of bonds between first neighbour atoms at a maximum radial distance of 3 Å, which was determined from the position of the first minimum after the first PDF peak.

These bond angle distributions have been smoothed for clarity. The smoothing process did not alter their general behavior, and the associated peaks can be seen clearly in the smoothed data. Following is a description of each of these bond angle distribution functions:

・ :

This distribution spreads over the entire range with no well defined peaks (except a little hump at around 60˚). The general theme of this distribution is flat, which is due to the very little fraction of Ge-Ge homopolar bonds in the first PDF shell.

・ :

The main peak in this distribution is broad and extends from 85˚ - 125˚ and centered at 105˚. A little hump also occurs at around 60˚. This distribution describes the connectivity between neighbouring tetrahedra. In the high-temperature phase of GeSe₂ glass (HT-GeSe₂), edge-sharing tetrahedra (EST) show angles close to 80˚ and corner-sharing tetrahedra (CST) show angles between 96˚ - 100˚ [44] [45] . Thus, the disappearance of the peak at 80˚ in the RMC-generated model indicates that EST are very few in Ge_0.20Se_0.80 glass, while the peak at 105˚ is due to CST. Its extension from 85˚ - 125˚ is consistent with the different linkage schemes available for this bond angle as can be seen in the right panel of Figure 9.

・ :

This distribution has a peak at around 60˚ which is associated with three-fold rings. The little hump seen around 106˚ is related to tetrahedral angles and n-fold rings present in the glass.

・ :

This distribution has two peaks, the first one occurs at around 60˚ and a second broad peak centered at around 109˚ which is consistent with the ideal value in a perfect tetrahedron (109.5˚), as shown in the right panel of Figure 9.

・ :

This distribution is relatively similar to that of. Here, a peak is observed at around 60˚ which is due to the occasional presence of three-fold rings, while the peak centered at around 102˚ characterizes the angle at which Se chains connect to GeSe₄ tetrahedra.

・ :

This distribution has two main peaks, the first one is sharp and centered at around 60˚, while the second peak is broad and extends from 95˚ - 120˚, with a maximum at 110˚. As indicated in Figure 9, the Se-Se-Se angles in perfect tetrahedra are 60˚. This indicates that the GeSe₄ tetrahedra in Ge_0.20Se_0.80 glass are ideal. This finding is consistent with the ratio of mentioned previously. In trigonal selenium [46] , the Se-Se-Se angle is 103˚ and the angles in small Se chains and rings range from 90˚ - 116˚. The second broad peak in this distribution indicates that Se chains and rings are formed in this glass.

Structural information about intermediate range order (IRO) is contained in the peaks beyond the nearest neighbor distances. As can be seen from Figure 6, the three partial atomic pair distribution functions have structural correlations that extend till about 8 Å. Of particular interest is the Ge-Ge partial distribution function. Peaks beyond the first shell in this function are associated with Ge-Ge correlations among the

GeSe₄ tetrahedra. Careful analysis of this distribution function shows a small peak at about 3.1 Å, which is the distance of Ge-Ge correlation when the GeSe₄ tetrahedra share edges. The peak at around 3.6 Å is due to Ge-Ge correlations in corner-sharing configuration.

The first sharp diffraction peak (FSDP) in the reduced structure function is considered as a signature of intermediate range order present in this glass [39] . It indicates that the bonding takes a significant directional character. It occurs at around 1.12(3) Å^-1, and so, the periodicity of the associated intermediate ranged oscillations (given by:) is about 5.61 Å. On the other hand, the full width at half maximum of the FSDP was extracted through reflecting its lower part around its center, and it was found to be 0.32(2) Å^-1. This width determines the so-called coherence length (given by:), which controls the extent of the intermediate ranged oscillations in real space. This extent was found to be around 19.6 Å.

5. Summary and Conclusion

In conclusion, we have used constrained RMC modeling to build a three-dimensional structural model of the Ge_0.20Se_0.80 glass through simulating its experimental X-ray total atomic pair distribution function (PDF). The calculated correlation functions have excellent agreement with the experimental data. The obtained model indicates that the Ge_0.20Se_0.80 network is best described by a chemically ordered network, where all atoms are coordinated according to the “8-N” rule, and the number of hetropolar bonds is maximized. The Ge atoms are four-fold coordinated to Se atoms to form GeSe₄ tetrahedra, and with some Se atoms are necessarily forced to form homopolar Se bonds. The GeSe₄ tetrahedra are linked together with different configuration schemes, including CST, EST and linkage through short Se chains. The present investigation on Ge_0.20Se_0.80 glass provides structural insights on the network topology at both short and intermediate atomic length scales. Finally, this work shows the power of RMC simulation of experimental data to build a structural model of an amorphous material. Without such a model, much important structural information cannot be obtained.

Acknowledgements

It is our pleasure to acknowledge Prof. Simon J. L. Billinge and his research group where the current experimental data set was collected. The X-ray diffraction experiment was performed at the 6ID-D beamline in the Midwest Universities Collaborative Access Team (MUCAT) sector at the Advanced Photon Source (APS). Use of the APS is supported by the US DOE, Office of Science, Office of Basic Energy Sciences, under Contract No. W-31-109-Eng-38. The MUCAT sector at the APS is supported by the US DOE, Office of Science, Office of Basic Energy Sciences, through the Ames Laboratory under Contract No. W-7405-Eng-82. We also thank Prof. Punit Boolchand from the University of Cincinnati, and his former graduate student Ping Chen for making up the studied sample.

References