Journal of Crystallization Process and Technology
Vol.04 No.04(2014), Article ID:50286,7 pages
10.4236/jcpt.2014.44023
Low Pressure Chemical Vapor Deposition of TiO2 Layer in Hydrogen-Ambient
Satoshi Yamauchi*, Kazuhiro Ishibashi, Sakura Hatakeyama
Department of Biomolecular Functional Engineering, Ibaraki University, Hitachi, Japan
Email: *ysatoshi@mx.ibaraki.ac.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 July 2014; revised 22 August 2014; accepted 16 September 2014
ABSTRACT
Low pressure chemical vapor deposition (LPCVD) of anatase TiO2 layer using metalorganic precursor of titanium-tetra-iso-propoxide (TTIP) and H2 as a reduction gas was demonstrated at pres- sure of 3 mtorr in comparison to that using TTIP and O2 with study for the property of the layers. Dissociation energy of TTIP in H2 was higher than that in O2 but resistivity of the layer deposited in H2 was significantly decreased to 0.2 Ω cm in contrast to the high resistivity beyond 100 Ω cm of the layer deposited in O2. UV-Vis optical transmission spectra showed absorption around 2.2 eV was increased in the layer deposited by TTIP + H2 in addition to decrease of forbidden energy gap due to increase of Urbach tail. Resistivity at low temperature below 100 K indicating the layer deposited in H2-ambient was degenerated by the high electron density but the resistivity was decreased with temperature above 100 K with the activation energy about 100 meV. A possible electronic conduction model based on kernel, grain boundary and surface trap to clarify the temperature dependent resistivity suggesting resistivity of the layer was limited by depletion region in the grain-boundary extended from the surface and the kernel with significantly low resistivity in 10−3 Ω cm order was formed in the layer.
Keywords:
LPCVD, TTIP+H2, Anatase-TiO2, Low Resistive TiO2

1. Introduction
TiO2 has been extensively investigated in view of photo-induced applications using the photo-catalytic reactions and the hydrophilicity [1] [2] in addition to dielectric applications using the high dielectric constant and optoelectronic applications by the high refractive index [3] [4] . On the other hand, the material has been also expected
for transparent conduction oxide (TCO) because of the wide band gap of 3.2 eV. In addition, the conductive TiO2 with significantly high resistance in acid and alkaline solutions has interesting potentials to fabricate solar-cells, chemical sensors etc. However, it is easily recognized that the conductivity control is more difficult than the other TCO such as ITO, Sn2O and ZnO since d-orbital contributes to forming TiO2. Recently, laser-ab- lation and reactive sputtering with the post-annealing in reduction ambient have been applied to form highly conductive TiO2 layer by using Nb as a donor-dopant [5] [6] . In such process, oxygen-deficiency is seemed to be required to enhance the electronic activation of the donor [7] , in which Ti3+ reduced from Ti4+ probably plays an important role of the conduction in TiO2. On the other hand, chemical vapor deposition (CVD) which is able to form thin film with step coverage better than that by physical vapor deposition has been studied on TiO2 fabrication. In the CVD process, suitable primary-source is fundamentally required in addition to control of the deposition condition. It has been well recognized that titanium-tetra-iso-propoxide (TTIP: Ti(O-i-C3H7)4) is a suitable metalorganic precursor for the TiO2 deposition and the thermally dissociated species is crystallized in the anatase-phase around 400˚C [8] . However, few studies have been reported for the conductivity control of TiO2 layer by CVD. Also in the CVD process, it can be believed that Ti3+ in TiO2 layer plays an important role for the conductivity. Previously, we demonstrated low pressure chemical vapor deposition (LPCVD) of TiO2 layer using TTIP + O2 and Nb-F co-doping by using the dopant of NbF5, in which the resistivity was decreased to 0.2 Ω cm by the doping in contrast to high resistivity of the undoped layer beyond 100 Ω cm [9] . Further, XPS study showed that F substituted to the O-site contributes to the reduction of resistivity, which can be recognized; the F reduced Ti4+ to Ti3+ and Ti3+ supports the activation of Nb-donor, but oxygen-vacancy increases the resistivity. These results are qualitatively in agreement with the results of molecular orbital calculations [9] , in which the donor level due to 6-fold-coordinated Ti3+ is shallower than that of Ti3+ associated with oxygen-va- cancy. These results indicate that Ti3+ ions or the complex defects are essentially required to control in the density and the nature for increase of the conductivity.
In this paper, LPCVD of TiO2 layer using TTIP and reduction gas of H2 is demonstrated to increase Ti3+ density and control the conductivity. The deposited layer is characterized by X-ray diffraction, UV-Vis transparent spectroscopy and the temperature dependent resistivity.
2. Experimental
2.1. LPCVD of TiO2 Layer
A bell-jar type reactor with the base pressure under 1 × 10−5 torr by a combination of diffusion pump and a rotary pump was used for LPCVD of titanium-oxide. Titanium tetra-iso-propoxide (TTIP, Ti(O-i-C3H7)4: 99.7% purity) was used as source gas after purification in vacuum. Details of the apparatus configuration and the purification sequence of TTIP were already shown elsewhere [9] . High purity hydrogen gas (99.99999%) was simultaneously introduced into the reactor through an individual gas inlet during the deposition. In the case of the deposition in O2, high purity oxygen gas (99.9999%) instead of H2 was introduced into the reactor. The gas sup- ply ratio of TTIP/H2 or TTIP/O2 were controlled by monitoring the reactor pressure using Shultz gage when TTIP and H2 or O2 were introduced into the reactor, in which sensitivity of the ion gage for H2 and O2 was taken into account to determine the gas supply ratio to TTIP. Substrate of 1 mm-thick quartz plate with optically flat surface was mounted on a substrate holder after chemical cleaning. Temperature of the substrate holder on resistive heater was monitored by K-type thermo-couple and controlled by PID-system.
2.2. Evaluation of LCVD-TiO2 Layer
Thickness of the layer was checked by a surface profiler (Veeco, DEKTAK150). Resistivity was evaluated by Van Der Pauw (VDP) method using symmetric four ohmic contacts of Indium-dots, in which the temperature was varied from 10 to 300 K in vacuum and dark by a cryogenic system (Janis Research, CCS-150). Crystallographic behavior was examined by θ - 2θ X-ray diffraction (RIGAKU: RAD-C) using CuKα. UV-Vis optical transmission spectra were obtained by UV-Vis spectrometer (OCEAN OPTICS: USB-2000) using a light source of Halogen lamp.
3. Results and Discussions
3.1. Deposition Rate and Resistivity of TiO2 Layer
Figure 1(a) shows Arrhenius plot of TiO2 deposition rate in O2 (open-circle) and H2 (solid-circle) ambient for the deposition temperature, in which supply rate of the gas to TTIP was kept at 1. The deposition rate of the layer deposited in O2 (TiO2/O2) and in H2 (TiO2/H2) was increased with the temperature and then saturated above 360˚C. At such low temperatures, the layers were poly-crystallized into anatase-phase as shown by XRD spectra in Figure 1(b), in which the spectra of TiO2/O2 and TiO2/H2 deposited at 360˚C is shown by black-line and red-line respectively. In the both spectra, diffraction peaks originated from (101) and (200) anatase-TiO2 were observed but not any peaks due to another phase such as rutile and brookite. The diffraction peak intensities of the TiO2/H2 layer were weaker than that of the TiO2/O2 layer but the peak angle shift was not observed in the spectrum. Activation energy of 138 kJ/mol for the deposition of TiO2/O2 obtained the result in Figure 1(a) showed that TTIP-dissociation feature was scarcely influenced by O2 because the energy was similar to CVD by TTIP single precursor [10] . In this case, it can be recognized TTIP is thermally dissociated then anatase-TiO2 is formed with propene and isopropanol at such low temperatures as follow reaction [11] .
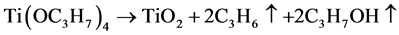 ,
,
where it is expected Ti=O bonds are formed on the deposition surface [12] . Further, it is considered the surface Ti=O bonds act as adsorption-site of the precursor and enhance the dissociation of TTIP as depicted in Figure 2(a). In contrast, the activation energy for TiO2/H2 was obtained as 230 kJ/mol. Previously, Shmakov et al. demonstrated quantum chemical calculations using B3LYP for monomolecular dissociation of TTIP and suggested

Figure 1. (a) Deposition rate in O2 (open-circle) and H2 (solid-circle) for the temperature and (b) typical θ - 2θ XRD spectra of 200 nm-thick TiO2 layer deposited at 360˚C in O2 (black-line) and H2 (red-line), where the miller indicate shows anatase-TiO2 surface.


Figure 2. Expected scheme of TTIP-dissociation on deposition surface (a) without (b) with hydrogen contribution. Blue-bowline in (b) shows thermal dissociation of monomolecular TTIP.
the activation barrier to form Ti(OC3H7)3(OH) and propene via O-H-CH2 interaction in isopropyl group of TTIP is 56.9 kcal/mol (238 kJ/mol) [13] . The calculated value is in good agreement with the activation energy for the deposition TiO2/H2, however, very high as compared to that for TiO2/O2 and the previous report using TTIP single precursor. It can be recognized the large different of the activation energy is owing to hydrogen at the deposition surface as shown in Figure 2(b). When H2 gas is simultaneously supplied with TTIP, methyl-group of TTIP cannot be allowed in the reaction to Ti-O or Ti on the deposition surface, because the surface consists of Ti=O is terminated by hydrogen. Therefore, the adsorption of the precursor is achieved after monomolecular dissociation to form Ti(OC3H7)3(OH), then the adsorbed species is dissociated to TiOx. It is noted Ti-H is probably remained in the deposited layer and the hydrogen is partially desorbed by thermal dissociation. In the scheme of the hydrogen-desorption, it is expected Ti4+ is reduced to Ti3+ and resulted in generation of donor- defect. Figure 3 shows dependence of resistivity of TiO2/H2 on the deposition temperature, in which the layers were deposited with the thickness about 200 nm and the resistivity was evaluated by VDP method at room- temperature. Although all of TiO2/O2 layer was with high resistivity above 100 Ω cm beyond the evaluation limit of our system, resistivity of the TiO2/H2 layer deposited in H2 was decreased with the deposition temperature and then gradually increased above 360˚C. The activation energy of 244 kJ/mol obtained below 350˚C suggested that donor concentration was increased with the temperature. Recently, it was reported that hydrogen acts as donor in TiO2 by experimental results for anatase-TiO2 powder (Degussa P25) treated by atomic-hydrogen [14] and molecular orbital theoretical results [15] , in which hydrogen was found to be bound to lattice oxygen in TiO2. In this work, it is however considered that the door species in the layer was not the hydrogen bound to O, because the absorption due to Ti-OH (Chemisorbed OH) which was identified in IR-spectrum of amorphous Ti- Ox layer deposited by plasma-assisted deposition at room-temperature [16] could not be observed in the TiO2/H2 layers. On the other, Nakamura et al. studied reduction treatment of anatase-TiO2 powder by radio-frequency hydrogen-gas plasma at 400˚C to enhance the visible light activity for NO removal [17] . In the report, ECR spectra indicated the anatase-TiO2 is reduced by hydrogen excited in the plasma and oxygen-vacancies are for- med with the double defect levels of 0.75 and 1.18 eV below the conduction band minimum. Although non-ex- cited hydrogen gas was supplied below 380˚C during the deposition in this work, it can be considered hydrogen was adsorbed to Ti as shown in Figure 3 and maybe form oxygen-vacancies in the layer. However, the defect level is too deep to decrease the resistivity at room-temperature. Therefore, the defect to reduce the resistivity is not oxygen-vacancy but Ti3+ with the defect level shallower than the complex centers predicted by theoretical calculations [15] . Indeed, the activation energy of 244 kJ/mol obtained by the result in Figure 3 was similar to the dissociation energy of 208 kJ/mol for Ti-H bond [18] .
3.2. Optical Absorption
Figures 4 shows optical absorption spectra in UV-Vis region. Dot-lines in Figure 4(a) show transmission spectra of TiO2/H2 (red-line) and TiO2/O2 (black-line) layers grown at 360˚C with the thickness about 200 nm. Gra- dual increase and relatively low value of optical transmittance in Vis-region suggested deep-level defects were included in the forbidden energy gap. The spectra were successfully deconvoluted into two-spectra with the peak at 2.2 eV and 3.0 eV, which were described by Gaussian-function, and near band edge absorption obtained after removal the two-spectra from the raw transmission spectrum. In Figure 4(a), the deconvoluted spectra and
Figure 3. Resistivity of TiO2/H2 for the deposition temperature, in which the layers were deposited with thickness about 200 nm.

Figure 4. (a) Transmission spectra (dot-lines) and the deconvoluted spectra (solid-lines) with the fitting lines (blue-lines) of TiO2/O2 (black-lines) and TiO2/H2 (red-lines); (b) (αhν)1/2 plots for photon energy with the linear relation line (dash-lines) to determine the optical band gap; and (c) absorption coefficient in near band edge region after removal the absorptions due to deep-levels centered at 2.2 eV and 3.0 eV.
the fitting curves are shown by solid-line (red-line: TiO2/H2, black-line: TiO2/O2) and blue-lines, respectively. Previously, Sekiya et al. suggested the origin of absorption at 3.0 eV and in between 2.2 and 2.3 eV, which were coincident to peak energies of the deconvoluted spectra in Figure 4(a), is attributed to oxygen-vacancies with two-trapped electrons and electron transition of Ti3+ from 2T2 to 2E state contributed by crystal field interaction with surrounding oxygen, respectively [19] . They also showed intensity of the absorption in between 2.2 and 2.3 eV is decreased by post-annealing above 300˚C with decreasing electrical conductivity. In this work, the absorption peak at 2.2 eV was significantly increased in the intensity for TiO2/H2 whereas the absorption peak at 3.0 eV was scarcely different as compared with TiO2/O2. From these results, it is considered that increase of Ti3+ density in TiO2/H2 was independent from the increase of oxygen-vacancy and resulted in the reduction of resistivity. It is noted significant broadening of the absorption around 2.2 eV was also observed for the TiO2/H2 in comparison with TiO2/O2 as shown in Figure 4(a), in which the full-with at half-maximum (FWHM) was 1.4 eV and 0.86 eV for the TiO2/H2 and TiO2/O2 respectively. The absorption broadening could be recognized crystal field around Ti3+ was more fluctuated in the layer as compared with the TiO2/O2, that is, structural disordering of TiO2/H2 was higher than that of TiO2/O2. Indeed, XRD spectra showed crystallinity of TiO2/H2 was inferior to that of TiO2/O2 as shown in Figure 1(b). Further, it has been reported structural disordering causes band gap narrowing in crystal. Figure 4(b) shows Tauc plot in (αhν)1/2 vs. photon energy (hν) to determine the optical band gap of TiO2/H2 (red-line) and TiO2/O2 (black-line), where α is absorption coefficient. The band gap of 3.16 eV given by the extrapolated linear line (black dot-line) for the TiO2/O2 was scarcely smaller than that of 3.2 eV for anatase-TiO2. In contrast, the band gap was significantly reduced to 3.0 eV for the TiO2/H2. The estimated band gap of 3.0 eV was similar to that for rutil-TiO2 but the lowering of band gap could be considered to be originated from defect states in the band gap, because any XRD diffraction peak corresponding to rutile phase could not be observed in the layer. On the other, it has been recognized localized defect states originated from structural disordering are extended form an optical absorption tail to lower energy side below the band gap and resulted in origin of the optical band gap narrowing, in which the tail is referred as Urbach tail represented by α = αoexp(hν/Eu) using Urbach energy (Eu) [20] . Figure 4(c) shows absorption coefficient of the TiO2/H2 (red- line) and TiO2/O2 (black-line) in log-scale against photon energy, where two-absorption spectra centered at 2.2 eV and 3.0 eV were numerically removed. Urbach energy obtained by the linear relationship in log(α) vs. photon energy below band gap was 153 meV and 114 meV for the TiO2/H2 and TiO2/O2, respectively. Previously, Choudhury et al. [21] reported the Urbach energy is dependent on anneal condition for sol-gel TiO2, and the energy of 140 meV for the anatase-TiO2 annealed in vacuum and about 100 meV for anatase/rutile mixed TiO2. They concluded such increase of the Urbach energy is come from oxygen-vacancies or structural disordering at interface with different crystal phases. In this work, Urbach energy for the TiO2/H2 was higher than that for the TiO2/O2, however, the density of oxygen-vacancy was similar for the both layers as shown by the absorption intensity around 3.0 eV in Figure 4(a). In contrast, from the result that the absorption around 2.2 eV was increased in the intensity for the TiO2/H2, it can be suggested not only the oxygen-vacancy but also the Ti3+-re- lated defects and/or the complexes contributed the band gap narrowing.
3.3. Temperature Dependence of Resistivity
Figure 5(a) shows dependence of resistivity evaluated by VDP method for TiO2/H2 layer. The electrodes using Indium-dots were ohmic at overall temperatures as shown in Figure 5(b), in which the current-voltage characteristics at 10 K (open-circle) and 300 K (solid-circle) are plotted. The saturated feature at low temperature indicated the layer was degenerated by the high density of conduction electron originated from shallow donors. In contrast, the resistivity was exponentially decreased with increasing temperature above 100K in Arrhenius relationship with the activation energy of 96.1 meV. Since it is difficult to attribute the activation energy to donor-level energy below conduction-band minimum in the degenerated semiconductor, influence in the grain boundary region should be taken into account in the electric conduction of the layer. In the grain boundary region, it is easy to consider deep level defects are formed by significantly disordered structures. The defects in the boundary region trap the carriers or compensate the shallow donors. In the case that the carriers are traps in the deep defects, depletion region is introduced toward the kernel. Previously, Blom et al. presented a conduction model for poly-crystalline layer consists of kernels and grain-boundaries and applied the analysis for temperature dependent conduction of ZnO layer [22] . In the model, resistivity of the layer parallel to the substrate is limited by that of grain boundaries surrounding kernel, because Schottky barrier is formed by traps in the grain- boundary because the resistivity of kernel can be expected to be much lower than that of the boundary region. Since the density of thermally emitted carrier across the barrier is increased with temperature, resistivity of the layer is decreased with temperature and then saturated to the resistivity due to the kernels at high temperature. However, the model is insufficient to the result in this work because the resistivity was saturated at low temperature. On the other, in the case that the carrier density is significantly reduced by compensation of shallow donors in the boundary region, resistivity in the region is much higher than in the kernel and dependent on the temperature. The resistivity in grain-boundary region is expected to be decreased with temperature. In this case, although resistivity of the layer limited by the resistance in grain-boundary is saturated at low temperature and reduced with temperature, the activation energy experimentally obtained by the result of Figure 5(a) is too large to explain the result of temperature dependent resistivity. Here, it should be noted that defects at deep level are also formed at surface. When electrons are captured by the traps at the surface, depletion region is extended in the boundary region with low carrier density from the TiO2 surface. The depletion length can be estimated by density of the trapped electron in the surface state (Nsse) and effective donor density in the boundary region (Nbd) in the relationship of Nbd/Nsse. The depletion region acts to cut off carrier transport across the boundary region and the depleted length is decreased with temperature due to activation of electrons captured the traps, which is resulted in decrease of the resistivity with temperature. Details based on the model including surface treatment of the layer are in progress, but the simulated result can explain well the temperature dependent resistivity as shown by solid-line in Figure 5(a). The result indicated Nbd/Nsse, peak energy of the surface trap below conduction band minimum, FWHM of surface trap distribution for electron energy and resistivity without the cut-off of electron transport in grain boundary is 1.8 × 10−5, 195 meV, 136 meV and 4.2 × 10−3 Ω cm, respectively. The obtained parameters suggested resistivity of the kernel is much lower than the effective resistivity limited by the grain boundary.

Figure 5. (a) Arrhenius plot of resistivity for TiO2/H2, in which the resistivity was evaluated by VDP method and (b) I-V property of the layer at 10 K (open-circle) and 300 K (solid-circle).
4. Conclusion
Low pressure chemical vapor deposition of TiO2 layer was performed in H2-ambient. The deposition rate and activation energy for the deposition were decreased and decreased as compared with the deposition in O2-am- bient. Crystallographic property of the layer deposited in H2 was inferior to that in O2 but the resistivity was drastically reduced by using H2 during the deposition. Optical absorption around 2.2 eV was notably increased by the deposition in H2 with scarce increase around 3.0 eV. These results and a possible dissociation scheme of TTIP on the deposition surface suggested that donor in the layer was originated from Ti3+ and/or Ti3+-related complex, which was increased by hydrogen. Temperature dependent resistivity was also evaluated for the layer deposited in H2, in which the resistivity was saturated at low temperature region but decreased with temperature above 100 K. A possible model consisted of kernel, grain-boundary and surface trapped electrons was applied to clarify the conduction mechanism of the layer. As a result, the temperature dependent result could be well fitted by the model and showed that electron transport in the layer was limited by depletion region in the grain- boundary, Further, the obtained parameters indicated that the grain with the resistivity of 4 × 10−3 Ω cm was formed with the surface traps around 200 meV below the conduction band minimum by the demonstrated deposition process, and the boundary and the surface engineering were fundamentally necessary to perform transparent conductive TiO2 layer.
References
- Wang, R., Hashimoto, K. and Fujishima, A. (1997) Light-Induced Amphiphilic Surfaces. Nature, 388, 431-432. http://dx.doi.org/10.1038/41233
- Mills, A., Lepre, A., Elliott, N., Bhopal, A., Parkin, I.P. and Neill, S.A. (2003) Characterisation of the Photocatalyst Pilkington ActivTM: A Reference Film Photocatalyst? Journal of Photochemistry and Photobiology A: Chemistry, 160, 213-224. http://dx.doi.org/10.1016/S1010-6030(03)00205-3
- Campbell, S.A., Kim, H.S., Gilmer, D.C., He, B., Ma, T. and Gladfelter, W.L. (1999) Titanium Dioxide (TiO2)-Based Gate Insulators. IBM Journal of Research and Development, 43, 383-392. http://dx.doi.org/10.1147/rd.433.0383
- Martinet, C., Paillard, V., Gagnaire A. and Joseph, J. (1997) Deposition of SiO2 and TiO2 Thin Films by Plasma Enhanced Chemical Vapor Deposition for Antireflection Coating. Journal of Non-Crystalline Solids, 216, 77-82. http://dx.doi.org/10.1016/S0022-3093(97)00175-0
- Hitosugi, T., Ueda, A., Furubayashi, Y., Hirose, Y., Konuma, S., Shimada, T. and Hasegawa, T. (2006) Fabrication of TiO2-Based Transparent Conducting Oxide Films on Glass by Pulsed Laser Deposition. Japanese Journal of Applied Physics, 46, L86-L88. http://dx.doi.org/10.1143/JJAP.46.L86
- Gillispie, M.A., van Hest, M.F.A.M., Dabney, M.S., Perkins, J.D. and Ginley, D.S. (2007) rf Magnetron Sputter Deposition of Transparent Conducting Nb-doped TiO2 Films on SrTiO3, Journal of Applied Physics, 101, Article Id: 033125.http://dx.doi.org/10.1063/1.2434005
- Hoang, N.L., Yamada, N., Hitosugi, T., Kasai, J., Nakao, S., Shimada, T. and Hasegawa, T. (2008) Low-Temperature Fabrication of Transparent Conducting Anatase Nb-Doped TiO2 Films by Sputtering. Applied Physics Express, 1, 115001-115003. http://dx.doi.org/143/APEX.1.115001
- Zhang, A. and Griffin, L. (1995) Gas-Phase Kinetics for TiO2: Hot-Wall Reactor Results. Thin Solid Films, 263, 65-71. http://dx.doi.org/10.1016/0040-6090(95)06580-6
- Yamauchi, S., Saiki, S., Ishibashi, K., Nakagawa. A. and Hatakeyama, S. (2014) Low Pressure Chemical Vapor Deposition of Nb and F Co-Doped TiO2 Layer. Journal of Crystallization Process and Technology, 4, 79-88. http://dx.doi.org/10.4236/jcpt.2014.42011
- Siefering, K.L. and Griffin, G.L. (1990) Kinetics of Low-Pressure Chemical Vapor Deposition of TiO2 from Titanium Tetraisopropoxide. Journal of the Electrochemical Society, 137, 814-818. http://dx.doi.org/10.1149/1.2086561
- Fictorie, C.P., Evans, J.F. and Gladfelter, W.L. (1994) Kinetic and Mechanistic Study of the Chemical Vapor Deposition of Titanium Dioxide Thin Films using Tetrakis-(Isopropoxo)-Titanium(IV). Journal of Vacuum Science & Technology A, 12, 1108-1113. http://dx.doi.org/10.1116/1.579173
- Ahn, K.H., Park, Y.B. and Park, D.W. (2003) Kinetic and Mechanistic Study on the Chemical Vapor Deposition of Titanium Dioxide Thin Films by in Situ FT-IR Using TTIP. Surface and Coating Technology, 171, 198-204. http://dx.doi.org/10.1016/S0257-8972(03)00271-8
- Shmakov, A.G., Korobeinichev, O.P., Knyazkov, D.A., Paletsky, A.A., Maksutov, R.A., Gerasimov, I.E., Bolshova, T.A., Kiselev, V.G. and Gritsan, N.P. (2013) Combustion Chemistry of Ti(OC3H7)4 in Premixed Flat Burner-Stabilized H2/O2/Ar Flame at 1 atm, Proceedings of the Combustion Institute, 34 ,1143-1149. http://dx.doi.org/10.1016/j.proci.2012.05.081
- Panayotov, D.A. and Yates Jr., J.T. (2007) n-Type Doping of TiO2 with Atomic Hydrogen-Observation of the Production of Conduction Band Electrons by Infrared Spectroscopy. Chemical Physics Letters, 436, 204-208. http://dx.doi.org/10.1016/j.cplett.2007.01.039
- Valentin, C.D. and Pacchioni, G. (2009) Reduced and n-Type Doped TiO2: Nature of Ti3+ Species. The Journal of Phy- sical Chemistry C, 113, 20543-20552. http://dx.doi.org/10.1021/jp9061797
- Yamauchi, S., Suzuki, H. and Akutsu, R. (2014) Plasma-Assisted Chemical Vapor Deposition of Titanium Oxide Layer at Room-Temperature. Journal of Crystallization Process and Technology, 4, 20-26. http://dx.doi.org/10.4236/jcpt.2014.41003
- Nakamura, I., Negishi, N., Kutsuna, S., Ihara, T., Sugihara, S. and Takeuchi, K. (2000) Role of Oxygen Vacancy in the Plasma-Treated TiO2 Photocatalyst with Visible Light Activity for NO Removal. Journal of Molecular Catalysis A: Chemical, 161, 205-212. http://dx.doi.org/10.1016/S1381-1169(00)00362-9
- Ride, D.R. (2005) CRC Handbook of Chemistry and Physics. CRC Press L.L.C., Boca Raton.
- Sekiya, T., Ichimura, K., Igarashi, M. and Kurita, S. (2000) Absorption Spectra of Anatase TiO2 Single Crystals Heat- Treated under Oxygen Atmosphere. Journal of Physics and Chemistry of Solids, 61, 1237-1242. http://dx.doi.org/S-0022-3697(99)00424-2
- Urbach, F. (1953) The Long-Wavelength Edge of Photographic Sensitivity and of the Electronic Absorption of Solids. Physical Review, 92, 1324. http://dx.doi.org/10.1103/PhysRev.92.1324
- Choudhury, B. and Choudhury, A. (2014) Oxygen Defect Dependent Variation of Band Gap, Urbach Energy and Luminescence Property of Anatase, Anatase-Rutile Mixed Phase and of Rutile Phases of TiO2 Nanoparticles. Physica E: Low-Dimensional Systems and Nanostructures, 56, 364-371. http://dx.doi.org/10.1016/j.physe.2013.10.014
- Blom, F.R., van de Pol, F.C.M., Bauhuis, G. and Popma, T.J.A. (1991) R.F. Planar Magnetron Sputtered ZnO Films II: Electrical Properties. Thin Solid Films, 204, 365-376. http://dx.doi.org/10.1016/0040-6090(91)90075-9
NOTES
*Corresponding author.







