Journal of Crystallization Process and Technology
Vol.4 No.2(2014), Article ID:44499,8 pages DOI:10.4236/jcpt.2014.42010
Reaction Rate Models for the Thermal Decomposition of Ibuprofen Crystals
Sundaram Ramukutty, Esakki Ramachandran
Department of Physics, Thiruvalluvar College, Papanasam, India
Email: esakkiramachandran@yahoo.co.in
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 18 January 2014; revised 18 February 2014; accepted 25 February 2014
ABSTRACT
Kinetics of the decomposition of racemic ibuprofen crystals were studied by non-isothermal analysis. Thermogravimetric analysis revealed that ibuprofen is thermally stable up to 152.6˚C and the initial loss of mass was due to evaporation only. Activation energy, pre-exponential factor, activation entropy and Gibbs free energy for the decomposition of ibuprofen were determined using the integral method of Coats-Redfern (CR). Geometrical contraction models were found to be the best fits. The Arrheinus equation for the thermal decomposition of ibuprofen is k = (1.1 × 107) e–79125/RT sec–1.
Keywords
Ibuprofen, Model Fitting, Kinetics, Decomposition, Coats-Redfern Method

1. Introduction
Thermal analysis is one of the most frequently used instrumental techniques in the pharmaceutical research. TGA/ DTA and differential scanning calorimetry help to solve pharmaceutical problems like the purity level, qualitative and quantitative analysis of drug formulations and polymorphism [1] [2] . Also, determination of the kinetic parameters helps to estimate the thermal stability [3] and hence the shelf-life of drugs.
Kinetic analysis has been the subject of interest for many investigators involved in the field of thermal decomposition. Solid-state kinetics studies have increasing importance in thermal analysis and being helpful in the calculation of the parameters of Arrhenius equation and to determine the mechanism of decomposition reaction. Various methods were proposed for the kinetic study of the thermal decomposition of materials and are generally classified under model-fitting and model-free methods. In each case, isothermal and non-isothermal data can be used. These analyses can provide valuable information about the shelf-life period and conditions of storage.
Ibuprofen or 2-(4-isobutylphenyl)-propionic acid belongs to a group of drugs called nonsteroidal anti-inflammatory drugs (NSAIDs). For many years, it has been used in the treatment of rheumatoid arthritis and other inflammatory diseases. Recently, renewed interest in this compound has arisen as new therapeutic properties have been discovered. Ibuprofen was shown to protect neurons from glutamate toxicity in-vitro [4] . The kinetic parameters of ibuprofen were determined by Bogdan Tita et al. [5] earlier. A renewed attempt is made by the authors. Since single crystal is the purest form of a compound, ibuprofen was synthesized from crystalline powder. Presently ibuprofen single crystals were grown by gel growth method. The grown crystal was confirmed using single crystal X-ray diffraction analysis. The kinetic parameters were determined for various solid state reaction models using the CR method under non-isothermal condition. The best fitting and suited model was determined using these parameters. Gibbs free energy and the entropy of activation were also calculated.
2. Experimental Details
Ibuprofen (99.9%) was purchased from Gopish Pharma Ltd., India. Silica gel prepared from an aqueous solution of sodium metasilicate (Na2SiO3.5H2O) (s.d. fine-Chem Ltd, Mumbai) was used as crystal growth medium. Organic solvent assays of 99% (Spectrum Reagent & Chemicals Pvt, Ltd., Cochin) were used for the preparation of binary mixtures. An aqueous solution of sodium metasilicate of specific gravity 1.06g/cm3 was prepared and the pH of the solution was adjusted using 5M acetic acid (Nice Chemicals Pvt. Ltd, Cochin). 2% w/v of ibuprofen in methanol-diethyl ether mixture (0.5:1) solution was placed over the set gel taken in a test tube. The pH of the gel solution was varied to get the best conditions for crystal growth and the crystal growth experiments were carried out at ambient temperature (≈ 27˚C). Transparent, platy crystals crystallized (Figure 1). The crystals were removed after a growth period of four weeks.
Enraf-Nonius CAD-4 Diffractometer, with MoKα (λ = 0.71073 Å) radiation was used to obtain the accurate cell parameters of the grown ibuprofen single crystal at room temperature. Cell parameters were obtained from least-squares refinement of the setting angles of 87 reflections.
TGA/DTA of ibuprofen (Figure 2) was carried out using a Perkin Elmer Pyris Diamond thermogravimetric/differential thermal analyzer instrument with an alumina crucible, applying a heating rate 10˚C min–1 in the temperature range of 40˚C - 610˚C, under nitrogen atmosphere with a flow rate 40 mL min–1. Crystalline powder of mass 10.776 mg of the grown crystals was used for the thermal analysis.
3. Results and Discussion
The unit cell parameters were determined from the collected X-ray data. Lattice parameters of racemic ibuprofen are: a = 10.768(18) Å, b = 7.881(16) Å, c = 14.674(31) Å, β = 99.50(9)˚ and the space group is P21/c. These values agree well with the reported values [6] in the literature.
The TGA/DTA curve is shown in Figure 2. Two non-symmetrical endothermic peaks were observed in the DTA curve at 76.2˚C and 255˚C. The endothermic peak at 76.2˚C, and the absence of loss of mass in the TGA indicates that it is the melting point of ibuprofen. Also the melting point of racemic ibuprofen reported earlier [7] agrees with the experimental data. The other peak at 255˚C indicates the boiling point. The evaporation of ibuprofen is intiated at 152.6˚C, and is followed by the exothermic behaviour between 189.7˚C and 255˚C.
Thermodynamical parameters, enthalpy of fusion (∆Hf) at the melting point and enthalpy of vaporization(∆Hvap) were determined using the Gibbs function and by Trouton’s rule as 28.10 kJ/mol and 46.47 kJ/mol

Figure 1. Ibuprofen crystals: (a) in gel (b) in mixtures of diethyl ether-methanol.
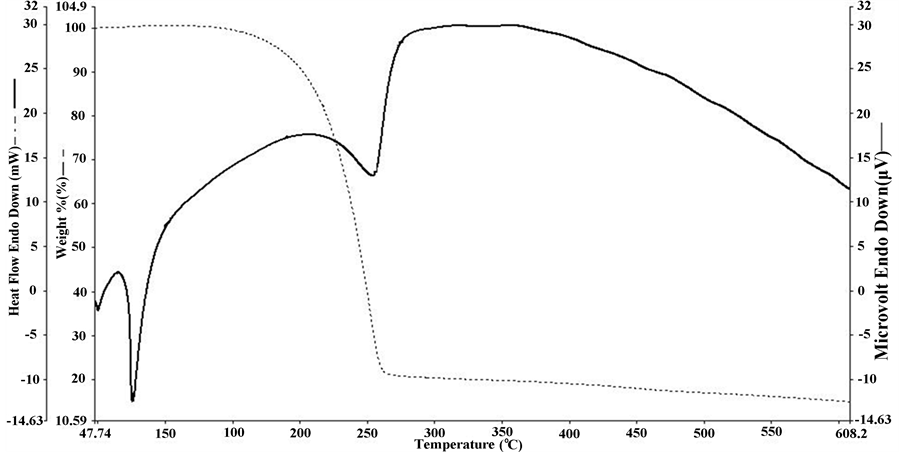
Figure 2. TGA/DTA of ibuprofen.
respectively. It is found that the activation energy of ibuprofen is twice that for enthalpy of vaporization (Table 1). This suggests that ibuprofen continue the dimer structure in liquid state and becomes a monomer in vapour state. The dimer structure is also confirmed by single crystal X-ray diffraction data. Hence the loss of mass of 50% may be attributed to evaporation of ibuprofen molecules in liquid phase, which is complete at a temperature nearly 245˚C. This behavior is also observered in the work of Lerdkanchanaporn et al [8] . The thermal decomposition of ibuprofen starts at 255˚C, transforming into a monomer and decompose with the release of CO2 molecule and hydrogen from the carboxylic acid chain accounting for a loss of mass of 21.8% that happens in the neighbourhood of the boiling point. Further decomposition results in a loss of mass of 7.76% and is due to the release of CH4 molecule at 274˚C, leaving carbonaceous residue behind. The material is found to be thermally stable up to 152.6˚C.
3.1. Kinetic Parameters
Kinetic parameters primarily depend on the rate of reaction. The TGA data is useful in the determination of the extent of reaction [9] . Kinetic analysis of decomposition process involves the reaction model and the Arrhenius equation. The reaction models are classified as nucleation model, diffusion model and reaction order model. Each model depends on the function extent of reaction (α). The extent of reaction was determined from the TGA/DTA (Figure 2) using the relation,
 (1)
(1)
where mt is the mass of the sample at particular temperature. mo and mf are the initial and final masses of the reaction respectively. Pre-exponential factor and activation energy were calculated for every model and the goodness of fit is analyzed. Kinetic parameters were determined from solid state rate reaction and integral rate law. The general form of solid state rate reaction Equation (2) and integral rate law Equation (3) are:
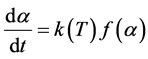 (2)
(2)
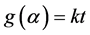 (3)
(3)
where t is time, T—temperature, f(α)—reaction model and g(α) is the integral reaction model. The rate constant k is determined using Arrhenius equation.
Equations (2) & (3) are modified using the Arrhenius equation as
Table 1 . Arrhenius parameters for non-isothermal decomposition of ibuprofen.
 (4)
(4)
 (5)
(5)
where A and E are the pre-exponential factor and activation energy; R is the gas constant.
The Arrhenius parameters (A and E) together with the reaction model are called as the kinetics triplet. Under non-isothermal condition equations incorporating β the heating rate (4) & (5) can be written as,
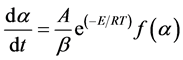 (6)
(6)
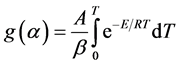 (7)
(7)
Replacing 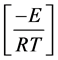 as “x” and transforming the limits in the Equation (7),
as “x” and transforming the limits in the Equation (7),
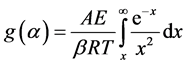 (8)
(8)
The exponential integral is replaced with p(x) which is a standard one, has no analytical solution but has approximations.
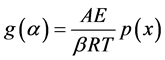 (9)
(9)
Kinetics parameters may be obtained from non-isothermal rate laws by both model-fitting and model-free methods. Model-fitting methods involve fitting of different models to the extent of reaction—temperature curves and simultaneous determination of the activation energy and frequency factor. Though there are several non-isothermal model-fitting methods, one of the most popular being the CR method [10] was used. It is an integral method that assumes various order of reaction and compares the linearity in each case to select the correct order. This method uses the asymptotic series expansion for approximating the exponential integral in Equation (9) and hence becomes,
 (10)
(10)
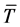 is the mean experimental temperature. Plotting
is the mean experimental temperature. Plotting  vs.
vs. 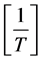 of Equation (10), gives E and A from the slope and intercept respectively. The model that gives the best linear fit is selected as the chosen model for the decomposition. Different reaction models available in the literature are listed in Table 2 [11] [12] . Arrhenius Parameters for non-isothermal decomposition of Ibuprofen were also determined for various models.
of Equation (10), gives E and A from the slope and intercept respectively. The model that gives the best linear fit is selected as the chosen model for the decomposition. Different reaction models available in the literature are listed in Table 2 [11] [12] . Arrhenius Parameters for non-isothermal decomposition of Ibuprofen were also determined for various models.
Kinetic analysis of ibuprofen was made using the TGA/DTA ( Figure 1) and the thermal degradation ibuprofen in the range 152.6˚C to 255˚C was chosen as it is linear. The graphs between ln{g(α)/T2} vs. 1/T of Equation (10) for the models 1 - 3 and 4 - 12 are plotted and depicted in Figures 3(a) & 3(b) respectively. Two
Table 2 . Solid state reaction models.

Figure 3. Plot of ln [g(α)/T2] vs. 1/T, TGA/DTA of ibuprofen.
separate plots were presented to view the response distinctly. The activation energy and pre-exponential factor were determined from the graph and are listed in Table 1. The activation energy should be positive for the absence of phase transition [13] . The calculated activation energies are positive for all the models, indicating that no phase transition took place in the selected temperature range. Moreover the best fitting model is decided from the correlation coefficient (r2) and it should approach 1. Though all the models seem to be better fits for α < 0.80, the reaction order models 8, 11 and 12 seem to be the best fitted models for the decomposition of ibuprofen in the chosen temperature range. But the Arrhenius parameters obtained from the models 11 and 12 almost matched with that of the reported values [5] [14] . Hence the mean value of activation energy and preexponential factors these models are presented and are: 79.1 kJ/mol and 1.162 × 107 sec–1 respectively. The Arrhenius equation for the thermal decomposition of ibuprofen is k = (1.1 × 107) e–79125/RT sec–1. This equation agrees with that of the values reported earlier [15] . Further a graph (Figure 4) is drawn between the activation energy (E) and pre exponential factor (A) obtained in Table 1. This indicates that there is a linear relation between E and A.
3.2. Thermodynamic Parameters
Entropy of activation is defined as the difference between the entropy of the transition state and the sum of entropies of the reactants. Free energy of change of decomposition is the driving force of a chemical reaction and hence is the difference between the enthalpy of the transition state and the sum of enthalpies of the reactants in the ground state.
The Thermodynamic parameters of ibuprofen: entropy of activation (∆S), enthalpy of activation (∆H) and Gibbs free energy (∆G) were calculated using Equations (11)-(13).
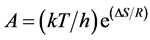 (11)
(11)
where h and k are Planck’s constant and Boltzmann constant respectively.
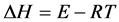 (12)
(12)
![]() (13)
(13)
The calculated rate constant and thermodynamic parameters or different models are listed in Table 3. It is observed that the entropy of activation increases with the increase of activation energy. The positive value of ∆G shows that the reaction involved in the decomposition of ibuprofen is not spontaneous. It is noted that the activation energy is nearly equal to enthalpy of activation (Table 3) suggesting that ibuprofen is in condensed phase between 152.6˚C to 255˚C. The mean values of ∆S, ∆H and ∆G for the models 11 & 12 are:39.60 J/K mol, 75.17 kJ/mol and 56.32 kJ/mol respectively.
4. Conclusion
Single crystals of ibuprofen were grown by gel growth method. Monoclinic form of the crystal was confirmed

Figure 4. Plot of E vs. ln A.
Table 3. Thermodynamic parameters of ibuprofen
using single crystal X-ray diffraction analysis. Thermal decomposition kinetics of ibuprofen was analyzed. Ibuprofen is thermally stable up to 152.6˚C. It is concluded that ibuprofen exists in dimer before the boiling point and in monomer after the boiling point. The thermal decomposition of ibuprofen occurred in a single step after the melting point. This happened in the form of evaporation only up to the boiling point. The kinetic parameters were determined using CR method. Thermodynamic parameters also confirmed that the decomposition of ibuprofen is due to non-spontaneous reaction. Geometrical contraction models were found to be the best fits.
Acknowledgements
The authors thank the University Grants Commission, Government of India, for providing Major Research Project; the Secretary of Thiruvalluvar College, Papanasam and Dr. K. Ravikumar, Dr. B. Sridhar, Laboratory of X-ray Crystallography, IICT, Hyderabad.
References
- Macedo, R.O., Aragao, C.F.S., do Nascimento, T.G. and Macedo, A.M.C. (1999) Application of Thermogravimerty in the Quality Control of Chloramphenicol Tablets. Journal of Thermal Analysis and Calorimetry, 56, 1323-1327. http://dx.doi.org/10.1023/A:1010102422381
- Moura, E.A., Correia, L.P., Pinto, M.F., Procopic, V.V., De Sousa, F.S. and Macedo, R.O. (2010) Thermal Characterization of the Solid State and Raw Material Fluconazole by Thermal Analysis and Pyrolysis Coupled to GC/MS. Journal of Thermal Analysis and Calorimetry, 100, 289-293. http://dx.doi.org/10.1007/s10973-009-0473-x
- Picciochi, R., Diogo, H.P. and Minas Da Piedade, M.E. (2010) Thermochemistry of Paracetamol. Journal of Thermal Analysis and Calorimetry, 100, 391-401. http://dx.doi.org/10.1007/s10973-009-0634-y
- Casper, D., Yaparpalvi, U., Rempel, N. and Werner, P. (2000) Ibuprofen Protects Dopaminergic Neutrons against Glutamate Toxicity in Vitro. Neuroscience Letters, 289, 201-204. http://dx.doi.org/10.1016/S0304-3940(00)01294-5
- Tita, B., Fulias, A., Bandur, G., Rusu, G. and Tita, D. (2010) Thermal Stability of Ibuprofen. Kinetic Study under Non-Isothermal Conditions. Revue Roumaine de Chimie, 55, 553-558.
- Stone, K.H., Lapidus S.H. and Stephens, P.W. (2009) Implementation and Use of Robust Refinement in Powder Diffraction in the Presence of Impurities. Journal of Applied Crystallography, 42, 385-391. http://dx.doi.org/10.1107/S0021889809008450
- Romero, A.J. and Rhodes, C.T. (1993) Stereochemical Aspects of the Molecular Pharmaceutics of Ibuprofen. Journal of Pharmacology and Pharmacotherapeutics, 45, 258-262. http://dx.doi.org/10.1111/j.2042-7158.1993.tb05549.x
- Lerdkanchanaporn, S. and Dollimore, D. (2000) The Evaporation of Ibuprofen from Ibuprofen-Starch Mixtures Using Simultaneous TG-DTA. Thermochimica Acta, 357, 71-78. http://dx.doi.org/10.1016/S0040-6031(00)00370-1
- Liu, Z.S., Wang, Q., Zou, Z.S. and Tan, G.L. (2011) Arrhenius Parameters Detemination in Non-Isothermal Conditions for the Uncatalyzed Gasification of Carbon by Carbon Dioxide. Thermochimica Acta, 512, 1-4. http://dx.doi.org/10.1016/j.tca.2010.08.014
- Coats, A.W. and Redfern, J.P. (1964) Kinetic Parameters from Thermogravimetric Data. Nature, 201, 68-69. http://dx.doi.org/10.1038/201068a0
- Ebrahimi Kahrizsangi, R., Abbasi, M.H. and Saidi, A. (2007) Model Fitting Approach to Kinetic Analysis of NonIsothermal Oxidation of Molybdenite. Iranian Journal of Chemistry & Chemical Engineering, 26, 119-123.
- Brown, M.E. and Gallagher, P.K. (2007) Handbook of Thermal Analysis and Calorimetry: Recent Advances, Techniques and Applications. Elsevier, The Netherlands, 5, 532.
- Brown, M.E. and Gallagher, P.K. (2007) Handbook of Thermal Analysis and Calorimetry: Recent Advances, Techniques and Applications. Elsevier, The Netherlands, 5, 517.
- Xu, F., Sun, L.X., Tan, Z.C., Liang, J.G. and Li, R.L. (2004) Thermodynamic Study of Ibuprofen by Adiabatic Calorimetry and Thermal Analysis. Thermochimica Acta, 412, 33-57. http://dx.doi.org/10.1016/j.tca.2003.08.021
- Ramukutty, S. and Ramachandran, E. (2012) Mechanical and Thermal Studies on Gel Grown Racemic Ibuprofen Crystals. World Science and Technology, 2, 36-38.


