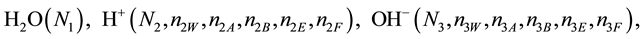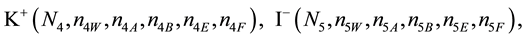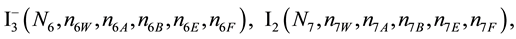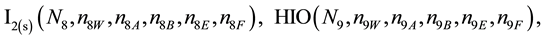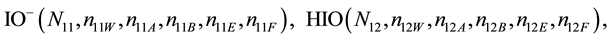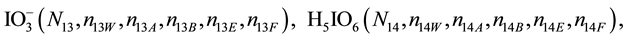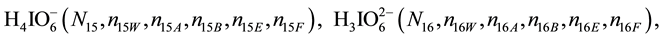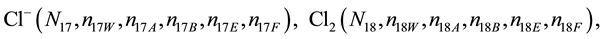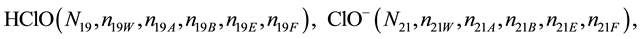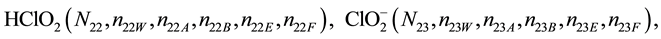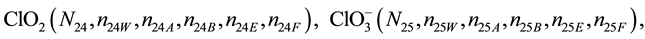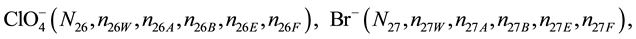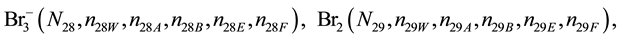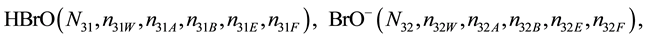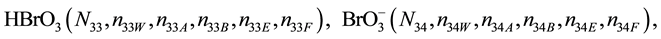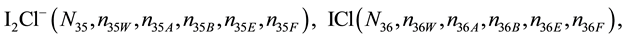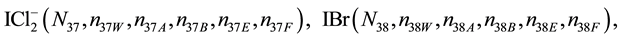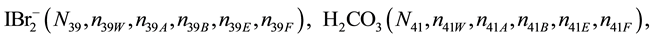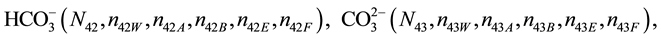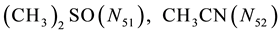Journal of Analytical Sciences, Methods and Instrumentation
Vol.04 No.04(2014), Article ID:52018,7 pages
10.4236/jasmi.2014.44014
Generalized Electron Balance for Dynamic Redox Systems in Mixed-Solvent Media
Anna Maria Michałowska-Kaczmarczyk1, Tadeusz Michałowski2*
1Department of Oncology, The University Hospital in Cracow, Cracow, Poland
2Faculty of Engineering and Chemical Technology, Cracow University of Technology, Cracow, Poland
Email: *michalot@o2.pl
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 September 2014; revised 25 October 2014; accepted 5 November 2014
ABSTRACT
A complex example of electrolytic redox system involving 47 species, 3 electron-active elements and five (3 amphiprotic + 2 aprotic) co-solvents, is presented. Mixed solvates of the species thus formed are admitted in the system considered. It is proved that the Generalized Electron Balance (GEB) in its simplest form obtained according to the Approach II to GEB is identical with the one obtained for aqueous media and binary-solvent system, and is equivalent to the Approach I to GEB.
Keywords:
Electrolytic Redox Systems, Generalized Electron Balance, Mixed-Solvent Media

1. Introduction
Motto: “Everything should be made as simple as possible, but not simpler” [1] .
In the previous issues [2] - [8] and in earlier papers cited therein, the concept of Generalized Electron Balance (GEB), completing the set of compatible equations necessary for quantitative/mathematical solution of electrolytic redox systems, was introduced as two alternative options, named as Approach I and Approach II to GEB. In both Approaches it is assumed/admitted, that all the species 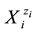 exist in an electrolytic system in their natural form, i.e., as solvates. In particular, there are hydrates
exist in an electrolytic system in their natural form, i.e., as solvates. In particular, there are hydrates 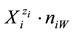 in aqueous (W = H2O) media,
in aqueous (W = H2O) media, 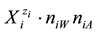 ,
, 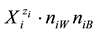 or
or 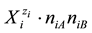 in binary-solvent media (W, A), (W, B) or (A, B) [9] -[11] , respectively. The values of nWi, nAi and nBi, considered as mean numbers of W, A and B attached to
in binary-solvent media (W, A), (W, B) or (A, B) [9] -[11] , respectively. The values of nWi, nAi and nBi, considered as mean numbers of W, A and B attached to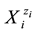 , are unknown, in principle, and vary with the co-solvent(s) composition, and solute(s) concentration.
, are unknown, in principle, and vary with the co-solvent(s) composition, and solute(s) concentration.
In this paper, we refer also to more complex media with the mixture of co-solvents: W, A, B, E and F. We assume that the co-solvents are mutually miscible and at least one of the co-solvents has amphiprotic properties
[5] . Eeach of the co-solvents has potential/real solvating properties, i.e., 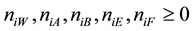 in the solvated species
in the solvated species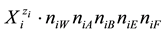 . Let
. Let 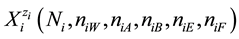 denotes Ni entities of these species in the related
denotes Ni entities of these species in the related
system. In further part of the paper, we assume W = H2O, A = CH3OH, B = C2H5OH, E = (CH3)2SO, F = CH3CN;
W, A, B have amphiprotic properties, and E, F―have not. In particular, N15 ions 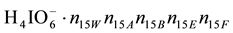 contain:
contain: 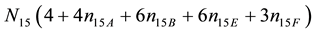 atoms of H,
atoms of H, 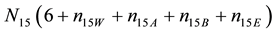 atoms of O, N15
atoms of O, N15
atoms of I, 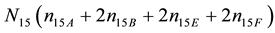 atoms of C, N15n15E atoms of S, and N15n15F atoms of N. It is as-
atoms of C, N15n15E atoms of S, and N15n15F atoms of N. It is as-
sumed that the solvents do not form―with solvates―the species 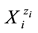 other than those formed in (known from) aqueous media. In other words, W, A, B, E, F enter (potentially) the solvating sphere of
other than those formed in (known from) aqueous media. In other words, W, A, B, E, F enter (potentially) the solvating sphere of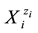 . On this basis, the elemental balances f(E(i)) for particular elements E(i) are formulated. For ordering purposes, we denote: E(1) = H, E(2) = O, E(3) = I, E(4) = C, E(5) = S, E(6) = N. We apply also the balances f(C(Y)) for the cores C(Y), Y = A, B, E, F. The “core” is a cluster of elements of the same composition, structure and charge, that does not undergo a change in the system in question; e.g., CH3OH,
. On this basis, the elemental balances f(E(i)) for particular elements E(i) are formulated. For ordering purposes, we denote: E(1) = H, E(2) = O, E(3) = I, E(4) = C, E(5) = S, E(6) = N. We apply also the balances f(C(Y)) for the cores C(Y), Y = A, B, E, F. The “core” is a cluster of elements of the same composition, structure and charge, that does not undergo a change in the system in question; e.g., CH3OH, 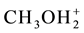 and CH3O? contain the cluster CH3O?, considered as the core. We denote C(A) = CH3O?, C(B) = C2H5O?, C(E) = (CH3)2SO = E, C(F) = CH5CN = F. The species: H2CO3,
and CH3O? contain the cluster CH3O?, considered as the core. We denote C(A) = CH3O?, C(B) = C2H5O?, C(E) = (CH3)2SO = E, C(F) = CH5CN = F. The species: H2CO3, 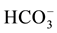
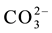
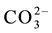
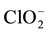
All the balances in this paper will be presented explicitly, to check the validity of the reasoning and accept it without reservations.
2. Formulation of Balances
Let us consider a system obtained after addition of V mL of titrant (T) containing I2 (C) + KI (C1) + CO2 (C2) in A + B + E + F into V0 mL of titrand (D) containing KBrO3 (C0) + HCl (C01) + CO2 (C02) in W + A + E; all concentrations are expressed in mol/L. The volume V0 mL of D is composed of N01 molecules of KBrO3, N02 molecules of HCl, N03 molecules of CO2, N04 molecules of W, N05 molecules of A, and N06 molecules of E; V mL of T is composed of N07 molecules of I2, N08 molecules of KI, N09 molecules of CO2 and N011 molecules of A, N012 molecules of B, N013 molecules of E, and N014 molecules of F.
We assume that the solutes composing D and T were introduced in single solvents or mixtures of solvents. In ca. V0 + V mL of a D + T mixture thus obtained, we have the following species (all changes in oxidation degrees are admitted).
where I2(s)―solid iodine, I2―soluble iodine. In the above list of species, H2O (N1), CH3OH (N44), C2H5OH (N47), (CH3)2SO (N51) and CH3CN (N52) are free molecules of the corresponding solvents, i.e., not involved in the solvates. We prove that the numbers: N1, N44, N47, N51 and N52 of the free molecules and the numbers: niW, niA, niB, niE, niF of these molecules in the solvates do not enter the simplest form of the resulting GEB.
The elemental balances: f(H) for H, and f(O) for O are as follows:
・ f(H)

・ f(O)

From (1) and (2) we obtain
・ 2・f(O) ? f(H)

As we see, Equation (3) does not involve the terms N1, N04, and {niW} related to water. To cancel the terms involved with A, B, E and F, we add Equation (3) to the core balances (4) - (7): 2・f(CH3O) (4), 4・f(C2H5O) (5), 4・f((CH3)2SO) (6), 3・f(CH3CN) (7) and charge balance (8). Further simplification gives addition of the balance for K (9), and of the core balance 4・f(CO3) (10):
・ 2・f(CH3O)
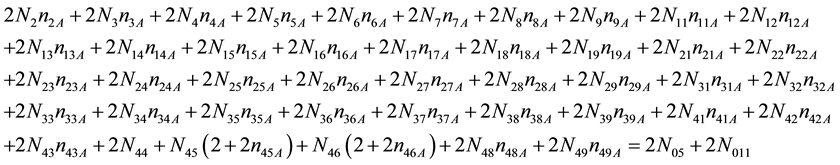
・ 4・f(C2H5O)
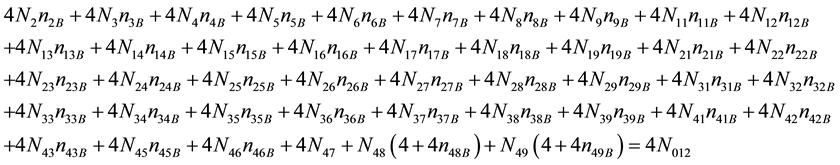
・ 4・f((CH3)2SO)
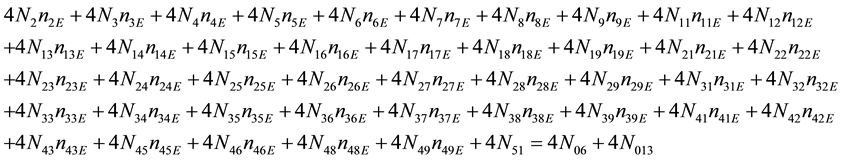
・ 3・f(CH3CN)
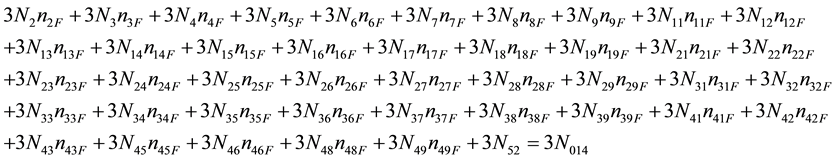
・ Charge balance
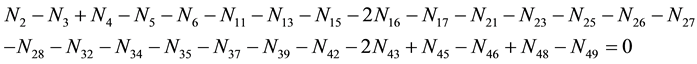
・ f(K)
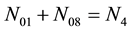
・ 4・f(CO3)
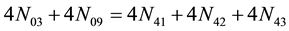
As the result of this addition, considered as a kind of linear combination [4] , we obtain the simplest form of GEB, expressed in terms of numbers of entities:
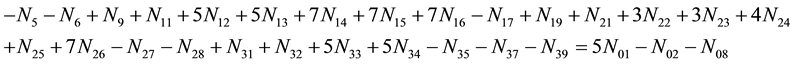
Applying the relations:
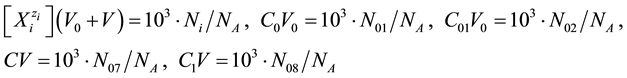
(where NA―Avogadro’s constant), from Equations (11), (12) we have
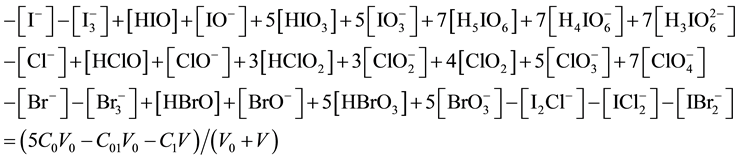
Elemental balances for electro-active elements (“players”) are as follows:
f(Br)
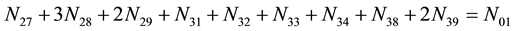
f(Cl)
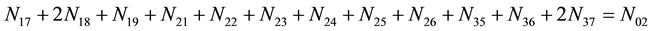
f(I)
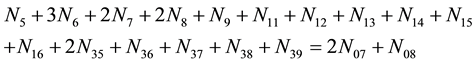
Multiplying (14) - (16) by atomic numbers: ZBr = 35, ZCl = 17, ZI = 53, for Br, Cl and I, respectively, adding them and applying Equation (12), we have:
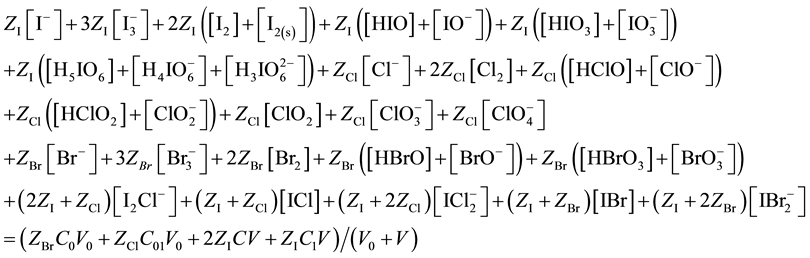
After subtracting (13) from (17), we get the equation for GEB, identical with one obtained according to Approach I to GEB
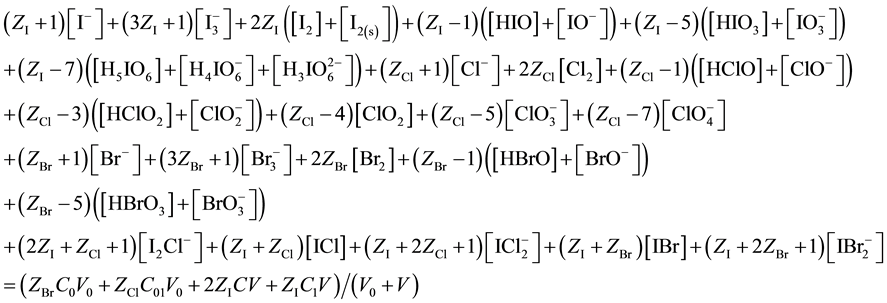
The balance (18) is equivalent to the balance (13).
A remark is needed in relation to the charge balance. Rewriting Equation (8) in terms of concentrations (see Equation (12)), we have
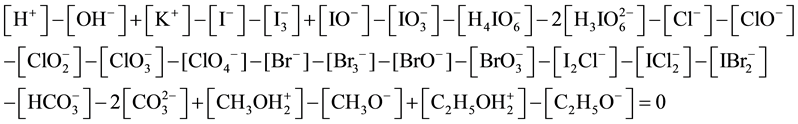
As we see, Equation (19) involves the ionic species related to amphiprotic co-solvents. However, in accordance with the remarks presented in [5] , the solvates of pairs of ions: (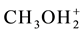
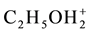
3. Final Comments
The complex redox system in a mixture with five solvents is considered. The discussion can be extended on mixtures with S solvents, 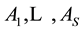
systems, the solvates 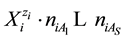
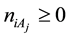
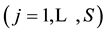
Equation (13) was obtained from linear combination of the related balance 2・f(O) ? f(H) (Equation (3)) with: charge balance (Equation (8)), elemental balances for other “fans” (C, K) (Equations (9), (10)), and core balances (Equations (4) - (7)) related to organic solvents in this system. This GEB does not involve the species composed only of “fans”: H, O, C, K. In particular, it does not contain the components explicitly related to the solvent species. The paper is an illustration of the compact formulation of redox systems according to GATES/ GEB Principles, presented in Ref. [5] .
One can notice that uncharged (neutral) species: I2, I2(s), Cl2, Br2, ICl, IBr are not present in Equation (13). Note also that Cl−, Br−, I−, Cl2, Br2, I2, I2(s), 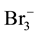
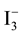
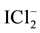
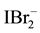
Note that―at the start―the Approach II does not distinguish between “fans” and “players”; the terms “fans” and “players” are used here only for the needs of the Approach I to GEB. In further parts of this text, the “players” (the electro-active elements) are distinguished later only to indicate the equivalency of the Approaches I and II.
References
- http://quoteinvestigator.com/2011/05/13/einstein-simple/
- Michałowski, T., Toporek, M., Michałowska-Kaczmarczyk, A.M. and Asuero, A.G. (2013) New Trends in Studies on Electrolytic Redox Systems. Electrochimica Acta, 109, 519-531. http://dx.doi.org/10.1016/j.electacta.2013.07.125
- Michałowski, T., Michałowska-Kaczmarczyk, A.M. and Toporek, M. (2013) Formulation of General Criterion Distinguishing between Non-Redox and Redox Systems, Electrochimica Acta, 112, 199-211. http://dx.doi.org/10.1016/j.electacta.2013.08.153
- Michałowska-Kaczmarczyk, A.M. and Michałowski, T. (2013) Comparative Balancing of Non-Redox and Redox Electrolytic Systems and Its Consequences. American Journal of Analytical Chemistry, 4, 46-53. http://dx.doi.org/10.4236/ajac.2013.410A1006
- Michałowska-Kaczmarczyk, A.M. and Michałowski, T. (2014) Compact Formulation of Redox Systems According to GATES/GEB Principles, Journal of Analytical Sciences, Methods and Instrumentation, 4, 39-45. http://dx.doi.org/10.4236/jasmi.2014.42006
- Michałowski, T., Ponikvar-Svet, M., Asuero, A.G. and Kupiec, K. (2012) Thermodynamic and Kinetic Effects Involved with pH Titration of As(III) with Iodine in a Buffered Malonate System. Journal of Solution Chemistry, 41, 436-446. http://dx.doi.org/10.1007/s10953-012-9815-6
- Michałowski, T. (2011) Application of GATES and MATLAB for Resolution of Equilibrium, Metastable and Non- Equilibrium Electrolytic Systems, Chapter 1. In: Michałowski, T., Ed., Applications of MATLAB in Science and Engineering, InTech―Open Access Publisher in the Fields of Science, Technology and Medicine, 1-34. http://www.intechopen.com/books/show/title/applications-of-matlab-in-science-and-engineering
- Michałowska-Kaczmarczyk, A.M., Michałowski, T., Asuero, A.G., Rymanowski, M. and Toporek, M. (2014) Formulation of Titration Curves for Some Redox Systems. American Journal of Analytical Chemistry, 5, 861-878. http://dx.doi.org/10.4236/ajac.2014.513095
- Pilarski, B., Dobkowska, A., Foks, H. and Michałowski, T. (2010) Modeling of Acid-Base Equilibria in Binary-Sol- vent Systems: A Comparative Study. Talanta, 80, 1073-1080. http://dx.doi.org/10.1016/j.talanta.2009.07.033
- Asuero, A.G., Pilarski, B., Dobkowska, A. and Michałowski, T. (2013) On the Isohydricity Concept―Some Comments, Talanta 112, 49-54. http://dx.doi.org/10.1016/j.talanta.2013.03.067
- Michałowski, T., Pilarski, B., Asuero, A.G. and Michałowska-Kaczmarczyk, A.M. (2014) Modeling of Acid-Base Pro- perties in Binary-Solvent Systems, Chapter 9.4. In: Wypych. G., Ed., Handbook of Solvents, Vol. 1 Properties, ChemTec Publishing, Toronto, 623-648.
NOTES
*Corresponding author.